Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers
Abstract
:1. Introduction
2. Pedestrian Load Model
2.1. Single-Person Foot Force Model
2.2. Multi-Person Foot Force Model
3. Analysis of Structural Dynamic Response under Pedestrian Load Excitation
3.1. Establishment of FE Models
3.2. Structural Dynamic Characteristics Analysis
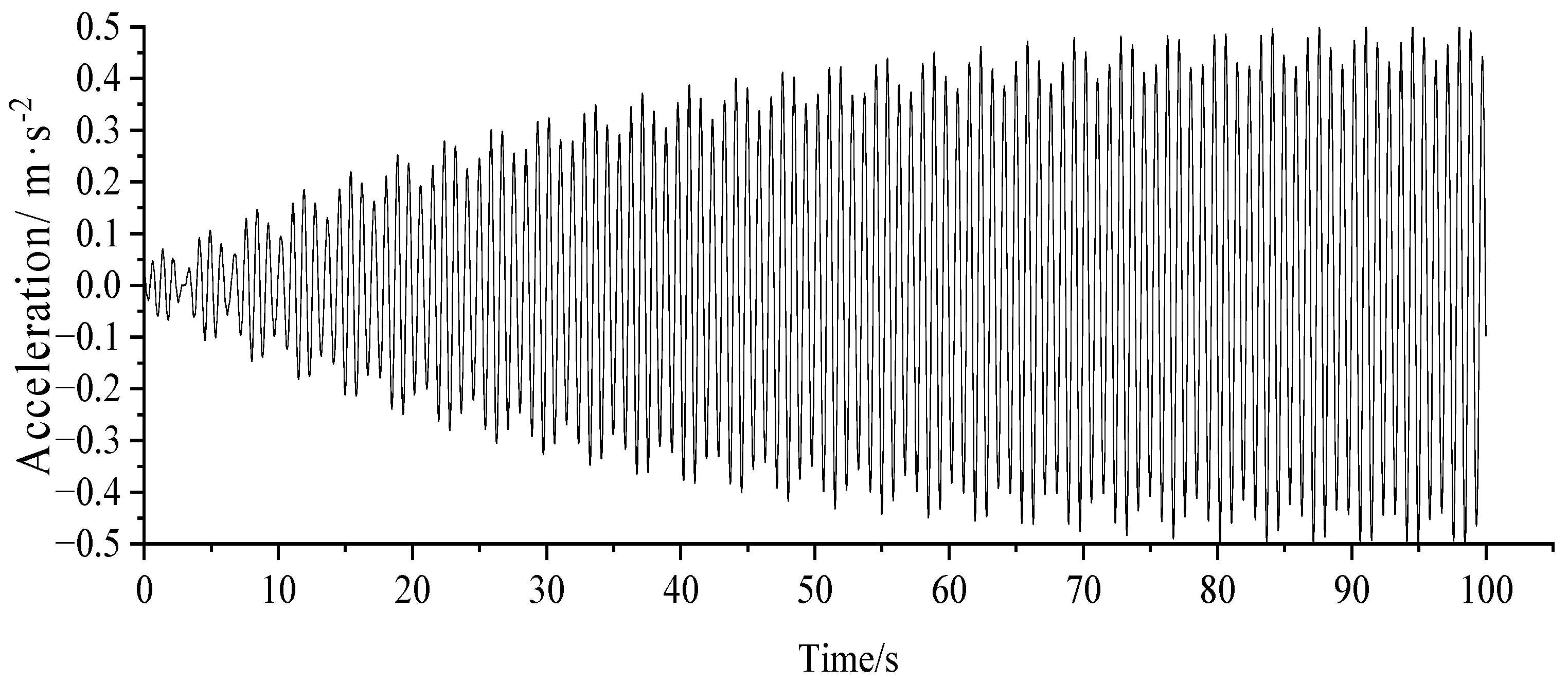
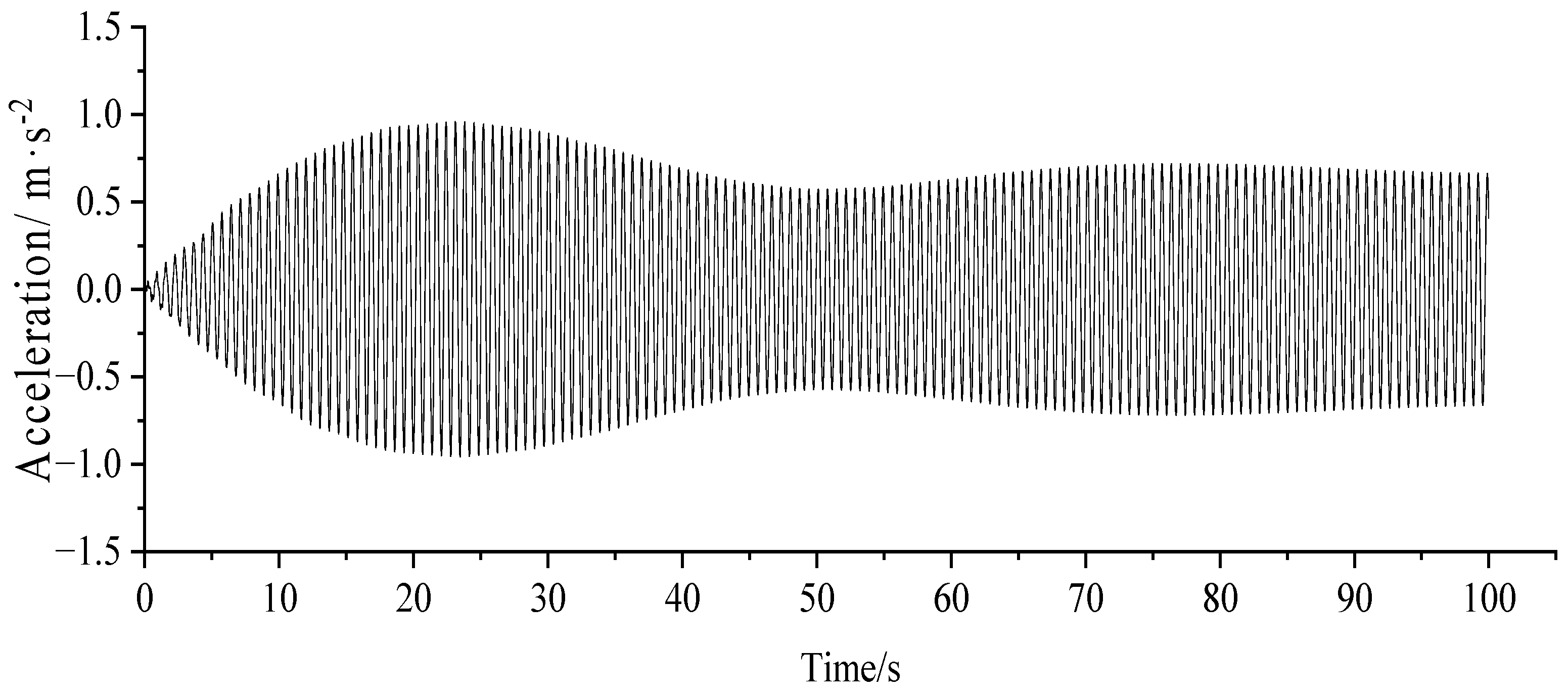
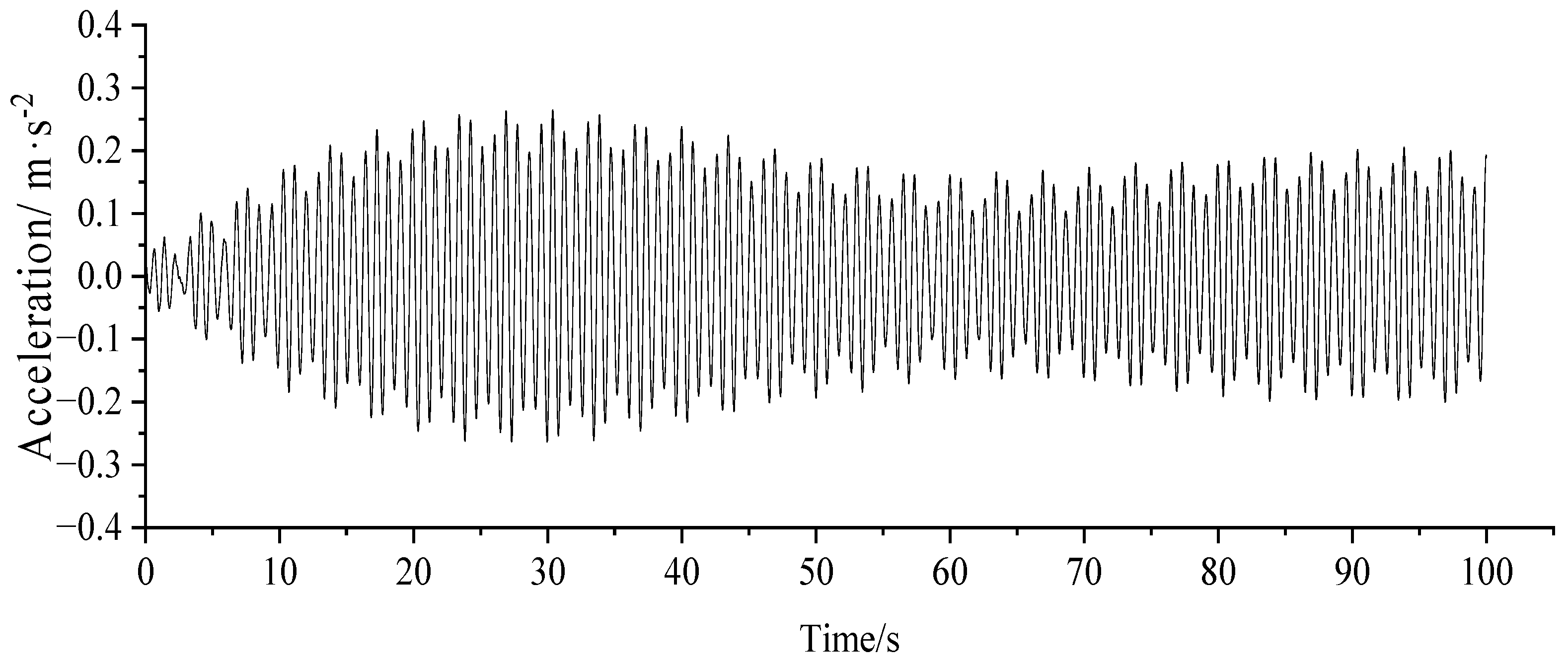
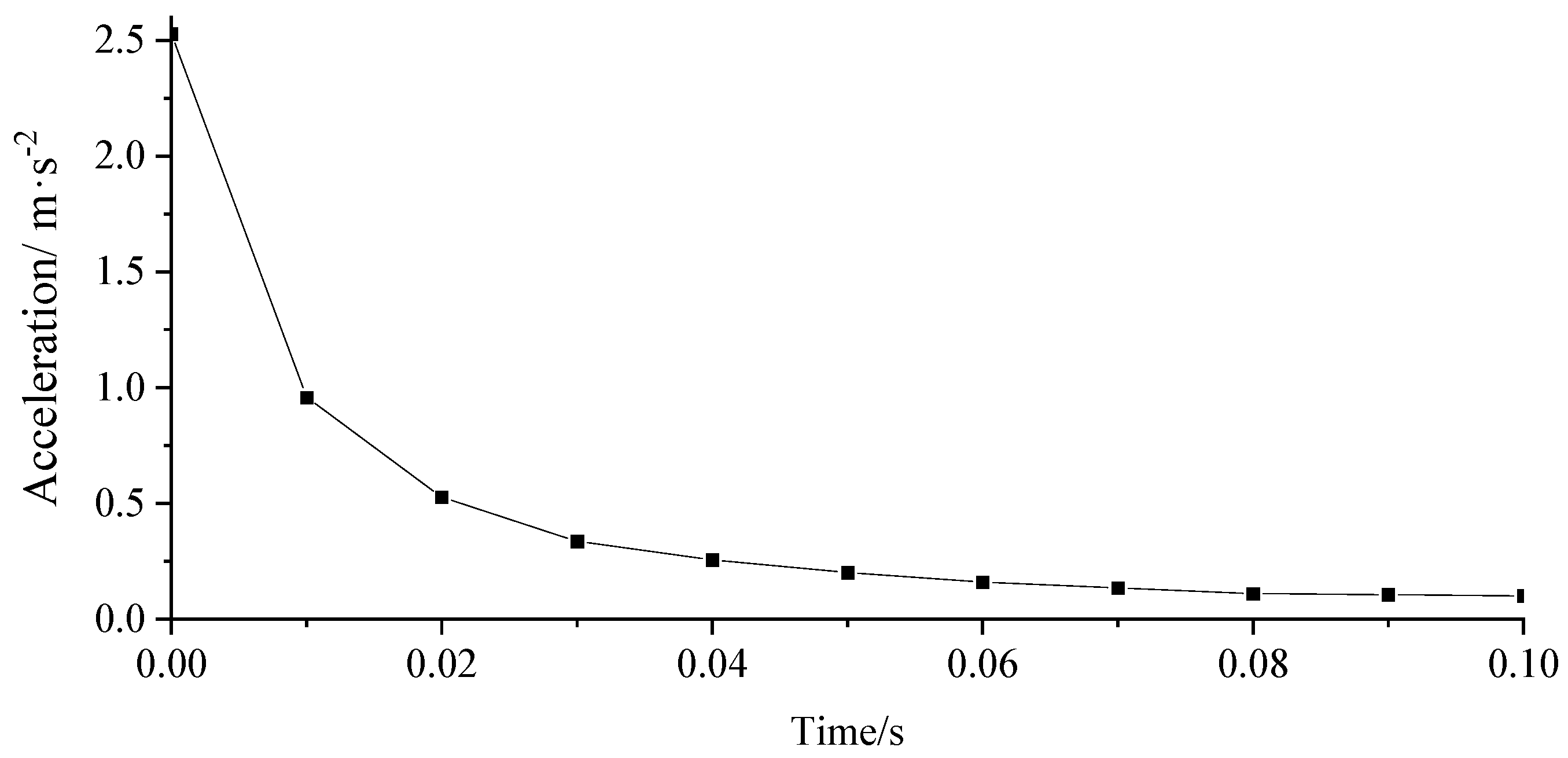
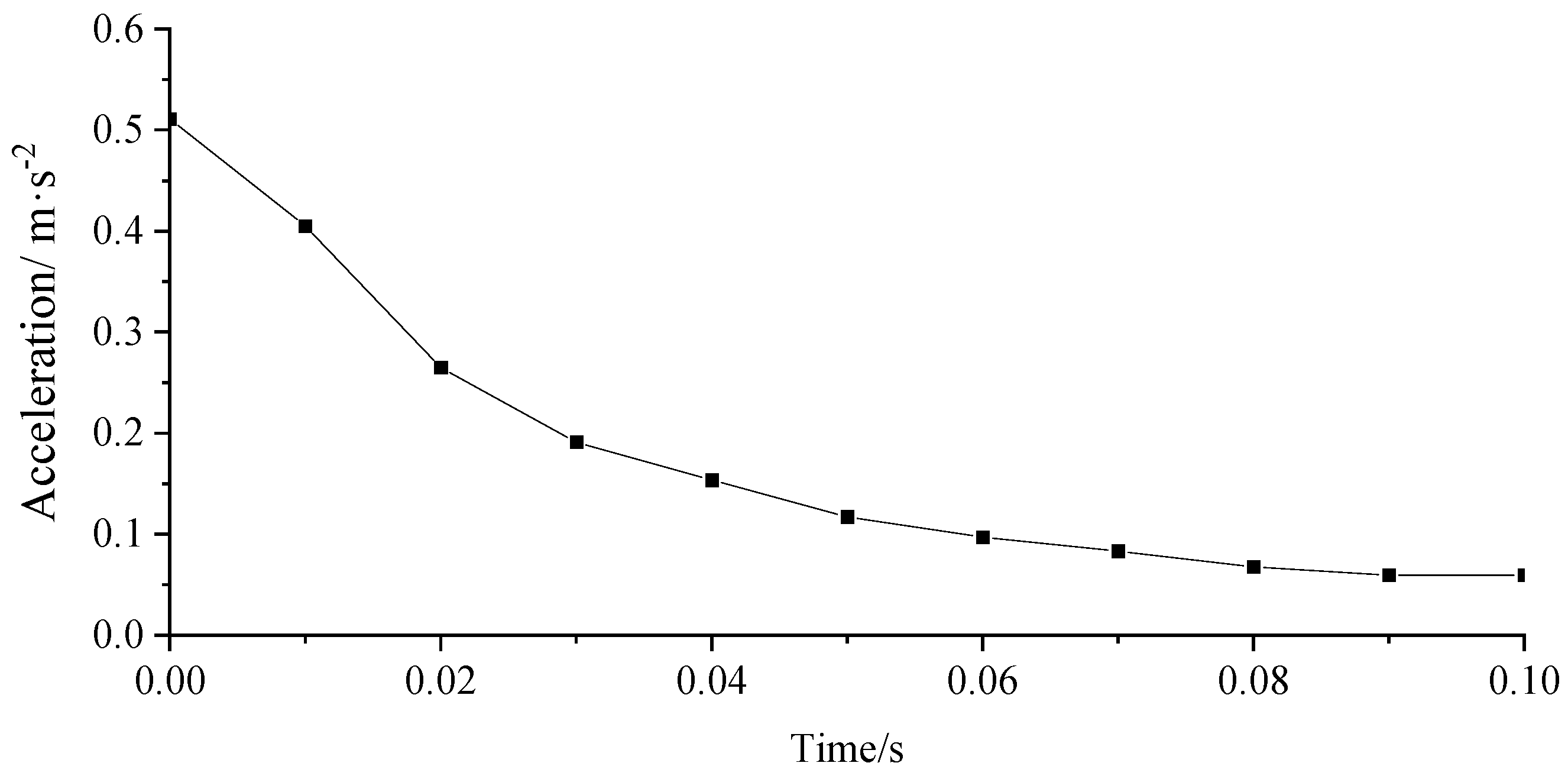
3.3. Human-Induced Vibration Response Analysis
4. Criteria for Comfort Evaluation
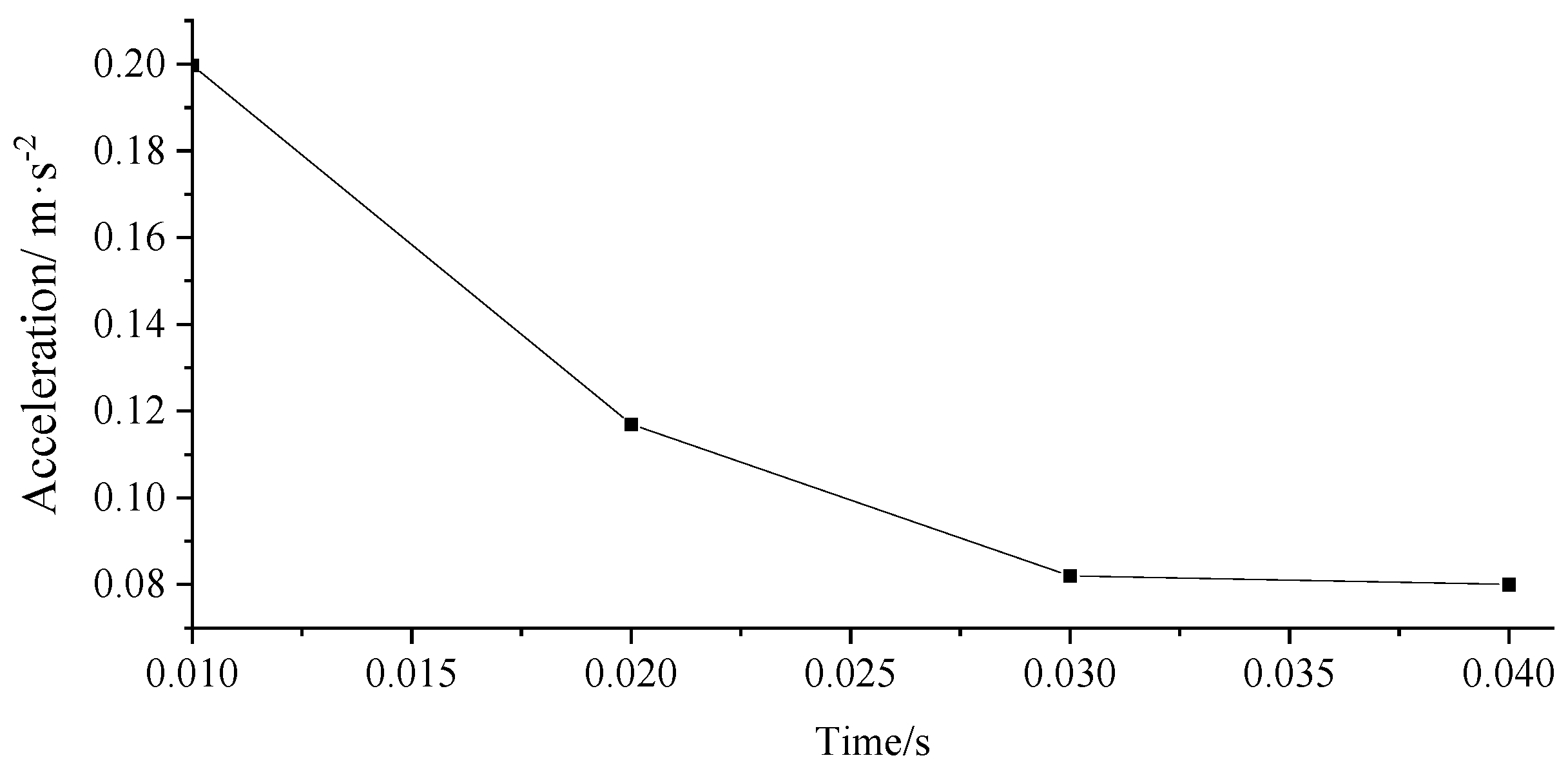
5. TMD Damping Analysis
- (1)
- The ratio u of the TMD mass to the generalized mass of the damping mode is selected.
- (2)
- According to the type of external load and the damping response, the optimal frequency ratio and the optimal damping ratio are determined, and the frequency of the tuning device calculated as below:
- (3)
- Physical parameters of TMD can be calculated as:
6. Conclusions
- (1)
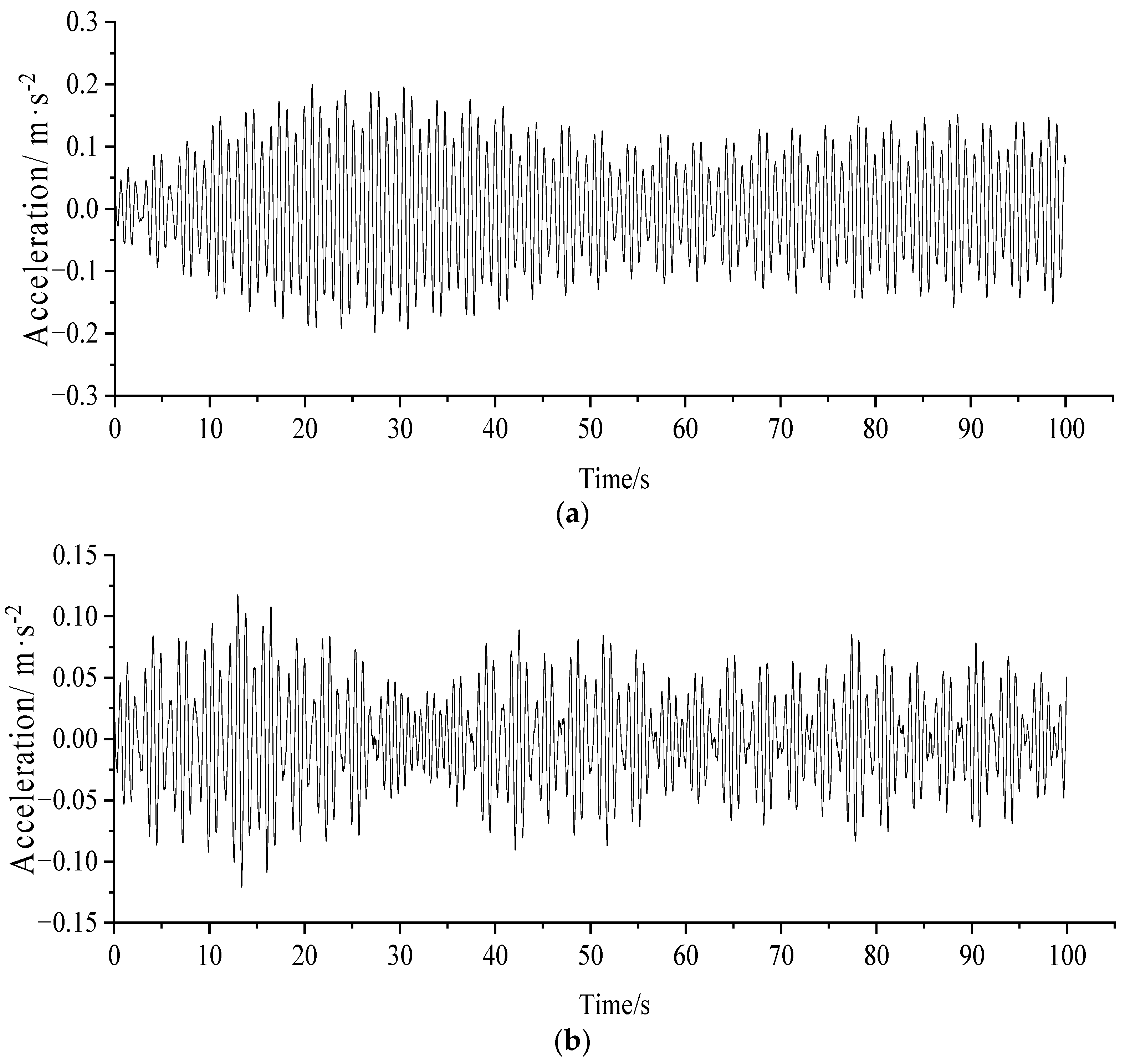
- Under the pedestrian load, the maximum lateral acceleration of the case bridge deck reached 0.511 m/s2 and the maximum vertical acceleration reached 2.528 m/s2, which exceeded the limits specified in EN03 and affected the comfort level of pedestrians. Setting the TMD on the bridge and adopting reasonably suitable TMD parameters, a better damping effect was obtained, by which the vertical acceleration was reduced to below 0.5 m/s2 and the lateral to below 0.1 m/s2, meeting the code requirements.
- (2)
- According to the analysis of the dynamic response of the structure without using the generalized mass ratio, for the large span pedestrian arch bridge, the vibration reduction efficiency was higher when the generalized mass ratio u was taken as 0.01–0.03.
- (3)
- Considering that the first-order lateral vibration of the arch bridge was the coupled vibration of the bridge deck and arch ribs, setting TMD at both of the arch ribs and the bridge deck was found to suppress better the transverse vibration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bachmann, H. Case studies of structures with man-induced vibrations. J. Struct. Eng. ASCE 1992, 118, 631–647. [Google Scholar] [CrossRef]
- Nakamura, S.; Kawasaki, T. Lateral vibration of footbridges by synchronous walking. J. Constr. Steel Res. 2006, 62, 1148–1160. [Google Scholar] [CrossRef]
- Fujino, Y.; Pacheco, B.M.; Nakamura, S.-I.; Warnitchai, P. Synchronization of Human Walking Observed during Lateral Vibration of a Congested Pedestrian Bridge. Earthq. Eng. Struct. Dyn. 1993, 22, 741–758. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Fu, T.N. Vibration excitation and control of a pedestrian walkway by individuals and crowds. Shock. Vib. 2005, 12, 333–347. [Google Scholar] [CrossRef] [Green Version]
- Beijing Municipal Engineering Research Institute. CJJ 69-1995, Technical Specifications of Urban Pedestrian Overcrossing and Underpass; China Architecture and Building Press: Beijing, China, 1996. (In Chinese) [Google Scholar]
- BS 5400-3; Steel, Concrete and Composite Bridges. British Standers Institution: London, UK, 2000.
- EN 2004-2; Eurocode 4: Design of Composite Steel and Concrete Structures. European Committee for Standardization: Brussels, Belgium, 2005.
- BD 29/03; Design Manual for Roads and Bridges. The Highways Agency: London, UK, 2020.
- IS0 10137-2007; Bases for Design of Structures—Serviceability of Buildings and Walkways against Vibrations. International Standardization Organization: Geneva, Switzerland, 2007.
- Wang, D.; Tse, T.K.; Zhou, Y.; Li, Q. Structural performance and cost analysis of wind-induced vibration control schemes for a real super-tall building. Struct. Infrastruct. Eng. 2014, 11, 990–1011. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Liu, W.; Feng, D.; Li, X. Investigation of the wind-resistant performance of seismic viscous dampers on a cable-stayed bridge. Eng. Struct. 2017, 145, 283–292. [Google Scholar] [CrossRef]
- Kandemir, E.C.; Mazda, T.; Nurui, H.; Miyamoto, H. Seismic Retrofit of an Existing Steel Arch Bridge Using Viscous Damper. Procedia Eng. 2011, 14, 2301–2306. [Google Scholar] [CrossRef] [Green Version]
- Mokrani, B.; Zhui, T.; Alaluf, D.; Meng, F.H.; Preumont, A. Passive damping of suspension bridges using multi-degree of freedom tuned mass dampers. Eng. Struct. 2017, 153, 749–756. [Google Scholar] [CrossRef]
- Shinsuke, Y.; Tsutomu, U.; Tetsuya, N. Developing a new hysteretic type seismic damper (BRRP) for steel bridges. Eng. Struct. 2016, 124, 286–301. [Google Scholar]
- Preumont, A.; Voltan, M.; Sangiovanni, A.; Mokrani, B.; Alaluf, D. Active tendon control of suspension bridges. Smart Struct. Syst. 2016, 18, 31–52. [Google Scholar] [CrossRef] [Green Version]
- Crusells-Girona, M.; Aparicio, A.C. Active control implementation in cable-stayed bridges for quasi-static loading patterns. Eng. Struct. 2016, 118, 394–406. [Google Scholar] [CrossRef] [Green Version]
- Blekherman, A.N. Swaying of pedestrian bridges. J. Bridge Eng. ASCE 2005, 10, 142–150. [Google Scholar] [CrossRef]
- Bruno, L.; Venuti, F.; Nascé, V. Pedestrian-induced torsional vibrations of suspended footbridges: Proposal and evaluation of vibration countermeasures. Eng. Struct. 2012, 36, 228–238. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Magalhães, F.; Moutinho, C. Studies for controlling human-induced vibration of the Pedro e Inês footbridge, Portugal. Part 1: Assessment of dynamic behavior. Eng. Struct. 2010, 32, 1069–1081. [Google Scholar] [CrossRef]
- Caetano, E.; Cunha, A.; Magalhães, F.; Moutinho, C. Studies for controlling human-induced vibration of the Pedro e Ines footbridge, Portugal. Part 2: Implementation of tuned mass dampers. Eng. Struct. 2010, 32, 1082–1091. [Google Scholar] [CrossRef]
- Li, Q.; Fan, J.; Nie, J.; Li, Q.; Chen, Y. Crowd-induced random vibration of footbridge and vibration control using multiple tuned mass dampers. J. Sound Vib. 2010, 329, 4068–4092. [Google Scholar] [CrossRef]
- Van Nimmen, K.; Verbeke, P.; Lombaert, G.; De Roeck, G. Numerical and experimental evaluation of the dynamic performance of a footbridge with tuned mass dampers. J. Bridg. Eng. ASCE 2016, 21, C4016001. [Google Scholar] [CrossRef]
- Brock, J.E. Theory of the damped dynamic vibration absorber for inertial disturbances. J. Appl. Mech. 1949, 14, 86–92. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Ragni, L.; Zona, A.; Nardini, L.; Salvatore, W. Design and experimental analysis of an externally prestressed steel and concrete footbridge equipped with vibration mitigation devices. J. Bridge Eng. 2016, 21, C5015001. [Google Scholar] [CrossRef]
- Chen, S.R.; Wu, J. Performance enhancement of bridge infrastructure systems: Long-span bridge, moving trucks and wind with tuned mass dampers. Eng. Struct. 2008, 30, 3316–3324. [Google Scholar] [CrossRef]
- Lin, C.C.; Wang, J.F.; Chen, B.L. Train-induced vibration control of high-speed railway bridges equipped with multiple tuned mass dampers. J. Bridge Eng. ASCE 2005, 10, 398–414. [Google Scholar] [CrossRef]
- Poovarodom, N.; Sopak, K.; Pennung, W. Application of non-linear multiple tuned mass dampers to suppress man-induced vibrations of a pedestrian bridge. Earthq. Eng. Struct. Dyn. 2003, 32, 1117–1131. [Google Scholar] [CrossRef]
- Song, Y. Comfort analysis and TMD vibration reduction design of long-span footbridge. Urban Roads Bridges Flood Control 2021, 7, 118–120+149+15–16. (In Chinese) [Google Scholar]
- Den, H.J.P. Mechanical Vibrations; Courier Corporation: Chelmsford, UK, 2011. [Google Scholar]
- Werkle, H.; Butz, R.; Tatar, R. Effectiveness of “detuned” TMD’s for beam-like footbridges. Adv. Struct. Eng. 2013, 16, 21–31. [Google Scholar] [CrossRef]
- Fan, J.S.; Chen, Y.; Nie, J.G. Optimum design of tuned mass damper for footbridge. Eng. Mech. 2012, 29, 133–140. (In Chinese) [Google Scholar]
- Andriacchi, T.P.; Ogle, J.A.; Galante, J.O. Walking speed as a basis for normal and abnormal gait measurements. J. Biomech. 1977, 10, 261–268. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, S.I.; Kawasaki, T.; Katsuura, H.; Yokoyama, K. Experimental studies on lateral forces induced by pedestrians. J. Constr. Steel Res. 2007, 64, 247–252. [Google Scholar] [CrossRef]
- Ricciardelli, F.; Pizzimenti, A.D. Lateral walking-induced forces on footbridges. J. Bridge Eng. ASCE 2007, 12, 677–688. [Google Scholar] [CrossRef]
- Zoltowski, K.; Piotr, Z. Dynamic Analysis of Pedestrian Bridges with Fem and Cfd; Gdnask University of Technology: Gdańsk, Poland, 2005. [Google Scholar]
- Young, P. Improved Floor Vibration Prediction Methodologies; ARUP Vibration Seminar: London, UK, 2001. [Google Scholar]
- AASHTO GSDPB-2009; LRFD Guide specifications for the Design of Pedestrian Bridges. American Association of State Highway and Transportation Officials: Washington, DC, USA, 2009.
- FIB Bulletin 32; Guidelines for the Design of Footbridges. International Federation for Structural Concrete: Geneva, Switzerland, 2005.
- RFS2-CT-2007-00033; Design of Footbridges-Guidelines and Background Document. Research Found for Coal and Steel: Brussels, Belgium, 2007.
- Wu, Y.; Li, J.; Sun, Q. Study on human-induced vibration of a cable-stayed bridge without backstays located in abrupt valley. Adv. Struct. Eng. 2021, 24, 3101–3117. [Google Scholar] [CrossRef]
- Blanchard, J.; Davies, B.L.; Smith, J.W. Design criteria and analysis for dynamic loading of footbridges. In Proceedings of the DOE and DOT TRRL Symposium on Dynamic Behaviour of Bridge, Crowthorne, UK, 19 May 1977; pp. 90–106. [Google Scholar]
- Research Fund for Coal and Steel. HiVoSS: Design of Footbridges; Guideline EN03; Research Fund for Coal and Steel: Luxembourg, 2008. [Google Scholar]
- Soong, T.T.; Dargush, G.F. Passive Energy Dissipation Systems in Structural Engineering; John Wiley and Sons: Hoboken, NJ, USA, 1997. [Google Scholar]

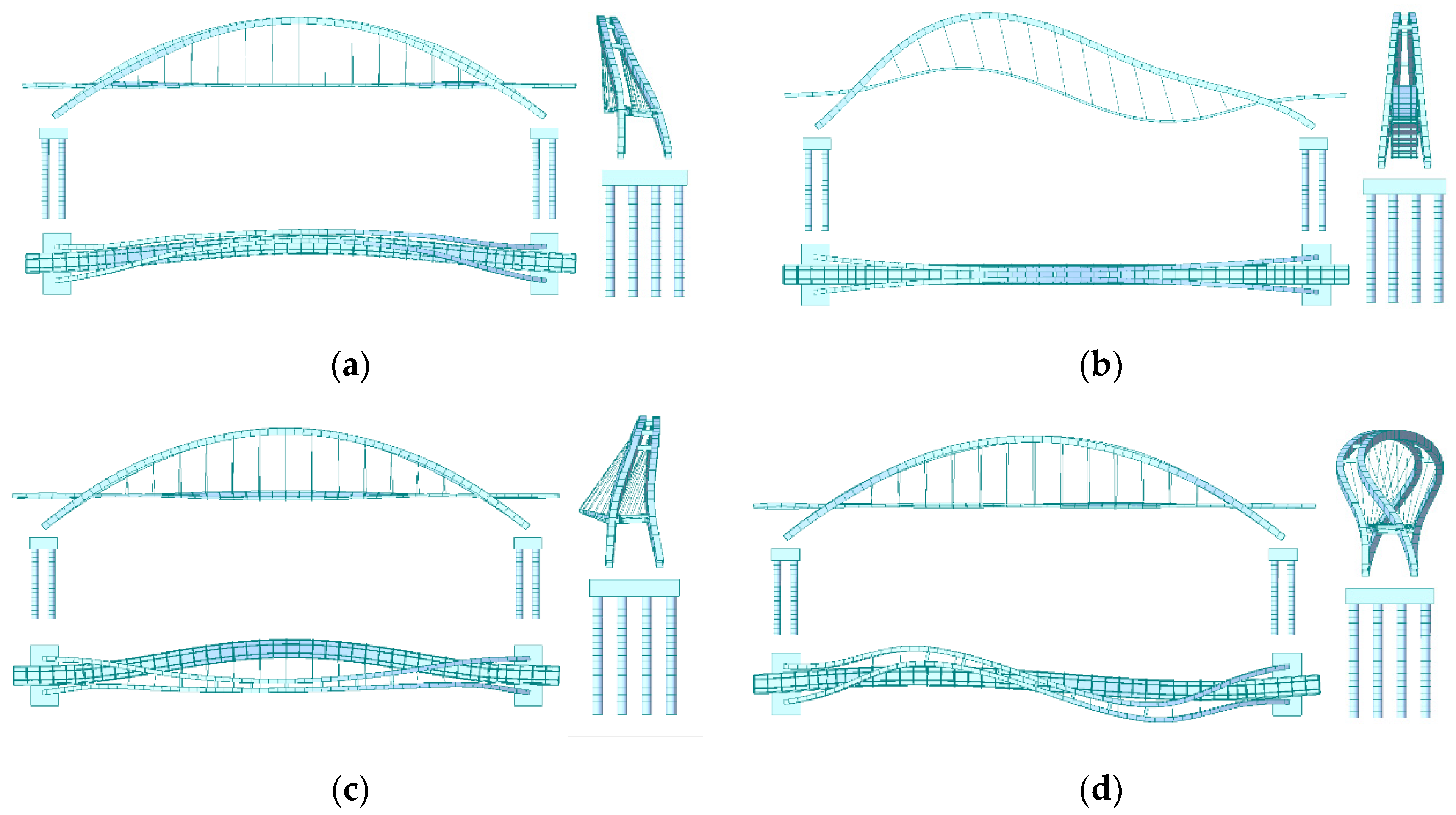


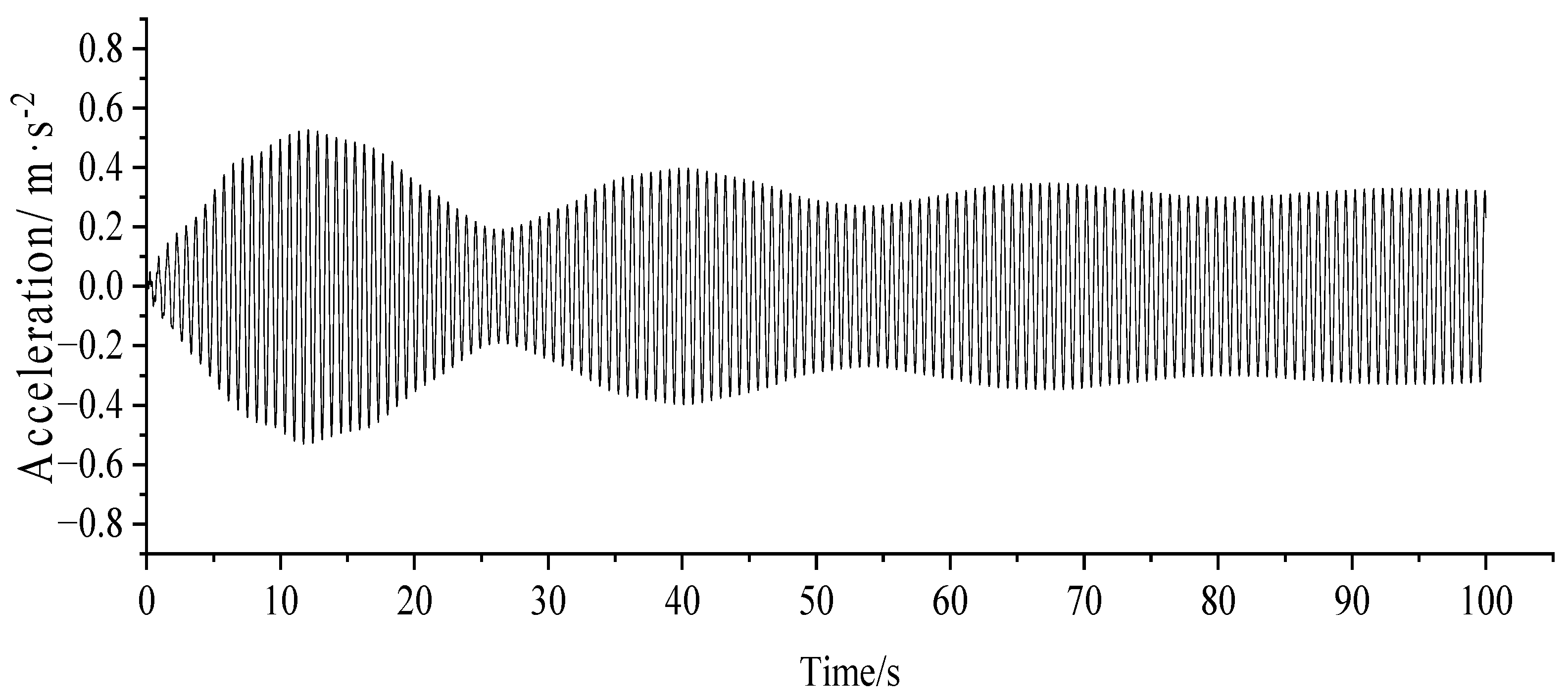
| Vibration Type | Frequency (Hz) | Description |
|---|---|---|
| 1 | 1.150896 | First-order lateral bending of bridge deck and arch ribs |
| 2 | 1.427685 | First-order vertical bend of bridge deck + vertical bend of arch rib |
| 3 | 1.446180 | Antisymmetric vertical bend of bridge deck + vertical bend of arch rib |
| 4 | 1.854052 | Arch rib lateral antisymmetric side bend |
| 5 | 2.499991 | Bridge deck and arch rib vertical bend |
| 6 | 3.392810 | Bridge deck with arch rib second-order lateral bend |
| 7 | 3.521042 | Bridge deck second-order lateral bend + arch rib third-order lateral bend |
| 8 | 3.922015 | Bridge deck second-order vertical bend + arch rib second-order vertical bend |
| 9 | 3.981197 | Bridge deck third-order vertical bend + arch rib second-order vertical bend |
| 10 | 4.763216 | Bridge deck third-order vertical bend + arch rib third-order vertical bend |
| Level | Description | Vertical Acceleration Limit (m/s2) | Lateral Acceleration Limit (m/s2) |
|---|---|---|---|
| CL1 | Best | <0.5 | <0.1 |
| CL2 | Moderate | 0.5–1 | 0.1–0.3 |
| CL3 | Poor | 1–2.5 | 0.3–0.8 |
| CL4 | Unacceptable | >2.5 | >0.8 |
| u | mTMD (kg) | kTMD (N/m) | c (m/s2) |
|---|---|---|---|
| 0.01 | 486.91 | 39,400.32 | 533.77 |
| 0.02 | 973.81 | 77,263.09 | 1487.59 |
| 0.03 | 1460.72 | 113,655.18 | 2693.18 |
| 0.04 | 1947.63 | 148,640.02 | 4086.77 |
| 0.05 | 2434.54 | 182,277.83 | 5630.03 |
| 0.06 | 2921.44 | 214,625.82 | 7296.39 |
| 0.07 | 3408.35 | 245,738.34 | 9065.91 |
| u | mTMD (kg) | kTMD (N/m) | c (m/s2) |
|---|---|---|---|
| 0.01 | 507.23 | 25,960.92 | 442.23 |
| 0.02 | 1014.47 | 50,908.76 | 1232.47 |
| 0.03 | 1521.70 | 74,887.56 | 2231.29 |
| 0.04 | 2028.93 | 97,939.12 | 3385.87 |
| 0.05 | 2536.16 | 120,103.11 | 4664.47 |
| 0.06 | 3043.40 | 141,417.25 | 6045.04 |
| 0.07 | 3550.63 | 161,917.34 | 7511.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, X. Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers. Appl. Sci. 2023, 13, 8263. https://doi.org/10.3390/app13148263
Li J, Liu X. Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers. Applied Sciences. 2023; 13(14):8263. https://doi.org/10.3390/app13148263
Chicago/Turabian StyleLi, Jialu, and Xi Liu. 2023. "Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers" Applied Sciences 13, no. 14: 8263. https://doi.org/10.3390/app13148263
APA StyleLi, J., & Liu, X. (2023). Human-Induced Vibration Analysis and Reduction Design for Super Long Span Pedestrian Arch Bridges with Tuned Mass Dampers. Applied Sciences, 13(14), 8263. https://doi.org/10.3390/app13148263







