Multicriteria Decision Making and Water Infrastructure: An Application of the Analytic Hierarchy Process for a Sustainable Ranking of Investments

Featured Application

The authors apply the analytic hierarchy process (AHP) in a ranking problem which consists of the ranking of water infrastructure investments (recovery or maintenance interventions) according to a sustainable temporal priority.

Abstract

The United Nations SDG6 goal of ensuring universal access to safe drinking water and sanitation by 2030 will require increased investment in the rehabilitation and maintenance of water infrastructure. In Italy, the water sector has not yet reached the performance of other European countries. The hierarchization of investments is essential for identifying priorities and efficiently allocating resources. This issue is part of the debate on the reconciliation of public and private needs in the management of water services. The present research proposes a model based on the analytic hierarchy process (AHP). Taking into account the design alternatives considered optimal that contribute to the resolution of territorial criticalities, the model organizes them in a ranking that indicates the chronological priorities to be respected in the investments to be made. The evaluation criteria are set in compliance with the norms defined by the National Authority (ARERA). The model is tested on a water manager in the Campania region. Among the main results, it is found that the two extremes of the ranking are shared between the two actors involved in the investment strategy (the private operator and public regulator). The model represents an effective tool for identifying shared planning strategies between public and private operators.

1. Introduction

The topic of water resource management represents a subject of frequent debate both in the political and scientific fields, since it implies the protection of fundamental rights and, at the same time, involves significant economic interests. Therefore, the management of water resources assumes a central role in the contemporary social and environmental context, in which the availability of drinking water represents a priority to guarantee the well-being of the population and the sustainability of productive activities [1]. The planning of water resource management activities presents various critical aspects since it is necessary to satisfy the demand for water in many territories and countries. The planning process requires the implementation of infrastructure, such as dams, sub-basins and reservoirs, both efficiently and effectively [2]. For this reason, many researchers are investigating the present and future challenges inherent in the sustainable management of water in urban areas [3,4].

In recent years, demographic growth on a global scale and sectoral pressures have generated a considerable increase in water demand, triggering multiple critical issues. Among the main problems in the water sector, we highlight water scarcity, the decrease in the quality standards of the resource, losses along the distribution network and the irregularity of water supplies. These factors present a challenge for the integration of water management approaches to ensure the sustainability of the resource. Therefore, it becomes essential to adopt effective policies and strategies that ensure sustainable water management for the benefit of present and future generations [5]. The need for investment in the water sector is urgent and cannot be underestimated. Globally, around one billion people currently lack access to drinking water services, while around two billion people are unable to access adequate sanitation services. Huge investments are therefore needed in the water sector, which, unfortunately, does not receive the priority it deserves from potential investors. Lack of investment is therefore a significant obstacle. Therefore, it becomes essential to adopt appropriate measures and policies to incentivize investments in the water sector and ensure that all people have access to safe drinking water and sanitation [6]. By 2030, water demand is expected to grow by about 41%. This will require new investments in capital and knowledge to ensure the sustainability of water resources. The drinking water sector presents numerous critical issues. To be carried out efficiently, supply, collection and distribution services must incorporate innovative and sustainable technological solutions. Only in this way will it be possible to reduce waste and comply with quality standards. In general, the decrease in the final reserves of drinking water represents an important challenge that requires significant investments in water production and treatment technologies [7]. It is, therefore, necessary to increase investments in the integrated water resource management (IWRM) sector to ensure a sufficient supply of drinking water, but also an adequate treatment of wastewater. Such investments can contribute to the promotion of economic, social and environmental development. The availability of safe drinking water and adequate sanitation is essential for public health. Furthermore, investments in the IWRM sector can improve the quality of life of local communities, promote social equity and provide an opportunity for public participation in water resource management [8].

To achieve the United Nations Sustainable Development Goal 6 (SDG6), which provides universal access to safe drinking water and sanitation by 2030, a considerable increase in investments in the sector will be required. According to estimates, the necessary financing would amount to USD 114 billion a year, or three times the current level of investments. In addition to initial investments, it is also important to consider the significant resources required to manage and maintain water and sanitation infrastructure, as well as to ensure universal coverage. These recurring costs will exceed 1.4 to 1.6 times the infrastructure construction costs by 2029. However, it will be necessary to consider not only the investments required for the construction, operation and maintenance of infrastructure, but also funding for improving water quality, increasing the percentage of treated wastewater, increasing water efficiency, implementing integrated water resources management, protecting and restoring water ecosystems, and adopting climate-change-resilient technologies. Without a significant increase in investments in water projects, it will be nearly impossible to achieve the objectives set out in SDG 6. Therefore, a significant long-term financial commitment will be required, which will require particular attention on the sustainability of funding sources and the efficient management of resources [9].

There are three main means used worldwide to finance investments in the water services sector: tariffs, money transfers and taxes. Tariffs represent sums paid by users, a portion of which generally increases as the volumes of water consumed increase. In most cases, the rates provide for cost recovery, i.e., they are estimated to fully cover the costs of the services offered or specific parts of them. The remainder of the costs not recovered through tariffs is covered through a mix of money transfers and taxes. The funding sources used to fund the IWRM sector can vary significantly from one country to another. A recent study conducted by the World Bank has shown that only 35% of water companies can cover their operating and maintenance costs through the revenues generated by the tariffs, while only 14% can face all the economic costs associated with the supply of services. In addition, few companies can cover upfront capital costs, which often are equal to or exceed operating and maintenance costs. This occurs, for example, in the UK, where capital costs represent 49% of the total costs of a water company. As a consequence, the rest of the expenses are covered by subsidies, which can be explicit (direct money transfer) or implicit (such as subsidies in terms of the cost of production factors). In the absence of adequate subsidies, water managers are forced to postpone maintenance interventions, but this often causes a significant deterioration of the structures [10].

As regards the main European countries, in 2015, in per capita terms, 100 EUR per inhabitant per year was invested in the water sector in the United Kingdom, 80 EUR per inhabitant per year in Germany, 90 EUR per inhabitant per year in France and 30 EUR per inhabitant per year in Italy. In 2020, 175 EUR per inhabitant per year was invested in the water sector in the United Kingdom, 82 EUR per inhabitant per year in Germany, 149 EUR per inhabitant per year in France and 92 EUR per inhabitant per year in Italy (of which 56 EUR per inhabitant per year was allocated to investments in the IWRM) [11]. The water sector in Italy has not yet reached the performance of other European countries in terms of investments. To fill this gap, it would be necessary to invest 12.5 billion EUR by 2030. Furthermore, to guarantee the maintenance of water infrastructures, a further 6 billion EUR of annual investments would be needed (equivalent to around 100 EUR per inhabitant). However, water utilities are currently only investing around 3.5 billion EUR a year [12]. An attempt is being made to make up for this lack with the recent National Recovery and Resilience Plan (PNRR) prepared by the Italian government, which provides for the use of funds allocated by the European Union through the Next Generation EU program. Issues relating to the efficient management of water services are included in Mission 2 (M2—Green Revolution and Ecological Transition) and, specifically, in Component 4 (C4—Protection of the Territory and Water Resources) of the PNRR. The interventions planned in the context of M2C4 concern the maintenance of the reservoirs, the completion of the water networks and the sustainable management of water resources. The objective of the investments is to ensure the security of the water supply and improve water quality, while at the same time optimizing the distribution of water between the various sectors [13]. The various water infrastructures in Italy have distinct economic and financial return profiles, with some generating private economic benefits, others public and still others both public and private. Furthermore, some installations are financially supported by user fees, while others are mainly financed through grants. It is essential to understand the different economic benefits and financial returns to identify financing mechanisms and evaluate investment opportunities in such infrastructures. In any case, all water infrastructures must undergo cost–benefit analyses (CBA) to determine the best allocation of financial resources. Water infrastructures can use a variety of funding modalities from governments and the private sector to finance the delivery of water services, such as drinking water, wastewater, irrigation and hydroelectric power [10].

Concerning the issues just examined, it emerges that in the design and planning of investments in water infrastructures, the need for a temporal hierarchization of interventions becomes increasingly important. This hierarchization must consider the needs of the public regulators, private managers and the community in terms of economic and financial returns, benefits, and environmental and social impacts. In particular, the temporal hierarchization of investments is essential for identifying priorities and efficiently allocating the limited financial resources available to maximize the return on investment and minimize negative impacts on the public budget and the quality of the service offered. In recent years, various strategies have been proposed and developed aimed at defining project priorities through an expert opinion elicitation (EE) process [14,15,16]. The prioritization of projects must be done in a logical, clear, explicit and well-defined way [17]. The subject of the hierarchization of investments in the water sector is part of the broader debate on the reconciliation of public and private needs in the management of water services [18]. Indeed, the water sector requires an effective collaboration between the public and private sectors, as both have different but complementary objectives. The public sector is responsible for regulation and strategic planning, while the private sector is responsible for the implementation and operational management of services. However, the complex and multifaceted reality of the water sector requires close collaboration between the two sectors to ensure the provision of effective, efficient and economically sustainable water services for the community. Due to tight budget constraints and insufficient financial resources, it is of primary importance to identify the top priorities in ranking water investments. In this context, the temporal hierarchization of investments plays a crucial role, as it allows us to optimize of the allocation of financial resources and to maximize the benefits for all parties involved [19].

The present research, focused on the theme of water management in the Italian context, proposes a multicriteria model for the temporal hierarchization of the investments considered optimal for the management of the territories of competence. This model makes it possible to compare the results of a time schedule set based on the needs of the public regulator, which takes into account the needs of the community indicated in the Area Plan (PdA), the planning tool that defines the quality objectives of the integrated water service management (IWSM) and the infrastructural interventions necessary to satisfy them, with another time schedule calibrated based on the objectives of optimizing the entrepreneurial return typical of private management. In this way, an attempt is made to balance the interests of the stakeholders involved. The proposed model is based on the application of the analytic hierarchy process (AHP) within an innovative logical scheme designed in compliance with the current national legislation established by the Regulatory Authority for Energy, Networks and the Environment (ARERA), an independent body that carries out regulation and control activities in the areas of energy, natural gas, water services, the waste cycle and district heating. The ultimate goal of the proposed model is to guarantee the sustainable management of water resources and the protection of the fundamental rights of the populations concerned.

The proposed model is in continuity with a previous study, in which the AHP technique was used to choose the best design alternatives (which mainly concerned restoration/replacement interventions or extraordinary maintenance interventions) capable of mitigating the impacts of the main infrastructural, managerial, economic and environmental criticalities found at a territorial level (the choice problem) [20]. Instead, in the present work, the AHP technique is used to organize the optimal design alternatives previously selected in a ranking that indicates the chronological priorities to be respected in the investments to be made (the ranking problem). The approach adopted is innovative for several reasons: first, although the AHP method is among those recommended by the ARERA for the selection of investments to be included in the PdA, the proposed model innovates the regulatory approach by proposing and configuring a final hierarchization route of the selected interventions; second, unlike ordinary applications in the context of the IWSM, the model does not limit itself to ranking the technical solutions under a temporal profile, but returns a flexible classification concerning both the social interests of the regulatory entity and the industrial interests of the water operator; finally, differing from the other operational approaches present in the literature, the model fits into a broader water investment evaluation protocol which distinguishes and integrates the investment choice phase from the investment ranking phase.

The model was tested by applying it to a concrete case of the IWSM of the Campania region (Italy). Among the main results, it was found that the results placed at the two extremes of the ranking are shared between the two players in the investment strategy (the private operator and public territorial body). Furthermore, both actors considered interventions on purification plants a priority. The model, therefore, is proven to be a sufficiently effective tool in identifying shared planning strategies between public and private operators.

The work is structured as follows: Section 2 is dedicated to the analysis of the reference literature on the application of multiple-criteria decision analyses (MCDA) and, specifically, on the AHP technique for the selection and temporal hierarchization of investments typical of the sector; in Section 3, the model is described in detai and subsequently applied to a real manager of the IWSM of the Campania region (in Southern Italy); in Section 4, the obtained results are presented and discussed; Section 5 shows the main conclusions and possible future research ideas; and finally, Appendix A provides a theoretical insight into the AHP, the technique used in this work within the temporal hierarchy model of investments in the water sector.

2. State of the Art

Since the management of water resources also involves intangible components, such as strategic profiles, socio-political conditioning and ethical/moral considerations of an intangible asset such as water, for the characterization of the model, we decided to use the analytic hierarchy process (AHP), a method extensively structured in the literature.

This section examines the main examples of the application of a multiple-criteria decision analysis (MCDA) in the field of water resources management found in the literature. We focus above all on the AHP, a technique that allows for addressing complex issues in the field of water resources management, offering valid support to the decision-making process. Thanks to the use of a hierarchy of criteria and the definition of relative weights, the AHP allows one to carry out objective assessments and identify effective solutions for the sustainable management of water resources [21]. The most commonly applied methods for planning and managing water resources are the fuzzy set analysis, compromise programming (CP), the analytic hierarchy process (AHP), ELECTRE and PROMETHEE [22]. Some of the main application cases developed in the last twenty years are detailed below.

The first study analyzed in this section presents a multi-criteria decision support methodology for the selection of projects to be included in the annual rehabilitation programs of drinking water networks in the European context [23]. To select the best wastewater treatment alternative, another study proposes a multi-criteria analysis methodology using both the analytic hierarchy process (AHP) and gray relational analysis (GRA). The AHP is used to manage multiple criteria and objectives during the decision-making process, while the GRA focuses on analyzing uncertain relationships between a major factor and all other factors in a system [24]. A third example proposes a multi-criteria decision analysis (MCDA) based on the analytic hierarchy process (AHP) within the framework of the IWRM in Bolivia to support stakeholders in the sustainable management of water resources [25]. Another research study uses a combination of methods, including a system dynamics study (SD) and the analytical hierarchy process (AHP), to create a rating index system and model for the ecological carrying capacity of water in a region [26]. A subsequent study presents a conceptual model of a three-phase strategic approach (3-SSA) for integrated water resources management, focusing on the first phase of minimization and the prevention of contamination at the source. A case study is presented in the expansion area of the city of Cali, Colombia, to evaluate different alternatives through a multi-criteria analysis [27]. Another study proposes the combined use of SD, the AHP and the creation of an integrated decision support system (DSS) for the sustainable management of water resources [28]. Other researchers have evaluated the water security of the Yellow River by integrating the fuzzy analytical hierarchy process (FAHP) with various other models (SPA, TOPSIS, GRA, VS and ME) [29]. Another example presents a multi-criteria analysis tool (MCA) to evaluate water resource management (WRM) strategies and select the most appropriate ones using four techniques (MAUT, AHP, ELECTRE and TOPSIS) [30]. In a recent work, a model was introduced to develop a multi-criteria spatial decision support system, which was designed to assist decision makers in defining and analyzing the investment priorities of individual water utilities [31]. Moreoever, recently, a decision support system was developed for emergency managers, to identify and rank the best options for water supply in crises. The approach used, based on the AHP, made it possible to integrate scientific and specialist knowledge into the decision-making process and to include criteria that are often overlooked in other methods and tools, such as social impacts [32]. Another work presents a multi-criteria decision support methodology for the selection and ranking of rehabilitation interventions in urban water infrastructures [33]. In a 2021 study, researchers used the FAHP method to prioritize the contracting methods needed to determine the most suitable contracting option for water and wastewater projects (WWP) [34]. Finally, another recent work is reported in which SWOT techniques were combined with the AHP to identify the essential elements influencing the implementation of the IWRM in the Philippines [35].

As can also be seen from the literature analyzed, the evaluation of infrastructural projects in the water sector generally requires the resolution of the following three main types of problems [36,37]:

• The choice problem: the goal is to select the best project or identify a subset of projects deemed optimal starting from a larger starting set;
• The sorting problem: projects are ordered and classified into two or more predefined categories based on common or divergent characteristics;
• The ranking problem: projects are ordered in descending order (from best to worst) based on a specific characteristic (for example, according to their time priority).

The focus of this work is on ranking problems. From the analysis of the examples found in the literature, it emerges that less importance is given to ranking problems within the IWSM. The MCDA method used is the AHP. This method is mainly useful for solving ranking problems and, occasionally, choice problems. Conversely, the AHP (at least in its original version) is less suitable for solving sorting problems [38]. The proposed model is described in the next section.

3. Model and Application

3.1. The Proposed Model: The AHP for the Temporal Hierarchy of Optimal Investments in the Water Sector

The temporal hierarchization model proposed in this work represents the third and final phase of a complex original protocol to support the public decision maker, aimed at the process of allocating resources to investments in the water sector in a territory [20]. The purpose of the innovative protocol, which meets the requirements imposed by the ARERA for the selection of project alternatives, is to build an architecture capable of rationalizing the design choices for investments in water infrastructures of the Area Plan (PdA). As mentioned, this document constitutes the main means of technical-economic and financial planning at a territorial level, defining the status of the service as well as establishing the objectives to aim for, the technical and organizational standards, the investments to be made in the respect for available resources, the tariff impact and the organizational and management model. The area government bodies (EGA) draw up the PdA. The latter are bodies identified by the regions for each optimal territorial area (ATO), a supra-municipal geographical area in which the IWSM is organized. All municipalities falling within the ATO are compulsorily participating in the EGAs. The exercise of the responsibilities of the municipalities themselves in the field of water resource management, including the planning of water infrastructures, is transferred to the EGAs. The PdA drawn up by the EGAs consists of four parts: (i) a reconnaissance of the infrastructures; (ii) a program of interventions (PdI); (iii) a management and organizational model; (iv) an economic/financial plan [8].

The proposed original protocol, of which the model presented therein is an integral part, can be a useful tool for drafting the PdI. In fact, in the PdI, the EGA highlights the investments that the water manager must make in the four-year planning period to respond to emerging needs in the area of competence. The needs of the entire ATO are represented in the PdI through a set of criticalities {CA}. This set is, in turn, deduced from a broader set of criticalities {C} defined by the national authority (ARERA), which groups the individual criticalities c_i into areas and sub-areas. If the reference ATO is not managed by a single utility, but by several water operators who deal with different portions of the territory T, the subset {CA} will have to be analyzed based on the specificities of each operator. In this way, it will be possible to identify a subset of {CT} criticalities within {CA}, for which coherent and adequate investments will be required. 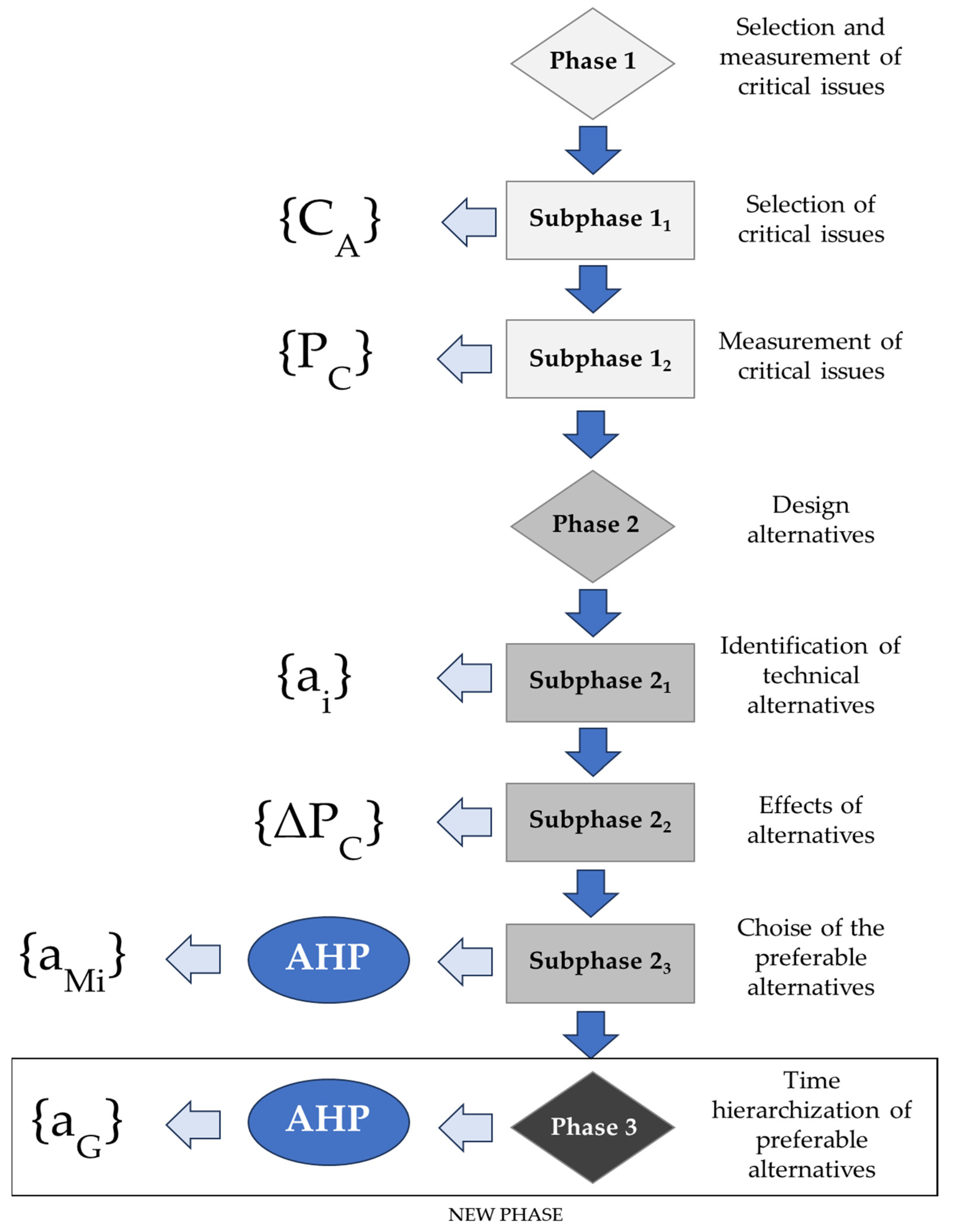For each criticality c_i of the sub-set {CT}, thanks to the collaboration with the operator, the EGA will have to identify the project a_j to be included in the PdI to decrease the impact of the criticality c_i, starting with a multiplicity of possible design solutions a_i. The proposed original protocol, which is substantiated in three phases (summarized in Figure 1), aims to facilitate the EGA in carrying out the operations just described.

The first two phases of the operative protocol were defined and tested in a previous study, to which reference is made for further details [20]. These phases are summarized as follows:

• Phase 1—The selection and measurement of critical issues: First of all, the EGA and the operator must define the criticalities c_i of the subset {CT} by deducing them from those already exposed by the EGA in the subset {CA}, which, as mentioned, can be deduced from the set {C} defined by the ARERA (Subphase 1₁). Subsequently, the EGA and the operator must identify the Pc_i technical parameter capable of allowing the measurement of the impact level of the c_i criticality. This passage is essential to circumscribe the problems that the investments have and to provide a quantitative survey (Subphase 1₂).
• Phase 2—Design alternatives: In this phase, the design alternatives useful for reducing or cancelling the impact of each criticality must first be identified (Subphase 2₁). The effects derived from the potential implementation of each design alternative on each criticality must then be measured using the variation in the value of the Pc_i indicators (Subphase 2₂). Finally, through the multicriteria AHP application, the best alternative a_Mi must be selected for each criticality. In this subphase, a novelty introduced by the model consists of integrating the ARERA criticalities with three other new criteria K_i (the impact of the design alternative on the population, investment cost of the design alternative and maintenance cost of the design alternative). It can therefore be said that in this subphase, the AHP is used to solve a choice problem (Subphase 2₃).

Here, Phase 3—Investment hierarchization of the operational protocol is introduced, defined and tested through an application case. Once the optimal a_Mi design alternatives have been defined, which contribute to the resolution of the critical issues found in {CT}, Phase 3 arranges for them to be organized in a ranking that indicates the chronological priorities to be respected in the investments to be made.

As mentioned, the timing of investment expenditure is a delicate subject of negotiation between the public and private sectors, given the different and conflicting objectives. On the one hand, there are the public purposes set out in the Area Plan, for which the EGA has identified deficiencies and objectives in-depth to be pursued in the territorial area to be governed. On the other hand, there are the entrepreneurial goals of the manager, who tends to invest in segments that ensure greater and more immediate profitability. In fact, among the a_Mis defined to respond to the various questions, some are more oriented in favor of the public, while others are in favor of the private sector. It is evident that each manager tends to favor investment in the segments (for example, water compared to sewage) or in the activities (for example, the reduction in losses for populous agglomerations compared to the construction of a new branch of the network useful for a small urban fraction) that are of greater and more immediate financial profitability. For this reason, with the model proposed in this paper, our intention is to define a tool capable of directing the negotiation between the water operator and the EGA to consider not only the entrepreneurial objectives but also the interests of the community.

The model envisages a new application of the AHP in addition to Subphase 2₃, in which the goal is the temporal hierarchy of the optimal a_Mi design proposals. The criteria remain unchanged compared to Subphase 2₃, with the elimination of the additional criteria K_i.

However, the vector of the weights of the criteria (which are assumed to be constant and equal in Subphase 2₃) is modified by the priorities that the PdA attributes to each criticality. The AHP was chosen to implement Phase 3 for several reasons. First of all, it was chosen because the issues inherent to the IWSM reconcile public objectives with a high social content and private objectives of a predominantly entrepreneurial nature. In this sense, the AHP is recognized as having the ability to effectively manage the inputs provided by multiple decision makers, being designed to manage these decision-making environments in which subjective judgements are made. Secondly, the existence of intrinsic conditions of uncertainty, deriving from the approximation of the qualitative/quantitative parameters for measuring the variables, refers to the MCDA approaches. In this case, it was preferrable to resort to a compensatory method given the information asymmetry between the parties and the moderate reliability of the information framework. Finally, as previously stated, the AHP is considered a sufficiently reliable technique in ranking problems [38,39]

The hierarchy of priorities is not always evident or explicit in the PdA. Indeed, it is sometimes expressed in verbal and discursive terms but is rarely defined through performance indicators. Therefore, the temporal hierarchy model proposed in this work represents an absolute novelty concerning the norms and practices followed in Italy. Therefore, the hierarchy of the design alternatives concerning time represents a completely original passage concerning the current indications of the law.

In applying the model, the vector of weights is drawn up by submitting the judgment on the temporal urgency of resolving the different critical issues to the EGA, along with a pairwise comparison procedure. Based on the results obtained, it is necessary to redesign the PdA through the use of quantitative parameters representative of the priority that the public attributes to the solution of the various critical issues. The judgment on the carrier of the weights must also be requested from the operator to ensure that his interests are taken into consideration.

Figure 2 defines the comparative hierarchy for the theorized model, understood as the final phase of an original protocol supporting the EGA for the definition of the PdA.

In the next subsection, the model is applied to a case study. Furthermore, the main obtained results are presented and discussed.

3.2. Application of the Model to a Case Study

The investment hierarchy model described in Section 3.1 was applied to a concrete case of an intervention program (PdI) developed by a water manager in Southern Italy. The research group responsible for the creation of this paper guided the implementation of the model, with the collaboration of the company involved in the experimentation. The utility in question is responsible for managing the integrated water service of 20 municipalities in the Campania region, which hosts a population of approximately 118,000 inhabitants over a total area of 677 km².

The analysis of the PdA made it possible to obtain detailed information on the population served by the distribution and sewage services in the various municipalities. The specific data broken down by municipality have not been reported in this paper for reasons of synthesis but can be requested directly from the authors. In general, the water distribution service covers 97% of the resident population, while access to the sewage system is only available for around 82% of the population. Furthermore, the responsible body only partially manages the wastewater treatment service.

The utility involved in the experiment has demonstrated its willingness to allow the implementation of the proposed model. It is important to underline that the collaboration between the scientific community and the utilities involved in the experimentation is essential to ensure the success of the PdIs.

Once the optimal design alternatives are selected a_Mi (an operation which, in the case in question, was performed using the AHP methodology and considering the indications and new criteria introduced in Subphase 2₃ of the proposed original protocol), the ARERA also requires the operator to define a time schedule for the identified interventions. In this regard, the model provides for the definition of a ranking that indicates the chronological priorities to be respected in the investments to be made. To identify a shared solution between the public aims set out in the Area Plan and the entrepreneurial aims of the utility, the model envisages a new application of the AHP, in which the goal is the temporal hierarchy of the project proposal’s optimal terms a_Mi.

The criteria for defining the ranking of the alternatives and the relative weights (unlike the previous phase, the criteria are now no longer equivalent) vary according to the following two scenarios:

• Scenario 1 is representative of the strategic intervention priorities defined in the PdA. Specifically, the vector of weights is drawn up by submitting the judgment on the temporal urgency of the resolution of the different critical issues to the EGA, along with a pairwise comparison procedure;
• Scenario 2 is instead representative of the operator’s business goals. The operator tends to invest in segments that ensure greater and more immediate profitability. In this scenario, therefore, the judgment on the weight vector is required of the utility to ensure that its interests are taken into account.

Depending on the scenario, therefore, the EGA or the utility compare, according to their points of view, the critical areas, the subareas and finally the critical issues themselves (a reference was made to the classification scheme of the critical issues suggested by the ARERA). The comparative hierarchy (defined on a theoretical/conceptual level in Figure A1 of Appendix A) for this specific application of the AHP methodology is illustrated in Figure 3.

The {CT} criticalities identified, grouped into areas and subareas, are summarized in

Table 1. Identified critical issues grouped into areas and subareas.

Areas		Subareas	Critical Issues
B	Critical issues in water supply	B1	B1.1	Inadequate physical condition of distribution network pipelines
			B1.2	Inadequate physical condition of the civil works of the plants
			B1.3	Inadequate physical condition of mechanical and electromechanical equipment
			B1.4	High pipeline rupture rate
		B4	B4.1	High level of water losses along distribution networks
		B10	B10.2	Malfunction or age of user meters
C	Critical issues in the sewerage service	C2	C2.1	Inadequate physical condition of sewer pipes
			C2.6	High pipeline rupture rate
			C2.7	Joint sealing defects
D	Critical issues of purification plants	D2	D2.2	Inadequate physical condition of civil works
			D2.3	Excessive failure rate of mechanical and electromechanical equipment
K	Critical issues in the knowledge of infrastructures	K2	K2.1	Imperfect knowledge of the operating parameters of the infrastructures
		K3	K3.1	Absence or inadequacy of infrastructure measurement and control systems
M	General management critical issues	M1	M1.3; M1.4; M1.5	Margins for improvement in the economic and functional efficiency of infrastructure management
		M3	M3.1	Safety of working conditions

. As anticipated, in Section 3.1, each criticality c_i of the set {CT} was identified following a phase of consultation between the utility and EGA (even if the standard formally attributes this responsibility to the EGA). These criticalities, which characterize the specific portion of the territory served by the utility, were selected from the set of criticalities {CA} that the EGA identified for the entire ATO (a supra-municipal geographical area that can be served by several utilities). In turn, the set {CA} is deduced from the general scheme of criticalities {C}, prepared by the ARERA and valid at the national level, which defines all the potential problems that may concern the IWSM. The criticalities of the set {C} (initially introduced by the ARERA with resolution 3/2014 DISD, then increased in number and partially modified with resolutions 2/2026 DISD and 1/2018 DISD) have been classified by the authority into areas and subareas. This classification can therefore also be applied to the {CA} and {CT} subsets. To identify the {CT} criticalities, the utility, supervised by the EGA, carried out a complete survey of the water infrastructures, as well as sewage and purification systems, assessing their technical quality through a series of indicators introduced by the ARERA with resolution 917/2017/R/Idr. Furthermore, feedback was collected on the degree of user satisfaction with the service offered. It was therefore possible to evaluate the contractual quality through a series of indicators introduced by the ARERA with resolution 655/2015/R/Idr. For further and more detailed information about the criticality selection and measurement processes {CT}, which are described in Phase 1 of the protocol of Figure 1, the reader can refer to the previous study published by the authors [20]. Compared to Phase 1, the authors carried out consultancy activities directing the utility in data collection and providing assistance regarding the correct interpretation of the technical and contractual quality indicators.

The investments to be ranked according to the time priority of implementation were identified, analyzed and selected in Phase 2. In this phase, the water operator presented a proposal for intervention consisting of a series of design alternatives to the EGA for each criticality to be mitigated. In Subphase 2₂, the best design alternative (a_Mi) was selected for each criticality, therefore, for each group of design alternatives. Downstream of this selection process, the 11 design alternatives considered the best were identified, as shown in

Table 2. The best alternatives chosen for each intervention.

Intervention ID	Intervention Description	The Best Alternative Chosen (aMI)	Critical Issues Potentially Eliminated or Reduced
1	Rehabilitation of deteriorated water network	Alternative 1: replacement of a part (about 4600 m) of the portion of the network considered most critical by the utility	B1.1—B1.4—B4.1
2	Implementation/modernization of remote-control services	Alternative 2: construction and modernization of 36 remote control stations on the plants with consequent implementation of the SCADA system	K3.1
3	Adaptation of distribution systems	Alternative 2: Restoration of 22 plants both in terms of civil works and electromechanical equipment	B1.2—B1.3—M3.1
4	Creation of water districts	Alternative 2: Creation of 23 water districts	K2.1
5	Rehabilitation of the deteriorated sewerage system	Alternative 2: Replacement of the sewerage system for a total of 5700 m	C2.1—C2.6
6	Adjustment of manholes	Alternative 2: Restoration and waterproofing of all 720 damaged wells	C2.7
7	Adaptation of purification plants	Alternative 2: Renovation of some structural parts and the fence, waterproofing the roof, the replacement of certain valves and adaptation of the electrical system to the appropriate safety standards for 13 sewage treatment plants	D2.2—D2.3—M3.1
9	Adoption of management software	Alternative 1: Adoption of an SAP management software	M1.3—M1.4—M1.5
10	Replacement of user meters	Alternative 1: Replacement of 1200 old meters with drinking water meters equipped with remote reading module	B10.2
11	Adaptation of the collection system	Alternative 1: Waterproofing the roof, the restoration of the fence, replacement of certain valves and adaptation of the electrical system to safety standards	M3.1

. The selected alternatives can contribute to reducing more criticalities. For more information on the identification of design alternatives and on the process of selecting the best alternatives through the AHP (Phase 2 of the protocol of Figure 1), the reader can refer to the previous study published by the authors [20]. However, it is useful to underline that, for the preliminary definition of the set of alternatives proposed for each criticality, we used a consultancy of engineers and civil companies specialized, respectively, in the design and construction/maintenance of hydraulic infrastructures. Instead, the authors of this study dealt with the estimation of investment and maintenance costs for each project alternative. Furthermore, we dealt with the definition of the financial criteria to be considered for the implementation of the AHP.

In Table 2, intervention 8 was not reported, which consists of the replacement of a 350 m long section of pipeline in order to improve the criticalities A7.1 (the average age of the pipeline) and A7.4 (the breakage of the pipelines of the adduction networks). These critical issues impacted six of the twenty municipalities managed by the utility. By virtue of this, both the utility and the EGA agreed in deeming the intervention a priority, and it was therefore carried out with extreme urgency. Otherwise, they were perplexed about the order of implementation of the other seven interventions. For this reason, the need arose to add to the first two phases of the protocol of Figure 1 a third phase aimed at the temporal hierarchy of the interventions. Naturally, intervention 8 was excluded from this phase as it had already been completed. Both for Scenario 1 (representative of the strategic priorities of the EGA) and for Scenario 2 (representative of the utility’s business goals), it was possible to construct a matrix of the pairwise comparisons of the criteria (criticalities) and the alternatives by following the methods described in Appendix A. In particular, their structure is similar to that of matrix (A1) in Appendix A. Since the judgments expressed are not fully consistent, Equation (A2) is not valid for these matrices. The dominance coefficients of the matrices were defined using the semantic scale of Saaty represented in

Table A1. A representation of the Saaty’s semantic scale (data from [49,50,51,52]).

Preference Index (aij) 1,2	1	3	5	7	9
How important is C1 relative to C2?	Equally important	Moderately more important	Strongly more important	Very strongly more important	Overwhelmingly more important

¹ It is also possible to use the intermediate (or compromise) values of 2, 4, 6 and 8; ² If C₁ is less important than C₂, the scale of reciprocal values is used: 1, 1/3, 1/5, 1/7 and 1/9 (it is also possible to use the intermediate values of 1/2, 1/4, 1/6 and 1/8).

. The definition phase of these coefficients is quite delicate as it is influenced by the subjective perception of the decision maker regarding the urgency in mitigating a specific criticality. The suggestion given to the EGA and utility was to formulate judgments that may be useful not only with respect to their own sphere of competence but in terms of the benefits for the other stakeholders involved (the end users of the services, funding bodies, administrations municipal authorities, utility employees, etc.) and minimizing negative impacts on the environment and society. The results of Phase 3 of the protocol are reported in the next section.

4. Results and Discussion

4.1. Results

Overall, the following 32 pairwise comparison matrices were defined:

• One matrix for the five criticality areas compared in pairs concerning the time priority objective;
• Five matrices for the nine criticality sub-areas compared in pairs concerning the five criticality areas;
• Nine matrices for the seventeen criticalities compared in pairs concerning the nine criticality sub-areas;
• Seventeen matrices for the ten projects to be implemented compared in pairs concerning the seventeen criticalities.

The relative weights of the criteria (criticalities), sub-criteria (areas and sub-areas of criticality) and alternatives (projects) were defined using the approximate method in Equation (A3). Furthermore, the consistency of each of the 32 matrices was evaluated by calculating the CI index using Equation (A4), the RCI index was defined using the values reported in

Table A2. A representation of the Random consistency ratio (RCI) values (data from [49,50,51,52]).

m	1	2	3	4	5	6	7	8	9
RCI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45

, and the CR index was obtained by dividing the CI by the RCI. The CR index associated with each matrix was then compared with one of the thresholds represented by the inequalities (A5). In cases of imperfect consistency, the decision makers were invited to formulate a partial revision of the pairwise comparisons. Finally, the total score of each alternative was calculated using Equation (A6).

Figure 4 illustrates the results obtained by the AHP for Scenario 1.

Figure 5 illustrates the results obtained by the AHP for Scenario 2.

Analyzing the results obtained for the two scenarios, some patterns emerge.

First of all, it is possible to state that the critical areas considered a priority by both stakeholders are those relating to purification, distribution and sewerage, as can be seen from the types of intervention which are in the first four positions of both rankings.

The central band of the hierarchy, on the other hand, has a more marked differentiation for the two points of view: in the scenario of the PdA, the criticality area relating to knowledge of the infrastructures appears; on the other hand, in the reference scenario of the utility, an intervention that impacts management criticalities is preferred. The latter occupy the lowest level of the hierarchy drawn up by the EGA. Lastly, on behalf of the manager, less importance is given to critical issues regarding knowledge of the infrastructure.

As for the merits of the individual project activities, for both scenarios, the following patterns emerge:

• A shared priority for Tasks 7, 1 and 5;
• A lesser importance attributed to Interventions 4 and 11.

Table 3. Shared time schedule of interventions.

Intervention ID	Intervention Description
7	Adaptation of purification plants
1	Rehabilitation of deteriorated water network
5	Rehabilitation of the deteriorated sewerage system
10	Replacement of user meters
3	Adaptation of distribution systems
9	Adoption of management software
2	Implementation/modernization of remote-control services
6	Adjustment of manholes
4	Creation of water districts
11	Adaptation of the collection system

illustrates the time schedule which summarizes the results of this phase.

In the phase of the formulation of the judgment on the temporal urgency, we proceeded by respecting the indications emerging from the concordances of the two economic actors (the EGA and water operator), basically favoring public objectives and safeguarding the operator’s expressions of preference when not in open conflict with collective ambitions.

4.2. Discussion

Our results from applying a hierarchy model of water investments, in which the winning solutions are framed in a time schedule of priorities, are surprising. The extremes of the ranking appear unpredictably shared between the two players in the investment strategy: the public one is entrusted with the safeguarding of the principles of social interest, and the private one is entrusted with the mandate of making the sector more efficient. Both consider interventions on purification plants (ID 7) as a priority. In Campania, given the various infringement procedures in recent years, it could not be otherwise. Furthermore, purification allows for business prospects of greater profitability compared to the other two areas of the IWSM. The two players also consider investments in the deteriorated parts of the water distribution network (ID 1) as a priority, as pressure control and loss reduction are certainly two of the most urgent battles both from an environmental and entrepreneurial point of view. Moreover, concerning the usefulness of the interventions in restoring the sewage system (ID 5), the utility and EGA are in strong agreement. For the utility, if the efficiency of the sewage network can translate into higher tariff revenues and a better relationship with the user, this certainly represents an opportunity in terms of pursuing the SDG6 for the EGA.

Likewise, the congruence of objectives also emerges in the final part of the ranking: the interventions of the technical sub-partition of the management district (ID 4) and the improvement of the safety conditions in the collection plants (ID 11). This is because, from the user’s point of view, for not very extensively managed territories, there is not a great difference in the perception of the quality of the service of the various administrative schemes adopted, and from the entrepreneur’s point of view, the partition into sub-domains represents a second-level objective in corporate strategies. However, this is also true because the collection systems ordinarily require a low concentration of work activity, for which the safety standards lead to a reduced number of man-hours, with the containment of the relative risks of accidents (compared to, for example, a more real risk in sewage treatment plants).

However, for the central part of the ranking, there is a substantial divergence of views. In particular, the replacement of the utility meters (ID 10) represents a fundamental objective for the utility for the following reasons: the better and punctual billing of consumption; a more transparent relationship with customers; and compliance with regulations without incurring penalties. This intervention leads to substantial monetary benefits for the utility, while it is less relevant for the EGA. Another intervention considered quite important for the utility is that relating to the adoption of management software (ID 9), now considered essential to fulfilling a series of regulatory obligations and for the fast and reliable management of information. It is obvious that, from the point of view of the EGA, this investment appears to be less of a priority. On the other hand, the intervention relating to the adaptation of the distribution systems (ID 3) is more relevant for the local authority, which consists of the restoration of civil works as well as the mechanical and electromagnetic equipment of 23 systems. This intervention is perceived as urgent for the EGA since, being a public body, it is personally involved in solving the environmental problem relating to the reduction in water losses. However, the utility is not indifferent to the intervention, as it is necessary to reduce energy and maintenance costs. Moreover, the restoration and waterproofing project of the damaged manholes is of more interest to the EGA than to the utility given the benefits that can be obtained in terms of the environment and human health. The intervention relating to the construction/modernization of remote-control stations in the plants (ID 2) is only slightly more relevant for the EGA than for the utility. From the point of view of the public operator, these stations can contribute to introducing a much lower volume of water per year into the distribution networks. Once again, therefore, the objective of environmental protection prevails for the EGA. However, the benefits are also evident for the utility, such as the faster identification of faults or significant savings in terms of personnel costs resulting from automating processes that were previously exclusively manual.

As can be seen, the greatest differences emerged in the central part of the ranking. One of the challenges consisted in overcoming these differences between the utility and EGA. The final ranking that summarizes the results of Phase 3, reported in Table 3, seems to have largely levelled these differences. This final ranking has found a positive opinion from both players involved. The results obtained by the model can be defined as satisfactory when the judgments expressed by the decision makers also consider the needs of the respective counterparty, as well as those of the environment and the community.

If it is necessary to carry out interventions relating to areas different from those considered in the present case study, the critical issues to be considered can be based on the classification suggested by the ARERA with resolution 1/2018 DISD, to which one can refer to for further details. To verify the effective presence and relevance of these critical issues, it is suggested to use the threshold, technical and contractual quality indicators, introduced respectively by resolutions 917/2017/R/Idr and 655/2015/R/Idr.

The model proposed in the present work seems to corroborate the position of Cai et al. (2004), who state that multi-objective analysis and multicriteria decision-making methods can be effective and useful for group decisions in water resource planning, facilitating the dissemination of information, the development of participatory models, processes of learning and the achievement of shared goals [39].

5. Conclusions

Water is not only a necessity and a fundamental human right but also a key element for global economic development. Lack of access to sanitation and clean, reliable water limits residential and industrial development. This is obvious; however, many areas have to deal with deteriorating and often deficient water infrastructures, which require huge costs for their restoration and maintenance. Therefore, if we want to incentivize these costly infrastructure improvements, it is essential to evaluate the positive benefits that water infrastructure can provide to the entire economy [40]. Often, global water crises are mainly caused by poor governance, despite the presence of important factors such as natural limitations in water supply, lack of funding and institutional problems [41]. The management of water resources requires a constant balance between the investments necessary to guarantee a reliable water supply and the entrepreneurial needs of the water operators, without losing sight of the interests of the entire community [42]. To face this challenge, it is necessary to adopt an integrated perspective that takes into account the different interests at stake. In this sense, the temporal hierarchization of water projects plays a central role. It can be achieved through the adoption of multicriteria evaluation methodologies, which allow projects to be evaluated based on multiple objectives, including effectiveness, efficiency, fairness, and environmental and economic sustainability. In this way, it is possible to define a ranking of the projects that takes into account all the interests at stake. The temporal hierarchization of the water projects to be implemented at a territorial level based on their priority is a fundamental aspect of the planning and management of water resources. This hierarchization makes it possible to define an order of priority for the interventions and to establish a roadmap for the implementation of the projects to guarantee the efficient and sustainable use of the available resources.

The present research proposes a multicriteria model for the temporal hierarchy of optimal investments in the management of water resources in Italy. The model, based on the application of the analytic hierarchy process (AHP) and designed in compliance with the current national legislation, is tested on a case study set in Campania (Italy). Among the main results, it is noted that the details of the ranking appear to be shared between the two players in the investment strategy (the private operator and EGA). The model is proven to be an effective tool in identifying shared planning strategies between public and private operators, helping to ensure the sustainable management of water resources and the protection of the fundamental rights of the populations concerned. As regards the application case analyzed in this work, both the utility and the EGA have expressed a positive opinion regarding both the proposed model and the results obtained. In particular, the AHP method was recognized by both as an effective tool that is quick to apply and easy to understand. Furthermore, the final hierarchy of projects to be carried out has been accepted and, so far, followed.

However, it is important to note that the proposed model does not completely resolve the information asymmetry that often exists between the water operator, who has detailed knowledge of the assets, stocks and costs of production factors, and the regulator, who remains a passive observer without adequate quantification of the representative parameters of the IWSM. Furthermore, since the AHP does not provide information on the cardinal differentials between the positions assumed by the projects, the results obtained cannot be considered in an absolute way and could be further integrated with other appropriate methodologies, such as the MAUT, to obtain a more accurate evaluation of the design alternatives [43].

Despite the limitations highlighted, the result of the temporal ranking performed on the case study appears satisfactory. From the tendential coincidence between the primary goals of the public and private operators, a positive perspective can be derived on the potential collaboration for the development of the water sector, especially in the most disadvantaged areas. In terms of future perspectives, it could be interesting to apply the multicriteria model proposed in other Italian regions or other countries to evaluate its effectiveness in different contexts and compare the results obtained. Secondly, it could be useful to test the model concerning other relevant criticalities that characterize the water resources management process. Thirdly, it could be useful to evaluate the impact of the investment strategy suggested by the model on the sustainable management of water resources and the rights of the populations concerned through the analysis of field data and the study of the outcomes of the implemented policies. Furthermore, the model could be used for improving investment planning in other sectors, such as energy and sustainable construction, using specific criteria defined based on recurring criticalities and integrating sector regulations.