A Finite Element Model for a 6 × K31WS + FC Wire Rope and a Study on Its Mechanical Responses with or without Wire Breakage

Abstract

The special spatial structure and the long-term harsh working environment make the transient response of wire rope complicated, so accurate assessment and prediction of its mechanical characteristics are of great significance to ensure the safe and stable operation of related equipment. In this paper, a method is proposed for the analysis of the mechanical characteristics of a 6 × K31WS + FC wire rope with or without wire breakage. Firstly, an accurate parametric geometric model of the wire rope is established based on the Frenet frame method, the material properties of the wire rope are acquired by experiments, and the finite element model of the wire rope is built. Then, a mechanical model of the wire rope is proposed to verify the validity of the finite element model. Finally, the influences of the number, distribution, and location of the broken wires on the mechanical characteristics of the wire rope are thoroughly analyzed. This work proposes a comprehensive framework that can quantitatively analyze the mechanical characteristics of the complex wire rope with or without wire breakage, which provides a practical method for its reliability and maintenance evaluation and has guiding significance for the shape design and structural optimization of the wire rope.

1. Introduction

A wire rope is a kind of component with a special spatial helix structure. It has good resistance to wear, fatigue, and shock, and is widely used in civil engineering, shipbuilding, aerospace engineering, and other industrial fields [1,2]. The core of a 6 × K31WS + FC wire rope is made of fiber, which has good performance in oil storage. This type of wire rope has excellent resistance to corrosion and fatigue, so it is widely used on various important occasions. However, due to its complex spatial structure and large number of wires, the contact between wires and strands under loading is complicated, and the internal wires bear a variety of loads such as tensile stress, bending stress, and shear stress. It is very difficult to accurately measure these loads of the wire rope, even though these loads play a very important role in the safe operation of a wire rope. As a result, accidents caused by wire rope failures occur from time to time, so there is an urgent need to propose an approach to effectively and accurately assess the mechanical characteristics of the wire rope with complex structures, such as a 6 × K31WS + FC wire rope.

At present, research on the mechanical characteristics of the wire rope mainly focuses on analytical analysis and numerical simulation. Hruska and Hall [3,4] first developed theoretical models to study the stress of a simple straight strand. They derived expressions of tangential, radial, and tensile forces in the strands, but ignored the bending stiffness, torsional stiffness, and the contact condition between wires. Costello [5,6] established the mechanical equilibrium equation between a single wire and a simple straight strand based on Love’s curved bar theory, on the basis of which he explored the nonlinear static response of a wire rope with an independent wire rope core (IWRC) structure when subjected to axial strain and torsion. Lee and Casey [7,8] applied differential geometric equations to establish a parametric equation for the three-dimensional helix structure of lang lay and regular lay wire rope, which is necessary for the geometric modeling of the wire rope. Based on Costello’s work, Kumar and Cochran [9] proposed a linear model to analyze the elastic deformation characteristics of multi-layer strands under tensile and torsional loads. Jiang [10] considered wire strands and wire ropes as typical structures defined by seven stiffness coefficients and deformation constants, proposing a common formula for linear and nonlinear analyses of wire ropes. Wang et al. [11] established a geometric model for all kinds of wire ropes with round strands. Li et al. [12] proposed a theoretical and numerical method for calculating the mechanical response of cables, and the effectiveness of the proposed method has been validated by comparisons with existing research. Meng et al. [13] established a mathematical model of a wire rope under axial tensile and torsional loads, and they accurately calculated the contact deformation, contact pressure, and internal stress of the wire rope due to line contact using the semi-analytical method.

With the rapid development of numerical simulation technology, its accuracy and efficiency have been greatly improved. Jiang et al. [14,15] established a simplified finite element model of the sector-shaped rope strands, where the overall response of the wire rope was basically consistent with the analytical solution and experimental data. Fedorko et al. [16] proposed an accurate geometric modeling method that can be used for modeling the special-shaped strand wire rope, and the accuracy of the model was verified by finite element analysis. Nawrocki and Labrosse [17] established a finite element model of a simple straight strand, using different contact settings to study the mechanical characteristics of the wire rope under a combination of axial tensile load and bending load. Stanova et al. [18,19] predicted the response of wire ropes with different shapes and structures by ABAQUS and analyzed the stress and deformation of these different wire ropes. Ma et al. [20,21] analyzed the stress and strain distribution of four types of wire rope with different lay directions under axial tensile force and compared the simulation result with the experimental result to verify the effectiveness of the finite element model. Cao and Wu [22] simulated the deflection experiment with a wire rope, and the error of the simulation result was 11.16% compared with the actual experimental result. Chen et al. [23] proposed a fine modeling method for locking coil wire ropes, studying the stress distribution pattern of the wire during the tensioning process. The theoretical and simulation results showed that the stress of the central wire was greater than the stress of the external wire, and the failure usually occurred near the end of the wire. Fontanari et al. [24] conducted tensile experiments to determine the strain-stress curve of the wire rope and studied the stress and strain evolution of the wire rope in the elastic state by finite element analysis. Wang et al. [25] predicted the stress response of a 6 × 19 + IWS wire rope in the linear region by finite element analysis and established a life model of crack extension based on elastic fracture mechanics. Du [26,27] established a 1/6 pitch finite element model of a 6 × 6 + IWS wire rope, compared the contact stress of a 1 × 7 + IWS wire rope under different broken wire conditions, and found that wires around the broken wire will bear a greater load. With the increase in the number of broken wires, the bearing capacity of the wire rope is rapidly weakened. Ma et al. [28] proposed an accurate and efficient finite element model for the mechanical analysis of wire ropes and studied the axial mechanical properties of a 6 × 36SW + IWR wire rope using experimental, theoretical, and numerical methods.

At present, studies on the mechanical characteristics of wire rope based on analytical analysis and numerical simulation have obtained certain results. However, the related studies based on analytical analysis often focus on dealing with wire ropes with simple structures. The vast majority of the numerical studies are based on the FEM (finite element method) and focus on simple wire ropes such as single-helix wire ropes, because the convergence of the FEM could be very difficult due to the complex geometry of wire ropes and complex contact conditions under loading. Overall, there are few studies on wire ropes with complex double-helix structures, such as the 6 × K31WS + FC wire rope. In addition, most of the above studies failed to establish a finite element model of the wire rope with a full pitch, so the simulation results are not convincible enough to reflect the actual mechanical response of the wire rope under loading. Furthermore, current research on the broken wires of wire ropes only focuses on explaining the patterns of broken wire in experiments or actual working conditions, and the influences of broken wires on the mechanical characteristics of wire ropes have not been fully analyzed.

Thus, the main objectives of this paper are to propose a comprehensive framework for analyzing the mechanical characteristics of wire ropes with complex structures with high efficiency and accuracy, and quantitatively study the influence of broken wires on the mechanical response of a 6 × K31WS + FC wire rope in detail. This work will provide a practical method for the performance evaluation of wire ropes under broken wire conditions, and partly fills the gap in the relevant research.

This article is arranged as follows: In Section 2, a precise geometric model of a 6 × K31WS + FC wire rope is proposed. In Section 3, a finite element model of the wire rope is established and the mechanical response of the wire rope under axial strain has been obtained. In Section 4, the effectiveness of the proposed model is validated by analytical analysis. In Section 5, the mechanical response of the wire rope under broken wire conditions is studied in detail. Finally, the conclusions are rendered in Section 6.

2. Geometric Modeling of 6 × K31WS + FC Wire Rope

The good bearing properties of wire rope benefit from its special helix geometry, so it is a prerequisite of the high-precision finite element model and the analytical model to establish an accurate geometric model of the wire rope.

2.1. Geometry of the Wire Rope

A 6 × K31WS + FC wire rope consists of a fiber core and six identical strands. Each strand is composed of 31 wires which can be divided into the center wire, the wire in the inner layer, the wire in the middle layer, and the wire in the outer layer according to their positions in the strand. The cross-section of a 6 × K31WS + FC wire rope is shown in Figure 1 and the radii of each type of wire are listed in

Table 1. Radius of the rope core and wires in a 6 × K31WS + FC wire rope.

Type	Serial Number	Mark	Number of Wires	Radius (mm)
Rope core	I	R1	1	7.4
Center wire	II	R2	1	0.85
Wire in inner layer	II	R3	6	0.85
Wire in middle layer	IV	R4	6	0.75
	V	R5	6	0.95
Wire in outer layer	VI	R6	12	1.35

. The radii of wires (including the rope core) numbered from I to VI are represented by R_i (I = 1, 2, …6), and the radius of the strand is represented by R_c. The pitch, diameter, and helix angle of a 6 × K31WS + FC wire rope are I_p = 240 mm, R_r = 37 mm, and β = 25.84°, respectively.

2.2. Parametric Equation of the Wire Centroid Line

The precise 3D geometry of the wire rope can be obtained by sweeping the cross-section of the wire along the centroid line of each wire constituting the wire rope. Thus, the parametric equations of the wire rope need to be acquired in advance. The global coordinate system O₁-XYZ and the relative coordinate system $O_2-\overrightarrow{n}\overrightarrow{b}\overrightarrow{t}$ or the Frenet frame, are established to obtain the parametric equations of the wire centroid line. As shown in Figure 2, the origin O₁ is located at the center of the bottom of the rope core, the origin O₂ is located at the center of the outer wire section, which is the endpoint of the centroid line of a single-helix wire, $\overrightarrow{n}$, $\overrightarrow{b}$, $\overrightarrow{t}$ are the unit principal normal vector, the unit slave normal vector, and the unit tangent vector at this point, respectively. The position of point A on the centroid line of the single-helix wire is represented by vector $\overrightarrow{R}$ in O₁-XYZ, the position of point B on the centroid line of the double-helix line is represented by vector $\overrightarrow{Q}$, the vector formed by the connection between point B and the origin O₁ is represented by $\overrightarrow{P}$, and θ is the angle between vector $\overrightarrow{R}$ and the X axis in the XO₁Y plane.

The parameter equation of the centroid line of a single-helix wire is R(θ) = [r_rcosθ_r, r_rsinθ_r, r_rθ_rtanβ_r]^T, where r_r, θ_r, and β_r are the helix radius, position angle, and helix angle of the wire, respectively. Then, the unit vectors of the Frenet frame can be obtained as:

$$\{\begin{array}{l}\overrightarrow{t}=\frac{R^{\prime }(\theta )}{R^{″}(\theta )}=\left[\begin{array}{c}-\sin {\theta }_{\mathrm{r}}\sin {\beta }_{\mathrm{r}}\\ \cos {\theta }_{\mathrm{r}}\cos {\beta }_{\mathrm{r}}\\ \sin {\beta }_{\mathrm{r}}\end{array}\right]\\ \overrightarrow{b}=\frac{R^{\prime }(\theta )\times R^{″}(\theta )}{\left|R^{\prime }(\theta )\times R^{″}(\theta )\right|}=\left[\begin{array}{c}\sin {\theta }_{\mathrm{r}}\sin {\beta }_{\mathrm{r}}\\ -\cos {\theta }_{\mathrm{r}}\sin {\beta }_{\mathrm{r}}\\ \cos {\beta }_{\mathrm{r}}\end{array}\right]\\ \overrightarrow{n}=\overrightarrow{b}\times \overrightarrow{t}=\left[\begin{array}{c}-\cos {\theta }_{\mathrm{r}}\\ -\sin {\theta }_{\mathrm{r}}\\ 0\end{array}\right]\end{array}$$

(1)

The transfer matrix from the global coordinate system to the Frenet frame is represented by T:

$$T={\left\{\begin{array}{ccc}\overrightarrow{n}& \overrightarrow{b}& \overrightarrow{t}\end{array}\right\}}^T=\left[\begin{array}{ccc}-\cos {\theta }_{\mathrm{r}}& -\sin {\theta }_{\mathrm{r}}& 0\\ \sin {\theta }_{\mathrm{r}}& -\cos {\theta }_{\mathrm{r}}\sin {\beta }_{\mathrm{r}}& \cos {\beta }_{\mathrm{r}}\\ -\sin {\theta }_{\mathrm{r}}\cos {\beta }_{\mathrm{r}}& \cos {\theta }_{\mathrm{r}}\cos {\beta }_{\mathrm{r}}& \sin {\beta }_{\mathrm{r}}\end{array}\right]$$

(2)

Any point on the centroid line of a double-helix wire is represented in the Frenet frame as [r_sicosθ_si, r_sisinθ_si, 0]^T, where r_si and θ_si represent the helix radius and position angle of each kind of double-helix wire, respectively, and it can be represented in O₁-XYZ as:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{x}_{\mathrm{s}i}\\ y_{\mathrm{s}i}\\ z_{\mathrm{s}i}\end{array}\right]& =\left[\begin{array}{c}{r}_{\mathrm{r}}\cos {\theta }_{\mathrm{r}}\\ r_{\mathrm{r}}\sin {\theta }_{\mathrm{r}}\\ r_{\mathrm{r}}{\theta }_{\mathrm{r}}\tan {\beta }_{\mathrm{r}}\end{array}\right]+T^{-1}\cdot \left[\begin{array}{c}{r}_{\mathrm{s}i}\cos {\theta }_{\mathrm{s}i}\\ r_{\mathrm{s}i}\sin {\theta }_{\mathrm{s}i}\\ 0\end{array}\right]\hfill \\ & =\left[\begin{array}{c}{r}_{\mathrm{r}}\cos {\theta }_{\mathrm{r}}-r_{\mathrm{s}i}\cos {\theta }_{\mathrm{r}}\cos {\theta }_{\mathrm{s}i}+r_{\mathrm{s}i}\sin {\theta }_{\mathrm{r}}\sin {\beta }_{\mathrm{r}}\sin {\theta }_{\mathrm{s}i}\\ r_{\mathrm{r}}\sin {\theta }_{\mathrm{r}}-r_{\mathrm{s}i}\sin {\theta }_{\mathrm{r}}\cos {\theta }_{\mathrm{s}i}-r_{\mathrm{s}i}\cos {\theta }_{\mathrm{r}}\sin {\beta }_{\mathrm{r}}\sin {\theta }_{\mathrm{s}i}\\ r_{\mathrm{r}}{\theta }_{\mathrm{r}}\tan {\beta }_{\mathrm{r}}+r_{\mathrm{s}i}\cos {\beta }_{\mathrm{r}}\sin {\theta }_{\mathrm{s}i}\end{array}\right]\hfill \end{array}$$

(3)

Here, the factor n is introduced to limit the rotational direction of the wires, which can guarantee that the wires are evenly distributed in each layer:

$$n=\frac{{\theta }_{\mathrm{s}i}}{{\theta }_{\mathrm{r}}}=\frac{r_{\mathrm{r}}}{r_{\mathrm{s}i}\tan {\beta }_{\mathrm{s}i}\cos {\beta }_{\mathrm{r}}}$$

(4)

Then, the parametric equation of a double-helix wire in O₁-XYZ is obtained as:

$$\left[\begin{array}{c}{x}_{\mathrm{s}i}\\ y_{\mathrm{s}i}\\ z_{\mathrm{s}i}\end{array}\right]=\left[\begin{array}{c}{r}_{\mathrm{r}}\cos \frac{{\theta }_{\mathrm{s}i}}{n}-r_{\mathrm{s}i}\cos \frac{{\theta }_{\mathrm{s}i}}{n}\cos {\theta }_{\mathrm{s}i}+r_{\mathrm{s}i}\sin \frac{{\theta }_{\mathrm{s}i}}{n}\sin {\beta }_{\mathrm{r}}\sin {\theta }_{\mathrm{s}i}\\ r_{\mathrm{r}}\sin \frac{{\theta }_{\mathrm{s}i}}{n}-r_{\mathrm{s}i}\sin \frac{{\theta }_{\mathrm{s}i}}{n}\cos {\theta }_{\mathrm{s}i}-r_{\mathrm{s}i}\cos \frac{{\theta }_{\mathrm{s}i}}{n}\sin {\beta }_{\mathrm{r}}\sin {\theta }_{\mathrm{s}i}\\ r_{\mathrm{r}}\frac{{\theta }_{\mathrm{s}i}}{n}\tan {\beta }_{\mathrm{r}}+r_{\mathrm{s}i}\cos {\beta }_{\mathrm{r}}\sin {\theta }_{\mathrm{s}i}\end{array}\right]$$

(5)

Based on the above process, the centroid equations that constitute all the wires of the wire rope are obtained, and an example is shown in Figure 3.

Based on the obtained centroid of each wire, the exact 3D geometry of a 6 × K31WS + FC wire rope with a full pitch is acquired and presented in Figure 4 according to the parameters described in Section 2.1. The helix radius and helix angle of each wire can be calculated based on the geometry of the wire rope, as shown in

Table 2. Helix radius and helix angle of the rope core and wires in a 6 × K31WS + FC wire rope.

Type	Serial Number	Mark	Helix Radius (mm)	Helix Angle (Rad)
Rope core	I	R1	\	\
Center wire	II	R2	1.90	1.23
Wire in inner layer	III	R3	1.85	1.52
Wire in middle layer	I	R4	3.49	1.48
	V	R5	2.62	1.50
Wire in outer layer	VI	R6	5.22	1.44

.

3. Finite Element Model of a 6 × K31WS + FC Wire Rope

With the aid of the precise 3D geometry model, an accurate and efficient finite element model of a 6 × K31WS + FC wire rope can be expected. To obtain the actual mechanical response of the wire rope and improve its solution efficiency, a finite element model of a 6 × K31WS + FC wire rope with a full pitch is established in the following sections.

3.1. Material Properties of the Wire

The material parameters are critical to establishing an accurate finite element model of the wire rope. There are four kinds of specimens, corresponding to four different diameters (1.5 mm, 1.7 mm, 1.9 mm, and 2.7 mm) of wires in a 6 × K31WS + FC wire rope. Each type of specimen contains 15 identical wires with lengths of 200 mm. Note that the steel wires in a 6 × K31WS + FC wire rope are made of the same material. The wires have been straightened carefully by special equipment in advance without introducing any damage. Here, a schematic illustration of the tensile experiment is shown in Figure 5a. The equipment used is an Instron 68FM-300 Floor Model Universal Testing Machine, the maximum speed and force capacity of which is 560 mm/min and 300 kN, respectively. Then, experiments are conducted according to GB/T228.1-2021 [29] to acquire the material parameters of the wires. To enhance the credibility of the experiment result, each type of wire has been tested 15 times. The experimental result of a typical wire sample is shown in Figure 5b.

After data processing, we discover that the experiment results (strain-stress curves) of the same type of wire are in good consistency. Therefore, an arbitrary strain-stress curve of each type of wire is selected as a representative, as depicted in Figure 6. In Figure 6, the strain at a fracture of R = [0.75 mm, 0.85 mm, 0.95 mm, and 1.35 mm] is 0.336, 0.185, 0.323, and 0.0446, respectively.

Based on the experiment results, the Poisson’s ratio μ and elastic modulus E of each type of wire are obtained, and they are all approximately 0.29 and 196, GPa respectively, and the deviations are less than 5%. This indicates that μ and E are insensitive to the variation in wire radius. Therefore, we can safely assume that μ and E of each type of wire are the same, i.e., μ = 0.29 and E = 196 GPa. The material parameters of the fiber core are obtained according to the reference [30], and all the material parameters obtained are listed in

Table 3. Material parameters of the wire specimens.

Radius of Wire Specimen (mm)	Density (g/cm3)	Tensile Load (kN)	Tensile Strength (MPa)	Poisson’s Ratio	Elastic Module (MPa)
0.75	7.85	3.62	2.03 × 103	0.29	1.96 × 105
0.85		5.29	2.05 × 103
0.95		5.93	2.09 × 103
1.35		10.02	2.13 × 105
Rope core	1.15	\	\	0.3	8 × 103

.

3.2. Pre-Processing of the Finite Element Model

3.2.1. Contact Properties

The contact of a 6 × K31WS + FC wire rope under load conditions is very complicated due to its complex geometry and large number of wires. In a finite element simulation of a complex wire rope, such as the 6 × K31WS + FC, the solution is often difficult to converge if the general contact algorithm is adopted. Thus, the contact problem is tricky, and it can severely influence the efficiency and accuracy of the finite element analysis. In this paper, the “Surface-to-Surface” contact algorithm is adopted to simulate the real contact of the wire rope. The adjacent surfaces of wires are the master and slave surfaces of each other, and a total of 378 contact pairs are set. The penalty friction algorithm is set for the tangential friction property of lateral surfaces among wires and the friction coefficient is 0.15. Normal behavior is defined as hard contact.

As shown in Figure 7, reference points RP1 and RP2 are defined at the center of each end surface of the rope core, respectively. The corresponding nodes on each end surface of the wire rope are coupled with RP1 and RP2. All the degrees of freedom of RP1 are constrained, and only the axial rotational freedom of RP2 is constrained. An axial strain of 0.01 is set on RP2 as the load of the wire rope.

3.2.2. Mesh Setup

To improve the efficiency and convergence of the proposed finite element model, the seeding edges method is used and the wire rope is carefully gridded. The number of seeds on the end face and generatrix of each wire is 12 and 300, respectively. The neutral axis algorithm is adopted to generate an inerratic grid for the model, which is meshed into a hexahedron element with 402,135 nodes and 308,800 elements, as shown in Figure 8.

To find the most suitable element type in the analysis of the wire rope, a model with 1/6 pitch of a 6 × K31WS + FC wire rope loaded by axial strain ε = 0.01 is established, which is depicted in Figure 9.

The contact properties are identical, as specified in Section 3.2.1. The simulation results of six feasible element types are listed in

Table 4. Analysis results of 6 feasible element types.

Element Type	Severe Discontinuous Iterations	Time (s)	Number of Elements	Number of Nodes	Maximum Stress (MPa)	Maximum Deformation (mm)
C3D8	0	1.34 × 103	5.69 × 105	1.09 × 106	1.35 × 103	8.82 × 10−2
C3D8R	0	1.39 × 103	5.69 × 105	1.09 × 106	1.18 × 103	1.10 × 10−1
C3D8I	0	1.27 × 103	5.69 × 105	1.55 × 106	1.53 × 103	9.397 × 10−2
C3D8S	0	1.43 × 103	5.69 × 105	1.09 × 106	1.37 × 103	8.82 × 10−2
C3D20	7	4.18 × 103	1.72 × 106	3.80 × 106	1.42 × 103	9.17 × 10−2
C3D20R	5	3.55 × 103	1.05 × 106	2.40 × 106	1.42 × 103	8.64 × 10−2

.

In Table 4, the model meshed by quadratic elements C3D20 and C3D20R have a much greater number of elements and nodes than the other element types. Moreover, the excessive elements and nodes of C3D20 and C3D20R caused severe discontinuous iterations during the calculation. The aforementioned reasons make the analysis efficiency of C3D20 and C3D20R much lower than other types of elements, while the values of maximum stress and maximum deformation do not show many differences. In addition, the solution time of quadratic elements is about three times longer than that of linear elements. Thus, C3D20 and C3D20R are not suitable for the finite element simulation of a 6 × K31WS + FC wire rope. Although the hourglass effect is well suppressed by the additional degrees of freedom in C3D8I, it can cause greater stress and deformation. The rigidity of C3D8S and C3D8 is too large. All three types of elements, C3D8I, C3D8S, and C3D8, are not consistent with the actual material properties of the wire rope. As for C3D8R, it overcame the shortcomings of the above element types in the finite element simulation of a 6 × K31WS + FC wire rope and had good computational efficiency and accuracy, so it is adopted in the following analysis.

3.3. Results and Discussion

Based on the material properties obtained, contact properties set, mesh methods defined, and element type (C3D8R) chosen, the stress distribution of a 6 × K31WS + FC wire rope under an axial strain of 0.01 is solved, as shown in Figure 10.

In Figure 10, along the axial direction of the rope, stresses at both ends of the wire rope are bigger than the other areas, which explains the phenomenon that the breaking of wires often occurs at both ends of a wire rope in actual working conditions. Along the radial direction, we discover that the stress near the rope core is relatively smaller than that away from the core. This is consistent with the phenomenon that the wire that lies outside of the wire rope often fractures earlier. The maximum stress S_max located at both ends of the wire rope is shown in Figure 10, S_max = 1497.65 MPa.

Taken together, the simulated results are consistent with the actual situations. To further enhance the credibility of the proposed finite element model of a 6 × K31WS + FC wire rope, a mechanical analysis of the wire rope is presented in Section 4.

4. Analytical Analysis of a 6 × K31WS + FC Wire Rope

In this section, the validity of the finite element model of a 6 × K31WS + FC wire rope is verified by mechanical analysis.

4.1. Analytical Model of a Simple Straight Strand

First, the mechanical response of a straight strand, which is displayed in Figure 11, is analyzed. In addition, the mechanical response of the wire rope with a more complex double-helix structure can be derived.

The original curvatures of the center wire and outer wire are κ₂ and ${\kappa }_2^{\prime }$. The torsion per unit length of the outer wire is τ₂, and:

$${\kappa }_2=0,{\kappa }_2^{\prime }=\frac{{\cos }^2{\alpha }_2}{r_2},{\tau }_2=\frac{\sin {\alpha }_2\cos {\alpha }_2}{r_2}$$

(6)

where r₂, α₂ are the helix radius and helix angle of the outer wire, respectively, which are shown in Figure 11.

The outer wire is transferred into a new single-helix structure under the load of strain, as shown in Figure 12. $h$ and $\overline{h}$ are the initial and final length of the strand. ${\theta }_2$ and $\overline{{\theta }_2}$ are the initial and final position angle, respectively, which define the position of the center of the outer wire, and ${\theta }_2$ = $\frac{h}{r_2\tan {\alpha }_2}$, $\overline{{\theta }_2}$ = $\frac{h}{\overline{r_2}\tan \overline{{\alpha }_2}}$. ξ₁ and ξ₂ are the axial strains of the center wire and the outer wire, respectively. The original curvature and the torsion per unit length are transformed into:

$$\overline{{\kappa }_2}=0,\overline{{\kappa }_2^{\prime }}=\frac{{\cos }^2\overline{{\alpha }_2}}{\overline{r_2}},{\tau }_2=\frac{\sin \overline{{\alpha }_2}\cos \overline{{\alpha }_2}}{\overline{r_2}}$$

(7)

where $\overline{r_2}$, $\overline{{\alpha }_2}$ are the new helix radius and new helix angle of the outer wire, $\overline{r_2}$ = R₁(1 − ξ₁) + R₂(1 − νξ₂), R₁ and R₂ are the radius of the core wire and the outer wire, respectively, ν is the Poisson’s ratio of the wire, and higher-order variables such as ξ₂Δα are ignored.

The torsion per unit length τ_s, the axial strain of the center wire ξ₁, and the rotational strain of the outer wire β₂ are:

$$\{\begin{array}{l}{\tau }_{\mathrm{s}}=\frac{\overline{{\theta }_2}-{\theta }_2}{h}\\ {\xi }_1=\frac{\overline{h}-h}{h}=\left(1+{\xi }_2\right)\frac{\sin \overline{{\alpha }_2}}{\sin {\alpha }_2}-1\\ {\beta }_2=r_2{\tau }_{\mathrm{s}}=\frac{{\xi }_2}{\tan {\alpha }_2}-\Delta {\alpha }_2+\nu \frac{R_1{\xi }_1+R_2{\xi }_2}{r_2\tan {\alpha }_2}\end{array}$$

(8)

The curvature variation $\Delta {\kappa }_2^{\prime }$ and the variation of torsion per unit length $\Delta {\tau }_2$ can be linearized and expressed as:

$$\{\begin{array}{l}{R}_2\Delta {\kappa }_2^{\prime }=\frac{R_2}{r_2}\left[\left(\nu \frac{R_1}{r_2}\frac{{\cos }^2{\alpha }_2}{\tan {\alpha }_2}-2\sin {\alpha }_2\cos {\alpha }_2\right)\Delta {\alpha }_2+\left(\nu {\cos }^2{\alpha }_2{\xi }_2\right)\right]\\ R_2\Delta {\tau }_2=\frac{R_2}{r_2}\left[\left(1-2{\sin }^2{\alpha }_2+\nu \frac{R_1}{r_2}{\cos }^2{\alpha }_2\right)\Delta {\alpha }_2+\left(\nu \sin {\alpha }_2\cos {\alpha }_2\right){\xi }_2\right]\end{array}$$

(9)

Then, the mechanical responses of the outer wire can be expressed as:

$$\{\begin{array}{l}{H}_2=\frac{\pi E{R}_2^3}{4\left(1+\nu \right)}{R}_2\Delta {\tau }_2\\ G_2^{\prime }=\frac{\pi E{R}_2^3}{4}{R}_2\Delta {\kappa }_2^{\prime }\\ N_2^{\prime }=H_2\frac{{\cos }^2{\alpha }_2}{r_2}-G_2^{\prime }\frac{\sin {\alpha }_2\cos {\alpha }_2}{r_2}\\ T_2=\pi E{R}_2^2{\xi }_2\\ X_2=N_2^{\prime }\frac{\sin {\alpha }_2\cos {\alpha }_2}{r_2}-T_2\frac{{\cos }^2{\alpha }_2}{r_2}\end{array}$$

(10)

where E and H₂ are the elastic modulus and axial torque of the outer wire, $G_2^{\prime }$ is the bending moment, $N_2^{\prime }$ is the shearing force, T₂ is the axial force, and X₂ is the contact force per unit length, as Figure 13 shows.

The total axial force F₂ and bending moment M₂ acting on the outer wires are:

$$\{\begin{array}{l}{F}_2=m_2\left(T_2\sin {\alpha }_2+N_2^{\prime }\cos {\alpha }_2\right)\\ M_2=m_2\left(H_2\sin {\alpha }_2+G_2^{\prime }\cos {\alpha }_2+T_2{r}_2\cos {\alpha }_2-N_2^{\prime }{r}_2\sin {\alpha }_2\right)\end{array}$$

(11)

where m₂ is the number of outer wires of the strand. Assuming that the wires are initially stress free, the tensile stress of the strand T_σ2 caused by load T₂, the maximum normal stress $G_{\sigma 2}^{\prime }$ caused by bending moment $G_2^{\prime }$, and the maximum shear stress H_σ2 caused by torque H₂ are [5]:

$$\{\begin{array}{l}{T}_{\sigma 2}=\frac{T_2}{\pi R_2^2}\\ G_{\sigma 2}^{\prime }=\frac{4G_2^{\prime }}{\pi R_2^3}\\ H_{\sigma 2}=\frac{2H_2}{\pi R_2^3}\end{array}$$

(12)

4.2. Analytical Analysis of a 6 × K31WS + FC Wire Rope

It is difficult to obtain the mechanical response directly according to the classical theory due to the complex structure of a 6 × K31WS + FC wire rope, so appropriate assumptions must be made. First, the 6 × K31WS + FC wire rope can be treated as a straight strand by regarding each strand of the wire rope as a steel wire with a helix structure, as shown in Figure 14a,b. Then, the mechanical response of each strand of the wire rope can be obtained according to Section 4.1. Finally, the mechanical responses of wires in the strand can be obtained by the same method specified in Section 4.1 with an input load calculated in the first step.

The helix radii of wires in each layer of strand are rr₃, rr₄, rr₅, and rr₆, respectively, which are:

$$\{\begin{array}{l}r{r}_3=R_2+R_3\\ r{r}_4=R_2+2R_3+R_4\\ r{r}_5=\sqrt{R_2^2+R_3^2}+\sqrt{R_3^2+R_5^2}\\ r{r}_6=\frac{\sqrt{{\left(R_4+R_6\right)}^2-R_6^2}+R_4+2R_3+R_2}{\cos \gamma }\end{array}$$

(13)

where γ is the angle between two lines, which is the line between the center of the rope core and the strand core wire, and the line between the center of the strand core wire and the outer wire, and it is illustrated in Figure 14c, γ = 15.14°.

If there is no initial torsion in the wire rope (β = 0), and the 6 × K31WS + FC wire rope is loaded with an axial strain ε = 0.01, which is located at the center of the end surface of the wire rope, the whole rope is regarded as a 1 × 7 simple straight strand and the radius of the center wire (rope core) R₁ = 7.4 mm, the radius of the outer wire (strand of rope) R_c = 6.27 mm, and the helix radius of the outer wire r_c^* = 13.67 mm.

The equivalent modulus E_c is used to represent the elastic modulus of each strand [31], E_c can be calculated as:

$$E_{\mathrm{c}}=E\left(R_2^2+m_3{R}_3^2+m_4{R}_4^2+m_5{R}_5^2+m_6{R}_6^2\right)/R_{\mathrm{c}}^2$$

(14)

where m_i is the number of each type of wire in one strand, R_i is the radius of each type of wire in one strand, E is the elasticity modulus, and E_c = 1.67 × 10¹¹ Pa.

Then, the following parameters could be calculated as described in Section 4.1. The axial strain of the strand ξ_c* = 8.55 × 10⁻³, the helix angle variation Δα_c* = 4.06 × 10⁻³, and the helix radius of the loaded strand ${\overline{r}}_{\mathrm{c}}^{*}$ = 13.63 mm. The curvature variation of the strand Δκ_c* = −1.65 × 10⁻⁴ mm⁻¹, the torsion per unit length Δτ_c* = −1.65 × 10⁻³ mm⁻¹, and the rotational strain of the strand β_c* = −1.76 × 10⁻¹⁷ N·m. Then, the mechanical responses of the simplified 6 × K31WS + FC wire rope is figured out, as listed in

Table 5. Mechanical response of the simplified 6 × K31WS + FC wire rope.

Mechanical Response	Result
Bending moment Gc*	−37.87 N·m
Axial torque Hc*	−29.04 N·m
Shearing force Nc*	637.76 N
Axial force Tc*	1.87 × 105 N
Uniformly distributed radial load Xc*	−1.54 × 106 N/m
Total axial force of strand Fc*	1.06 × 106 N
Total torque of strand Mc*	4.89 × 103 N·m

.

Note that the axial stress and bending moment of the rope core are regarded as 0, since the load of the fiber rope core is relatively small compared with the strand in a 6 × K31WS + FC wire rope.

Based on the mechanical responses of the simplified 6 × K31WS + FC wire rope, the mechanical responses of each wire in each strand could be figured out, and the axial stress T_σ2 = 1.42 × 10³ MPa, the normal stress $G_{\sigma 2}^{\prime }$ = 178.08 MPa, and the shear stress H_σ2 = 68.28 MPa. According to the previous assumption, the axial strain ξ_c* and helix angle variation Δα_c of the simplified center wire are equal to the axial strain ξ₂ and the helical angle variation Δα₂ of the simplified outer wire, that is, ξ₂ = ξ_c* = 8.55 × 10⁻³, Δα₂ = Δα_c = 4.06 × 10⁻³.

Table 6. Parameters of the wire in each layer of the strand.

Serial Number of Wires	Axial Strain ξi	Helix Angle Variation Δαi	Curvature Variation Δκi (m−1)	Torsion per Unit Length Δτi (m−1)
III	8.52 × 10−3	5.29 × 10−4	−2.41 × 10−2	−0.219
I	8.46 × 10−3	9.92 × 10−4	−4.49 × 10−2	−0.214
V	8.50 × 10−3	7.47 × 10−4	−3.39 × 10−2	−0.217
VI	8.35 × 10−3	1.47 × 10−3	−1.81 × 10−2	−0.207

lists the axial strain and helix angle variation of wires in each layer of the strand.

Table 7. Mechanical responses of wires in each layer of the strand.

Serial Number of Wires	Bending Moment Gi (N·m)	Axial Torque Hi (N·m)	Shearing Force Ni (N)	Axial Force Ti (N)	Uniformly Distributed Radial Load Xi (N/m)
III	−2.61 × 10−3	−1.82 × 10−2	4.48 × 10−2	4.55 × 103	−5.60 × 103
IV	−2.22 × 10−3	−8.15 × 10−3	3.81 × 10−2	3.06 × 103	−7.05 × 103
V	−4.56 × 10−3	−2.24 × 10−2	7.82 × 10−2	5.06 × 103	−8.78 × 103
VI	−7.30 × 10−3	−6.40 × 10−2	−3.35 × 10−2	8.61 × 103	−2.94 × 105

lists the mechanical responses of wires in each layer of a strand of a 6 × K31WS + FC wire rope, which are obtained by Equation (10).

According to Equation (11), the total axial force of the outer wires in a strand F_H = 1.78 × 10⁵ N, the axial torque M_H = 2.30 N·m, the axial force of the center wire F₂ = 5.09 × 10³ N, and the axial torque M₂ = −1.70 × 10⁻⁵ N·m. Then, the stress and the Von Mises stress of the wires in each layer of the strand can be solved by Equation (12), as listed in

Table 8. Stress of wires in each layer of strand.

Serial Number of Wires	Axial Stress Tσi (MPa)	Normal Stress Gσi (MPa)	Shear Stress Hσi (MPa)	Equivalent Stress (MPa)
II	1794.98	\	−0.013	1794.98
III	1789.67	−4.56	−15.91	1785.22
IV	1776.21	−6.98	−12.81	1769.30
V	1784.39	−6.77	−16.65	1777.72
VI	1753.45	−4.76	−20.87	1748.82

.

The maximum stress of the 6 × K31WS + FC wire rope S_max = 1794.98 MPa, while axial strain ε = 0.01. As stated before, the maximum stress obtained from finite element simulation is 1497.65 Mpa. Obviously, the maximum stress obtained by the analytical analysis is 297.33 Mpa bigger, the deviation is 19.85%. The reasons accounting for the deviation could be summarized as: (1) The assumption that the fiber core does not bear any load in the analytical model may lead to a bigger result; (2) The equivalent modulus E_c may overestimate the stiffness of the assumed strand; (3) The strand of wire rope is not straight thus our assumption will certainly increase the stiffness of the strand.

Based on the above analysis, it can be safely said that the proposed finite element model of the 6 × K31WS + FC wire rope is accurate, and it can be used in further analysis of the wire rope.

5. Finite Element Analysis of a 6 × K31WS + FC Wire Rope with Broken Wires

The main damage patterns of a wire rope in working conditions are wire breakage, wear, rust, and kink [32], of which wire breakage is the most common form of wire rope failure [33]. Vukelic and Vizentin [34] studied the influence of broken wires on the mechanical characteristics of 6 × 7, 7 × 7, and 8 × 7 wire ropes. However, they did not provide further analysis of wire ropes with more complex structures, which are made of more than 100 wires. More importantly, a wire rope with a complex structure and composed of a large number of wires is at a greater risk of wire breakage. However, there are few studies focusing on this issue, which is vital to ensure its safe operation and maintenance.

Wire ropes mainly bear tensile loads, and broken wires can no longer bear any tensile loads. Thus, the broken wires could be omitted when carrying out finite element analysis. Figure 15 shows the finite element model of a 6 × K31WS + FC wire rope with a broken wire in the center of the strand. This simplification is conventional because scholars adopted the same methodology when studying wire breakage problems [34].

In this part, the mechanical response of a 6 × K31WS + FC wire rope with broken wires is thoroughly investigated by adopting the model proposed in Section 3. A tensile load of 30 kN is applied on one end of the rope, and the other end of the rope is fastened reliably. The other setups of the finite element model are identical as stated in Section 3. Then, 12 scenarios with different broken wire numbers and locations have been carefully studied, and the initial broken wire is determined according to the stress distribution of the intact wire rope. The 12 scenarios are (a) intact wire rope; (b) the wire that bears the maximum stress in scenario (a) is broken; (c) the core wire of the strand is broken; (d) one wire in the outer layer near the rope core is broken; (e) two wires in the outer layer near the rope core are broken; (f) two wires in the outer layer away from the rope core are broken; (g) three wires in the outer layer near the rope core are broken; (h) three wires in the outer layer away from the rope core are broken; (i) five wires in the outer layer near the rope core are broken; (j) five wires in the outer layer away from the rope core are broken; (k) nine wires in the outer layer near the rope core are broken; (l) nine wires in the outer layer away from the rope core are broken. These 12 scenarios are clearly demonstrated in Figure 16.

Then, the mechanical responses of the 12 cases could be obtained, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 represent the stress distribution of the maximum stress section of 12 scenarios.

Table 9. The cross-section area and corresponding maximum stress in different cases.

Serial Number	Number of Broken Wires	Cross-Section Area Decrease	Maximum Stress (MPa)	Maximum Stress Increase	Maximum Stress in Middle Cross-Section (MPa)	Maximum Stress in Middle Cross-Section Increase
a	0	0	658.02	/	311.73	/
b	1	0.45%	663.10	0.77%	305.52	−1.99%
c	1	0.45%	678.33	3.09%	317.49	1.85%
d	1	0.78%	665.61	1.15%	311.26	−0.15%
e	2	1.57%	673.79	2.40%	311.40	−0.11%
f	2	1.57%	686.33	4.30%	336.29	7.88%
g	3	2.35%	680.40	3.40%	308.11	−1.16%
h	3	2.35%	722.20	9.75%	374.09	20.00%
i	5	3.92%	695.98	5.77%	324.33	4.04%
j	5	3.92%	760.30	15.54%	400.13	28.36%
k	9	7.06%	771.56	17.26%	399.52	28.16%
l	9	7.06%	796.71	21.08%	420.77	34.98%

clearly demonstrates the simulation results. Note that the symbols used to mark the working scenarios in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21 are correlated with the symbols in Table 9.

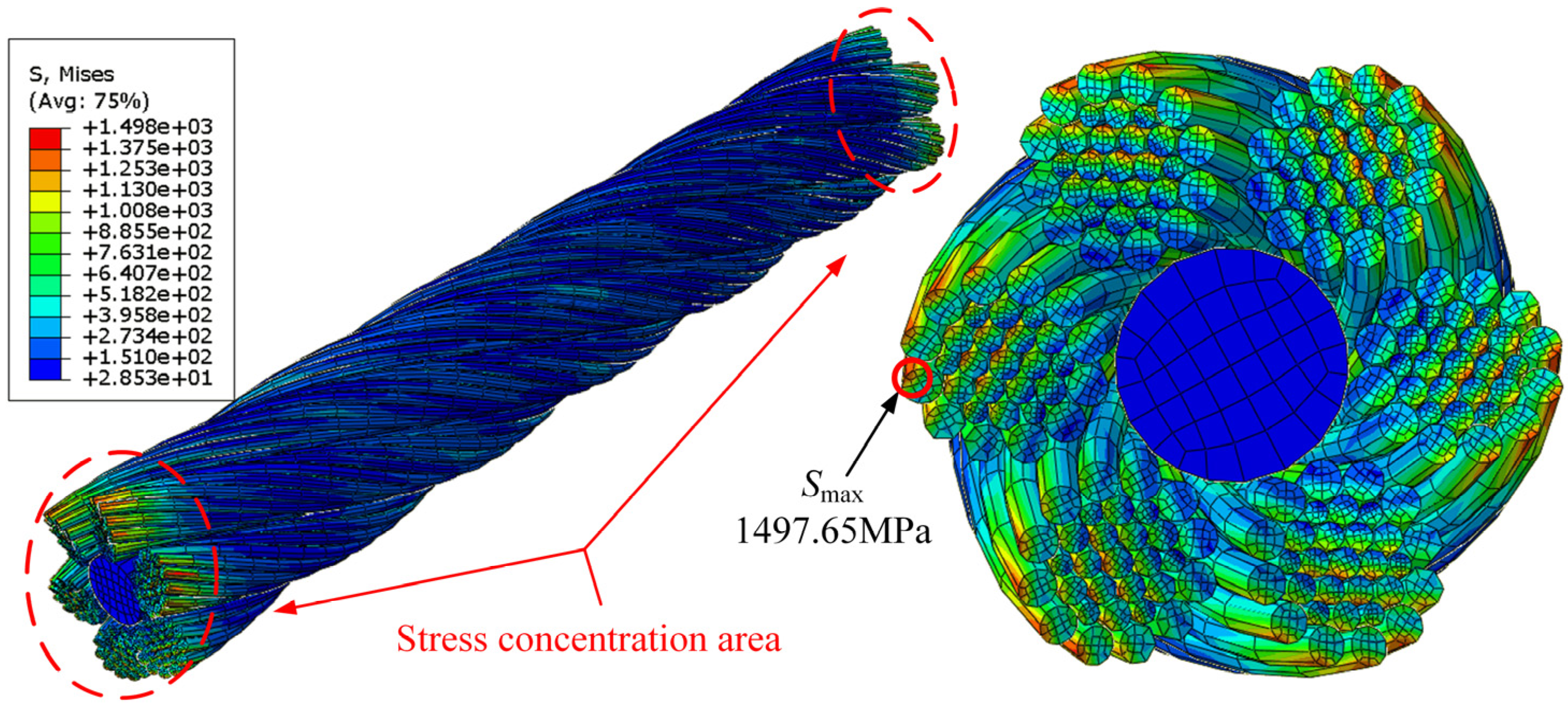
After careful observation of Figure 17, while the wire rope is intact as depicted in Figure 16a, the maximum stress σ^a_max = 658.02 MPa, and it is located at the wire marked by a red circle. According to the simulation results, the maximum stress cross-section appears at both ends of the wire rope in all 12 cases. This is consistent with the facts that wire breakage always occurs at both ends of the wire rope during actual operation.

In Figure 16b,c, only one wire is broken, and the broken wire shares the same radius R = 0.85 mm, which denotes that the decrease in the cross-section area of the wire rope is 0.45%. The corresponding maximum stress are σ^b_max = 663.10 MPa and σ^c_max = 678.33 MPa, respectively. The maximum stress shown in Figure 17 is increased by 0.77% and 3.09% when compared with σ^a_max. Apparently, the location of the broken wire has a dramatic impact on the maximum stress.

In Figure 16d, one wire R = 1.35 mm is broken and the maximum stress σ^d_max = 665.61 MPa, which is larger than σ^a_max by 1.15%. The increases in maximum stress due to the broken wire in cases (c) and (d) are 3.09% and 1.15%, while the decreases in the cross-section area are 0.45% and 0.78%. This is more evidence that the location of wire breakage is influential to the maximum stress of the wire rope. In addition, it seems that the breakage of a strand core wire could have a more dramatic influence on the maximum stress of the rope than if it was another wire in the strand.

However, the wires in the outer layer of a strand are more susceptible to damage, such as striking, scraping, rusting, etc., by interacting with other components or the environment. Thus, the influence of the number and position of the broken wires in the outer layer of a strand on the wire rope’s performance is thoroughly studied.

Figure 16e,f demonstrates the stress distribution when two wires of a strand are broken. The maximum stresses shown in Figure 18 are σ^e_max = 673.79 MPa and σ^f_max = 686.33 MPa, the corresponding increases in the maximum stress are 2.40% and 4.30%, while the decrease in the cross-section area is 1.57%.

Figure 16g,h demonstrates the stress distribution when three wires of a strand are broken. The maximum stresses shown in Figure 19 are σ^g_max = 680.40 MPa and σ^h_max = 722.20 MPa, the corresponding increases in maximum stress are 3.40% and 9.75%, while the decrease in the cross-section area is 2.35%.

Figure 16i,j demonstrates the stress distribution when five wires of a strand are broken. The maximum stresses shown in Figure 20 are σⁱ_max = 695.98 MPa and σ^j_max = 760.30 MPa, the corresponding increases in the maximum stress are 5.77% and 15.54%, while the decrease in the cross-section area is 3.92%.

Figure 16k,l demonstrates the stress distribution when nine wires of a strand are broken. The maximum stresses shown in Figure 21 are σ^k_max = 771.56 MPa and σ^l_max = 796.71 MPa, the corresponding increases in maximum stress are 17.26% and 21.08%, while the decrease in the cross-section area is 7.06%. The simulation results are also listed in Table 9.

In Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21, the maximum stress seems to always appear adjacent to the strand with a broken wire. In addition, there is a strong correlation between the decrease in the cross-section area of the wire rope (due to wire breakage) and the increase in the maximum stress of the wire rope. If the cross-section area of the wire rope decreases, there will be a remarkable increase in the maximum stress of the wire rope. For example, in case (j), a decrease in the cross-section area of 3.92% leads to an increase in the maximum stress of 15.54%. This indicates that wire breakage has a critical influence on the maximum stress of the wire rope in operation. Moreover, the breakage of the wire away from the core in the outer layer of the strand has a greater effect on the maximum stress of the wire rope than the breakage of the wire near the core.

Figure 22 displays the maximum stress and cross-section area of the wire rope along different wire-breaking conditions.

Figure 23 shows the stress distribution in the middle cross-section of the wire rope under 12 scenarios and the details are listed in Table 9. In the middle of the wire rope, the maximum stress is located at either the core or the inner wire of the strand, and the maximum stress in the middle of the wire rope is about half of that at the end of the wire rope. As the number of broken wires increases, the maximum stress of the middle cross-section also increases, and it most likely appears adjacent to the strand with the broken wire. It seems that the bearing capacity of the strand with broken wires gradually decreases, and it is shown in Figure 23 that the stress of the remaining wires in the strand with broken wires is less than that of the wires in the same position in the intact strands. Figure 23i,j demonstrates that the bearing capacity of the wire rope will greatly decrease when the number of broken wires in a strand reaches five and the stress distribution of the wire rope is no longer symmetrical, which means that the excellent bearing capacity is damaged.

6. Conclusions

This paper proposed an accurate and efficient framework for analyzing the mechanical characteristics of a wire rope with a complex structure, and also provided a practical method to quantitatively evaluate the performance of a complex wire rope with wire breakage. First, an accurate 3D geometry modeling method for a wire rope with a complex structure has been proposed. Second, the material properties of the wire constituting the rope have been tested to facilitate the building of the finite element model of the wire rope. Third, the most feasible element type in the finite element analysis of a wire rope with a complex structure has been investigated. Then, the finite element model of the wire rope with a complex structure is built, and the mechanical characteristics of a 6 × K31WS + FC wire rope are figured out, with its effectiveness having been validated by theoretical analysis. Finally, a quantitative relation of the number and location of broken wires with the mechanical characteristics of the wire rope is thoroughly analyzed. The approach proposed in this work can facilitate the optimization of the structure of the wire rope, such as lay angle, lay direction, wire radius, etc., and it also can provide valuable data for reliability and maintenance evaluation of the wire rope in practical operation. The main conclusions of this work are as follows:

(1) C3D8R is an appropriate element type, and it is advisable for it to be adopted in finite element analysis of wire ropes with complex structures in terms of computational accuracy, efficiency, and convergence.

(2) The maximum stress cross-section appears at both ends of a 6 × K31WS + FC wire rope regardless of whether there is a broken wire. Thus, we should carefully check the region at both ends of the wire rope when examining the wire rope condition.

(3) The number and location of the broken wires have a great influence on the maximum stress of the wire rope. A small cross-section area decrease could induce a dramatic increase in the maximum stress. Thus, the wire rope must be carefully examined and analyzed before it can be continued to be used when there is wire breakage.

(4) Stress distribution in the middle cross-section of the wire rope reveals that the stress of the remaining wires in the strand with broken wires is less than that of the wires in the same position in the intact strands. This phenomenon indicates the bearing capacity of the strand has been weakened, especially when the number of broken wires increases.