Experimental and Theoretical Study on Operation Characteristics of an Oscillating Heat Pipe

Abstract

An oscillating heat pipe (OHP) is an effective heat transfer device for the thermal management of electronic devices. However, the heat transfer mechanism of the OHP was not fully understood due to its complicated operation characteristics. In this paper, the thermal performance of an OHP was experimentally studied. The condensation and evaporation temperature variations were monitored under different heat inputs and were then used to evaluate the OHP system operating characteristics. Thermal resistance was used as a key parameter to evaluate the thermal performance of the OHP system. The results indicated that as the heat input increased from 25 to 100 W, the average thermal resistance decreased while the stable evaporating and condensing temperatures increased. The equivalent heat transfer coefficient was derived theoretically. It showed that the reciprocal of the radial heat transfer coefficient increased with increasing liquid film thickness. Based on this result, an empirical correlation was proposed to evaluate the thermal resistance of an OHP system. This correlation was validated using both the experimental data provided in this study and the data collected from the open literature. The comparison results indicated that the proposed empirical correlation could reasonably predict the thermal resistance under different filling ratios and heat inputs.

1. Introduction

As a passive heat transmission device, the heat pipe can effectively transfer heat using both thermal conduction and phase transition. It was widely used in electronic cooling to take advantage of simple structures, flexible operations, and good applicability. The oscillating heat pipe has better performance and flexibility in comparison to the traditional heat pipe. It was introduced by Akachi [1] in the 1990s. The OHP is a capillary tube that is fabricated with several turns and partially filled with a working fluid. It has three sections. Heat is received in the evaporation section; then, the working fluid is vaporized to produce a driving force. The vapor plug is separated by liquid slugs, and the oscillating motion is generated in the OHP channel. At the same time, the heat can be removed from the wall in the condensation section.

The OHP has distinguished features that the plug/slug flow can significantly improve the convection and phase change heat transfer. It can be designed without a wick structure and is independent of gravity [2].

Operation characteristics on OHPs are still in an exploratory stage. The visualization technique was widely used by researchers to investigate the flow regime. Khandekar et al. [3] investigated the operating mechanism and heat transfer characteristics and found that slug flow gradually shifted to annular flow as the heating load increased. The transformation of the two-phase flow is a critical factor contributing to the operation characteristics and heat transfer mechanism in the OHP. The same research group [4] further studied the parametric effect of a visualized OHP with an inner tube diameter of 2 mm. They considered that the gravity effect is still an important factor influencing the distributions of the working fluid in the OHPs. Ghiaasiaan [5] conducted a visualization experiment to study the dominant flow regime during the start-up and stable operation of an OHP. Xu et al. [6] observed the bubbly flow, slug/plug flow, and churn flow in the process from the start-up to the steady operation.

Some other researchers investigated the effect of geometric structure and operating conditions on the thermal performance of OHPs. Li et al. [7] studied the operation characteristics of three types of OHPs under different working conditions. They found that the thermal performance can be enhanced by varying channel diameter and adopting a three-dimensional configuration. Xu et al. [8] investigated the cooling ability of two aluminum flat-plate OHPs with different working fluids. The effect of heat flux, operating angle, length of the cooling section, heating area, cooling strategy, and working fluid were comprehensively studied. The results indicated that the OHP using HFC-134a exhibited better cooling ability. Smoot et al. [9] experimentally investigated the role of heat conduction in the thermal performance of an OHP system. Thompson et al. [10] used neutron radiography to capture the internal flow behavior in a flat-plate OHP incorporated with a Tesla-type check valve. The results indicated that the thermal resistance was reduced in the order of 15 to 25%, depending on the power input. They also found that the effective thermal conductivity is independent of gravity [11]. Cui et al. [12] studied the operation characteristics and heat transfer mechanism of an OHP. The results indicated that the limit of thermal performance was strongly affected by the geometric structure, material, and operating angle. Rahman et al. [13] investigated the effect of fins on the performance of a closed-loop OHP. Kearney et al. [14] studied the cooling ability of a PCB-embedded OHP for power electronic applications. Qu et al. [15] investigated the effect of multi-heat source cooling and high heating flux cooling on the thermal performance of a three-dimensional OHP with different working conditions. The results demonstrated that the start-up, oscillation, and dry-out of OHP were significantly affected by the cooling air velocity and operating orientation. Dang et al. [16] studied the thermal design of an OHP-based rack to achieve better cooling performance. Tokuda et al. [17] studied the heat transport characteristics of an OHP charged with sodium for high-temperature conditions. They found that the temperature increase in the evaporation section and temperature decrease in the condensation section can improve the heat transport rate. Ando et al. [18] experimentally studied the thermal performance of OHPs with an optimal check valve arrangement. They found that start-up reliability and steady-state thermal performance can be achieved with a check valve arrangement. Iwata et al. [19] studied the thermal performance of a metallic micro-oscillating heat pipe. They conducted dynamic stiffness tests to verify the flexibility of a micro-OHP. Wang et al. [20] studied the tubular oscillating heat pipe (OHP) with sintered copper particles (SCPs) inside a flat-plate evaporator. They proposed the best relationship between the filling ratio, temperature, and the illumination intensity of LEDs.

From the above literature review, the OHP has been widely studied for different working fluids and with different design structures. However, there is still a lack of deep theoretical analysis that could guide OHP design and application. In this paper, an OHP was investigated under different cooling conditions. An experimental setup was developed for this purpose. The temperature variations were monitored, and the thermal resistance in the OHP was evaluated under different heating inputs. A mathematical model was proposed, which used an equivalent heat transfer coefficient to study the heat transfer in the OHP. By combining the experimental and theoretical analysis, an empirical correlation was developed to estimate the thermal resistance based on the equivalent heat transfer coefficient curve. It was validated using data from the open literature. This study provides useful information for engineers and researchers in the design and optimization of the OHP.

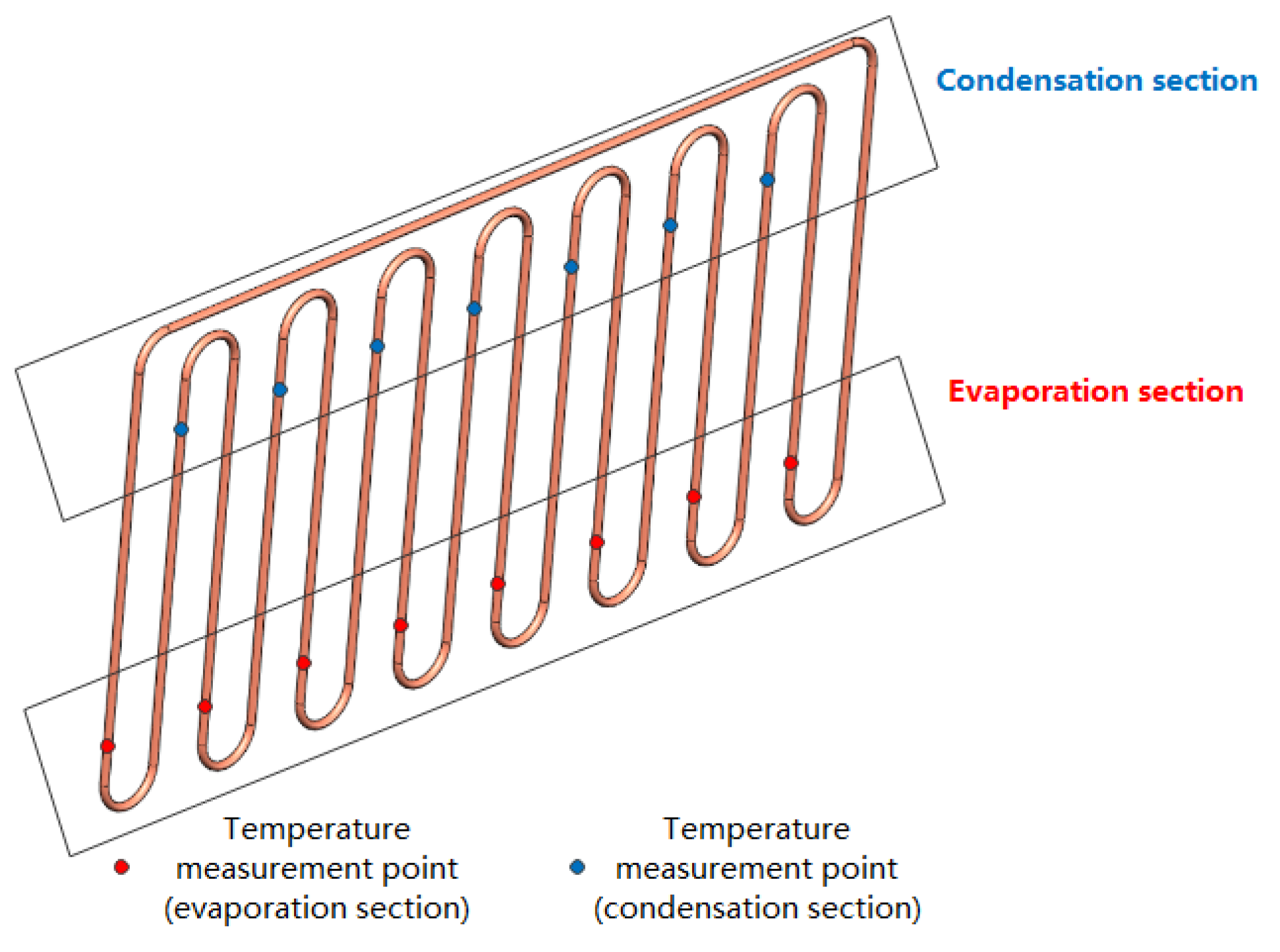
2. Experimental Setup

2.1. OHP Test System

Figure 1 shows a schematic geometry of an OHP system and measurement points in the test. The condensation section is 40 mm, and the evaporation section is 60 mm.

The width (L) and height (H) of the OHP is 450 mm and 180 mm, respectively. The pipe diameter can be determined using the Bond number:

$$\mathrm{Bo}=\frac{r^{2}g\left({\rho }_l-{\rho }_v\right)}{\sigma }$$

(1)

where Bo is the Bond number, r is the hydraulic radius of an OHP, ${\rho }_l$ is the liquid density, ${\rho }_v$ is the vapor density, $\sigma$ is the surface tension, and $g$ is the gravitational acceleration. As reported by Taft et al. [21], a value of 0.85 could be used to determine the maximum hydraulic radius for the OHP. Then, the maximum radius in an OHP system is expressed as follows:

$$r_{h,\max }\le 0.92\sqrt{\frac{\sigma }{g\left({\rho }_l-{\rho }_v\right)}}$$

(2)

Based on Equation (2), the inner diameter of 3 mm is chosen for the studied OHP system. Copper tubes with inner diameter of 3 mm and outer diameter of 5 mm are bent in a U-shape, as shown in Figure 1. Deionized water is used as the working fluid, and the filling ratio is 62%.

$$FR=\frac{V_l}{V_{HP}}$$

(3)

where FR is the filling ratio of the OHP, %; V_l is the liquid volume, m³; V_HP is the liquid volume, m³.

The OHP tester includes a thermal isolation box, heating elements, and a cooler. The box has an insulation layer filled with glass wool. Three resistance heating wires, each having resistance of 840 Ω, are wrapped in the evaporation section. The heating power is controlled between 25 and 100 W by adjusting the voltage transformer. The condensation section of the OHP is cooled by the water cooler. The water cooler is connected to the thermostatic bath, which can provide the chilled water with a specified temperature of 15 ± 0.05 °C. The water temperatures at the inlet and outlet are measured using thermometers and recorded via the data acquisition system. The test unit is shown in Figure 2.

2.2. Experimental Data Reduction

The experiment is conducted under heating input between 25 and 100 W. The thermal resistance is defined by Equations (4)–(6) as follows:

$$R=\frac{\left({\overline{T}}_e-{\overline{T}}_c\right)}{Q}$$

(4)

where R is the thermal resistance of the OHP, °C/W; Q is the electric heating capacity, W; $\overline{T_e}$ and $\overline{T_c}$ are the mean temperatures of the evaporation and condensation sections, °C, and can be obtained as follows:

$${\overline{T}}_e=\frac{1}{8}{\displaystyle {\sum }_{i=1}^8{T}_{ei}}$$

(5)

$${\overline{T}}_c=\frac{1}{7}{\displaystyle {\sum }_{i=9}^{15}{T}_{ci}}$$

(6)

where i is the number of the points measured using the K-type thermocouples (with an accuracy of $\pm 0.75\mathrm{\%}$ of the reading). The temperature measuring points are shown in Figure 1.

2.3. Uncertainty Analysis

The standard uncertainty is an important index to estimate the measurement quality [22], which can be expressed by the following:

$$\frac{u(R)}{R}=\sqrt{{\left(\frac{u({\overline{T}}_e)}{\Delta T}\right)}^2+{\left(\frac{u({\overline{T}}_c)}{\Delta T}\right)}^2+{\left(\frac{u(Q)}{Q}\right)}^2}$$

(7)

The voltage transformer is employed to adjust the output voltage (with an accuracy of $\pm 0.5\mathrm{V}$). An Agilent 34,972 A data acquisition unit and 34,901 modules are utilized to record the data. The output power is calculated from the formula $Q=U^2/R_e$. R_e is the electric resistance, which is divided into three parts. Each part is measured using a UNI-T 201 multi-meter (with an accuracy of ±1% of reading). For a heating power of 25 W, the measured value of voltage and resistance are 83.67 V and 840 Ω, respectively. Then, the uncertainties for the heating power and thermal resistance are expressed as follows:

$$\frac{u(Q)}{Q}=\sqrt{{\left(\frac{2u(U)}{U}\right)}^2+{\left(\frac{u(R_e)}{R_e}\right)}^2}=1.55\%$$

(8)

$$\frac{u(R)}{R}=\sqrt{{\left(\frac{u({\overline{T}}_e)}{\Delta T}\right)}^2+{\left(\frac{u({\overline{T}}_c)}{\Delta T}\right)}^2+{\left(\frac{u(Q)}{Q}\right)}^2}=2.55\%$$

(9)

The expanded uncertainty is obtained by the following equation:

$$u_{\max }=K\times u_c=5.04\%$$

(10)

The expanded uncertainty is based on a standard uncertainty multiplied by a coverage factor $K=2$, providing a level of confidence of approximately 95%.

3. Mathematical Analysis

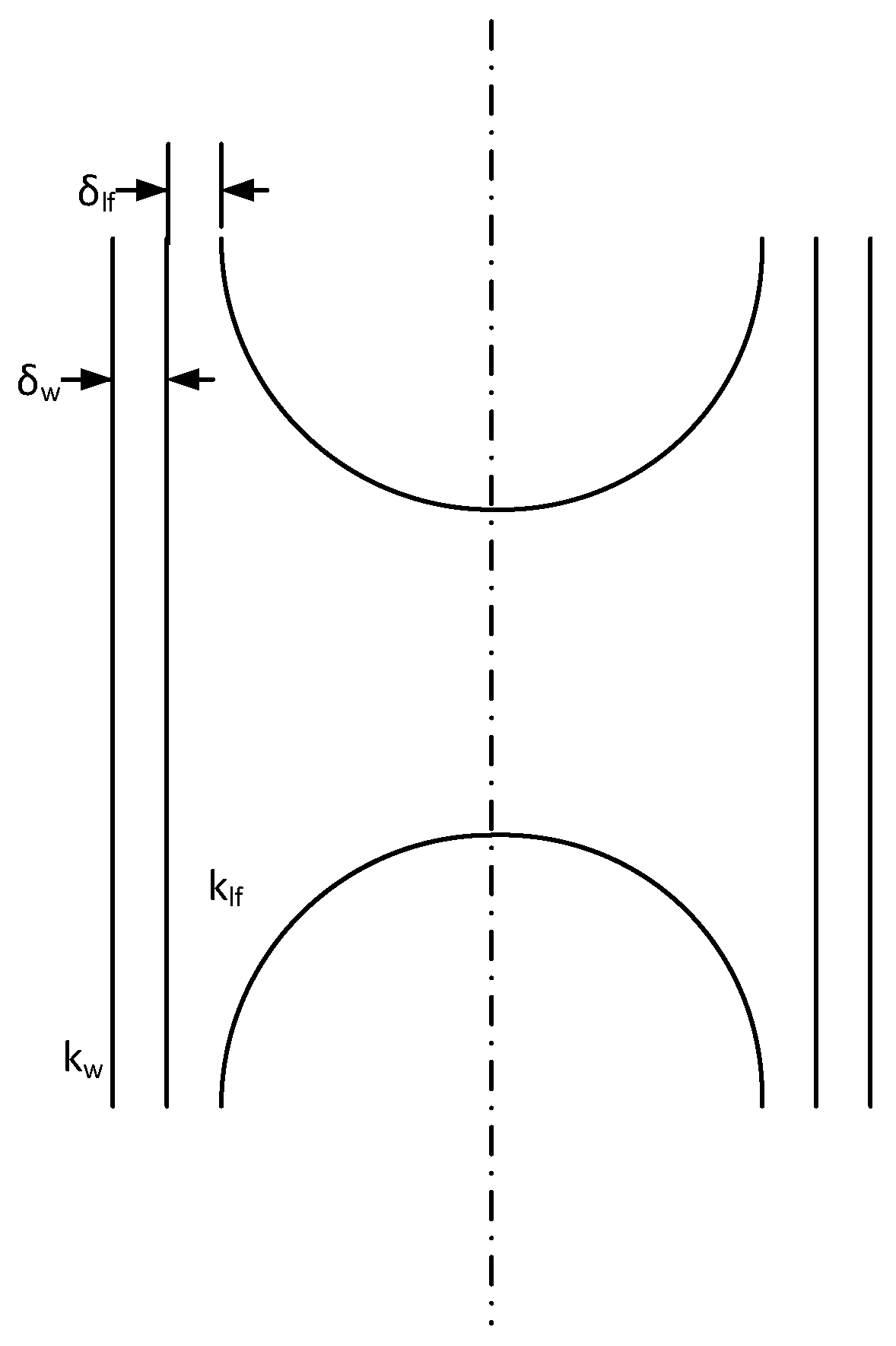
3.1. Equivalent Thermal Conductivity

To better understand the thermal performance of the OHP, the equivalent thermal conductivity is deduced theoretically. The OHP is simplified as a unit consisting of one liquid plug and two halves of the vapor bubbles. The OHP is assumed to be two-dimensional. Figure 3 shows the simplified model.

When the heat flux direction is parallel to the axial direction, the thermal resistance can be described as a parallel thermal resistance circuit. The temperature gradient across the OHP is the same, while the heat fluxes are different. The effect of the liquid film region on the axial heat conduction is ignored due to its small magnitude. Therefore, the axial thermal conductivity is determined by the following:

$$k_a=\frac{d_i^2}{d_o^2}{k}_l+\left(1-\frac{d_i^2}{d_o^2}\right)k_w$$

(11)

where $k_a$ is the axial thermal conductivity, W/(m·K); $d_i$ is the inner diameter, m; $d_o$ is the outer diameter, m; $k_l$ is the thermal conductivity of the liquid, W/(m·K); and $k_w$ is the thermal conductivity of the copper, W/(m·K).

When the heat flux direction is perpendicular to the axial direction, the thermal resistance can be described as a series thermal resistance circuit. The heat flux passed through the wall and the liquid film. Assuming that the wall and the liquid film have the same flow area, the heat fluxes are equal. The radial thermal conductivity is determined as follows:

$$\frac{1}{k_r}=\frac{{\delta }_w}{k_w\left({\delta }_w+{\delta }_{lf}(x)\right)}+\frac{{\delta }_{lf}}{k_{lf}\left({\delta }_w+{\delta }_{lf}(x)\right)}$$

(12)

where $k_r$ is the radial thermal conductivity, W/(m·K); and ${\delta }_{lf}$ is the liquid film thickness, m.

According to the literature [23,24], the magnitude of the liquid film is around ${10}^{-8}~{10}^{-6},{\delta }_w\gg {\delta }_{lf}$. It is assumed that the influence of the absorbed region is negligible, Equation (12) can be expressed as follows:

$$\frac{1}{k_r}=\frac{1}{k_w}+\frac{{\delta }_{lf}}{k_{lf}{\delta }_w}$$

(13)

Substituting the thermal conductivity of the copper and liquid film into Equation (13), the value of characteristic thermal conductivity can be calculated. When the thickness of the liquid film becomes smaller, heat is transferred more effectively through the liquid film.

For copper and water, the thermal conductivity can be calculated using a correlation that is a function of temperature [25]. It is given by the following:

$$k=A+B\cdot \mathrm{T}+C\cdot T^2$$

(14)

For inorganic compounds, the correlation is expressed as follows:

$$\log k=A+B{\left(1-\frac{T}{C}\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$7$}\right.}$$

(15)

where A, B, and C are the regression coefficients for a chemical compound, and T is in Kelvin temperature scale. In this study, the mean temperature (70 °C) of the evaporation section after heating for twenty minutes is chosen as the reference temperature.

3.2. Extended Thermal Resistance

As mentioned in the literature, the thermal performance of OHPs has been experimentally studied for different structures, working fluids, and other operating conditions. However, no formulation was proposed to evaluate the thermal performance of OHPs theoretically, which limits the wide application of findings in the literature. It is well known that the liquid film heat conduction and phase transition are the major factors influencing thermal resistance. In this paper, an empirical correlation is proposed to describe the relationship between thermal resistance and heat input based on experimental and mathematical results.

According to the literature [5,6,24], the thermal resistance of the OHP mainly depends on the radial thermal conductivity. The other influencing factors could be corrected using a correlation coefficient. Using this assumption, the relationship between the heat input and liquid film thickness is almost linear, and, hence, the thermal resistance can be determined as follows:

$$R=\epsilon \cdot \frac{1}{k_r}+\theta \cdot \frac{1}{k_a}$$

(16)

$$Q=\frac{1}{\phi {\delta }_{lf}}$$

(17)

where the two terms in the right hand of Equation (16) are the radial heat conduction term and the axial heat conduction term, respectively. $E$ and $\theta$ are the regression coefficients for thermal resistance, which are measures of the importance of radial and axial heat conductions relative to the thermal resistance. These two coefficients are influenced by the geometric parameters such as thickness and area as well as the OHP characteristics such as filling ratio and working fluid. $\phi$ is the regression coefficient for heat inputs. It reflects the relationship between heat input and liquid film thickness. The correlation function of $\phi$ leads the value of $1/\left(\phi \cdot Q\right)$ to approach the magnitude of ${\delta }_{lf}$. To simplify the calculation, Equation (13) can be substituted into Equation (16).

$$R=\epsilon \left[\frac{1}{k_w}+\frac{{\delta }_{lf}}{k_{lf}{\delta }_w}\right]+\theta \cdot \frac{1}{k_a}$$

(18)

Substituting Equation (17) in Equation (18), the equivalent thermal resistance formula relative to the heat input can be expressed as follows:

$$R=\frac{\epsilon }{\phi }\cdot \frac{1}{k_{lf}{\delta }_w}\cdot \frac{1}{Q}+\left(\theta \cdot \frac{1}{k_a}+\epsilon \cdot \frac{1}{k_w}\right)$$

(19)

According to Equation (19), the linear correlation is expressed. The slope is described by the liquid film term. The intercept is described as a function of the axial thermal conductivity term and the wall thermal conductivity term. Then, Equation (18) can be expressed as follows:

$$R=\frac{\epsilon }{\phi }\cdot \frac{1}{k_{lf}{\delta }_w}\cdot \frac{1}{Q}+C(k_w,k_a)$$

(20)

where $C(k_w,k_a)$ is a constant associated with the thermal conductivities k_w and k_a for a given condition. The value of $\epsilon /\phi$ and $C(k_w,k_a)$ can be determined by the experimental data. The validation of this correlation will be discussed in the following section.

4. Results and Discussion

The performance of the proposed OHP was comprehensively studied under heating inputs between 25 and 100 W. The temperatures were monitored and recorded. The thermal resistance of the OHP was calculated to evaluate the characteristics of the OHP.

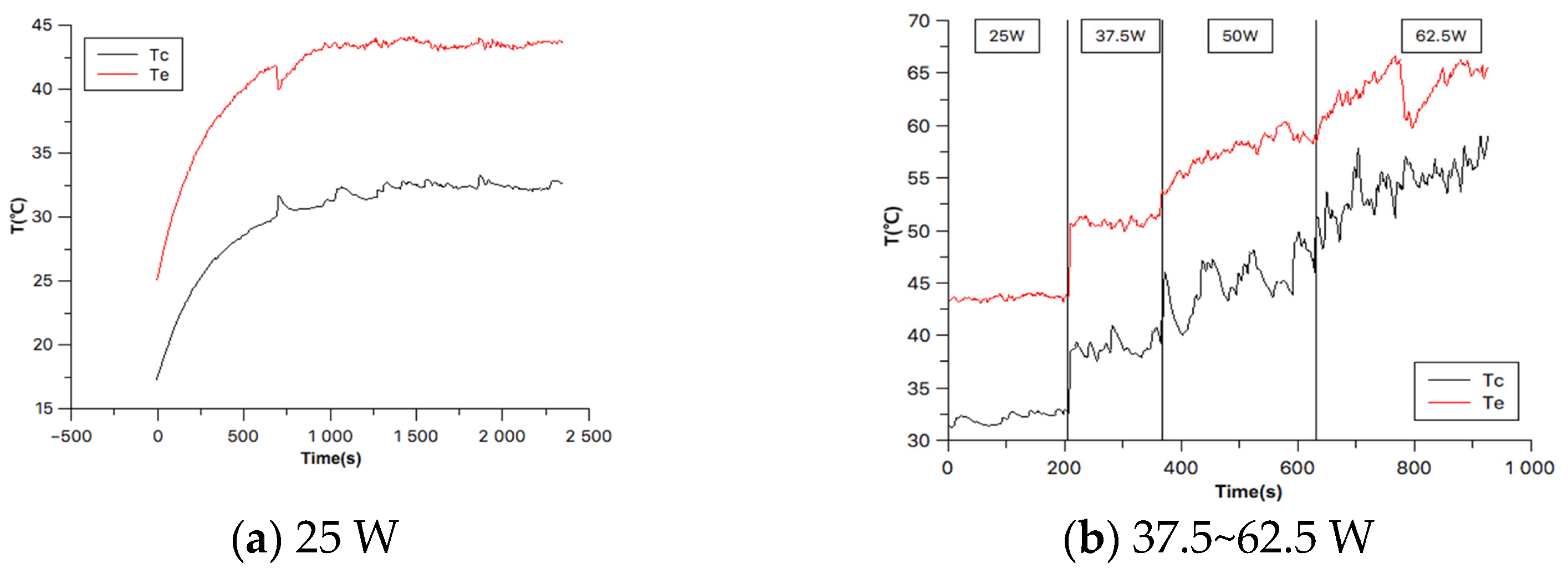
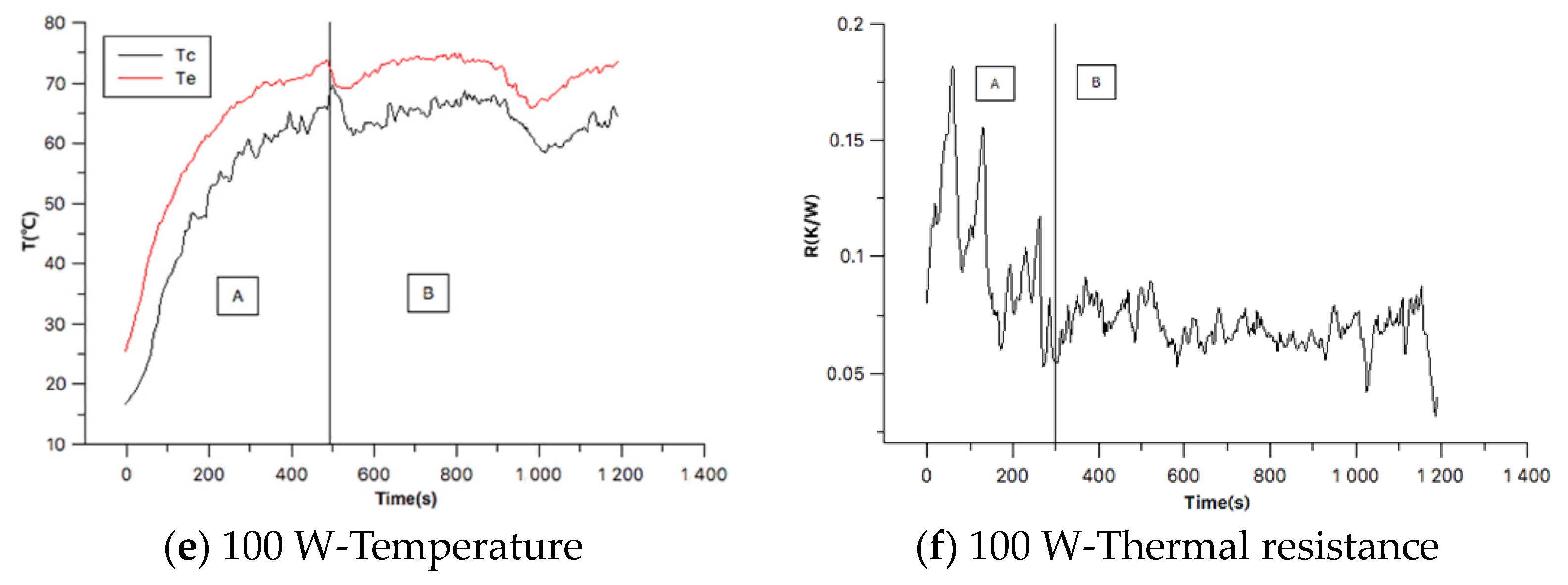
4.1. Temperature Variation

Figure 4a shows the temperature oscillations of the OHP under a heating power of 25 W. Two periods can be defined: the initial start-up period and the stable oscillating period. The temperature oscillation differs in different periods. During the first period, no oscillation was observed. The temperatures increased significantly on both sides of the OHP. During the stable oscillating period, the amplitude of the temperature oscillation was small, and the frequency is high.

As the heating power increased from 25 to 62.5 W, the temperature oscillation presented a large fluctuation associated with the occasional large amplitude and low frequency at the high heating input, as shown in Figure 4b. This might occur due to the boiling phenomena. At the low heating input, the temperature of the heat pipe surface is slightly higher than the working fluid temperature, which forms nucleate boiling. The heat flux is small, so the amplitude of the temperature variation is small. As the heating input increases, boiling enters the transition boiling phase driven by a large temperature difference. It is an unstable boiling, which led to large amplitude and low frequency of the temperature oscillation. As the heating input increased up to 75 and 100 W, the heating input increases, and the boiling enters the film boiling. During this period, a thin layer of vapor that has low thermal conductivity insulates the surface. The temperature oscillation is moderate with small amplitude and high frequency, as shown in Figure 5a,c,e.

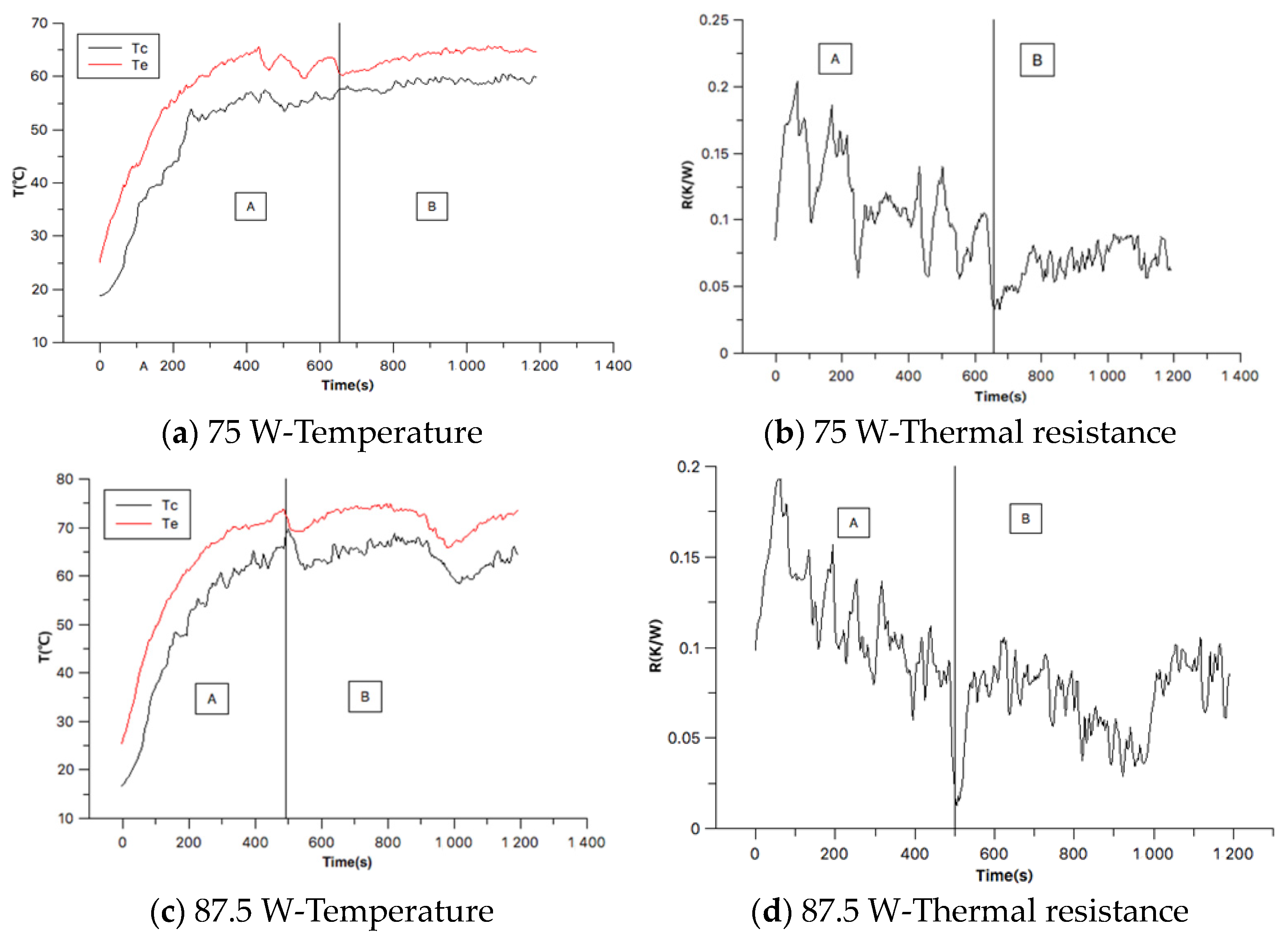
4.2. Thermal Resistance Analysis

Figure 5 shows the temperature variation in the evaporation and condenser sections and the thermal resistance of the OHP under different heat inputs. The thermal resistance clearly indicates two different periods as highlighted by A and B, which are associated with the heating periods in the OHP. In the first period, the thermal resistance presented a large amplitude and low frequency as the heat is added into the evaporation section of the OHP. This showed that the OHP is in an unstable situation. As the heat was added to the evaporation section, the whole evaporator wall was heated up, and the working fluid received thermal energy via radial conduction. The fluid vaporized to produce the vapor volume expansion. The heat was transferred to the condenser section via axial conduction. In the condenser section, the heat was removed via radial conduction, and the vapor was condensed leading to the vapor volume contraction in the condenser section. The expansion and contraction of the vapor volume generated the large amplitude and low-frequency thermal resistance oscillation in the OHP. The vapor volume variation acted as a spring in the system, generating oscillating motion accompanied by heat and mass transfer. As the heat was continuously added to the evaporation section wall, the temperatures in both the evaporator and condenser sections were becoming stable. Then, the heat transfer rates from the wall to the liquid in the evaporation section and from the liquid to the wall in the condenser section were becoming stable. This stable heat transfer rate lowered the oscillation of the thermal resistance. Then, the system entered a stable period during which the oscillation of the thermal resistance exhibited a moderate amplitude and high frequency. The average thermal resistance had stabilized.

Figure 6 shows the thermal resistance of OHP under different heating powers. Data were collected after the system was running for at least twenty minutes to ensure the system was stable. The thermal resistance was found to decrease almost linearly as the heating input increased from 25 to 75 W. However, as the heating input increased from 75 to 100 W, the thermal resistance did not show a significant change. This indicated that the proposed OHP system provided the highest heat transmission efficiency and entered the optimum operation condition when the heating input is 75 W. A further increase in heating power will not substantially enhance the heat transfer. This finding is consistent with those presented in the literature [15].

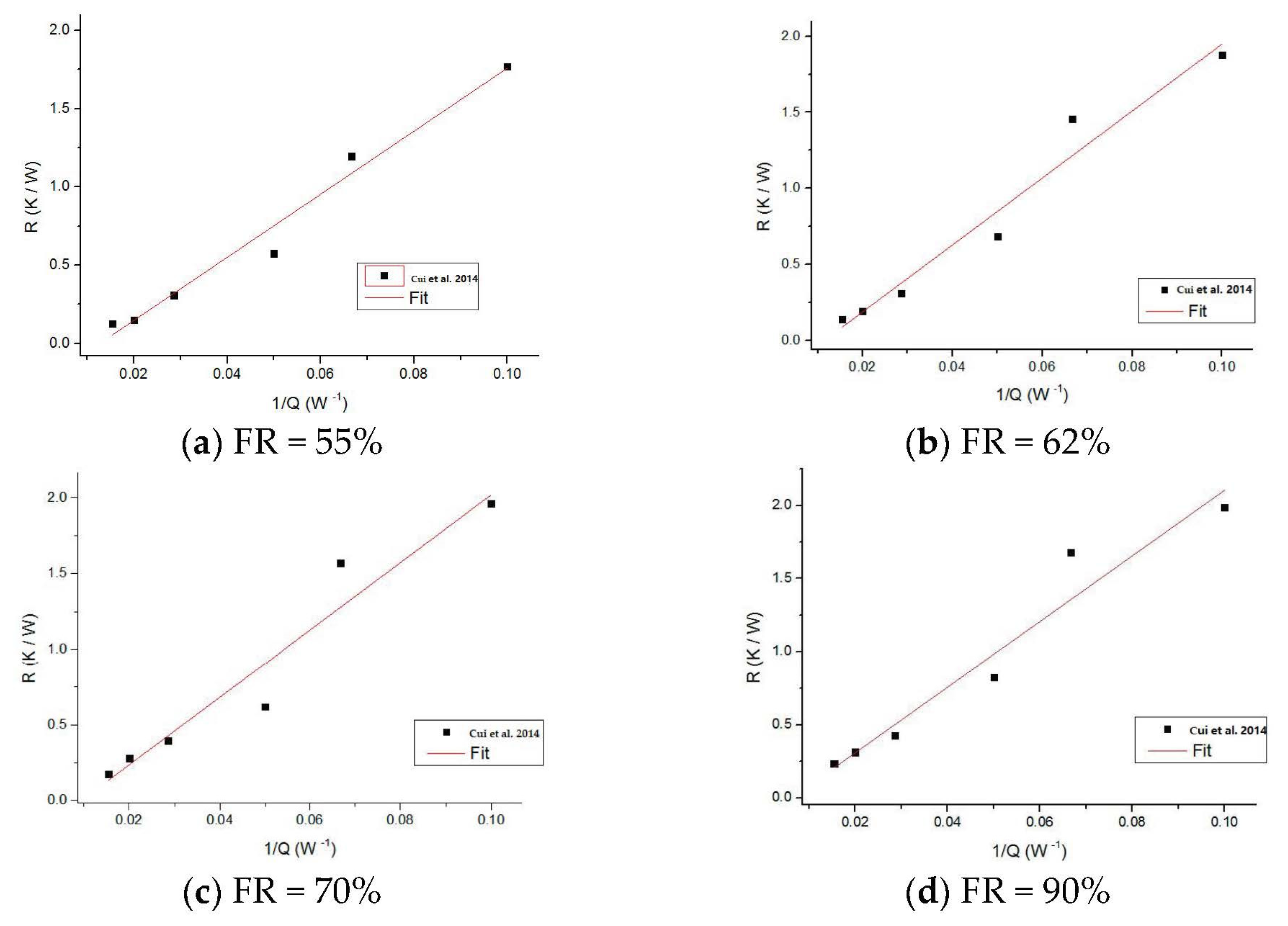
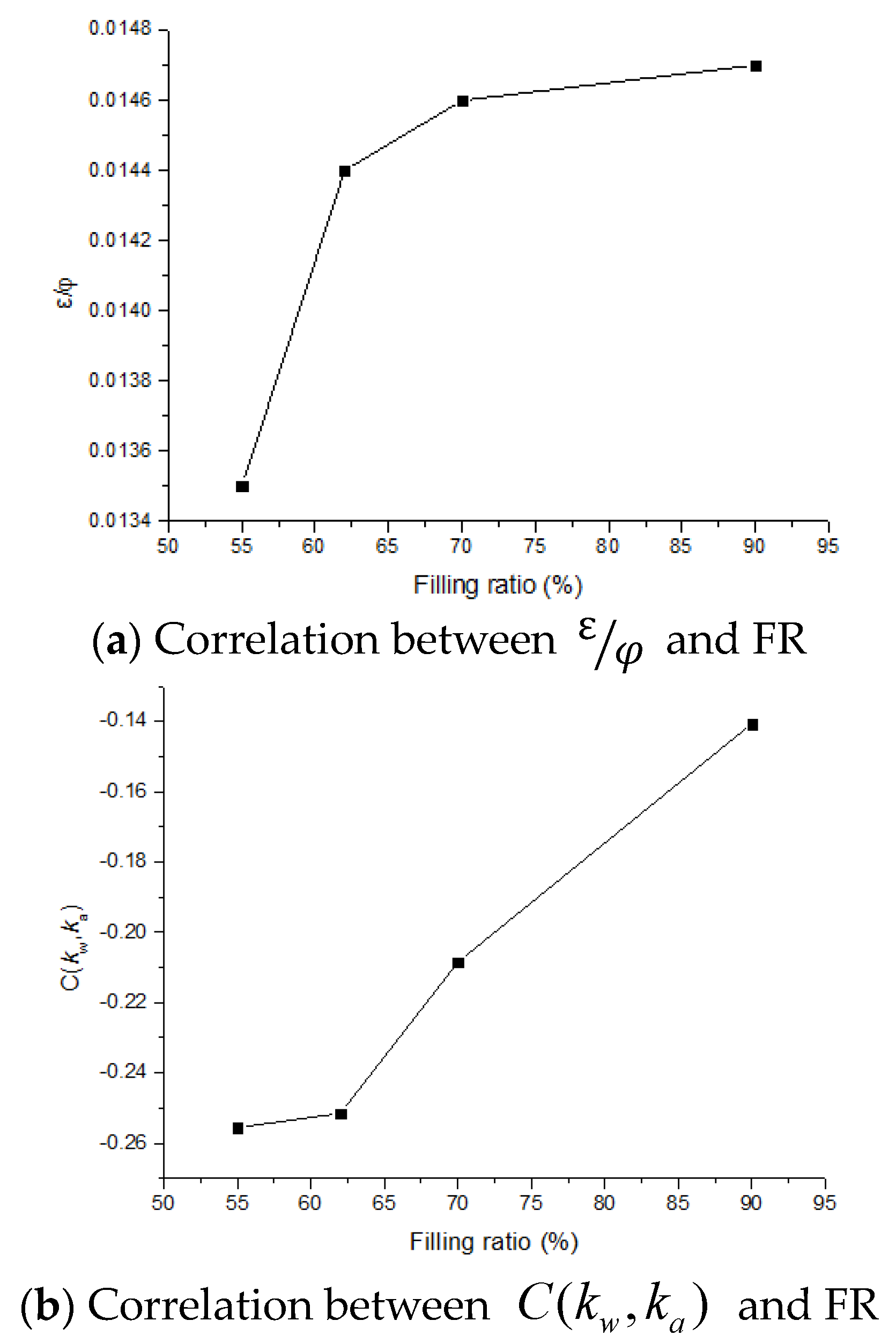
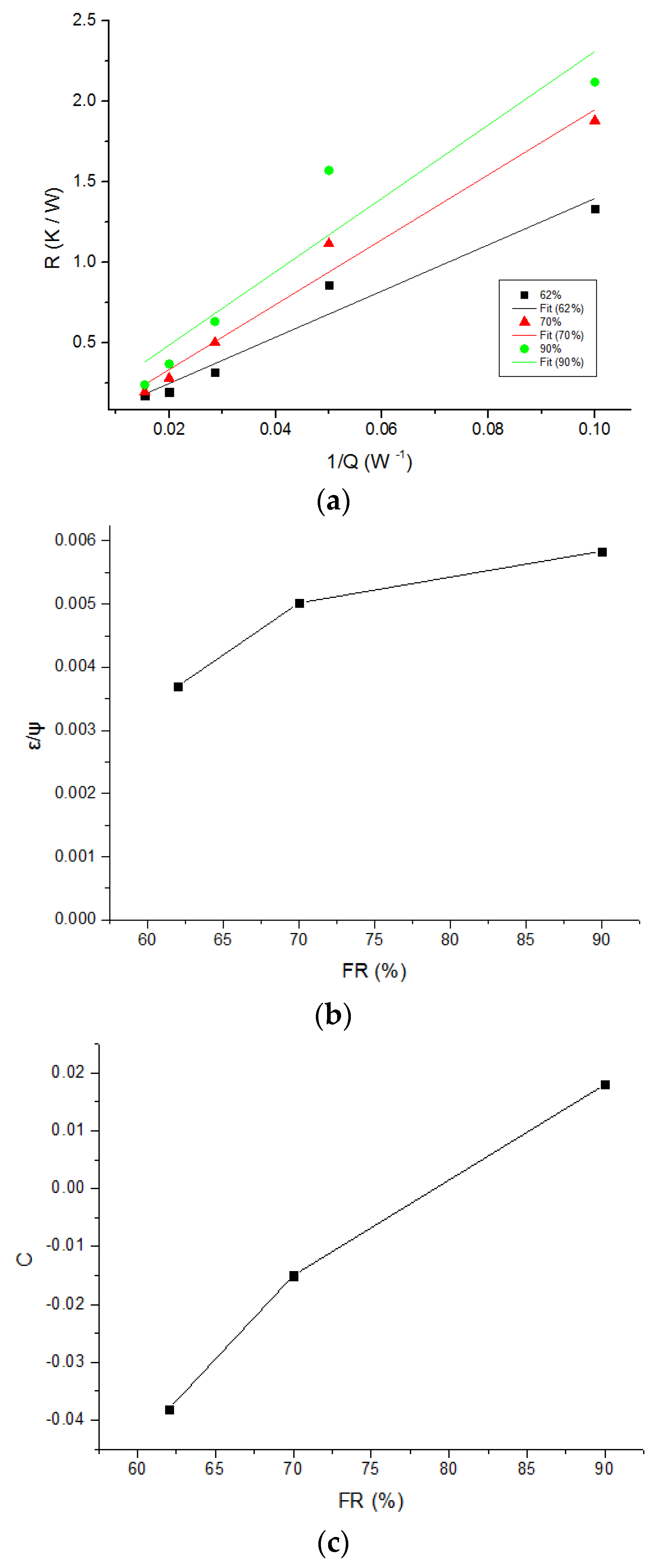
4.3. Thermal Resistance Correlation

Figure 7 shows the modified thermal resistance curve. The modified conductivity curve is calculated by substituting Equation (14) into Equation (12). The thermal resistance curve is modified from the experimental data in Figure 6 by changing the heating input to the reciprocal of the heating input. It is observed that these two curves have a similar trend. It proves that the temperature variation influences the growth of the bubbles and the meniscus radium. This is consistent with that reported in the literature [5,6,26]. It proves that the assumption made for Equation (16), that the thermal resistance of the OHP mainly depends on the radial thermal conductivity and the other influencing factors, could be corrected by a correlation coefficient.

Figure 8 shows the linear curve fitting using Equation (20), which is derived from Equation (16). The two constants $\raisebox{1ex}{$\mathsf{\epsilon }$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.$ and $C(k_w,k_a)$ are $8.55\times {10}^{-3}$ and −0.05, respectively. Using the Root Mean Square (RMS) method in statistical analysis, the standard deviation for the difference in the thermal resistance between the curve fitting and the experimental data was 0.026. It is found that the proposed linear correlation could be used to reasonably predict thermal resistance. The error was mainly due to (i) thermal conductivity was based on the two-dimensional hypothesis; (ii) thermal conductivity of copper and liquid was calculated from the average temperature, which could be improved using the varying temperature; and (iii) the relationship between heating input and the liquid film thickness was assumed to be linear, which could be improved using the real relationship obtained from visualization experimental study. Furthermore, as the heating power increases, local and periodical dry-out may occur, which may cause a sharp increase in temperature in the evaporator section and, hence, cause the heat transfer performance to deteriorate. Therefore, in this analysis, the heat input was limited to 100 W.

Figure 9 shows the linear curve fitted with the experimental data reported in the literature [12]. It demonstrated that the proposed linear relation could be used to describe the performance characteristics of the OHP system under different filling ratios. As depicted in Figure 10, the two constants, $\epsilon /\phi$ and $C(k_w,k_a)$, varied with different filling ratios. This is consistent with that reported in the literature [12]. The filling ratio has a large effect on the OHP performance. As a result, the thermal resistance depends on the heating input and filling ratio.

Figure 11 demonstrated the application of the theory in the OHP system using Methanol as a working fluid. Once again, the results show that the proposed linear correlation could be used to present the relationship between the thermal resistance and heating input for this methanol OHP system. Compared to the water OHP system presented in Figure 9, the two constants $\epsilon /\phi$ and $C(k_w,k_a)$ were very different. Furthermore, the proposed linear correlation was also verified in OHP systems using Ethanol and Acetone as working fluids reported in the literature [12]. It was found that the linear correlation was also applicable to these working fluids. However, the two constant values change significantly for different working fluids as shown in

Table 1. Regression coefficients of the OHP using different working fluids at a filling ratio of 62% based on Ref. [12].

	Deionized Water	Methanol	Ethanol	Acetone
$\raisebox{1ex}{$\mathsf{\epsilon }$}\!\left/ \!\raisebox{-1ex}{$\phi $}\right.$	$14.4\times {10}^{-3}$	$3.7\times {10}^{-3}$	$4.52\times {10}^{-3}$	$2.89\times {10}^{-3}$
$C(k_w,k_a)$	−0.25154	−0.0381	−0.4767	−0.041

. This could be explained by the equivalent thermal conductivity. Different working fluids have different thermal conductivity, which leads to a large change in the thermal conductivity in the liquid film and, hence, causes thermal resistance variation.

5. Conclusions

This study focused on the thermal performance of an OHP system under server cooling conditions. The temperature variations were recorded to monitor the operating characteristics of the studied OHP. The thermal resistance was used to evaluate the OHP performance. A linear empirical correlation was derived to predict the OHP performance under different heating inputs by introducing a concept of equivalent thermal conductivity. The following specific conclusions were drawn:

(1)

The initial start-up period and stable oscillating period can be clarified during the operation of an OHP. As the heating power increased from 25 to 62.5 W, the trends of the temperature oscillation were similar. However, the temperature oscillation presented a large fluctuation associated with the occasional large amplitude and low frequency at the high heating input.

(2)

Thermal resistance showed an oscillation with a large amplitude and lower frequency during the start-up period. During the stable operation period, the oscillation exhibited small amplitude and high frequency. As the heating power increases, the thermal resistance decreases simultaneously. It showed an optimal thermal performance at a heating input of 75 W for the studied OHP system.

(3)

The reciprocal of the radial heat transfer coefficient increased with increasing liquid film thickness. As a result, an empirical linear correlation using regression coefficients was found to be able to describe the relationship between the thermal resistances and heating inputs. This has been proven using experimental data both in this study and from the literature.