Calculation of Consistent Plasma Parameters for DEMO-FNS Using Ionic Transport Equations and Simulation of the Tritium Fuel Cycle

Featured Application

The research was carried out within the framework of the federal project Development of technologies for controlled fusion and innovative plasma technologies of the comprehensive program of the State Corporation Rosatom, Development of equipment, technologies and scientific research in the field of the use of atomic energy in the Russian Federation for the period up to 2030. The developed methodology and the results obtained can be used in the design of fusion neutron sources and hybrid reactor facilities.

Abstract

Modeling the D and T fluxes in Fusion Neutron Source based on a tokamak fuel cycle systems was performed consistently with the core and divertor plasma. An indirect integration of ASTRA, SOLPS4.3, and FC-FNS codes is used. The feedback coupling is realized between the pumping and puffing systems in the form of changes in the isotopic composition of the core and edge plasma. In the ASTRA code, instead of electrons, ions were used in the particle transport equations. This allows better estimates of the flows of the D/T components of the fuel that have to be provided by the gas puffing and processing systems. The particle flows into the plasma from pellets, required to maintain the target plasma density <n_e> = (6–8) × 10¹⁹ m⁻³ are 10²² particles/s. In the majority of the working range of parameters, additional ELM stimulation is necessary (by ~1-mm³-size pellets from the low magnetic field side) in order to maintain the controlled energy losses at the level δW_ELM~0.5 MJ. For the starting load of the FC and steady-state operation of the facility, up to 500 g of tritium are required taking into account the radioactive decay losses.

1. Introduction

To provide an exact estimate of the flows of fuel components in ITER, DEMO, and other fusion facilities under construction, it is necessary to conduct detailed integrated simulations of the plasma, outside the scope of the simple studies of particle balance and plasma transport in the active zone that are usually used for this purpose [1]. This is necessary because the conditions necessary for ensuring parameters and fusion plasma confinement can have a substantial effect on plasma replenishment by the recycled particles and on the transfer of edge particles [2,3]. It was noted in [1] that the results obtained from integrated simulations can differ by more than one order of magnitude from the estimates obtained by simpler models (in particular, [4,5]).

Earlier, an approach was developed and discussed to simulations of tritium FC systems and calculation of the amount of tritium at the facility, consistently with the core and divertor plasma [6,7,8]. In this approach, similarly to [9], the state of the core (inside the separatrix) and edge (outside the separatrix) plasma is simulated by a combination of the ASTRA [10] and SOLPS4.3 [11] codes and the particle flows in the FC systems are simulated by the FC-FNS [12] code. The integration between these three independent codes is carried out by an indirect scheme, where the output data from one code is parametrized and further used as input data in the other code [13]. This allowed us to create an effective calculation workflow that describes the interaction of different components of the model with strongly different calculation times.

In the developed approach, SOL modeling was carried out with parameterization of the results [13], then these data were used as boundary conditions in the core modeling [6,8]. Based on the obtained simulations, the characteristic particle retention times were calculated (see below) and zero-dimensional modeling of the particle balance inside the vacuum chamber was carried out:

$$\begin{array}{r}{N}_{core}^{}=N_{sep}^{}+S_{NB}^{}{\tau }_{NB}^{}+(S_{pel(LFS)}^{}+S_{pel(HFS)}^{}-{\alpha }_{ELM}{P}_{SOL}/3\times T_{ped}){\tau }_{pel}^{}+\\ +S_{sep}^{}{\tau }_{sep}^{}-S_{fus}^{}{\tau }_{tot}^{}\end{array}$$

(1)

by which the flows in the pumping, processing and injection systems were modeled.

$$S_{sep}^T=S_{sep}^{}(S_{puff}^T+S_{out}^T)/(S_{pump}^{}+S_{sep}^{})$$

$$\begin{array}{r}{S}_{puff}^T=S_{pel(HFS)}^T(1/k_{eff\_HFS}^{}-1)+S_{GIS}^T\\ S_{puff}^D=S_{NB}^D(1/k_{eff\_NBI}^{}-1)+S_{pel(HFS)}^D(1/k_{eff\_HFS}^{}-1)+\\ +S_{pel(LFS)}^D(1/k_{eff\_LFS}^{}-1)+S_{GIS}^D\end{array}$$

(2)

et al. (see [8]).

The earlier used model assumes that the core plasma is replenished by particles from three different sources (neutral beam injection, pellet injection, and gas supply to edge/SOL) that have different confinement times. These “partial” confinement times were determined after some sources were artificially decreased by ~10% [7]. Since, in earlier simulations by the ASTRA and SOLPS codes the hydrogen isotopes were not distinguished, in order to estimate that deuterium and tritium flows by the FC-FNS code, we used an additional assumption that the transport coefficients of the D and T particles were equal in the core plasma. This assumption is rather rough and may carry a potential inaccuracy for the result (so the flows may be in opposite directions for D and T—see [3,14]). Theoretically, it is possible to introduce different transport coefficients for different isotopes, yet there is no detailed data on the particle transport of different isotopes, and in particular on the mixing of isotopes. The existing theoretical estimates and experimental data (see, e.g., [15]) indicate that the dependence of particle confinement on its mass is relatively weak, ~m^1/2. Therefore, taking into account the ratio of T/D masses that is equal to 1.5, the above assumption appears reasonable. The relative concentration of tritium in the core plasma is determined by the ratio of intensities of the D and T sources and by the distribution of the different sources across the cross section of the core plasma. Note that, in simulations by the ASTRA code in [7], the diffusion coefficients were normalized so as to provide the given global particle confinement times τ_p in the plasma column.

In this article, the further development of the proposed approach is described, where in the ASTRA code, transport equations for ions instead of electrons are used. This allows us to treat all isotopes as distinct species and estimate and estimate the “partial confinement times” of ions from different sources (neutral beams, pellets, gas puffing, and recycling) to improve estimation precision.

2. Transport Model

The transport model used in the ASTRA code for heat is similar to previous simulations [13,16]. To model the plasma density, in this work, ion transport equations are used, and the continuity equations are written separately for each of the isotopes of the main gas and each of the plasma fueling systems. Thus, a set of six continuity equations is formed,

$$\begin{array}{l}{D}^{+}:\left\{\begin{array}{l}\frac{\partial }{\partial t}{n}_{beam}^{D^{+}}+\mathrm{div}\left(-D\nabla n_{beam}^{D^{+}}+V{n}_{beam}^{D^{+}}\right)=S_{beam}^{D^{+}}-R_{beam}^{D^{+}},\\ \frac{\partial }{\partial t}{n}_{pel}^{D^{+}}+\mathrm{div}\left(-D\nabla n_{pel}^{D^{+}}+V{n}_{pel}^{D^{+}}\right)=S_{pel}^{D^{+}}-R_{pel}^{D^{+}},\\ \frac{\partial }{\partial t}{n}_{sep}^{D^{+}}+\mathrm{div}\left(-D\nabla n_{sep}^{D^{+}}+V{n}_{sep}^{D^{+}}\right)=S_{sep}^{D^{+}}-R_{sep}^{D^{+}},\end{array}\right.\\ T^{+}\hspace{0.17em}\hspace{0.17em}:\left\{\begin{array}{l}\frac{\partial }{\partial t}{n}_{beam}^{T^{+}}+\mathrm{div}\left(-D\nabla n_{beam}^{T^{+}}+V{n}_{beam}^{T^{+}}\right)=S_{beam}^{T^{+}}-R_{beam}^{T^{+}},\\ \frac{\partial }{\partial t}{n}_{pel}^{T^{+}}+\mathrm{div}\left(-D\nabla n_{pel}^{T^{+}}+V{n}_{pel}^{T^{+}}\right)=S_{pel}^{T^{+}}-R_{pel}^{T^{+}},\\ \frac{\partial }{\partial t}{n}_{sep}^{T^{+}}+\mathrm{div}\left(-D\nabla n_{sep}^{T^{+}}+V{n}_{sep}^{T^{+}}\right)=S_{sep}^{T^{+}}-R_{sep}^{T^{+}},\end{array}\right.\end{array}$$

(3)

where n is the density of deuterium (D⁺) or tritium (T⁺) ions in the fast ion beam (beam), pellets (pel) or particles that arrive from the divertor zone through the separatrix (sep), S is the ionization source, R is the recombination sink, D is the diffusion coefficient, and V is the convection velocity (particle pinch). It is easy to see that the equations do not contain charge exchange terms (see, for example, [3]), since it is difficult to take them into account in the chosen approach. Estimates made for the typical parameters with which the simulations were performed (Section 3 et seq.) showed that the influence of the charge exchange effect (including charge exchange on beam atoms) can be neglected, given the other assumptions used, which seems to be acceptable at the moment.

It is seen that the sum of the equations for each isotope gives the full continuity equation. Therefore, the solutions for the flux and total ion density are the same as in the case of solving the single full equation. Although the separation of one type of particle into “partial” components is quite artificial from the viewpoint of transport processes, such an approach allows one to quite naturally feed the answers obtained by the 1D plasma transport simulations into the 0D simulations of the tritium FC flows.

For each equation, boundary conditions are set at the last closed magnetic surface,

$$\begin{array}{l}{D}^{+}:\left\{\begin{array}{l}{n}_{beam}^{D^{+}}\left(a\right)=0,\\ n_{pel}^{D^{+}}\left(a\right)=0,\\ n_{sep}^{D^{+}}\left(a\right)=\left(1-f_{sep}^T\right)\times n_i^{SOLPS},\end{array}\right.\\ T^{+}:\left\{\begin{array}{l}{n}_{beam}^{T^{+}}\left(a\right)=0,\\ n_{pel}^{T^{+}}\left(a\right)=0,\\ n_{sep}^{T^{+}}\left(a\right)=f_{sep}^T\times n_i^{SOLPS},\end{array}\right.\end{array}$$

(4)

where f_sep^T = S_sep^T+/(S_sep^D+ + S_sep^T+) is the fraction of the tritium source and n_i ^SOLPS is the density of main gas ions at the plasma boundary obtained by SOLPS calculations [13]. Separation of the consistent value S_sep (S_0sep in terms of [13], etc.) cannot be performed in the ASTRA code since S_out^T depends on S_sep^T, which gives a nonlinear equation in the system. The total density of Maxwellized ions is determined as the sum

$$n_i=n_{beam}^{D^{+}}+n_{pel}^{D^{+}}+n_{sep}^{D^{+}}+n_{beam}^{T^{+}}+n_{pel}^{T^{+}}+n_{sep}^{T^{+}}.$$

(5)

Consequently, the electron density can be determined from the quasi neutrality condition taking into account the impurities and the fast ions,

$$n_e=n_i+n_{fast}^{D^{+}}+n_{fast}^{T^{+}}+{\displaystyle \sum _{Z=\mathrm{He},\mathrm{Be},\mathrm{Ne}}Z\times n_Z},$$

(6)

where n_fast^D+ (n_fast^T+) is the density of fast deuterium (tritium) ions, and n_Z is the density of the impurity with charge Z (the sum is over all charge states of the He, Be, and Ne impurities).

The set of Equation (3) allows us to explicitly obtain the partial ion concentrations and, consequently, determine the “partial confinement times” for each plasma fueling system,

$${\tau }_{beam}^{D^{+}/T^{+}}=\frac{{\displaystyle \underset{V_{pl}}{\int }\left(n_{beam}^{D^{+}/T^{+}}+n_{fast}^{D^{+}/T^{+}}\right)d{V}_{pl}}}{{\displaystyle \int S_{beam}^{D^{+}/T^{+}}d{V}_{pl}}},$$

(7)

$${\tau }_{pel}^{D^{+}/T^{+}}=\frac{{\displaystyle \underset{V_{pl}}{\int }{n}_{pel}^{D^{+}/T^{+}}d{V}_{pl}}}{{\displaystyle \int S_{pel}^{D^{+}/T^{+}}d{V}_{pl}}},$$

(8)

$${\tau }_{sep}^{D^{+}/T^{+}}=\frac{{\displaystyle \underset{V_{pl}}{\int }\left(n_{sep}^{D^{+}/T^{+}}-n_{sep}^{D^{+}/T^{+}}(a)\right)d{V}_{pl}}}{{\displaystyle \int S_{sep}^{D^{+}/T^{+}}d{V}_{pl}}}.$$

(9)

Let us also determine the particle and energy confinement times as

$${\tau }_E^{}=\frac{\frac{3}{2}{\displaystyle \underset{V_{pl}}{\int }\left(n_e{T}_e+n_i{T}_i\right)d{V}_{pl}}}{{\displaystyle \int P_{tot}^{}d{V}_{pl}}},$$

(10)

$${\tau }_p^{}=\frac{{\displaystyle \underset{V_{pl}}{\int }{n}_{i}d{V}_{pl}}}{{\displaystyle \int S_i^{tot}d{V}_{pl}}},$$

(11)

$${\tau }_{tot}^{}=\frac{{\displaystyle \underset{V_{pl}}{\int }\left(n_i^{}-n_i^{}(a)\right)d{V}_{pl}}}{{\displaystyle \int S_i^{tot}d{V}_{pl}}},$$

(12)

where τ_E is energy confinement time, τ_p is ion confinement time, τ_tot is the ion confinement time without recycling, P_tot is the total plasma heating power, and S_i^tot is the total source of ions from all fueling systems.

To determine the set of Equation (3) unequivocally, it is necessary to provide the transport coefficients. In calculations made in this work, D and V were determined as

$$\left\{\begin{array}{l}D=C_n^{}\times \left(1-C_n^{ped}\times H\left({\rho }_{ped}\right)\right),\\ V=0.0,\end{array}\right.$$

(13)

where H(ρ) is the Heaviside function, C_n is a constant, and C_n ^ped is the height of the “step” that determines the given value of the density pedestal.

The solution of the set of Equation (3) is found by the reverse method, i.e., in the calculation process the values of flows required to provide the given regime of the average density and confinement are selected. The solution is found using the following feedbacks:

(i)

Feedback over the average density: the particle flow from the pellets (D + T) is chosen to provide the required value <n_e> = (6–8) × 10¹⁹ m⁻³.

(ii)

Feedback over energy confinement time: the ion and electron heat conductivity coefficients χ_e = χ_i are chosen so as to provide the required value of the factor H_IPB(y,2) = 1.3.

(iii)

Feedback over particle confinement time: the value of constant C_n is chosen to satisfy the given value τ_p/τ_E = 0.75–3.0.

(iv)

Feedback over the fraction of tritium in the pellets: the flow from the pellets is divided between D and T to provide the required value f ^T = 0.5.

During the calculation, <n_e> and τ_p/τ_E are considered free parameters and they are varied in the above-mentioned range in order to consider all the most probable DEMO-FNS operation regimes. It is seen that feedback links (i)–(iii) affect each other, meaning that we have to solve a nonlinear inverse problem.

3. Calculation Results

Simulation of plasma parameters in DEMO-FNS was carried out using different confinement parameters: e.g., in [6,13] and earlier works, τ_p/τ_E was taken to be equal to 3–4, while later, its range was extended to 2–4 [17] since it was shown [7] that, for higher values of τ_p/τ_E, the required value of density can be provided only by ion beam and particle flows from the divertor region. Such regimes without pellet injection are uncontrollable. Later, based on experimental data [18,19], it was proposed to consider the range τ_p/τ_E~1.5–3.0, which corresponds to the ratio of coefficients of diffusion and thermal conductivity D/χ_e = 0.3–0.5. In this work, calculations were carried out in the range τ_p/τ_E = 0.75–2.5 since this range covers the experimental values of D/χ_e [18,20].

It is shown in Figure 1 that, to provide higher values of τ_p/τ_E, it is necessary to decrease the particle diffusion coefficient. The range D/χ_e = 0.2–0.75 presented in [18] in the case of DEMO-FNS facility provides the variation of confinement parameters τ_p/τ_E = 0.5–2.25. At the same time, in calculations with higher density, the diffusion coefficients are lower (see Figure 1).

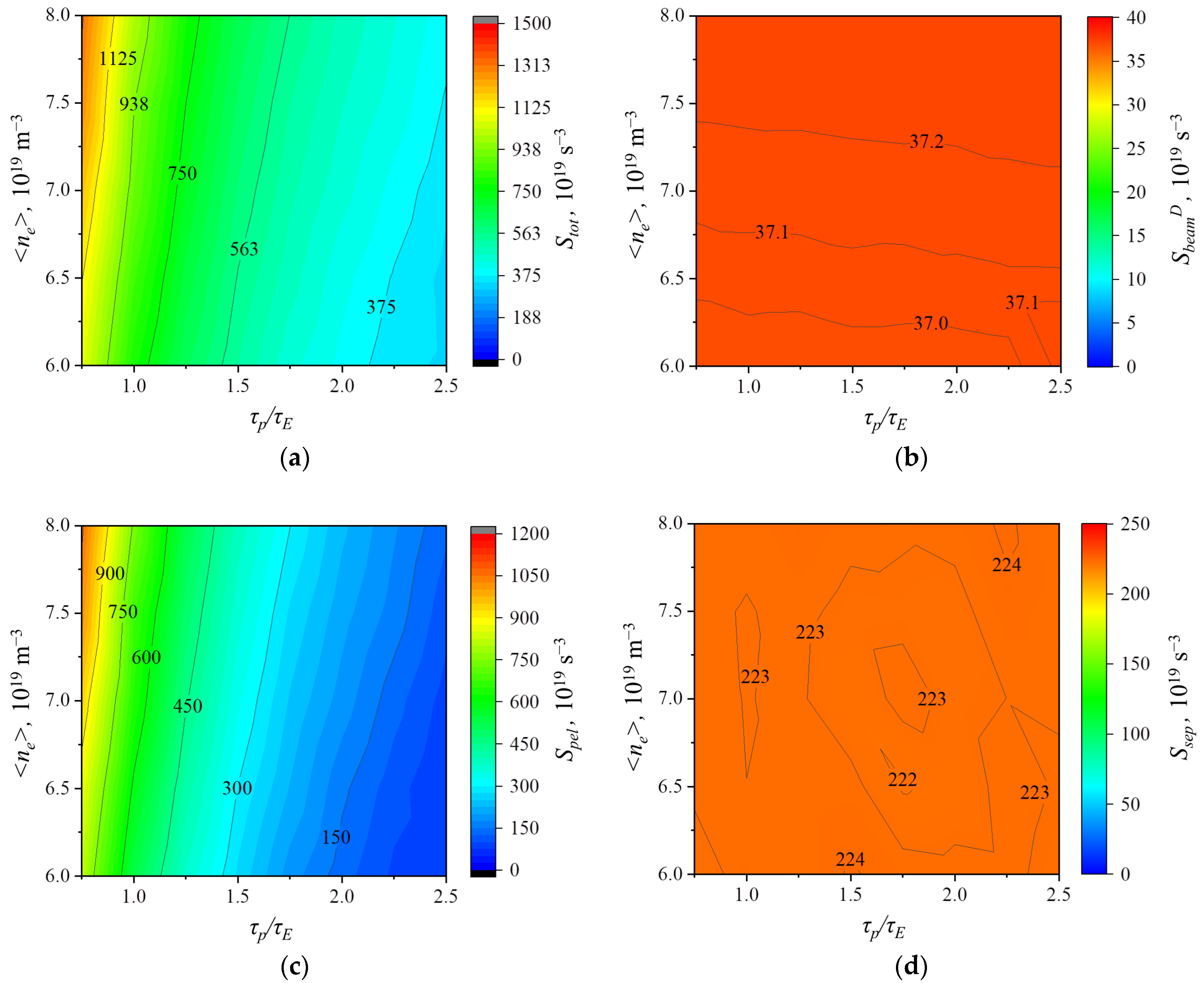
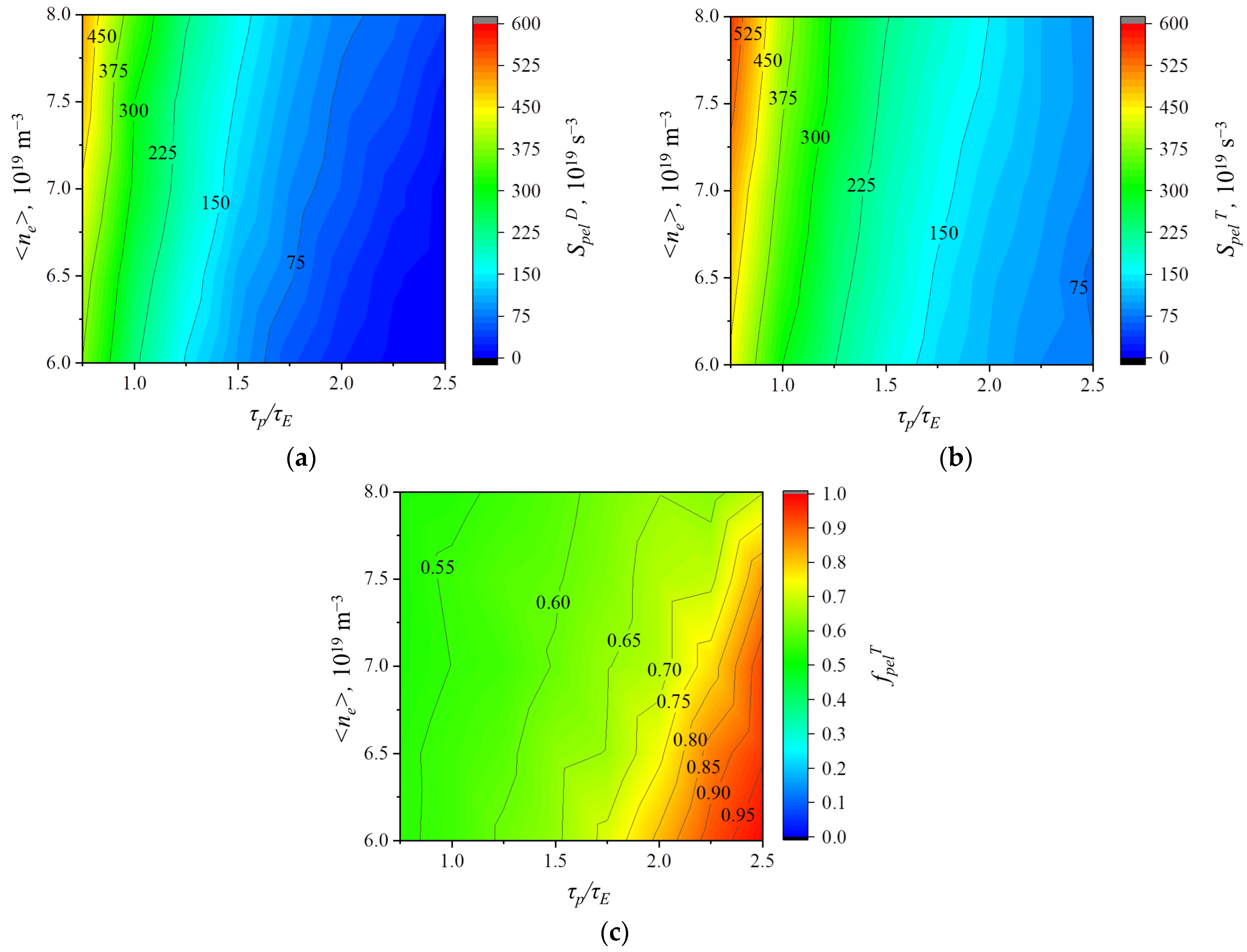
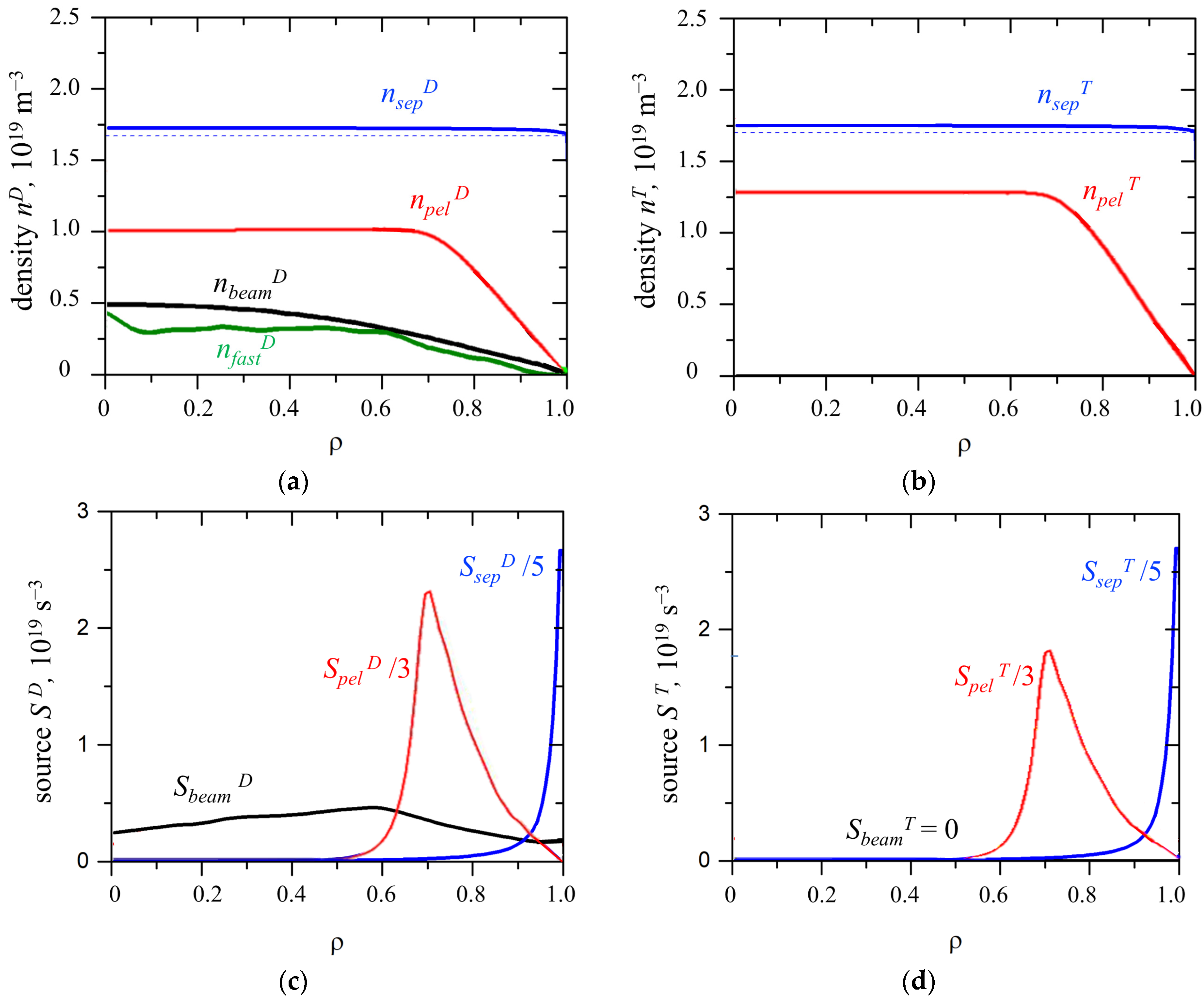
3.1. Particle Flows

The particle balance in the plasma is shown in Figure 2. To provide the given density, plasma fueling is necessary at the level 1.5 × 10²¹–1.3 × 10²² particles/s depending on confinement and target density. In all regimes, the 30 MW-power deuterium neutral beam injection (NBI) provides flows at the level of (36–37) × 10¹⁹ particles/s (absorption in the plasma taking into account the “shine-through” particles). The particle flow from the divertor is (2.2–2.3) × 10²¹ particles/s. The beam and neutrals from the divertor (that are provided by gas puffing) can provide the required density only in the case of high particle confinement. In the range τ_p/τ_E = 1–2, plasma fueling with pellets is needed. These values are lower than the ones calculated earlier via the parameterization of calculations by the ASTRA code [8] in the range τ_p/τ_E = 1.5–3.

Injection parameters and source profiles are discussed in detail in Section 3.3. For the fueling of DEMO-FNS, deuterium and tritium pellets are considered, which can be introduced separately or by using the same injection system [21,22]. In the absence of forced isotope content control in the divertor plasma by controlled gas puffing (f_div^T = f_core^T), the fraction of tritium in the plasma is determined mainly by the ratio of the flows S_pel^T and S_pel^D. In the described calculations, the parameters of injection of tritium pellets were chosen to provide the given ratio n_D+:n_T+ = 1:1, i.e., the fraction of tritium in the core plasma is f_core^T = 0.5,

$$f_{pel}^T=\frac{S_{pel}^T}{S_{pel}^D+S_{pel}^T}$$

(14)

The obtained data on pellet flows is shown in Figure 3. It is seen that, in the case of low density and high particle confinement, tritium-only pellets are sufficient to maintain the plasma parameters (together with the injection of deuterium form NBI). In all other cases, injection of both deuterium and tritium pellets is necessary, and their ratio should be f_pel^T = 0.5–0.8.

The performed calculations show that, in regimes with high confinement and low density, it is impossible to provide the required isotope composition of the core plasma because, in this case, all the density is provided by the beam and flow of neutrals through the separatrix (gas puffing), and the tritium flow through the separatrix is zero. This, once again, indicates that the parameter range of τ_p/τ_E was chosen correctly. Additional calculations can be carried out when ions are separated in SOLPS-ITER calculations (in this approach, the separation of the total flow through the separatrix S_sep was carried out proportionally to f_div^T, similar to [7,8]), yet currently this appears unnecessary. In all other cases, the flows S_sep^D and S_sep^S turn out to be approximately equal, as is shown in Figure 4.

Thus, by increasing the calculation precision due to the use of ion equations, it was shown that regimes with high confinement and low density can be non-optimum from the viewpoint of plasma fueling and control of the tritium fraction.

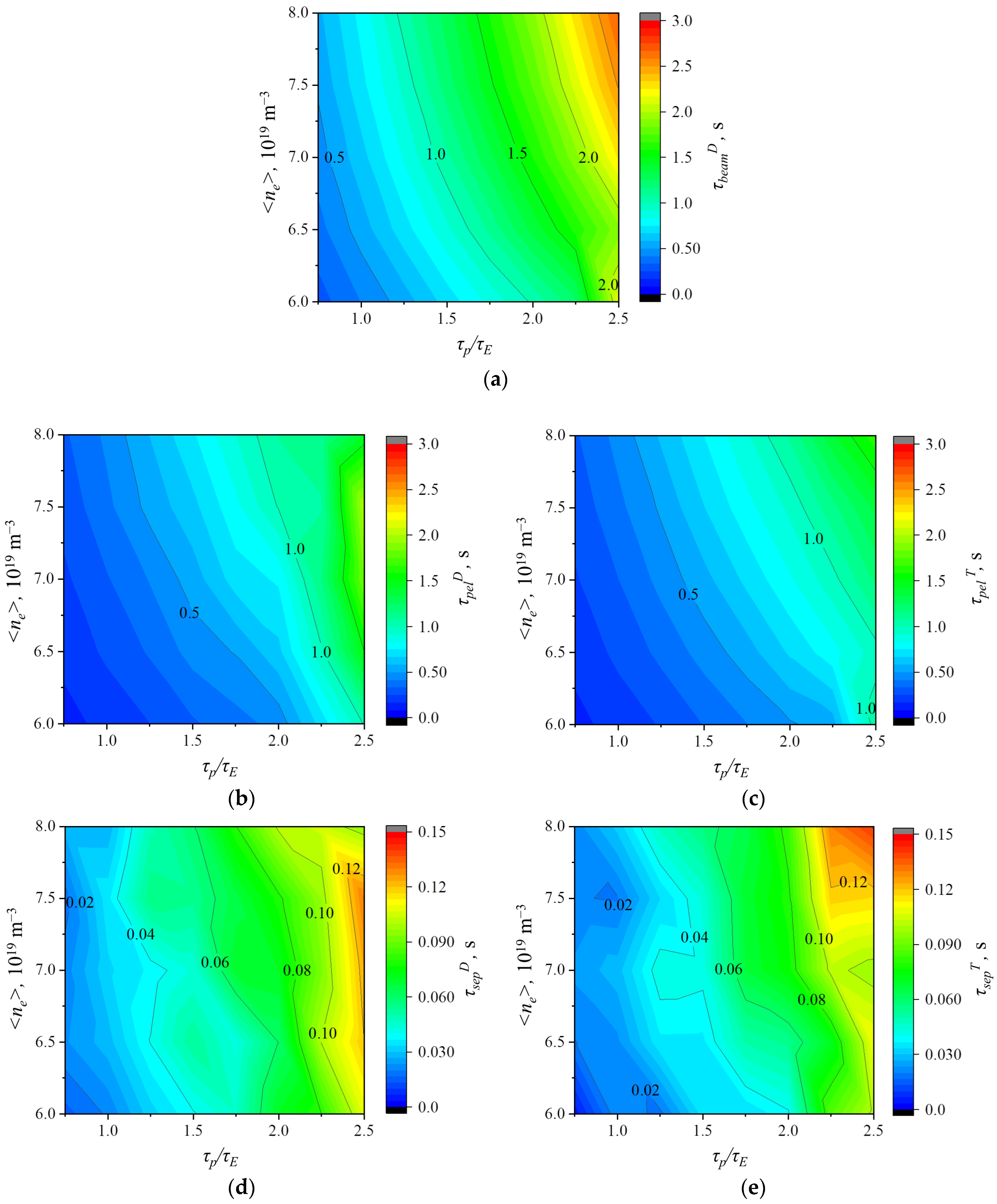
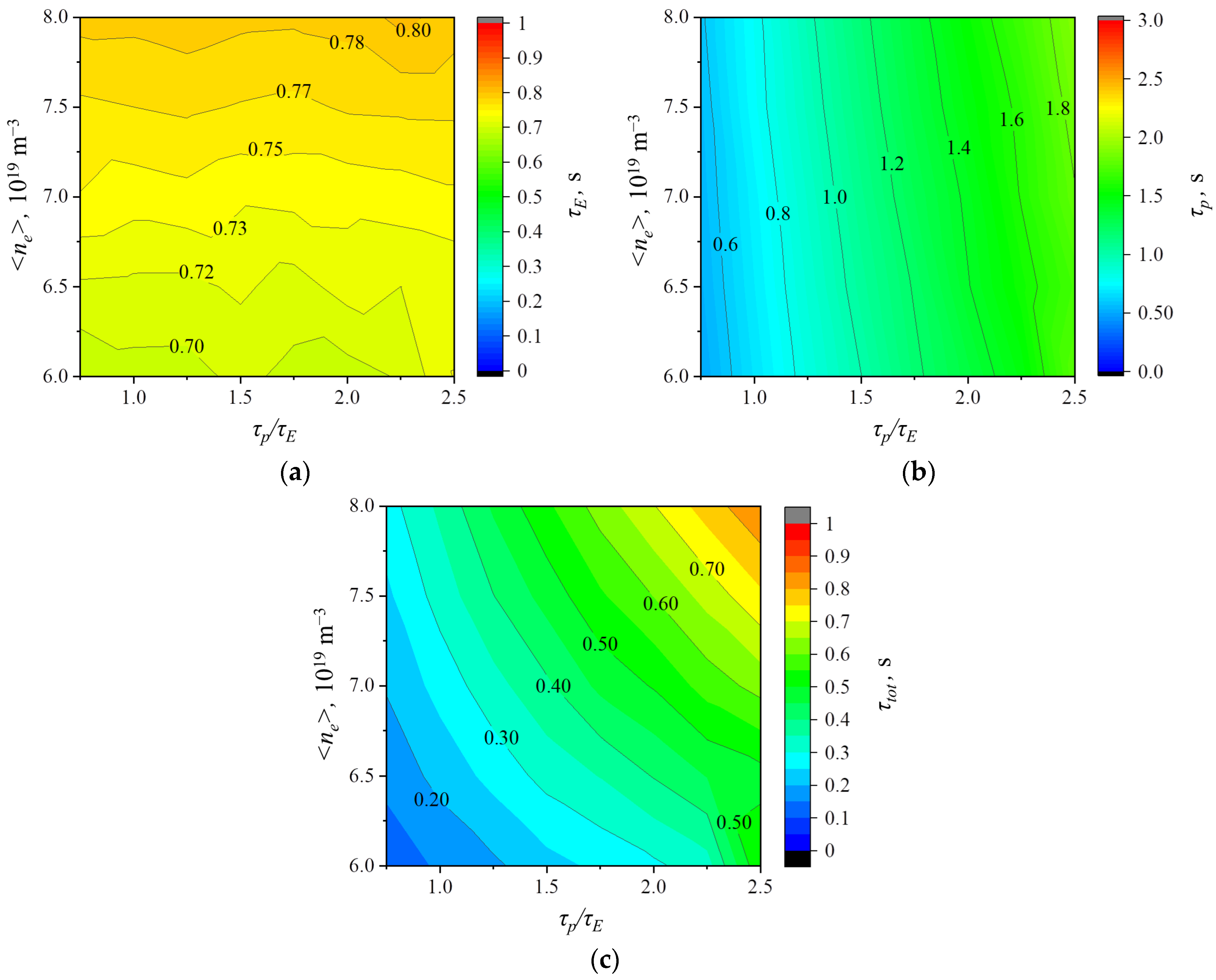
3.2. Confinement Times

Using the ion equations for calculations and the resulting more accurate determination of “partial confinement times” for particles in the plasma led to the increase of partial confinement times of beam particles and pellets by up to 2.5 times (in the corresponding working points). However, for the source of particles in the form of neutrals entering the plasma through the separatrix, the particle confinement times decreased up to 3 times. Due to this, the deposition of particles from different sources to the density of the core plasma changed compared to the previous estimates [8]. The increase of “partial particle confinement times” (Figure 5) led to the decrease of required particle flows (the strength of particle sources). Thus, Figure 2 shows the flows into the plasma from pellets, which are 2.7 times lower than those determined earlier (in the corresponding working points). The diffusion particle losses from the plasma are also lower than those calculated earlier, which leads to a proportional increase of gas puffing (see Equations (2) and (3) in [8]). Figure 5b–e shows the differences of corresponding times for different ions. The confinement times of ions from pellets shown in Figure 5b,c are longer than the injection times 1/f_pel < 0.1 s (see Section 3.3). This indicates that the estimates are reasonable, since pellet injection will occur more quickly than the characteristic density decay times.

The nonlinearity of the inverse problem that is being solved, as well as the effect of density on sources and sinks of particles and heat, leads to the change in particle flows not being obvious during the transition from one regime to another. The nonlinearity also makes the operation of feedback links more difficult, due to which the regime (defined by <n_e> and τ_p/τ_E) can differ within 10% from the required one. As a result, in addition to the difference of “partial times” when using the ion equations in the calculations, the global energy and ion confinement times are also different (compared to the previous estimates). At the same time, for the average values of plasma density, the values of τ_P and τ_E almost do not differ from those obtained in [8], and for higher and lower densities the confinement times decrease and increase by 15%, respectively.

Such implicit effects can be traced by analyzing the variation of the global parameters over the calculation mesh. It is seen in Figure 6 that the energy confinement time depends monotonously on the plasma density, while the ion confinement time is almost independent of <n_e>, yet it changes with the confinement parameter τ_p/τ_E. The time τ_tot that characterizes the ion confinement time without taking into account recycling depends uniformly on both <n_e> and τ_p/τ_E in the working window. The increase of the confinement time with increasing density is connected to the decrease of the diffusion coefficient.

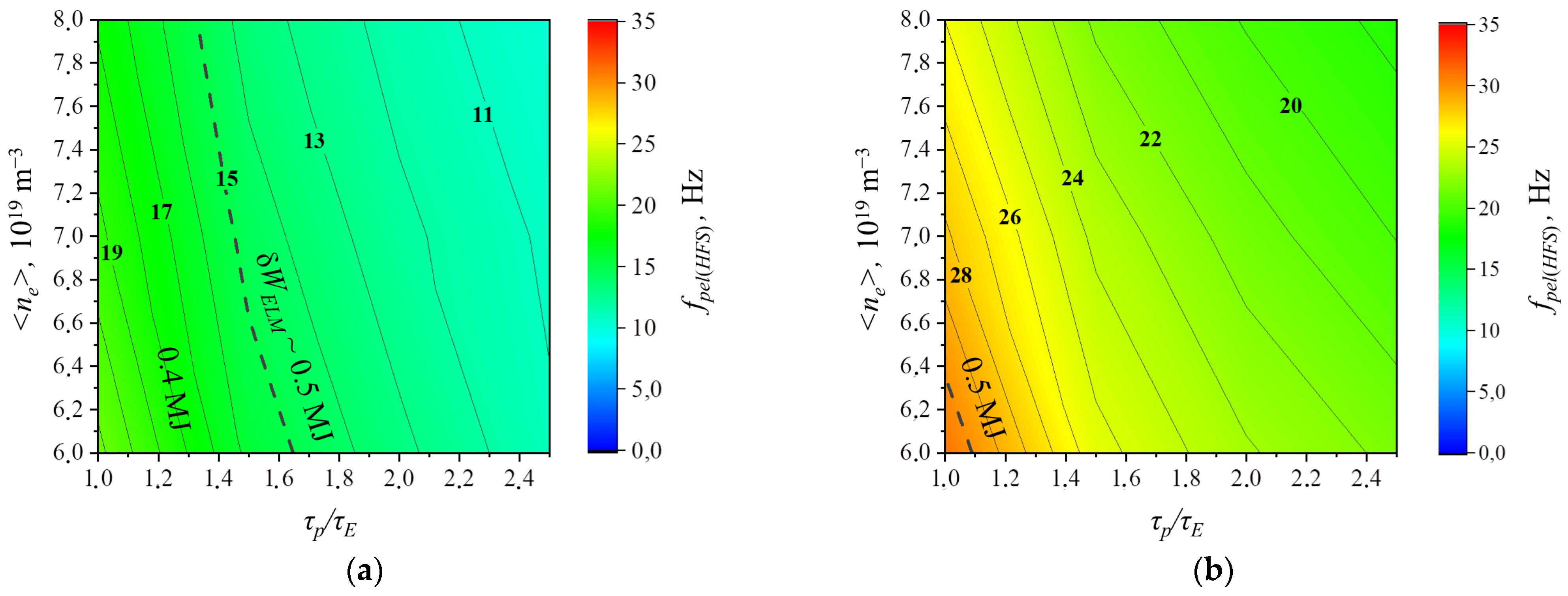
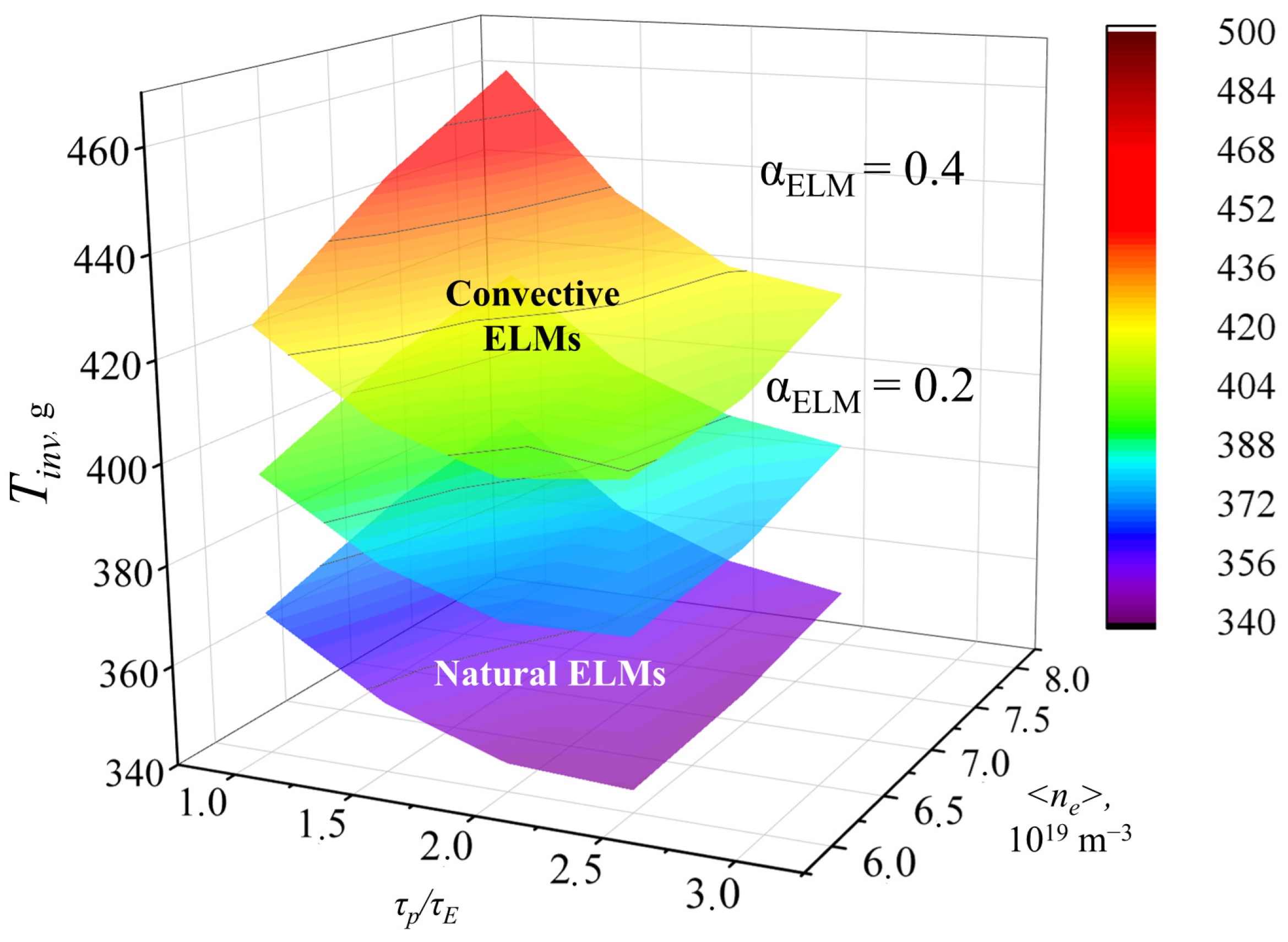
3.3. ELM Control by Pellet Injection

It is predicted that the natural (or “uncontrolled”) pulsed releases of particles from the column edge through the separatrix (edge localized modes, ELMs) in facilities under construction (including ITER) will lead to high pulsed heat loads on the plasma-facing components, which can substantially decrease their lifetime. It was shown [23] that the critical ELM parameters can be determined either by the loads on the divertor components or the first wall components, depending on the plasma configuration. Estimates made for ITER under the assumption that ELMs will affect the plasma Z_eff due to transport of impurities (including the first wall and divertor materials) show that the requirements to ELM control needed to maintain the necessary impurity concentration in the plasma are stricter than the requirements to prevent excessive erosion of the divertor and first wall components [23].

For conditions under which uncontrolled ELMs exceed the limits for the erosion of divertor components and the first wall, ELM control is needed. This can be carried out by suppressing type I ELMs by controlled ELM stimulation using the inverse dependence of the energy loss in ELMs (δW_ELM) and their frequency (f_ELM) [24],

$$f_{ELM}^{}={\alpha }_{ELM}\frac{P_{SOL}}{\delta W_{ELM}}$$

(15)

where P_SOL is the power flow from the core plasma into SOL and α_ELM is the fraction of the power that is deposited in ELMs. The expected minimum frequency of controlled ELMs will substantially depend on the requirements to the energy deposited in ELMs and the value of α_ELM, which, according to experimental measurements, is usually taken to be equal to 0.2–0.4 [25].

The change of the pellet ion source S_pel (i.e., the flow of D + T particles required to fuel the core plasma in the form of pellets injected from the high magnetic field side (HFS)), taking into account convective ELMs (in addition to “natural” ELMs) calculated in a manner similar to [8], is shown in Figure 7. It is seen that the increase in fuel flow to compensate for the particle losses in ELMs is 2–3 times, depending on α_ELM, which has to be accounted for in requirements for the system of pellet injection. The flows of particles from pellets into the plasma are up to 1.6 times lower than those calculated earlier (in the corresponding working points). The considered range of flows through the pellet injection system corresponds to the chosen requirements to the pellet injection system (PIS) of ITER and it is twice as small even for the maximum values of S_pel and α_ELM. From this, one can conclude that, even taking into account the additional flow of particles needed to stimulate ELMs from the low magnetic field side (LFS), the considered requirements for the PIS system are achievable from the engineering standpoint.

The frequency of fuel pellet injection (with maximum size for each separate plasma density) f_pel(HFS) is shown in Figure 8 depending on α_ELM for the working window of plasma parameters. The dashed line shows the levels of f_ELM necessary for stimulation of ELMs with δW_ELM~0.5 MJ (comparable to the value accepted for ITER) due to pellet injection. In Figure 8, frequencies f_ELM are also marked, necessary to stimulate ELMs with lower values of δW_ELM. The obtained result differs quantitatively from earlier obtained results [8] but it is the same in principle. It is seen that, in the significant fraction of the working window with τ_p/τ_E > 1.7 for α_ELM = 0.2 and with τ_p/τ_E > 1.2–1.4 for α_ELM = 0.4, additional stimulation of ELMs is necessary. This can be performed by injecting pellets from the LFS and/or decreasing the size of fuel pellets [8]. The specific solution should be chosen based on detailed simulations and determination of the size of the pellets injected from different directions.

Estimates of the size of LFS pellets required for reliable initiation of ELMs (for example, [26]) by the method described in [23] give the value of ~1.0 mm³. This agrees with modern experimental data from JET, DIII-D, and ASDEX Upgrade [23]. Since the fuel injection flows weakly depend on the LFS injection parameters (see [8]), we left the analysis of the minimum pellet size for ELM stimulation to the future.

Control of ELM frequency f_ELM and energy losses in ELMs δW_ELM by pellet injection is considered as the main scheme of ELM control for ITER and other facilities under construction. Experiments carried out at DIII-D showed the high efficiency of this method in decreasing the ELM energy released in the divertor [27]. It was shown experimentally that the energy of ELMs released in the divertor decreased 10 times for ELMs controlled by pellet injection compared with uncontrolled ELMs under the same discharge conditions [27]. To apply this method in constructed facilities including ITER and determine the requirements to the PIS, one needs to additionally study:

(a)

the size of the pellets required for reliable stimulation of ELMs and changes in the flows of fuel components in the FC caused by it;

(b)

the geometry of pellet injection for fueling the plasma and stimulating ELMs;

(c)

the effect of this control method on the parameters of density pedestal of the core plasma and, consequently, its confinement and the characteristics of the neutron source.

Figure 9 shows the density profiles of the main components of the plasma core provided by different ion sources: NBI, pellets, and neutrals through the separatrix. It is seen that the latter forms a relatively uniform profile despite the source having a peak at the plasma periphery (see Figure 9c,d). At the same time, the sources of pellets and the beam have maximums close to the system axis, which provide the characteristic density profiles. It was noted in [28] that the radial profile of the source of neutrals from the beam is calculated by the NUBEAM code [29] that is incorporated into the ASTRA transport code. The high boundary density of ions that are supplied in the form of atoms from the divertor zone is generated as a result of the decrease of the scrape-off layer (SOL) thickness λ_q due to the high magnetic field (see, e.g., [30]). Of the experimental data accessible in open literature, only the results from Alcator C-Mod [31,32] can be compared with the DEMO-FNS and ITER facilities.

In an accurate approach, it is necessary to simulate the profiles created in plasma (with given properties) during ablation of pellets with the given composition, size, velocity, frequency, and injection direction. Approach [33] allows one to calculate the evaporation rate of the pellet material, yet to obtain the source profile it is necessary to take into consideration the drift of the evaporated material after ablation. For this, specialized calculation codes can be used (e.g., HPI2 [34]) as well as simpler models [35,36]. In this work, the deposition profile of the pellet particles was simulated consistently by code [35] that is incorporated into the ASTRA. The DEMO-FNS geometry allows injection from HFS at angles α_pel = 0–80° relative to the equatorial plane. The speed varied in the range of 0.3–3.0 km/s. It was shown that the largest deposit was achieved at α_pel = 0° and the highest velocities, which was used in further simulations. The ablation depth does not change much with size, while the deposit depth doubled as the pellet size V_pel increased from 2.5 to 17.5 mm³. As a result, we simulated pellet injection with the maximum possible size V_pel = k_dens <n_e> V_plasma/(2p/m_mol)) equal to 10% of particles in the plasma, which corresponded to V_pel = 12–18 mm³ for scenarios <n_e> = 6–8 × 10¹⁹ m^–3, respectively.

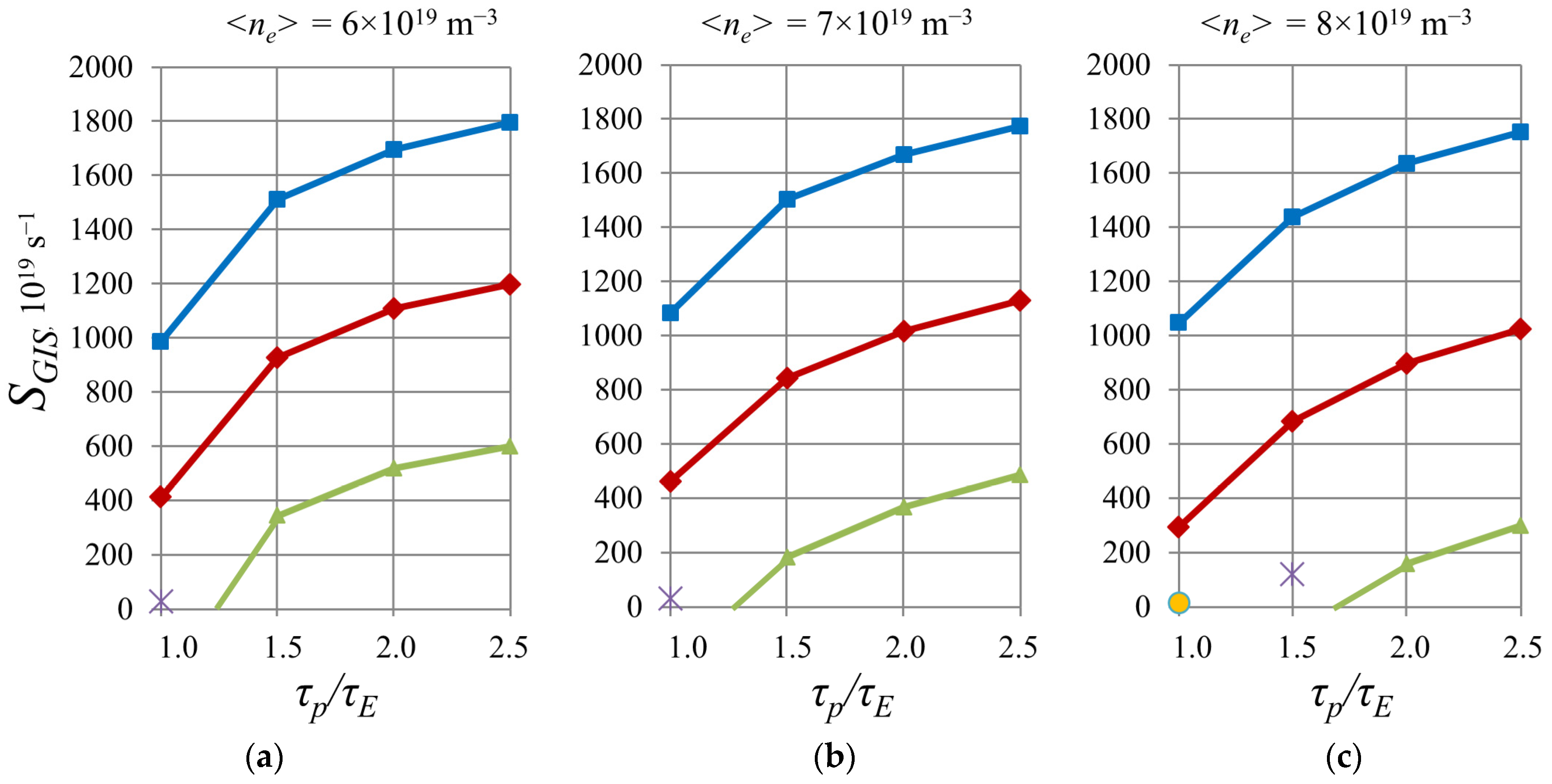
3.4. Gas Puffing into the Vacuum Vessel

Under stationary operation conditions of a facility with a gas-saturated vacuum vessel wall, particle exchange between the plasma and the wall leads to a dynamic equilibrium between the flows of particles from the plasma and flows of particles reflected or desorbed from the wall. Since these flows depend in different ways on the parameters of the plasma and the wall, every change in the state of the plasma or the wall can be expected to disrupt the balance to one side or to another and, consequently, lead to effective pumping or supply of the wall with the main gas.

While it is relatively simple to compensate for the effective pumping of the wall by increased gas puffing, it is much more difficult to compensate for the opposite effect. Since increasing the pumping rate two or more times is impossible, instead, it is necessary to constantly operate at a gas puffing rate close to maximum in order to have the necessary freedom for decreasing it in case of excess degassing from the wall [37].

The supposed effect can be estimated from the expected total flow of particles onto the wall. In the DEMO-FNS project, the ion and neutral flows onto the (internal and external) wall are 2 × 10²³ s⁻¹ in total and 3 × 10²⁴ s⁻¹ onto the divertor plates in total. In this case, the total flows of hydrogen (D, T) particles onto the surface of structural elements in DEMO-FNS are expected to be Γ ~ 3.2 × 10²⁴ s⁻¹ (ions and neutrals), which is about 15% of the same value for ITER [37]. Similarly to the calculations described in [37], one can estimate the equilibrium flows of particles absorbed and desorbed by the wall. The disruption of the balance of flows by, e.g., 1% [37] leads to the appearance of an effective source or sink of particles of the size 1.6 × 10²² s⁻¹. Consequently, to have the ability to decrease the intensity of gas puffing in case of excessive particle desorption from the wall, one has to provide additional gas injection (S_GIS to the difference from S_puff—see (2)) of no less than 33 Pa m³/s or 1600 × 10¹⁹ s⁻¹ (in the units given in the figures).

In scenarios with stimulated convective ELMs, an increase in particle losses from the plasma

$$\begin{gathered} S_{out}^T=S_{sep}^T+S_{pel}^T-S_{fus}^T, \\ {S}_{out}^D=S_{sep}^D+S_{pel(HFS)}^D+S_{pel(LFS)}^D+S_{NB}^D-S_{fus}^D \end{gathered}$$

(16)

is observed (see Figure 10). As a result of the increase of flows from the plasma and from pellets that miss the plasma, at a constant S_sep and constant pressure p_n, additional gas injection S_GIS has to be decreased. In the absence of a base value for S_GIS, in some working points (e.g., τ_p/τ_E ~ 1 for α_ELM = 0.4), the pumping rate 20 m³/s is insufficient to provide the required pressure of p_n = 2 Pa. It has to be increased to 22–25 m³/s (see the separate markers: the crosses and the yellow dot in Figure 11) when the value of S_GIS becomes almost zero. Since the additional flow of particles from the pellet “shards” that have missed the plasma core S_HFS (1/k_{eff_HFS} − 1) cannot be turned to zero in the case of unpredictable gas desorption from the wall, the only controlling parameter remains the value of S_GIS.

$$S_{out}^T+S_{out}^D+S_{puff}^T+S_{puff}^D=c_p\times p_n+S_{sep}^D+S_{sep}^T.$$

(17)

At a fixed value of gas injection S_GIS = 1600 × 10¹⁹ s⁻¹, the flow into the pumping system of the vacuum vessel will increase to 50 m³ Pa/s for the scenario with natural ELMs and to 65–80 m³ Pa/s for the scenario with particle losses in convective ELMs. In this case, the geometry of the pumping nozzles and the chosen pumping equipment need to provide the required conductivity and pumping rate. In the DEMO-FNS project, pumping will be carried out from the upper and lower divertors through 36 pumping nozzles, of which

-

the upper pipeline contains 18 branches, each of which consists of a 264-mm-diameter opening, a 264-mm-diameter 6900-mm-long pipeline, a 90° bend, and a further length of 304-mm-diameter 2200-mm-long pipeline;

-

the lower pipeline also contains 18 branches, each of which contains a 264-mm-diameter opening, a 264-mm-diameter 5330-mm-long pipeline, a 90° bend, and a further length of 304-mm-diameter 2284-mm-long pipeline.

The total hydrogen conductivity of these pipelines is 34 m³/s (at T = 20 °C) and 44 m³/s (at T = 200 °C). When pumps with a total nominal hydrogen conductivity of 111.6 m³/s are used (18 + 18 turbomolecular pumps with a capacity of 3.1 m³/s), the total pumping efficiency is ~30 m³/s. When the total nominal pumping efficiency is increased two times (by using cryopumps), the total effective pumping rate increases only by ~15%. In order to be able to pump out substantially larger flows, it is necessary to increase the conductivity of the pumping channels, i.e., increase their cross section and decrease their length.

The analysis of the gas flow rate S_GIS acceptable for the DEMO-FNS project showed that the current limitation of c_p~30 m³/s can provide gas injection up to S_GIS = 20 Pa m³/s, or 1000 × 10¹⁹ s⁻¹ for the considered working window (Figure 12). Consequently, at the calculated flows from the plasma onto the DEMO-FNS wall (that are lower than flows calculated for ITER), the requirements for gas injection exceeds the engineering limitations of the pumping system for some of the considered scenarios. Specification of gas conditions at the first wall is extremely important to optimize the gas injection and engineering solutions in the pumping system.

In calculations, one should also account for the fact that the violation of the top–bottom symmetry [38] in the double-zero configuration caused by the radiation–condensation instability (RCI) can lead to up to 5 times less efficient pumping. This means that nearly all pumping will be carried out from only one (colder) divertor, while the pumps connected to the other (warmer) divertor will be blocked. In this case, the total conductivity of the pumping system will decrease to 35 Pa m³/s, which will allow us to conduct gas injection within 10 Pa m³/s in the regimes with convective ELMs and within 20–30 Pa m³/s in the regimes with natural ELMs. To provide pumping in the range of 50–85 Pa m³/s, which corresponds to fixed gas injection of 33 Pa m³/s, in case of disruption of divertor symmetry, the required pumping rate is c_p = 40–70 m³/s (depending on the operation scenario).

Taking into account the fixed value of S_GIS and the connected increase in flows in the gas injection system (relative to the estimates that were made to date) will not affect the flows in the fuel injection systems and the hydrogen separation system that contain the maximum gas reserves. However, this will lead to an increase in the amount of tritium accumulated in the pumping, processing, and gas injection systems (in detail, this phenomenon is discussed in Section 3.6).

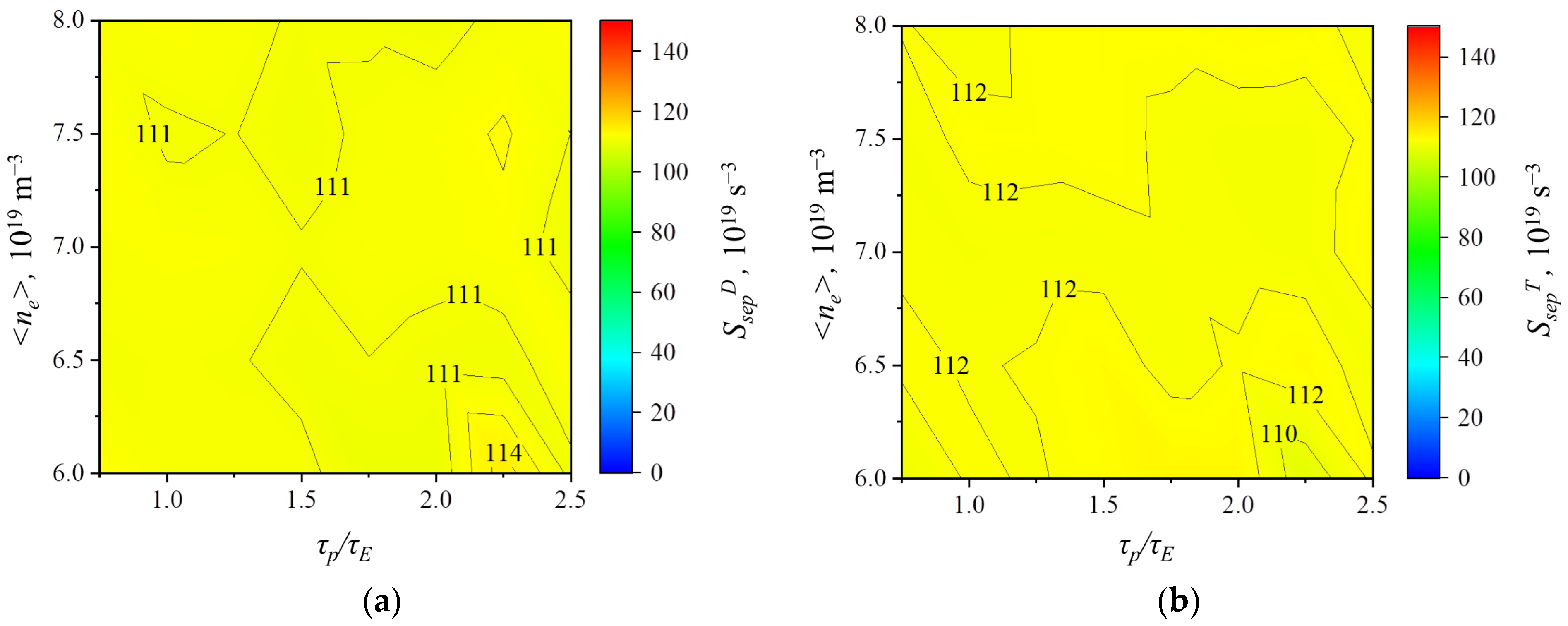
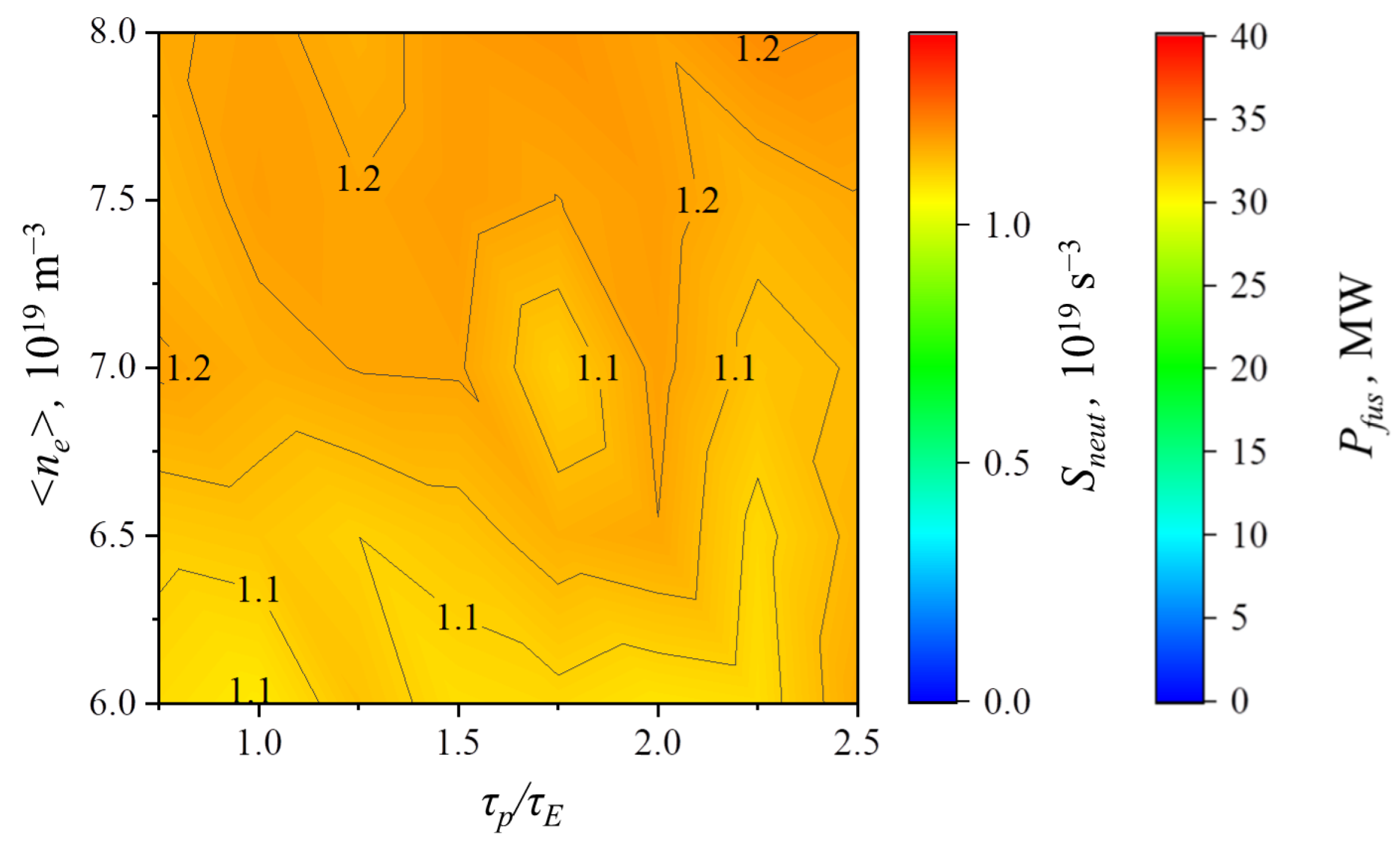
3.5. Parameters of the Neutron Source

Estimates of the maximum neutron yield for the volumetric fusion neutron source in the DEMO-FNS project with 40 MW of fusion power [39,40] give 1.42 × 10¹⁹ s⁻¹. At the same time, calculations by the ASTRA code did not provide [8,13] such values for neutron power and yield. Calculations showed that, in the working window of densities and confinement parameters, the achievable fusion power is >35 MW, which is higher than calculated earlier (see Figure 13). The achievable power increases with increasing plasma density.

It was already noted [13,41] that the total fusion power P_fus is formed by the plasma–plasma and beam–target components and the ratio of these values depends substantially on the plasma and beam compositions. Since, to date, the most promising variant is that using the deuterium NBI, calculations were carried out for this. The obtained dependences of neutron yield S_neut on f_core^T (see Figure 14) are in relatively good agreement with the earlier obtained results [13]. The maximum values of neutron flow can be obtained at f_core^T = 0.7 for the D⁰ beam. In the considered case with f_core^T = 0.5, the neutron yield turns out to be approximately 10% lower than expected, similar to the total fusion power. The dependence of neutron yield S_neut on plasma parameters: density <n_e> and confinement parameter τ_p/τ_E is shown in Figure 13. It is seen that, in the considered working window, the values are quite uniform.

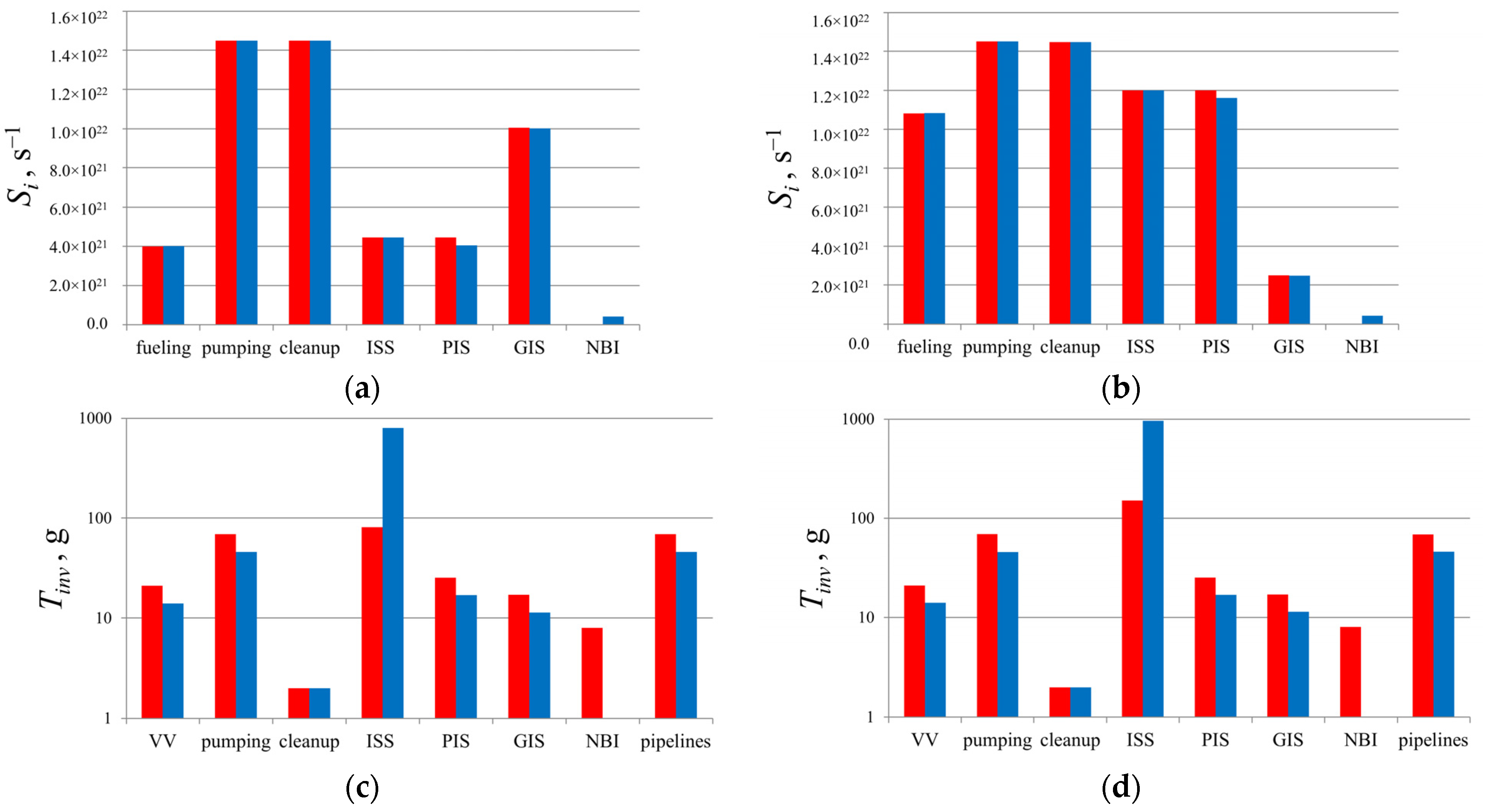
3.6. Tritium Inventories

The total store of tritium, as the most critical fuel component, is calculated by the FC-FNS code using estimates of the FC systems described in [6]. In [22], dependences were given for the tritium store in the FC of the DEMO-FNS facility on particle confinement time τ_p/τ_E for different plasma densities <n_e> for two types of beams (D + T and D). In addition to the case of natural ELMs, whose particle losses were included in the total diffuse losses, convective ELMs that are more frequent with lower stored energy were also considered. In this case, the ion losses from the plasma are expected to be much higher, which requires that its fueling be intensified and that the flows in the FC increase [8]. Note that, in a number of systems, the amount of accumulated isotopes will not change at different plasma parameters. However, in the majority of the FC components, there will be a correlation between flows in the FC and the hydrogen isotopes inventory in them. For this reason, during simulations by the FC-FNS code, for each separate set of plasma parameters, flows in FC and fuel component inventories are calculated [22].

Figure 15 shows the flows and distribution of the hydrogen isotopes inventory in the FC systems in the case of the deuterium beam. Figure 15a,c show the case with natural ELMs, in which the flows in the FC are lower than in the case of convective ELMs shown in Figure 15b,d. According to the accepted FC architecture [21,22], increasing the particle flows across the plasma increases the loads on the PIS and NBI systems and the hydrogen isotope separation system (ISS) that supply them. At the same time, the flow in the gas injection system (GIS), on the contrary, decreases due to the increase in particle flow in the vacuum vessel due to the partial penetration of pellets through the plasma (the penetration efficiency is <1). The maximum flows of particles through the pumping and cleaning systems are independent of the considered scenarios, since they are determined by the engineering parameters: the pressure in the divertor and the pumping rate [22].

Figure 15c,d show that the maximum amount of tritium is accumulated in the pipelines, the pumping system (if cryogenic pumps are used), and in the hydrogen isotope separation and the injection systems. The amount of tritium in the injection systems is determined, in the first place, by the construction of these systems. At the same time, the amounts of tritium and deuterium in the hydrogen isotope separation system are determined by the initial gas flows (from different FC components) and by the isotopic composition of these flows. It was noted in [42] that the method of estimating the amount of tritium inventories in the FC systems with a strong dependence of hydrogen isotope flows on plasma parameters determines the total store of tritium T_inv in the facility. In the described calculations, we use the earlier-developed specialized ISS module of the FC-FNS code to estimate the amount of tritium in the ISS [42].

The values calculated using the new ISS module for the FC-FNS code was lower than those obtained earlier [22]. The estimate of the contingency stock required during the temporary stop of the tritium reproduction systems (for repairs or maintenance) remained the same, and it is about 100 g of tritium. Without taking into account the tritium produced in the blanket of the facility and the tritium stored in the long-term storage for outside consumers, from 350 to 400 g of T₂ will be found at the facility site depending on the ELM scenario (taking into account the losses from radioactive decay). The store of T in the FC (without taking into account the long-term storage), including the particle losses in ELMs, depending on the particle confinement time τ_p/τ_E and plasma density <n_e>, are shown in Figure 16. The increase in the flows of fuel components through the injection system, the isotope separation system, and some other systems when convective ELMs are taken into account leads to an increase in the storage of T in the FC. The amount of T in the FC increases to 500 g in the working window of plasma parameters, the density <n_e> and the confinement τ_p/τ_E for α_ELM = 0.4 for convective ELMs.

As discussed above, the changes in flows in the gas injection system S_GIS do not lead to changes of flows in the fuel injection system or the hydrogen isotopes separation system, which can contain the maximum amounts of tritium. However, this leads to an increase in stored tritium in the gas pumping, processing, and puffing systems by up to 50 g in the considered window of parameters.

4. Conclusions

The tritium fuel cycle (FC) systems have to provide the conditions for burning and heating of the plasma and for current generation (by injection of fast atom beams), provide the residual detritylation of gases and processing of waste, and also contain minimum stores of hydrogen isotopes. The particle flows in the FC are determined by the flows into the pumping system from the vacuum chamber (the divertor region) and the flows in the injection system required the maintaining the necessary parameters of the core plasma. The simulation of flows of particles in the FC systems has to be conducted consistently with the core and divertor plasma.

For simultaneous simulations of the core and divertor plasma, the indirect integration of the ASTRA and SOLPS4.3 codes is used. The one-dimensional simulation of the main plasma by the ASTRA code is supplied with the boundary conditions and limitations presented in the form of scalings obtained by two-dimensional simulations of the edge plasma by the SOLPS4.3 code. Simulation of hydrogen flows in the FC systems is performed by the FC-FNS code. In the developed approach, feedback is realized between the pumping and injection systems in the form of changes to the isotopic composition of the core and divertor (edge) plasma.

In the article, the further development of the approach is described that uses ions instead of electrons in the particle transport equations in the ASTRA code. This allows one to estimate the “partial confinement times” in plasma of ions from different sources (neutral beam injection, pellets, gas injection, and recycling) more accurately. The case was simulated of the injection of a deuterium beam into the plasma of DEMO-FNS with the isotope density ratio D:T = 1:1. In this work, calculations were carried out in the range of confinement parameters τ_p/τ_E = 0.75–2.5, since this range covers the experimental values D/χ_e = 0.2–0.75. The calculated “partial confinement times” are presented for all sources. Estimates were made of the change in the particle flow through the pellet injection system that is required to compensate for the additional losses from the plasma in the case of stimulated convective ELMs. The stores of tritium in the FC systems of DEMO-FNS were estimated, including the case of convective ELMs.

It was shown that the values obtained by the ion equations are lower than the values obtained earlier by parameterizing the calculation results obtained by the ASTRA code. The losses from the plasma turn out to be up to 1.5 times lower than in earlier estimates in the working window of parameters. The flows of particles from pellets into the plasma required to provide the given density are also 1–2.7 times lower than those calculated earlier (in the corresponding working points) and are 10²² particles/s. The increase in the fuel flow needed to compensate for the particle losses in ELMs is 2–3 times, depending on the value of α_ELM, is 1–1.6 times lower than the earlier estimates.

The value of gas injection was analyzed, taking into account the possible degassing from the vacuum vessel wall. Limitations were shown, due to the chosen engineering solutions. Under the assumption of the total flow of particles onto the wall of DEMO-FNS, an estimate was obtained of the intensity of gas injection equal to 1.6 × 10²² s⁻¹ (33 Pa m³/s), which is necessary to be able to compensate for the excessive degassing from the vessel wall under steady-state operation mode of facility. At the same time, to date, the DEMO-FNS project allows the effective pumping rate of ~30 m³/s, which limits gas puffing at rates ≤ 10²² s⁻¹ (in the considered window of parameters). At the same time, the evacuated flows (taking into account the particle losses in convective ELMs) are close to or exceed the existing engineering limitations of the pumping system. Thus, refining the gas conditions at the first wall is extremely important for the optimization of the gas puffing system and the engineering solutions for the pumping system.

It was shown that, in a fraction of the considered working range, the injection frequencies of fuel HFS pellets that contain up to 10% of the number of particles in the plasma (N_pel ≤ 5.0–7.0 × 10²⁰ for <n_e> = 6.0–8.0 × 10²⁰ m⁻³, respectively) are lower than the obtained estimate f_pel < f_ELM (δW_ELM ~ 0.5 MJ). In this case, to control ELMs, it is necessary to decrease the size of the pellets or provide additional LFS injection. Preliminary estimates show that this is possible in the entire working window for α_ELM = 0.2–0.4. The controlled energy losses in ELMs δW_ELM can be decreased in a similar manner, but this requires additional analysis, which is being conducted currently and is outside the scope of this work.

For the starting load of the FC and stationary operation of the FC systems, about 400 g of T₂ are required, taking into account the losses from radioactive decay. The tritium stores at the site of the facility (without taking into account the long-term storage) in the convective ELMs scenario increase to 500 g.