Next Article in Journal
Health State Assessment of Road Tunnel Based on Improved Extension Cloud Model
Previous Article in Journal
Calculation of Consistent Plasma Parameters for DEMO-FNS Using Ionic Transport Equations and Simulation of the Tritium Fuel Cycle
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 13
Issue 14
10.3390/app13148553
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Finite Element Method (FEM) Modeling of Laser-Tissue Interaction during Hair Removal

by
Zan Klanecek
1,
Rok Hren
1,2,
Urban Simončič
1,3,
Blaz Tasic Muc
4,
Matjaž Lukač
1,2,3 and
Matija Milanič
1,3,*
1
Faculty of Mathematics and Physics, University of Ljubljana, 1000 Ljubljana, Slovenia
2
Institute of Mathematics, Physics, and Mechanics, 1000 Ljubljana, Slovenia
3
Jozef Stefan Institute, 1000 Ljubljana, Slovenia
4
Fotona d.o.o., 1000 Ljubljana, Slovenia
*
Author to whom correspondence should be addressed.
Appl. Sci. 2023, 13(14), 8553; https://doi.org/10.3390/app13148553
Submission received: 15 June 2023 / Revised: 17 July 2023 / Accepted: 20 July 2023 / Published: 24 July 2023
Browse Figures
Versions Notes

Abstract

:
In this study, a comprehensive and realistic model of laser light interaction with skin and hair was constructed. The model was applied to study the characteristics of laser-tissue interaction for the deeply penetrating Nd:YAG laser. Three types of finite element method (FEM) models were developed. In the first model, the hair shaft grew straight out of the follicle; in the second model, it grew at a variable angle; and in the third model, an array of hair was considered. The transport equation and heat diffusion equation were solved with the mesh-based Monte Carlo method and partial differential equations, respectively. The results of the simulations indicated that the area of necrosis increased with increasing fluence; cooling had a limited effect on the extent of necrosis, particularly at a fluence of 80 J/cm2. The thermal damage to hair follicles on the periphery of an irradiated array of hair may be insufficient for achieving necrosis. The pulse itself and the short cooling-down period after the pulse contributed the most to the final thermal damage to the hair follicle. The FEM modeling of laser-tissue interaction has proven to be a useful tool for studying the influence of different therapeutic parameters on the resulting hair and skin damage.

1. Introduction

In recent decades, laser technology has become an increasingly prevalent tool for hair removal, both for aesthetic and health-related purposes [1,2,3,4]. When compared to conventional practices such as shaving, waxing, chemical depilatories, and electrolysis, laser hair removal procedures appear to be fast, with long-lasting results and minimal side effects [5,6]. The mechanism of laser hair removal has been well described and is based on irreversible photothermal damage to hair follicles through the use of a light source at the red or infrared end of the spectrum [1]. Among the critical factors influencing the effectiveness of laser hair removal are the laser wavelength, duration of the pulse, fluence, and cooling method [1]. The main advantage of laser hair removal is selective photothermolysis, while most complications can be prevented by correctly selecting the laser type tailored to each patient and adjusting parameters and cooling [7]. It is imperative to have well-trained personnel with in-depth knowledge of the procedures to perform laser treatments effectively and safely [7].
The most frequently used laser hair removal systems are ruby laser (694 nm), alexandrite laser (755 nm), pulsed diode lasers (800, 810 nm), and Nd:YAG laser (1064 nm); in addition, intense pulsed light (IPL) sources with a broad spectrum (within 500–1200 nm) are also being used for hair removal [7]. In this article, we exclusively focus on the long-pulse Nd:YAG laser (1064 nm), which is characterized by the largest penetration within skin due to its low absorption and scattering, while at the same time the absorption in the hair follicle is sufficiently high to achieve irreversible damage to this area.
Ideally, the duration of the laser pulse should be shorter than the thermal relaxation time of the hair and longer than that of the epidermis in order to achieve effective hair removal while avoiding unnecessary skin damage [1]. However, since the epidermal and hair relaxation times both vary in the range of 1–100 ms, with thinner hair having a shorter relaxation time, this approach may not always be viable [8]. For example, one of the challenges involved with commercial diode laser hair removal systems is their very long pulse duration [1].
Most commonly, induced skin cooling is used to prevent epidermal damage. The fastest cooling method, albeit with certain risks involved, is a cryogenic cooling spray that evaporates immediately and very quickly removes heat from the epidermis without substantially changing the temperature in the deeper layers of the skin [9,10]. Safer methods include contact cooling with cold metal and induced cooling with cold air [11,12]. Most recently, a DMC (Dry Molecular Cooling) technology has been introduced that is based on a controlled fine water spray, combining the positive features of the cryogenic spray and cold air cooling [13].
Numerical modeling of laser-tissue interaction is useful as it can aid in optimizing the design and validation of laser hair removal protocols and systems by methodically assessing the influence of various parameters before submitting patients to unnecessary clinical trials. It is therefore somewhat surprising that, according to our knowledge, there has been only one published study [14] that applied an adequately realistic numerical modeling technique to simulate light and heat transport during laser hair removal. Specifically, Sun et al. [14] systematically simulated hair removal with an IPL device for wavelengths between 400 and 1200 nm, with fluences from 5.0–7.0 J/cm2 and pulse lengths of 2.5–25 ms. Their approach was based on the three-dimensional modular adaptable grid model of Pfefer et al. [15] and contained epidermis and dermis, while the hair was approximated as a cylindrical sleeve with a truncated sphere.
The primary aim of the present study was to extend the formalism of Sun et al. [14] by adding an additional tissue type to the finite element method (FEM) model in order to be able to study hair removal characteristics for the deeply penetrating (up to ~1 cm) Nd:YAG laser. The developed model was then used to study laser-tissue interaction depending on the exit angle of the hair relative to the skin surface and for a more realistic situation where multiple hairs are concurrently irradiated by a large spot-size laser beam. Additionally, the influence of externally applied cooling on the resulting skin and hair damage was evaluated.

2. Materials and Methods

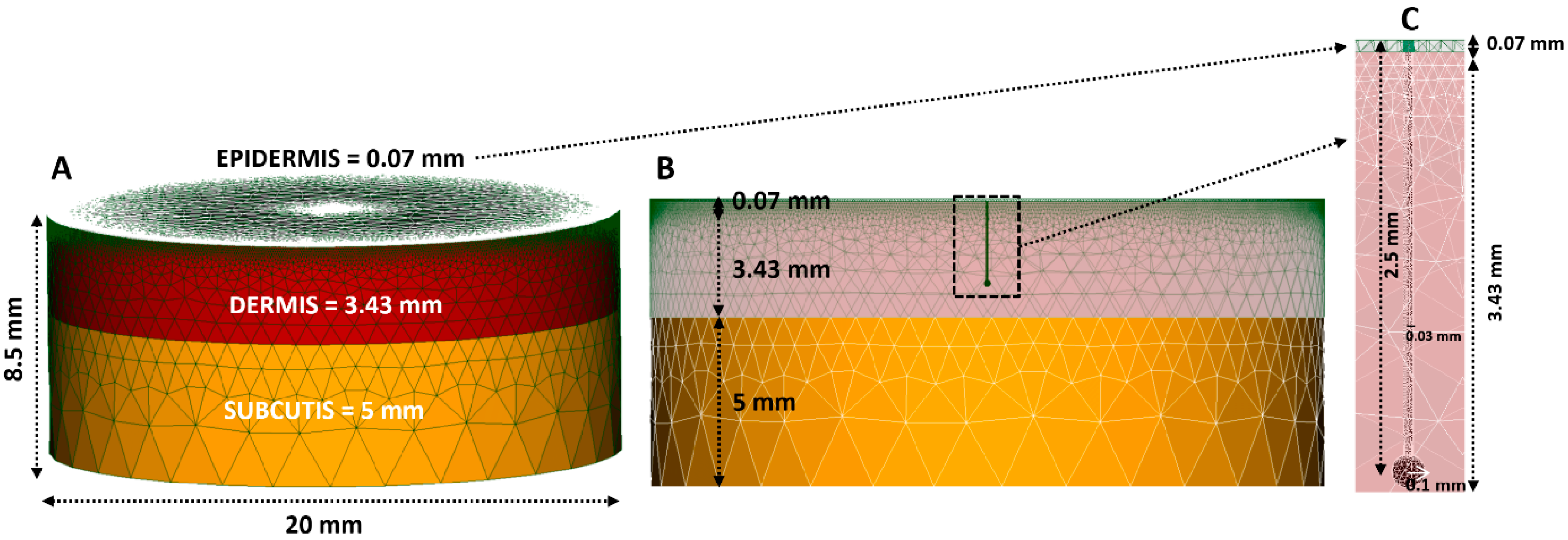
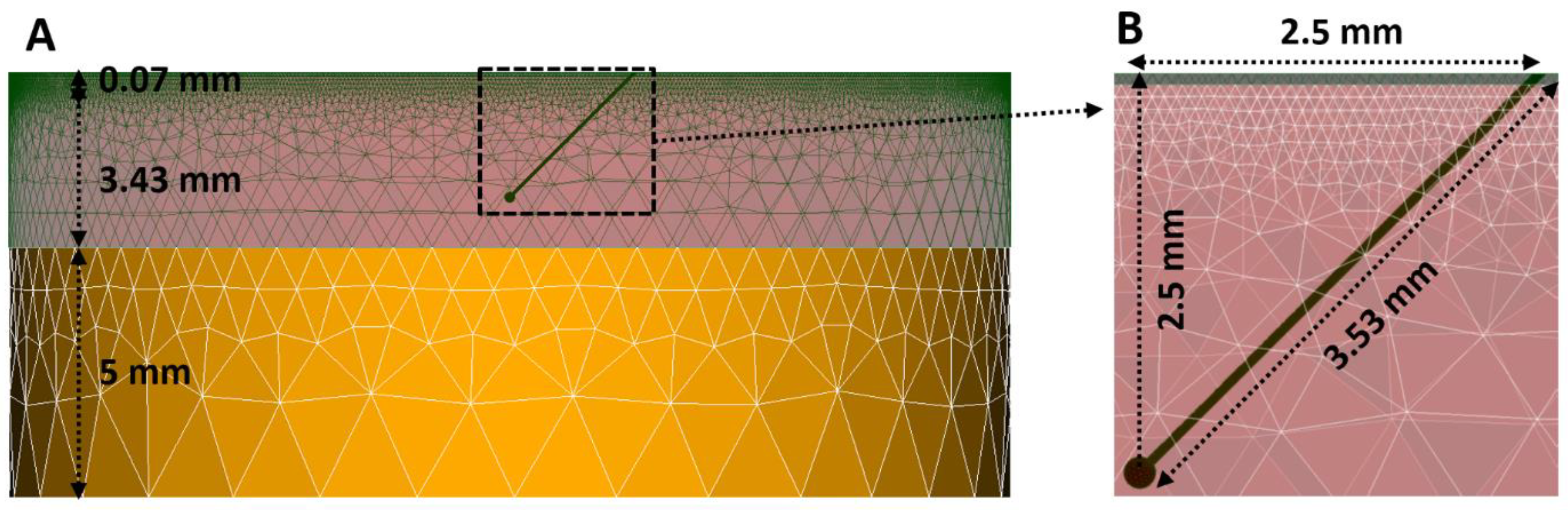
2.1. FEM (Finite Element Method) Modelling

We developed our skin and hair modeling for the Nd:YAG laser using the finite element method (FEM), building upon previous research [14,15]. To ensure accurate results, we adapted the model’s geometric shape to a cylinder instead of the conventional rectangular shape with sharp corners. This modification reduced the need for a larger number of volumetric elements while maintaining comparable accuracy. SALOME (v7) software was used to create mesh models. The process began by generating the geometry of the mesh, with careful consideration given to achieving a seamless connection between the surfaces to eliminate any gaps. Subsequently, the NETGEN [16] algorithm was employed to establish a surface mesh, which served as a foundation for generating the volumetric mesh.
Overall, we created three types of models: FEM Model #1, FEM Model #2, and FEM Model #3.
The FEM Model #1 had a radius of 10 mm, a height of 8.5 mm, and included the epidermis [14,17], dermis [14,18], subcutis [19], hair shaft [20], and follicle [21], as shown in Figure 1. The thicknesses of the epidermis, dermis, and subcutis were 0.07 mm, 3.43 mm, and 5 mm, respectively. The hair was placed at the center of the model cylinder. The hair shaft was modelled as a tiny cylinder with a radius of 0.03 mm and a length of 2.5 mm, oriented along the long axis of the larger cylinder, while the follicle had a radius of 0.1 mm and was located at a depth of 2.5 mm [19]. In simulations, we applied laser beams with a radius of no more than 4 mm; therefore, the width of the model was deemed sufficient to account for the multiple scatterings of photons [14].
Hair typically exits the skin at an angle, and for that purpose, FEM Model #2 was built, identical to FEM Model #1, with the only difference being that the hair shaft grew out of the follicle at different angles. In Figure 2, an example is depicted for the angle of 45°. In that specific case, the hair was 3.53 mm long, exiting the skin at the coordinates x = 2.5 mm and y = 0 mm (instead of x = 0 mm and y = 0 mm when considering straight hair). The exit point of the hair from the skin was thus still covered by a laser beam with a radius of 4 mm.
The surface density of hair on human skin has on average 14–32 hair follicles per square centimeter [20], which we have taken into account with the even more realistic FEM Model #3, with an array of hair arranged in the shape of a cross (Figure 3); this arrangement corresponded to a density of 18 follicles per square centimeter.

2.2. Laser-Tissue Interaction

The transport of photons in the tissue is the first of the two main physical processes occurring during laser hair removal. In the first step, we simulated the irradiation of each of our FEM models and, to that end, used the mesh-based Monte Carlo method (MMCM) [22] as an implementation algorithm for solving the transport equation. The MMCM algorithm assumed homogeneity of the optical properties of the tissue within each tetrahedral element and allowed for parallelization via several processor cores or a graphics card, which significantly accelerated the simulations [23]. Our software enabled varying the type, dimension, and direction of the laser beam. The optical properties of different tissue types used in simulations are summarized in Table 1. While a substantial amount of work has been carried out in determining the optical properties of human skin and hair [24,25], it has been noted [26] that the tabulated values of optical properties may have a range of values and may be determined only for specific wavelengths; additionally, the absorption coefficients of epidermis and hair have proven to be particularly difficult to assess because they contain melanin, which exhibits pronounced inter-subject variability [27,28,29,30,31,32]. For that reason, we have developed, verified, and piloted a protocol for in vivo measurement of absorption coefficients of epidermis and hair in human subjects, which is described in detail in Appendix A.
The second modeled physical process is heat diffusion within the tissue. The absorbance calculated by MMCM for each tissue type and each FEM element was converted into a heat source (W/mm3). The calculated heat source was then fed into the heat diffusion equation, subject to the initial conditions, the boundary conditions between the tissue surfaces, and the convective thermal boundary condition with a constant heat transfer coefficient h, as specified in Appendix B [14]. Again, homogeneity of the thermal properties of the tissue within each tetrahedral FEM element was assumed. We solved the heat diffusion equation in the MATLAB software environment (R2019b) using the PDE toolbox. The “createpde” function was employed with the parameters “thermal” and “transient” to simulate the time-varying temperature distribution in a model. To simulate different therapeutic protocols, we varied the laser fluence and pulse duration, or forced cooling parameters. The thermal properties of the tissues used in the simulations are summarized in Table 2.

2.3. Thermal Damage Estimation in the Tissues

Although thermal damage to the tissue depends on many complex mechanisms, it is accepted that the time course can be well approximated by a single process of protein denaturation. It is described by a simple kinetic first-order expression known as a damage integral Ω (x, y, z, t), based on the Arrhenius equation [33,34,35],
Ω x ,   y ,   z ,   t = ∫ 0 t A e − E a R T x ,   y ,   z ,   τ d τ
The values for the Arrhenius constants A and Ea were assumed to be the same for all tissue types and were set at 2.9 × 1037 s−1 and 240 J/mol [36]. When the value of Ω (x, y, z, t) equaled at least 1, then at least 63% of cells within the given tetrahedral FEM element were deemed to be dead. This meant that the skin tissue within that element was irreversibly damaged.

2.4. Simulation Protocols of Thermal Damage in the Tissue

Before applying simulation protocols, we thoroughly tested our FEM modeling approach by comparing the results of simulations with the publication of Sun et al. [14], as outlined in Appendix C.
In the first simulation protocol (Protocol #1), we applied the following:
-
The simulated laser beam, with a wavelength of 1064 nm and a disc-shaped radius of 4 mm, was directed perpendicularly to the short-axis center of FEM Model #1, FEM Model #2, and FEM Model #3.
-
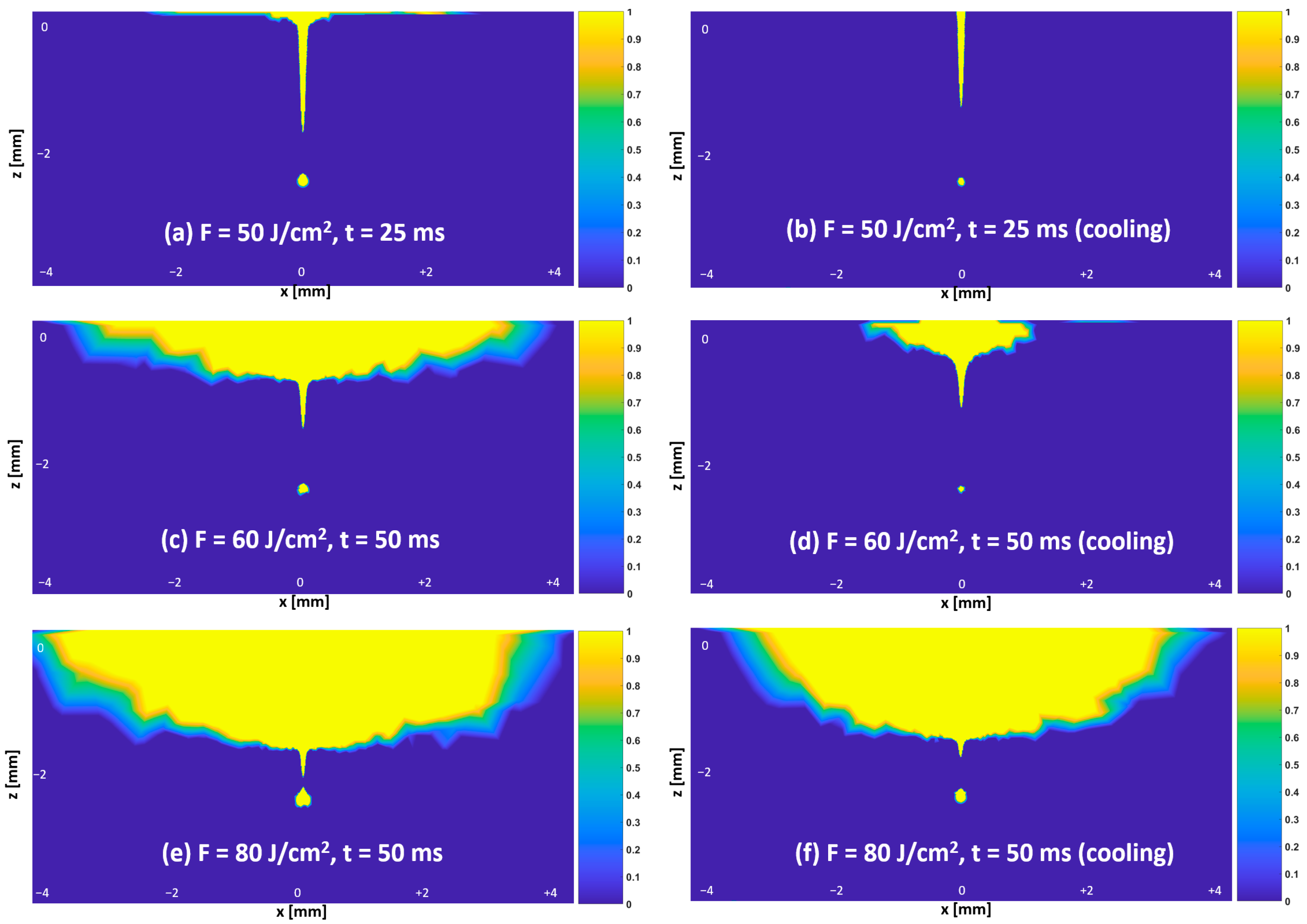
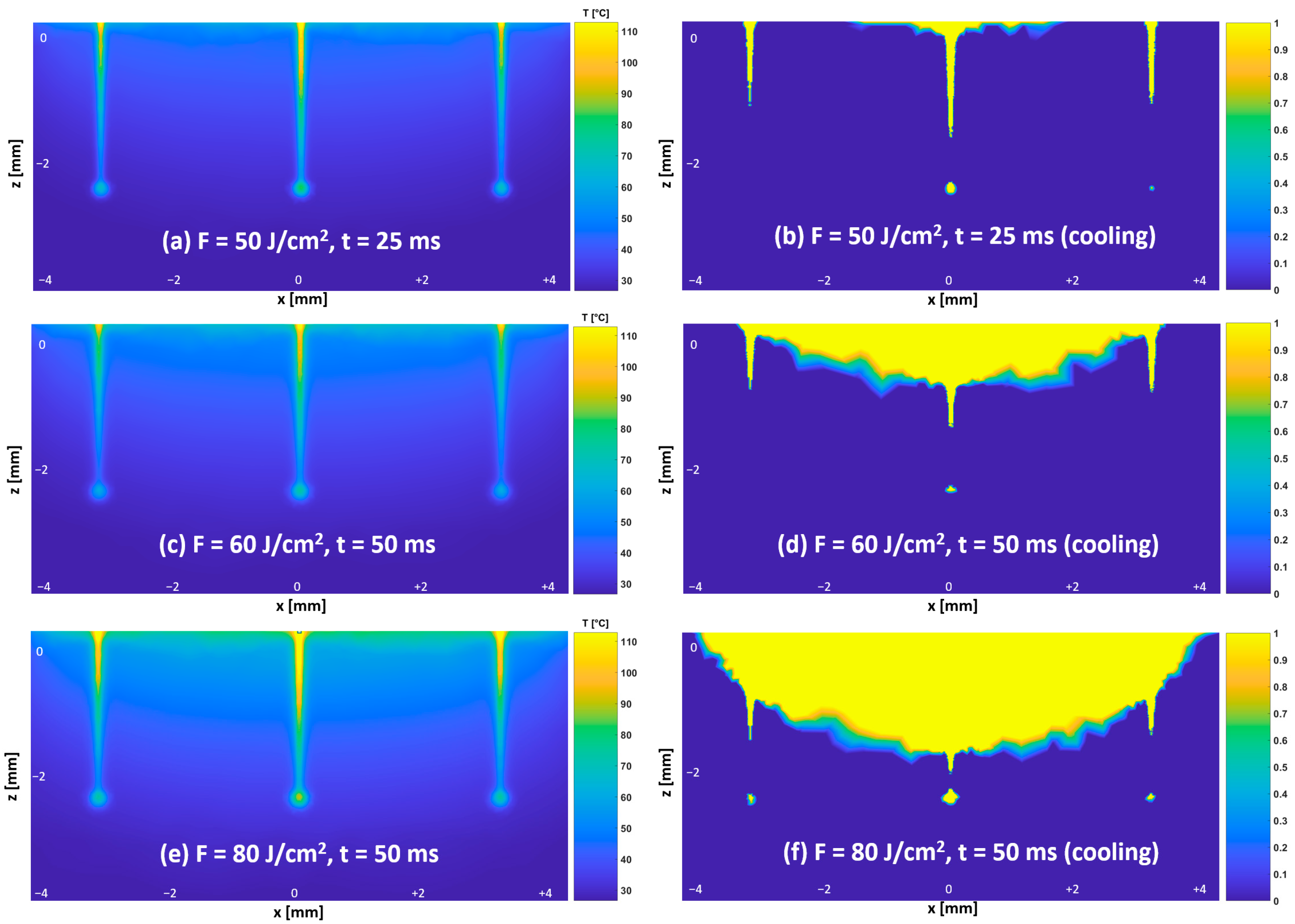
The parametric study was undertaken by varying the fluence and pulse duration: we closely followed the clinical study [37] and accordingly used combinations of fluence and pulse duration of (i) 50 J/cm2 and 25 ms, (ii) 60 J/cm2 and 50 ms, and (iii) 80 J/cm2 and 50 ms.
-
We explicitly considered the (i) mode without forced cooling, with a value of the free convection coefficient h of 10 W/m2K [14,38] and ambient temperature T = 22 °C for all three FEM models, and the (ii) mode with forced cooling by means of a cryogenic spray with a convection coefficient h of 5000 W/m2K [39] and spray temperature T = −50 °C [39] for FEM Model #1 and FEM Model #2 only. The forced cooling by cryogenic spray consisted of 10 ms of preliminary cooling, with a 5-ms pause immediately after the pulse and 15 ms of cooling thereafter, as outlined in the clinical study [37].
-
The main outcomes of the simulations were temperature and thermal damage distributions after the completion of the irradiation.
In the second simulation protocol (Protocol #2), we applied a wider laser beam with a diameter of 6 mm and a combination of fluence of 80 J/cm2 and a pulse duration of 50 ms; in this protocol, we considered only the mode without forced cooling. We used the more realistic models, FEM Model #2 and FEM Model #3. The main outcome was a time-dependent curve of cumulative hair-follicle damage for each of the two FEM models.

3. Results

3.1. Optimization of the Laser Beam

The Monte Carlo methodology is a stochastic technique with random sampling, and thus its accuracy inherently depends on the number of simulated photons. To address this attribute, we calculated the absorbance in the hair follicle of the FEM Model #1 for different numbers of photons, ranging from 104 to 109. The simulated laser beam was disc-shaped with a radius of 4 mm and directed perpendicularly to the short-axis center of the FEM Model #1. The average absorbance value of the entire hair follicle was determined by interpolating and spatially integrating values at its vertices. The mean value over the follicle was evaluated ten times (from ten independent simulations), and then the average and standard deviations were calculated, which are presented in Figure 4. The average absorbance was normalized, meaning that the source power was set at 1 W.
As can be clearly seen in Figure 4, average hair-follicle absorbance converged with an increasing number of photons, while the number of photons beyond 107 had virtually no impact on the results. Based on these results, we decided to use 108 photons as the optimal quantity in all simulations.

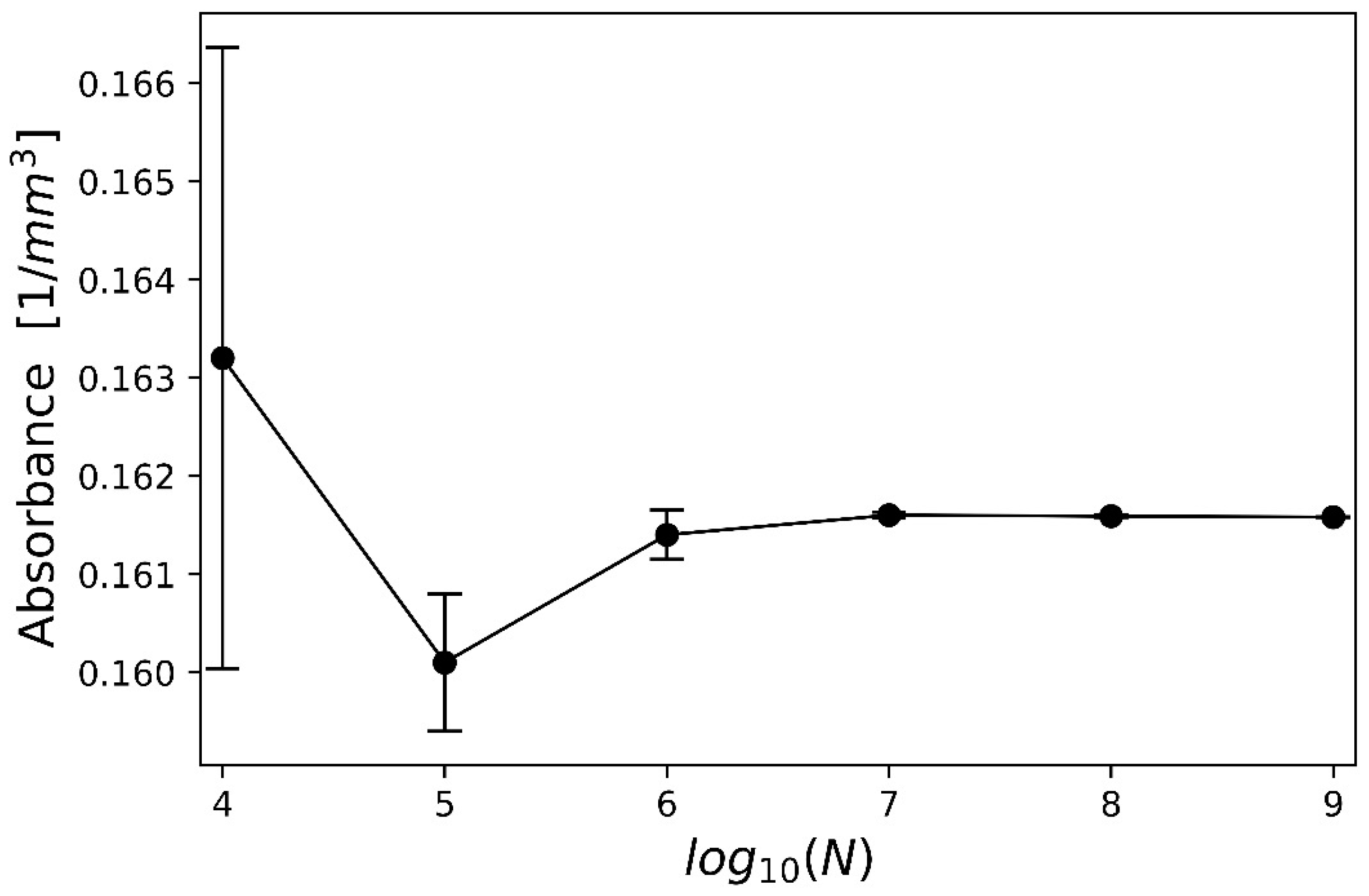
3.2. Optimization of the FEM Model

The FEM models were constructed so that the density of the tetrahedral elements close to the hair shaft and follicle was much higher than the density on the periphery. A high density of tetrahedral elements was also present in the whole epidermis, while in the dermis, far from the hair, the density of tetrahedral elements was lower, with the lowest in the subcutis. The reason for this is that the description of a homogeneous volume, for example the subcutis far from the hair, does not require as many elements as, e.g., a thin epidermis or a tiny hair shaft and follicle. We found that the following ratio in the number of tetrahedral elements between the hair shaft/follicle (Nhair), epidermis (Nepidermis), dermis (Ndermis), and subcutis (Nsubcutis) would be appropriate: Nhair:Nepidermis:Ndermis:Nsubcutis = 10:10:100:1.
To estimate the minimal number of tetrahedral elements, we simulated the average temperature within the hair follicle using a fluence of 5 J/cm2 and a sequence of three consecutive pulses with a duration of 2.5 ms and a pause of 200 ms between each pulse. The average temperature was calculated in the same manner as described above.
Figure 5 shows the dependence of the average temperature of the hair follicle immediately after the first, second, and third pulses, respectively, on the number of tetrahedral FEM elements. We can conclude that the average temperature of the hair follicle starts converging at roughly 500,000 elements, which was taken as the minimal number of elements in our simulations. FEM Model #1 thereby had 422,742 elements, FEM Model #2 had 453,775 elements, and FEM Model #3 had 586,633 elements.
For the selected three models, the simulation speed of the laser-tissue interaction on the Intel i5-8250u CPU was approximately 50,000 photons per second, while the single heat diffusion simulation took approximately 3 h to complete.

3.3. Temperature and Thermal Damage Distributions—Protocol #1

Figure 6 shows temperature distribution maps for FEM Model #1 immediately after irradiation for all three combinations of fluence and pulse duration, both without and with forced cooling. As expected, the maximal temperature (Table 3) occurred at the very tip of the hair shaft due to the hair having a larger absorption coefficient than the epidermis and dermis. The largest gradient was observed along the hair shaft. Interestingly, the temperature in the hair follicle was higher than in the hair shaft just above it, which can be attributed to the hair follicle absorbing a much larger number of scattered photons than the tiny hair shaft. All these observations are congruent with those of Sun et al. [14]. The combination of fluence and pulse duration had a non-intuitive effect, as the maximum temperature increased with increasing fluence but decreased with increasing pulse duration. The maximum temperature at the tip of the hair shaft was thus higher for a fluence of 50 J/cm2 and a pulse duration of 25 ms than for a fluence of 60 J/cm2 and a pulse duration of 50 ms. This happened because the difference in irradiation power normalized to the surface area of the laser beam (2000 W/cm2 in the first case and 1200 W/cm2 in the second case) was not compensated by delivering 17% more energy in twice the amount of time in the second case. The temperature was highest when irradiating the model with a fluence of 80 J/cm2 and a pulse duration of 50 ms. In this case, the irradiation power, normalized to the surface of the laser beam, equaled 1600 W/cm2, but the higher energy and longer pulse were sufficient to deliver the highest temperature among the three combinations. These observations were corroborated by the maximum temperatures calculated within the follicle (Table 3). We observed that cooling had no impact on the follicle temperature.
Figure 7 shows distribution maps of thermal damage Ω for FEM Model #1 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling. As expected, the area of thermal necrosis (where Ω exceeds 1) increased with increasing fluence, while cooling led to the area of necrosis in the epidermis being substantially smaller compared to that without cooling, particularly for the fluence of 50 J/cm2 with a pulse duration of 25 ms and the fluence of 60 J/cm2 with a pulse duration of 50 ms. It is notable that the area of thermal necrosis along the hair shaft toward the hair follicle was not connected, reflecting the temperature gradient along the hair shaft and the fact that the temperature was higher in the follicle than in the hair shaft just above it (Figure 6).
Figure 8 shows distribution maps of thermal damage for FEM Model #2 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling. The area of necrosis in the hair follicle is smaller than in FEM Model #1, and the discontinuity of thermal necrosis along the hair shaft is more extensive. The main reason for this was the lower temperature achieved in the hair follicle due to the hair shaft being longer and at an angle relative to the incoming laser beam. Table 4 reveals that the maximum follicle temperature in FEM Model #2 was consistently lower than in FEM Model #1.
Figure 9 shows temperature and thermal damage distribution maps for FEM Model #3 immediately after irradiation for three combinations of fluence and pulse duration, in a mode without forced cooling. The non-central hair shafts and follicles heated up substantially less than the central hair shaft and follicle; as a result, for a fluence of 50 J/cm2 and a pulse duration of 25 ms, no necrosis occurred in the non-central hair follicles. Table 5 indicates that the maximum temperature of the central follicle was lower than in FEM Model #1 and FEM Model #2 and that a non-central follicle had a 10 °C lower maximum temperature than the central follicle.

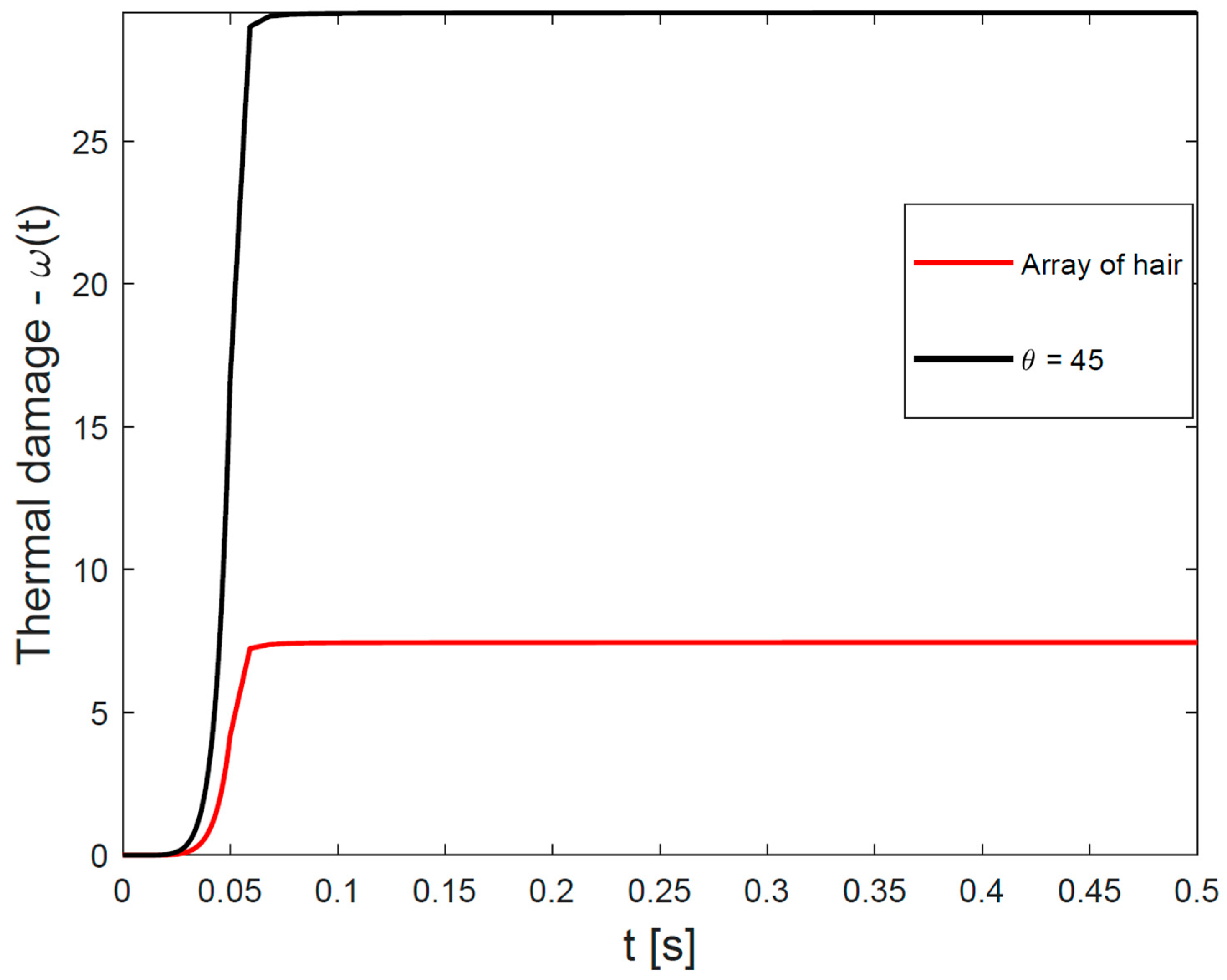
3.4. Time-Dependent Curve of Cumulative Hair-Follicle Damage—Protocol #2

When inspecting the results of cumulative heat damage to the hair follicle for FEM Model #2 and FEM Model #3, shown in Figure 10, we notice that the pulse itself and a short cooling-down period after the pulse contributed the most to the final thermal damage to the hair follicle; in our case, this amounted to 50 ms of the pulse duration and about 20 ms after the pulse, i.e., 70 ms in total. We can hypothesize that the heat damage to an array of hair may have been insufficient to reach necrosis of the hair follicle, which is in line with observations in FEM Model #3 under Protocol #1 (Figure 9).

4. Discussion

This is the first report of an approach to realistic modeling of skin and hair in which laser beam-tissue interaction was studied within an FEM framework. A modeling approach allowed us to examine temperature and thermal damage distributions following irradiation at a wavelength of 1064 nm for three combinations of fluence and pulse duration, with and without forced cooling. Our approach also accounted for the presence of angled hair and hair arrays and is comprehensive enough that it could be applied to further clinical research studies.
In this paper, we have undertaken a parametric study by varying light fluence and pulse duration, closely following the clinical study [37]. We have found that for all combinations of fluence and pulse duration, at least a partial necrosis of the hair follicle at a depth of 2.5 mm occurred, which corroborated the outcomes of the clinical study [37]. Increasing fluence resulted in an increased area of necrosis, particularly in the epidermis and dermis, which again agreed with the clinical study where an increase in the likelihood of damage to the epidermis and dermis was demonstrated, typically manifesting as erythema and perifocal edema [37]. The use of forced cooling made the area of necrosis less extensive, especially in the epidermis, which again agreed with the findings of the clinical study [37].
We have shown that the hair follicle of a hair exiting the skin surface at an angle undergoes less thermal damage than the follicle of a straight hair. In addition, we observed that the thermal exposure of hair follicles on the periphery of an irradiated array of hair may be insufficient for reaching necrosis. This is possibly a partial explanation for why laser hair removal does not remove all of the hair, since during the hair removal procedure, the laser beam is not centered on each hair separately but on a given area. Finally, our simulation study indicated that the pulse itself and a short relaxation time after the pulse contributed the most to the final thermal damage to the hair follicle.
We have also demonstrated that the FEM model of light-tissue interaction in combination with measurements of surface temperature has proven useful in assessing the absorption coefficients of human epidermis and hair. We attempted to develop, verify, and pilot a protocol for in vivo assessment of absorption coefficients of epidermis and hair in humans that could efficiently account for inter-subject variability. As the protocol of our study is simple and comprehensive enough, it may be potentially helpful in a clinical setting.
Because pulses significantly shorter than the hair’s thermal relaxation time are expected to provide the highest temperatures, the initial hair removal lasers were Q-switched Nd:YAG lasers with nanosecond-long pulse durations [40]. However, since the achievable pulse energies of Q-switched lasers limited the fluences to below 2–4 J/cm2 for spot radiuses of 6–4 mm, and typically required using a topical carbon-based solution to enhance hair absorption, most of today’s hair removal procedures are performed with lasers operating in the millisecond (1–50 ms) pulse duration regime [1,3,41,42]. The longer Nd:YAG laser pulse durations, in the range of 25–50 ms, as used in our simulations, are often a preferred choice in order to avoid overheating of the epidermis with a shorter thermal relaxation time. However, our model can be easily adapted to incorporate shorter pulses. Another potential extension of our FEM modeling approach would be to simulate laser treatment of keratinocyte carcinoma [43].
An obvious extension of our study would be to consider thinner hair at different depths and different dimensions of the epidermis, dermis, and subcutis. Another possibility would be to vary skin and hair types. While our study specifically focused on the Nd:YAG laser, it could be easily applied to other lasers operating at shorter wavelengths and then compared to the results of corresponding clinical studies. In our study, we used the well-established Arrhenius damage integral [44], however, we could also consider other models of thermal damage [45]. Further, the model could be applied to study hair removal while taking into account the recently reported “avalanche-type” enhancement of hair temperature increase under repetitive pulse exposures [46]. Our ultimate goal is that the developed FEM model of laser beam-tissue interaction would also prove useful in a clinical setting by aiding the optimal selection of treatment parameters during hair-removal procedures. Using the novel hyperspectral imaging modality [47] could aid in, e.g., collecting information about the quantity of melanin and estimating epidermal thickness, which would in turn be helpful for selecting optimal laser treatment parameters.
In this study, we focused on the Nd:YAG laser, which is known for its ability to treat darker skin tones since the longer wavelength bypasses the melanin in the skin. However, our approach could also be applied to evaluate the effects of other hair removal laser wavelengths and the effects of multiple wavelengths present during IPL treatments. The IPL (Intense Pulsed Light) uses broad-spectrum light to target and remove unwanted hair and is particularly efficient in removing dark hair on fair to medium skin tones. The method is fast and inexpensive, but the major drawback is that it may lead to pigmentation of the darker skin [48]. In spite of our focusing on the Nd:YAG wavelength only, we believe that the major conclusions of our study related to the dependence of the efficacy of the hair removal on the hair density and the angle of the hair shaft apply as well to other light-based hair removal methods.

Author Contributions

Conceptualization, M.M., M.L. and U.S.; methodology, Z.K., U.S. and M.M.; software, Z.K. and U.S.; writing—original draft preparation, R.H. and Z.K.; writing—review and editing, R.H., M.L., M.M., Z.K. and U.S.; visualization, Z.K. and B.T.M.; supervision, M.M. and U.S.; funding acquisition, M.M. and M.L. All authors have read and agreed to the published version of the manuscript.

Funding

The authors would like to thank to the Slovenian Research Agency for their financial support (research core funding No. P1-0389).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

M.L. and B.T.M. are affiliated with the company Fotona, d.o.o.; the remaining authors declare no conflicts of interest.

Appendix A. Protocol for In Vivo Measurement of Absorption Coefficients of Human Hair and the Epidermal Layer

Appendix A.1. Protocol

We assessed the absorption coefficients of the epidermis and hair by combining (i) in vivo measurement of the temperature increase on the surface of a shaved patch of skin with (ii) simulation of the transport of photons and heat diffusion in the tissue. The protocol was verified by measurements and simulations using a phantom with known optical and thermal properties.

Appendix A.2. Measurements

The experiments were performed with a Nd:YAG laser with a wavelength of 1064 nm (Dualis VP, Fotona d.o.o., Ljubljana, Slovenia). The laser beam, with a diameter of 6 mm, was directed at an angle of about 35° to the surface of the specimen. The pulse had a top-hat shape, while fluences of 20 and 40 J/cm2, both in combination with a duration of 30 ms, were used. The irradiated area was partially fixed by an aperture made of transparent plexiglass; temperature measurements on the surface were taken at approximately 1 s before the pulse, during the pulse, and approximately 4 s after irradiation using a high-speed IR (infrared) camera (SC7500 FLIR Systems, Boston, MA, USA) with a 50 mm lens and a nominal temperature sensitivity NEDT of 20 mK. Radiometric images were captured at a frequency of 1000 Hz, and a different spot on the skin was irradiated each time.
A male subject, aged 25, was enrolled in the study with Fitzpatrick II skin type and dark hair. The study was conducted according to the guidelines of the Declaration of Helsinki and was approved by the Medical Ethics Committee of the Republic of Slovenia (protocol number 0120-365/2017-9); the subject signed an informed consent form. Temperature rises on the skin surface were recorded in different areas of freshly shaved forearm skin, hand-cleaned with cotton wool and ethanol, and finally air-dried. This anatomical location was chosen because of its easy accessibility for the experimental setup and ease of handling. Experiments were also undertaken using a PlatSil SiliGlass type C tissue-mimicking phantom with known optical and thermal properties [49]. All personnel present during the laboratory experiment wore appropriate eye protection.

Appendix A.3. Simulations

To simulate the transport of photons and heat diffusion in the tissue, we used the finite element method framework (FEM) in combination with the mesh-based Monte Carlo method (MMCM), as described in the main body of this article and Appendix B. The FEM model of the PlatSil SiliGlass type C tissue-mimicking phantom had the following optical and thermal properties. The absorption and scattering coefficients µa and µs were 0.035 mm−1 and 5.9 mm−1, respectively; the anisotropy factor g was set to 0.7; the refractive index n was 1.44 [49], while the specific heat cp, thermal conductivity k, and density ρ were 703 J/kgK, 1.38 W/mK, and 2203 kg/m3, respectively [49]. The FEM model of the phantom was homogeneous, i.e., had only one tissue type and had 8,697 tetrahedral elements. To assess the absorption coefficients of the epidermis and hair, we used the realistic FEM Model #1 with the optical and thermal properties of different tissue types specified in Table 1 and Table 2, respectively, with the µa for the epidermis and hair obviously missing.
Verification of the protocol using the PlatSil SiliGlass type C tissue-mimicking phantom.
Figure A1 shows the temperature distribution map on the surface of the PlatSil SiliGlass type C phantom immediately following irradiation with a fluence of 50 J/cm2 and a pulse duration of 30 ms. In the center of the irradiated area, the temperature increase amounted to more than 30 K. The time course of the temperature change in the center of irradiation following the pulse is shown in Figure A1, where we can see that experimental measurements agree well with simulation results.
Applsci 13 08553 g0a1 550
Figure A1. Verification of the experimental protocol using a PlatSil SiliGlass type C tissue-mimicking phantom. (A) The temperature distribution map on the surface of the phantom immediately after irradiation with a fluence of 50 J/cm2 and pulse duration of 30 ms; (B) time course of the temperature change in the center of irradiation following the pulse. Dashed lines represent experimental measurements, and solid lines represent simulation results.
Figure A1. Verification of the experimental protocol using a PlatSil SiliGlass type C tissue-mimicking phantom. (A) The temperature distribution map on the surface of the phantom immediately after irradiation with a fluence of 50 J/cm2 and pulse duration of 30 ms; (B) time course of the temperature change in the center of irradiation following the pulse. Dashed lines represent experimental measurements, and solid lines represent simulation results.
Applsci 13 08553 g0a1

Appendix A.4. Skin Measurements

Figure A2 shows the time course of the temperature change in the human subject following irradiation of (i) hair on the skin surface and (ii) skin at two different locations distant from visible hair. For the case with a fluence of 20 J/cm2 and a duration of 30 ms, the temperature increase was 16 °C, while in the case with a fluence of 40 J/cm2 and a duration of 30 ms, the corresponding increase was 41 °C.
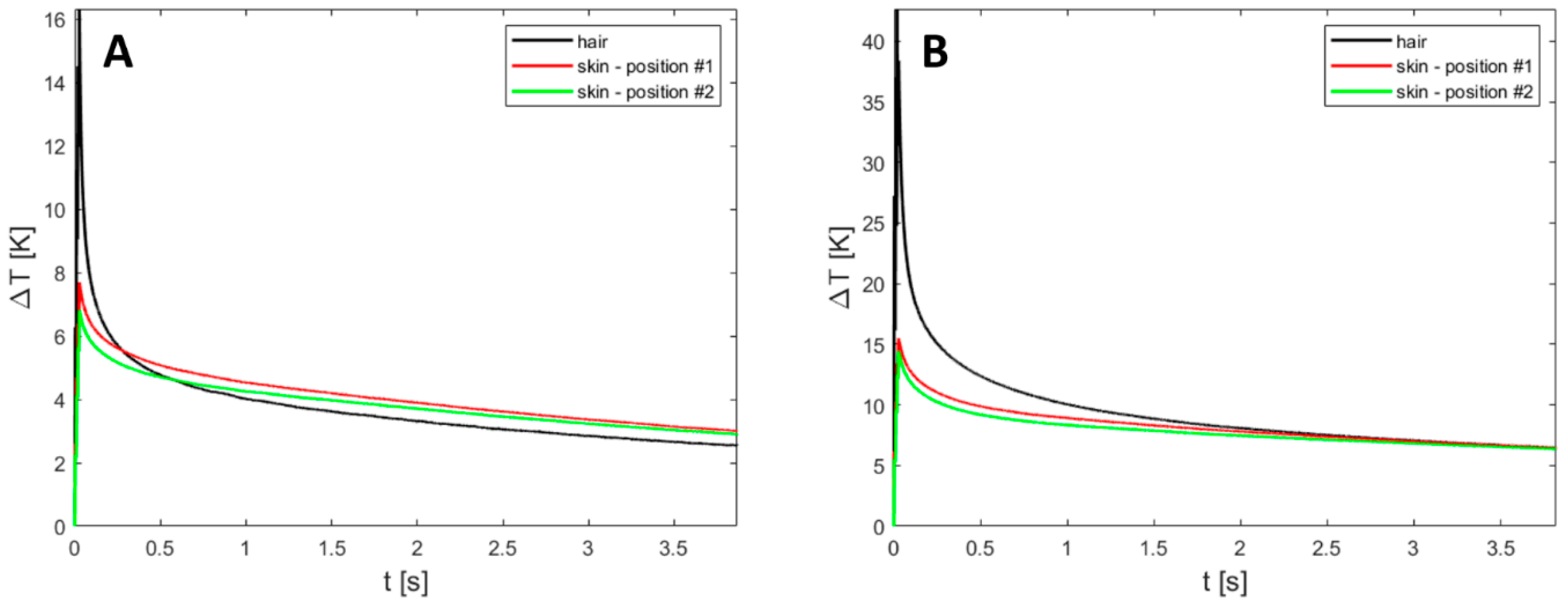
Applsci 13 08553 g0a2 550
Figure A2. Time course of the temperature change following irradiation of (i) hair and (ii) skin at two different locations distant from visible hair in a human subject. (A) Fluence of 20 J/cm2 and duration of 30 ms; (B) fluence of 40 J/cm2 and duration of 30 ms.
Figure A2. Time course of the temperature change following irradiation of (i) hair and (ii) skin at two different locations distant from visible hair in a human subject. (A) Fluence of 20 J/cm2 and duration of 30 ms; (B) fluence of 40 J/cm2 and duration of 30 ms.
Applsci 13 08553 g0a2

Appendix A.5. Simulations

As the absorption coefficient mainly affects the temperature increase on the surface of the skin during irradiation, we decided to assess the absorption coefficient of skin and hair in such a way that the experimental measurements and simulated results were matched at the moment of maximum temperature increase. Figure A3 shows the measured and simulated time course of the temperature change in both subjects following irradiation of hair and skin; we exhibit a fluence of 40 J/cm2 and a duration of 30 ms, while a fluence of 20 J/cm2 and a duration of 30 ms gave similar results. As we can see, the measured and simulated results for the epidermis matched very well, and the absorption coefficient of the epidermis µa was 0.069 mm−1. For hair, the correspondence between the measured and simulated time course of the temperature change was worse; we attribute this to the fact that the absorption coefficient regulates only the temperature increase but has no effect on relaxation, which may very much depend on the thickness of the hair and the proximity of adjacent hairs. The absorption coefficient of the hair µa was estimated at 0.56 mm−1.
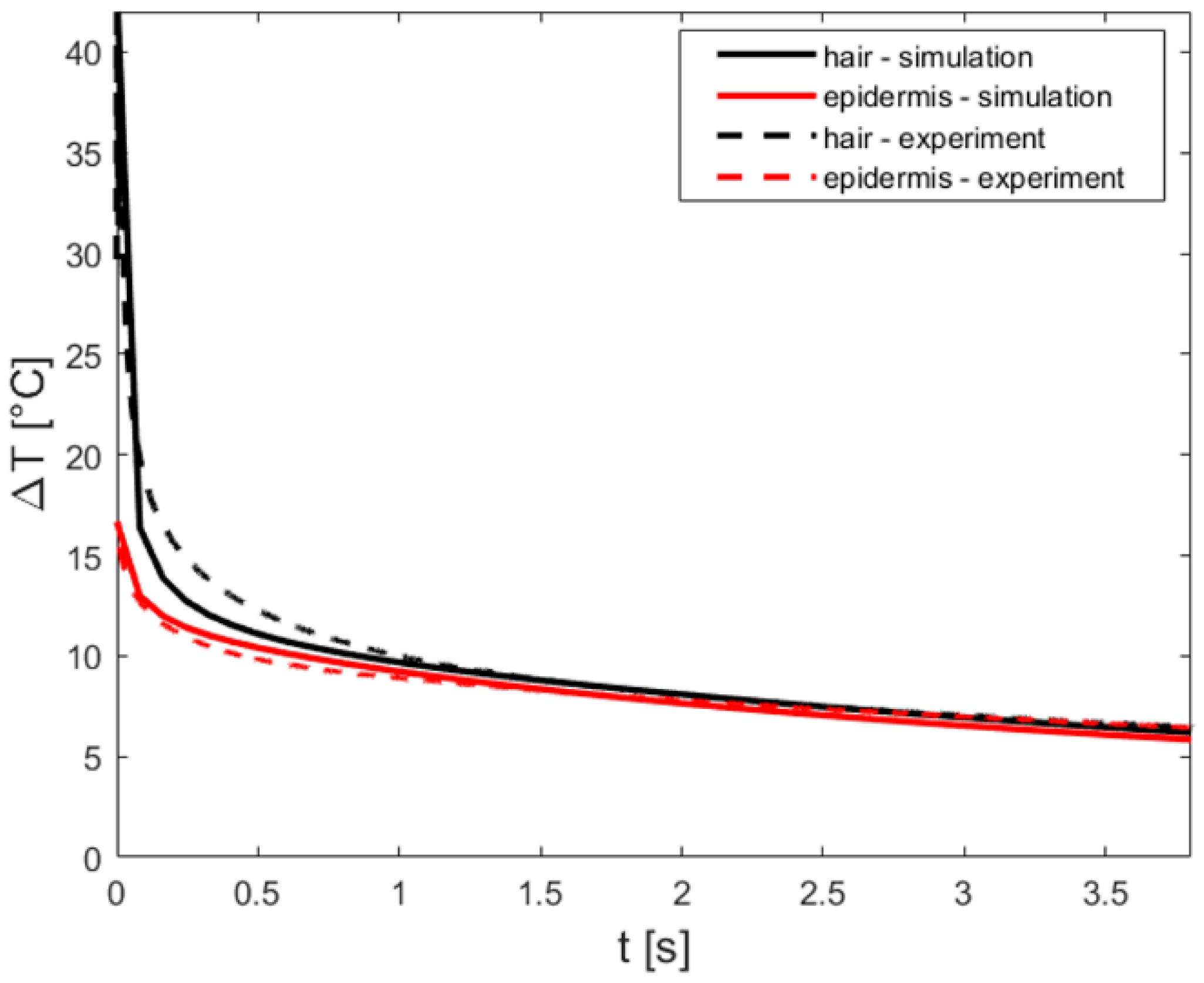
Applsci 13 08553 g0a3 550
Figure A3. Time course of the temperature change following irradiation in a human subject for a fluence of 40 J/cm2 and a duration of 30 ms. Dashed lines represent the experimental measurements, and the solid line represents the simulation results.
Figure A3. Time course of the temperature change following irradiation in a human subject for a fluence of 40 J/cm2 and a duration of 30 ms. Dashed lines represent the experimental measurements, and the solid line represents the simulation results.
Applsci 13 08553 g0a3

Appendix B. Heat Diffusion Equation

Formalism of the heat diffusion process was described for each tissue type and each FEM element as follows [14]:
ρ c p ∂ T ∂ t = ∇ k ∇ T + Q
where T is temperature, ρ is density, c p is specific heat capacity, k is thermal conductivity, and Q is the heat source due to absorption of photons, which was calculated by the mesh-based Monte Carlo method (MMCM). The initial temperature profile was in the form of a linear temperature gradient, namely, the temperature varied continuously from the surface of the skin (i.e., the top of the epidermis) to the bottom of the subcutis from 32 °C to 37 °C, after which it remained constant. The model was subject to the convective thermal boundary condition.
k ∂ T ∂ z = h T − T a i r
where k is the conductivity of hair or epidermis, h is a constant heat transfer coefficient, and T a i r is the ambient temperature (20 °C).

Appendix C. Validating a Finite-Element Method Model for Simulating Laser-Tissue Interaction in Hair Removal Systems

The FEM model for validating our simulations with the results of Sun et al. [14] had a cross section of 2 mm × 2 mm, a height of 3.5 mm, and included the epidermis, dermis, hair shaft, and follicle, as shown in Figure 1. The thicknesses of the epidermis and dermis were 0.07 mm and 3.43 mm, respectively. The hair was placed at the center of the model. The hair shaft was modeled as a tiny cylinder with a radius of 0.1 mm and a length of 3 mm, while the follicle had a radius of 0.5 mm and was located at a depth of 2.5 mm. In simulations, we applied laser beams with a radius of no more than 1 mm; therefore, the width of the model was deemed sufficient to account for the multiple scatterings of photons. The FEM model had a total of 800,000 tetrahedral elements.
Applsci 13 08553 g0a4 550
Figure A4. A three-dimensional representation of the Finite-Element Method (FEM) model of skin and hair for validating our simulations with the results of Sun et al. [14]. The model includes epidermis, dermis, hair shaft, and follicle and has a radius of 10 mm and a height of 8.5 mm; the thickness of epidermis and dermis is 0.07 mm and 3.43 mm, respectively; the cylindrical hair shaft has a radius of 0.1 mm and a length of 3 mm; the follicle has a radius of 0.5 mm and is located at a depth of 2.5 mm.
Figure A4. A three-dimensional representation of the Finite-Element Method (FEM) model of skin and hair for validating our simulations with the results of Sun et al. [14]. The model includes epidermis, dermis, hair shaft, and follicle and has a radius of 10 mm and a height of 8.5 mm; the thickness of epidermis and dermis is 0.07 mm and 3.43 mm, respectively; the cylindrical hair shaft has a radius of 0.1 mm and a length of 3 mm; the follicle has a radius of 0.5 mm and is located at a depth of 2.5 mm.
Applsci 13 08553 g0a4
In the simulation protocol, we applied the following:
-
The simulated disc-shaped laser beam (1064 nm) with a radius of 1 mm was directed perpendicularly to the cross-section of the FEM model.
-
The main outcomes of simulations were temperature distribution maps and the average temperature of the follicle.
-
Simulations were undertaken by varying the fluence and pulse duration: we closely followed the published study and accordingly used the sequence of three pulses of fluence and pulse duration of 4.8 J/cm2 and 2.5 ms, respectively, with a pause of 200 ms between each pulse when analyzing temperature distribution maps; when analyzing average temperature of the follicle, the fluence was between 5.0 J/cm2 and 7.0 J/cm2 with 0.5 J/cm2 steps, each pulse duration of 2.5 ms, with a 200 ms pause between each pulse.
Figure A5 shows the temperature distributions at y = 0 mm immediately after the first, second, and third pulses, respectively. Comparison with Figure 6 in the publication of Sun et al. [14] shows excellent qualitative correspondence; the only difference is due to the slightly different shape of follicles; in our simulations, the follicle was of a spherical shape, while in the publication it was of a truncated sphere.
Applsci 13 08553 g0a5 550
Figure A5. Temperature distribution maps shown in the y = 0 plane for the FEM model immediately (left) after the first pulse, (middle) after the second pulse, and (right) after the third pulse (fluence per pulse is 4.8 J/cm2 and the duration of pulse is 2.5 ms, with a 200 ms pause between each pulse). Compare with Figure 6 in the article published by Sun et al. [14].
Figure A5. Temperature distribution maps shown in the y = 0 plane for the FEM model immediately (left) after the first pulse, (middle) after the second pulse, and (right) after the third pulse (fluence per pulse is 4.8 J/cm2 and the duration of pulse is 2.5 ms, with a 200 ms pause between each pulse). Compare with Figure 6 in the article published by Sun et al. [14].
Applsci 13 08553 g0a5
The results of the analysis of the average temperature of the hair follicle are shown in Figure A6. Comparison with Figure 8 in the article by Sun et al. [14] shows agreement within 5 percent. There are a couple of potential reasons for the relatively minor deviation: one is due to the different shapes of the follicle, and the other is due to different ways of calculating the average temperatures when using FEM and finite-difference models [14].
Applsci 13 08553 g0a6 550
Figure A6. Effect of fluence (x axis) on average follicle temperature (y axis) immediately after the first pulse (purple line), second pulse (blue line), and third pulse (red line). Compare with Figure 8 in the article by Sun et al. [14].
Figure A6. Effect of fluence (x axis) on average follicle temperature (y axis) immediately after the first pulse (purple line), second pulse (blue line), and third pulse (red line). Compare with Figure 8 in the article by Sun et al. [14].
Applsci 13 08553 g0a6

References

  1. Goldberg, D. Laser complications: Hair removal. J. Cosmet. Laser Ther. 2006, 8, 197–202. [Google Scholar] [CrossRef] [PubMed]
  2. Fernandez, A.A.; França, K.; Chacon, A.H.; Nouri, K. From flint razors to lasers: A timeline of hair removal methods. J. Cosmet. Dermatol. 2013, 12, 153–162. [Google Scholar] [CrossRef] [PubMed]
  3. Gan, S.D.; Graber, E.M. Laser Hair Removal: A Review. Dermatol. Surg. 2013, 39, 823–838. [Google Scholar] [CrossRef] [PubMed]
  4. Haedersdal, M.; Haak, C.S. Hair Removal. In Current Problems in Dermatology: Basics in Dermatological Laser Applications; Bogdan Allemann, I., Goldberg, D.J., Eds.; S. Karger AG: Basel, Switzerland, 2011; pp. 111–121. Available online: https://www.karger.com/Article/FullText/328272 (accessed on 18 July 2023).
  5. Haedersdal, M. Wulf H. Evidence-based review of hair removal using lasers and light sources. J. Eur. Acad. Dermatol. Venerol. 2006, 20, 9–20. [Google Scholar] [CrossRef]
  6. Russe, E.; Purschke, M.; Herold, M.; Sakamoto, F.H.; Wechselberger, G.; Russe-Wilflingseder, K. Evaluation of Safety and Efficacy of Laser Hair Removal with the Long-Pulsed 755 nm Wavelength Laser: A Two-Center Study with 948 Patients. Lasers Surg. Med. 2020, 52, 77–83. [Google Scholar] [CrossRef] [Green Version]
  7. Vaidya, T.; Hohman, M.H.; Kumar, D.D. Laser Hair Removal; StatPearls: Treasure Island, FL, USA, 2023. Available online: https://www.ncbi.nlm.nih.gov/books/NBK507861/ (accessed on 18 July 2023).
  8. Lukač, M. Beyond Customary Paradigm: FRAC3 Nd:YAG Laser Hair Removal. LAHA (Online ed.). 2010. Available online: https://www.fotona.com/media/documents/97092_v1_hair_removal_leaflet_15_a4.pdf (accessed on 18 July 2023).
  9. Suzuki, H.; Anderson, R.R. Treatment of melanocytic nevi. Dermatol. Ther. 2005, 18, 217–226. [Google Scholar] [CrossRef]
  10. Majaron, B.; Kelly, K.M.; Park, H.B.; Verkruysse, W.; Nelson, J.S. Er:YAG laser skin resurfacing using repetitive long-pulse exposure and cryogen spray cooling: I. Histological study. Lasers Surg. Med. 2001, 28, 121–130. [Google Scholar] [CrossRef]
  11. Das, A.; Sarda, A.; De, A. Cooling devices in laser therapy. J. Cutan. Aesthet. Surg. 2016, 9, 215. [Google Scholar] [CrossRef]
  12. Grad, L.; Sult, T.; Sult, R. Scientic Evaluation of VSP Nd:YAG Lasers for Hair Removal. J. Laser Health Acad. 2007, 2, 1–11. [Google Scholar]
  13. Vella, D.; Jernejčič, U.; Kukovič, J.; Zorman, A.; Jezeršek, M.; Lukač, N.; Lukač, M. Enhanced Hair Removal based on the “Avalanche Effect” of the AvalancheLase® Hair Removal Laser System. J. Laser Health Acad. 2021, 1, 1–5. [Google Scholar]
  14. Sun, F.; Chaney, A.; Anderson, R.; Aguilar, G. Thermal modeling and experimental validation of human hair and skin heated by broadband light. Lasers Surg. Med. 2009, 41, 161–169. [Google Scholar] [CrossRef]
  15. Pfefer, T.J.; Kehlet Barton, J.; Chan, E.K.; Ducros, M.G.; Sorg, B.S.; Milner, T.E.; Nelson, J.S.; Welch, A.J. A three-dimensional modular adaptable grid numerical model for light propagation during laser irradiation of skin tissue. IEEE J Sel. Top. Quantum Electron. 1996, 2, 934–942. [Google Scholar] [CrossRef] [Green Version]
  16. Schöberl, J. NETGEN An advancing front 2D/3D-mesh generator based on abstract rules. Comput. Vis. Sci. 1997, 1, 41–52. [Google Scholar] [CrossRef] [Green Version]
  17. Sandby-Møller, J.; Poulsen, T.; Wulf, H.C. Epidermal Thickness at Different Body Sites: Relationship to Age, Gender, Pigmentation, Blood Content, Skin Type and Smoking Habits. Acta Dermato-Venereol. 2003, 83, 410–413. [Google Scholar] [CrossRef] [PubMed]
  18. Oltulu, P.; Ince, B.; Kokbudak, N.; Findik, S.; Kilinc, F. Measurement of epidermis, dermis, and total skin thicknesses from six different body regions with a new ethical histometric technique. Turk. J. Plast. Surg. 2018, 26, 56. [Google Scholar] [CrossRef]
  19. Abrahams, P. The Family Medical Encyclopedia: The Essential Guide to More than 120 Medical Conditions, Syndromes and Diseases; National Library: London, UK, 2005. [Google Scholar]
  20. Otberg, N.; Richter, H.; Schaefer, H.; Blume-Peytavi, U.; Sterry, W.; Lademann, J. Variations of Hair Follicle Size and Distribution in Different Body Sites. J. Investig. Dermatol. 2004, 122, 14–19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  21. Landthaler, M.; Brunner, R.; Braun-Falco, O.; Haina, D.; Waidelich, W. Effects of argon, dye, and Nd:YAG lasers on epidermis, dermis, and venous vessels. Lasers Surg. Med. 1986, 6, 87–93. [Google Scholar] [CrossRef]
  22. Fang, Q. Mesh-based Monte Carlo method using fast ray-tracing in Plücker coordinates. Biomed. Opt. Express 2010, 1, 165. [Google Scholar] [CrossRef]
  23. Alerstam, E.; Svensson, T.; Andersson-Engels, S. Parallel computing with graphics processing units for high-speed Monte Carlo simulation of photon migration. J. Biomed. Opt. 2008, 13, 060504. [Google Scholar] [CrossRef] [Green Version]
  24. Klaneček, Ž. Development of a Numerical Model of Laser Epilation. University of Ljubljana. Available online: https://repozitorij.uni-lj.si/IzpisGradiva.php?id=110385&lang=slv (accessed on 18 July 2023).
  25. Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef] [Green Version]
  26. Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, R37–R61. [Google Scholar] [CrossRef] [PubMed]
  27. Patwardhan, S.V.; Dhawan, A.P.; Relue, P.A. Monte Carlo Simulation of Light-Tissue Interaction: Three-Dimensional Simulation for Trans-Illumination-Based Imaging of Skin Lesions. IEEE Trans. Biomed. Eng. 2005, 52, 1227–1236. [Google Scholar] [CrossRef] [PubMed]
  28. Ding, H.; Lu, J.Q.; Wooden, A.W.; Kragel, P.J.; Hu, X.-H. Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm. Phys. Med. Biol. 2006, 51, 1479–1489. [Google Scholar] [CrossRef] [Green Version]
  29. Verdel, N.; Marin, A.; Milanič, M.; Majaron, B. Physiological and structural characterization of human skin in vivo using combined photothermal radiometry and diffuse reflectance spectroscopy. Biomed. Opt. Express 2019, 10, 944. [Google Scholar] [CrossRef] [PubMed]
  30. Nachabé, R.; Hendriks, B.H.W.; van der Voort, M.; Desjardins, A.E.; Sterenborg, H.J.C.M. Estimation of biological chromophores using diffuse optical spectroscopy: Benefit of extending the UV-VIS wavelength range to include 1000 to 1600 nm. Biomed. Opt. Express 2010, 1, 1432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  31. Mordon, S.R.; Wassmer, B.; Reynaud, J.; Zemmouri, J. Mathematical modeling of laser lipolysis. BioMed Eng. OnLine 2008, 7, 10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Bashkatov, A.N.; Genina, E.A.; Kochubei, V.I.; Tuchin, V.V. Estimate of the melanin content in human hairs by the inverse Monte-Carlo method using a system for digital image analysis. Quantum Electron. 2006, 36, 1111–1118. [Google Scholar] [CrossRef]
  33. Petrovicova, E.; Kamath, Y.K. Heat transfer in human hair: Heat transfer in human hair. Int. J. Cosmet. Sci. 2019, 41, 387–390. [Google Scholar] [CrossRef]
  34. Kim, T.-H.; Lee, G.-W.; Youn, J.-I. A comparison of temperature profile depending on skin types for laser hair removal therapy. Lasers Med. Sci. 2014, 29, 1829–1837. [Google Scholar] [CrossRef]
  35. Ataie-Fashtami, L.; Shirkavand, A.; Sarkar, S.; Alinaghizadeh, M.; Hejazi, M.; Fateh, M.; Djavid, G.E.; Zand, N.; Mohammadreza, H. Simulation of Heat Distribution and Thermal Damage Patterns of Diode Hair-Removal Lasers: An Applicable Method for Optimizing Treatment Parameters. Photomed. Laser Surg. 2011, 29, 509–515. [Google Scholar] [CrossRef] [Green Version]
  36. Gaylor, D.C. Physical Mechanisms of Cellular Injury in Electrical Trauma; Massachusetts Institute of Technology: Boston, MA, USA, 1989. [Google Scholar]
  37. Rogachefsky, A.S.; Becker, K.; Weiss, G.; Goldberg, D.J. Evaluation of a Long-Pulsed Nd:YAG Laser at Different Parameters: An Analysis of Both Fluence and Pulse Duration. Dermatol. Surg. 2002, 28, 932–936. [Google Scholar] [CrossRef] [PubMed]
  38. Milanic, M.; Muc, B.T.; Lukac, N.; Lukac, M. Numerical Study of Hyper-Thermic Laser Lipolysis With 1,064 nm Nd:YAG Laser in Human Subjects. Lasers Surg. Med. 2019, 51, 897–909. [Google Scholar] [CrossRef]
  39. Milanič, M.; Jia, W.; Nelson, J.S.; Majaron, B. Numerical optimization of sequential cryogen spray cooling and laser irradiation for improved therapy of port wine stain: Optimization of sequential laser irradiation. Lasers Surg. Med. 2011, 43, 164–175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  40. Nanni, C.A.; Alster, T.S. Optimizing treatment parameters for hair removal using a topical carbon-based solution and 1064-nm Q-switched neodymium:YAG laser energy. Arch. Dermatol. 1997, 133, 1546–1549. [Google Scholar] [CrossRef] [PubMed]
  41. Subodh, J.D.; Venkataram, M. Effectiveness of short-pulse width Nd:YAG in laser hair reduction. J. Cosmet. Dermatol. 2018, 17, 1046–1052. [Google Scholar] [CrossRef]
  42. Khatri, K.A.; Lee, R.A.; Goldberg, L.J.; Khatri, B.; Garcia, V. Efficacy and safety of a 0.65 millisecond pulsed portable ND:YAG laser for hair removal. J. Cosmet. Laser Ther. 2009, 11, 19–24. [Google Scholar] [CrossRef]
  43. Omland, S.H.; Wenande, E.C.; Svane, I.M.; Tam, J.; Olesen, U.H.; Hædersdal, M. Laser Immunotherapy: A Potential Treatment Modality for Keratinocyte Carcinoma. Cancers 2021, 13, 5405. [Google Scholar] [CrossRef]
  44. Chang, I.A. Considerations for Thermal Injury Analysis for RF Ablation Devices. Open Biomed. Eng. J. 2010, 4, 3–12. [Google Scholar] [CrossRef] [Green Version]
  45. Lukač, M.; Lozar, A.; Perhavec, T.; Bajd, F. Variable heat shock response model for medical laser procedures. Lasers Med. Sci. 2019, 34, 1147–1158. [Google Scholar] [CrossRef]
  46. Vella, D.; Lukač, M.; Jernejčič, U.; Lukač, N.; Klaneček, Ž.; Milanič, M.; Jezeršek, M. Measurements of hair temperature avalanche effect with alexandrite and Nd:YAG hair removal lasers. Lasers Surg. Med. 2023. submitted. [Google Scholar] [CrossRef]
  47. Hren, R.; Sersa, G.; Simoncic, U.; Milanic, M. Imaging perfusion changes in oncological clinical applications by hyperspectral imaging: A literature review. Radiol. Oncol. 2022, 56, 420–429. [Google Scholar] [CrossRef] [PubMed]
  48. Dorgham, N.A.; Dorgham, D.A. Lasers for reduction of unwanted hair in skin of colour: A systematic review and meta-analysis. J. Eur. Acad. Dermatol. Venereol. 2020, 34, 948–955. [Google Scholar] [CrossRef] [PubMed]
  49. Sekar, S.K.V.; Pacheco, A.; Martella, P.; Li, H.; Lanka, P.; Pifferi, A.; Andersson-Engels, S. Solid phantom recipe for diffuse optics in biophotonics applications: A step towards anatomically correct 3D tissue phantoms. Biomed. Opt. Express 2019, 10, 2090. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Applsci 13 08553 g001 550
Figure 1. Finite element method (FEM) Model #1 of skin and hair. The model includes the epidermis, dermis, subcutis, hair shaft, and follicle and has a radius of 10 mm and a height of 8.5 mm; the thickness of the epidermis, dermis, and subcutis is 0.07 mm, 3.43 mm, and 5 mm, respectively; the cylindrical hair shaft has a radius of 0.03 mm and a length of 2.5 mm. The follicle has a radius of 0.1 mm and is located at a depth of 2.5 mm. (A) 3D representation of the whole model; (B) cross-section through the model center; (C) detailed view of the hair shaft and follicle.
Figure 1. Finite element method (FEM) Model #1 of skin and hair. The model includes the epidermis, dermis, subcutis, hair shaft, and follicle and has a radius of 10 mm and a height of 8.5 mm; the thickness of the epidermis, dermis, and subcutis is 0.07 mm, 3.43 mm, and 5 mm, respectively; the cylindrical hair shaft has a radius of 0.03 mm and a length of 2.5 mm. The follicle has a radius of 0.1 mm and is located at a depth of 2.5 mm. (A) 3D representation of the whole model; (B) cross-section through the model center; (C) detailed view of the hair shaft and follicle.
Applsci 13 08553 g001
Applsci 13 08553 g002 550
Figure 2. Finite element method (FEM) Model #2 of skin and hair with the hair exiting the skin at an angle of 45°. (A) Cross-section through the model center; (B) detailed view of the hair shaft and follicle.
Figure 2. Finite element method (FEM) Model #2 of skin and hair with the hair exiting the skin at an angle of 45°. (A) Cross-section through the model center; (B) detailed view of the hair shaft and follicle.
Applsci 13 08553 g002
Applsci 13 08553 g003 550
Figure 3. Finite element method (FEM) Model #3 of skin and hair with an array of hair. (A) 3D representation of the model; (B) cross-section through the model center. An array of hair had the shape of a cross, with the central hair at x = y = 0 mm and each neighboring hair at 3 mm from the central one. All five hair shafts and follicles were identical to the ones presented in Figure 1.
Figure 3. Finite element method (FEM) Model #3 of skin and hair with an array of hair. (A) 3D representation of the model; (B) cross-section through the model center. An array of hair had the shape of a cross, with the central hair at x = y = 0 mm and each neighboring hair at 3 mm from the central one. All five hair shafts and follicles were identical to the ones presented in Figure 1.
Applsci 13 08553 g003
Applsci 13 08553 g004 550
Figure 4. Impact of the number of photons on the absorbance of the hair follicle, averaged over 10 simulation runs.
Figure 4. Impact of the number of photons on the absorbance of the hair follicle, averaged over 10 simulation runs.
Applsci 13 08553 g004
Applsci 13 08553 g005 550
Figure 5. Dependence of the average temperature of the hair follicle immediately after the first, second, and third pulses, respectively, on the number of tetrahedral FEM elements.
Figure 5. Dependence of the average temperature of the hair follicle immediately after the first, second, and third pulses, respectively, on the number of tetrahedral FEM elements.
Applsci 13 08553 g005
Applsci 13 08553 g006 550
Figure 6. Temperature distribution maps shown in the y = 0 plane for FEM Model #1 immediately after irradiation for three combinations of fluence, pulse duration, and modes without forced cooling and with forced cooling. The left column shows maps without forced cooling and the right column with forced cooling for fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Figure 6. Temperature distribution maps shown in the y = 0 plane for FEM Model #1 immediately after irradiation for three combinations of fluence, pulse duration, and modes without forced cooling and with forced cooling. The left column shows maps without forced cooling and the right column with forced cooling for fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Applsci 13 08553 g006
Applsci 13 08553 g007 550
Figure 7. Thermal damage distribution maps shown in the y = 0 plane for FEM Model #1 immediately after irradiation for three combinations of fluence, pulse duration, and modes without forced cooling and with forced cooling. The left column shows maps without forced cooling and the right column with forced cooling for fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Figure 7. Thermal damage distribution maps shown in the y = 0 plane for FEM Model #1 immediately after irradiation for three combinations of fluence, pulse duration, and modes without forced cooling and with forced cooling. The left column shows maps without forced cooling and the right column with forced cooling for fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Applsci 13 08553 g007
Applsci 13 08553 g008 550
Figure 8. Thermal damage distribution maps shown in the y = 0 plane for FEM Model #2 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling. The left column shows maps without forced cooling and the right column with forced cooling for fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Figure 8. Thermal damage distribution maps shown in the y = 0 plane for FEM Model #2 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling. The left column shows maps without forced cooling and the right column with forced cooling for fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Applsci 13 08553 g008
Applsci 13 08553 g009 550
Figure 9. Temperature and thermal damage distribution maps shown in the y = 0 plane for FEM Model #3 immediately after irradiation for three combinations of fluence and pulse duration for a mode without forced cooling. The left column shows temperature distribution maps, and the right column shows thermal damage distribution maps, with fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Figure 9. Temperature and thermal damage distribution maps shown in the y = 0 plane for FEM Model #3 immediately after irradiation for three combinations of fluence and pulse duration for a mode without forced cooling. The left column shows temperature distribution maps, and the right column shows thermal damage distribution maps, with fluences of: (a,b) 50 J/cm2 and 25 ms; (c,d) 60 J/cm2 and 50 ms; (e,f) 80 J/cm2 and 50 ms.
Applsci 13 08553 g009
Applsci 13 08553 g010 550
Figure 10. Time variation of cumulative heat damage to the hair follicle during laser irradiation with a beam of radius 6.0 mm, fluence of 80 J/cm2, and pulse duration of 50 ms without forced cooling. Results are shown for FEM Model #2 and FEM Model #3.
Figure 10. Time variation of cumulative heat damage to the hair follicle during laser irradiation with a beam of radius 6.0 mm, fluence of 80 J/cm2, and pulse duration of 50 ms without forced cooling. Results are shown for FEM Model #2 and FEM Model #3.
Applsci 13 08553 g010
Table
Table 1. Optical properties of different tissue types used in simulations along with references; µa and µs are absorption and scattering coefficients, respectively; n is the refractive index; and g is an anisotropy factor.
Table 1. Optical properties of different tissue types used in simulations along with references; µa and µs are absorption and scattering coefficients, respectively; n is the refractive index; and g is an anisotropy factor.
Tissueµa [mm−1]µs [mm−1]gn
Epidermis0.07 [1]26.1 [2]0.89 [3]1.42 [4]
Dermis0.038 [5]5.25 [2]0.72 [3]1.37 [4]
Subcutis0.008 [6]2.27 [6]0.78 [3]1.44 [7]
Hair0.56 [1]79.7 [8]0.9 [8]1.37 [9]
Table
Table 2. Thermal properties of the tissues used in simulations, along with references: cp is specific heat capacity; k is thermal conductivity; and ρ is density.
Table 2. Thermal properties of the tissues used in simulations, along with references: cp is specific heat capacity; k is thermal conductivity; and ρ is density.
Tissuecp [J/kgK]k [W/mK]ρ [kg/m3]
Epidermis3200 [10]0.34 [10]1120 [10]
Dermis3500 [10]0.41 [10]1090 [10]
Subcutis2870 [6]0.3 [6]860 [6]
Hair2512 [11]0.63 [11]1300 [12]
Table
Table 3. Maximum follicle temperature in FEM Model #1 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling.
Table 3. Maximum follicle temperature in FEM Model #1 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling.
Maximum Follicle Temperature after Pulse [°C]
Fluence of 50 J/cm2
Pulse Duration of 25 ms		Fluence of 60 J/cm2
Pulse Duration of 50 ms		Fluence of 80 J/cm2
Pulse Duration of 50 ms
No CoolingCoolingNo CoolingCoolingNo CoolingCooling
79.379.373.673.686.886.8
Table
Table 4. Maximum follicle temperature in FEM Model #2 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling.
Table 4. Maximum follicle temperature in FEM Model #2 immediately after irradiation for three combinations of fluence and pulse duration, for modes without forced cooling and with forced cooling.
Maximum Follicle Temperature after Pulse [°C]
Fluence of 50 J/cm2
Pulse Duration of 25 ms		Fluence of 60 J/cm2
Pulse Duration of 50 ms		Fluence of 80 J/cm2
Pulse Duration of 50 ms
No CoolingCoolingNO COOLINGCoolingNo CoolingCooling
77.977.972.672.685.585.5
Table
Table 5. Maximum temperature of the central and non-central follicles in FEM Model #3 immediately after irradiation for three combinations of fluence and pulse duration, in a mode without forced cooling.
Table 5. Maximum temperature of the central and non-central follicles in FEM Model #3 immediately after irradiation for three combinations of fluence and pulse duration, in a mode without forced cooling.
Maximum Follicle Temperature after Pulse [°C]
Fluence of 50 J/cm2
Pulse Duration of 25 ms		Fluence of 60 J/cm2
Pulse Duration of 50 ms		Fluence of 80 J/cm2
Pulse Duration of 50 ms
Central
Follicle		Non-Central
Follicle		Central
Follicle		Non-Central
Follicle		Central
Follicle		Non-Central
Follicle
73.063.068.860.080.468.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Klanecek, Z.; Hren, R.; Simončič, U.; Muc, B.T.; Lukač, M.; Milanič, M. Finite Element Method (FEM) Modeling of Laser-Tissue Interaction during Hair Removal. Appl. Sci. 2023, 13, 8553. https://doi.org/10.3390/app13148553

AMA Style

Klanecek Z, Hren R, Simončič U, Muc BT, Lukač M, Milanič M. Finite Element Method (FEM) Modeling of Laser-Tissue Interaction during Hair Removal. Applied Sciences. 2023; 13(14):8553. https://doi.org/10.3390/app13148553

Chicago/Turabian Style

Klanecek, Zan, Rok Hren, Urban Simončič, Blaz Tasic Muc, Matjaž Lukač, and Matija Milanič. 2023. "Finite Element Method (FEM) Modeling of Laser-Tissue Interaction during Hair Removal" Applied Sciences 13, no. 14: 8553. https://doi.org/10.3390/app13148553

APA Style

Klanecek, Z., Hren, R., Simončič, U., Muc, B. T., Lukač, M., & Milanič, M. (2023). Finite Element Method (FEM) Modeling of Laser-Tissue Interaction during Hair Removal. Applied Sciences, 13(14), 8553. https://doi.org/10.3390/app13148553

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop