Novel Methodology for Scaling and Simulating Structural Behaviour for Soil–Structure Systems Subjected to Extreme Loading Conditions
Abstract
1. Introduction
2. Background of Scale Model Similitude Theories
2.1. The Concept of Application of Scale Model Similitude to Soil Mechanics
2.2. Reference Case Study
3. Implied Prototype Scaling Methodology
3.1. General
3.2. Scale-Modelling Factors
4. Design of the Soil and Pile Models
4.1. Soil Model
4.1.1. Soil-Modelling Criteria
4.1.2. Prototype Soil Parameters
4.2. Design of the Pile Model
4.2.1. Pile-Modelling Criteria
4.2.2. Prototype Pile Parameters
4.3. Model Pile Development
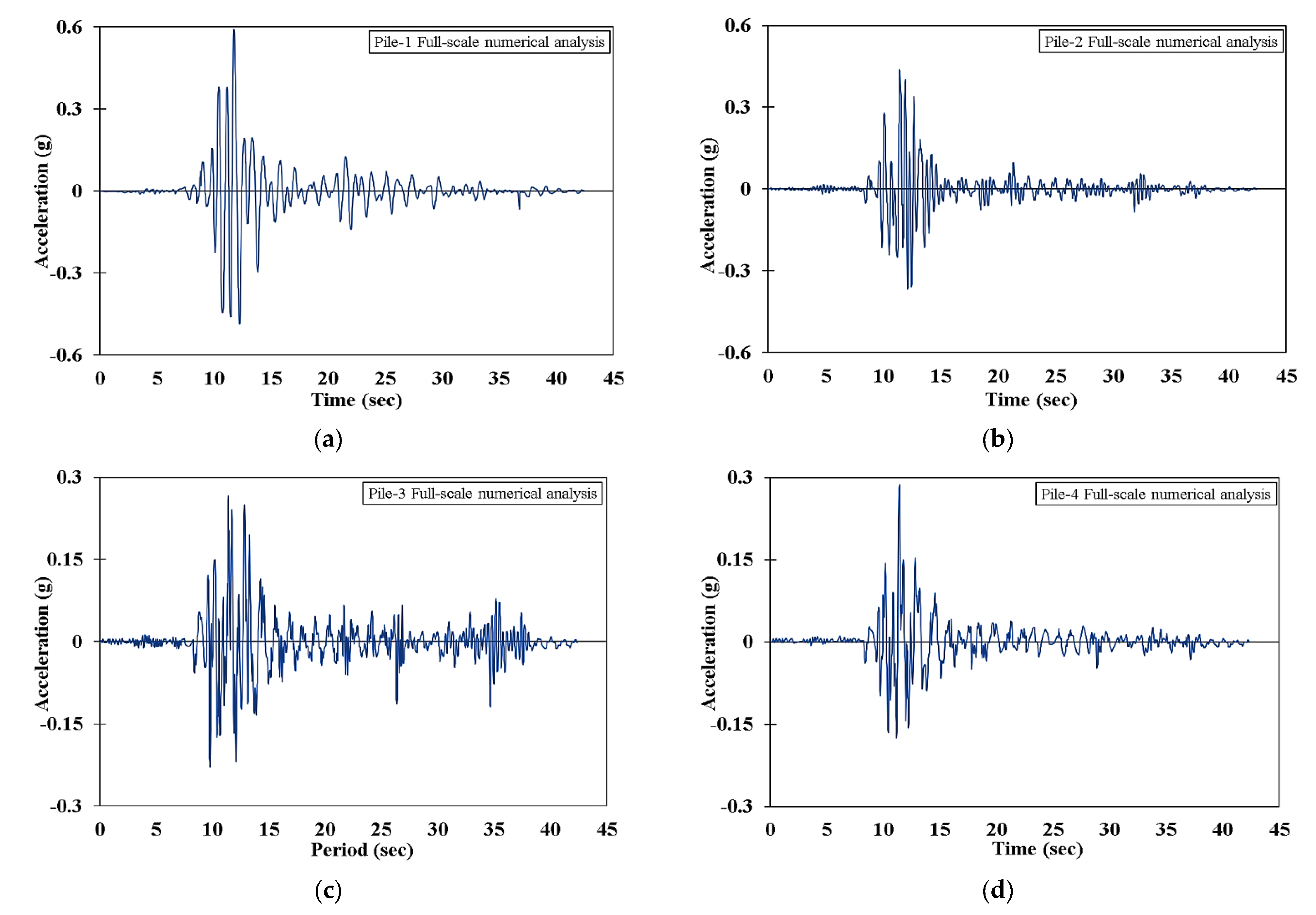
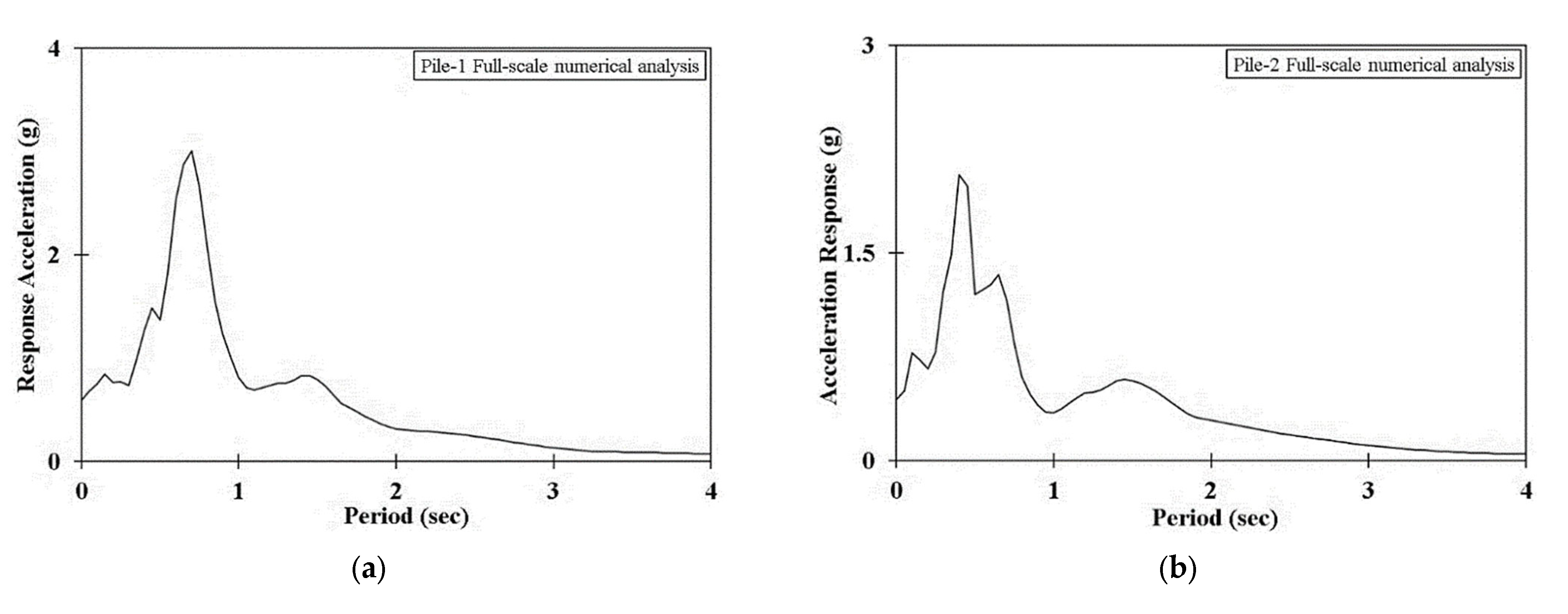
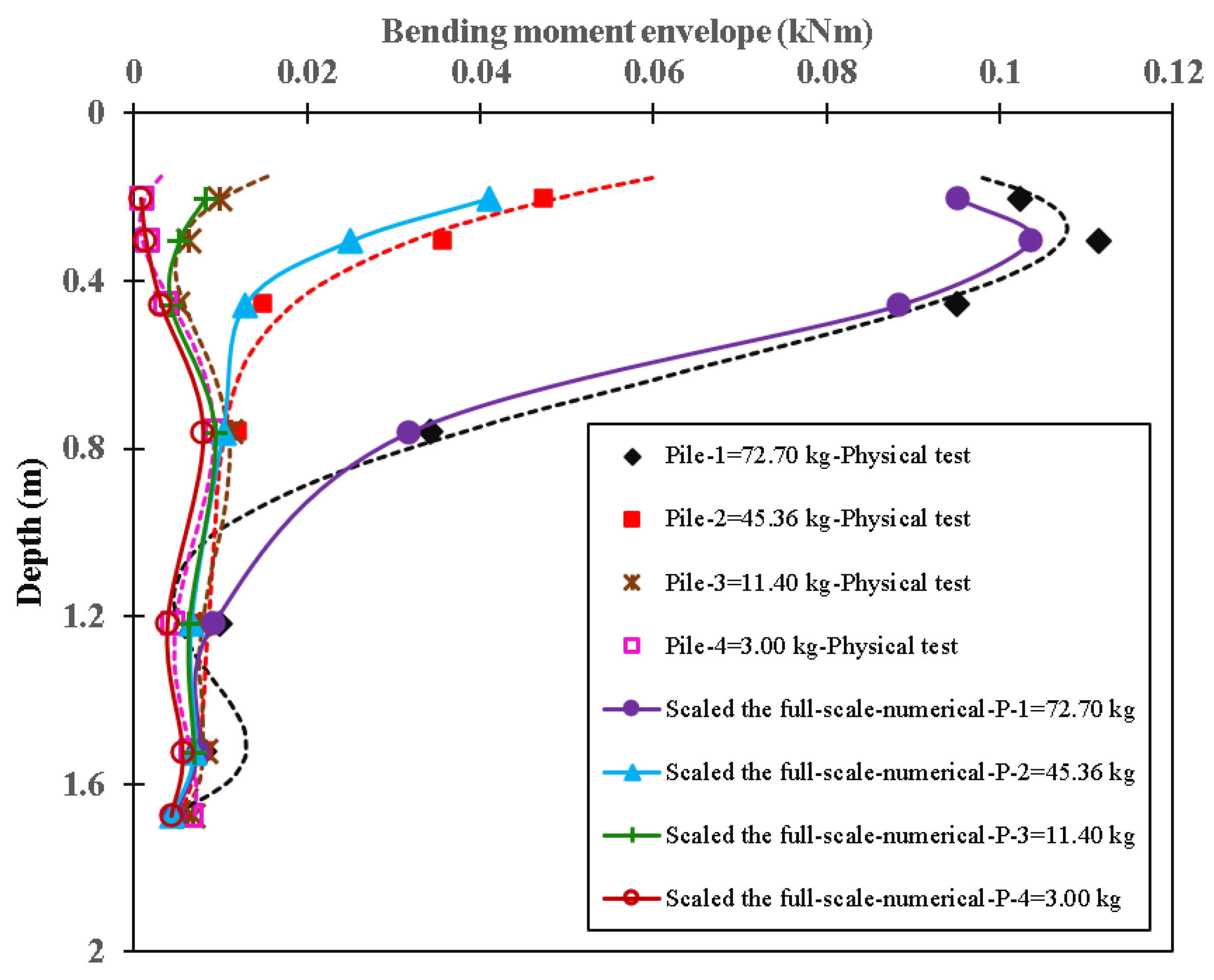
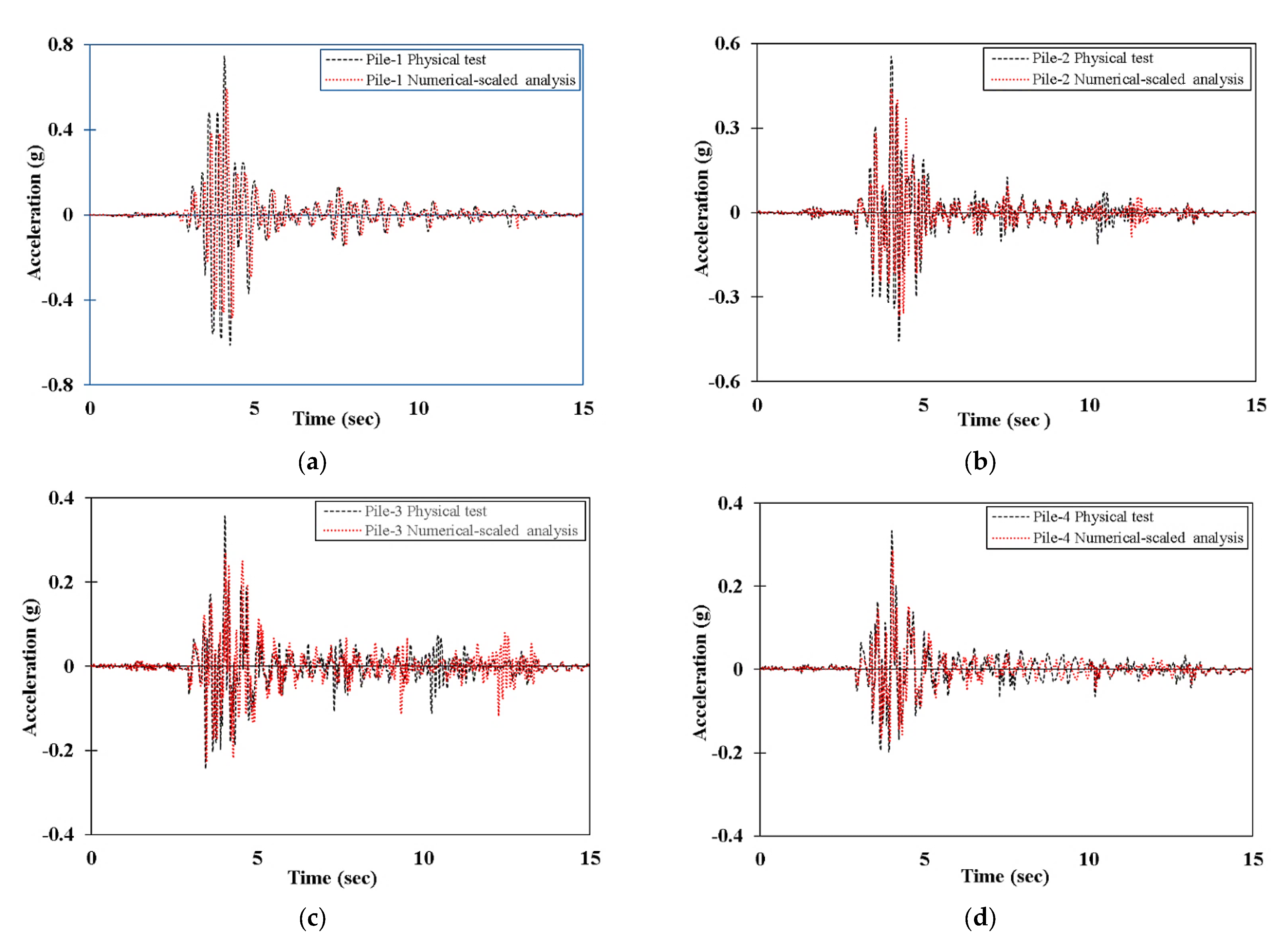
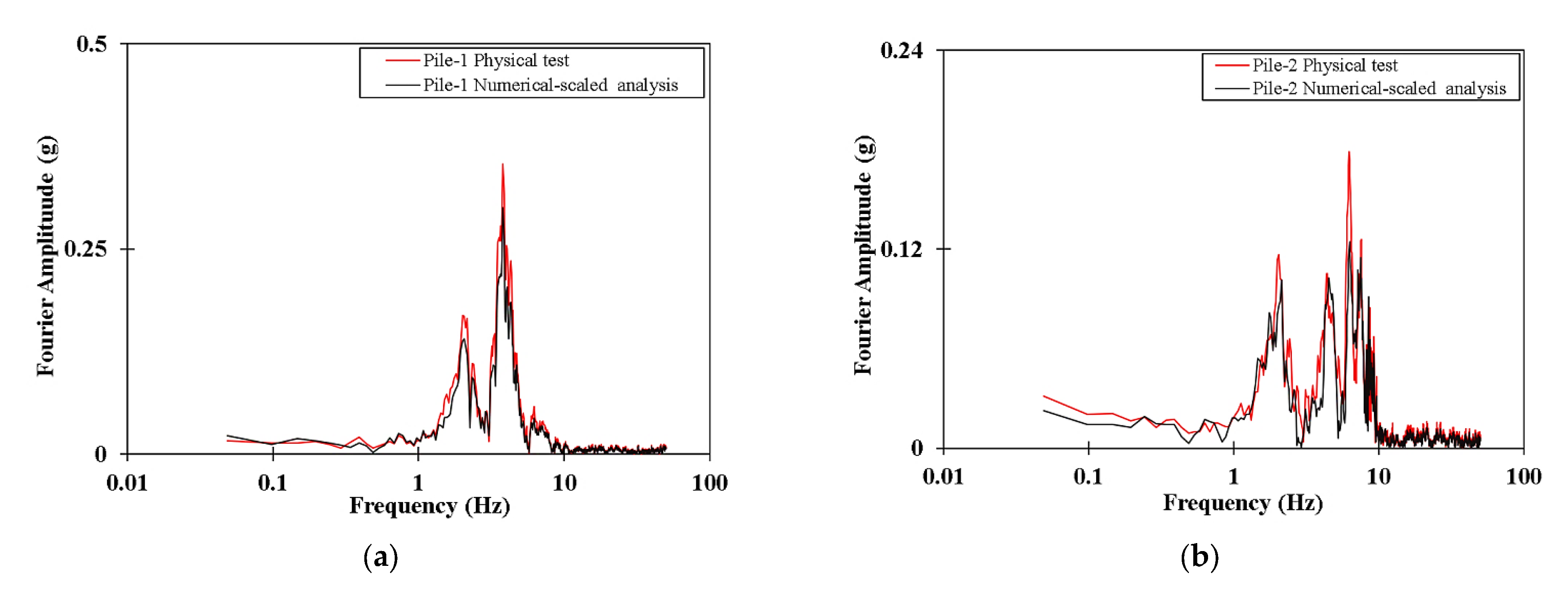
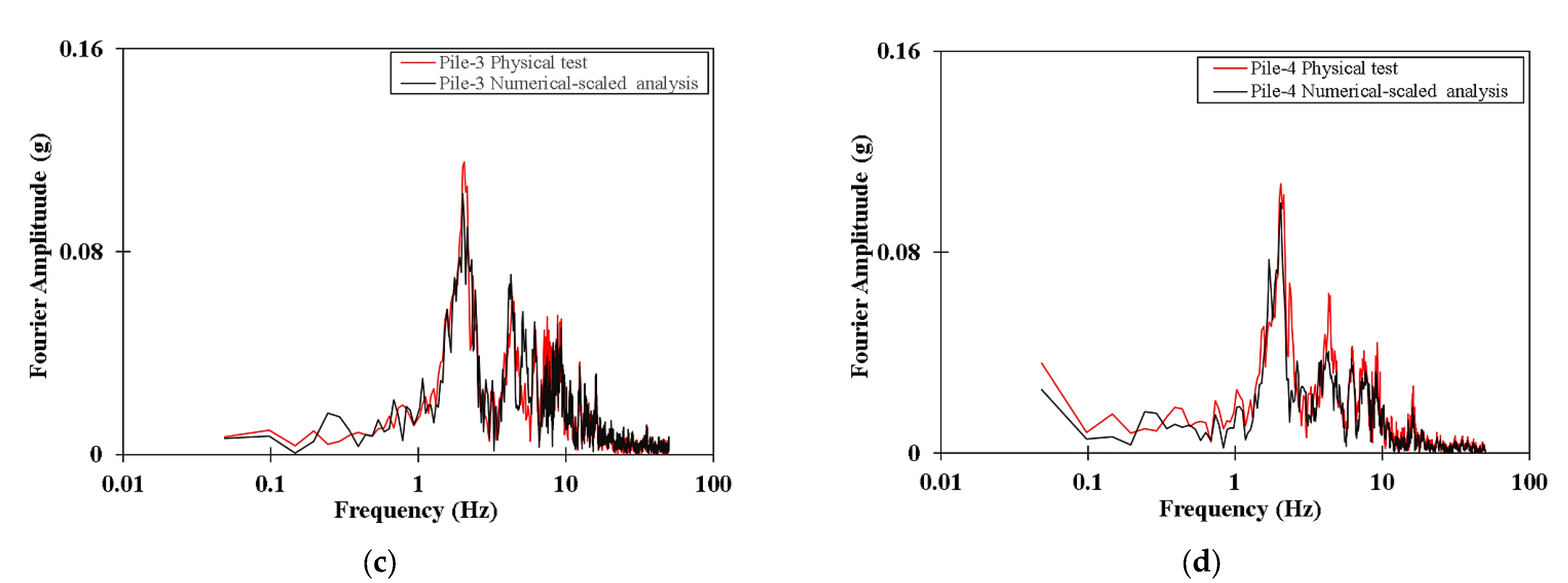
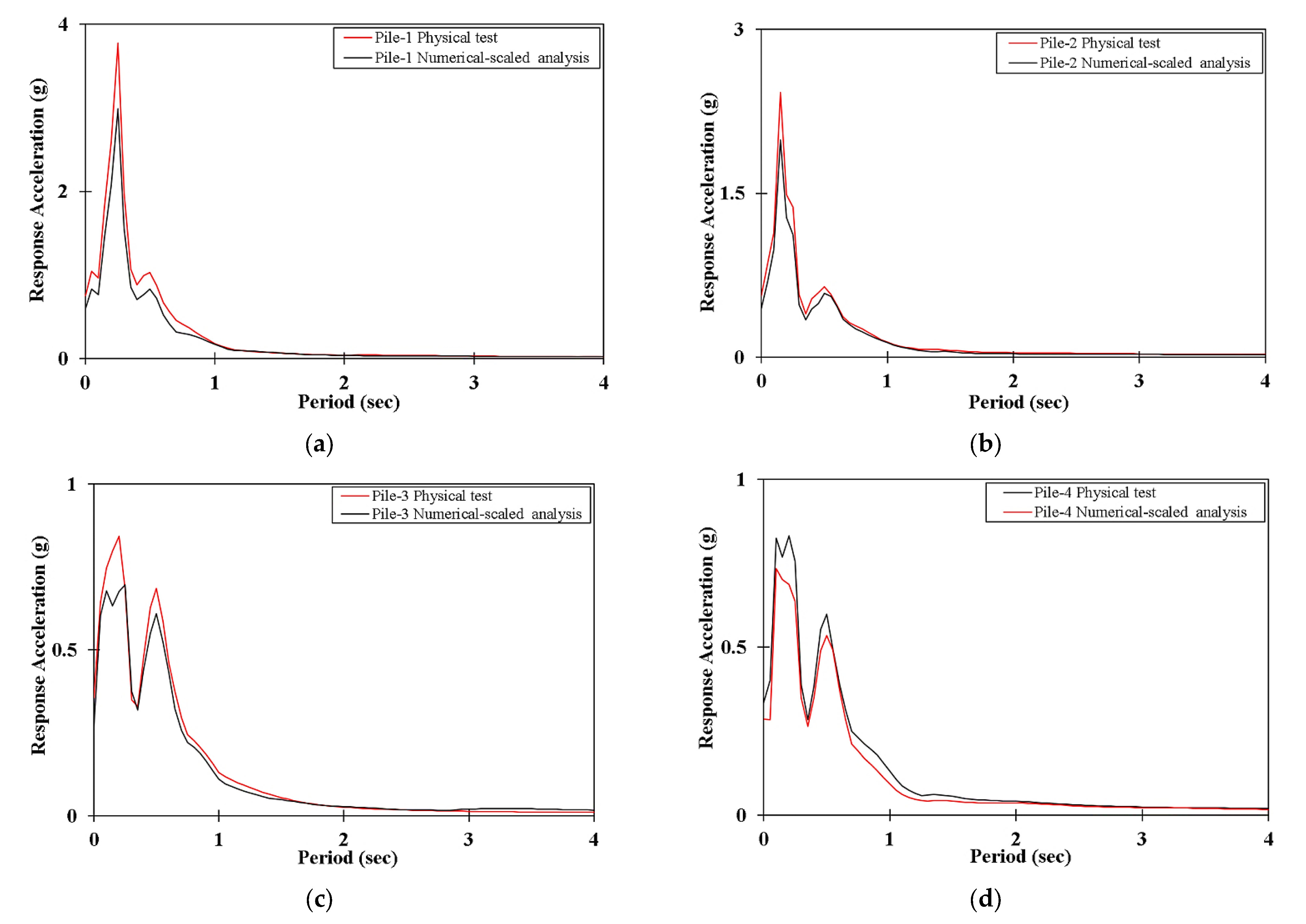
5. Validation Methodology
5.1. Numerical Modelling Characteristics
5.2. Validation of the Scaling Methodology
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al Heib, M.; Emeriault, F.; Caudron, M.; Nghiem, L.; Heib, M.A.; Emeriault, F.; Caudron, M.; Nghiem, L.; Boramy, H. Large-scale soil-structure physical model (1g)—Assessment of structure damages. Int. J. Phys. Model. Geotech. 2014, 12, 138–152. [Google Scholar]
- Meymand, P.J. Shaking Table Scale Model Tests of Nonlinear Soil-Pile-Superstructure Interaction in Soft Clay. 1998. Available online: http://nisee.berkeley.edu/meymand/files/intro.pdf (accessed on 15 July 2023).
- Kline, S.J. Similitude and Approximation Theory; Springer: Berlin/Heidelberg, Germany; Stanford, CA, USA; New York, NY, USA; Tokyo, Japan, 1986. [Google Scholar]
- Jonsson, D. Quantities, Dimensions and Dimensional Analysis. arXiv 2014, arXiv:1408.5024. Available online: http://arxiv.org/abs/1408.5024 (accessed on 15 July 2023).
- Szϋcs, E. Similitude and Modelling; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1980; Volume 2. [Google Scholar]
- Simitses, J. Structural Similitude and Scaling Laws for Laminated Beam-Plates; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Ramu, M.; Prabhu Raja, V.; Thyla, P.R. Establishment of structural similitude for elastic models and validation of scaling laws. KSCE J. Civ. Eng. 2013, 17, 139–144. [Google Scholar] [CrossRef]
- Coutinho, C.P.; Baptista, A.J.; Dias Rodrigues, J. Reduced scale models based on similitude theory: A review up to 2015. Eng. Struct. 2016, 119, 81–94. [Google Scholar] [CrossRef]
- Langhaar, H.L. Dimensional Analysis Theory Models, 13th ed.; Krieger Publishing Company: Malabar, FL, USA, 1980; ISBN 9780882756820. [Google Scholar]
- Moncarz, P.; Krawinkler, H. Theory and Application of Experimental Model Analysis in Earthquake Engineering; The John A. Blume Earthquake Engineering Centre: Stanford, CA, USA, 2006. [Google Scholar]
- Clough, R.W.; Pirtz, D. Earthquake Resistance of Rock-Fill Dams. J. Soil Mech. Found. Div. 1956, 82, 1–26. [Google Scholar] [CrossRef]
- Seed, H.B.; Clough, R.W. Earthquake Resistance of Sloping Core Dams. J. Soil Mech. Found. Div. 1964, 90, 169–170. [Google Scholar] [CrossRef]
- Candeias, P.X. Physical Modelling, Instrumentation and Testing; Seismic Engineering Research Infrastructures for European Synergies: Lisbon, Portugal, 2012. [Google Scholar]
- Rocha, M. Similarity conditions in model studies of soil mechanics problems. In Proceedings of the Prepared to be Distributed to the Members of the 3rd International Conference on Soil Mechanics and Foundation Engineering, Zurich, Switzerland, 16–27 August 1953; Laboratorio Nacional de Engenharia Civil: Zurich, Switzerland, 1953. [Google Scholar]
- Roscoe, K.H. Soils and model tests. J. Strain Anal. 1968, 3, 57–64. [Google Scholar] [CrossRef]
- Kana, D.D.; Boyce, L.; Blaney, G.W. Development of a scale model for the dynamic interaction of a pile in clay. J. Energy Resour. Technol. Trans. ASME 1986, 108, 254–261. [Google Scholar] [CrossRef]
- Iai, S. Similitude for Shaking Table Tests on Soil-Structure-Fluid Model in 1-g Gravitational Field. Soils Found. JSSMFE 1989, 29, 105–118. Available online: http://www.mendeley.com/research/geology-volcanic-history-eruptive-style-yakedake-volcano-group-central-japan/ (accessed on 15 July 2023).
- Gohl, W.B. Response of Pile Foundations to Simulated Earthquake Loading: Expermental and Analytical Results. Ph.D. Thesis, University of British Columbia, Vancouver, BC, USA, 1991. [Google Scholar]
- Scott, R.F. Centrifuge and modeling technology: A survey. Rev. Française Géotech. 1989, 48, 15–34. Available online: https://resolver.caltech.edu/CaltechAUTHORS:20140611-132033693 (accessed on 15 July 2023). [CrossRef]
- Gibson, A. Physical Scale Modeling of Geotechnical Structures at One-G. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1997. [Google Scholar]
- Al-Isawi, A.T.; Collins, P.E.F.; Cashell, K.A. Fully Non-Linear Numerical Simulation of a Shaking Table Test of Dynamic Soil-Pile-Structure Interactions in Soft Clay Using ABAQUS. Geotech. Spec. Publ. 2019, 2019, 252–265. [Google Scholar] [CrossRef]
- Mylonakis, G.; Nikolaou, A.; Gazetas, G. Soil-pile-bridge seismic interaction: Kinematic and inertial effects. Part I: Soft soil. Earthq. Eng. Struct. Dyn. 1997, 26, 337–359. [Google Scholar] [CrossRef]
- U.S. Geological Survey. PEER Ground Motion Database. Pacific Earthquake Engineering Research Centre. Available online: https://ngawest2.berkeley.edu/ (accessed on 15 July 2023).
- Schellart, W.P.; Strak, V. A review of analogue modelling of geodynamic processes: Approaches, scaling, materials and quantification, with an application to subduction experiments. J. Geodyn. 2016, 100, 7–32. [Google Scholar] [CrossRef]
- Harris, H.G.; Sabnis, G. Structural Modeling and Experimental Techniques; Taylor and Francis Group: Abingdon, UK, 1999. [Google Scholar]
- Bonaparte, R.; Mitchell, J.K. The Properties of San Francisco Bay Mud at Hamilton Air Force Base, California; Department of Civil Engineering, University of California: Berkeley, CA, USA, 1979. [Google Scholar]
- Dickenson, S.E. Dynamic Response of Soft and Deep Cohesive Soils during the Loma Prieta Earthquake of October 17, 1989; University of California: Berkeley, CA, USA, 1994. [Google Scholar]
- Raoul, J.; Sedlacek, G.; Tsionis, G.; Raoul, J.; Sedlacek, G.; Tsionis, G. Eurocode 8: Seismic Design of Buildings Worked Examples; Publications Office of the European Union: Luxemborge, 2012. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 3rd ed.; CRC Press: London, UK, 2012; pp. 1–1019. [Google Scholar] [CrossRef]
- Meymand, P.J.; Riemer, M.F.; Seed, R.B. Large scale shaking table tests of seismic soil-pile interaction in soft clay. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; p. 2817. [Google Scholar]
- Wang, S.T.; Reese, L.C. COM624P: Laterally Loaded Pile Analysis Program for the Microcomputer; Federal Highway Administration: Washington, DC, USA, 1993; p. 510. [Google Scholar]
- Brittsan, D. Indicator Pile Test Program for the Seismic Retrofit of the East Approach Structure of the San Francisco-Oakland Bay Bridge; Foundation Testing and Implementation: Sacramento, CA, USA, 1995. [Google Scholar]
- Langhaar, H. Dimensional Analysis and Theory of Models; John Wiley & Sons; Inc.: London, UK, 1951. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual; Version 2018; SIMULIA: Providence, RI, USA, 2018; p. 1146. [Google Scholar]
- Lucena, C.A.T.; Queiroz, P.C.O.; El Debs, A.L.H.C.; Mendonça, A.V. Dynamic Analysis of Buildings Using the Finite Element Method. In Proceedings of the 10th World Congress on Computational Mechanics, Sao Paolo, Brasil, 8–13 July 2012; pp. 4712–4726. [Google Scholar] [CrossRef]
- Helwany, S. Applied Soil Mechanics with ABAQUS Applications; John Wiley & Sons; Inc.: Hoboken, NJ, USA, 2009; ISBN 978-0-471-79107-2. [Google Scholar]
- Pitilakis, D.; Dietz, M.; Wood, D.M.; Clouteau, D.; Modaressi, A. Numerical simulation of dynamic soil-structure interaction in shaking table testing. Soil Dyn. Earthq. Eng. 2008, 28, 453–467. [Google Scholar] [CrossRef]
- Alisawi, A.T.; Collins, P.E.F.; Cashell, K.A. Nonlinear numerical simulation of physical shaking table test, using three different soil constitutive models. Soil Dyn. Earthq. Eng. 2021, 143, 106617. [Google Scholar] [CrossRef]
- SeismoSoft. Manual and program description of the program SeismoStruct. 2020. Available online: http://www.seismosoft.com (accessed on 15 July 2023).
- Reese, L.C.; Wang, S.T. Analysis of Piles Under Lateral Loading with Nonlinear Flexural Rigidity. In Proceedings of the International Conference on Design and Construction of Deep Foundations, Orlando, FL, USA, 6–8 December 1994; pp. 842–856. [Google Scholar]
- American Association of State Highway and Transportation Officials. AASHTO Provisional Standards 2021; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2021. [Google Scholar]
- Eurocode 7; Geotechnical design—Part 1: General Rules. British Standards Institution: London, UK, 2011; Volume 1.
- Byrne, B.W.; McAdam, R.A.; Burd, H.J.; Beuckelaers, W.J.A.P.; Gavin, K.G.; Houlsby, G.T.; Igoe, D.J.P.; Jardine, R.J.; Martin, C.M.; Muir Wood, A.; et al. Monotonic laterally loaded pile testing in a stiff glacial clay till at Cowden. Géotechnique 2020, 70, 970–985. [Google Scholar] [CrossRef]
- Bala, M. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms—Working Stress Design. Api Recomm. Pract. 2007, 2A–WSD, 242. [Google Scholar]
- Hannigan, J.P.; Goble, G.G.; Thendean, G.; Likins, G.E.; Rausche, F. Design and Construction of Driven Pile Foundations. U.S. Dep. Transp. Fed. Highw. Adm. 1997, I. [Google Scholar]


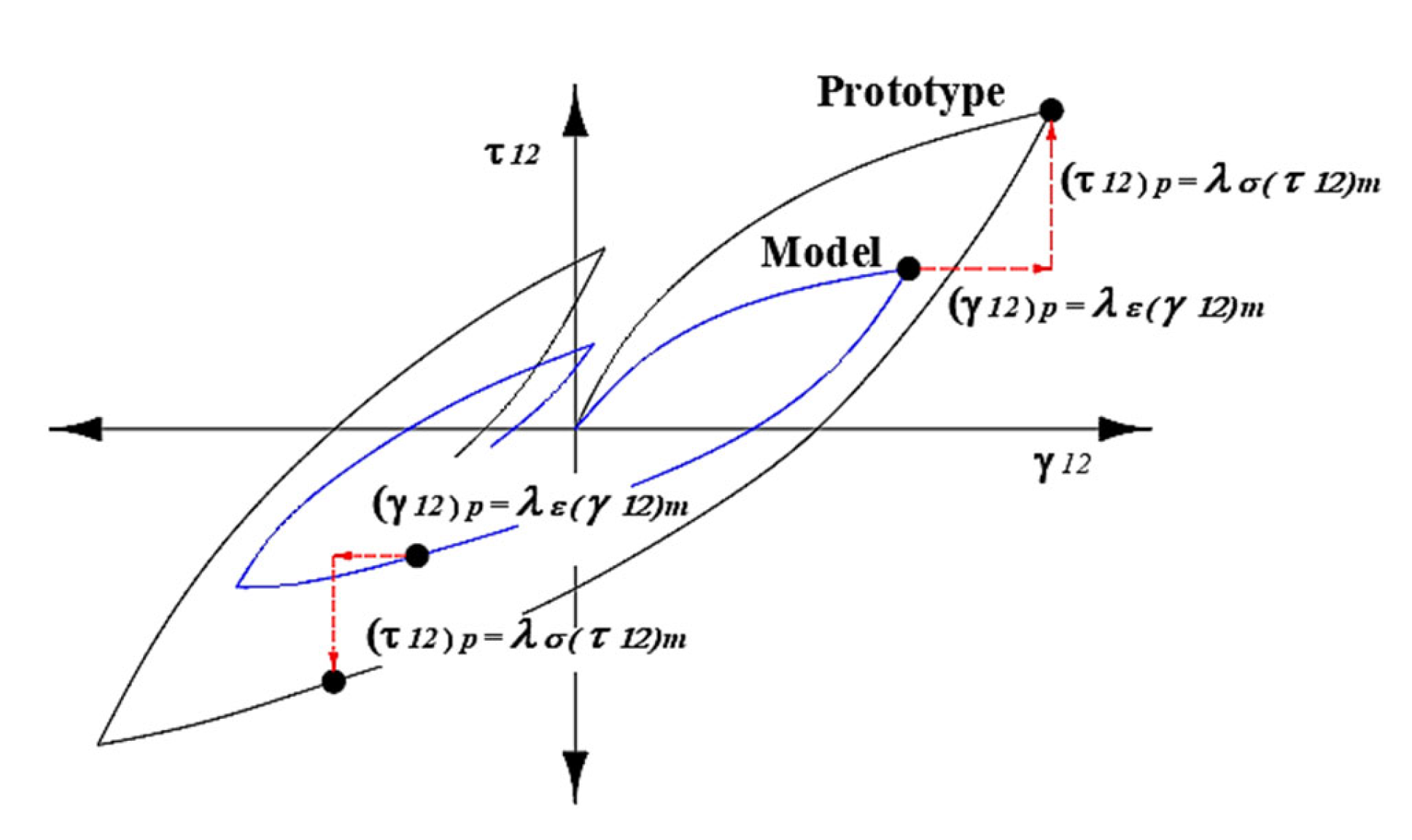
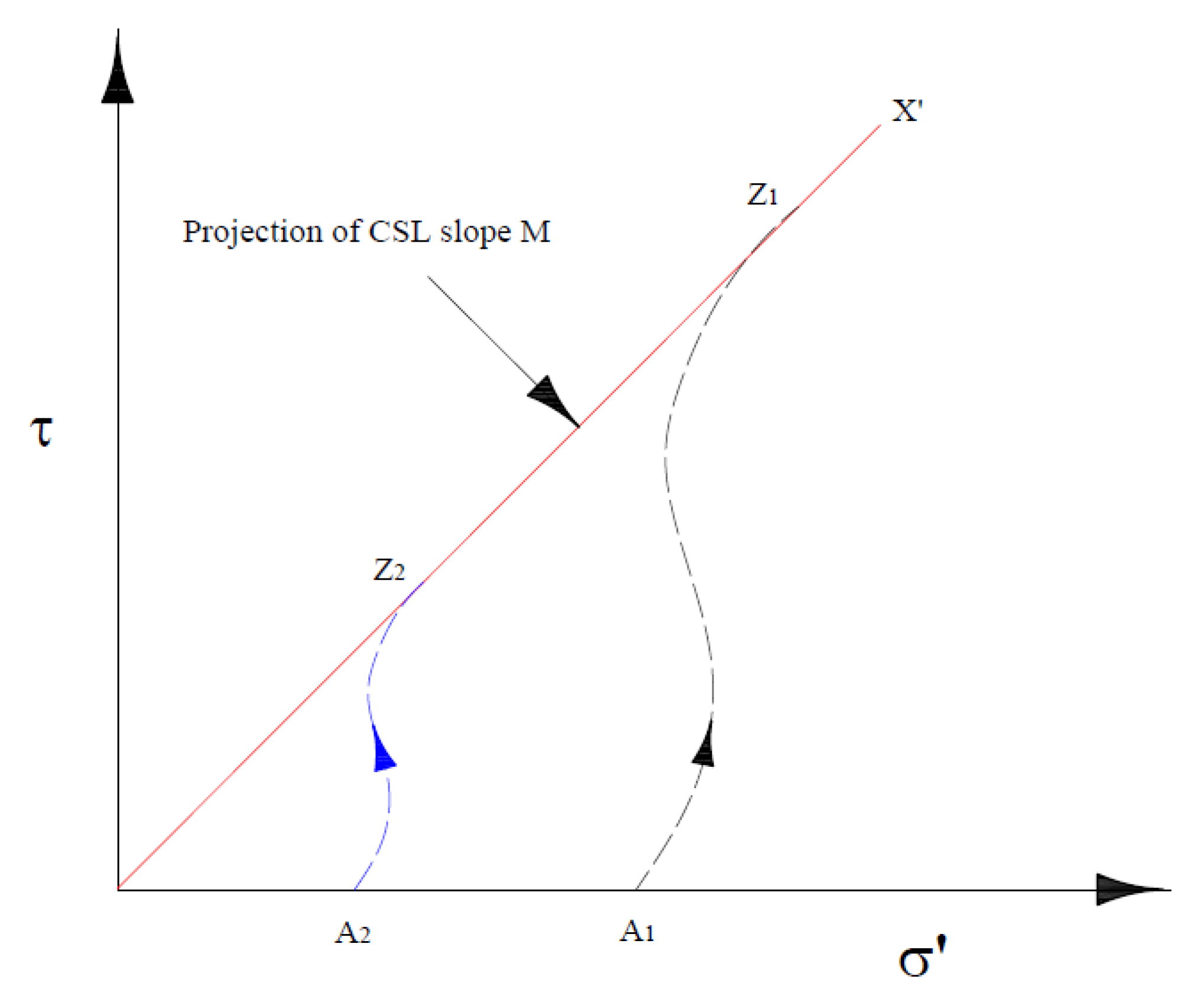



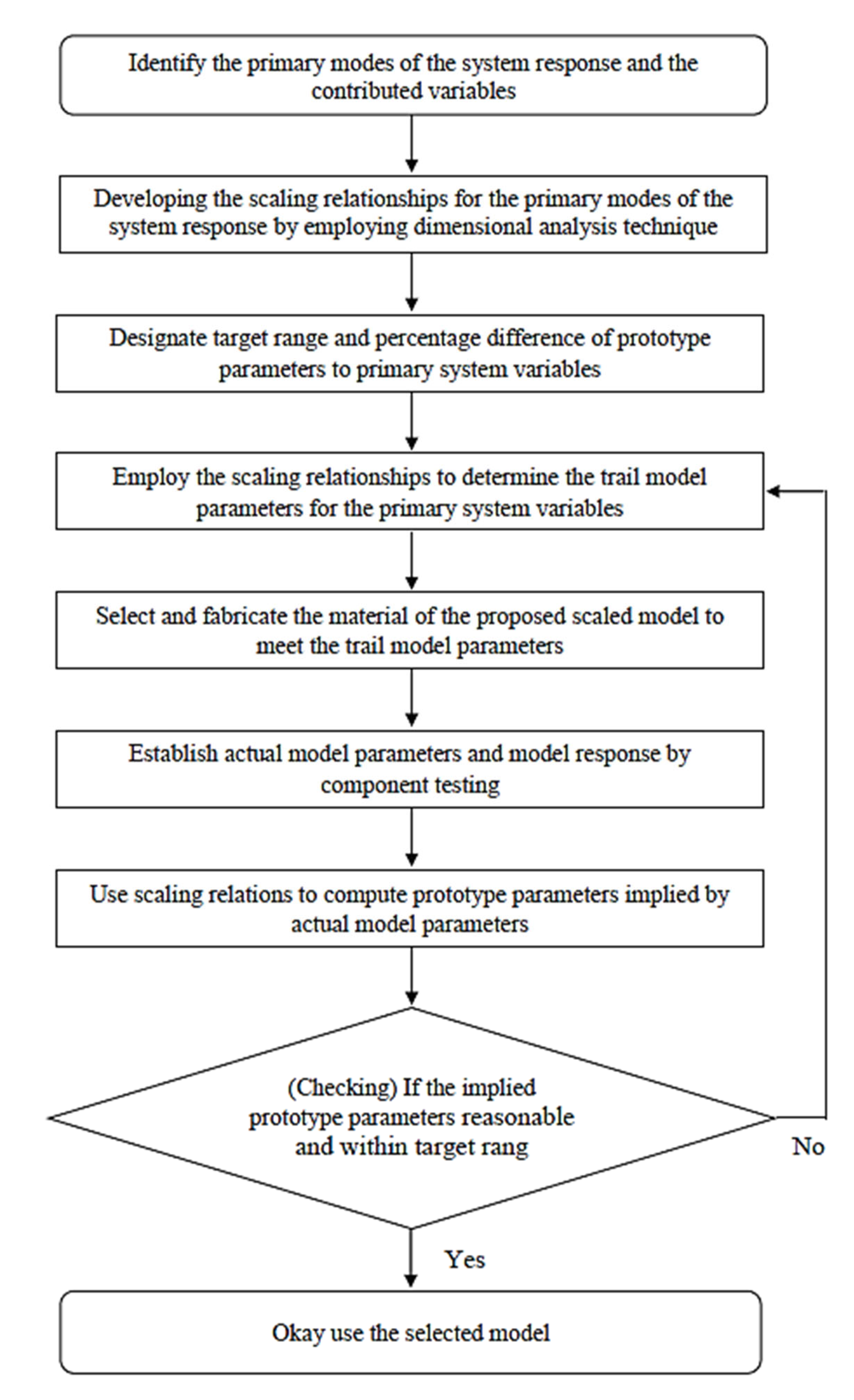


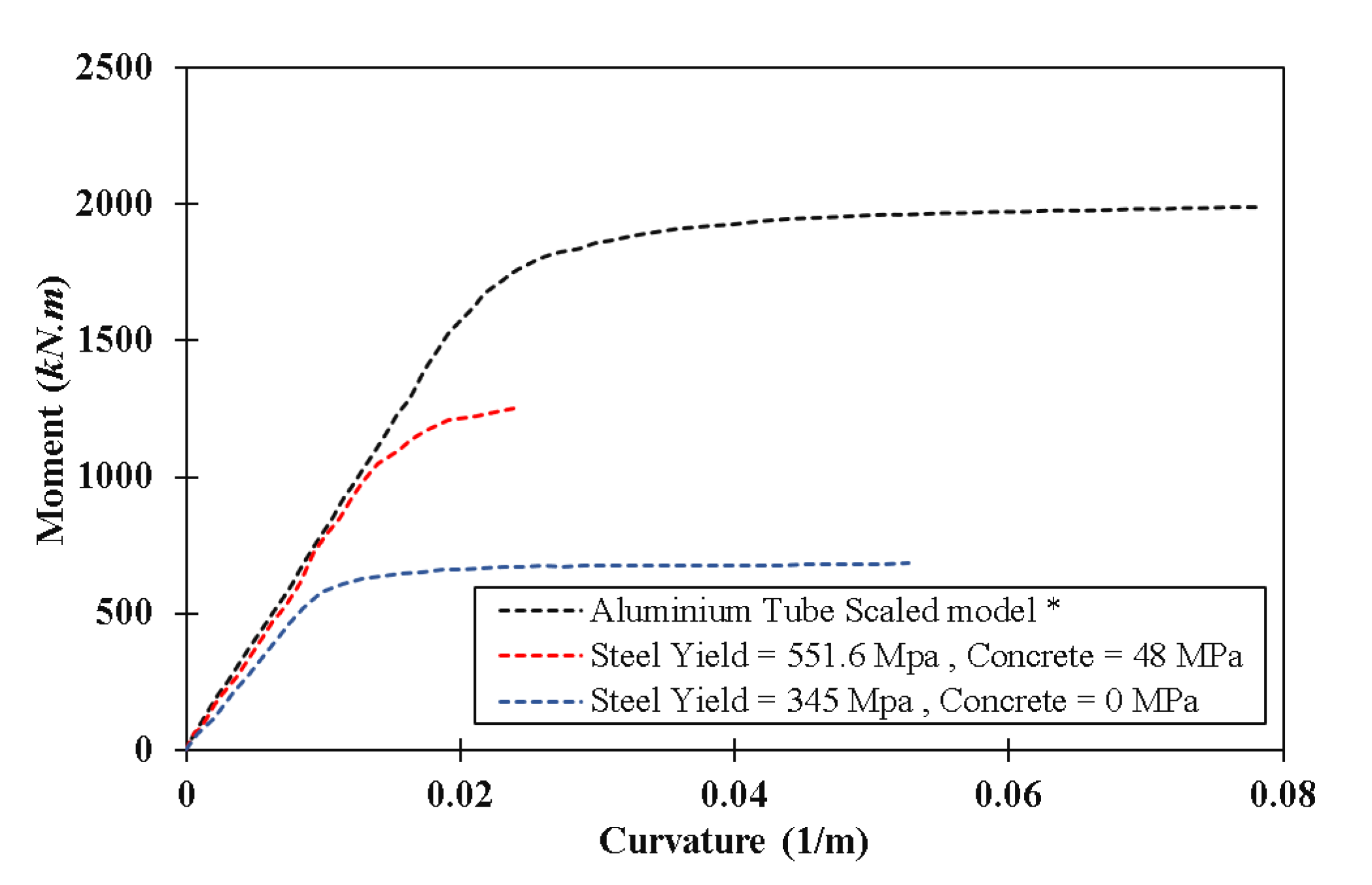
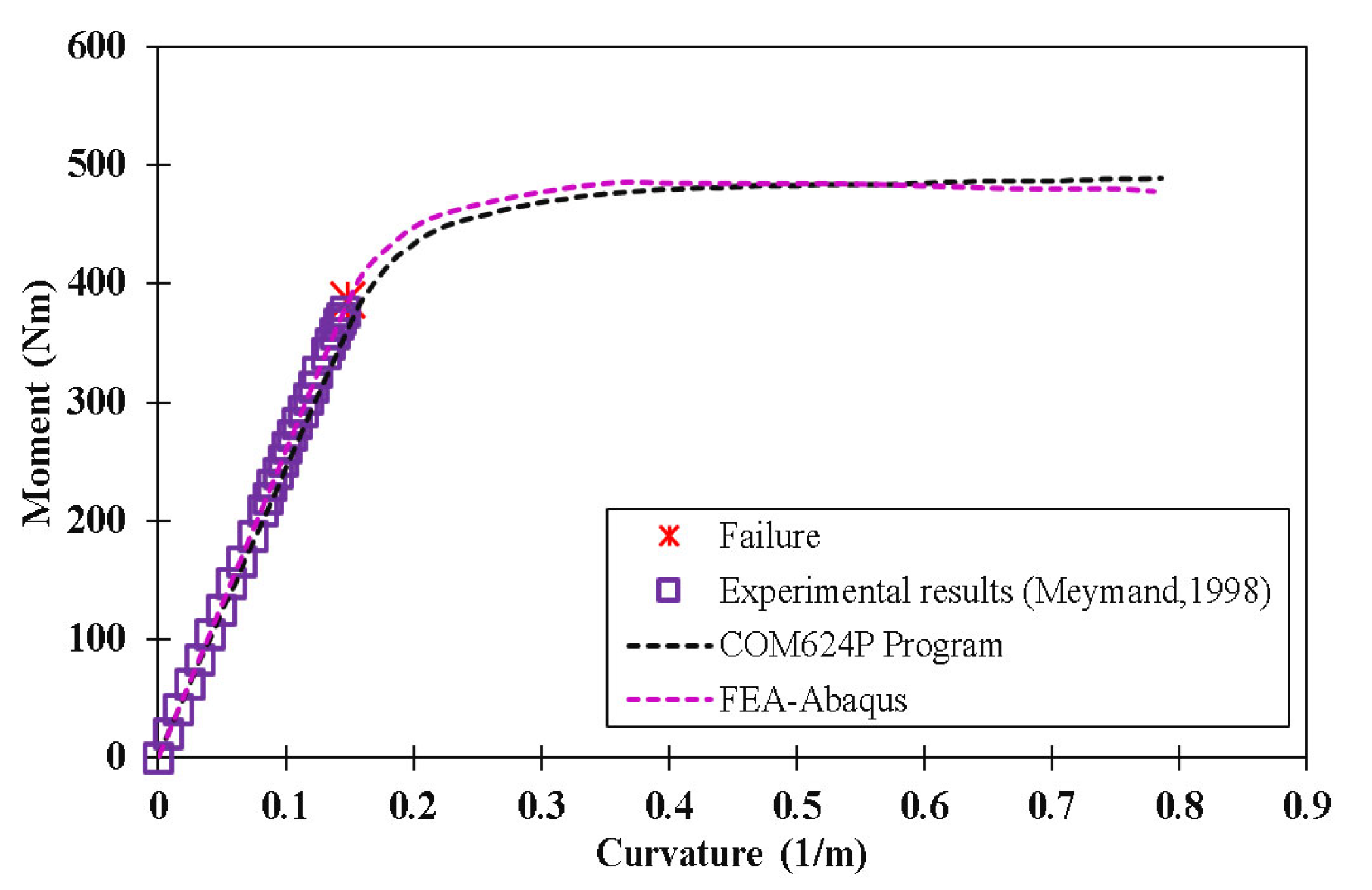

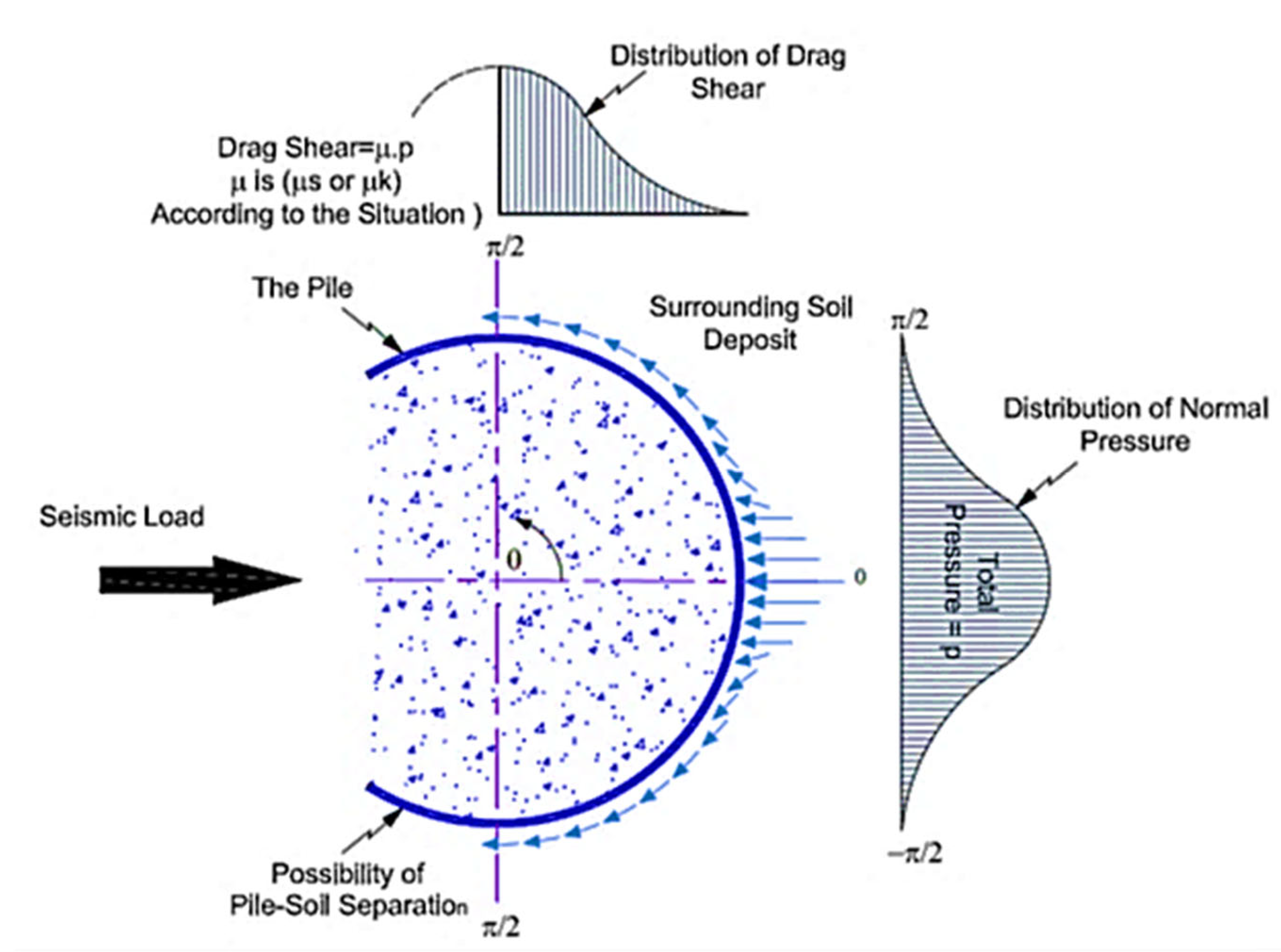

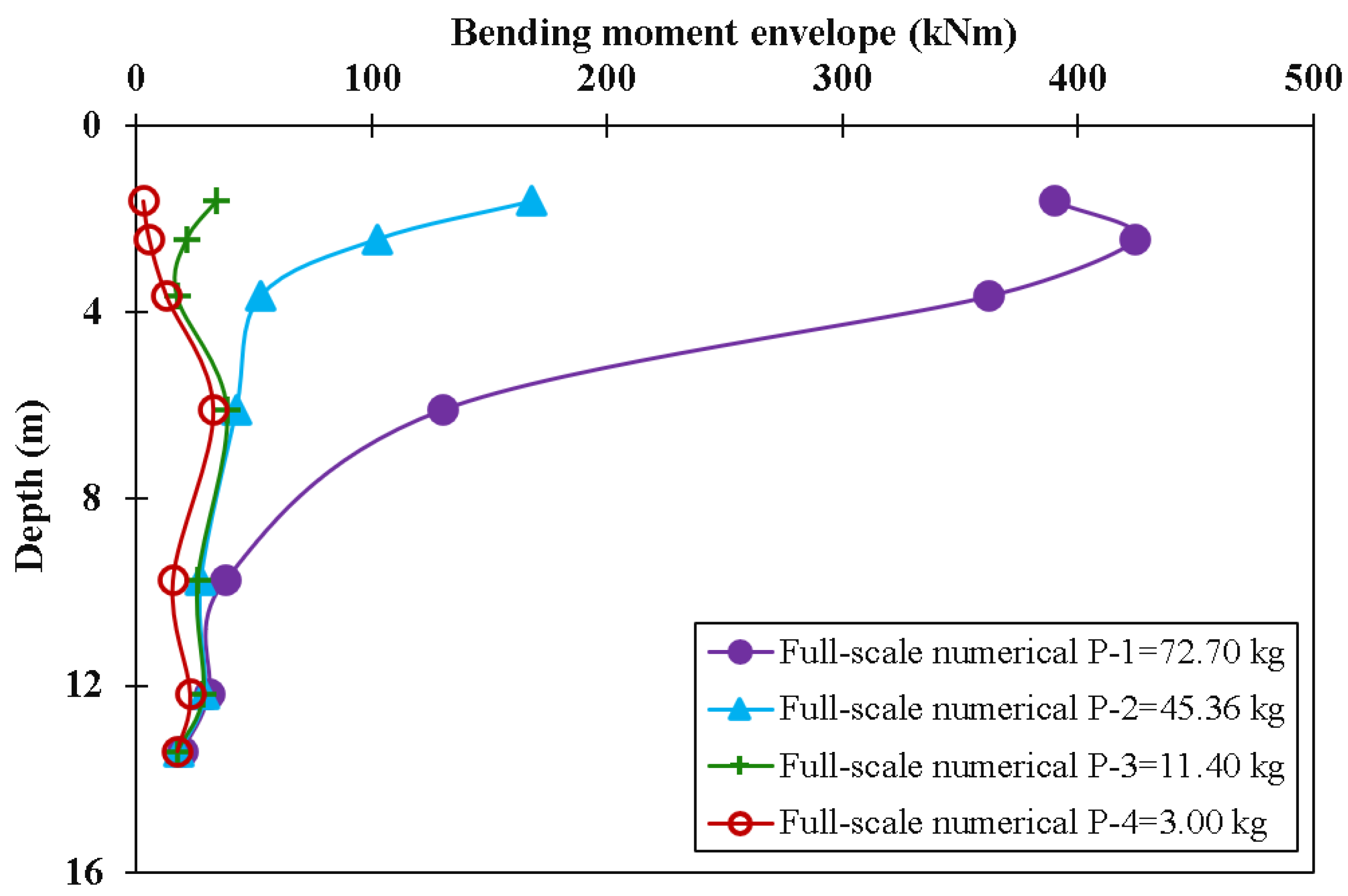


| No. | Interaction Mode (SSPSI) | Variables |
|---|---|---|
| I. | Free-field | modulus of degradation and damping |
| II. | Soil–pile lateral kinematic interaction | , |
| III. | Soil–pile lateral inertial interaction | |
| IV. | Soil–pile axial response | , |
| V. | Radiation damping |
| Variable | Symbol | Factor |
|---|---|---|
| Mass density of saturated soil and structure | 1 | |
| Acceleration of soil and or structure | ||
| Strain of soil and structure | ||
| Strain of the soil due to creep, temperature, etc. | ||
| Porosity of soil | ||
| Inclination of the beam | ||
| Density of pore water and/or external water | ||
| Inclination angle | ||
| Hydraulic gradient of external water | ||
| Length | ||
| Total stress of soil and structure | ||
| Effective stress of soil | ||
| Tangent modulus of soil | ||
| Bulk modulus of the solid grains of soil | ||
| Pressure of pore water and/or external water | ||
| Displacement of soil and/or structure | ||
| Bulk modulus of pore water and/or external water | ||
| Young’s modulus of the soil and structure | ||
| Shear modulus of the soil and structure | ||
| Displacement of the soil and/or the structure | ||
| Pressure of pore water and/or external water | ||
| Average displacement of pore water relative to the soil skeleton | ||
| Static soil shear strength | ||
| Dynamic soil shear strength | ||
| Time | ||
| Permeability of soil | ||
| Velocity of soil and/or structure | ||
| Rate of pore water flow | ||
| Shear wave velocity | ||
| Stiffness | ||
| Mass per unit length | ||
| Shear force | ||
| Axial force | ||
| Force | ||
| Mass | ||
| Longitudinal rigidity | ||
| Bending moment | ||
| Flexural rigidity | ||
| Frequency |
| Property | Symbol | Unit | Value |
|---|---|---|---|
| Saturated unit weight | 1505.74 | ||
| Natural water content | % | 90 | |
| Liquid limit | % | 88 | |
| Plastic limit | % | 48 | |
| Plasticity index | % | 40 | |
| Undrained strength ratio | Ratio | 0.32 | |
| Coefficient of consolidation |
| Prototype Input Parameters | Symbol | Value | Units |
|---|---|---|---|
| Pile outer diameter | 0.4064 | m | |
| Pile wall thickness | |||
| Pile length | |||
| Pile density | 7700 | ||
| Soil shear strength | |||
| Shear wave velocity | |||
| Steel Young’s modulus | |||
| Concrete Young’s modulus | |||
| Soil Young’s modulus | |||
| Soil shear modulus | 163.8 | MPa | |
| Percentage of concrete EI contribution |
| Model Input Parameters | Symbol | Value | Units | Criteria |
|---|---|---|---|---|
| Pile outer diameter | Target | |||
| Pile wall thickness | Target | |||
| Pile length | Target | |||
| Ratio | - | Target | ||
| Pile d/t Ratio | - | Target | ||
| Target | ||||
| 96 | Target | |||
| Soil shear strength | Target | |||
| Area of steel: | Scale | |||
| Steel moment of inertia | Scale | |||
| 60,915.6 | Scale | |||
| Area concrete | 0.114 | Scale | ||
| Concrete flexural rigidity EI | 14,263.4 | Scale | ||
| Composite concrete/steel flexural rigidity | 75,179 | Scale | ||
| Composite concrete/steel flexural rigidity | 2.294 | Target | ||
| Total Mass/m length | Ratio | 397.24 | Target | |
| Prototype first mode period | 0.7386 | Target |
| Model Parameters | Symbol | Value | Units | % Difference |
|---|---|---|---|---|
| Pile outer diameter | Scaled | |||
| Pile wall thickness | 76 | |||
| Pile length | Scaled | |||
| Pile Young’s modulus | Scaled | |||
| Pile density | Scaled | |||
| Soil shear strength (with 0.75 dynamic correction) | 2.4 | |||
| Shear wave velocity | Scaled | |||
| Pile cross sectional area | Scaled | |||
| Pile mass/m length | Ratio | Scaled | ||
| Pile moment of inertia | Scaled | |||
| Pile flexural rigidity/Unit length | ||||
| ratio | Dimensionless | |||
| Pile d/t ratio | Dimensionless | |||
| Dimensionless | ||||
| 101 | Dimensionless |
| Parameter | Value | ||
|---|---|---|---|
| Density (kg/m3) | 1505.75 | ||
| Log bulk modulus | 0.05 | ||
| Poisson’s ratio | 0.47 | ||
| Tensile limit | 0.00 | ||
| Log plasticity bulk modulus | 0.27 | ||
| Stress ratio | 1.26 | ||
| Wet yield surface size | 1.00 | ||
| Flow stress ratio | 0.78 | ||
| Initial void ratio | 1.50 | ||
| Cyclic loading parameters | |||
| Freq. (Hz) | Cyclic stress ratio (CSR) | ||
| cyclic degradation parameters | |||
| 0.1 | 0.6 | 4.2 | 75 |
| 0.25 | 0.6 | 4.2 | 97 |
| 1 | 0.6 | 4.1 | 420 |
| 2 | 0.6 | 4.1 | 600 |
| 5 | 0.6 | 4.2 | 825 |
| 10 | 0.6 | 4.2 | 1065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alisawi, A.T.; Collins, P.E.F.; Cashell, K.A. Novel Methodology for Scaling and Simulating Structural Behaviour for Soil–Structure Systems Subjected to Extreme Loading Conditions. Appl. Sci. 2023, 13, 8626. https://doi.org/10.3390/app13158626
Alisawi AT, Collins PEF, Cashell KA. Novel Methodology for Scaling and Simulating Structural Behaviour for Soil–Structure Systems Subjected to Extreme Loading Conditions. Applied Sciences. 2023; 13(15):8626. https://doi.org/10.3390/app13158626
Chicago/Turabian StyleAlisawi, Alaa T., Philip E. F. Collins, and Katherine A. Cashell. 2023. "Novel Methodology for Scaling and Simulating Structural Behaviour for Soil–Structure Systems Subjected to Extreme Loading Conditions" Applied Sciences 13, no. 15: 8626. https://doi.org/10.3390/app13158626
APA StyleAlisawi, A. T., Collins, P. E. F., & Cashell, K. A. (2023). Novel Methodology for Scaling and Simulating Structural Behaviour for Soil–Structure Systems Subjected to Extreme Loading Conditions. Applied Sciences, 13(15), 8626. https://doi.org/10.3390/app13158626








