An Improved Density Peak Clustering Algorithm Based on Chebyshev Inequality and Differential Privacy

Featured Application

Privacy protection and data mining.

Abstract

This study aims to improve the quality of the clustering results of the density peak clustering (DPC) algorithm and address the privacy protection problem in the clustering analysis process. To achieve this, a DPC algorithm based on Chebyshev inequality and differential privacy (DP-CDPC) is proposed. Firstly, the distance matrix is calculated using cosine distance instead of Euclidean distance when dealing with high-dimensional datasets, and the truncation distance is automatically calculated using the dichotomy method. Secondly, to solve the difficulty in selecting suitable clustering centers in the DPC algorithm, statistical constraints are constructed from the perspective of the decision graph using Chebyshev inequality, and the selection of clustering centers is achieved by adjusting the constraint parameters. Finally, to address the privacy leakage problem in the cluster analysis, the Laplace mechanism is applied to introduce noise to the local density in the process of cluster analysis, enabling the privacy protection of the algorithm. The experimental results demonstrate that the DP-CDPC algorithm can effectively select the clustering centers, improve the quality of clustering results, and provide good privacy protection performance.

1. Introduction

In the age of information, there has been an exponential surge in the volume of data, driving the need to extract valuable information and models, which has emerged as a central focus in current research [1]. Accompanying the swift advancements in machine learning, the application of data mining and data publishing [2] assumes paramount significance across diverse industries.

Clustering analysis serves as a fundamental aspect of data mining and finds relevance in numerous real-life scenarios [3,4]. The traditional clustering algorithms can be roughly divided into partition-based algorithms, hierarchy-based algorithms, density-based algorithms, grid-based algorithms, and model-based algorithms [5]. Currently, many scholars have conducted extensive research on clustering algorithms and continuously improved them to enhance their performance. S. Karthik et al. [6] proposed a method combining Kalman filter and K-means for improving the performance of Bayesian classification. This method was able to reduce the computational time for data clustering. Y. Tang et al. [7] proposed a novel CVI (Clustering Validity Index) for fuzzy clustering, i.e., tri-centered relation (TCR) index for noisy datasets. This index solved the difficulty of generating the correct number of clusters when the clustering centers are close to each other and possesses a simple separation processing mechanism. In order to improve the clustering quality of the K-means algorithm, T. Biswas et al. [8] applied the computational geometry method to initialize the clustering center, and proposed an Empty-Circles-based K-means (ECKM) Clustering algorithm. In order to improve the certainty and clarity of information security detection, Y. Zhang [9] proposed a DBSCAN clustering algorithm based on big data. This algorithm was a method of applying a big data clustering algorithm to information security detection.

In the era of data sharing, it becomes imperative to address the issue of privacy disclosure when dealing with vast amounts of data. Differential privacy technology [10], in comparison to other privacy protection techniques, offers a stringent mathematical definition and a rigorous proof process while providing a quantifiable degree of privacy protection.

In recent years, there has been a notable focus on differential privacy-based clustering algorithms, particularly on K-means and its derivative algorithms [11,12,13,14]. However, these algorithms have certain limitations that restrict their applicability to arbitrary types of datasets. These limitations include the need for predetermining the number of clustering centers and multiple iterations to reduce the sensitivity of the initial clustering center. In contrast, the combination of density-based clustering algorithms with differential privacy techniques offers a more versatile and noise-resistant approach. These algorithms do not require multiple iterations and can effectively handle various types of datasets, thereby demonstrating promising potential for practical applications. One noteworthy algorithm in this domain is the DP-DBSCAN algorithm proposed by W. Wu et al. [15]. This algorithm not only ensures clustering effectiveness but also achieves the desired level of differential privacy protection. Moreover, it is applicable to datasets of varying sizes and dimensions. Another proposed approach by L. N. Ni et al. [16] is the differential privacy protection multi-core DBSCAN clustering mode designed specifically for network user data. This approach effectively addresses privacy leakage issues encountered in the data mining process. However, it is worth noting that these algorithms have sensitive parameters and require complex parameter adjustments, which can pose challenges in obtaining stable clustering results. A balancing solution between privacy and availability is offered by the DP-OPTICS algorithm proposed by H. Wang et al. [17]. However, a key requirement for this algorithm is the need to assume query probabilities in advance and establish an appropriate privacy budget.

The Density Peak Clustering (DPC) algorithm [18] stands out from other density clustering algorithms due to its ability to efficiently identify density peak points and cluster data of arbitrary shapes [19]. Moreover, it requires fewer parameters, making it well-suited for large-scale data clustering analysis. The algorithm holds significant research value and shows promising application prospects. However, there are several challenges associated with this algorithm, including its limited adaptability to high-dimensional data, manual selection of truncation distance and clustering centers, and potential privacy leakage during the clustering process. Consequently, many researchers have conducted studies on the DPC algorithm to address these issues.

In response to the problem of distance convergence in the DPC algorithm for high-dimensional samples, S. C. Zhang et al. [20] proposed a novel density peak clustering algorithm for isolated nuclei and K-induction (IKDC), this algorithm addresses the issue by employing optimized isolation kernels to replace conventional distances. The new approach enhances the similarity between two samples in sparse domains, while reducing the similarity in dense domains. As a result, the convergence problem concerning distance measurements in high-dimensional samples is effectively resolved.

To address the issue of manual selection of clustering centers in the DPC algorithm, numerous improved algorithms have been proposed by researchers. Y. Lv et al. [21] introduced a fast search density peak clustering algorithm based on a shared neighbor and adaptive clustering center algorithm (DPC-SNNACC). This algorithm automatically determines the number of knee points in the decision graph by analyzing the characteristics of different datasets and eliminates the need for manual intervention in determining the number of clustering centers. Another approach was proposed by X. N. Yuan et al. [22], who developed a density peak clustering algorithm based on K-nearest neighbor and adaptive merge strategy (KNN-ADPC). This algorithm has only one parameter and performs clustering tasks automatically without human involvement. Y. Li et al. [23] defined local density using a reasonable granularity principle, they introduced the concept of relative semantic distance to select clustering centers in the decision graph, resulting in a new density peak clustering method based on fuzzy semantic units. W. Zhou et al. [24] replaced local density with the local deviation of spatial distance in datasets with diverse structures. By generating a more reasonable clustering center decision graph, they defined a threshold to accurately classify and process low-density points, thus proposing the bias density peak clustering algorithm (DeDPC). This algorithm effectively identifies outliers among low-density points. Furthermore, J. Y. Guan et al. [25] introduced the principal density peak clustering algorithm (MDPC+), which rapidly detects the principal density peak in the peak graph. The principal density peak represents the highest density peak in the cluster. Based on the new central hypothesis, MDPC+ can easily detect the true center of multi-peak clustering scenarios. Moreover, S. F. Ding et al. [26] proposed the density peak clustering algorithm based on natural adjacency and merge strategy (IDPC-NNMS). This algorithm identifies the natural neighborhood set of each data point and adaptively obtains its local density, effectively minimizing the influence of cutoff parameters on the final clustering result.

Table 1. The summarization of the applications and improvements of the clustering algorithm.

Reference	Solved Problems	Proposed Algorithm	Characteristics
S. Zhang et al. [18]	To make it easier to distinguish the density peaks of any two high-dimensional points and avoid producing “bad label” delivery	A novel density peaks clustering algorithm with isolation kernel and K-induction (IKDC)	It is superior to other algorithms
X. Yuan et al. [22]	To solve the subjectivity of determining cutoff distance cluster centers	A density peaks clustering algorithm based on K nearest neighbors with adaptive merging strategy (KNN-ADPC)	Higher accuracy of KNN-ADPC compared with DBSCAN, K-means++, DPC, and DPC-KNN.
Y. Li et al. [23]	To improve the performance of DPC on real datasets in practice	A novel method for density peaks clustering based on fuzzy semantic cells	Exhibits higher performance
J. Guan et al. [25]	To overcome the bad effect on multi-peak clusters of complex shapes of DPC algorithm time-consuming	A Main Density Peak Clustering algorithm (MDPC+)	Suitable for large datasets, superior in detecting center detection
S. Ding et al. [26]	To solve DPC algorithm works poorly on manifold data-sets with different densities, and sensitive to the cutoff parameter dc	An improved density peaks clustering algorithm based on natural neighbor with a merging strategy (IDPC-NNMS)	Effectively eliminate the impact of the cutoff parameter, and prove the effectiveness and superiority

summarizes the applications and improvements of the clustering algorithm.

In order to avoid the issue of privacy leakage during the clustering process in the DPC algorithm, researchers have proposed the integration of differential privacy techniques. Although there are limited studies on combining the DPC algorithm with differential privacy, some notable approaches have been introduced. Chen Yun incorporated the concept of reachable center points into the DPC algorithm and proposed DP-rcCFSFDP [27], which combines differential privacy technology. This approach achieves good clustering results. However, this algorithm still faces challenges such as subjective truncation distance and clustering center selection, as well as limited applicability to high-dimensional data. L. Sun, S. Bao, et al. proposed a DPC algorithm for differential privacy protection based on shared neighbor similarity DP-DPCSNNS [28]. This algorithm computes the local density of samples by combining shared neighbor similarity with Euclidean distance and utilizes shared neighbor similarity to detect clustering centers. This methodology facilitates the selection of appropriate clustering centers. H. Chen et al. proposed two improved density peak clustering algorithms based on differential privacy [29,30] with distinct perspectives. These approaches address various challenges, including weak clustering effects on high-dimensional datasets, manual selection of clustering centers and truncation distances, as well as privacy leakage during the clustering analysis in the DPC algorithm.

Table 2. The summarization of the applications and improvements of differential privacy techniques to clustering algorithms.

Reference	Solved Problems	Proposed Algorithm	Characteristics
L. Ni et al. [16]	Effectively leverage the privacy leakage issue in the process of data mining	A differential privacy preservation multiple cores DBSCAN clustering schema	Show better efficiency, accuracy, and privacy preservation effect than previous schemas
Y. Chen et al. [27]	To solve the poor performance of DPC algorithm on evenly distributed data and avoid privacy leakage	Optimize the clustering process with reachable-centers and propose DP-rcCFSFDP	Improve the clustering effectiveness while preserving data privacy compared with DP-CFSFDP
L. Sun et al. [28]	To solve the sensitive information leakage and security risk	Differential privacy-preserving density peaks’ clustering based on the shared near neighbors similarity method	Effectively protects the data privacy and improves the quality of the clustering results
Hua Chen et al. [29]	To solve the poor adaptability of high-dimensional data, inability to automatically determine clustering centers, and privacy problems in clustering analysis.	A new density peak clustering algorithm with adaptive clustering center based on differential privacy (DP-ADPC)	Can realize the automatic selection of clustering center, solve the privacy problem in clustering analysis, and improve clustering effect

summarizes the application of differential privacy techniques to clustering algorithms.

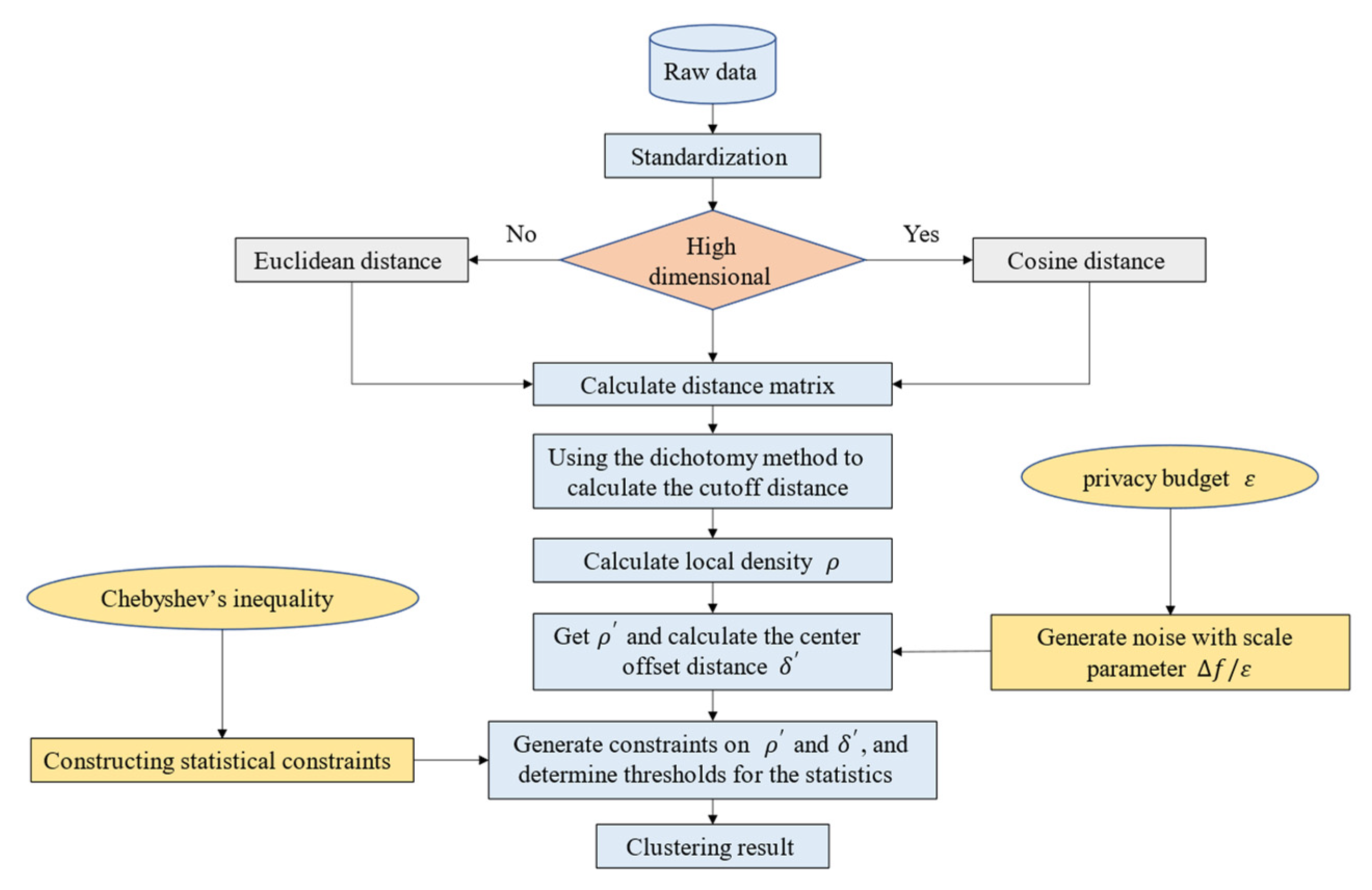
Building upon these studies, this paper proposes an improved DPC algorithm based on Chebyshev inequality and differential privacy called DP-CDPC from the perspective of the decision graph. The flowchart of the DP-CDPC algorithm is shown in Figure 1.

The specific contributions are as follows:

(1)

Aiming at the problem of manual selection of clustering centers in the traditional DPC algorithm, different from DP-ADPC proposed in the literature [29], this paper proposes an improved DPC algorithm based on Chebyshev inequality (CDPC). From the perspective of the decision graph, CDPC constructs constraint conditions for the statistics of the decision graph using Chebyshev inequality. By adjusting the parameters of the algorithm, the threshold of the statistics is determined, and CDPC automatically identifies the clustering centers.

(2)

In order to solve the problem of manual selection of truncation distance in the ADPC algorithm [29], dichotomy is used to determine the truncation distance adaptively.

(3)

To tackle the problem of privacy leakage in CDPC algorithm, this paper introduces the Laplace mechanism to add noise to the local density. Based upon these improvements, an extension of CDPC based on differential privacy (DP-CDPC) is proposed. To demonstrate the superiority of the algorithm, extensive tests and evaluations are conducted on multiple datasets.

The rest of this paper is organized as follows. Section 2 summarizes the related basic theoretical knowledge. Section 3 presents the core theory of the proposed algorithm, including its principles and steps. Section 4 includes specific experiments that validate the proposed algorithm on various datasets and compare its performance with other algorithms. Section 5 is the conclusion of this paper.

2. Related Basic Work

2.1. Differential Privacy

Definition 1

((Differential privacy) [10]). Let $\epsilon$ be a positive real number, $M$ be a random algorithm, $D$ denote the entire input dataset of the algorithm, and $S$ denote all output sets corresponding to the algorithm $M$. For any two non-single sample subsets $D_1$ and $D_2$ of the dataset $D$ that differ by only one sample, the algorithm $M$ is said to satisfy $\epsilon$-difference privacy if it satisfies Equation (1). Where $\epsilon$ represents privacy budget and $P[·]$ represents probability.

$$e^{-\epsilon }P[M(D_2)\in S]\le P[M(D_1)\in S]\le e^{\epsilon }P[M(D_2)\in S]$$

(1)

From the definition of differential privacy, it can be seen that, as $\epsilon$ becomes smaller, the more indistinguishable the left and right ends of the inequality, indicating that the degree of the privacy protection is larger, on the other hand, also indicating the lower availability of the algorithm. In order to achieve the balance between privacy and utility, it is necessary to choose an appropriate privacy budget.

Definition 2

((Sensitivity) [31]). Let $f(D)$ be a random function of the dataset $D$, $\Delta f$ represent the maximum value of the function change when a single sample is added or removed from any dataset, that is, if $\Delta f$ satisfies Equation (2), it is said that $\Delta f$ represents the sensitivity of the function $f(D)$.

$$\Delta f=\underset{D_1,D_2}{\max }|f(D_1)-f(D_2)|$$

(2)

2.2. Laplacian Noise Mechanism

The mechanisms employed to introduce noise into the algorithm for achieving differential privacy primarily consist of the Laplace mechanism [10] and the exponential mechanism [32]. In the case of continuous data, the Laplace mechanism is utilized to add noise, while the exponential mechanism is employed for discrete data types. In this paper, the noise will be added using the Laplace mechanism.

Definition 3

(Laplacian distribution). Suppose the density function of the random variable $X$ is shown in Equation (3), then $X$ is said to obey the Laplacian distribution of scale parameter $\lambda$ and displacement parameter $\mu$, where $\lambda >0$.

$$p(x|\mu ,\lambda )=\frac{1}{2b}\exp (-\frac{|x-\mu |}{\lambda })$$

(3)

Let $f(D)$ be the continuous variable, then the Laplacian mechanism can be expressed as:

$$M(D)=f(D)+lap(\mu ,\lambda )$$

(4)

where $lap(\mu ,\lambda )$ represents the random noise obeying the Laplacian distribution. In general, the displacement parameter $\mu$ equals 0, and the value of the scale parameter $\lambda$ can be determined by the sensitivity $\Delta f$ and the privacy budget $\epsilon$ of the statistic, which can be expressed as $\lambda =\Delta f/\epsilon$ [29].

2.3. DPC Algorithm

The DPC algorithm [18] introduces the concepts of the local density and the center offset distance, which can make it easier to understand the principle of the DPC algorithm. The algorithm works as follows: (1) it chooses the clustering center with both larger local density and center offset distance, and all other points in the cluster surrounding the clustering center. (2) The clustering centers are far from each other.

Definition 4

(Cutoff distance). Set $d_{ij}$ to represent the similarity between two different samples $i$ and $j$ of the dataset $D$. Traditional algorithms usually use Euclidean distance to measure the similarity of two samples. Let $R$ represent the sequence of $d_{ij}$ arranged in the order from the smallest to the largest, $R_i$ representing the $ith$ index of $R$. Set $d_c$ as the cutoff distance, $p$ as the cutoff percentage; $d_c$ of the DPC algorithm is determined by $p$, and its calculation can be expressed as $d_c=r_{p\times n}$, where $n$ represents the total number of samples in the dataset.

Definition 5

(Local density). Set $x_i$ as the $ith$ sample of the dataset $D$, $\rho$ as the local density, and ${\rho }_i$ to represent the local density of each point. There are two methods to define the local density [33]: if all attribute types of the dataset $D$ are discrete, Equation (5), which represents the calculation method of truncated kernel, can be used; if the attribute types of the dataset $D$ are continuous, the soft statistics method, which is based on Gaussian kernel, can be used, and its formula is given by Equation (6) [29].

$${\rho }_i={\displaystyle \sum _j\chi (d_{ij}-d_c)},\chi (d)=\left\{\begin{array}{c}0,d>0\\ 1,d\le 0\end{array}\right.$$

(5)

$${\rho }_i={\displaystyle \sum _j\exp (-{(\frac{d_{ij}}{d_c})}^2)}$$

(6)

Definition 6

(Center deviation distance). Set $\delta$ as the center deviation distance and ${\delta }_i$ as the center deviation distance of each point. The center deviation distance represents the minimum distance between point $x_i$ and the set of points whose local density is locally larger than $x_i$ For the point $x_i$ with the largest local density value, ${\delta }_i$ represents the maximum distance between that point and other points. The definition of center deviation distance can be expressed as the mathematical Equation (7) [29].

$${\delta }_i=\left\{\begin{array}{c}\underset{j}{\min }\left\{d_{ij}\right\},{\rho }_j>{\rho }_i\\ \underset{j}{\max }\left\{d_{ij}\right\},otherwise\end{array}\right.$$

(7)

2.4. Cosine Distance

According to the literature [29], algorithms using cosine distance for high-dimensional datasets tend to exhibit better performance. In order to further verify the impact of cosine distance on high-dimensional datasets, the principle and definition of cosine distance will be shown here.

Definition 7

(Cosine distance). Cosine similarity measures the cosine of the Angle between two vectors in the space. Let $x_{ik}$ represent the value of the $kth$ dimension of the $ith$ sample point in the dataset $D$, m represent the dimension of $D$, and let $\theta$ represent the included angle between two sample points, then the mathematical expression of cosine similarity is shown in Equation (8).

$$\cos (\theta )=\frac{x_i{x}_j}{\left|x_i\right|\left|x_j\right|}=\frac{{\displaystyle \sum _{k=1}^m{x}_{ik}{x}_{jk}}}{\sqrt{{\displaystyle \sum _{k=1}^m{x}_{ik}{}^2}\sqrt{{\displaystyle \sum _{k=1}^m{x}_{jk}{}^2}}}}$$

(8)

According to the principle of cosine similarity, as the value of $\theta$ decreases, the closer the cosine value is to 1, the more similar they are, and the cosine distance $d_{ij}$ can be expressed as Equation (9):

$$d_{ij}=1-\cos (\theta )$$

(9)

2.5. Determination of Cutoff Distance by Dichntomy

Using the dichotomy method [30] to determine the cutoff distance $d_c$ can solve the subjectivity of the traditional method by setting the truncation percentage $p$, the main process is as follows:

(1) Convert the distance list obtained by Euclidean distance or cosine distance into a distance matrix, and set the maximum value and minimum value of the distance matrix as $d_{\max }$ and $d_{\min }$, respectively;

(2) The value of the initial truncation distance $d_c$ is the average value of $d_{\max }$ and $d_{\min }$, namely $d_c=\frac{d_{\max }+d_{\min }}{2}$;

(3) Calculate the number $n\_neighs$ less than $d_c$ in the distance matrix, and calculate its ratio $r$ to the total number;

(4) If $r<a_1$, assign the initialized $d_c$ value to $d_{\min }$, return to step (2), and continue the loop;

(5) If $r>a_2$, assign the initialized $d_c$ value to $d_{\max }$, return to step (2), and continue the cycle with the new $d_c$ instead of the initial value;

(6) If $a_1\le r\le a_2$, or if $d_{\max }-d_{\min }<0.0001$, then exit the loop;

(7) Output $d_c$.

According to the value of truncation percentage $p$ in the traditional DPC algorithm and in the results of many experiments, in this paper $a_1$ and $a_2$ are set as 0.01 and 0.04, respectively.

3. An Improved DPC Algorithm Based on Chebyshev Inequality and Differential Privacy

Based on the literature [29,30], this paper proposes the use of cosine distance instead of Euclidean distance to measure the similarity of high-dimensional datasets, and the use of dichotomy to determine truncation distance adaptively. Aiming at the subjective selection of clustering centers, from the perspective of the decision graph, this paper establishes the constraint conditions of the decision graph statistics by Chebyshev inequality, and then the threshold of statistics $\rho$ and $\delta$ are obtained, and the selection of clustering centers is achieved by adjusting the constraint parameters, the improved DPC algorithm based on Chebyshev inequality (CDPC) is proposed. Finally, to avoid privacy disclosure, noise with suitable privacy budget is added to $\rho$ and a CDPC algorithm based on differential privacy (DP-CDPC) is proposed. The specific improvement process is described below.

According to the definition of local density, the maximum change in local density is 1 when a sample is added or deleted, so the value of $\Delta f$ is taken as 1. Furthermore, based on the mechanism of adding noise as illustrated in Equation (4), the expression for local density with the addition of noise can be expressed using Equation (10).

$${{\rho }^{\prime }}_i={\rho }_i+lap(0,\frac{1}{\epsilon })$$

(10)

3.1. Determination of Clustering Center Based on Chebyshev Inequality

The core of DPC algorithm to select the clustering centers based on the decision graph is to select the points with relatively large local density $\rho$ and center deviation distance $\delta$ from dataset $D$. While previous studies, such as those in the literature [34,35,36], have utilized the concept of Chebyshev inequality to achieve adaptive clustering center selection, their inequality parameters were determined as 3, 2, and 1, respectively, without universal adaptability.

This paper establishes the constraint conditions for $\rho$ and $\delta$ through Chebyshev inequality, and determines the threshold values by adjusting parameters $b_1$ and $b_2$ to obtain the clustering center. Through this process, the clustering centers are obtained. The procedure is shown as follows:

(1) The potential set of clustering centers $ELC$ is obtained based on $\delta$, and the constraint conditions of $\delta$ can be expressed by Equation (11), where $\mu (\delta )$ and $\sigma (\delta )$, respectively, represent the mean value and the standard deviation of $\delta$, $b_1$ represents the coefficient parameter of $\sigma (\delta )$, and $I_{\mathrm{s}}$ represents the set of all points.

$$ELC=\left\{i\right|{\delta }_i>\mu (\delta )+b_1\sigma (\delta ),i\in I_s\}$$

(11)

(2) The true set of clustering centers, denoted as $LC$, is screened from $ELC$. If the average of the local density of all the points in $ELC$ is less than that of all points in $D$, it indicates that $ELC$ contains a significant number of noise points; in this case, the true clustering center set can be obtained from Equation (12). Conversely, the true clustering center set can be obtained from Equation (13). Where $\mu (\rho )$,$\sigma (\rho )$ represents the mean value and the standard deviation of $\rho$, respectively, $ave$ represents the mean of $\rho$ of all points, and $b_2$ represents the coefficient parameter of $ave$.

$$LC=\left\{i\right|{\rho }_i>\mu (\rho )+\sigma (\rho ),i\in ELC\}$$

(12)

$$LC=\left\{i\right|{\rho }_i>b_{2}ave,i\in ELC\}$$

(13)

3.2. The Procedure of DP-CDPC Algorithm

Based on the above theory, a CDPC algorithm is proposed. For balancing between the algorithm effect and the degree of privacy protection, a CDPC algorithm based on differential privacy (DP-CDPC) (Algorithm 1) is proposed.

The specific procedure is shown as follows:

Algorithm 1: DP-CDPC algorithm

Input: dataset $D$, privacy budget $\epsilon$, clustering center parameters $b_1$, $b_2$

Output: clustering results

1. Processing of datasets and calculation of statistics: Firstly, standardize $D$ Then, Euclidean distance is usually used to calculate the distance between different samples of $D$, but for high-dimensional datasets using Equation (9). Then, the dichotomy is used to determine the truncation distance $d_c$ adaptively; the local density ${\rho }_i$ and the center deviation offset distance ${\delta }_i$ are calculated, respectively, according to Equations (6) and (7).

2. Add Laplacian noise: According to the privacy budget $\epsilon$ and the sensitivity $\Delta f$ of $\rho$ to generate Laplacian noise, the obtaining of the local density of added noise ${\rho }_i{}^{\prime }$ according to Equation (10), and the corresponding ${{\delta }^{\prime }}_i$ can be calculated by Equation (7).

3. Calculate the mean and the standard deviation of ${\rho }_i{}^{\prime }$ and ${{\delta }^{\prime }}_i$: Normalize ${\rho }_i{}^{\prime }$ and ${{\delta }^{\prime }}_i$ after adding noise and calculate their mean and standard deviation, respectively.

4. Selection of clustering centers: The set of local clustering center $ELC$ is obtained according to Equation (11). If the average of the local density in $ELC$ is less than that of the whole dataset, the set of real clustering centers can be selected from the $ELC$ according to Equation (12); otherwise, the final clustering centers are selected using Equation (13).

5. Distribution of non-clustering central points: Assign non-central points to each clustering center that are closer to the point.

3.3. Analysis of DP-CDPC Algorithm Complexity

This section provides an analysis of the complexity of the DP-CDPC algorithm. Compared with the DPC algorithm, the DP-CDPC algorithm introduces additional processes such as dichotomy for determining the truncation distance, addition of noise to the local density, and adjustment of parameters for determining the clustering centers. Let $N$ represent the size of the dataset, the time complexity of the DP-CDPC algorithm is mainly composed of the following components:

(1) Calculation of statistics. The time complexity of data standardization processing is $O(N^2)$. The time complexity of calculating the distance $d_{ij}$ between samples is $O(N^2)$. The time complexity of dichotomy method for determining the cutoff distance $d_c$ is $O(\log N)$. The time complexity of calculating the local density of each sample ${\rho }_i$ is $O(N^2)$. Adding noise to the local density can obtain the local density of each sample after adding noise ${\rho }_i{}^{\prime }$, and the time complexity is $O(N)$; The time complexity of calculating the center offset distance of each corresponding sample ${\delta }_i{}^{\prime }$ is $O(N^2)$; For the calculation of the mean and standard deviation of ${\rho }_i{}^{\prime }$ and ${\delta }_i{}^{\prime }$, the time complexity is $O(N^2)$ respectively. The total time complexity is: $O(N^2)+O(N^2)+O(\log N)+O(N^2)+O(N)+O(N^2)+4O(N)~O(N^2)$.

(2) Selection of clustering center. The time complexity of getting the threshold of ${\delta }_i{}^{\prime }$ and ${\rho }_i{}^{\prime }$ is $O(N)$. The total time complexity of getting the clustering centers is $O(N)$.

(3) Assignment of non-clustering centers. Assigning non-clustering center points to the closest points within the cluster based on the nearest neighbor principle has the same time complexity as the DPC algorithm, which is $O(N)$.

In summary, the overall time complexity of DP-CDPC algorithm is consistent with that of DPC algorithm, which is $O(N)$.

3.4. Privacy Analysis of DP-CDPC Algorithm

The DP-CDPC algorithm implements privacy protection by introducing appropriate noise to the core statistic of the CDPC algorithm, this section aims to analyze and establish this claim, and the proof process is presented as follows:

Let $D$ and $D^{\prime }$ denote a group of adjacent datasets of local density, $M(D)$ and $M(D^{\prime })$ respectively represent the set of all output results of adjacent datasets through DP-CDPC algorithm, and $S$ represent all output results of algorithm. Since the inequality $|a-c|-|b-c|\le |a-b|$ holds, and exponential function $e^x$ is an increasing function, then:

$$\begin{array}{l}\frac{P(M(D)\in S)}{P(M(D^{\prime })\in S)}=\frac{\frac{1}{2b}\exp (-\frac{|D-\mu |}{b})}{\frac{1}{2b}\exp (-\frac{|D^{\prime }-\mu |}{b})}\\ =\exp (\frac{|D^{\prime }-\mu |}{b}-\frac{|D-\mu |}{b})\\ \le \exp (\frac{|D-D^{\prime }|}{b})\\ \le \exp (\frac{\max |D-D^{\prime }|}{b}) \\ =\exp (\frac{\Delta f}{\Delta f/\epsilon })\\ =e^{\epsilon }\end{array}$$

(14)

In the DP-CDPC algorithm, each generated cluster family is independent of each other, and the clustering process does not involve iterative steps. Hence, there is no need to allocate the privacy budget. Therefore, the DP-CDPC algorithm guarantees $\epsilon$ differential privacy protection.

4. Experimental Results and Analysis

4.1. Experimental Environment and Dataset

In this paper, python3.8.3 is used to verify the validity of the proposed algorithm. The experimental environment is Windows10, Intel^®Core (TM) i3-7130U CPU, 8.00 GB memory, 64-bit operating system. Several synthetic datasets and UCI datasets are used as experimental datasets, and the characteristics of these datasets are provided in

Table 3. Experimental datasets.

Dataset	Attributes	Size	Clusters	Sources
flame	2	240	2	Synthetic
spiral	2	312	3	Synthetic
compound	2	399	6	Synthetic
aggregation	2	788	7	Synthetic
R15	2	600	15	Synthetic
D31	2	3100	31	Synthetic
seeds	7	210	3	UCI
ecoli	7	336	8	UCI
movement	90	360	15	UCI
dermatology	33	366	6	UCI
banknote	4	1372	2	UCI
abalone	8	4177	3	UCI

.

The datasets flame, spiral, compound, aggregation, R15, and D31 are all two-dimensional composite datasets commonly employed for algorithm testing, and these datasets exhibit different density distributions and shapes.

The datasets seeds, ecoli, movement, dermatology, banknote, and abalone are all real-world datasets obtained from the UCI Machine Learning Repository. The seeds dataset describes the grain characteristics of three wheat varieties, namely, Kama, Rosa, and Canadian. Each wheat variety contains 70 samples, and each sample contains 7 attributes such as grain area, perimeter, tightness, kernel length, kernel width, asymmetry index, and core groove length. The ecoli dataset is regarding protein localization sites, and contains 336 samples, with each sample containing 7 features divided into 8 categories. The movement dataset comprises 15 classes, each of which contains 24 instances, and each sample includes 46 features. The dermatology dataset is a classified dataset for diagnosing skin diseases: it includes 366 samples, with each containing 33 attributes, grouped into 6 categories. The banknote dataset contains 1372 samples, divided into two categories—genuine banknote and counterfeit banknote. Each sample contains four features extracted from the images used to evaluate the banknote authentication process through wavelet transform tools. The abalone dataset measures the age of abalone: it contains 4177 samples and is divided into 3 categories by measuring 8 characteristics of each sample.

To evaluate the effectiveness of the DP-CDPC algorithm, several comparison experiments are conducted. Firstly, different methods for measuring the similarity of UCI datasets are compared. Secondly, the CDPC algorithm is compared with the ADPC [29], K-means [8], DBSCAN [9], and SNNDPC [37] algorithms. Thirdly, the DP-CDPC algorithm is compared with the CDPC and DP-ADPC. Lastly, the clustering effects of different privacy budgets are compared. The Fowlkes and Mallows index [38] ($FMI$), Adjusted Rand index [39] ($ARI$), and Adjusted Mutual Information index [39] ($AMI$) are used in these experiments to assess the clustering performance of the proposed algorithm.

4.2. The Settings of Clustering Center and Privacy Budget Parameters

The CDPC algorithm determines the clustering center by adjusting parameters $b_1$ and $b_2$, which have great influence on the result of the algorithm. In order to study the influence of different privacy budgets on the clustering effect of the algorithm under different combinations of $b_1$ and $b_2$, experiments are conducted on several composite datasets and UCI datasets, respectively. Line graphs are drawn to illustrate the change in the clustering effect with respect to privacy budget $\epsilon$. Due to the inherent randomness associated with the added Laplacian noise, the clustering effect showed a fluctuation change. To mitigate this, the experiments are repeated 20 times, and the average values are computed to obtain the final results. Since the three-evaluation metrics show similar trends, only the results of $ARI$ changing are presented here.

4.2.1. Synthetic Datasets

In terms of synthetic datasets, the clustering effect of different combinations of $b_1$ and $b_2$ of the DP-CDPC algorithm varies with the privacy budget, as shown in Figure 2, where the numbers in the algorithm label, respectively, represent the values of parameters $b_1$ and $b_2$.

From Figure 2, several characteristics of the DP-CDPC algorithm can be observed. Overall, as the privacy budget $\epsilon$ increases gradually, the clustering evaluation index of the algorithm initially improves and then stabilizes. It can be seen that, within a certain range, increasing the privacy budget leads to better clustering effectiveness.

For the flame dataset, when parameter $b_2$ is set as 1 and $b_1$ is set as 3, the algorithm achieves the best performance after reaching the steady state, and the critical value $\epsilon$ for reaching the stationary state is 15.

For the spiral dataset, when parameter $b_2$ is set as 1 and $b_1$ is set as 1, 2, or 3, respectively, the algorithms show a consistent trend of change when different amounts of noise are added. When the same amount of noise is added, the clustering effect does not differ significantly with varying parameter values. For the compound and aggregation datasets, when parameter $b_1$ and $b_2$ are set as 3 and 0.5, respectively, the algorithm has the best effect after reaching the stationary state, and the critical value $\epsilon$ for reaching the stationary state is 1.5 and 2, respectively. For dataset R15, when parameters $b_1$ and $b_2$ are set as 1 and 0.5, respectively, the algorithm achieves the best effect after reaching the stationary state, and the critical value $\epsilon$ for reaching the stationary state is 0.5. For the D31 dataset, when parameter $b_2$ is set as 0.5 and $b_1$ is set as 2 or 3, the algorithm achieves the best effect after reaching the stationary state, and the critical value $\epsilon$ for reaching the stationary state is 0.5.

4.2.2. UCI Datasets

For the UCI datasets, the line graph of the clustering effect of algorithms under different combinations of $b_1$ and $b_2$ changes with privacy budget $\epsilon$, as shown in Figure 3, where the label contains “eu” indicating the use of Euclidian distance, while “cos” indicates the use of cosine distance.

As observed in Figure 3a, for dataset seeds, the clustering effect of DP-CDPC using Euclidean distance is better than that of using cosine distance on the whole; when parameter $b_1$ is set as 2 and $b_2$ is set as 1, the clustering effect of reaching the stationary state is better, and the critical value $\epsilon$ of reaching the stationary state is 4. In Figure 3b, for the ecoli dataset, the clustering effect of the DP-CDPC using cosine distance is better than that of using Euclidean distance overall. When cosine distance is adopted, a better clustering performance is achieved after setting the algorithm’s parameters to 2 and 0.5, respectively, and the critical value $\epsilon$ of reaching the stationary state is 0.5. When Euclidean distance is used, the clustering effect is better when both parameters $b_1$ and $b_2$ are set to 1, and the critical value is 1.5. Figure 3c reveals that, for the movement dataset, cosine distance also leads to a better clustering performance. When cosine distance is used, the clustering effect is better when parameters $b_1$ and $b_2$ are set as 1 and 0.5, respectively, and the critical value is 1. When Euclidean distance is used, the clustering effect is better when both $b_1$ and $b_2$ are set as 1, respectively, and the critical value is 0.5. In Figure 3d, for the dermatology dataset, the effect of cosine distance is also better. In the case of cosine distance, when $b_2$ is 0.5 and $b_1$ is 3, respectively, the algorithm achieves a better clustering performance when reaching the stable state, and the critical value is 0.5. When Euclidean distance is used, the clustering effect is better when both parameters $b_1$ and $b_2$ are set as 1, respectively, and the critical value is 1.5. Figure 3e indicates that, for the banknote dataset, the clustering effect using Euclidean distance is better than that using cosine distance. When the parameters are set as 3 and 1, respectively, the algorithm achieves a better clustering effect in the stationary state, and the critical value of reaching the stationary state is 8. When cosine distance is adopted, $b_2$ is set as 0.5, and $b_1$ is set as 2, the effect is better after reaching the stationary state, and the critical value $\epsilon$ is 2. It can be seen from Figure 3f that, for the abalone dataset, the clustering effect using cosine distance is better. When $b_2$ is set as 1 and $b_1$ is set as 1, 2 or 3, respectively, the algorithms present the same trend of change when different amounts of noise are added. After adding noise of the same $\epsilon$, the clustering effect of algorithms with different parameter values is not significantly different, and the critical value of $\epsilon$ is 0.5.

In conclusion, the experiments conducted on both the synthetic datasets and UCI datasets demonstrate that the parameter $b_1$ in the DP-CDPC algorithm can be set to 1, 2, or 3, while the parameter $b_2$ can be set to 0.5 or 1. By choosing an appropriate privacy budget, the DP-CDPC algorithm achieves a balance between privacy protection and clustering effectiveness. For low-dimensional datasets such as seeds, banknote, and the synthetic datasets, the clustering performance is better when using the similarity measured by Euclidean distance. On the other hand, for high-dimensional datasets like ecoli, movement, dermatology, and abalone, the clustering performance is better when using the similarity measured by cosine distance. These findings suggest that the choice of similarity measure depends on the dimensionality of the dataset. Cosine distance appears to be more effective for high-dimensional datasets, while Euclidean distance is more suitable for low-dimensional datasets.

4.3. Analysis of Algorithm Results

To further verify the effectiveness of the DP-CDPC algorithm, this paper compares it with several other algorithms including the K-means, DBSCAN, SNNDPC, CDPC, ADPC, and DP-ADPC algorithms. The parameters for the DP-CDPC and CDPC algorithms are set based on the parameters that yield better clustering results in Section 4.2, the parameters’ truncation percentage $p$ of DP-ADPC and ADPC can be set according to the literature [29]. The parameters of the K-means and SNNDPC algorithms can be obtained from the actual number of categories in each dataset. The parameters of the DBSCAN algorithm are determined by the standard of the maximum $ARI$.

Table 4. Parameter settings.

Dataset	DBSCAN		DP-ADPC		DP-CDPC
	$\mathit{e}\mathit{p}\mathit{s}$	$\mathit{m}\mathit{p}\mathit{t}\mathit{s}$	$\mathit{p}$	$\mathit{\epsilon }$	$\mathit{\epsilon }$	${\mathit{b}}_1$	${\mathit{b}}_2$
flame	0.4	10	3	16	15	3	1
spiral	0.4	1	2	24	24	3	1
compound	0.4	19	6	18	1.5	3	0.5
aggregation	0.4	1	4	3	2	1	0.5
R15	0.4	1	4	6	3	3	0.5
D31	0.01	1	1	2	0.5	2	0.5
seeds	1.2	17	0.9	5	4	2	1
ecoli	0.8	4	0.1	4.5	0.5	2	0.5
movement	2.8	1	0.1	2	1	1	0.5
dermatology	4	4	0.1	5	0.5	3	0.5
banknote	0.4	4	2.5	2	1	3	1
abalone	0.4	19	2.9	1	1	1	1

shows an overview of the parameter settings for each algorithm, including $eps$ and $mpts$ of the DBSCAN algorithm, $p$ and $\epsilon$ of the DP-ADPC algorithm, $b_1$, $b_2$ and $\epsilon$ of the DP-CDPC algorithm on each dataset.

4.3.1. Synthetic Datasets

According to the parameter settings of each algorithm in different datasets in Table 4, the effectiveness of each algorithm on synthetic datasets is shown in

Table 5. The clustering evaluation index of each algorithm for synthetic datasets.

Dataset	Algorithm	ARI	AMI	FMI
flame	K-means	0.409	0.368	0.715
	DBSCAN	0.934	0.866	0.969
	SNNDPC	0.950	0.911	0.977
	ADPC	1.000	1.000	1.000
	CDPC	1.000	1.000	1.000
	DP-ADPC	0.966	0.968	0.983
	DP-CDPC	0.970	0.970	0.990
spiral	K-means	−0.006	−0.005	0.328
	DBSCAN	1.000	1.000	1.000
	SNNDPC	1.000	1.000	1.000
	ADPC	1.000	1.000	1.000
	CDPC	1.000	1.000	1.000
	DP-ADPC	0.850	0.853	0.901
	DP-CDPC	0.885	0.885	0.923
compound	K-means	0.581	0.722	0.677
	DBSCAN	0.786	0.795	0.852
	SNNDPC	0.640	0.727	0.745
	ADPC	0.740	0.804	0.830
	CDPC	0.740	0.804	0.830
	DP-ADPC	0.768	0.849	0.843
	DP-CDPC	0.770	0.835	0.846
aggregation	K-means	0.715	0.828	0.776
	DBSCAN	0.734	0.835	0.819
	SNNDPC	0.891	0.895	0.915
	ADPC	0.996	0.992	0.997
	CDPC	0.996	0.992	0.997
	DP-ADPC	0.956	0.978	0.967
	DP-CDPC	0.962	0.981	0.971
R15	K-means	0.993	0.994	0.993
	DBSCAN	0.264	0.731	0.455
	SNNDPC	0.993	0.994	0.993
	ADPC	0.993	0.994	0.993
	CDPC	0.993	0.994	0.993
	DP-ADPC	0.993	0.994	0.993
	DP-CDPC	0.993	0.994	0.993
D31	K-means	0.956	0.968	0.957
	DBSCAN	0.005	0.061	0.050
	SNNDPC	0.946	0.962	0.948
	ADPC	0.938	0.957	0.940
	CDPC	0.938	0.956	0.940
	DP-ADPC	0.909	0.952	0.913
	DP-CDPC	0.935	0.955	0.937

; the bolded values in the table represent the optimal experimental results.

As can be seen from Table 5, for the flame dataset, the clustering result of the CDPC and ADPC are same, and they achieve higher values for all three external evaluation indexes compared to other algorithms. After adding noise, the evaluation values slightly decrease but remain higher than other algorithms. Moreover, the DP-CDPC algorithm outperforms the DP-ADPC algorithm in terms of external evaluation indexes.

In the case of the spiral dataset, the CDPC, DBSCAN, SNNDPC, and ADPC algorithms all achieve optimal values for each clustering evaluation index, namely, $ARI$, $AMI$, and $FMI$ all reaching 1. These algorithms exhibit superior clustering effects compared to the K-means algorithm. The values of $ARI$, $AMI$, and $FMI$ for the DP-CDPC algorithm are 0.8845, 0.8851, and 0.9232, respectively, which are larger than those of the DP-ADPC algorithm. However, compared to the CDPC algorithm, the clustering effect of the DP-CDPC algorithm shows a significant reduction. For dataset compound, $ARI$ of the DBSCAN is larger than other algorithms, while $AMI$ and $FMI$ of the CDPC and ADPC are the same and larger than other algorithms. The evaluation indexes of the DP-ADPC and DP-CDPC are slightly lower than the ADPC and CDPC, but still higher than the other three algorithms in general, while the indexes of the DP-ADPC are slightly smaller than those of the DP-CDPC. For dataset aggregation, the clustering effect of the ADPC and CDPC is consistent and superior to the K-means, DBSCAN, and SNNDPC, while the clustering evaluation indexes of the DP-ADPC and DP-CDPC are slightly lower than the CDPC, but still higher than the others. Furthermore, the DP-CDPC algorithm exhibits a better effect than the DP-ADPC algorithm. In the case of the R15 dataset, all the values of the evaluation indexes of each algorithm are the same, except for the DBSCAN algorithm, and larger than that of the DBSCAN algorithm. For the D31 dataset, the values of the three external evaluation indicators of the K-means algorithm are the largest compared to those of the other algorithms, followed by the SNNDPC algorithm, while the values of all the external evaluation indicators of the DBSCAN algorithm are the smallest. The clustering results of the ADPC and CDPC algorithms are consistent and the clustering effect is better than that of the algorithm after adding noise, among which the DP-CDPC algorithm is better than the DP-ADPC algorithm.

In summary, the ADPC and CDPC algorithms demonstrate consistent clustering effects across all synthetic datasets and exhibit the best clustering performance compared to other algorithms on the flame, spiral, aggregation, and R15 datasets. In general, the DP-CDPC algorithm exhibits higher values for cluster evaluation indexes than the DP-ADPC algorithm, indicating its superior clustering effect. By comparing the clustering effect of the ADPC and CDPC algorithms, it is evident that using dichotomy to determine the truncation distance effectively addresses the problem of subjective selection. Furthermore, the CDPC algorithm shows improvement compared to the K-means, DBSCAN, and SNNDPC algorithms. Comparing the clustering effect of the DP-CDPC algorithm and the CDPC algorithm demonstrates that the clustering effectiveness of the algorithm after adding some noise is not necessarily weaker than the original algorithm due to the random and fluctuating nature of the noise.

4.3.2. UCI Datasets

This section further verifies the effect of the DP-CDPC algorithm on the UCI datasets, and the experimental results of each algorithm on the UCI datasets are shown in

Table 6. The clustering evaluation index of each algorithm for UCI datasets.

Dataset	Algorithm	ARI	AMI	FMI
seeds	K-means	0.773	0.725	0.848
	DBSCAN	0.408	0.453	0.648
	SNNDPC	0.745	0.737	0.830
	ADPC	0.800	0.754	0.866
	CDPC	0.800	0.754	0.866
	DP-ADPC	0.768	0.727	0.846
	DP-CDPC	0.771	0.726	0.847
ecoli	K-means	0.500	0.618	0.620
	DBSCAN	0.463	0.444	0.638
	SNNDPC	0.674	0.630	0.769
	ADPC	0.671	0.633	0.772
	CDPC	0.671	0.633	0.772
	DP-ADPC	0.647	0.621	0.749
	DP-CDPC	0.687	0.646	0.781
movement	K-means	0.336	0.564	0.383
	DBSCAN	0.255	0.479	0.299
	SNNDPC	0.278	0.462	0.342
	ADPC	0.394	0.595	0.436
	CDPC	0.391	0.618	0.441
	DP-ADPC	0.367	0.580	0.416
	DP-CDPC	0.364	0.588	0.423
dermatology	K-means	0.698	0.856	0.758
	DBSCAN	0.440	0.631	0.583
	SNNDPC	0.825	0.883	0.868
	ADPC	0.837	0.900	0.877
	CDPC	0.837	0.900	0.877
	DP-ADPC	0.837	0.901	0.879
	DP-CDPC	0.852	0.911	0.889
banknote	K-means	0.013	0.010	0.509
	DBSCAN	0.611	0.568	0.784
	SNNDPC	−0.003	0.013	0.704
	ADPC	0.962	0.932	0.981
	CDPC	0.962	0.932	0.981
	DP-ADPC	0.886	0.859	0.940
	DP-CDPC	0.961	0.929	0.980
abalone	K-means	0.136	0.163	0.430
	DBSCAN	0.149	0.136	0.501
	SNNDPC	0.031	0.105	0.538
	ADPC	0.197	0.183	0.530
	CDPC	0.189	0.176	0.525
	DP-ADPC	0.195	0.181	0.529
	DP-CDPC	0.185	0.170	0.523

.

An analysis of Table 6 reveals the following observations. For the seeds dataset, the clustering results of the ADPC and CDPC algorithms are consistent, and they achieve the largest values for each external evaluation index among all the algorithms. The DP-ADPC and DP-CDPC algorithms yield lower values for each evaluation index compared to the CDPC algorithm. However, the clustering effectiveness of the DP-CDPC algorithm is better than that of the DP-ADPC algorithm. In the case of the ecoli dataset, the clustering effect of the CDPC and ADPC algorithms is the same and superior to the K-means, DBSCAN, SNNDPC, and DP-ADPC algorithms. However, the value of $ARI$ is slightly lower than that of the SNNDPC algorithm. The DP-CDPC algorithm outperforms other algorithms in terms of each clustering evaluation index, demonstrating its effectiveness. Regarding the movement dataset, the values of $ARI$ and $FMI$ for the ADPC algorithm are higher than those of other algorithms, while the value of $AMI$ for the CDPC algorithm is the largest among all the algorithms. Adding appropriate noise to these algorithms will have a certain impact on their clustering effect. The values of $ARI$ and $FMI$ for the DP-ADPC algorithm are larger than those of the DP-CDPC algorithm, but the value of $AMI$ is lower than that of the DP-CDPC algorithm. In terms of the dermatology dataset, the clustering evaluation indexes of the CDPC and ADPC algorithms are the same and slightly lower than those of the DP-CDPC and DP-ADPC algorithms. However, they are higher than other algorithms, indicating the superior clustering effect of the DP-CDPC algorithm. For the banknote dataset, the clustering evaluations of the CDPC and ADPC algorithms are consistent and superior to other algorithms. The clustering evaluations of the DP-CDPC algorithm are slightly lower than those of the CDPC algorithm but superior to other algorithms. For the abalone dataset, the ADPC algorithm achieves the largest $ARI$ and $AMI$, while the SNNDPC algorithm achieves the largest $FMI$. The values of each evaluation index for the DP-CDPC algorithm are lower than those of the CDPC algorithm. The values of each external evaluation index for the DP-ADPC algorithm are slightly lower than those of the ADPC algorithm. Overall, these algorithms exhibit better clustering effects compared to the K-means, DBSCAN, and SNNDPC algorithms.

In summary, the clustering results of the ADPC and CDPC algorithms are consistent on the whole. In general, both the ADPC and CDPC algorithms outperform the K-means, DBSCAN, and SNNDPC algorithms.

By comparing the performance of the ADPC, CDPC, K-means, DBSCAN, and SNNDPC algorithms on different UCI datasets, the effectiveness of the CDPC algorithm, which employs dichotomy to determine the truncation distance, is verified once again. When comparing the clustering indicators of the DP-CDPC and DP-ADPC algorithms, it can be concluded that the clustering of the DP-CDPC is better than that of the DP-ADPC on the whole. When comparing the clustering indicators of the DP-CDPC and CDPC algorithms, it can be concluded that they do not necessarily weaken the effectiveness of the algorithm. Noise is volatile and, after selecting an appropriate privacy budget, the effectiveness of the algorithm will fluctuate within a certain range after adding noise.

5. Discussions

In this paper, an improved density peak clustering algorithm based on Chebyshev inequality and differential privacy (DP-CDPC) is proposed. The algorithm employs the dichotomy approach to achieve the adaptive determination of truncation distance, and introduces Chebyshev inequality to construct statistical constraints. Finally, combined with differential privacy technology, appropriate privacy budget noise is added to the local density of the algorithm to avoid privacy leakage in the process of clustering analysis. Through privacy analysis and time complexity analysis, it is theoretically proven that the proposed algorithm not only conforms to the definition of differential privacy but also does not need to add extra complexity. By comparing the experimental results of the DP-CDPC algorithm and other algorithms on multiple datasets, it is proven that, when the constraint conditions of constructing decision graph statistics are set by introducing Chebyshev inequality, and the inequality parameters are set to $b_1\in \{1,2,3\}$ and $b_2\in \{0.5,1\}$, respectively, the clustering center can be selected well, and the clustering effect is better than other algorithms.

This paper verifies the clustering effect of the algorithm by setting up several groups of comparative experiments. The K-means algorithm is a widely used partition-based clustering algorithm. The DBSCAN and DPC algorithms are two typical density-based clustering algorithms. The SNNDPC [37] and ADPC [29] algorithms are improvements on the traditional DPC algorithms, respectively. Through the clustering effect of these algorithms and the CDPC algorithm on several experimental datasets, we can see that the clustering result of the CDPC algorithm is consistent with that of the ADPC algorithm, and better than the other algorithms. Compared with the ADPC algorithm, the CDPC algorithm uses the dichotomous method to determine cluster center adaptively, and the clustering results are consistent, which verifies the rationality of applying the dichotomous method to the DPC algorithm.

By comparing the effect of the DP-CDPC with the change in privacy budget, we can see that, within a certain range, the bigger the privacy budget, the better the clustering effectiveness

The DP-ADPC algorithm is an ADPC algorithm based on differential privacy. By comparing the DP-CDPC algorithm with the DP-ADPC algorithm, it can be seen that the DP-CDPC algorithm has a smaller privacy budget critical value for the same data, indicating a higher level of privacy protection and better clustering performance. It has achieved privacy protection while maintaining clustering quality.

6. Conclusions

In the information age, the problem of data leakage is becoming more and more serious, and people are paying more and more attention to privacy and security issues, which requires data miners to pay attention to privacy protection issues in the process of modeling. This paper presents an improved density peak clustering algorithm based on differential privacy and Chebyshev inequality (DP-CDPC). Through theoretical analysis and experiments, compared with the DP-ADPC algorithm, it is proven that the proposed algorithm cannot only select the cluster centers well, but also realize differentiated privacy protection. The clustering effect of the DP-ADPC algorithm is better than that of the DP-CDPC, and the DP-CDPC algorithm achieves a smaller privacy budget critical value compared to the DP-ADPC, indicating a higher level of privacy protection.

However, it is important to note that the algorithm proposed in this paper only studies continuous datasets and only studies strict differential privacy. Future work should focus on extending algorithms to discrete and mixed datasets, in addition to focusing on the advantages of existing improved techniques, investigating relaxed forms of differential privacy protection, and applying them to real-world problems.