Seismic Fragility Analysis of a High-Pier Bridge under Pulse-like Ground Motion, Based on a PCA and K-Means Approach
Abstract
:1. Introduction
2. Selection of Pulse-like Ground Motions and the Engineering Background
2.1. Selection of Pulse-like Ground Motions
2.2. Engineering Background and Finite Element Modeling
3. Correlation Analysis of Seismic IMs
3.1. Initial Candidate Seismic IMs
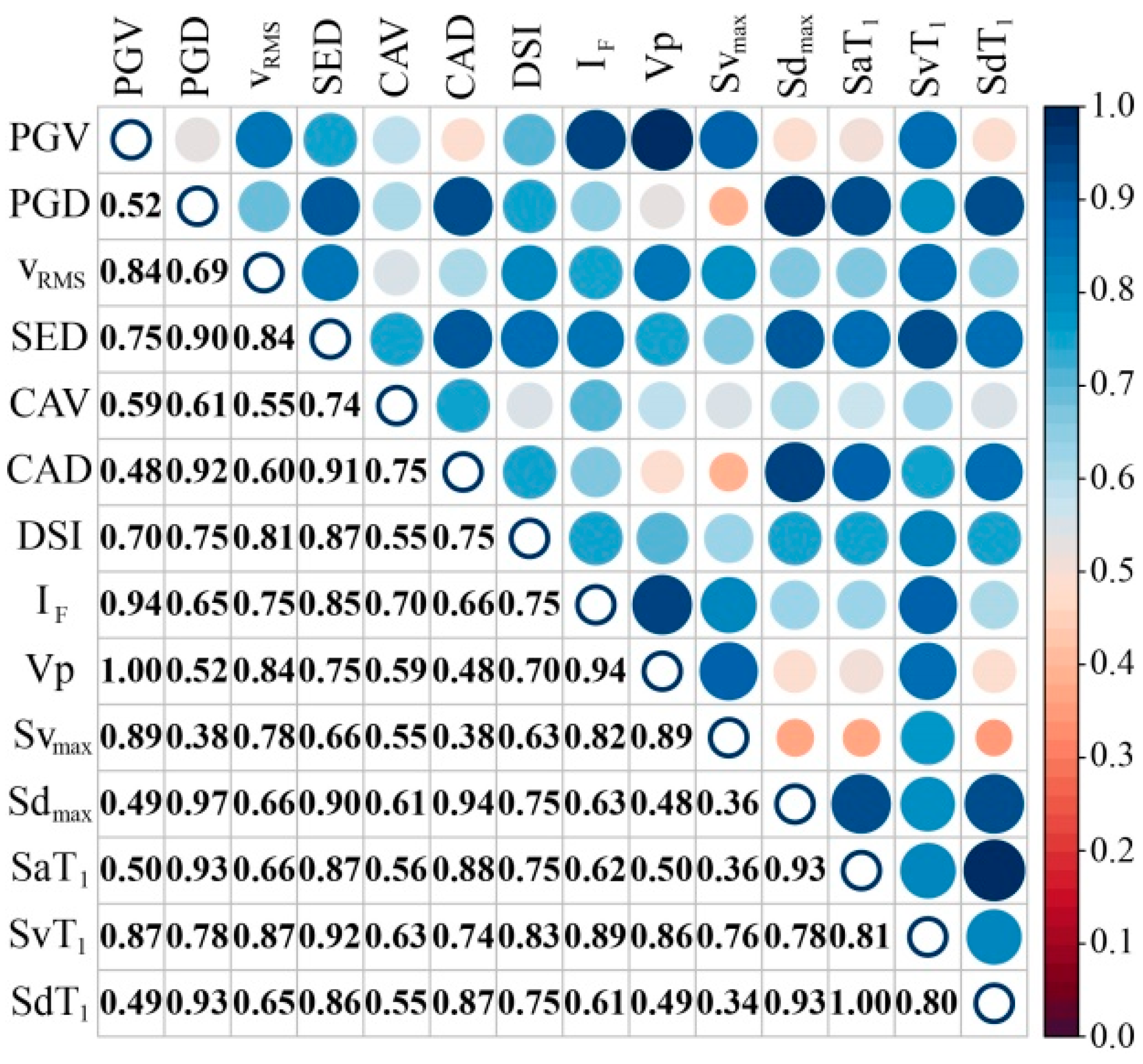
3.2. Correlation Analysis between Seismic IMs
4. Selection of Seismic IMs for the PCA Algorithm
4.1. PCA Algorithm
4.2. Removal of Weakly Correlated IMs
- (1)
- A longitudinal earthquake;
- (2)
- A transverse earthquake;
- (3)
- A biaxial earthquake (longitudinal direction + transverse direction);
- (4)
- A triaxial earthquake (longitudinal direction + transverse direction + vertical direction).
4.3. Elimination of Multicollinearity IMs
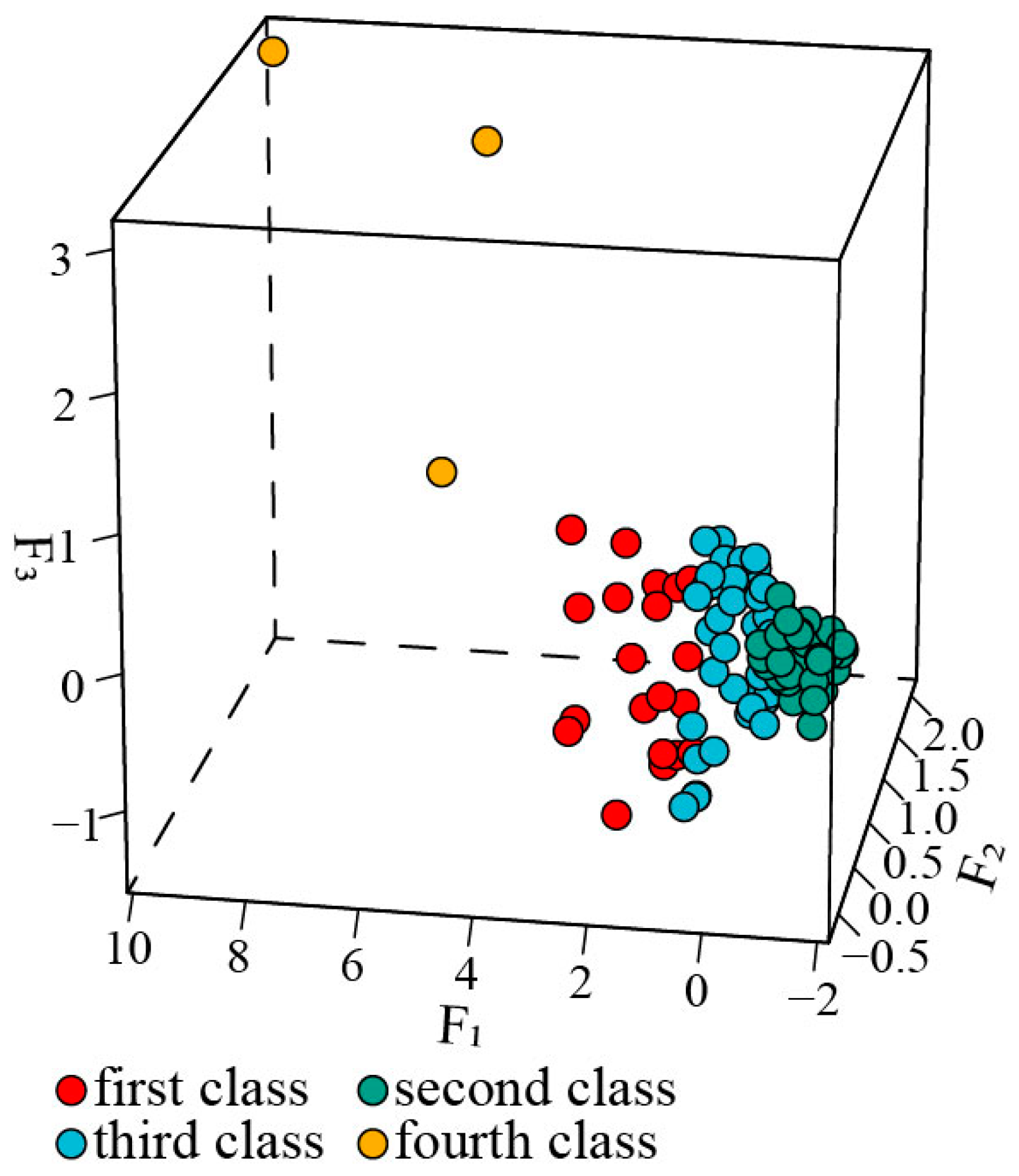
4.4. Principal Component Analysis of IMs
5. Clustering Analysis of the Selected Ground Motions Based on a K-Means Algorithm
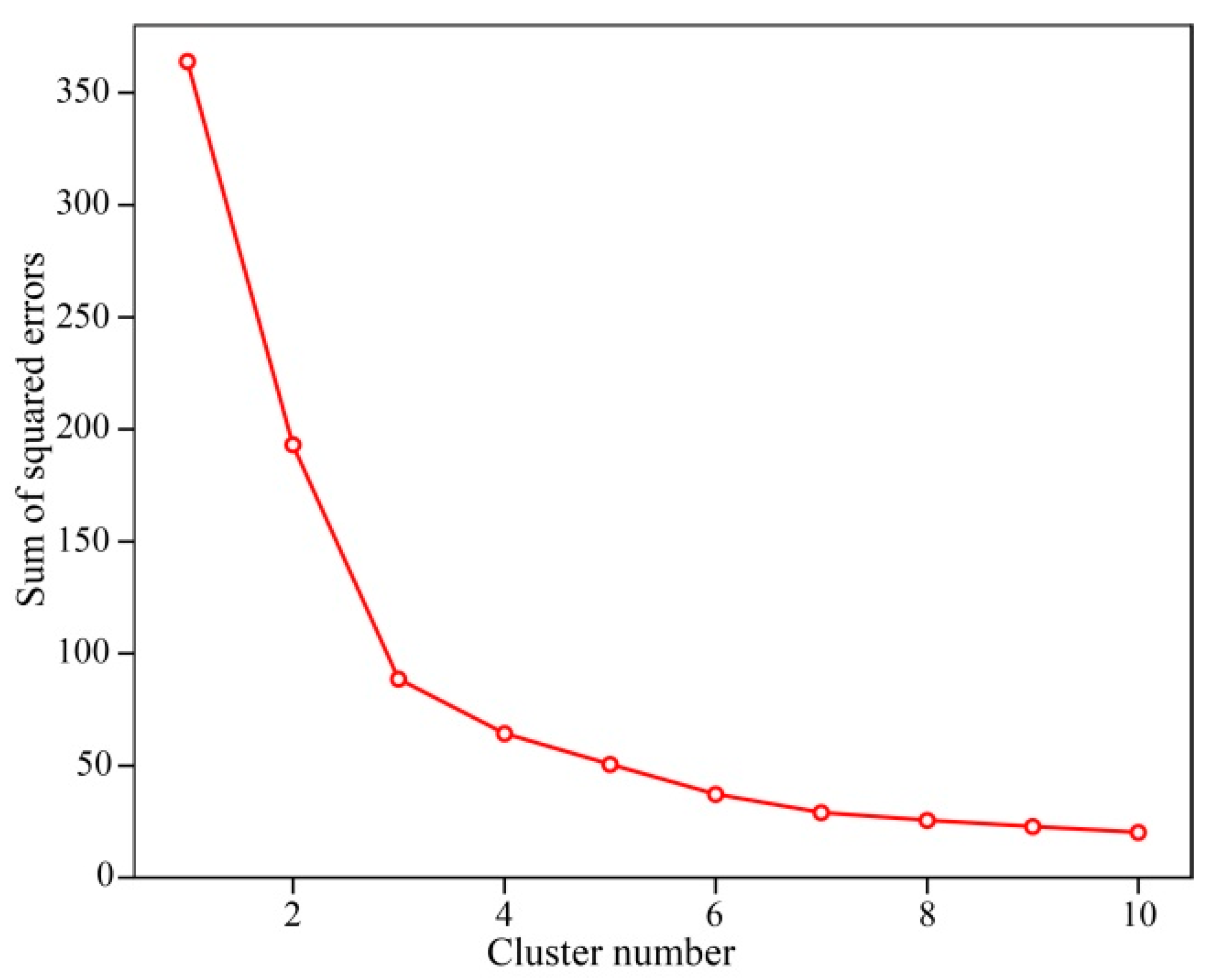
5.1. K-Means Clustering Algorithm
- (1)
- Assuming that the ground motions are divided into K initial classes, K data points are randomly selected as the initial clustering centers.
- (2)
- Assuming that the first three principal component values of ground motion are , and the principal component value of the j-th cluster center is , then the Euclidean distance between the i-th ground motion and the j-th cluster center is:
- (3)
- Using Equation (13), the Euclidean distance from each ground motion to each cluster center point is calculated separately, and the ground motions are assigned to the nearest cluster center, according to the principle of minimum distance, then the ground motions are classified into K classes;
- (4)
- Calculating the sum of squared errors (SSE), , which reflects the distortion degree of clustering, according to Equation (14):where represents the principal component of the l-th ground motion in the j-th class, and represents the number of ground motions in the j-th class.
- (5)
- Calculating the mean values of the ground motions assigned to each class in step (3) according to Equation (15) and updating the cluster center for each class by using the mean values as the new centroid, then recalculating the sum of squared errors, :where is the mean value of the ground motion data in the j-th class, and is the number of ground motions in the j-th class.
- (6)
- Performing step (2) to recalculate the Euclidean distance between each ground motion and the updated cluster center in step (5), we then perform step (3) to reclassify each ground motion. We then perform step (5) to update each cluster center point and calculate the sum of squared errors, . We repeat this process until the sum of squared errors has not changed for two consecutive iterations, then terminate the algorithm and output the final cluster analysis results.
5.2. Pulse-like Ground Motion Clustering Analysis
6. Seismic Fragility Analysis of a High-Pier Bridge
6.1. Probability Seismic Fragility Analysis Model
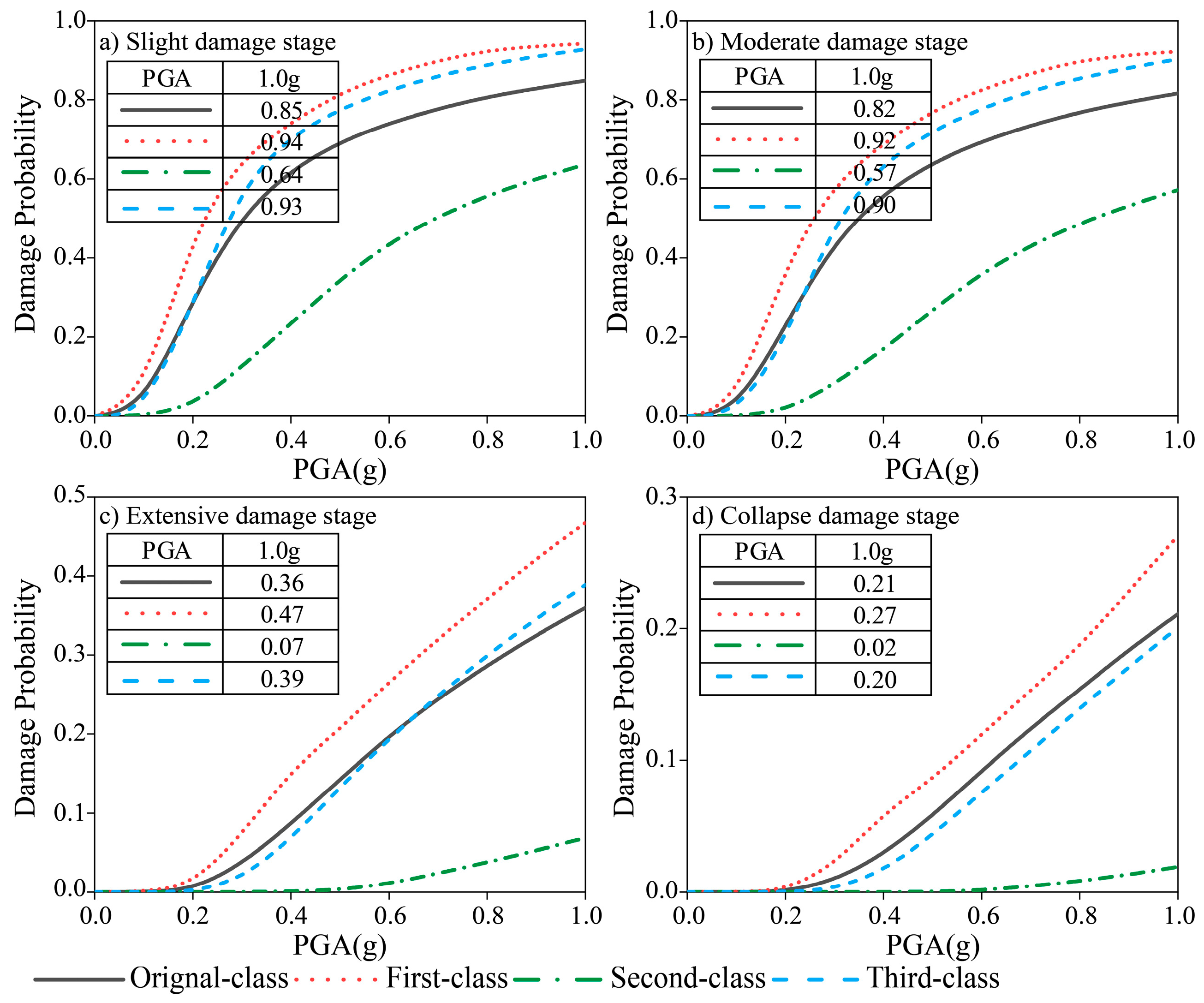
6.2. Seismic Fragility Analysis of the High-Pier Bridge
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Housner, G.W.; Hudson, D.E. The Port Hueneme earthquake of March 18, 1957. Bull. Seismol. Soc. Am. 1958, 48, 163–168. [Google Scholar] [CrossRef]
- Liu, Q.F.; Yuan, Y.F.; Jin, X.; Ding, H.P. Basic characteristics of near-fault ground motion. Earthq. Eng. Eng. Vib. 2006, 26, 1–10. (In Chinese) [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhou, X.Y.; Zhang, P.Z.; Igel, H. Characteristic of amplitude and duration for near fault strong ground motion from the 1999 Chi-Chi, Taiwan Earthquake. Soil Dyn. Earthq. Eng. 2002, 22, 73–96. [Google Scholar] [CrossRef]
- Khakzand, L.; Jalali, R.S.; Veisi, M. Near-fault ground motion effects on pounding and unseating using an example of a three-span, simply supported bridge. Earthq. Eng. Resil. 2022, 1, 164–195. [Google Scholar] [CrossRef]
- Liao, W.I.; Loh, C.H.; Wan, S. Earthquake response of RC moment frames subjected to near-fault ground motions. Struct. Des. Tall Build. 2001, 10, 219–229. [Google Scholar] [CrossRef]
- Liao, W.I.; Loh, C.H.; Wan, S.; Jean, W.Y.; Chai, J.F. Dynamic responses of bridges subjected to near-fault ground motions. J. Chin. Inst. Eng. 2000, 23, 455–464. [Google Scholar] [CrossRef]
- Geng, P.; Zeng, G.X.; Guo, X.Y.; He, Y.; Ding, T.; He, C. Seismic response of tunnel structures passing through fault zone under near-field pulsed earthquakes. China J. Highw. Transp. 2020, 33, 122–131. (In Chinese) [Google Scholar] [CrossRef]
- Li, B.X.; Liao, Q.; Zeng, X.L.; Chen, B. Effects on earthquake intensity and peak of near-fault velocity pulse on seismic response of the simply supported slab bridge. Adv. Eng. Sci. 2018, 50, 1–7. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, J.G.; Jia, H.Y.; Zhan, Y.L. Seismic vulnerability analysis of multi-main-span high pier continuous rigid-frame bridge in terms of cloud method. KSCE J. Civ. Eng. 2023, 27, 2519–2534. [Google Scholar] [CrossRef]
- Jia, H.Y.; Zhang, D.Y.; Zheng, S.X.; Xie, W.C.; Pandey, M.D. Local site effects on a high-pier railway bridge under tridirectional spatial excitations: Nonstationary stochastic analysis. Soil Dyn. Earthq. Eng. 2013, 52, 55–69. [Google Scholar] [CrossRef]
- JTG/T 2231-01-2020; Specifications for Seismic Design of Highway Bridges. People’s Republic of China Ministry of Transportation: Beijing, China, 2020.
- Whitman, R.V.; Biggs, J.M.; Brennan, J.E.; Cornell, C.A.; de Neufville, R.L.; Vanmarcke, E.H. Seismic design decision analysis. ASCE J. Struct. Div. 1975, 101, 1067–1084. [Google Scholar] [CrossRef]
- Mosleh, A.; Jara, J.; Razzaghi, M.S.; Varum, H. Probabilistic seismic performance analysis of RC Bridges. J. Earthq. Eng. 2018, 24, 1704–1728. [Google Scholar] [CrossRef]
- Mackie, K.; Stojadinovic, B. Seismic Demands for Performance-Based Design of Bridges; PEER Report No. 2003/16; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Zhuang, L.J.; Yin, P.C.; Pang, Y.T. E-Cloud: Efficient seismic fragility assessment of structures based on enhanced cloud analysis. Earthq. Spectra 2022, 38, 2994–3016. [Google Scholar] [CrossRef]
- Lu, D.G.; Liu, Y.; Yu, X.H.; Huang, M.G. Probabilistic seismic demand models and fragility analysis of RC continuous girder bridges. In Proceedings of the Symposium on Reliability of Engineering System (SRES’2015), Hangzhou, China, 15–17 October 2015. [Google Scholar]
- Billah, A.H.M.M.; Alam, M.S. Seismic fragility assessment of highway bridges: A state-of-the-art review. Struct. Infrastruct. Eng. 2015, 11, 804–832. [Google Scholar] [CrossRef]
- Franchini, A.; Sebastian, W.; D’Ayala, D. Surrogate-based fragility analysis and probabilistic optimisation of cable-stayed bridges subject to seismic loads. Eng. Struct. 2022, 256, 113949. [Google Scholar] [CrossRef]
- Karim, K.R.; Yamazaki, F. Effect of earthquake ground motions on fragility curves of highway bridge piers based on numerical simulation. Earthq. Eng. Struct. Dyn. 2001, 30, 1839–1856. [Google Scholar] [CrossRef]
- Billah, A.H.M.M.; Alam, M.S.; Bhuiyan, A.R. Fragility analysis of retrofitted multi-column bridge bent subjected to near fault and far field ground motion. J. Bridge Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- Mogheisi, M.; Tavakoli, H.; Peyghaleh, E. Fragility curve development of highway bridges using probabilistic evaluation (case study: Tehran City). Asian J. Civ. Eng. 2023, 24, 1783–1800. [Google Scholar] [CrossRef]
- Zhong, J.; Pang, Y.T.; Jeon, J.S.; DesRoches, R.; Yuan, W.C. Seismic fragility assessment of long-span cable-stayed bridges in China. Adv. Struct. Eng. 2016, 19, 1797–1812. [Google Scholar] [CrossRef]
- Chen, X. System fragility assessment of tall-pier bridges subjected to near-fault ground motions. J. Bridge Eng. 2020, 25, 04019143. [Google Scholar] [CrossRef]
- Wu, F.W.; Zhou, J.W.; Zhao, Y.Y.; Wang, G.; Tang, W.; Luo, J.; Meng, Y. Performance-Based Seismic Fragility and Risk Assessment of Five-Span Continuous Rigid Frame Bridges. Adv. Civ. Eng. 2021, 2021, 6657663. [Google Scholar] [CrossRef]
- Zhao, J.G.; Jia, H.Y.; Zhan, Y.L.; Xiang, Z.; Zheng, S.; Bi, K. Combination of LS-SVM algorithm and JC method for fragility analysis of deep-water high piers subjected to near-field ground motions. Structures 2020, 24, 282–295. [Google Scholar] [CrossRef]
- Cao, X.Y.; Feng, D.C.; Beer, M. Consistent seismic hazard and fragility analysis considering combined capacity-demand uncertainties via probability density evolution method. Struct. Saf. 2023, 103, 102330. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Zhao, J.G.; Du, B.; Zhan, Y.L.; Zhao, K. Comparison of constitutive concrete models in OpenSees for hysteretic behavior of structures. J. Guilin Univ. Technol. 2017, 37, 59–67. (In Chinese) [Google Scholar]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 11, 559–572. [Google Scholar] [CrossRef] [Green Version]
- Hotelling, H. Analysis of a complex of statistical variables into principal components, Part 1. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2016.
- He, X.Q.; Liu, W.Q. Applied Regression Analysis, 5th ed.; China Renmin University Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Mackie, K.; Stojadinovic, B. Fragility curves for reinforced concrete highway overpass bridges. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Gu, X.Y.; Shan, D.S.; Dong, J.; Li, Q. Seismic fragility analysis of irregular continuous rigid frame girder bridge. Cogent Eng. 2018, 5, 1545741. [Google Scholar] [CrossRef]
- Zhang, J.; Huo, Y.L. Evaluating effectiveness and optimum design of isolation devices for highway bridges using the fragility function method. Eng. Struct. 2009, 31, 1640–1648. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Applied incremental dynamic analysis. Earthq. Spectra 2004, 20, 523–553. [Google Scholar] [CrossRef]
- Pang, Y.; Wang, X. Cloud-IDA-MSA conversion of fragility curves for efficient and high-fidelity resilience assessment. J. Struct. Eng. 2021, 147, 04021049. [Google Scholar] [CrossRef]
- Padgett, J.; Nielson, B.; DesRoches, R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq. Eng. Struct. Dyn. 2008, 37, 711–725. [Google Scholar] [CrossRef]
- Chen, L.B.; Huang, C.G.; Chen, H.Q.; Zheng, Z.F. Seismic fragility models of a bridge system based on copula method. Earthq. Spectra 2022, 38, 1417–1437. [Google Scholar] [CrossRef]
- Zhao, J.G.; Jia, H.Y.; Zhan, Y.L. Effects of near-field rotating seismic waves on seismic waves on seismic vulnerability of multi-span high-pier continuous rigid frame bridge. J. Vib. Shock. 2023, 42, 154–167. (In Chinese) [Google Scholar] [CrossRef]
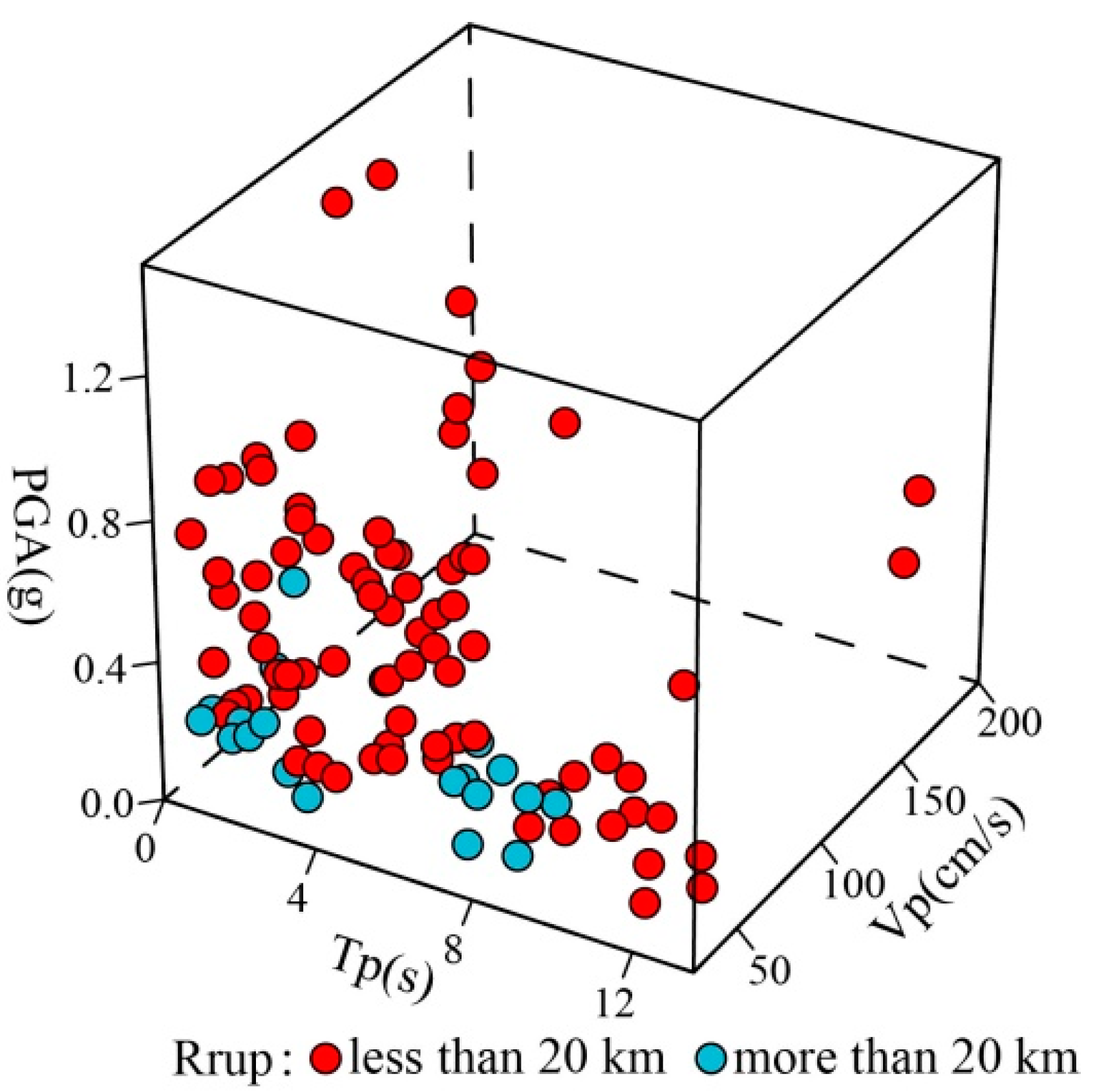

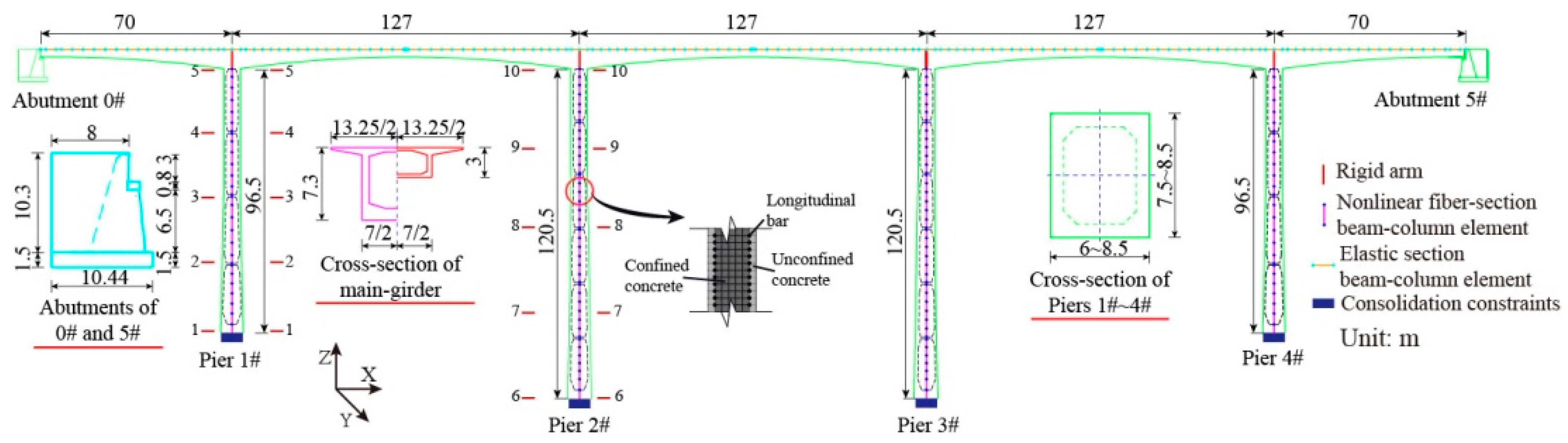
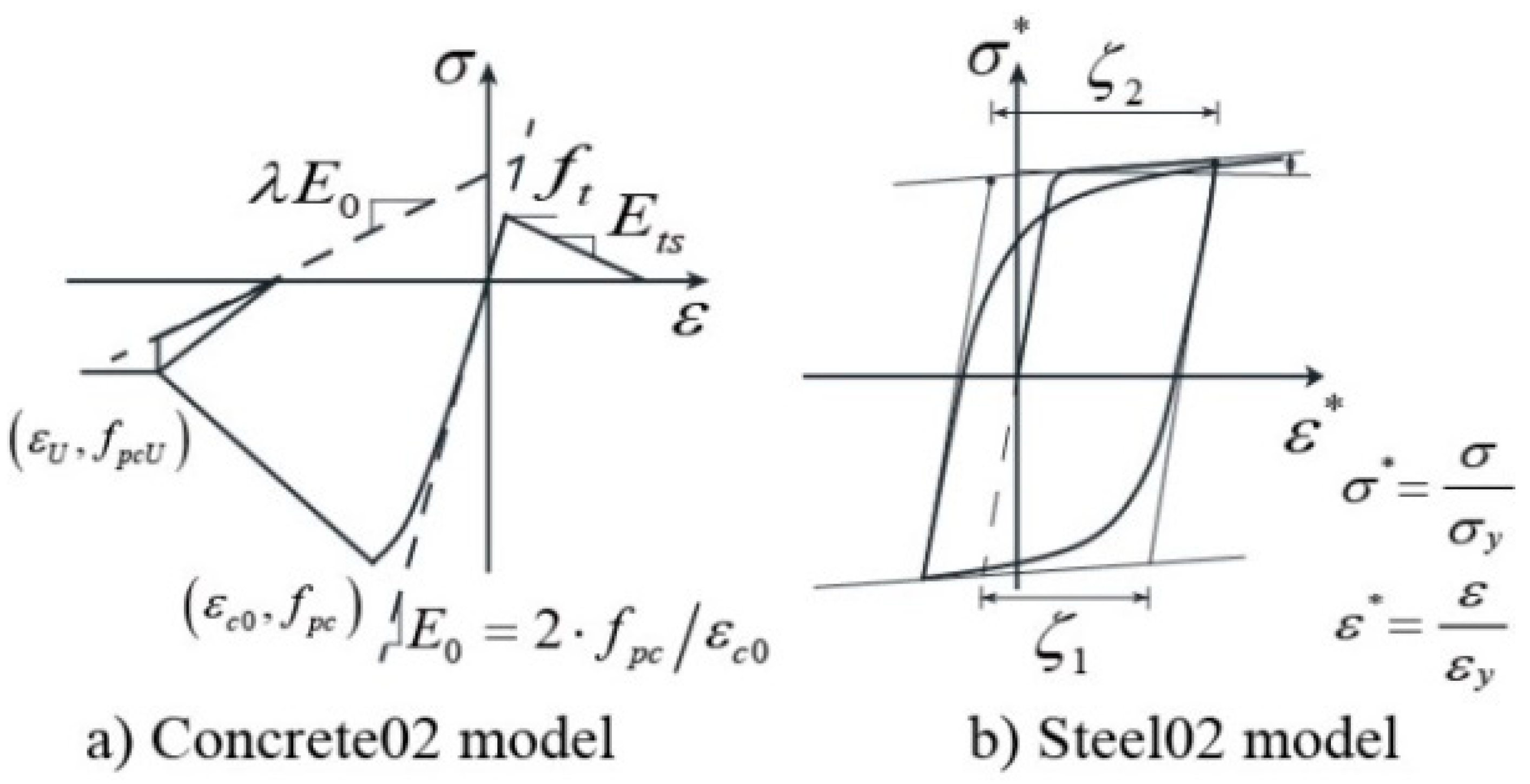


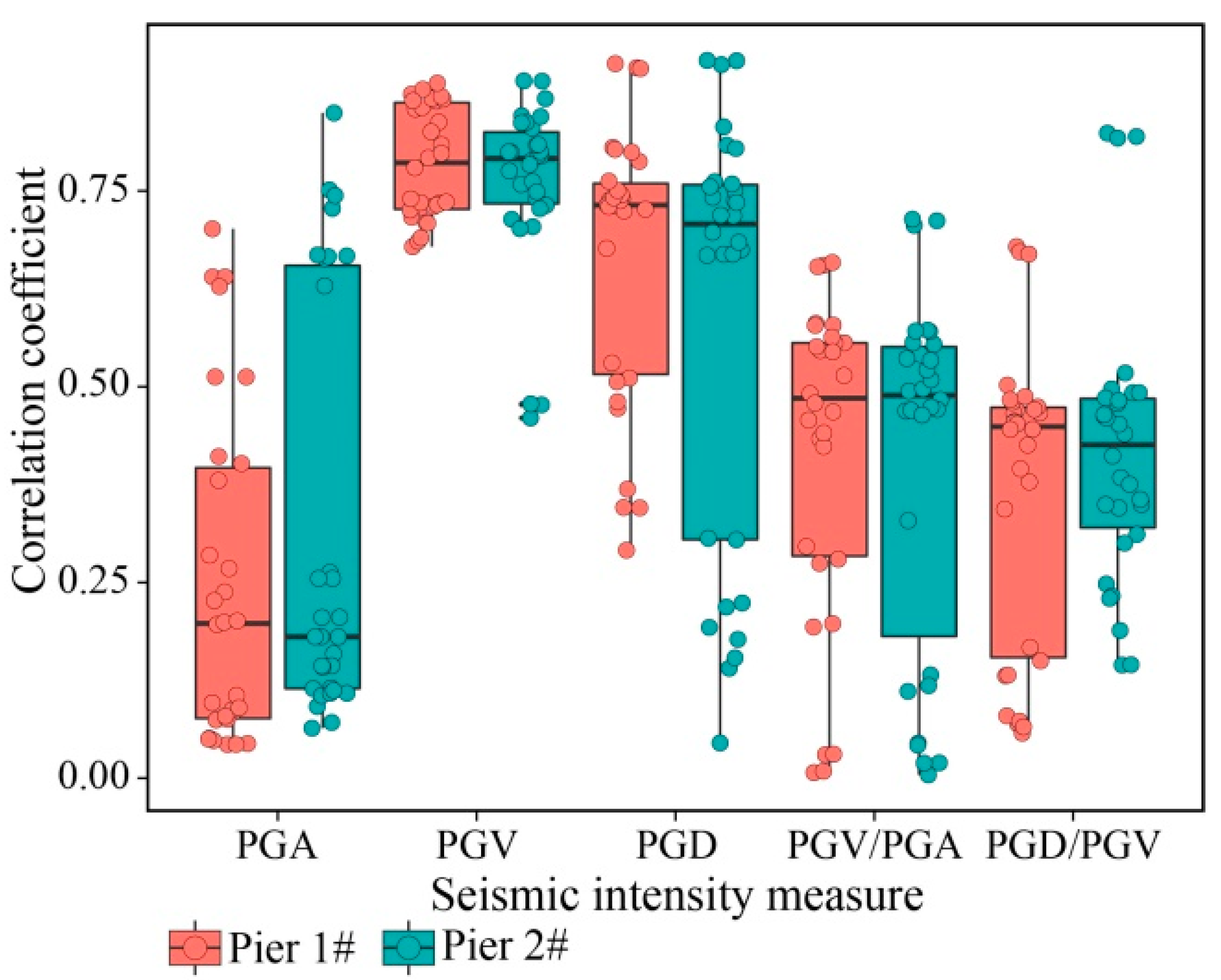



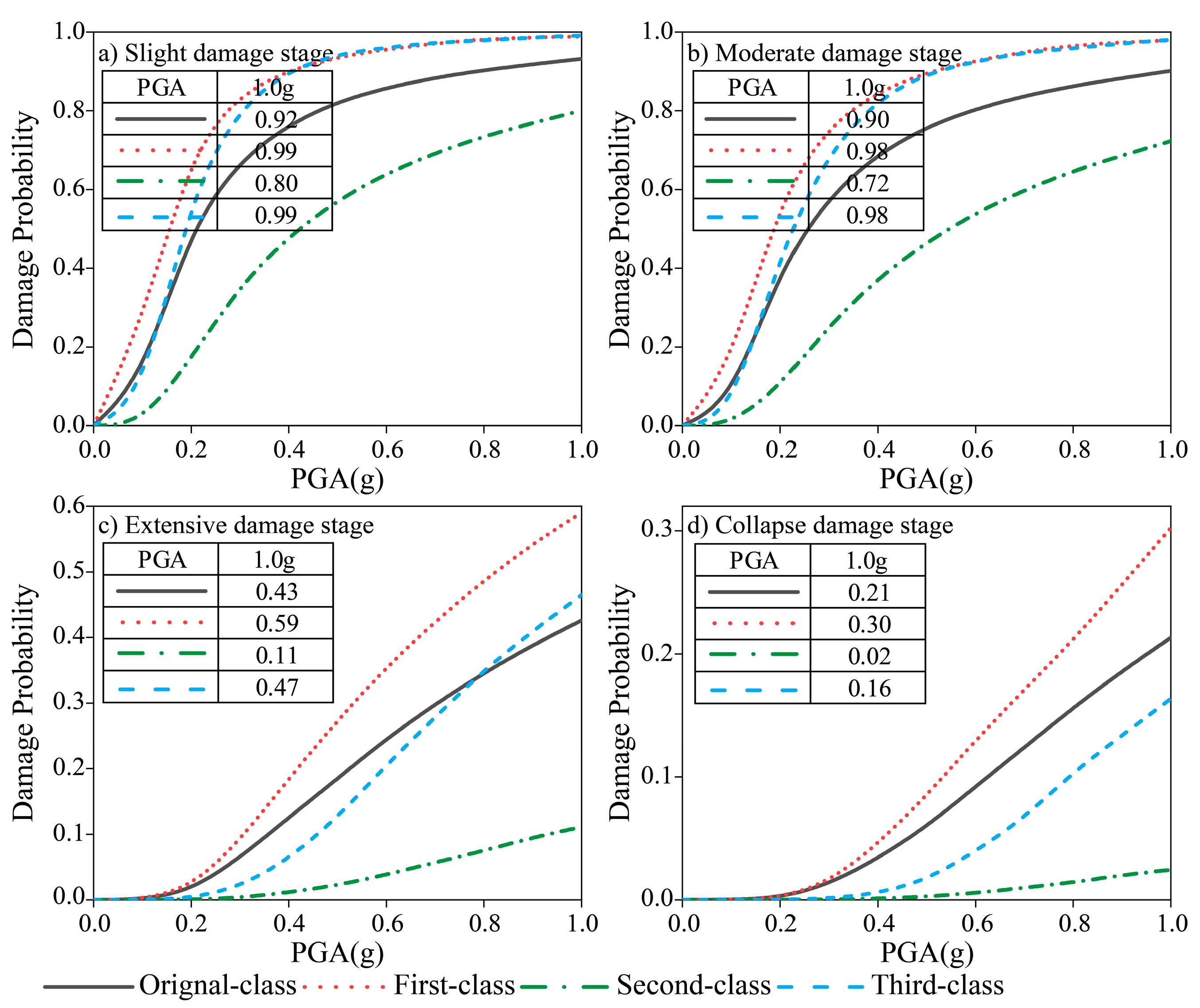
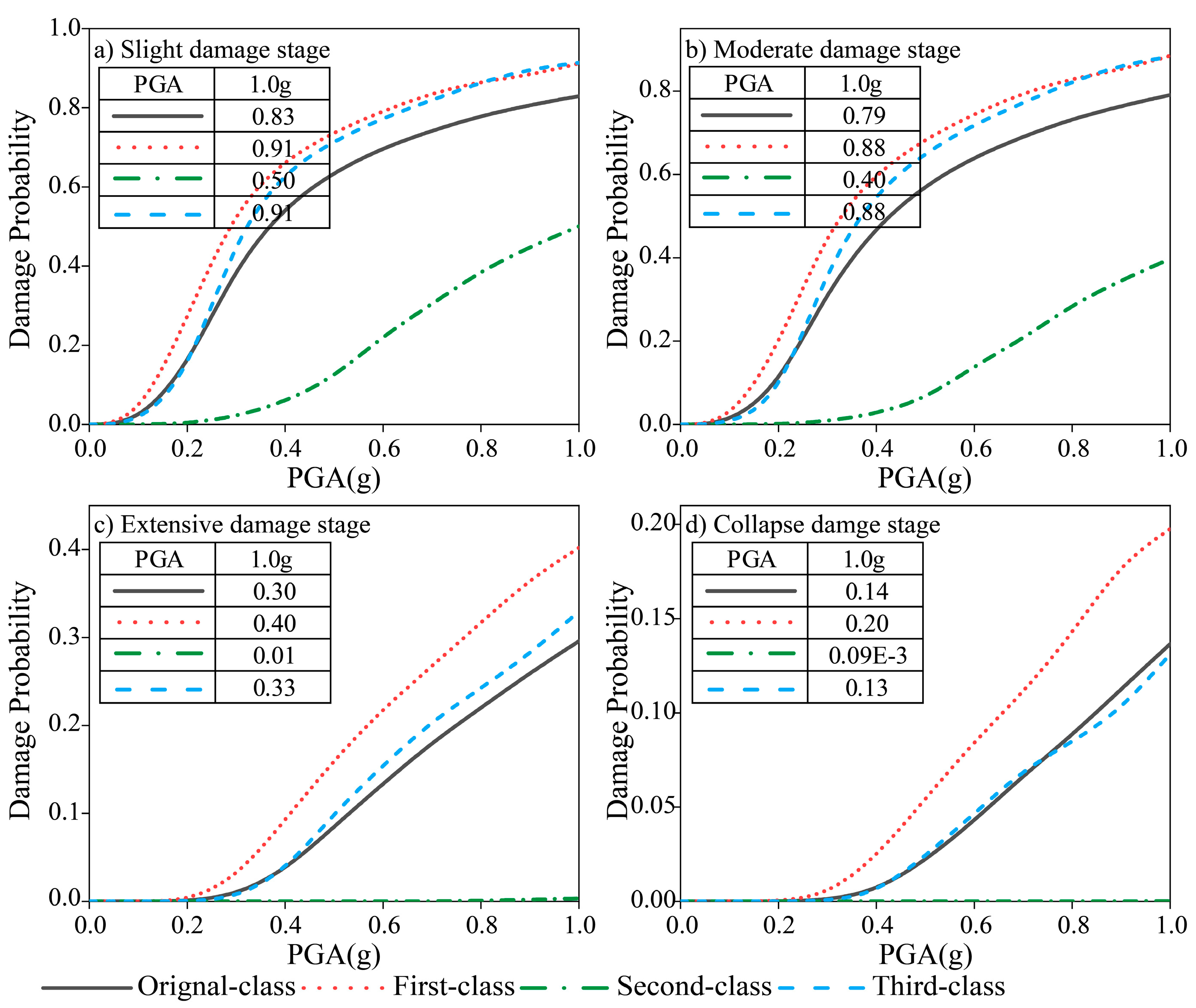
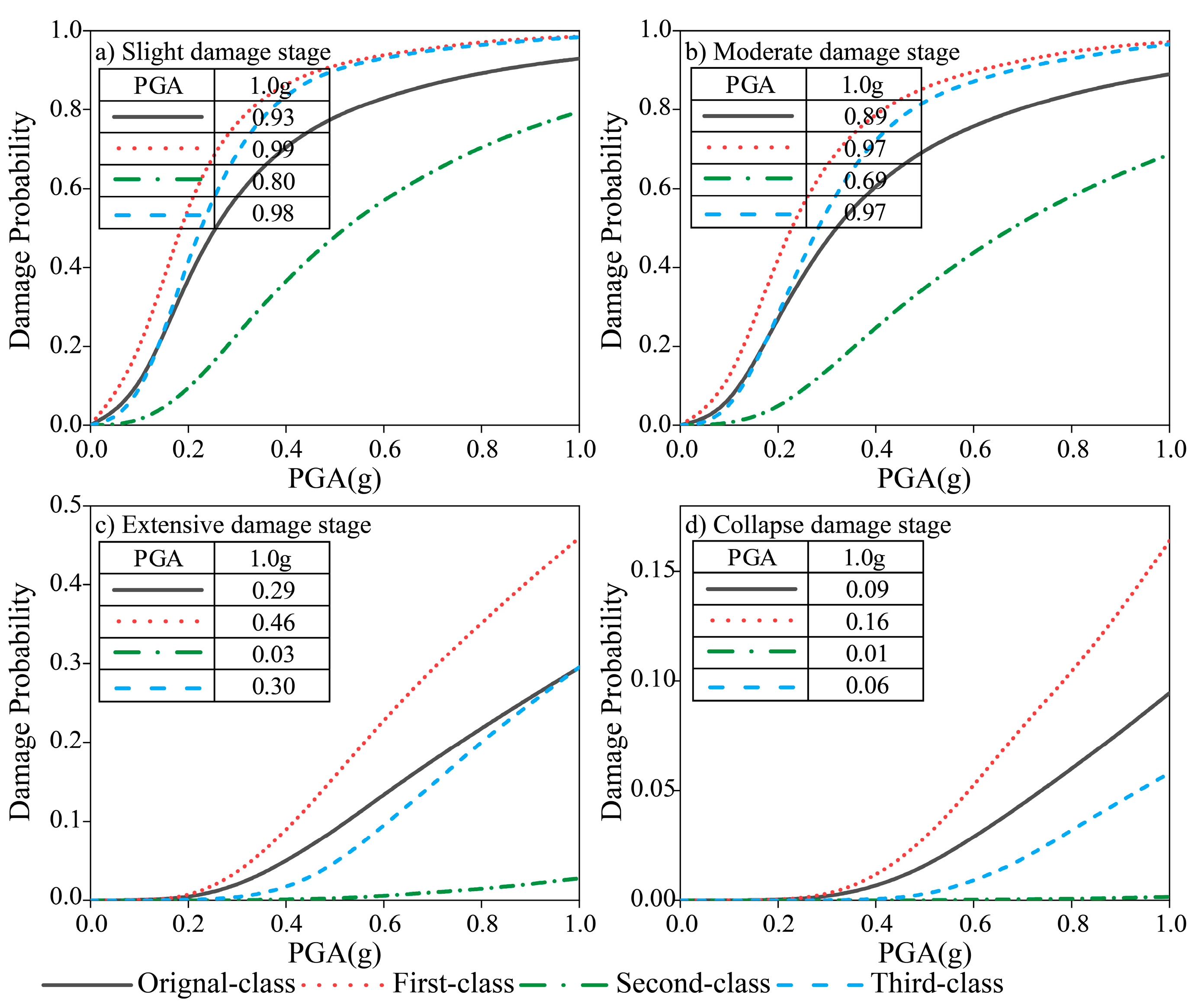
| Number | Time (Year) | Event | Station | Mag | Tp (s) | Vp (cm/s) | Rrup (km) |
|---|---|---|---|---|---|---|---|
| 1 | 1999 | Chi-Chi, Taiwan | TCU052 | 7.6 | 12.55 | 172.34 | 0.70 |
| 2 | 2004 | Parkfield-02, CA | Parkfield—Fault Zone 1 | 6.0 | 1.06 | 81.40 | 2.50 |
| 3 | 1986 | San Salvador | National Geografical Inst | 5.8 | 1.02 | 73.01 | 7.00 |
| 4 | 1989 | Loma Prieta | Los Gatos—Lexington Dam | 6.9 | 1.69 | 95.86 | 5.00 |
| 5 | 1979 | Imperial Valley-06 | El Centro—Meloland Geot. Array | 6.5 | 3.56 | 92.62 | 0.10 |
| 6 | 1992 | Cape Mendocino | Bunker Hill FAA | 7.0 | 5.63 | 67.88 | 12.20 |
| 7 | 1979 | Montenegro, Yugo | Ulcinj—Hotel Olimpic | 7.1 | 1.90 | 51.64 | 5.80 |
| 8 | 1992 | Cape Mendocino | Centerville Beach, Naval Fac | 7.0 | 1.91 | 49.55 | 18.30 |
| 9 | 1995 | Kobe, Japan | Port Island (0 m) | 6.9 | 2.83 | 90.69 | 3.30 |
| Intensity Measure | Description | Unit | Intensity Measure | Description | Unit | ||
|---|---|---|---|---|---|---|---|
| 1 | PGA | Peak ground acceleration | cm/s2 | 16 | Arms | Housner root mean square measure | cm/s2 |
| 2 | PGV | Peak ground velocity | cm/s | 17 | ASI | Acceleration spectrum intensity | cm/s |
| 3 | PGD | Peak ground displacement | cm | 18 | VSI | Velocity spectrum intensity | cm |
| 4 | PGV/PGA | Peak ground velocity to peak ground acceleration ratio | s | 19 | DSI | Displacement spectrum intensity | cm‧s |
| 5 | PGD/PGV | Peak ground displacement to peak ground velocity ratio | s | 20 | IAM | Modified Arias intensity | cm/s |
| 6 | SI | Housner intensity | cm | 21 | IF | Fajfar measure | / |
| 7 | aRMS | Root mean square of acceleration | cm/s2 | 22 | Tp | Velocity pulse period | s |
| 8 | vRMS | Root mean square of velocity | cm/s | 23 | Vp | Velocity pulse amplitude | cm/s |
| 9 | dRMS | Root mean square of displacement | cm | 24 | Samax | Peak acceleration spectrum | cm/s2 |
| 10 | Td | The interval of time between the 5% and 95% thresholds of the total Arias intensity | s | 25 | Svmax | Peak velocity spectrum | cm/s |
| 11 | IA | Arias intensity | cm/s | 26 | Sdmax | Peak displacement spectrum | cm |
| 12 | IC | Characteristic intensity | / | 27 | Sa(T1) | Spectral acceleration at first mode period | cm/s2 |
| 13 | SED | Specific energy density | cm2/s | 28 | Sv(T1) | Spectral velocity at first mode period | cm/s |
| 14 | CAV | Cumulative absolute velocity | cm/s | 29 | Sd(T1) | Spectral displacement at first mode period | cm |
| 15 | CAD | Cumulative absolute displacement | cm | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Jia, H.; Yang, C.; Du, B. Seismic Fragility Analysis of a High-Pier Bridge under Pulse-like Ground Motion, Based on a PCA and K-Means Approach. Appl. Sci. 2023, 13, 8721. https://doi.org/10.3390/app13158721
Zhao J, Jia H, Yang C, Du B. Seismic Fragility Analysis of a High-Pier Bridge under Pulse-like Ground Motion, Based on a PCA and K-Means Approach. Applied Sciences. 2023; 13(15):8721. https://doi.org/10.3390/app13158721
Chicago/Turabian StyleZhao, Jingang, Hongyu Jia, Can Yang, and Bin Du. 2023. "Seismic Fragility Analysis of a High-Pier Bridge under Pulse-like Ground Motion, Based on a PCA and K-Means Approach" Applied Sciences 13, no. 15: 8721. https://doi.org/10.3390/app13158721








