Analysis of Dynamic Characteristics of Attached High Rise Risers
Abstract
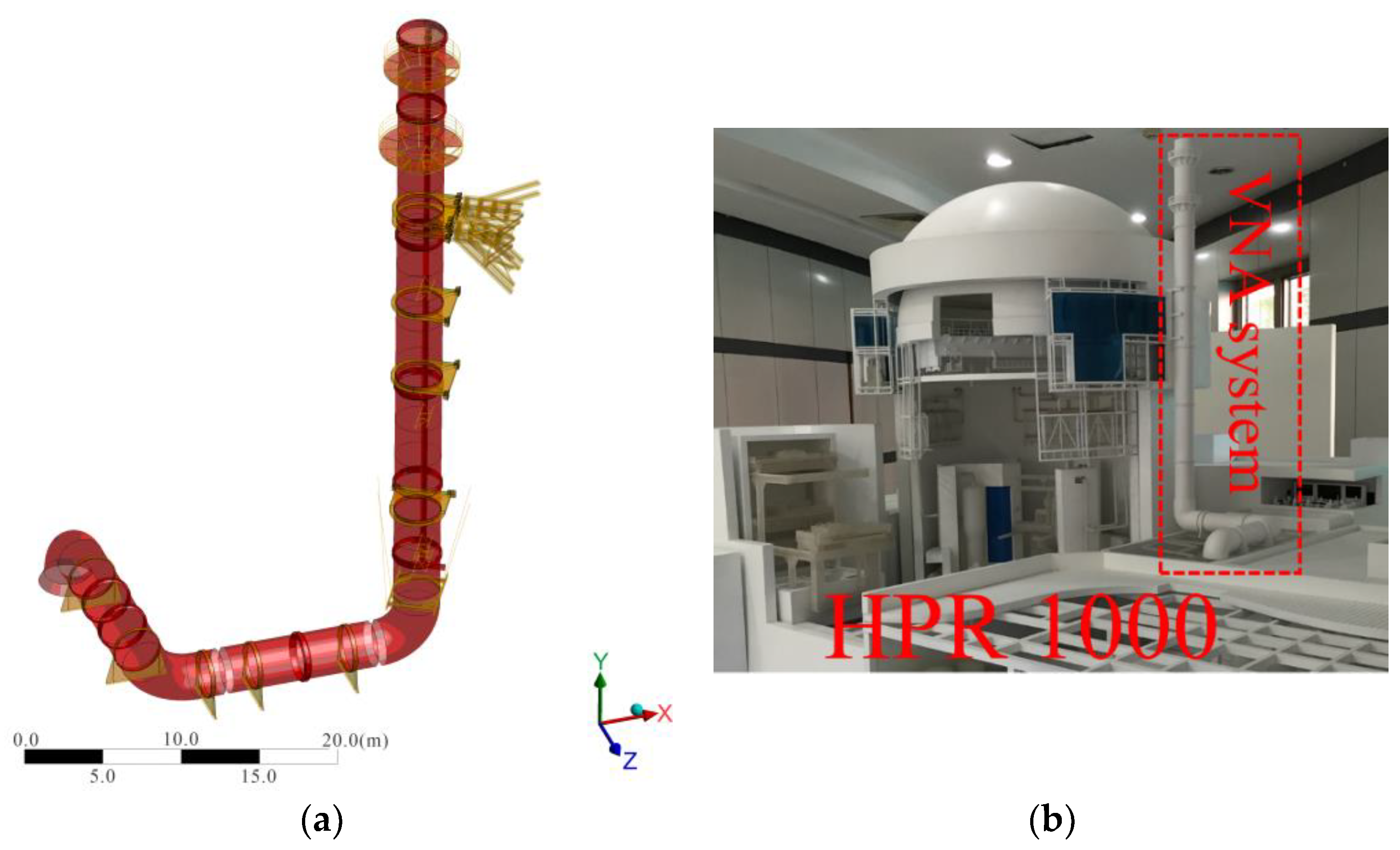
:1. Introduction
2. Natural Vibration Characteristics Analysis
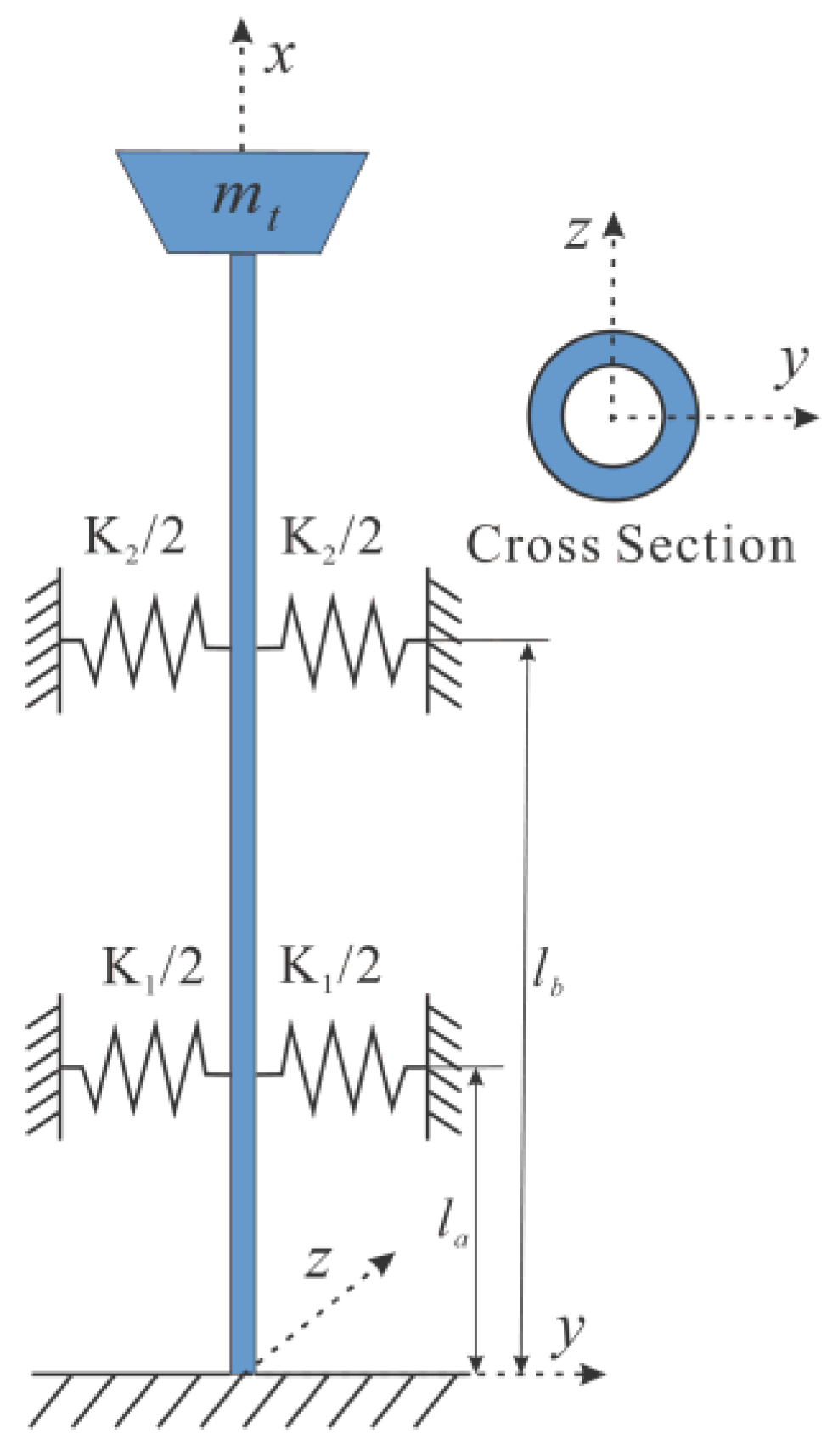
2.1. Theoretical Model
2.2. DTM Analysis
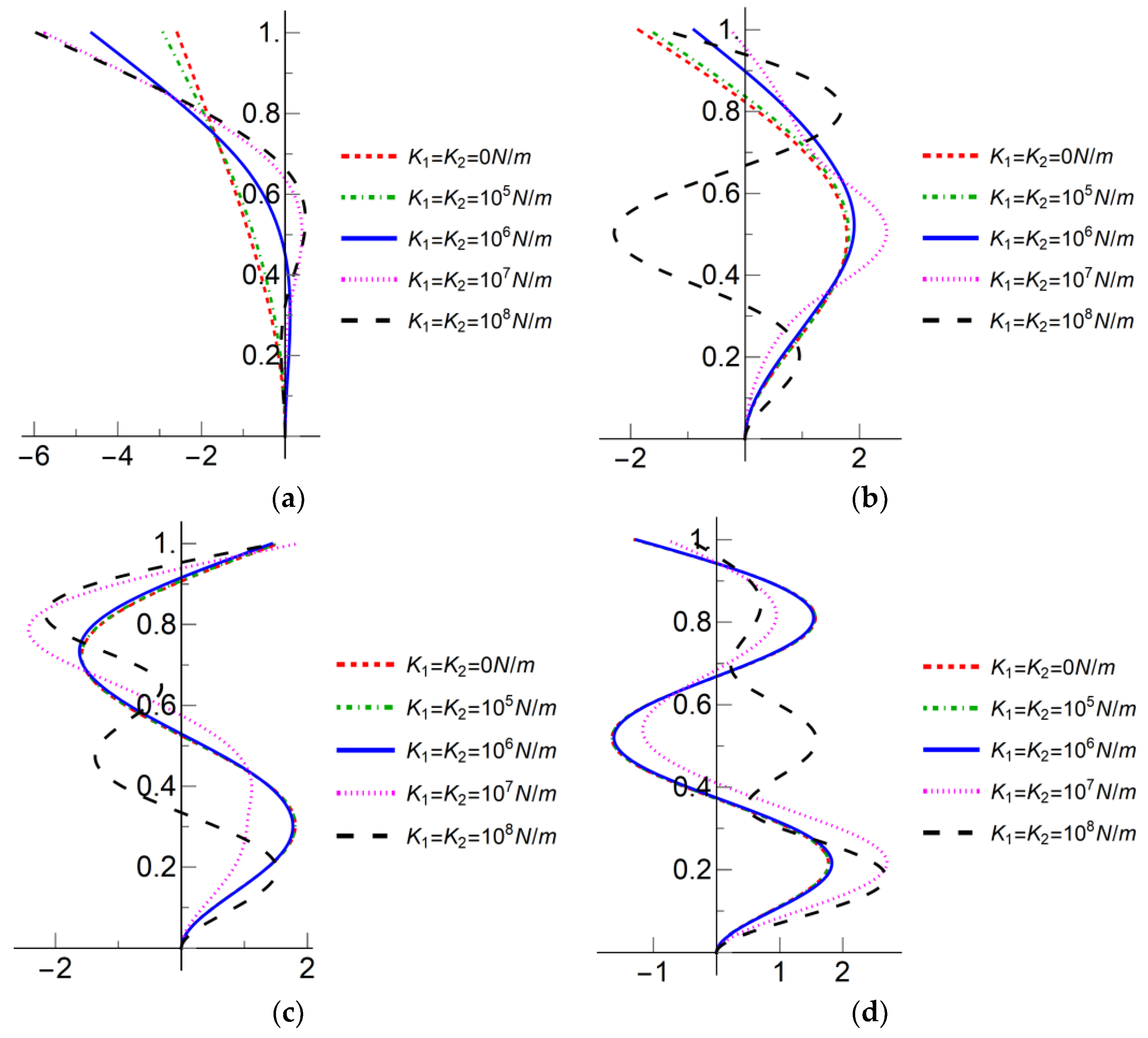
2.3. Constraint Stiffness on Vibration Mode Analysis
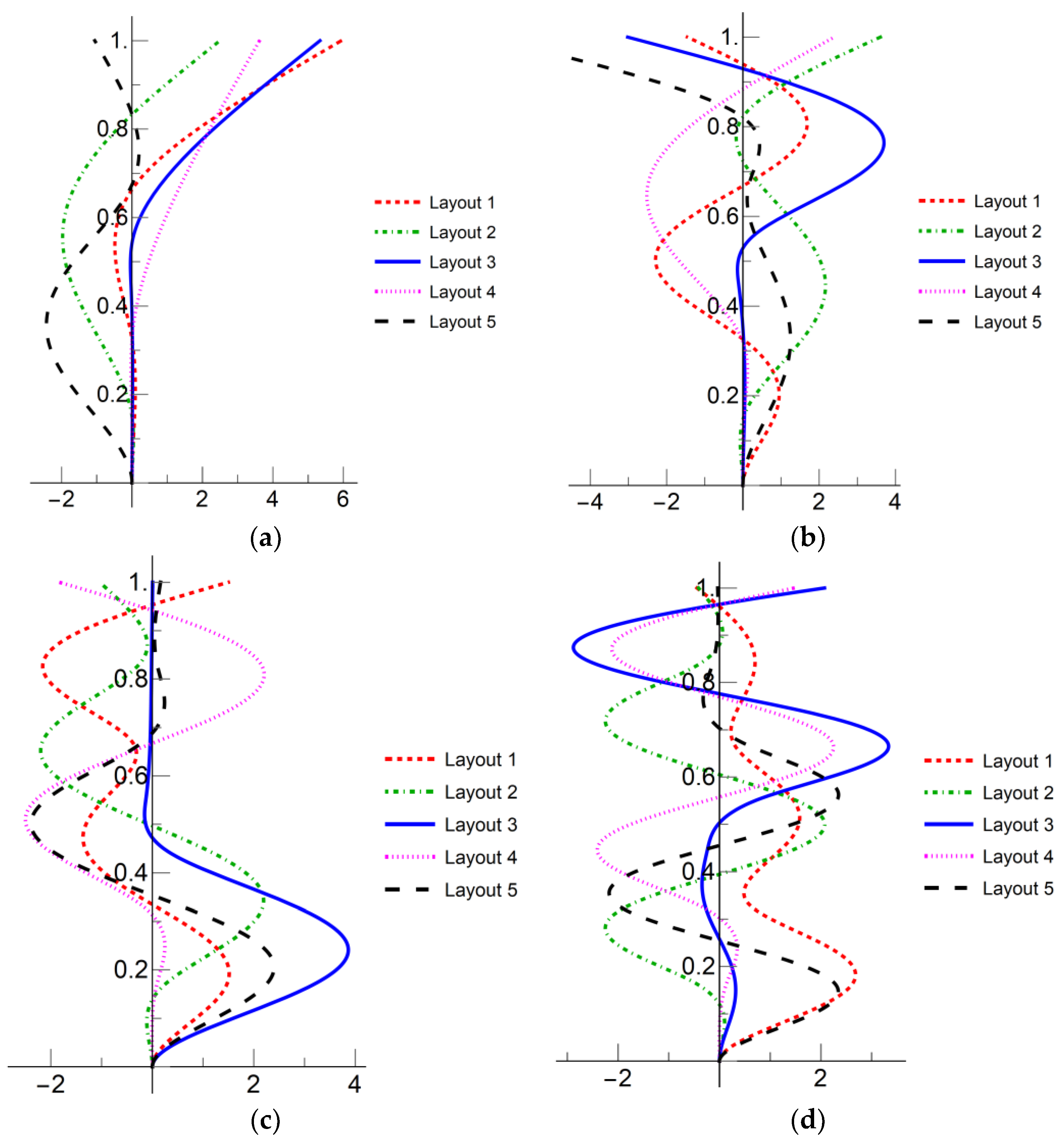
2.4. Constraint Arrangement Analysis
- →
- Layout 1: Low constraint elevation is 30 m and high constraint elevation is 60 m,
- →
- Layout 2: Low constraint elevation is 15 m and high constraint elevation is 75 m,
- →
- Layout 3: Low constraint elevation is 40 m and high constraint elevation is 50 m,
- →
- Layout 4: Low constraint elevation is 15 m and high constraint elevation is 30 m,
- →
- Layout 5: Low constraint elevation is 60 m and high constraint elevation is 75 m.
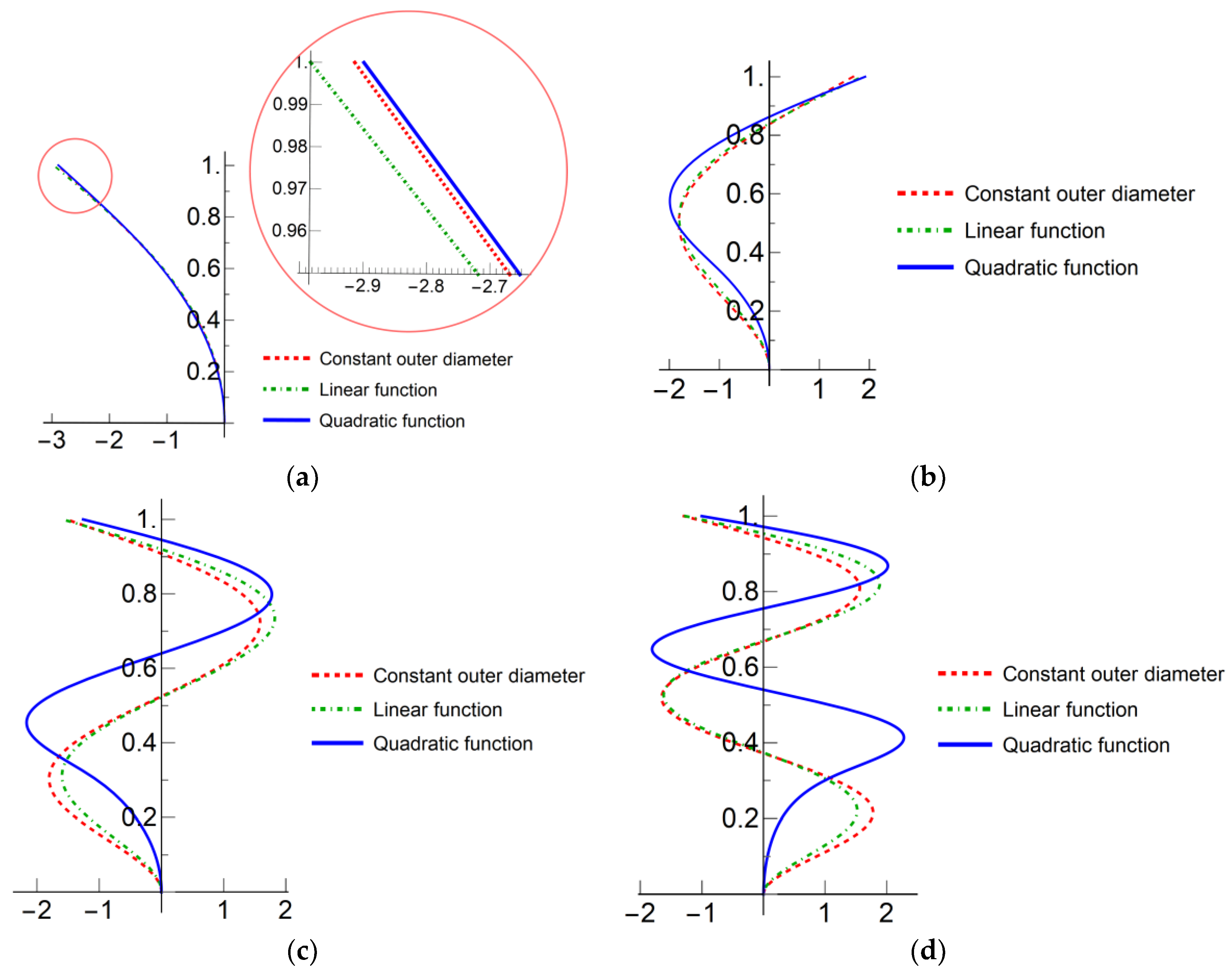
2.5. Outer Diameter Function on Vibration Mode Analysis
3. Dynamic Analysis of VNA System under Combined Excitation
3.1. Mathematical Model
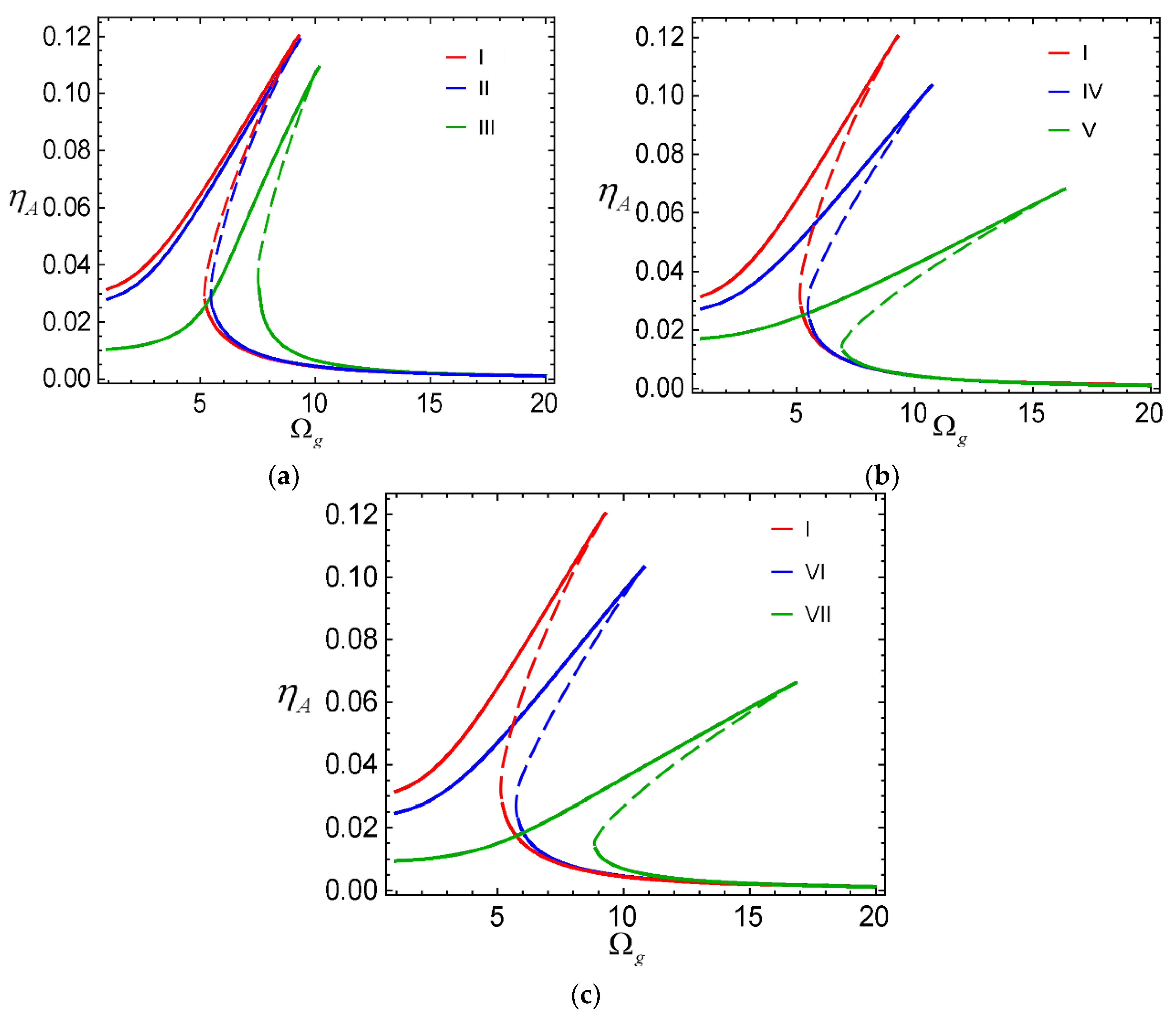
3.2. Vibration Response of the VNA System under First Order Frequency Locking
- I:
- linear stiffness 103 N/m, nonlinear stiffness 103 N/m3;
- II:
- Linear stiffness 104 N/m, nonlinear stiffness 103 N/m3;
- III:
- Linear stiffness 105 N/m, nonlinear stiffness 103 N/m3;
- IV:
- Linear stiffness 103 N/m, nonlinear stiffness 104 N/m3;
- V:
- Linear stiffness 103 N/m, nonlinear stiffness 105 N/m3;
- VI:
- Linear stiffness 104 N/m, nonlinear stiffness 104 N/m3;
- VII:
- Linear stiffness 105 N/m, nonlinear stiffness 105 N/m3.
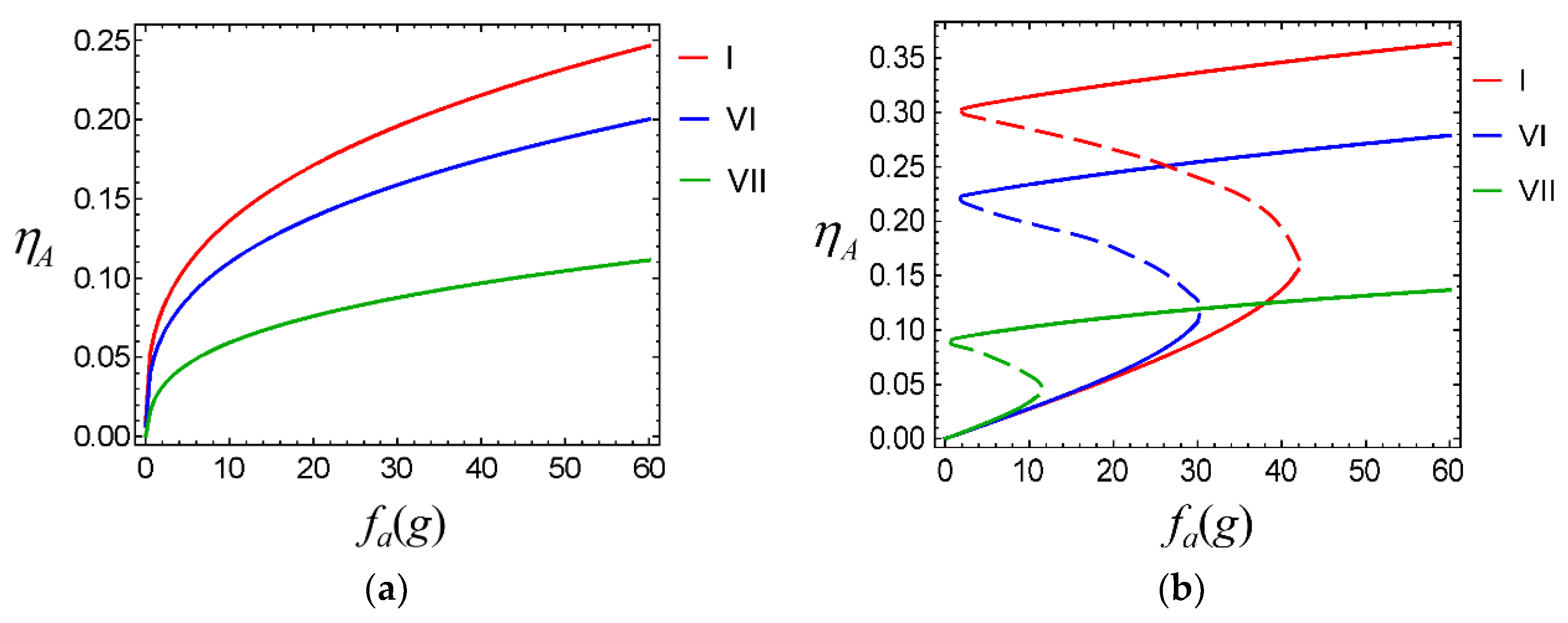
- I:
- Linear stiffness 103 N/m, nonlinear stiffness 103 N/m3;
- VI:
- Linear stiffness 104 N/m, nonlinear stiffness 104 N/m3;
- VII:
- Linear stiffness 105 N/m, nonlinear stiffness 105 N/m3.
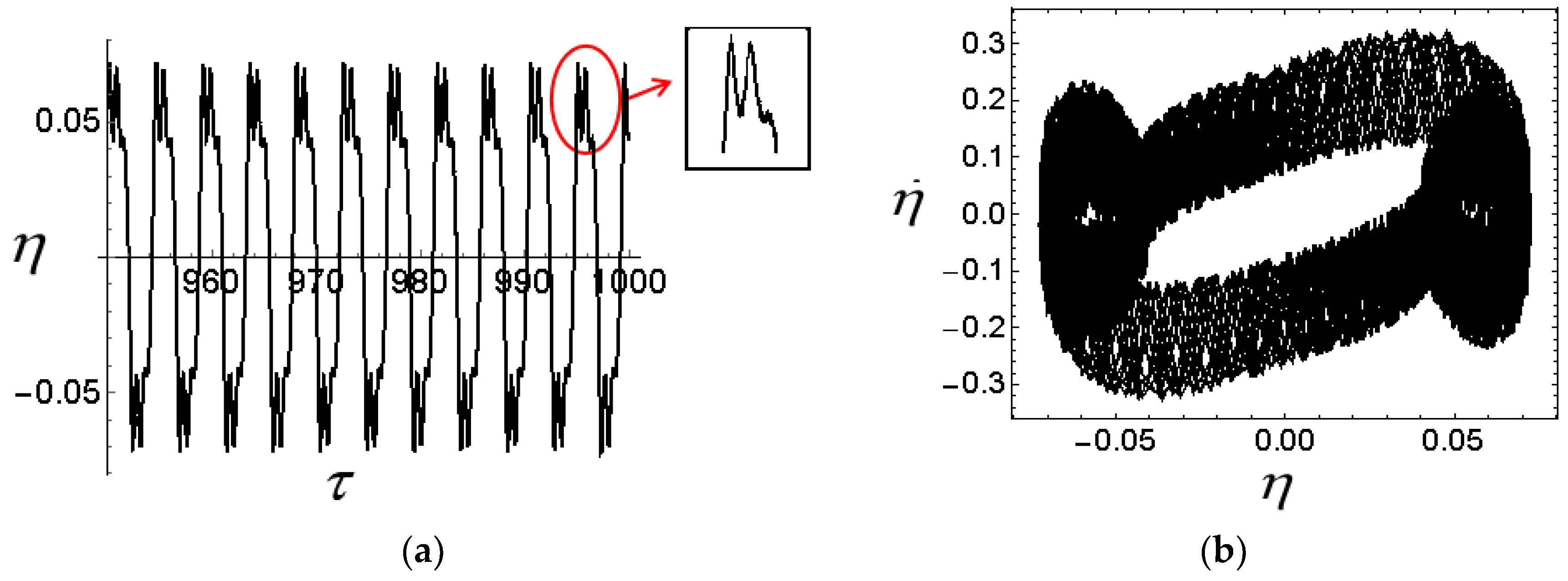
3.3. System Vibration Response Analysis under Design and Accident Conditions
- (1)
- Design condition (level O, level A): dead weight + accessory load + OBE seismic load + 100 year return period strong wind load.
- (2)
- Accident condition (level D): (1) dead weight + accessory load + 71.4 m/s tornado load; (2) dead weight +accessory load + SSE seismic load.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Primitive Function | Differential Transformation Function |
|---|---|
References
- Ashley, H.; Haviland, G. Bending vibrations of a pipe line containing flowing fluid. J. Appl. Mech. 1950, 17, 229–232. [Google Scholar] [CrossRef]
- Long, R.H.J. Experimental and theoretical study of transverse vibration of a tube containing flowing fluid. J. Appl. Mech. 1955, 22, 65–68. [Google Scholar] [CrossRef]
- Benjamin, T.B. Dynamics of a system of articulated pipes conveying fluid I Theory. Proc. R. Soc. London Ser. A 1961, 261, 487–499. [Google Scholar]
- Benjamin, T.B. Dynamics of a system of articulated pipes conveying fluid II Experiments. Proc. R. Soc. London Ser. A 1961, 261, 87–99. [Google Scholar]
- Gregory, W.R.; Païdoussis, M.P. Unstable oscillation of tubular cantilevers flowing fluid-theory and experiments. Proc. R. Soc. London Ser. A 1966, 293, 512–542. [Google Scholar]
- Païdoussis, M.P.; Issid, N.T. Dynamic stability of pipes conveying fluid. J. Sound Vib. 1974, 33, 267–294. [Google Scholar] [CrossRef]
- Païdoussis, M.P. Flow-induced instabilities of cylindrical structures. Appl. Mech. Rev. 1987, 40, 163–175. [Google Scholar] [CrossRef]
- Olson, G.; Jamison, D. Application of a general purpose finite element method to elastic pipes conveying fluid. J. Fluids Struct. 1997, 11, 207–222. [Google Scholar] [CrossRef]
- Seiranyan, A.P. Collision of eigenvalues in linear oscillatory systems. J. Appl. Math. Mech. 1994, 58, 805–813. [Google Scholar] [CrossRef]
- Xu, J.; Huang, Y.Y. Bifurcation of a cantilevered pipe conveying stead fluid with a terminal nozzle. Acta Mech. Sin. 2000, 16, 264–272. [Google Scholar]
- Marzani, A.; Mazzotti, M.; Viola, E.; Vittori, P.; Elishakoff, I. FEM formulation for dynamic instability of fluid-conveying pipe on non-uniform elastic foundation. Mech. Based Des. Struct. Mach. 2012, 40, 83–95. [Google Scholar] [CrossRef]
- Ryu, S.U.; Sugiyama, Y.; Ryu, B.J. Eigenvalue branches and modes for flutter of cantilevered pipes conveying fluid. Comput. Struct. 2002, 80, 1231–1241. [Google Scholar] [CrossRef]
- Sinha, J.K.; Singh, S.; Rao, A.R. Finite element simulation of dynamic behaviour of an open-ended cantilever pipe conveying fluid. J. Sound Vib. 2012, 40, 189–194. [Google Scholar] [CrossRef]
- Firouz AR, D.; Askariana, A.R.; Kheiri, M. Bending-torsional flutter of a cantilevered pipe conveying fluid with an inclined terminal nozzle. J. Sound Vib. 2013, 332, 3002–3014. [Google Scholar] [CrossRef]
- Yu, D.L.; Païdoussis, M.P.; Shen, H.J.; Wang, L. Dynamic stability of periodic pipes conveying fluid. J. Appl. Mech. 2013, 81, 011008. [Google Scholar] [CrossRef]
- Sinir, B.G. Bifurcation and chaos of slightly curved pipes. Math. Comput. Appl. 2010, 15, 490–502. [Google Scholar] [CrossRef] [Green Version]
- Koo, G.H.; Yoo, B. Dynamic characteristics of kalimer IHTS hot leg piping system conveying hot liquid sodium. Int. J. Press. Vessel. Pip. 2000, 77, 679–689. [Google Scholar] [CrossRef]
- Dai, H.L.; Wang, L.; Qian, Q.; Gan, J. Vibration analysis of three-dimensional pipes conveying fluid with consideration of steady combined force by transfer matrix method. Appl. Math. Comput. 2012, 219, 2453–2464. [Google Scholar] [CrossRef]
- Thurman, A.L.; Mote, C.D., Jr. Non-linear oscillation of a cylinder containing flowing fluid. ASME J. Eng. Ind. 1969, 91, 1147–1155. [Google Scholar] [CrossRef]
- Semler, C.; Li, G.X.; Païdoussis, M.P. The nonlinear equations of motion of pipes conveying fluid. J. Sound Vib. 1994, 169, 577–599. [Google Scholar] [CrossRef]
- Holmes, P.J. Bifurcations to divergence and flutter in flow-induced oscillations: An infinite dimensional analysis. J. Sound Vib. 1977, 53, 471–503. [Google Scholar] [CrossRef]
- Holmes, P.J. Pipes supported at both ends cannot flutter. J. Appl. Mech. 1978, 45, 619–622. [Google Scholar] [CrossRef]
- Modarres, S.Y.; Païdoussis, M.P. Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends. J. Fluids Struct. 2009, 25, 535–543. [Google Scholar] [CrossRef]
- Sri, N.N.; Tien, W.M. Bifurcation behavior of nonlinear pipes conveying pulsating flow. J. Fluids Struct. 1989, 3, 609–629. [Google Scholar]
- Wang, L. A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid. Int. J. Non-Linear Mechanics. 2009, 44, 115–121. [Google Scholar] [CrossRef]
- Jaroszewicz, J.; Zoryi, L. Investigation of the effect of axial loads on the transverse vibrations of a vertical cantilever with variable parameters. Int. Appl. Mech. 2000, 36, 1242–1251. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y. Further Analysis of the Natural Vibration Characteristics of Deep Sea Risers. Ship Mech. 2014, 18, 165–171. [Google Scholar]
- Kim, Y.C.; Triantafyllou, M.S. The nonlinear dynamics of long slender cylinders. J. Energy Resour. Technol. 1984, 106, 250–256. [Google Scholar] [CrossRef]
- Soltanahmadi, A. Determination of flexible riser natural frequencies using Fourier analysis. Mar. Struct. 1992, 5, 193–203. [Google Scholar] [CrossRef]
- Cheng, Y.; Vandiver, J.K.; Moe, G. The linear vibration analysis of marine risers using WKB-based dynamic stiffness method. J. Sound Vib. 2002, 251, 750–760. [Google Scholar] [CrossRef]
- Park, H.I.; Jung, D.H. A finite element method for dynamic analysis of long slender marine structures under combined parametric and forcing excitations. Ocean Eng. 2002, 29, 1313–1325. [Google Scholar] [CrossRef]
- Sparks, C.P. Transverse modal vibrations of vertical tensioned risers: A simplified analytical approach. Oil Gas Sci. Technol. 2002, 57, 71–86. [Google Scholar] [CrossRef]
- Almitani, K.H.; Mohamed, N.; Alazwari, M.A.; Mohamed, S.A.; Eltaher, M.A. Exact solution of nonlinear behaviors of imperfect bioinspired helicoidal composite beams resting on elastic foundations. Mathematics 2022, 10, 887. [Google Scholar] [CrossRef]
- Lee, J.K. Lateral free vibration of rectangular barrettes subjected to vertical loading. Mar. Georesources Geotechnol. 2022, 40, 995–1003. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Mohamed, S.A.; Eltaher, M.A. Vibration analysis of laminated composite higher order beams under varying axial loads. Ocean Eng. 2022, 252, 111203. [Google Scholar] [CrossRef]
- Virgin, L.N.; Santillan, S.T.; Holland, D.B. Effect of gravity on the vibration of vertical cantilevers. Mech. Res. Commun. 2007, 34, 312–317. [Google Scholar] [CrossRef]
- Xi, L.Y.; Li, X.F.; Tang, G.J. Free vibration of standing and hanging gravity-loaded Rayleigh cantilevers. Int. J. Mech. Sci. 2013, 66, 233–238. [Google Scholar] [CrossRef]
- Song, L.; Zheng, X.; Zhang, W.; Lin, J.; Yue, Q. Natural frequencies and vibration modes of marine riser suspension. Ship Mech. 2015, 19, 1267–1274. [Google Scholar]
- Chen, Y.F.; Chai, Y.H.; Li, X.; Zhou, J. An extraction of the natural frequencies and mode shapes of marine risers by the method of differential transformation. Comput. Struct. 2009, 87, 1384–1393. [Google Scholar] [CrossRef]
- Zhou, C.Y.; So, R.M.C.; Lam, K. Vortex-induced vibration of an elastic circular cylinder. J. Fluids Struct. 1999, 13, 165–189. [Google Scholar] [CrossRef]
- Newman, D.J.; Karniadakis, G. A direct numerical simulation study of flow past a freely vibrating cable. J. Fluid Mech. 1997, 344, 95–136. [Google Scholar] [CrossRef]
- Moe, G.; Wu, Z.J. The lift force on a cylinder vibrating in a current. ASME J. Offshore Mech. Arct. Eng. 1990, 112, 297–303. [Google Scholar] [CrossRef]
- Huse, E.; Nielsen, F.G.; Soreide, T. Coupling between in-line and transverse VIV response. In Proceedings of the 21st International Conference on Offshore and Arctic Mechanics, Oslo, Norway, 23–28 June 2002; paper OAME 2002-28618. Amer Society of Mechanical: New York, NY, USA, 2002. [Google Scholar]
- Cao, P.; Niu, K.; Sun, J.; Zhao, S.; Liu, Y. Reordering of vertical vibration modes in an axially compressed beam on a Winkler foundation. J. Sound Vib. 2022, 526, 116841. [Google Scholar] [CrossRef]
- Zhou, F. Research on Nonlinear Dynamics of a Class of MEMS Resonators. Master’s Thesis, Tianjin University, Tianjin, China, 2014. [Google Scholar]
- RCC-M 2000 + 2002; Specification Design and Construction Rules for Mechanical Components of PWR Nuclear Islands. AFCEN: Paris, France, 2002.
- GB50267-97; Code for Seismic Design of Nuclear Power Plants. State Seismological Bureau: Beijing, China, 1998.


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modulus | 1.4 × 1010 MPa | Low position constraint stiffness | 1 × 105 N/m |
| Outer diameter | 1.52 m | High position constraint stiffness | 1 × 105 N/m |
| Inner diameter | 1.5 m | Low position constraint elevation | 30 m |
| Riser density | 1856 kg/m3 | High position constraint elevation | 60 m |
| Additional mass | 2000 kg | riser length | 90 m |
| Additional rotational inertia | 5000 kg·m² | Gas density | 1.225 kg/m3 |
| ω1 (rad/s) | ω2 (rad/s) | ω3 (rad/s) | ω4 (rad/s) | ω5 (rad/s) | |
|---|---|---|---|---|---|
| DTM | 2.0108 | 7.6238 | 20.2602 | 38.6768 | 62.5487 |
| FEM | 2.0086 | 7.5970 | 20.1703 | 38.4927 | 62.2990 |
| f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | |
|---|---|---|---|---|
| Layout 1 | 0.9249 | 5.8070 | 7.4536 | 8.7769 |
| Layout 2 | 1.4401 | 3.0100 | 6.0971 | 11.303 |
| Layout 3 | 0.6700 | 4.3996 | 5.0971 | 11.987 |
| Layout 4 | 0.3239 | 2.1522 | 6.0335 | 11.529 |
| Layout 5 | 2.4147 | 2.4887 | 6.5410 | 12.259 |
| External Diameter | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) |
|---|---|---|---|---|
| Constant value | 0.3200 | 1.2140 | 3.2245 | 6.1556 |
| Linear function | 0.3798 | 1.2645 | 3.2312 | 6.1269 |
| Quadratic function | 0.3367 | 1.1608 | 3.0977 | 5.9339 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Han, M.; Zhang, Q.; Hao, S.; Zhen, J. Analysis of Dynamic Characteristics of Attached High Rise Risers. Appl. Sci. 2023, 13, 8767. https://doi.org/10.3390/app13158767
Zhang L, Han M, Zhang Q, Hao S, Zhen J. Analysis of Dynamic Characteristics of Attached High Rise Risers. Applied Sciences. 2023; 13(15):8767. https://doi.org/10.3390/app13158767
Chicago/Turabian StyleZhang, Linghao, Mingjiang Han, Qichang Zhang, Shuying Hao, and Jianwei Zhen. 2023. "Analysis of Dynamic Characteristics of Attached High Rise Risers" Applied Sciences 13, no. 15: 8767. https://doi.org/10.3390/app13158767





