Design of a Miniaturized Electron Cyclotron Resonance Ion Source for High-Voltage Proton Accelerator
Abstract
:Featured Application
Abstract
1. Introduction
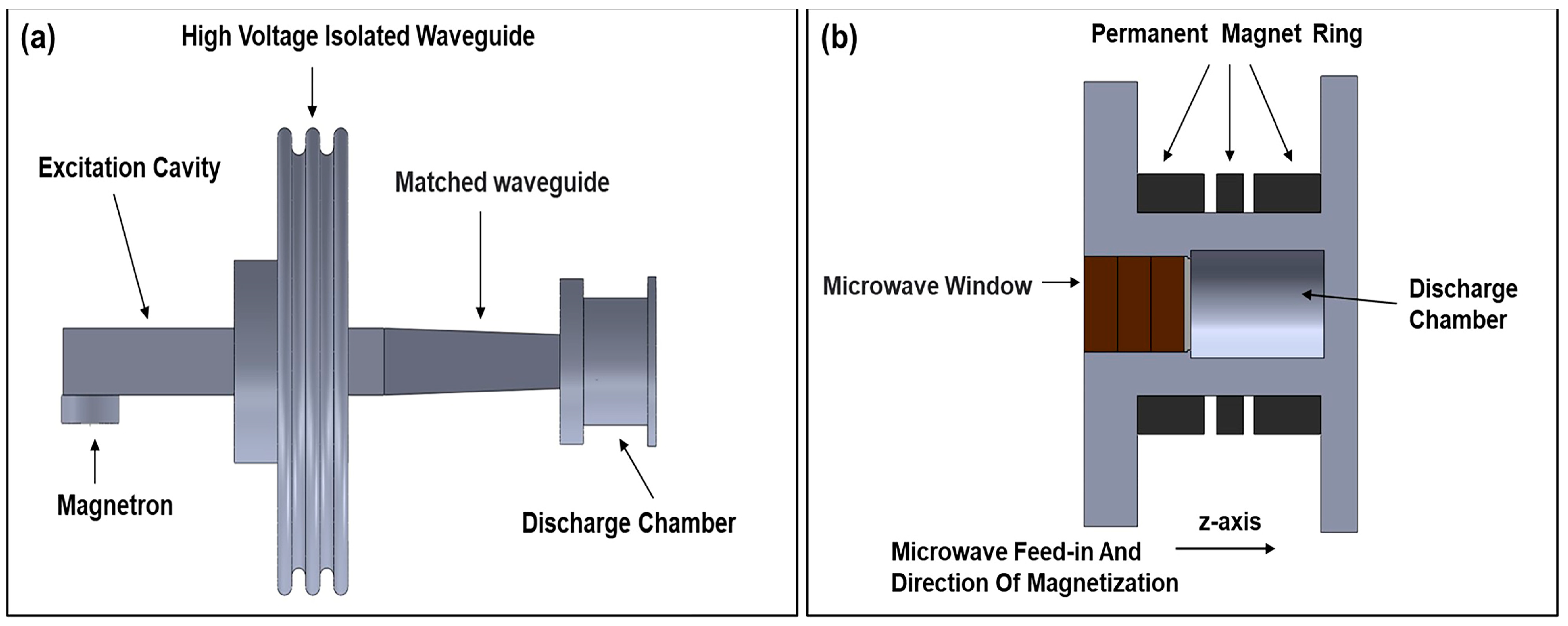
2. Miniaturization of the Microwave System
2.1. Conventional Microwave System
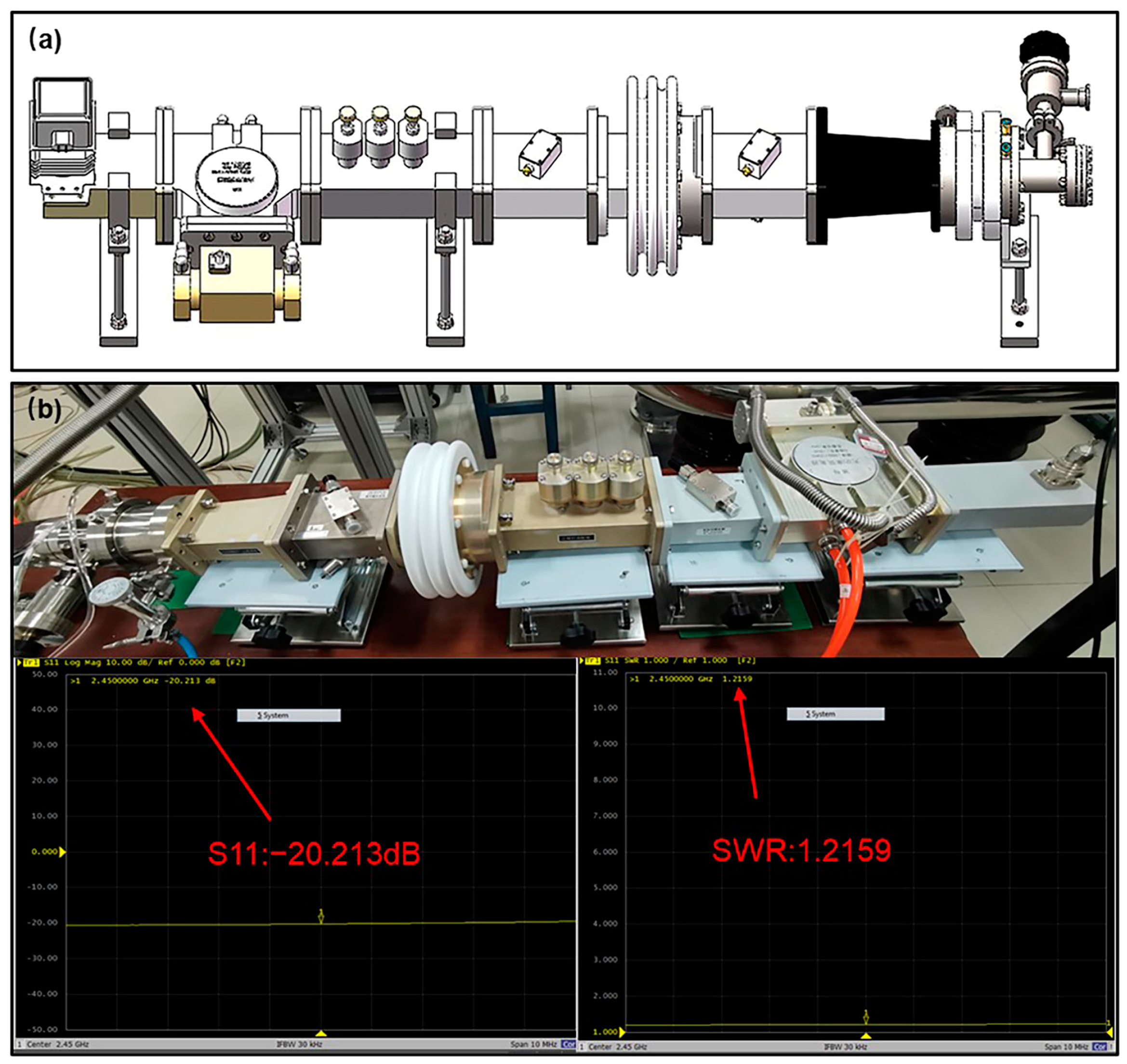
2.2. Microwave Transmission System Miniaturization Design
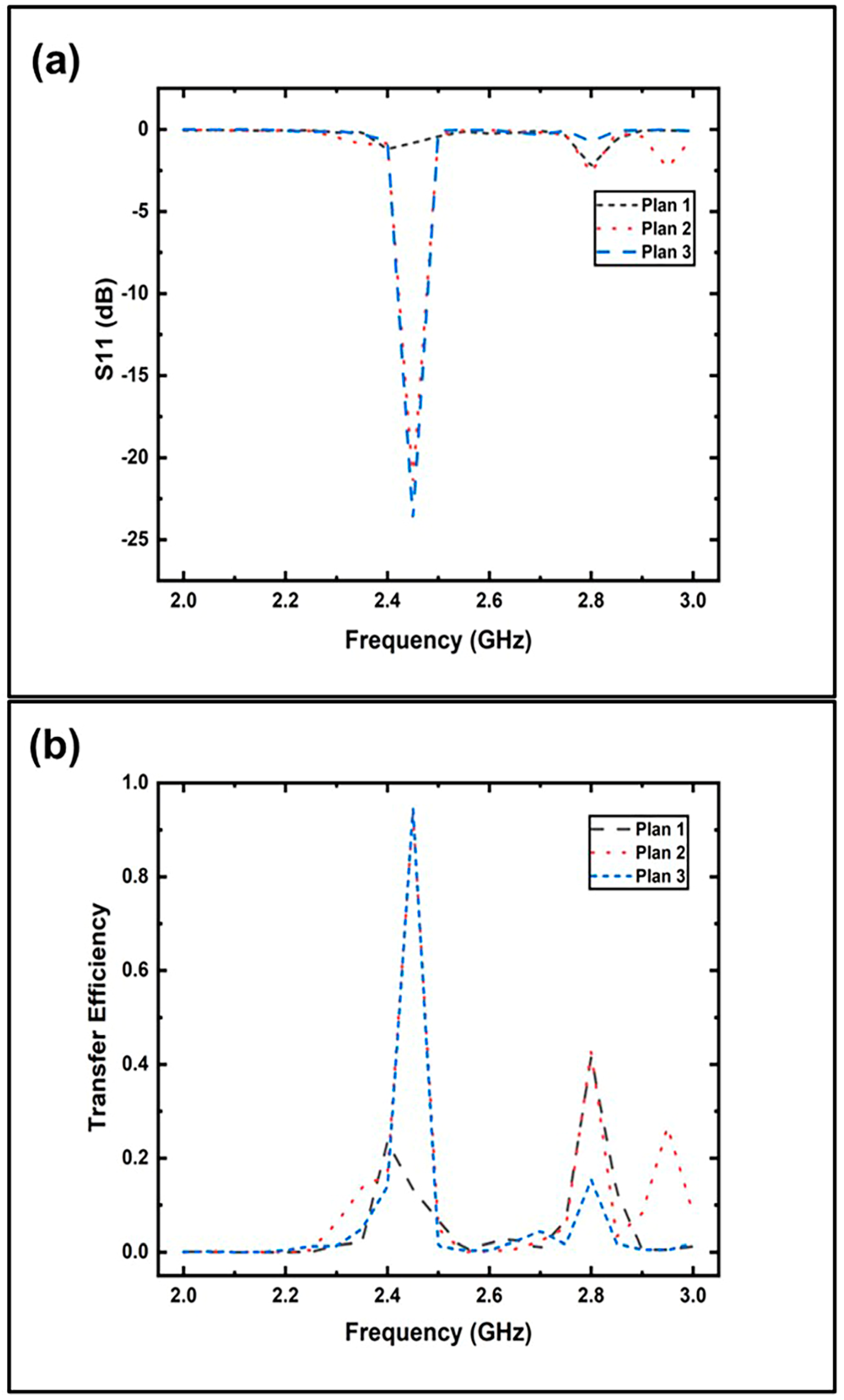
2.2.1. Conventional Length Waveguide Plus Transition Waveguide
2.2.2. Conventional Length Waveguide Plus Miniaturized Ridged Waveguide
2.2.3. Reduced Length Waveguide Plus Miniaturized Ridge Waveguide
3. Optimization of Discharge Chamber Size and Magnetic Field
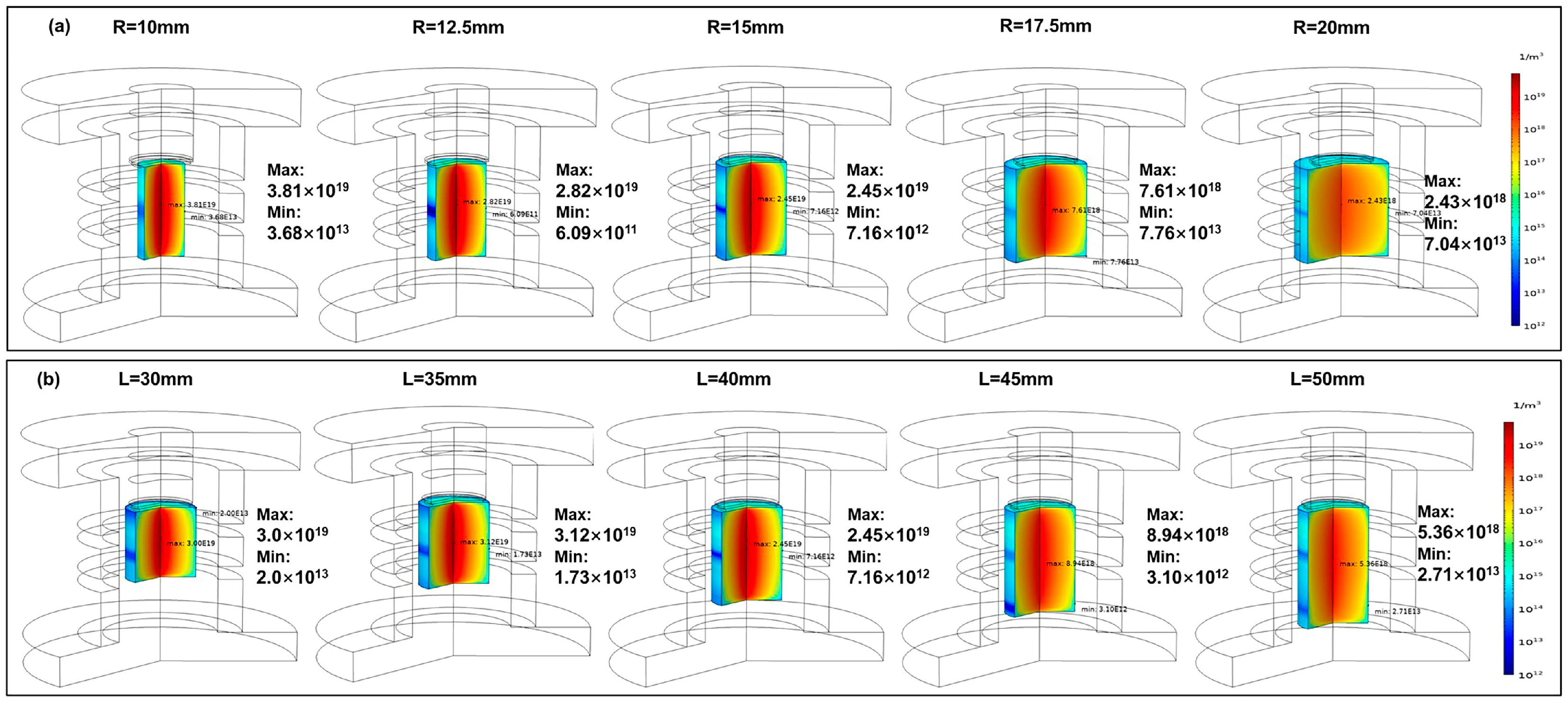
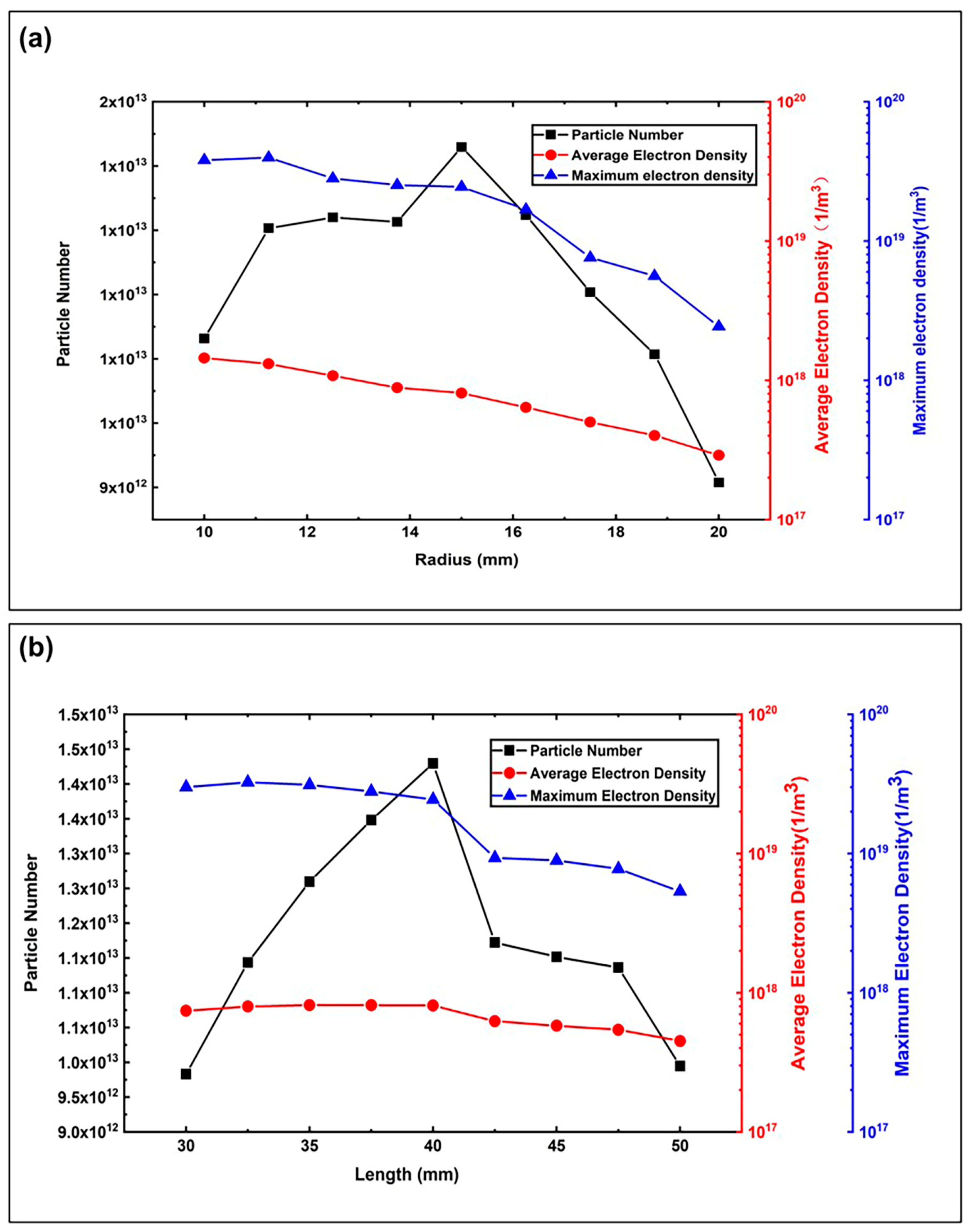
3.1. The Impact of the Discharge Chamber’s Dimensions on the Ionization Properties
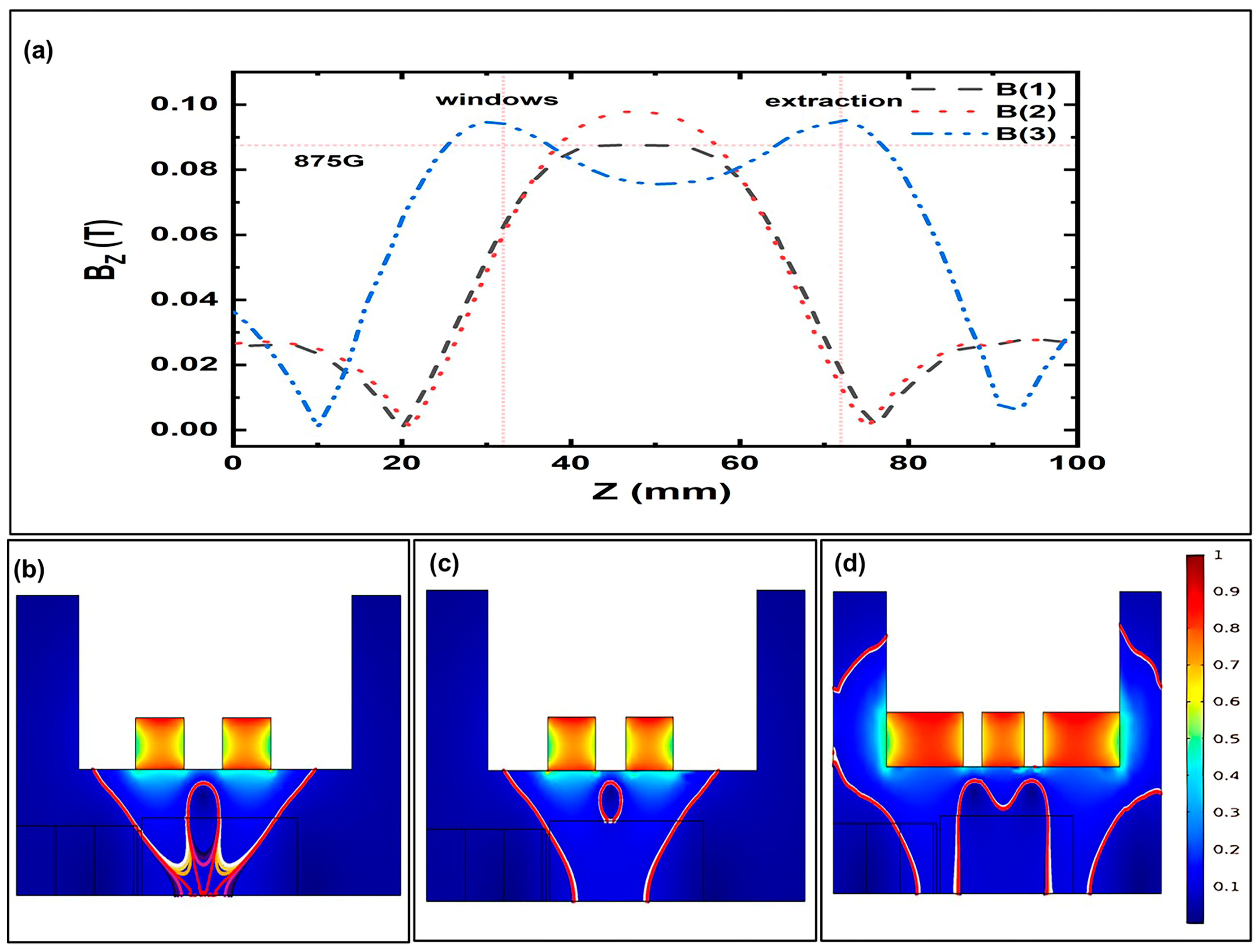
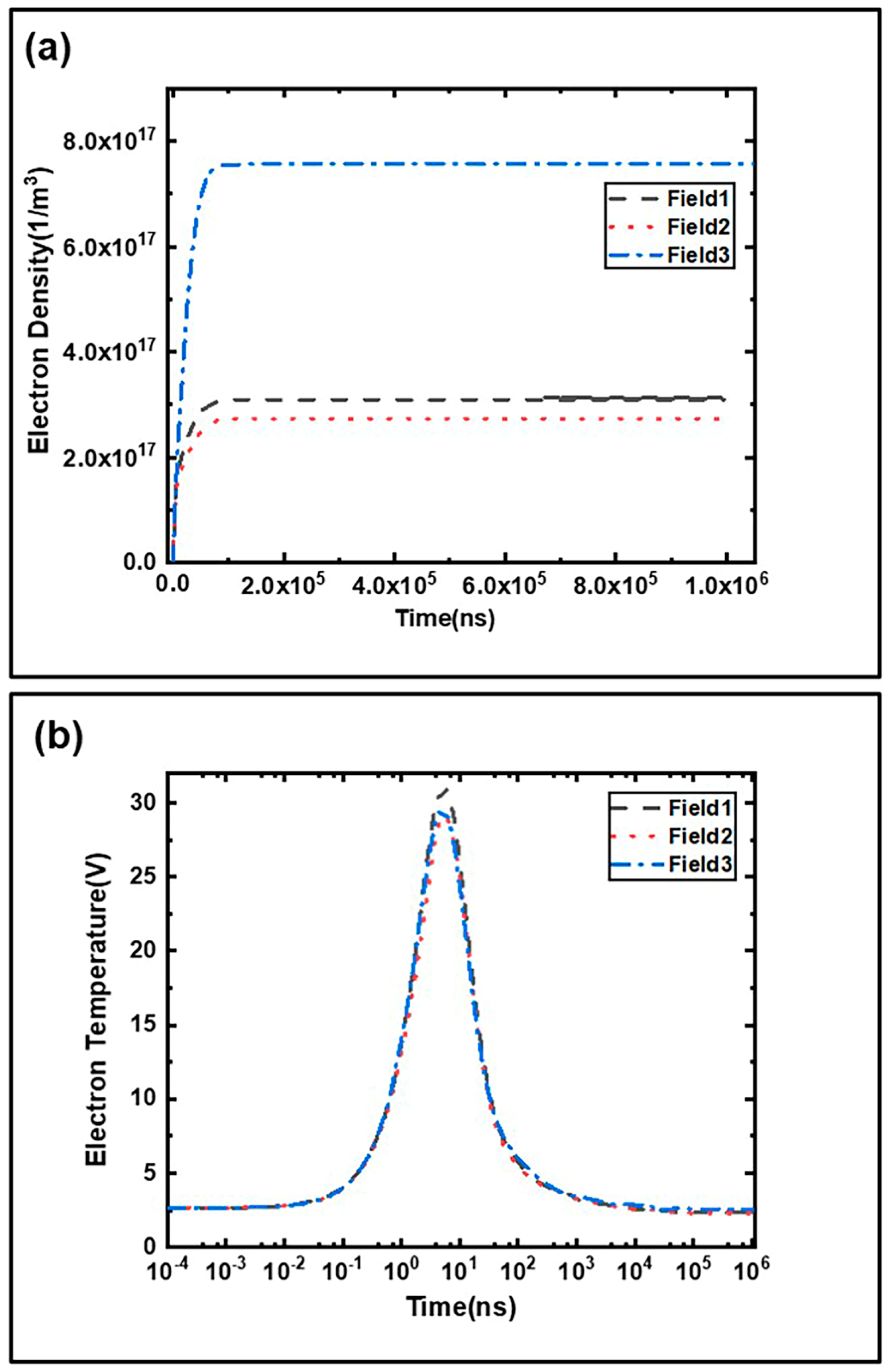
3.2. Effects of Three Classical Axial Magnetic Field Distributions on Ionization Characteristics
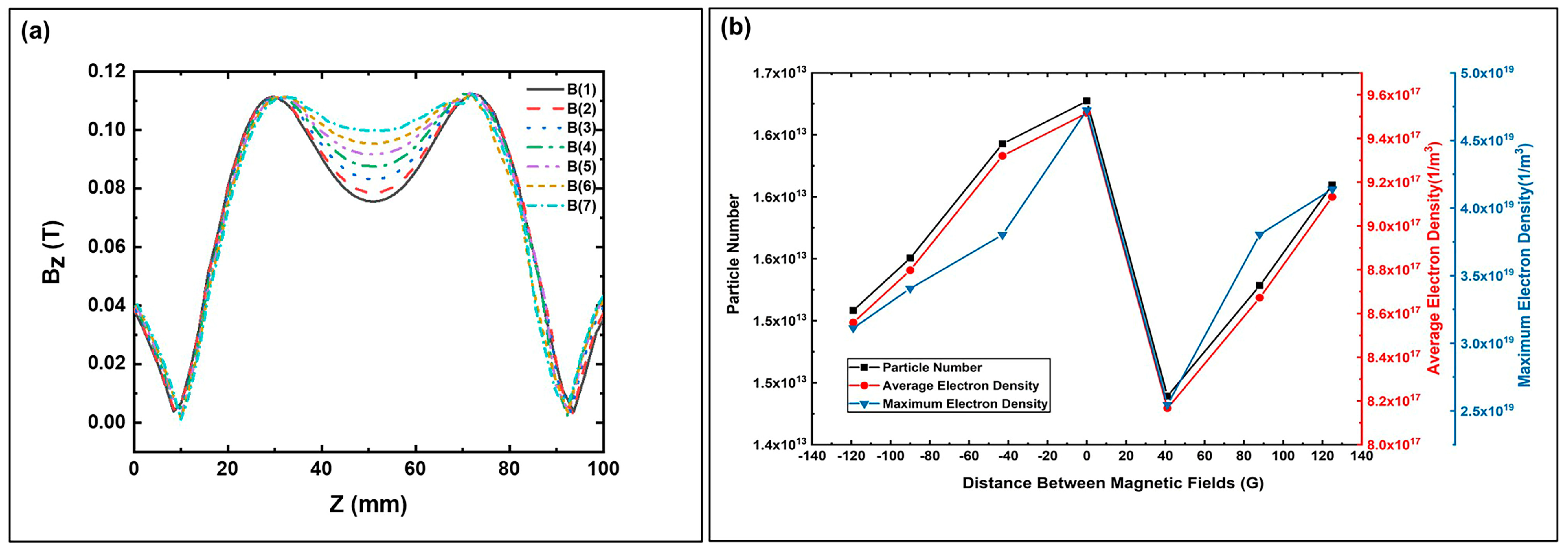
3.3. Improvement of the Saddle Magnetic Field
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kasatov, D.; Koshkarev, A.; Kuznetsov, A.; Makarov, A.; Ostreinov, Y.; Shchudlo, I.; Sorokin, I.; Sycheva, T.; Taskaev, S.; Zaidi, L. The accelerator neutron source for boron neutron capture therapy. J. Phys. Conf. Ser. 2016, 769, 012064. [Google Scholar] [CrossRef]
- Kiyanagi, Y.; Sakurai, Y.; Kumada, H.; Tanaka, H. Status of accelerator-based BNCT projects worldwide. AIP Conf. Proc. 2019, 2160, 050012. [Google Scholar] [CrossRef]
- Honda, S.; Yoshihashi, S.; Tomita, S.; Tsuchida, K.; Kiyanagi, Y.; Tsurita, Y.; Watanabe, K.; Yamazaki, A.; Uritani, A. Development of a Sealed Li target as an accelerator-driven neutron source for Boron neutron capture therapy at Nagoya University. Nucl. Instrum. Methods A 2022, 1040, 167140. [Google Scholar] [CrossRef]
- Yoshioka, M. Review of accelerator-based boron neutron capture therapy machines. In Proceedings of the 7th International Particle Accelerator Conference (IPAC’16), Busan, Republic of Korea, 8–13 May 2016; pp. 3171–3175. [Google Scholar] [CrossRef]
- Porra, L.; Seppala, T.; Wendland, L.; Revitzer, H.; Joensuu, H.; Eide, P.; Koivunoro, H.; Smick, N.; Smick, T.; Tenhunen, M. Accelerator-based boron neutron capture therapy facility at the Helsinki University Hospital. Acta Oncol. 2022, 61, 269–273. [Google Scholar] [CrossRef]
- Chen, G.; Xu, S.W.; Xie, Y.H.; Song, Y.T.; Chen, Y.Q.; Hu, C.D.; Zhao, Y.P.; Samsonov, E.V.; Karamysheva, G.; Shirkov, G.; et al. The construction of the inner ion source for SC200 compact superconducting cyclotron. AIP Conf. Proc. 2018, 2011, 090009. [Google Scholar] [CrossRef]
- Ji, Q.; Sy, A.; Kwan, J.W. Radio frequency-driven proton source with a back-streaming electron dump. Rev. Sci. Instrum. 2010, 81, 02B312. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.T.; Peng, S.X.; Zhang, M.; Zhou, Q.F.; Song, Z.Z.; Yuan, Z.X.; Lu, P.N.; Xu, R.; Zhao, J.; Yu, J.X.; et al. The deuteron injector progress of the Peking University Neutron Imaging Facility project. Rev. Sci. Instrum. 2010, 81, 02B714. [Google Scholar] [CrossRef]
- Gobin, R.; Beauvais, P.; Ismail, A.B.; Bogard, D.; Delferriere, O.; De Menezes, D.; Duperrier, R.; Gauthier, Y.; Harrault, F.; Leroy, P.; et al. ECR light ion sources at CEA/Saclay. Chin. Phys. C 2007, 31, 46–50. [Google Scholar]
- Peng, S.X.; Zhang, A.L.; Wu, W.B.; Ma, T.H.; Jiang, Y.X.; Li, K.; Zhang, J.F.; Zhang, T.; Wen, J.M.; Xu, Y.; et al. Plasma simulation and optimization for a miniaturized antenna ECR ion source. Nucl. Instrum. Methods A 2021, 1011, 165586. [Google Scholar] [CrossRef]
- Wen, J.M.; Peng, S.X.; Ren, H.T.; Zhang, T.; Zhang, J.F.; Wu, W.B.; Sun, J.; Guo, Z.Y.; Chen, J.E. A miniaturized 2.45 GHz ECR ion source at Peking University. Chin. Phys. B 2018, 27, 055204. [Google Scholar] [CrossRef]
- Fatkullin, R.; Bogomolov, S.; Efremov, A.; Loginov, V.; Kostukhov, Y.; Bondarchenko, A. Current status of the compact 2.45 GHz ECR Ion Source at FLNR JINR. EPJ Web. Conf. 2019, 201, 08002. [Google Scholar] [CrossRef] [Green Version]
- Delferrière, O.; Gobin, R.; Harrault, F.; Nyckees, S.; Sauce, Y.; Tuske, O. Advanced light ion source extraction system for a new electron cyclotron resonance ion source geometry at Saclay. Rev. Sci. Instrum. 2012, 83, 02A307. [Google Scholar] [CrossRef]
- Shimada, M.; Watanabe, I.; Torii, Y. Compact electron cyclotron resonance ion source with high density plasma. J. Vac. Sci. Technol. A 1991, 9, 707–710. [Google Scholar] [CrossRef]
- Qian, C.; Chen, Z.; Wu, Q.; Zhang, W.H.; Wang, Y.; Yang, Y.; Ma, H.Y.; Fang, X.; Sun, L.T.; Zhang, X.Z.; et al. Microwave impedance matching of A 2.45 GHz ECR ion source. Nucl. Phys. Rev. 2013, 30, 32–37. [Google Scholar] [CrossRef]
- Swaroop, R.; Kumar, N.; Rodrigues, G.; Kanjilal, D.; Banerjee, I.; Mahapatra, S.K. Design and development of a compact ion implanter and plasma diagnosis facility based on a 2.45 GHz microwave ion source. Rev. Sci. Instrum. 2021, 92, 053306. [Google Scholar] [CrossRef]
- Misra, A.; Pandit, V.S. Studies on the coupling transformer to improve the performance of microwave ion source. Rev. Sci. Instrum. 2014, 85, 063301. [Google Scholar] [CrossRef]
- Wang, P. The Parameter Calculation for Ridge Waveguide. Fire Control Radar Technol. 2004, 3, 014. [Google Scholar] [CrossRef]
- Sun, W.M.; Balanis, C.A. MFIE analysis and design of ridged waveguides. IEEE Trans. Microw. Theory 1993, 41, 1965–1971. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Makasheva, K.; Garrigues, L.; Boeuf, J.P. Modelling of a dipolar microwave plasma sustained by electron cyclotron resonance. J. Phys. D Appl. Phys. 2009, 42, 194019. [Google Scholar] [CrossRef]
- Mallick, C.; Bandyopadhyay, M.; Kumar, R. Spatio-temporal evolution of electric field inside a microwave discharge plasma during initial phase of ignition and its effect on power coupling. Phys. Plasmas 2019, 26, 043507. [Google Scholar] [CrossRef] [Green Version]
- Mallick, C.; Bandyopadhyay, M.; Kumar, R. Plasma characterization of a microwave discharge ion source with mirror magnetic field configuration. Rev. Sci. Instrum. 2018, 89, 125112. [Google Scholar] [CrossRef]
- Kinder, R.L.; Kushner, M.J. Consequences of mode structure on plasma properties in electron cyclotron resonance sources. J. Vac. Sci. Technol. A 1999, 17, 2421–2430. [Google Scholar] [CrossRef]
- Gammino, S.; Ciavola, G. ECR ion sources and scaling laws. In Proceedings of the 14th International Conference, Cyclotrons and Their Applications, Cape Town, South Africa, 8–13 October 1995; pp. 377–380. [Google Scholar] [CrossRef]
- Cortazar, O.D.; Megia-Macias, A.; Vizcaino-de-Julian, A. Experimental Study of Breakdown Time in a Pulsed 2.45-GHz ECR Hydrogen Plasma Reactor. IEEE Trans. Plasma Sci. 2012, 40, 3409–3419. [Google Scholar] [CrossRef]
- Song, Z.Z.; Peng, S.X.; Yu, J.X.; Ming, J.C.; Yuan, Z.Y.; Qian, F.; Guo, Z.Y. Minipermanent magnet high-current microwave ion source. Rev. Sci. Instrum. 2006, 77, 03A305. [Google Scholar] [CrossRef]
- Wei, X.B.; Li, G.P.; Pan, X.D.; Wu, Q.; Liu, Y.G. Proton beam intensity and proton fraction measurement of the 2.45 GHz ECR ion source. J. Instrum. 2020, 15, T04005. [Google Scholar] [CrossRef]
- Liu, Y.G.; Ke, J.L.; Zhao, G.Y.; Lou, B.C.; Hu, Y.H.; Liu, R. Effect of magnetic field distribution on ECR ion source discharge. Nucl. Sci. Tech. 2018, 29, 126. [Google Scholar] [CrossRef]
- Ke, J.L.; Liu, Y.G.; Liu, B.L.; Hu, Y.H.; Liu, M.; Tang, J.; Zheng, P.; Li, Y.; Wu, C.L.; Lou, B.C. Development of a Compact Deuterium–Deuterium Neutron Generator for Prompt Gamma Neutron Activation Analysis. Instrum. Exp. Tech. 2020, 63, 616–620. [Google Scholar] [CrossRef]
- Liu, Y.G.; Liu, J.L.; Wu, Q.; Sun, L.T. Ion beam production with an antenna type 2.45 GHz electron cyclotron resonance ion source. Rev. Sci. Instrum. 2020, 91, 023301. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, S.; Wu, W.; Ma, T.; Zhang, J.; Ren, H.; Li, K.; Zhang, T.; Wen, J.; Xu, Y. A miniaturized ECR plasma flood gun for wafer charge neutralization. Rev. Sci. Instrum. 2020, 91, 033319. [Google Scholar] [CrossRef]



| Index Parameter | Design Indexes |
|---|---|
| Maximum energy | 2.5 MeV |
| Maximum current intensity | 15 mA |
| Minimum current intensity | 10 mA |
| Energy stability | ≤0.5% |
| Beam scanning range | 100 mm × 100 mm |
| Index Parameter | Design Indexes |
|---|---|
| Beam intensity | ≥20 mA |
| Extraction voltage | 40 kV |
| Proton ratio | ≥85% |
| Normalized emittance | ≤0.25 π mm. mrad |
| External contour size | 600 mm(length) × 300 mm(width) × 300 mm(high) |
| Maximum magnetic field | 1100 G |
| Vacuum level | 10−5 Pa–10−3 Pa |
| Microwave frequency | 2.45 GHz |
| Microwave power | 300 W–500 W |
| Organization | Ion Source Type | Ion Species | Extraction Voltage (kV) | Beam (mA) |
|---|---|---|---|---|
| Institute of Plasma Physics, CAS [6] | Penning ion source | H+ | 40 | 0.1 |
| Lawrence Berkeley National Laboratory [7] | High frequency source | H+ | 15.5 | 16 |
| Peking University [8] | ECR source | H+ | 50 | 100 |
| CEA/Saclay [9] | ECR source | H+ | 85 | >100 |
| Organization | Microwave Transmission Mode | Overall Size of the Ion Source System (mm) | Miniaturized Component | Power (W) | Magnetic Field Generation Mode | Extraction Voltage (kV) | Beam (mA) |
|---|---|---|---|---|---|---|---|
| Peking University [10,11] | waveguide + coaxial line | >600 (without coaxial line length) | microwave system + discharge chamber | 180 | permanent magnet ring | 40 | 21.7 |
| antenna + coaxial line | <200 (without coaxial line length) | microwave system + discharge chamber | 200 | permanent magnet ring | 35 | 4.5 | |
| Institute for Theoretical and Experimental Physics(ITEP) [12] | coaxial line | <200 (without coaxial line length) | microwave system + discharge chamber | 100 | permanent magnet ring | 15 | 0.5 |
| CEA/Saclay [13] | waveguide | >1000 mm | extraction system | -- | focus coil | 50 | 48.5 |
| Our work | waveguide | <350 mm | microwave system + discharge chamber | >300 | permanent magnet ring | 40 | >20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.-F.; He, Z.-F.; Zhao, M.-H.; Wan, W.-S.; Liu, H.-L.; Wu, Y.; Lv, W.-Z.; Zhou, D.-Y.; Lu, H.-T. Design of a Miniaturized Electron Cyclotron Resonance Ion Source for High-Voltage Proton Accelerator. Appl. Sci. 2023, 13, 8831. https://doi.org/10.3390/app13158831
Yu H-F, He Z-F, Zhao M-H, Wan W-S, Liu H-L, Wu Y, Lv W-Z, Zhou D-Y, Lu H-T. Design of a Miniaturized Electron Cyclotron Resonance Ion Source for High-Voltage Proton Accelerator. Applied Sciences. 2023; 13(15):8831. https://doi.org/10.3390/app13158831
Chicago/Turabian StyleYu, Hua-Fei, Zi-Feng He, Ming-Hua Zhao, Wei-Shi Wan, Huan-Ling Liu, Yue Wu, Wen-Zhuang Lv, Da-Yong Zhou, and Huan-Ting Lu. 2023. "Design of a Miniaturized Electron Cyclotron Resonance Ion Source for High-Voltage Proton Accelerator" Applied Sciences 13, no. 15: 8831. https://doi.org/10.3390/app13158831
APA StyleYu, H.-F., He, Z.-F., Zhao, M.-H., Wan, W.-S., Liu, H.-L., Wu, Y., Lv, W.-Z., Zhou, D.-Y., & Lu, H.-T. (2023). Design of a Miniaturized Electron Cyclotron Resonance Ion Source for High-Voltage Proton Accelerator. Applied Sciences, 13(15), 8831. https://doi.org/10.3390/app13158831





