Unequal Interval Dynamic Traffic Flow Prediction with Singular Point Detection

Abstract

Analysis of traffic flow signals plays an important role in traffic prediction and management. As an intrinsic property, the singular point of a traffic flow signal labels a new nonsteady status. Therefore, detecting the singular point is an effective approach to determine the moment of traffic flow prediction. In this paper, an improved wavelet transform is proposed to detect singular points of real-time traffic flow signals. The number of detected singular points is output via the heuristic selection of multiple scales. Then, a weighted similarity measurement of historical traffic flow signals is utilized to predict the next singular point. The position of the next singular point decides the duration of prediction adaptively. The detected and predicted singular points are applied to dynamically update the unequal interval prediction of traffic flow. Furthermore, a Vasicek model is used to predict the traffic flow by minimizing the sum of the relative mean standard error (RMSE) between the traffic flow increment in the predicted interval and the sampled increments of previous intervals. A decomposition method is used to solve the unequal matrix problem. Based on the scenario and traffic flow imported from the real-world map, the simulation results show that the proposed algorithm outperforms existing approaches with high prediction accuracy and much lower computing cost.

1. Introduction

Traffic flow predictions have been used widely as metrics in traffic management, e.g., planning routes for commuters, alleviating traffic congestion, and improving traffic operation efficiency [1,2]. Depending on the real-time and historical traffic information [3], many prediction models have been proposed to forecast traffic flow [4], including linear prediction models (autoregression, multivariate adaptive regression splines), neural network models, echo state, support vector machine, adaptive filter, deep learning system, etc. Prediction accuracy depends on the parameter adjustment and model training. However, researchers also pointed out that training models have drawbacks, i.e., scenario limitation and training cost [5]. Analysis of a traffic flow signal is suitable for solving the bottleneck of fixed-interval prediction to capture the dynamics of a traffic flow [4].

The singular point of a time-series signal is an intrinsic property of traffic flow, and it can reflect changes in a continuous process. The singular point of a traffic flow signal labels a nonstationary traffic flow status, which might be caused by a traffic congestion or accident [6]. In wavelet multiresolution analysis, an important decision is to select the decomposition level [7]. Guo et al., proposed a hybrid model that combined the discrete wavelet decomposition and prophet framework [8]. The model decomposed the traffic flow from low frequency to high frequency and then was trained to predict the components. The adjusted components were reconstructed to complete the prediction. Jiang et al., gave a nonparametric dynamic time-delay recurrent wavelet neural network model to predict the traffic flow [9]. The concept of wavelet frame was introduced and exploited in the model to provide flexibility in the design of wavelets and to add extra features. Wavelet denoising and phase space reconstructions improve the prediction model in terms of accuracy [10]. Singular point detection is an effective approach to provide the basis for traffic flow status division, and singular points should be redetected to keep the prediction accuracy. The precision of singular point detection is balanced by the accuracy and computing time of further traffic flow prediction. It is apparent that a wavelet transform is an effective method for multiscale signal analysis, which can detect traffic flow signals’ singular points. However, it is still challenging to decide when the traffic flow prediction should be dynamically updated to balance the prediction accuracy and computing time.

In this paper, we aim at developing a method for efficiently and dynamically updating traffic flow prediction by analyzing the singular points in real-time and historic traffic flow signals. The overall architecture contains three subprocesses, i.e., (1) traffic flow analysis that detects the multiscale singular points via an improved wavelet transform, (2) unequal interval decision considering the accuracy and computing time comprehensively, and (3) traffic flow prediction based on a Vasicek model involving a matrix decomposition method. The work in this paper can realize the accurate and rapid dynamic traffic flow prediction in the road segment scenario, which acquires its continuous historical and real-time traffic flow data. The main contributions of this paper are emphasized as follows:

• The paper gives a framework to use singular point detection to analyze the traffic flow signal. An improved wavelet transform method is proposed to detect singular points dynamically based on the wavelet’s adjustable scale. Based on the position of the singular points, the traffic flow signal is divided into unequal slots in time series, which is determined via the multiscale.
• Depending on the real-time observation and historical traffic data, we propose an algorithm to predict the position of the next singular point in the observed process based on similarity measurement via a weighted function. The forecasting of the next singular point position decides the interval of traffic flow prediction.
• We use the Vasicek model to predict the traffic flow’s trend from the current moment to the predicted next singular point. The matrix decomposition is imported to deal with the unequal size problem during an optimization solution.

The rest of the paper is organized as follows: Section 2 discusses related work about short-term traffic flow predictions. The framework and main process of the traffic flow prediction are proposed in Section 3. Section 4 introduces the singular point detection and prediction methods based on the multiscale wavelet transform. The prediction of the next singular point position with the weighted function is also given. Section 5 proposes an algorithm of unequal interval traffic flow prediction based on the Vasicek model. Performance evaluations are presented in Section 6. Finally, the concluding remarks are drawn in Section 7.

2. Related Work

According to the time interval, traffic flow prediction can be classified into short-term prediction and long-term prediction. Xing et al., pointed out that short-term prediction aims to forecast the traffic trend in the next few seconds to hours based on real-time and historical traffic information [11], while Li et al., mentioned that long-term prediction forecasts a full day or weeks of traffic in the future [12]. This paper mainly focuses on the short-term prediction of traffic flow.

Many researchers designed various prediction models and adjusted parameters to increase performance. Chu et al., proposed a stochastic Lagrangian traffic flow model to capture the transition points in traffic flow [13]. The model used an unscented Kalman filter to update the parameters and real-time information that were probed from the first and last vehicles in the cell. Based on the prediction results, an advanced warning was provided for stop-and-go traffic jams. The model combined traffic prediction and data completion via Graph Laplace to recover missing data and predicted the traffic flow in a large-scale network [14]. Hu et al., used a digital twin-assisted real-time traffic data prediction method to analyze the traffic flow and velocity data to realize a quick response with high accuracy [15]. The duration of real-time data was collected by 5G, and the prediction slot was fixed to 15 min in the experiments. Ali et al., proposed a microscopic model that identifies drivers’ response to increase the reaction and sensitivity of traffic flow prediction [16]. Based on the application of machine learning methods, analysis of historical flight tracks, weather forecasts, and airport operational data was used in multilayer clustering to predict the results. Chen et al., focused on the influences of traffic conditions on decision makers and proposed the traffic-condition-aware ensemble approach by stacking multiple predictions [17]. The model collected spatiotemporal patterns embedded in traffic flow by a convolutional neural network, and the extracted high-level features weighted the values of parameters. The improvements of prediction models achieved high accuracy in traffic flow forecasting. However, the complexity is usually quantified by the number of internal parameters [5]. The system needs to spend time on debugging the parameters in the complex road network. Additionally, the parameters should be updated and trained once the scenario changes.

Due to the computing time and the scenario limitation, the insights and structure of a traffic flow signal can benefit traffic prediction [5]. Some studies have studied the relative algorithms and methods on time-varying or spatial series to analyze the traffic flow signal. Ma et al., performed time series analysis on traffic flow data and performed smoothing and standardization processing to obtain a stable time series as a model input [18]. The first layer of the model learned the input time series, and the further layers learned and were trained to reduce prediction errors. The evaluation increased by 5 min among simulations to test the prediction accuracy. The singular point is the intrinsic property of the time-varying traffic flow signal. As a nonstationary sequence, the singular point marks that the previous steady state is broken by a traffic jam or accident. The methods are used to detect and predict the agnostic points of the signal. Hou et al., proposed a hybrid model to predict a short-term traffic flow combining an autoregressive integrated moving average model (ARIMA) and wavelet neutral network (WNN), which can improve the accuracy of prediction [19]. Long short-term memory (LSTM) with an attention mechanism was used for traffic flow forecasting [20]. The study of a traffic flow’s regular pattern can achieve the robustness of a training dataset. Wang et al., tried to solve the prediction issue via convolutional neural networks (CNN) and LSTM [21]. The spatiotemporal characteristics of traffic flow were input as a regression prediction layer to learn more key data features for improving performance. Wang et al., proposed a method to obtain the spatiotemporal state and spatiotemporal dependency automatically based on a multigraph adversarial neural network, which extracted the spatiotemporal state of the data in real time and broke the constraints of traditional generative adversarial networks (GAN) [22].

Existing short-term traffic flow prediction models are constantly improved, and prediction accuracy is gradually increased. However, there are still some problems seldom discussed in the complex road network in an urban area: (1) There is no effective method or model to detect and analyze intrinsic properties based on the acquired real-time traffic flow information, which can reflect the change of status in the continuous process of traffic flow. (2) The same fixed interval is not suitable for the complex and changeable road network. The repetitive prediction interval should be dynamic and varying to balance between accuracy and computing time based on the analysis of the traffic flow signal. (3) The unequal matrix size problem should be considered during the prediction solution, which is caused by the unequal interval division. This paper mainly aims to solve these issues. Regarding the first issue, this paper selects singular points as the analyzed characteristic of traffic flow. Considering the application in a real traffic road network, the singular point detection and prediction are adaptively filtered based on multiscales. The frequent singular point selection benefits the prediction accuracy, while the sparse singular point selection can save on computing cost. A model with unequal intervals is extracted to balance two metrics, which is involved in a decomposition method during the solution.

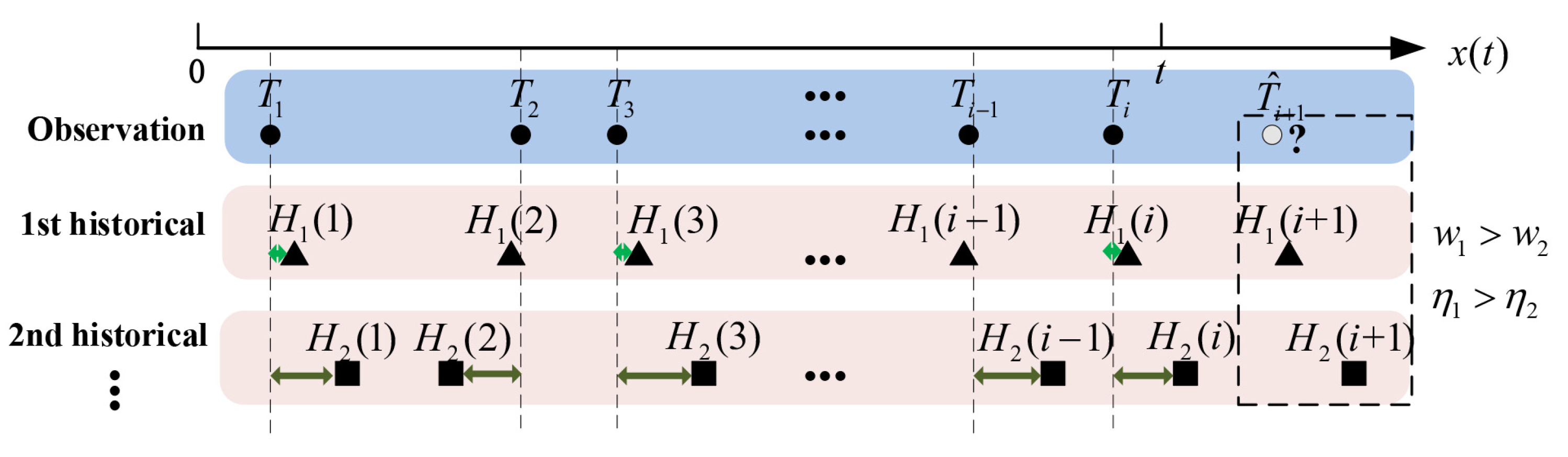
3. System Model

This section presents an overview of a system model, including the framework and process of the proposed dynamic prediction for the system model. Notations in this paper are described in

Table 1. Summary of the main mathematical notations.

Notation	Description
a	scale parameter of wavelet
$x\left(t\right)$	original traffic flow signal
${\phi }_a\left(t\right)$	wavelet signal with scale a
$T_i$	ith singular point’s position in real-time traffic data
$H\left(i\right)$	ith singular point’s position in historical traffic data
$w_k$	weighed parameter of kth historical traffic data
${\epsilon }_k$	relative error of the kth historical traffic data
${\lambda }_k$	antirandom interference factor of the kth historical traffic data
${\eta }_k$	correction factor of the kth historical traffic data
$X_t$	current observation process
$\widetilde{X_t}(i+1)$	traffic flow prediction results from t to $T_{i+1}$
$W_t$	stochastic disturbance in the traffic flow process

.

Figure 1 shows the main framework for the unabridged dynamic unequal interval of a traffic flow prediction process. The entire process involves three categories of data, i.e., observed data, training data, and predicted results. Observed data are the real-time traffic flow data that are acquired via the VANETs based on our previous work, which depends on the vehicle-to-vehicle (V2V) communication [23], vehicle-to-roadside unit (V2R) communication [24], and roadside-unit-to-roadside unit (R2R) information sharing mechanism [25]. Real-time traffic information can be acquired and stored in the roadside unit (RSU). The obtained real-time traffic flow information is a continuous-time process and will be used to predict the traffic flow trend in a later specific duration. The continuous and incomplete real-time traffic flow information is also called observation value in the following discussion [26]. The complete historical traffic data of the same road segment on different days are used to analyze the singular point distribution of the real-time observed traffic flow signal. The system forecasts the next singular point position of the observation traffic flow sequence via the historical data analysis results. Therefore, multigroups of historical data are also called training data in the paper, which are used for predicting the next singular point of the observed traffic flow signal.

The main idea of the proposed prediction framework is to analyze the singular points in a real-time traffic flow signal obtained by a wavelet transform. Singular points can be used to divide the observed traffic flow signal into several unequal slots. Meanwhile, the historical traffic information is used as the training data and processed via the same scale wavelet transform as observed data. Considering the distribution of singular points between the historical data and observed information, the position of the next singular point can be predicted via a similarity measurement with a weighted parameter and correction factor. Then the dynamic intervals of the observed traffic flow signal can be determined, including the analyzed singular points and the predicted next singular point. Finally, the system uses a Vasicek model to predict the traffic flow’s trend from the current moment to the predicted next singular point. According to a comparison between predicted and observed traffic flow results, the system corrects and adjusts the parameters of the model to improve the accuracy. The process is updated and looped.

4. Singular Point Detection and Prediction via Wavelet Transform

In this section, we will discuss how to use a wavelet transform to analyze and detect singular points of a traffic flow signal. The relation between a wavelet scale and the number of detected singular points is also analyzed. The section proposes a weighted similarity measurement to predict the next singular point, which will be used for the latter dynamic unequal interval traffic flow prediction.

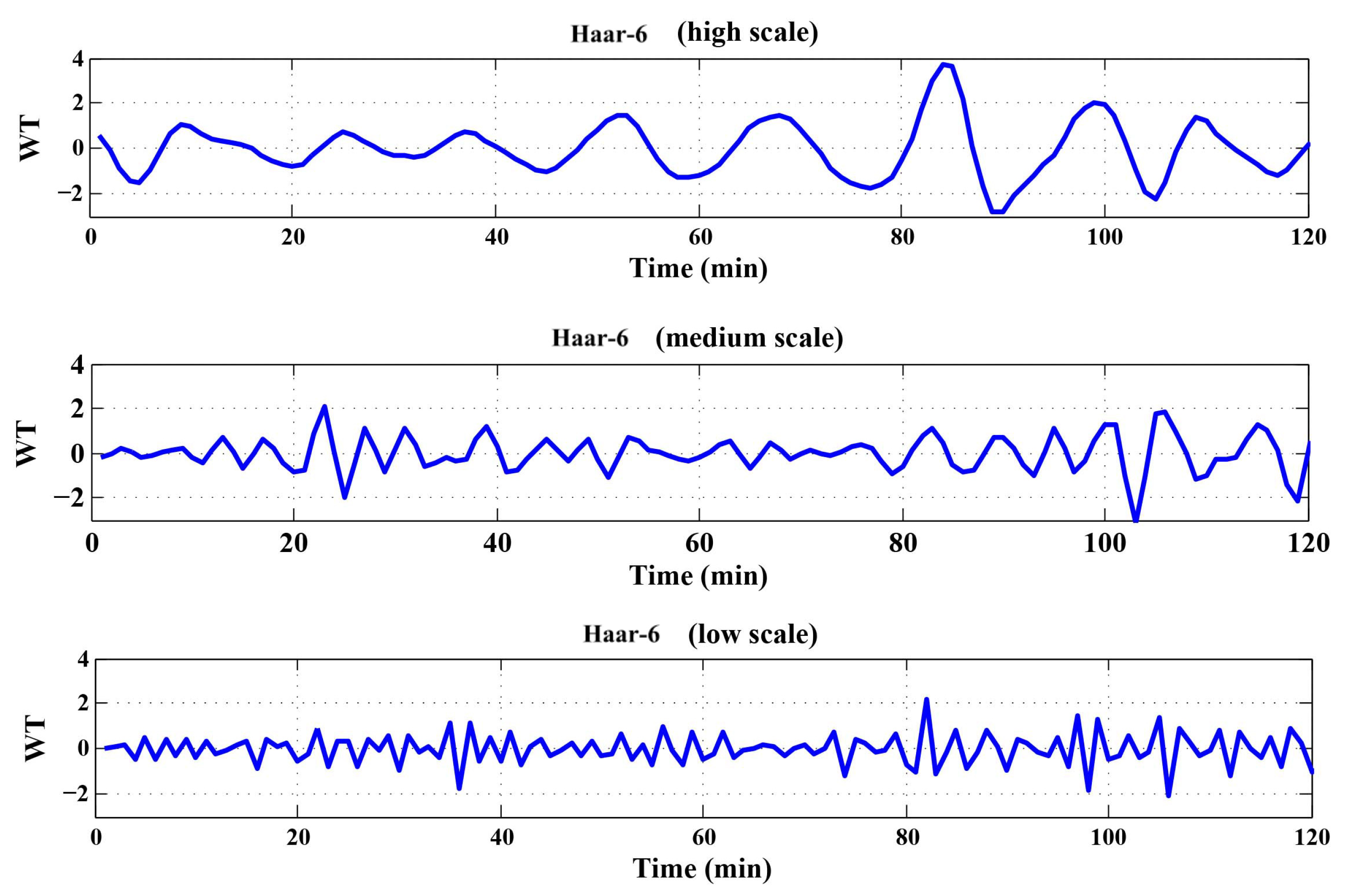
4.1. Singular Point Detection via Multiscale Wavelet Transform

According to the aforementioned discussion, the singular point of a traffic flow timing signal reflects the intrinsic traffic condition. The trend of a traffic flow is relatively stable between two successive singular points, and the parameters within this interval fluctuate via a certain predictable range. Once a singular point appears in the traffic flow signal, it means that a traffic congestion occurs in this road segment due to heavy traffic or a sudden traffic accident, which leads the previous relatively stable status to be broken. The parameters in the new trend and situation need to be predicted again. Therefore, this section mainly discusses how to detect the singular points of a traffic flow timing signal and filtrate the singular points via a multiscale.

A wavelet transform can be used to highlight the local characteristics of a signal in time and frequency [27]. The crossing zero points and extreme points can better describe the details of signals, which play an important role in analyzing the signal’s local character. Therefore, the conversion of the original traffic flow timing signal through a wavelet transform can reflect the comprehensive performance in a multiscale, especially its potential singular points of the traffic flow. Based on the definition of wavelet transform, the original signal can be transformed as

$$\mathrm{W}{\mathrm{F}}_{a}x\left(t\right)=\frac{1}{a}\int x\left(\tau \right)\phi \left(\frac{t-\tau }{a}\right)d\tau =x\left(t\right)\ast {\phi }_a\left(t\right),$$

(1)

where $x\left(t\right)$ is the original signal representing the traffic flow timing signal. The wavelet ${\phi }_a\left(t\right)$ denotes $\frac{1}{a}\phi \left(\frac{t}{a}\right)$. A wavelet transform can be used as the original signal’s output after an impulse response that denotes ${\phi }_a\left(t\right)$. Furthermore, using the wavelet transform to detect a signal’s singular points, the multiscale wavelet ${\phi }_a\left(t\right)$ depends on the low-pass smoothing function $\theta \left(t\right)$, which should satisfy the following two conditions [28]:

• The order of smoothing and derivation of a signal does not influence the wavelet transform performance.
• The first-order derivative and second-order derivative of this low-pass smoothing function $\theta \left(t\right)$ should be a band-pass function, which denotes

  $$\begin{array}{c}\int \theta (t)dt\ne 0,\\ \mathrm{\Theta }(\mathrm{\Omega }=0)\ne 0.\end{array}$$

  (2)

Therefore, when $\theta \left(t\right)$ satisfies the above two conditions,

$${\theta }^{\left(1\right)}\left(t\right)=\frac{d\theta }{dt},{\theta }^{\left(2\right)}\left(t\right)=\frac{d^2\theta }{d{t}^2}$$

(3)

can be the basic wavelets in the transform. Furthermore, based on the scale property of the Fourier transform [29], the scale changes of $\frac{d\theta }{dt}$ and $\frac{d^2\theta }{d{t}^2}$ do not affect the performance, which denotes ${\phi }_a\left(t\right)$ in Equation (1) as

$${\phi }_a\left(t\right)={\theta }_a^{\left(1\right)}\left(t\right)=\frac{1}{a}{\theta }^{\left(1\right)}(\frac{t}{a}),$$

(4)

or

$${\phi }_a^{{}^{\prime }}\left(t\right)={\theta }_a^{\left(2\right)}\left(t\right)=\frac{1}{a}{\theta }^{\left(2\right)}(\frac{t}{a}).$$

(5)

The selection of the wavelet scale parameter a further influences singular point detection [28]. The wavelet with a small scale a detects more singular points but increases the probability of false detection because of the superposition effect. The wavelet with a large scale a detects few and sharp singular points. Parts of singular points are ignored and smoothed as noise of the signal. For instance, the traffic flow on the specific road segment has a sharp increment, which can be detected as a singular point. The algorithm decides whether a reprediction is needed. Based on the selected scale, the algorithm regards this change of traffic flow as a normal disturbance if it relates to a weak singular point. This case will be ignored and released by itself. Conversely, if it is a strong singular point, the algorithm judges that it cannot resume in a short time and will repredict the traffic flow tendency with an unequal interval. It can also transform other characteristics, such as signalized and unsignalized junctions on a road segment, into the singular point implicitly. When the signal operation of the traffic light influences the traffic status strongly, this kind of singular point will not be smoothed, and reprediction is executed.

Respectively, the selection of a wavelet relates to the traffic flow singular point detection as in the following two cases:

Case 1: The maximal  values of  $\mathrm{W}{\mathrm{F}}_{a}x\left(t\right)$ correspond to the singular points. The minimal values of $\mathrm{W}{\mathrm{F}}_{a}x\left(t\right)$ are the fake singular points that are caused by the superposition, when the basic wavelet denotes the first-order derivative ${\theta }_a^{\left(1\right)}\left(t\right)$ of the a specific low-pass smooth function $\theta \left(t\right)$. The singular point $T_i$ satisfies that

$$\begin{array}{c}\mathrm{W}{\mathrm{F}}_a^{{}^{\prime }}x\left(T_i\right)=0,\\ \mathrm{W}{\mathrm{F}}_a^{{}^{\prime \prime }}x\left(T_i\right)<0.\end{array}$$

(6)

Case 2: The zero cross points of $\mathrm{W}{\mathrm{F}}_{a}x\left(t\right)$ need further constraint to select the correct singular points when the basic wavelet denotes the second-order derivative ${\theta }_a^{\left(2\right)}\left(t\right)$ of a specific low-pass smooth function $\theta \left(t\right)$. The singular point $T_i$ satisfies that

$$\begin{array}{c}\mathrm{W}{\mathrm{F}}_{a}x\left(T_i\right)=0,\\ \mathrm{W}{\mathrm{F}}_{a}x(T_i+ϵ)>0,\\ \mathrm{W}{\mathrm{F}}_{a}x(T_i-ϵ)<0.\end{array}$$

(7)

Here, $ϵ$ denotes a tiny positive value.

Based on the multiscale a and Equations (6) and (7), the system detects a sequence of successive singular points of $\mathrm{W}{\mathrm{F}}_{a}x\left(t\right)$ that combines as a set:

$$SPS=\{T_1,T_2,\dots ,T_i\}.$$

(8)

The elements in the set are a moment where the traffic flow has the abrupt abnormal points. Regarding the real-time traffic information as the original signal, the number of all the observed singular points denotes i. The current observation process $X_t$ is divided into a number of intervals, which are presented as unequal and nonuniform intervals. The duration of the kth interval is denoted as

$$\mathrm{\Delta }T{S}_k=T_k-T_{k-1},k\in 1,2,\dots ,i.$$

(9)

Depending on the above equations, the system can detect all the singular points in both the real-time (observation) and historical (training) traffic flow data. Additionally, the continuous process is divided into several dynamic intervals, in which the duration of each interval is not a constant. The number of singular points depends on the wavelet scale, which is determined via iterations of an improved wavelet transform. The multiscale a is decreased during iterations. The stop criterion of multiscale iteration is expressed as $\frac{\partial i}{\partial m}<\xi$. Here, i denotes the number of singular points detected by the multiscale a in the mth iteration. m is smaller than the maximum value of iteration. $\xi$ is the threshold of the interval increment gradient. Based on the improved wavelet transform, the framework achieves the dynamic and adaptive singular point detection.

4.2. Next Singular Point Prediction via Weighted Similarity Measurement

The system predicts the position of the next singular point of the observed process to determine the dynamic traffic flow prediction duration, considering the singular point distribution characters of the observed and historical traffic flow signal.

The traffic flow data have periodic characteristics. In a long-term traffic flow analysis, Fang et al., found that the same characteristics, e.g., weekday/weekends, workday/holiday, and weather, of the same road segment share similar trends of traffic flow [30]. In a short-term traffic flow analysis, the road segments’ traffic flow trend has similarity in peak hours or off-peak period [31]. Therefore, the characteristics of the historical data’s singular points provide a basic similarity measurement of a real-time traffic flow’s next singular point prediction. Unlike using different reprediction intervals based on the characters of the day [30], or dividing the day into the peak/off-peak periods [31], our method divides the observed process based on the singular point position, which presents the specific and unique traffic flow characters of the real-time data.

Since the real-time information (observations) can be used to predict the trend of the traffic flow in the following duration but cannot predict the next traffic flow singular point position itself, the historical traffic data of the same road segment are used to make the next singular point prediction. Through the similarity measurement with weighted parameters, the dynamic unequal interval can be determined and the next singular point position can be predicted.

As shown in Figure 2, there are i detected singular points in the observation before the current time t via our proposed multiscale wavelet transform method. The historical data have a sequence of completed singular points. Due to the analysis of the similarity measurement [32] with the weighted parameters, the next singular point position is predicted based on historical data results. The weight factor $w_k$ and correction factor ${\eta }_k$ quantify the similarity measurement results of different historical data. For instance, the patterns of the first historical data are more similar to the observation’s than the second historical data. Therefore, the values of $w_1$ and ${\eta }_1$ are larger than $w_2$ and ${\eta }_2$, respectively.

The position of the next singular point of the observation process can be predicted via the historical data’s similarity measurement results by

$${\tilde{T}}_{i+1}=\sum _{k=1}^N{w}_k\left[(1+{\eta }_k)H_k(i+1)\right],$$

(10)

where ${\tilde{T}}_{i+1}$ denotes the predicted value of the real-time traffic data’s next singular point. The number of the historical traffic data group is N. $H_k(i+1)$ denotes the position of the $i+1$th singular point of the kthhistorical traffic data. $w_k$ is the weight factor of the kth historical data. It depends on the similarity between the observation value and historical traffic data. The large value of $w_k$ means that the kth historical traffic data’s singular point distribution is similar to the observation. Its next singular point position has more weight factor in determining ${\tilde{T}}_{i+1}$ during prediction, which is presented by

$$w_k=\frac{{\epsilon }_k}{{\displaystyle \sum _{k=1}^N}{\epsilon }_k},$$

(11)

where ${\epsilon }_k$ denotes the relative error between the observation and historical data that presents as

$${\epsilon }_k=\frac{1}{\sum _{j=1}^i[\frac{|T_j-H_k\left(j\right)|}{(T_j+H_k\left(j\right))/2}]-{\lambda }_k}.$$

(12)

Here, the number of the observation’s detected singular point is i. $T_j$ denotes the jth singular point of the observation. $H_k\left(j\right)$ denotes the jth singular point in the kth historical traffic data. Aiming to avoid the measurement error caused by abnormal data, there is an antirandom interference factor, ${\lambda }_k$, to remove the max error of the kth training data, which denotes

$$\begin{array}{c}{\lambda }_k=max\{\frac{|T_j-H_k\left(j\right)|}{(T_j+H_k\left(j\right))/2}\},j=0,1,2,\dots ,i.\end{array}$$

(13)

The factor ${\eta }_k$ in Equation (10) denotes the correction factor between the observation and the kth historical data, which reflects the influence of the singular point distribution. It is represented by

$${\eta }_k=\frac{\gamma [T_j-H\left(i\right)]+(1-\gamma )c_k[T_j-T_{i-1}]}{H_k(i+1)}.$$

(14)

The numerator in the fraction corresponds to the exponential smoothing value of the current time, which reflects the changing trend between the singular point of the observation and historical data. $\gamma$ and $c_k$ construct the exponential smoothing function to represent the difference of the singular points in the prediction model, which can make the predicted result more close to the actual situation.

Algorithm 1 presents the pseudo code of the proposed singular point detection and prediction via a multiscale wavelet transform and weighted similarity measurement (SPDP-wtsm). Lines 1–15 present the process of singular point detection for real-time traffic data via an improved multiscale wavelet transform. As the preparation for the next singular point prediction, the N historical data loop the same process, which is shown as lines 16–22. Lines 23–35 present the prediction for the next singular point via a weighed similarity measurement.

Algorithm 1 Singular point detection and prediction via multiscale wavelet transform and weighted similarity measurement (SPDP-wtsm).

1: /*Singular point detection*/ 2: Input: Observation process x from 0 $\sim t$ 3: Choose suitable wavelet function: $\phi \left(t\right)$ 4: Wavelet initialization: a, m, and $\xi$ 5: $\phi \left(t\right)\leftarrow {\theta }_a^{\left(1\right)}\left(t\right)$ or ${\theta }_a^{\left(2\right)}\left(t\right)$ 6: Do WT-function: $R=X\left(t\right)*\phi \left(t\right)$ 7: Determine zero crossing point: $R=0$ 8: Output: $SPS\left[obs\right]=\{T_1,T_2,\dots ,T_i\}$ 9: if$\frac{\partial i}{\partial m}<\xi$  then 10:    Determine multiscale value: a 11: else 12:    Shrink a 13:    $m++$ 14:    Go to line5 to line8 15: end if 16: /*Historical data preparation*/ 17: Input N historical data: $H_1\left(X\right)$ to $H_N\left(X\right)$ 18: for  $k=1:1:N$  do 19:    $X\leftarrow H_k\left(X\right)$ 20:    Go to line5 to line8 21:    Output: $SPS\left[tra\left(k\right)\right]=\{H^k\left(1\right),H^k\left(2\right),\dots ,H^k\left(i\right)\}$ 22: end for 23: /*Next singular point prediction*/ 24: for  $k=1:1:N$  do 25:    for $j=1:1:i$ do 26:      singular point error: $erro{r}_j^k:$ 27:      $abs:\frac{2\left\{SPS\right[obs\left(j\right)]-SPS[tra\left(k\right)\left(j\right)\left]\right\}}{\left\{SPS\right[obs\left(j\right)]+SPS[tra\left(k\right)\left(j\right)\left]\right\}}$ 28:    end for 29:    ${\lambda }_k=max\left\{error\left[k\right]\right\}$ 30:    Determine the weight of kth historical data: 31:    $w_k=1/sum\left\{error\left[k\right]\right\}-{\lambda }_k$ 32:    Set ${\eta }_k$ as Equation (12) 33:    Do prediction: ${\tilde{T}}_{i+1}=w_k[1+{\eta }_k]H_k(i+1)$ 34: end for 35: Output the predicted next singular point: ${\tilde{T}}_{i+1}$

5. Multiscale Traffic Flow Prediction via Vasicek Model

In this section, we will design the traffic flow prediction based on a Vasicek model. The observed traffic flow signal is divided into a number of unequal intervals according to the detected and predicted singular points. The objective and the algorithm of a dynamic unequal traffic flow prediction are also presented in this section.

5.1. Unequal Interval Dynamic Traffic Flow Prediction Design Based on Vasicek Model

The Vasicek model is a mathematical model used to describe the evolution of interest rates in the financial field [33]. It is a single-factor short-term interest rate model that describes the interest rate change in the case of only one source of market risk. The general model denotes

$$d{r}_t=l(b-r_t)dt+\sigma d{W}_t.$$

(15)

Here, $W_t$ denotes the Wiener process under the risk-neutral framework. $\sigma$ denotes the parameter of a standard deviation, which influences the fluctuation of the interest. b denotes the long-term mean value, which produces a series of orbital values. l presents the return rate, and $r_t$ is the momentary fluctuation that measures the amplitude of random factors in the system at each time point.

Because the short-term prediction of a traffic flow variation trend also has a similar slope fluctuation, Rajabzadeh et al., predicted the short-term traffic flow variation trend by the Vasicek model via a stochastic differential equation [26]. Considering the singular point detection and prediction in Section 4, the model’s elements denote unequal size.

The first term in Equation (15) represents the average trend of the predicted traffic flow, and the second term denotes the random disturbance to the predicted traffic flow. It can be assumed that the trend of the traffic flow in the current interval is relatively stable except for random disturbance. Additionally, the parameters of the differential equation of traffic flow in this interval remain unchanged until the next singular point of the traffic flow occurs. The parameters of the prediction model should be recalculated once the next interval generation is divided via a singular point. Our proposed model can not only consider the accuracy of the traffic flow prediction but also reduce the times of reprediction that saves the computing resource in the system. Further, the prediction is a dynamic unequal interval according to the position of traffic flow singular points. The relationship between time and the traffic flow can be described via the Vasicek model as

$$d{X}_t=({\alpha }_0\left(t\right)+{\alpha }_1\left(t\right)X_t)dt+{\beta }_{0}d{W}_t.$$

(16)

Here, $X_t$ denotes the observed process of the real-time traffic flow. Both ${\alpha }_0\left(t\right)$ and ${\alpha }_1\left(t\right)$ are the parameters that relate to the trend of the traffic flow. The parameters depend on the time and present the traffic flow’s slope and amplitude. $W_t$ denotes a random process that disturbs the traffic flow and ${\beta }_0$ denotes its system factor.

Figure 3 shows the definition and division of the observation process, in which slots are unequal and nonuniform intervals. The dynamic division for the interval depends on the position of the detected and predicted singular points. The observation process is divided into $i+1$ intervals, which are i intervals by detected singular points and the last predicted slot.

The traffic flow in each interval is sampled without loss of authenticity. For the interval $T{S}_k$, $k\in \{1,2,\dots ,i\}$, the length of the sampled traffic flow is $▵t_k$. Additionally, the increment of the traffic flow in $▵t_k$ denotes ${▵}_{k}X$, which is described as

$${▵}_{k}X=({\alpha }_0\left(k\right)+{\alpha }_1\left(k\right)X_k){▵}_{k}t+{\beta }_0\left(k\right){▵}_{k}W.$$

(17)

The last term in Equation (17) is regarded as the random disturbance, and Equation (17) can be described as

$$\frac{{▵}_{k}X}{{▵}_{k}t}=({\alpha }_0\left(k\right)+{\alpha }_1\left(k\right)X_k)+{\zeta }_k.$$

(18)

The increment of the traffic flow in the interval $i+1$ can be attained when the parameters ${\alpha }_0\left(k\right)$ and ${\alpha }_1\left(k\right)$ are determined. Then the system predicts the traffic flow from the current time to the next predicted singular point.

The relative mean standard error (RMSE) between the increment of the traffic flow in the ith interval $\frac{{▵}_{k}X}{{▵}_{k}t}$ and the sampled increments of the observation from the 1st to ith interval is used as the metric of the prediction model. The sum of the RMSE [26] will be minimized based on the weighted linear function to determine the value of the parameters as

$$\underset{{\alpha }_1\left(k\right),{\alpha }_0\left(k\right)}{min}\sum _{j=1}^k{\{\frac{{▵}_{j}X}{{▵}_{j}t}-[{\alpha }_0\left(k\right)+{\alpha }_1\left(k\right)X_j]\}}^2{K}_h(\frac{t_j-t_k}{h}),$$

(19)

where $\frac{{▵}_{j}X}{{▵}_{j}t}$ denotes the predicted value of the traffic flow’s increments in the jth interval. $K_h(\frac{t_j-t_k}{h})$ denotes the weighted linear function, which can be described as

$$K_h\left(t\right)=\left\{\begin{array}{cc}\frac{3}{4h}(1-t^2),\hfill & -1\le t<0\hfill \\ 0,\hfill & t<-1,t\ge 0.\hfill \end{array}\right.$$

(20)

Here, h denotes the bandwidth parameter of the one-sided Epanechnikov.

Based on the algorithm [34], the optimization problem can be solved, and the parameter $\alpha$ can be obtained by

$$\alpha ={\left(X^{T}WX\right)}^{-1}{X}^{T}WY,$$

(21)

where W, Y, $\alpha$, and X can be described as

$$W=diag[K_h(t_1-t_k),K_h(t_2-t_k),\dots ,K_h(t_i-t_k)],$$

(22)

$$Y=[\frac{{▵}_{1}X}{{▵}_{1}t},\frac{{▵}_{2}X}{{▵}_{2}t},\dots ,\frac{{▵}_{i}X}{{▵}_{i}t}],$$

(23)

$$\alpha ={[{\alpha }_0\left(k\right),{\alpha }_1\left(k\right)]}^T,$$

(24)

and

$$X=\left[X_1,X_2,\cdots ,X_i\right].$$

(25)

Based on the determined value of the parameters, the increment of the traffic flow in the ith interval ${▵}_{i}X$ can be obtained. The traffic flow trend before the next predicted singular point can be output.

5.2. Unequal Element Solution via Matrix Decomposition

The prediction model is designed via Equation (18) and sets the RMSE as the metric of prediction objection via Equation (19). However, because the observation is divided into several unequal intervals and the elements in the matrix are unequal, the solution of the parameter $\alpha$ considers the unequal elements. Based on the decomposition model [35], we extend the observation as a matrix, andthe algorithm will deal with the unequal elements by matrix decomposition and composition during the algorithm solution [36]. In the following, we present an approach delivering the efficient solution of offsetting the unequal size elements in $X^{T}WX$.

$X_k$ in the set $\{X_1,\dots ,X_i\}$ is an unequal element, which depends on the dynamic interval division in the above section. $X_k$ can be decomposed further into a smaller subelement, which denotes

$$X_k=[x_1,\dots ,x_p],$$

(26)

in which the length of $X_k$ denotes p, and it relates to the kth interval’s length. Therefore, p is a variable and different for all the divided process from $X_1$ to $X_i$. This relation between the size of the matrix $X_k$ and the length of the kth interval can be described as

$$p\propto \mathrm{\Delta }T{S}_k.$$

(27)

Here, $\mathrm{\Delta }T{S}_k$ is the length of the interval k, which can be obtained by Equation (9). Therefore, all the elements in the matrix X can be decomposed to offset the difference among these unequal intervals. Suppose that $X_1$ to $X_i$ are all decomposed based on Equations (26) and (27), and then the original matrix X can be decomposed along its column as

$$X=[x_1,x_2,\dots ,x_m].$$

(28)

Furthermore, the complexity process can omit parts of a useless calculation and be simplified via a quadratic form. Since $W\in {\left(diag\right)}^{m\times m}$ is a diagonal matrix that has the property of ${\left(W^{\frac{1}{2}}\right)}^T{W}^{\frac{1}{2}}=W$, W is decomposed via $W^{\frac{1}{2}}$ along its row, which presents it as $\mathrm{\Lambda }=W^{\frac{1}{2}}$ and denotes

$$\mathrm{\Lambda }=\left(\begin{array}{c}{\mathrm{\Lambda }}_1\\ {\mathrm{\Lambda }}_2\\ ⋮\\ {\mathrm{\Lambda }}_m\end{array}\right).$$

(29)

Then, the original unequal elements $X^{T}WX$ can be transformed as

$$\begin{array}{cc}\hfill X^{T}WX& =\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}\right){\left(\begin{array}{c}{\mathrm{\Lambda }}_1\\ {\mathrm{\Lambda }}_2\\ ⋮\\ {\mathrm{\Lambda }}_m\end{array}\right)}^T\left(\begin{array}{c}{\mathrm{\Lambda }}_1\\ {\mathrm{\Lambda }}_2\\ ⋮\\ {\mathrm{\Lambda }}_m\end{array}\right){\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}\right)}^T\hfill \\ \hfill & ={\left(\sum _{c=1}^m{x}_c{\mathrm{\Lambda }}_c\right)}^T\left(\sum _{d=1}^m{\mathrm{\Lambda }}_d{x}_d\right)\hfill \\ \hfill & =\sum _{c=1}^m\sum _{d=1}^m{x}_c^T{\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_d{x}_d.\hfill \end{array}$$

(30)

$\mathrm{\Lambda }$ gives an orthogonal decomposition as

$${\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_d=\left\{\begin{array}{cc}0\hfill & c\ne d\hfill \\ {\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_c\hfill & c=d.\hfill \end{array}\right.$$

(31)

Therefore, Equation (30) can be transformed as

$$\begin{array}{cc}\hfill X^{T}WX& =\sum _{c=1}^m\sum _{d=1}^m{x}_c^T{\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_d{x}_d\hfill \\ \hfill & =\sum _{c=1}^m{x}_c^T{\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_c{x}_c.\hfill \end{array}$$

(32)

Therefore, the unequal size element of $X^{T}WX$ can be transformed and output the optimization solution based on Equation (32). Accordingly, since Y denotes the discrete integral that is sampled from X and has the same size as X, the other term $X^{T}WY$ of Equation (24) can be obtained in the same method that is denoted as

$$\begin{array}{cc}\hfill X^{T}WY& =\sum _{c=1}^m\sum _{d=1}^m{x}_c^T{\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_d{y}_d\hfill \\ \hfill & =\sum _{c=1}^m{x}_c^T{\mathrm{\Lambda }}_c^T{\mathrm{\Lambda }}_c{y}_c.\hfill \end{array}$$

(33)

After the decomposition and transformation steps, the solutions of $\alpha$, X, W, and Y are presented via $[x_1,\dots ,x_m]$ and $\mathrm{\Lambda }$. Correspondingly, the unequal size element $X_k$ can be obtained via the inverse operation of Equation (26) to locate the position in the dynamic interval. Therefore, the result of ${\left(X^{T}WX\right)}^{-1}$ can be obtained via Equation (32), and the result of $X^{T}WY$ can be obtained via Equation (33). Then the parameter $\alpha$ is calculated via Equation (24). The increment of the traffic flow ${▵}_{i}X$ is presented as Equation (17), which decides the traffic flow prediction result before the next singular point as

$${\tilde{X}}_{i+1}=X_i+{▵}_{i}X.$$

(34)

Algorithm 2 presents the pseudo code of the proposed dynamic unequal interval traffic flow prediction via the Vasicek model (DTFP-vm). Lines 1–5 present the initialization for the traffic data and the optimization. Lines 6–13 are the process of dynamic interval division based on the singular points. The optimal result for the Vasicek model is calculated via mixed-integer linear programming (MILP) in lines 14–24. Lines 25–37 present the results for the different requested time.

Algorithm 2 Dynamic unequal interval traffic flow prediction via the Vasicek model (DTFP-vm).

1: /*Initialization*/ 2: Input: Observation process: X, Current moment: t, 3: Input: Singular Points set: $\{T_1,T_2,\dots ,T_i\}$ 4: Input: The predicted next singular point: ${\tilde{T}}_{i+1}$ 5: error threshold: $ϵ$; iteration threshold: $i{n}_{max}$ 6: /*Dynamic intervals division*/ 7: for  $k=1:1:i$  do 8:    Divide $X_k$ from $T_{k-1}$ to $T_k$ 9:    Calculate the duration of interval: $T{S}_k=T_k-T_{k-1}$ 10:    Determine the sampled duration: ${▵}_{k}t$ 11:    Add kth observed value into matrix X: $X\bigcup \left\{X_k\right\}$ 12: end for 13: Set up X, Y, $\alpha$, and W 14: /*Traffic flow prediction via Vasicek model*/ 15: Set up optimization objective as Equation (19) 16: while  $in\le i{n}_{max}$  do 17:    Do MILP to solve the Equation (19) 18:    Attain W as Equation (22); Y as Equation (23), $\alpha$ as Equation (24), and X as Equation (25) 19:    if $|p-p^{*}|\ge ϵ$ then 20:      adjust $\alpha$ 21:      $in++$ 22:    end if 23: end while 24: Output W, Y, X, and $\alpha$ 25: Set up traffic flow via Vasicek model as Equation (16) 26: Input the time for prediction: $t^{\prime }$ 27: if  $t^{\prime }\le t$  then 28:    Output the observation value of $X_{t^{\prime }}$ 29: else 30:    if $t^{\prime }>{\tilde{T}}_{i+1}$ then 31:      Waiting for the next singular point via Algorithm 1 32:    end if 33: else 34:    Attain the increment ${▵}_{t^{\prime }}X$ via Equation (18) 35:    $X_{t^{\prime }}=X_t+{▵}_{t^{\prime }}X$ 36: end if 37: Respond the traffic flow results to the request

6. Performance Evaluations

The performance of our proposed method is discussed in this section. The evaluation aims to answer the following questions:

• Is the proposed algorithm effective and accurate for detecting and predicting the traffic flow’s singular points?
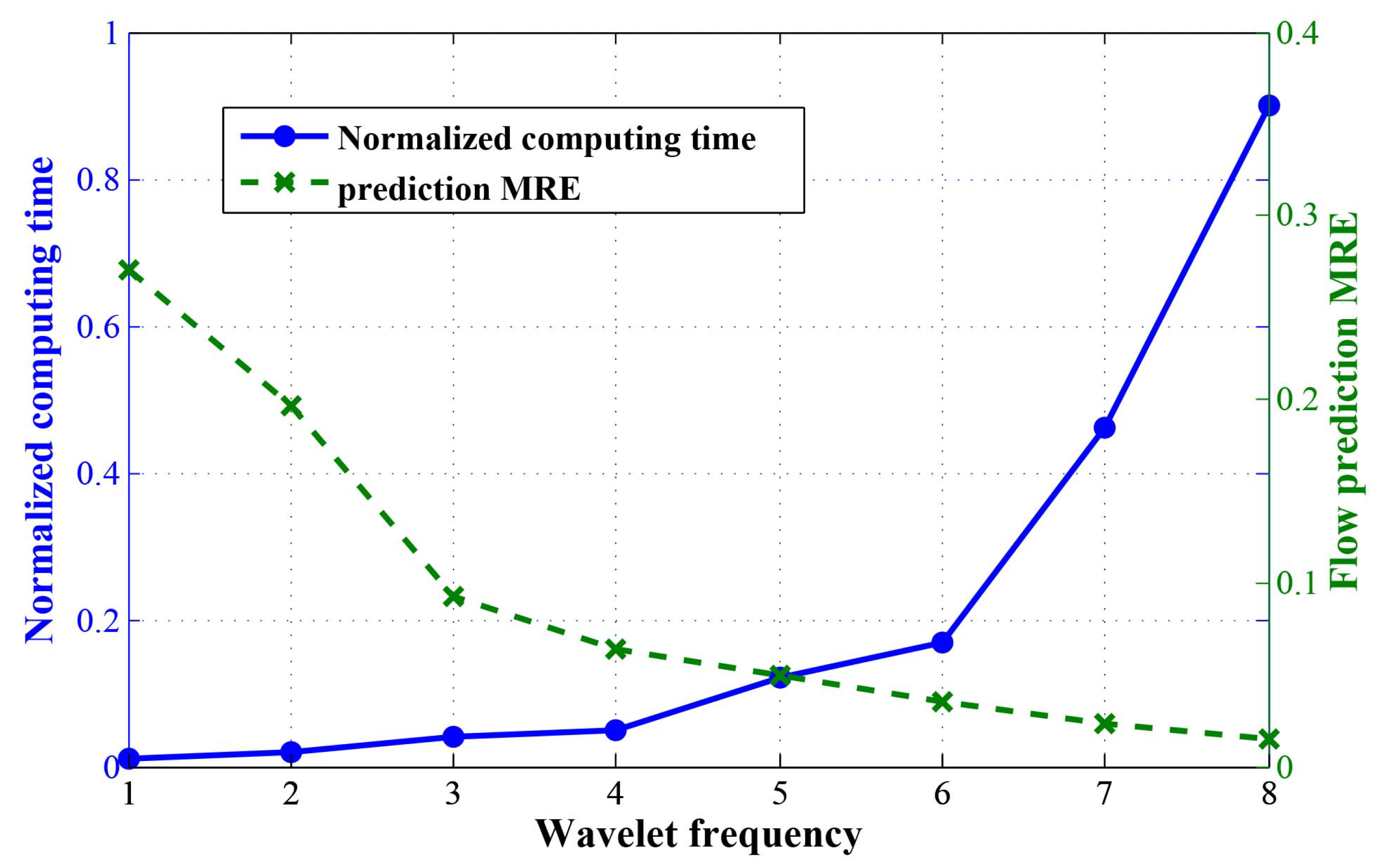
• How does the wavelet adaptive parameter a influence the traffic flow prediction performance?
• Is the proposed algorithm better than other traffic flow prediction methods?

6.1. Simulation Setup

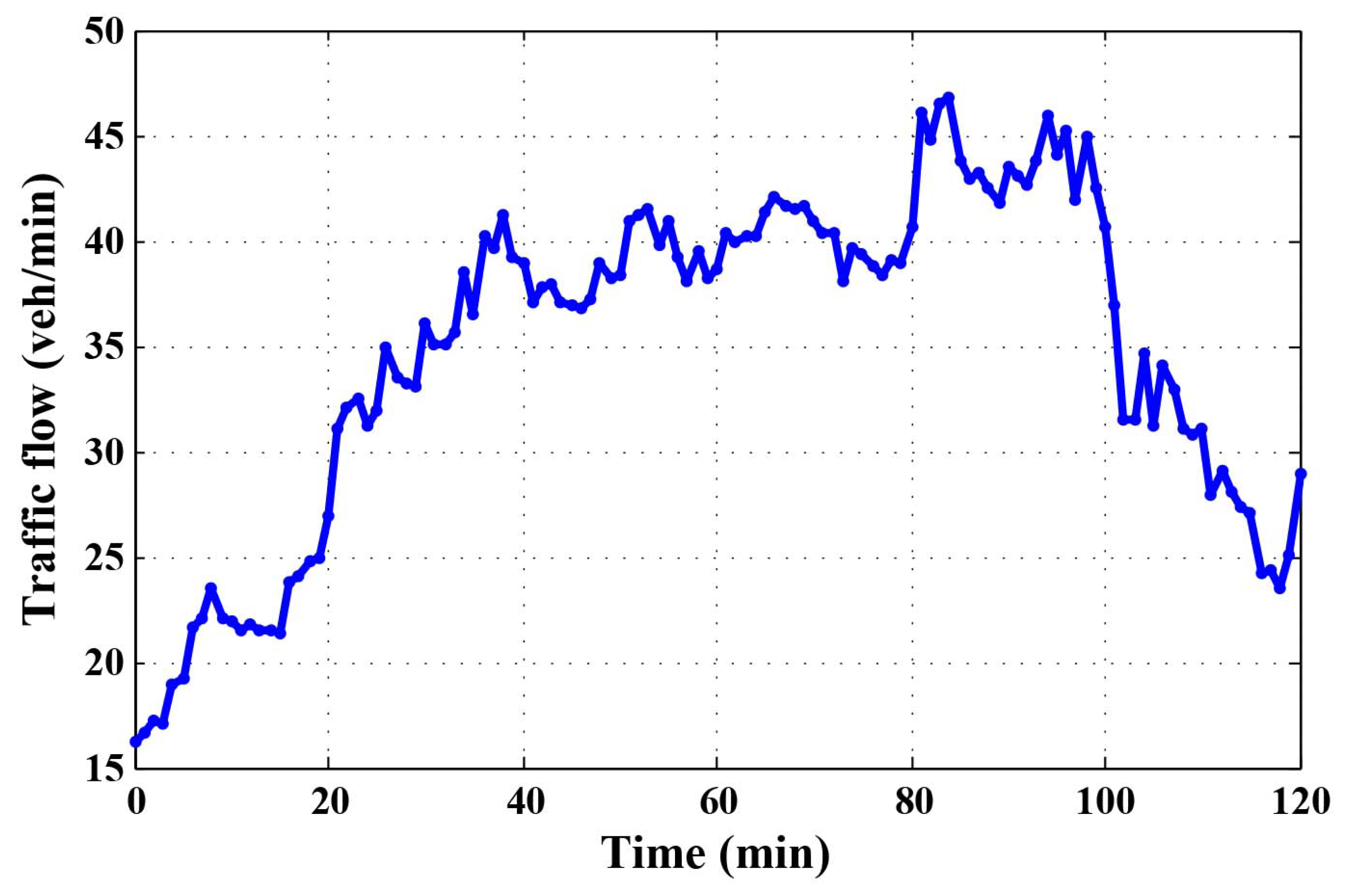
6.1.1. Simulation Scenario

We conduct the evaluation using Matlab, which runs on a Windows 10 computer with Core i7 and 8 GB memory. Especially, as shown in Figure 4, the traffic data used in the evaluation are realistic data collected in Yan’an Elevated Road, Shanghai, China [37]. The raw data are recorded every second, and the simulation uses the average traffic flow every minute. The traffic data in 2 h, i.e., 15:10–17:10, are used as the real-time observation data. The original datasets contain five characteristics, i.e., the interdistance between vehicles, the recorded vehicular speed, the ID of the lane, the traffic flow data, and the traffic density. We mainly used the fourth characteristic to execute our evaluations. The traffic flow data in the same period and the same road segment but on different dates are chosen as the historical (training) data, which have five groups of data provided via a database. Because our proposed algorithm repredicts the traffic flow based on the singular points’ amount and position, the prediction’s time interval is not fixed. Comparing algorithms’ time interval defaults as 12 min, which can attain 10 traffic flow repredictions during the whole process. The details of the traffic data are shown in

Table 2. Summary of the simulation parameters.

Simulation Parameter	Value
default vehicular lane in road segment	1
duration of the observation/prediction	120 min
interval of average traffic flow calculation	1 min
comparing methods’ default prediction time interval	12 min
maximum volume of wavelet scales	8
number of training data	5
level of Fourier series	8

. This table also contains a few other key parameters of the following simulation.

6.1.2. Metrics

The metrics used to evaluate the performance of the proposed algorithms and compare the methods are as follows:

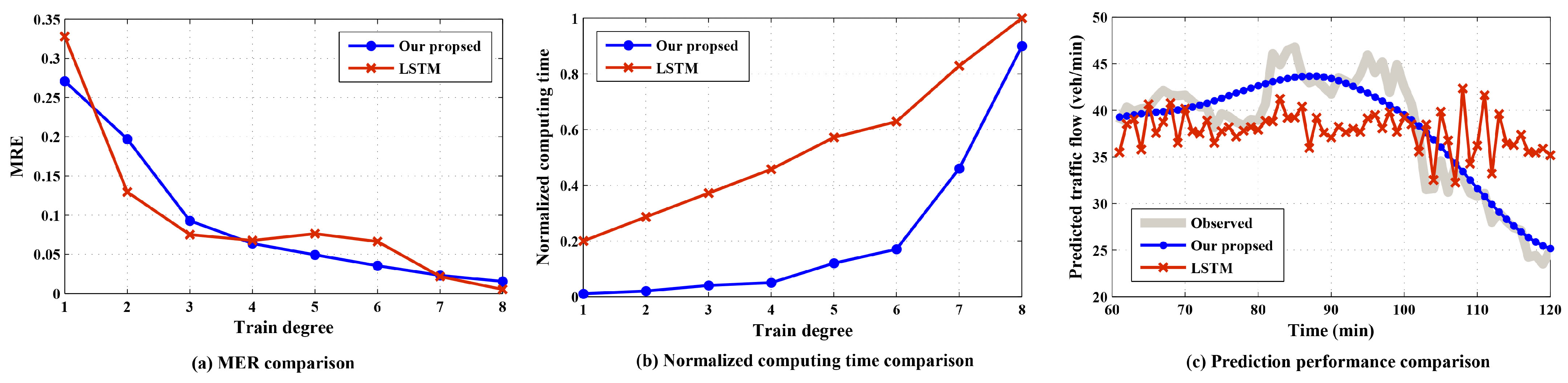
• Mean relative error (MRE): The ratio of absolute difference and observed value, in which absolute difference is between the predicted value and the corresponding observed value. MRE evaluates the accuracy of the traffic flow singular point detection and prediction.
• Normalized computing time: This metric is used to evaluate the algorithms’ computation cost. To balance the magnitudes of different algorithms, we normalize the computing time that can reflect the computation cost and computing increment directly.
• Sum of squares error (SSE) and coefficient of determination (R-square): The lower the SSE is, the closer are the predicted traffic flow and the observed value. The performance is better when the value of R-square closes to 1. These two metrics reflect the prediction robustness during the different processes.

6.1.3. Comparing Algorithms

Based on the aforementioned review and discussion, we select four comparing methods depending on related works to evaluate their performance:

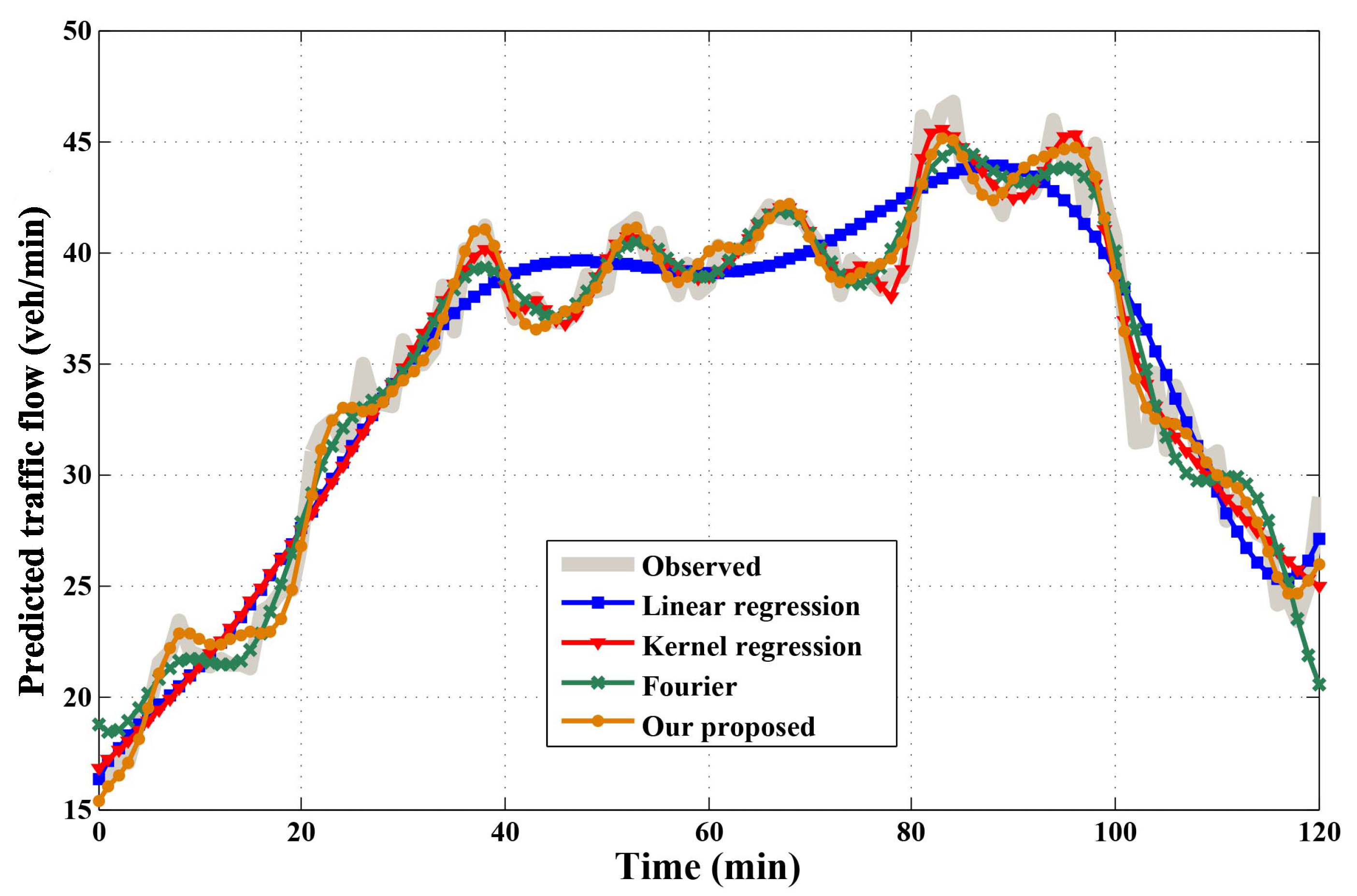
• Linear regression: Based on the confidence interval ($CI=\pm 10\%$), linear regression analyzes the distribution of the observed data in each time interval and uses the linear relation to express and smooth the curve, which predicts the traffic flow’s trend. The algorithm will shorten the time interval once the prediction leaks the $CI$ area.
• Kernel regression: Depending on the core of the support vector machine, kernel regression lies at the Gaussian process to label the observed and historical data. The Laplacian matrix is used for predicting and recovering the results.
• Fourier series: The intervals and prediction intervals of the observation process are divided evenly. The traffic flow trend in the observation process is fixed and predicted based on the Fourier series’ parameter determination. The Fourier method improves the prediction performance via the increment of the Fourier series degree and the adjustment of parameters.
• LSTM (long short-term memory): Besides the above three comparing algorithms, LSTM sets up a single-input-and-single-output recurrent neural network with 96 neural cells. During the training ratio determination and 250 iterations, LSTM can output the predicted results. Because the selected LSTM model needs some extent of observations as the training data, comparison with our proposed algorithm is separated.

6.2. Performance Evaluation of Singular Point Detection and Prediction by Multiscale Wavelet Transform

Figure 5 shows the traffic flow in 2 h of the observation that is preprocessed via average calculation per minute. Figure 6 shows the wavelet transform results of the observation of Figure 5 based on the Haar wavelet, which contains three different scales a of the selected wavelet. Figure 6 provides the different singular point detection results in different wavelet scales.

As shown in Figure 6, the positions of the max extreme points of the results are the traffic flow singular points because the system uses the first deviation of the low-pass function as the wavelet. The bottom subfigure detects the most singular points with the smallest scale. Additionally, the top of the subfigure detects the fewest singular points as its wavelet scale is the largest. Parts of the singular points are regarded as tiny noises and ignored. The numbers of singular points in three different wavelet scales are 18, 32, and 65. Moreover, all the singular points detected via a larger wavelet scale are included in the detected singular point set of a smaller wavelet scale. Therefore, it validated that our proposed algorithm can detect the traffic flow signal’s singular points adaptively by the scale a, and the intervals can be divided into different amounts and lengths.

Since the detected singular points divide the process into unequal intervals, Figure 7 shows the results of the the next singular point prediction MRE in different types of wavelets. Haar-1 and Haar-6 share the same envelope of a continuous signal but the different sampled intervals of the discrete signal. The sampled interval of Haar-1 is larger than Haar-6’s. It can be observed that both the Haar and Daubechies wavelets can predict the next singular point accurately and efficiently when the number of input-detected singular points is enough. The average MRE of the next singular point prediction is less than 20.0%. Additionally, in all wavelets, the MRE approaches stability when the number of input-detected singular points increases. This is because the smaller sampled interval leads to a better low-pass property of the wavelet. In the same type, the wavelet that has a smaller sampled interval outperforms the one with larger intervals. The next singular point prediction MRE of Daubechies-6 reduces by 83.6% compared with the MRE of Daubechies-1. Further, comparing Haar-1 and Haar-6 increases the accuracy of the next singular point prediction by 22.6%. The performance for the next singular point prediction by using a Haar wavelet is better than a Daubechies’s. Specifically for the 10th singular point prediction, the MRE of Haar is decreased, respectively, by 98.8% and 76.5% compared with Daubechies in the same sampled interval. It is because the low-pass performance of Haar’s first derivative is better than Daubechies’s. Especially, parts of the predicted singular points MRE increase, for instance, the 6th and 10th singular point predictions. It is caused by a traffic accident that never occurs in the training data. Therefore, the MRE is less than 15.0%, and increasing the number of training data can improve the performance.

Overall, the evaluations verify that the proposed multiscale wavelet transform can detect and predict the singular points of the traffic flow signal accurately and efficiently. In the next subsection, the comprehensive traffic flow prediction of our proposed algorithm will be discussed.

6.3. Performance Evaluation of Dynamic Traffic Flow Prediction via Unequal Interval Vasicek Approach

According to the aforementioned process, a series of detected and predicted singular points divide the process into finite unequal intervals, which are used for dynamic traffic flow prediction via our proposed algorithm. The number of unequal intervals is decided by the value of the wavelet scale. Figure 8 shows the traffic flow prediction performance in different numbers of unequal intervals. Based on the performances shown in Figure 7, we select the Haar-6 wavelet and evaluate eight different wavelet scales. The Vasicek model predicts the traffic flow trend with the biggest scale, which has the worst performance in traffic flow prediction. When the wavelet scale reduces, the number of detected singular points and the number of reprediction intervals increase, and the prediction results of the traffic flow become close to the real-time observation data. The smallest three wavelet scales divide the process into 17, 46, and 90 unequal dynamic intervals, respectively. Additionally, their traffic flow prediction results are limited to the realistic observation value. The remaining five bigger wavelet scales miss sorts of important singular points, and their traffic flow prediction cannot reflect the realistic signal trend.

The cost of a prediction performance improvement is caused by the wavelet scale decrement and the number of intervals’ increment, which reflects on the computing time of the prediction algorithm. Therefore, Figure 8 shows the relation between the MRE and the normalized computing time of the traffic flow prediction in different wavelet frequencies. Wavelet frequency is inversely proportional to wavelet scale, which means that the highest wavelet frequency corresponds to the smallest wavelet scale that can detect the most singular points. When wavelet frequency increases, the intervals for repredictions are increased, respectively, which can reflect the traffic condition in more detail and the MRE of prediction reduces from 27.1% at the beginning to 1.5%.

Accordingly, with the increment of intervals for reprediction, the normalized computing time increases from 0.01 to 0.90. Furthermore, since the wavelet frequency increases to 5, the speed of computing time rises rapidly. It is observed that the MRE of prediction reduces, but the computing time increases with the increment of the number of repredictions. The reason is that the recalculation of the Vasicek model rises once the unequal intervals increase. When the wavelet frequency is chosen as 5 or 6, the MRE of traffic flow prediction is less than 5.0%, and the computation time is relatively lower, shown as 0.12 and 0.17, which realizes a comprehensive traffic flow prediction performance and the trade-off between accuracy and computing time.

6.4. Traffic Flow Prediction Performance Comparison

Figure 9 shows the traffic flow prediction performances of our proposed algorithm and the other three comparing methods. Compared with the realistic real-time observation data, the ranking in terms of prediction performance is our proposed algorithm, kernel regression, Fourier method, and linear regression. The prediction accuracy of our proposed algorithm increases by 21.3%, 29.1%, and 83.4% respectively. The reason for the prediction performance improvement is that the unequal interval division via singular points can reflect the hidden traffic condition variations of the flow signal. Moreover, the Wiener process in the Vasicek model expresses the heuristic fluctuation of the traffic flow signal.The details of the traffic flow prediction performances of our proposed algorithm and the comparing methods are shown in

Table 3. Details of prediction performance comparisons in four methods.

	Our Proposed	Linear Regression	Kernel Regression	Fourier
unequal interval?	Y	N	N	N
reprediction times	46	90	10	10
multiscale?	Y	N	N	N
degree	7	-	-	8
MRE	0.841	1.543	1.021	1.087
SSE	137.009	432.321	216.668	283.275
RMSE	1.064	1.890	1.338	1.530
normalized computing time	0.256	0.500	1.000	0.500

.

As shown in Table 3, only our proposed algorithm predicts the traffic flow within dynamic unequal intervals. Linear regression adjusts the prediction interval to guarantee the confidence interval. However, it can predict the main trend of the traffic flow but cannot be a detailed expression, in which the SSE of the linear regression in limited to 3.15 times of our proposed algorithm’s performance. Kernel regression uses KNN (k-nearest neighbor) to train the parameter, which presents the best MRE in three comparing algorithms. It might outperform our proposed algorithm when it increases the number of iterations. However, the increment of training costs more computing time. Our proposed algorithm’s computing time is reduced by 74.4%. To obtain a better performance, we used an 8-degree Fourier model. The gap between our proposed algorithm and Fourier remains 22.4% because Fourier cannot detect the abnormal points of a traffic flow signal.

Furthermore, as LSTM needs parts of an observation as the input training data, the prediction performance comparison between our proposed algorithm and LSTM is separated as Figure 10. Train degree relates to the input training ratio of the observation, which means that the higher the train degree is, the more observation is used as training data. To be consistent with LSTM, our proposed algorithm selects eight different wavelet scales. Figure 10a shows an MRE comparison between the two algorithms. The MRE of both algorithms is limited to decrement and stability when it increases the training degree and wavelet frequency. The average MREs of both algorithms are similar, which are 0.093 and 0.096, respectively. However, the trend of MRE decrement of our proposed algorithm outperforms LSTM. LSTM has a tiny increment in the 5th and 6th degrees because of the limitation of iterations. Our proposed algorithm can maintain a stable trend via the determination of singular points. Figure 10b shows a normalized computing time comparison between the two algorithms. Because of the omission of repeat and iteration, our proposed algorithm saves 59.2% computing time compared with LSTM. Moreover, our proposed algorithm’s increase in computing time is also better than LSTM. The growth of computing time becomes sharp when the wavelet scale frequency rises relatively. Figure 10c shows the traffic prediction performance between two algorithms. The train degree of LSTM selects 4, which means that a half observation is used for training and predicts the remaining process. In the meanwhile, the wavelet frequency denotes 4, which contains 12 unequal intervals. Figure 10c shows that LSTM outperforms our proposed algorithm in the first half prediction process. Because the details can be better expressed after 250 iterations. However, our proposed algorithm is improved in the latter process. It is because the predicted singular points guide the adjustment of previous parameters, which cannot be changed once the training LSTM is finished.

7. Conclusions

As information and communication technologies advance signal processing, it becomes crucial to utilize real-time and historical traffic information for predicting traffic flow while balancing prediction accuracy and computing time. In this paper, we analyzed the relationship between singular points and the intrinsic properties of traffic flow. By identifying the location of singular points, we divided the continuous traffic flow process into different stable statuses for traffic prediction. Our proposed method employed an improved multiscale wavelet transform to detect and predict singular points for both real-time and historical data. We then utilized the Vasicek model with unequal time slots to meet the accuracy requirements. Furthermore, the proposed method dynamically adjusted the reprediction interval using the multiscale wavelet, achieving a balance between prediction accuracy and computing time. The reprediction interval was determined based on the traffic condition and its intrinsic property, rather than relying on a fixed prediction interval set by the management system. The simulation results demonstrated the effectiveness of the proposed method. Compared with four related algorithms, our method achieved a significant reduction in computing time with only a marginal sacrifice in prediction accuracy. Moreover, the majority of singular points were successfully detected. The proposed method considered the prediction accuracy and computing cost comprehensively on the rapid dynamic traffic flow status, which had the application prospect in the realistic transportation scenario. However, the present work has limitations: (1) the spatial relation among jointed road segments is seldom discussed, and (2) the impact factor only considered the singular point. In future works, we aim to extend our approach from a single road segment to the entire road network and explore a multiscale spatial division and consider more impact factors for the prediction performance, i.e., the signalized and unsignalized junctions on a road segment.