Lightweight Design and Evaluation of Square Reflector
Abstract
:1. Introduction
2. Square Reflector Lightweight Design
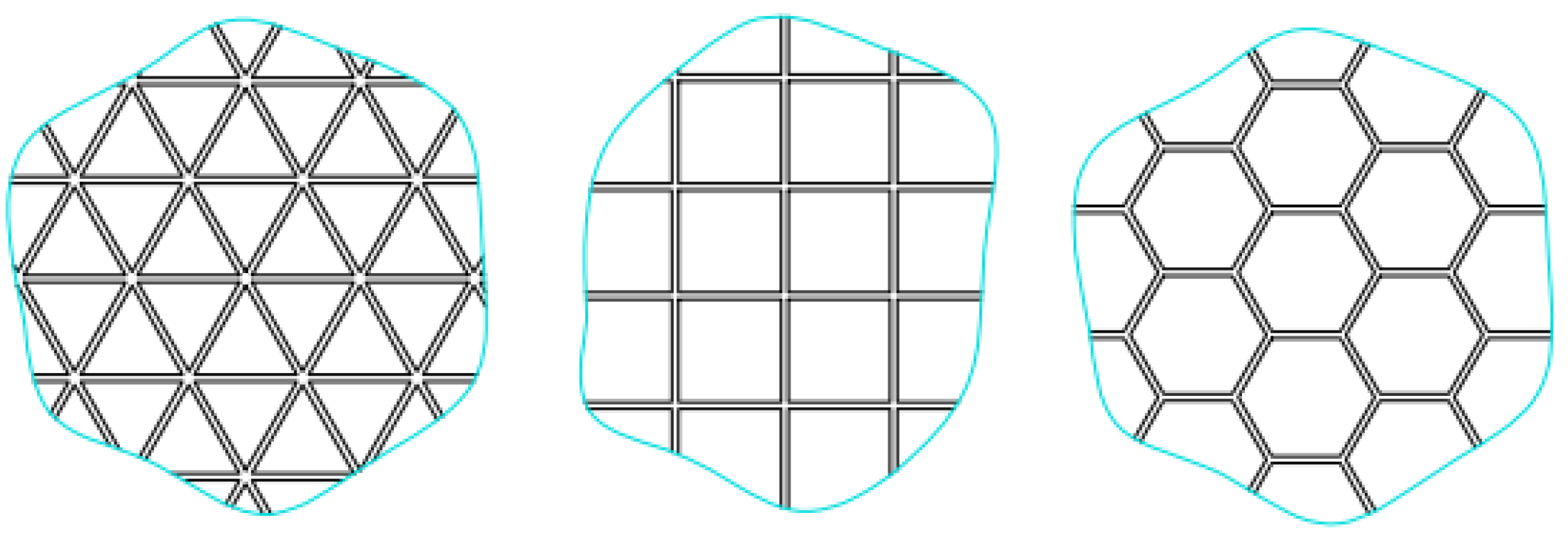
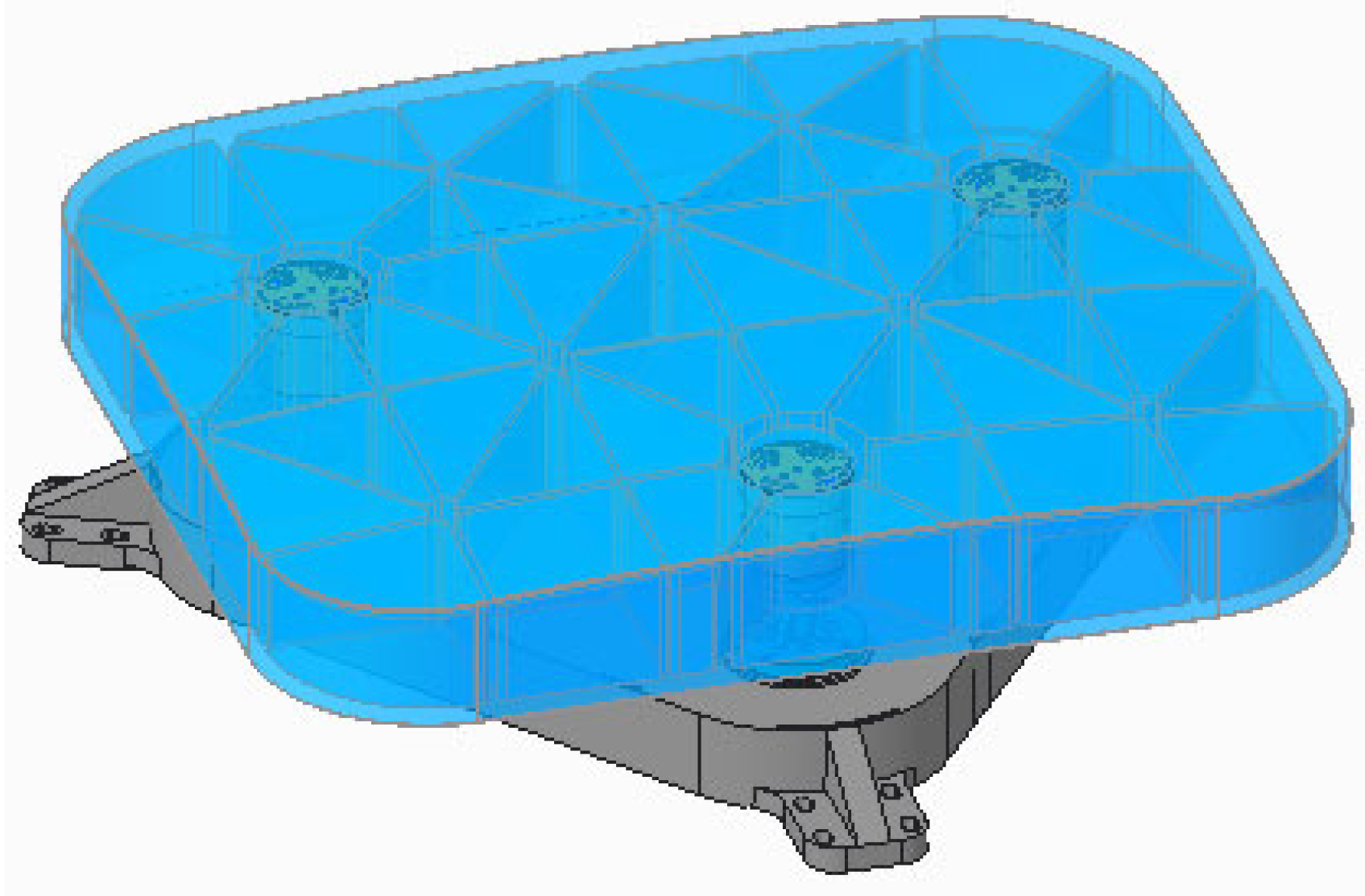
2.1. Mirrorr Structure Design
2.2. Mirror Thickness Design
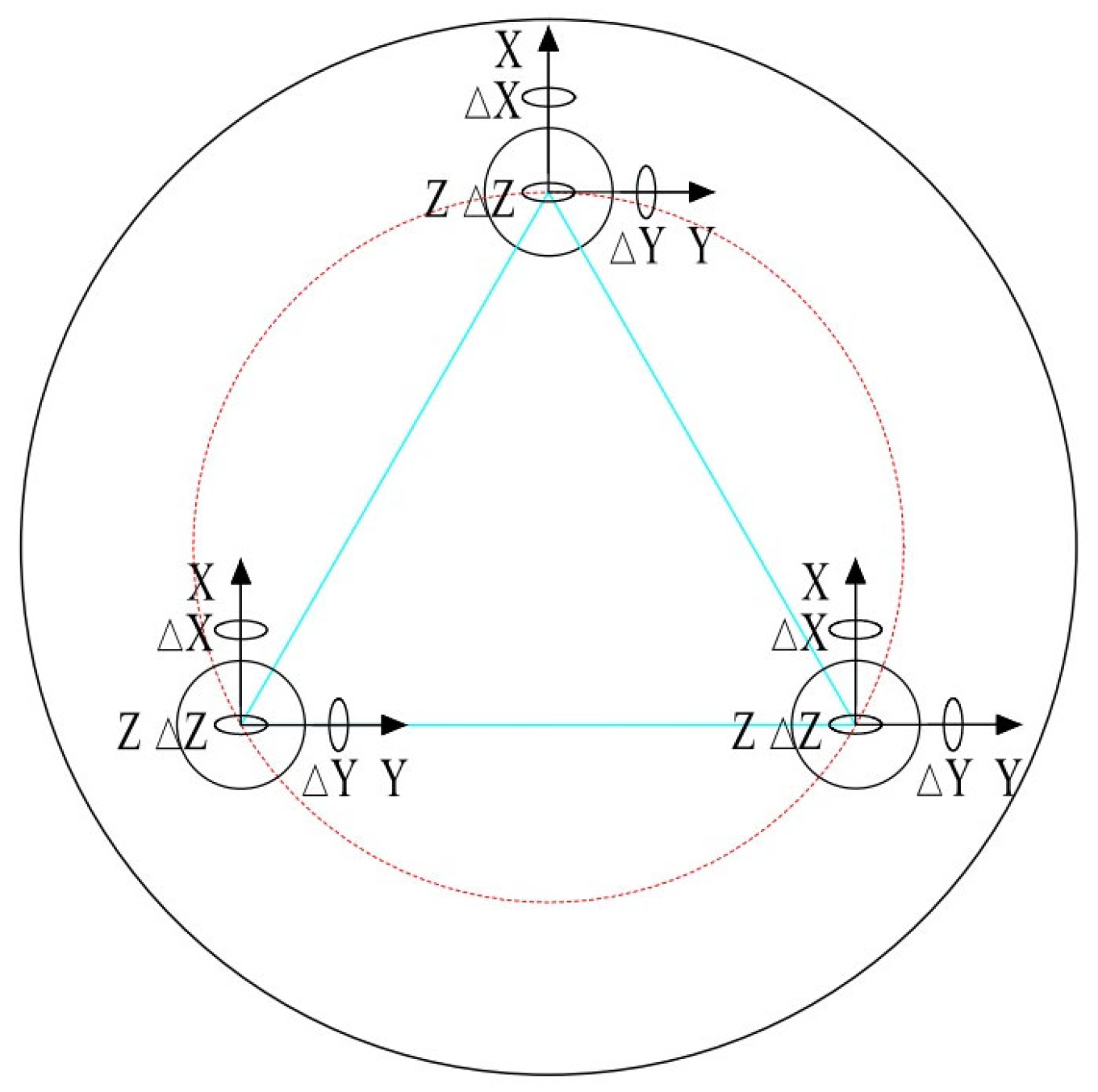
2.3. Design of Mirror Support Point Position
2.4. Design of Mirror Support Point Position
- (1)
- Simulation of Sandwich Structures
- (2)
- Stress simulation of mirrors
- (3)
- Rib optimization design
3. Analysis and Evaluation of Simulation Results
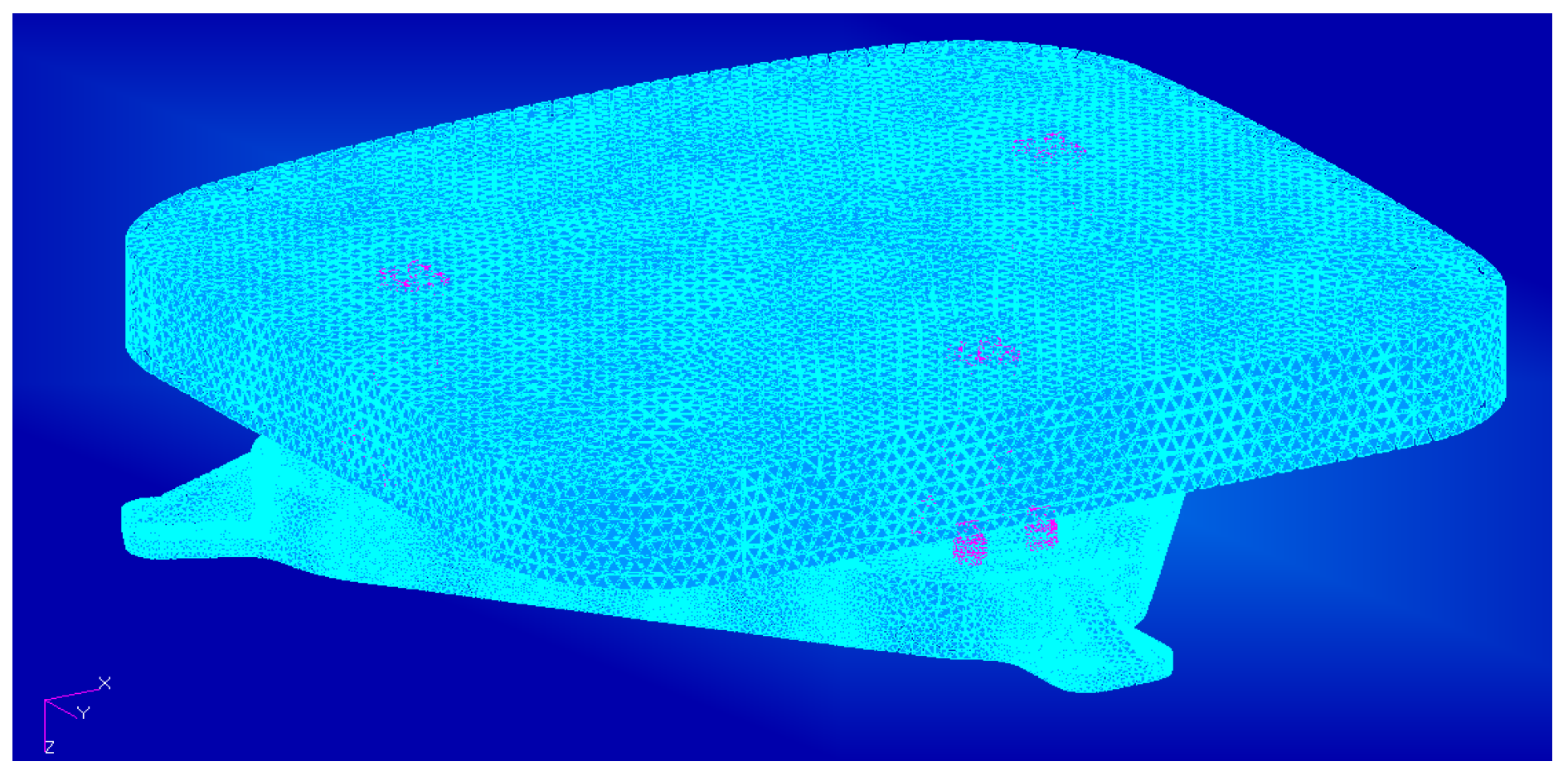
3.1. Firmness Tests and Analysis
3.2. Static Analysis
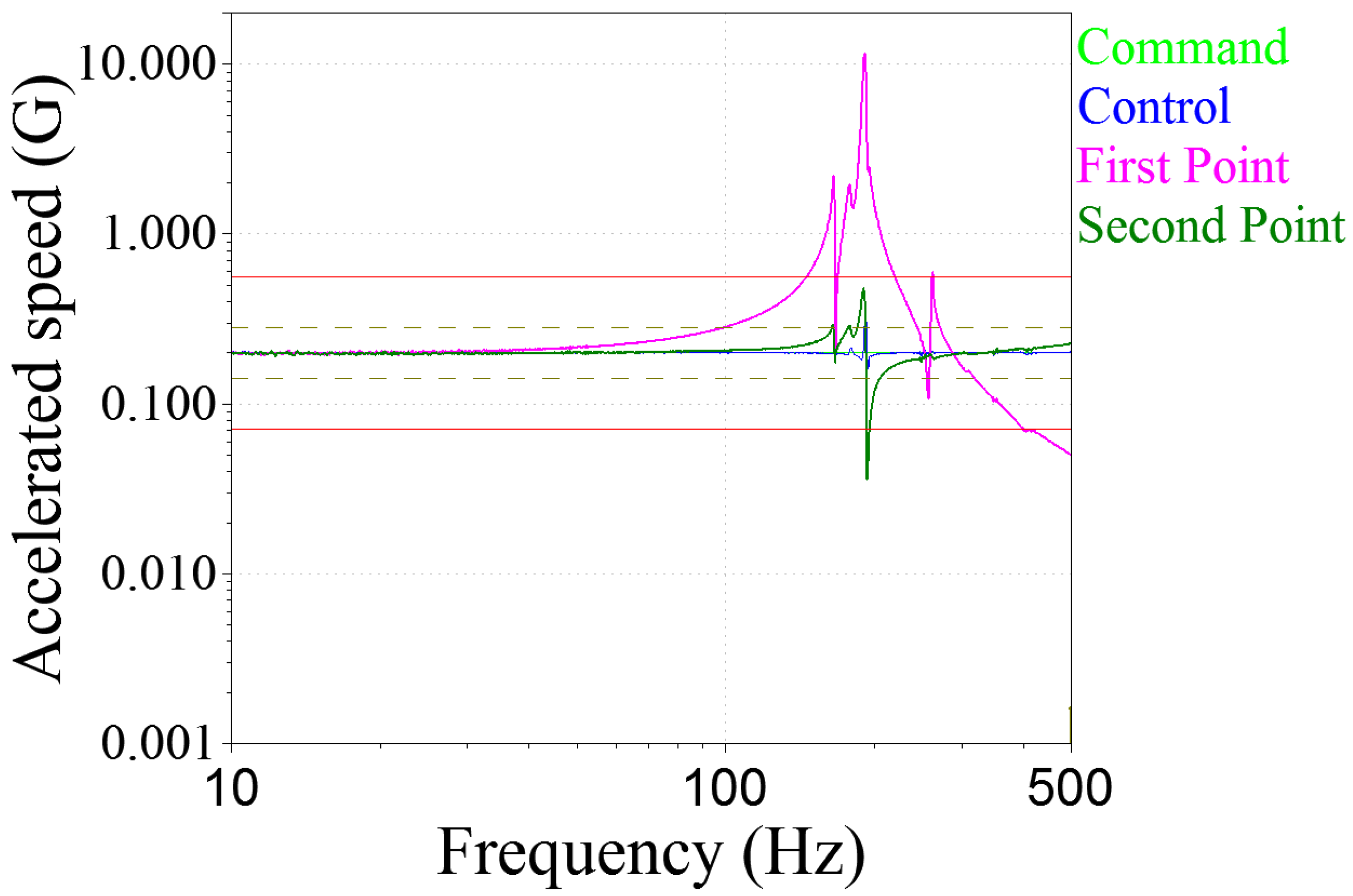
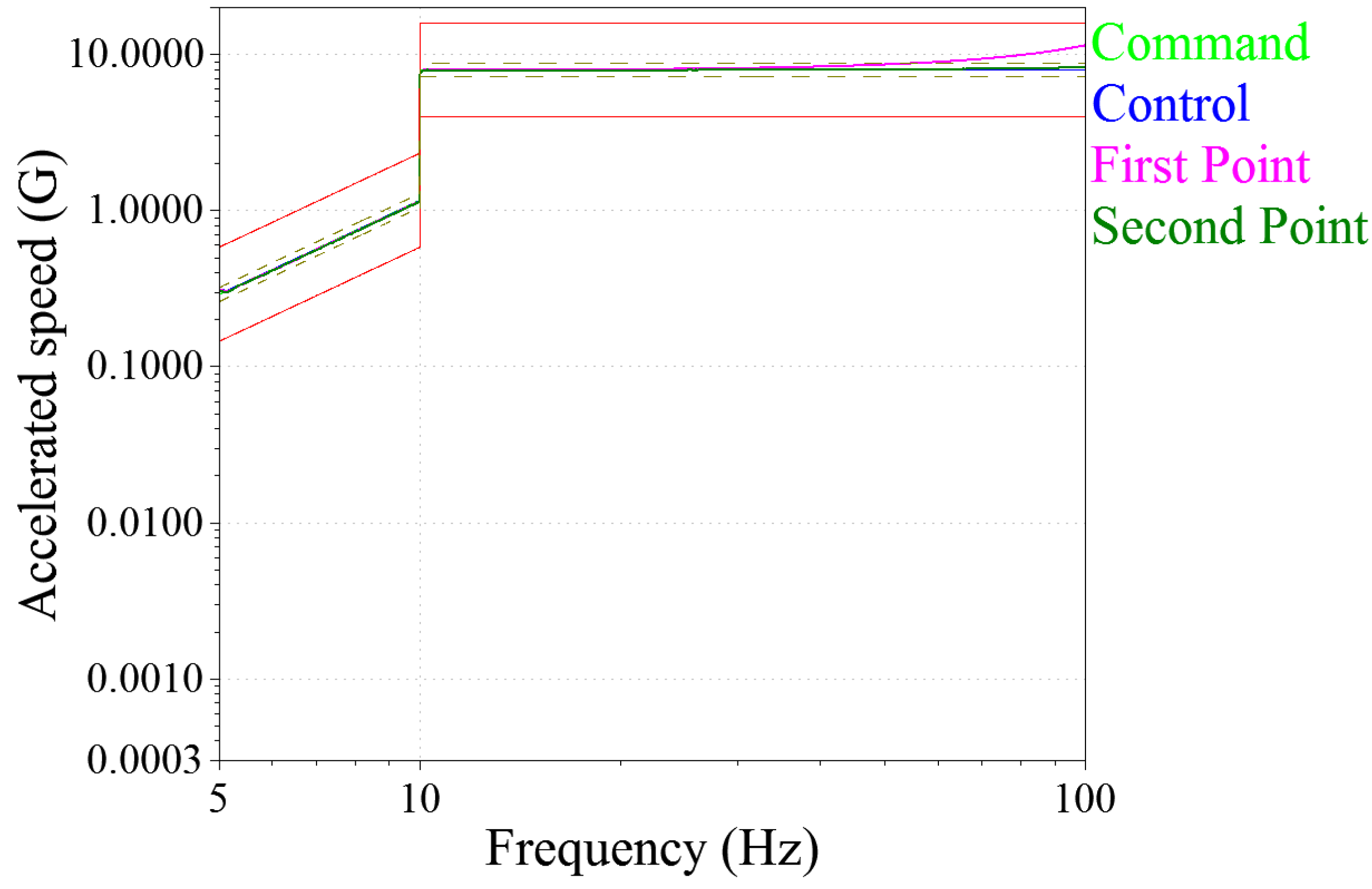
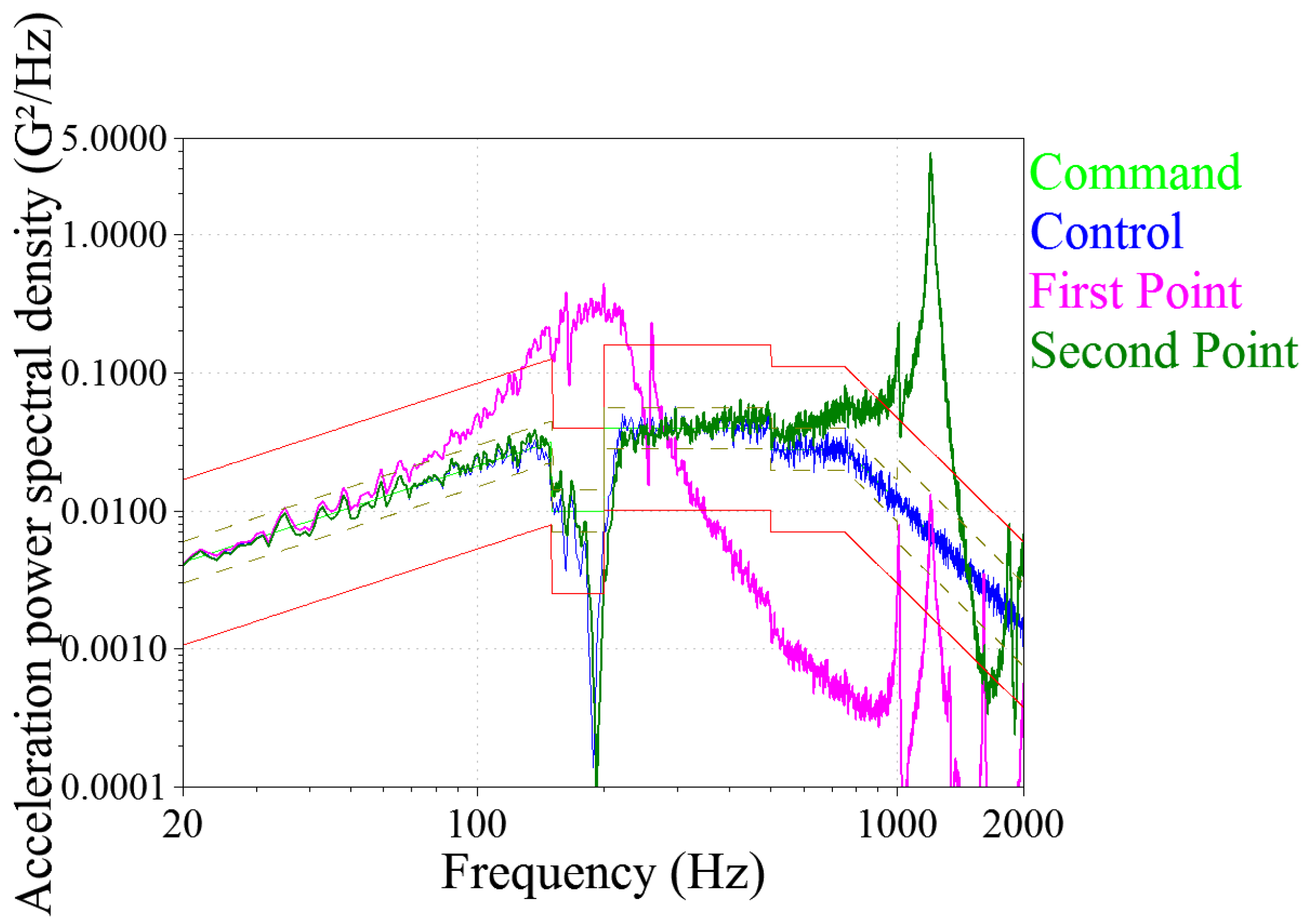
3.3. Vibration Test and System Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stahl, H.P.; Postman, M.; Mosier, G.; Smith, W.S.; Blaurock, C.; Ha, K.; Stark, C.C. AMTD: Update of engineering specifications derived from science requirements for future UVOIR space telescopes. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation, Montréal, QC, Canada, 22–27 June 2014. [Google Scholar]
- Miller, D.W.; de Weck, O.L.; Mosier, G.E. Framework for multidisciplinary integrated model-ing and analysis of space telescopes. In Proceedings of the Workshop on Integrated Modeling of Telescopes. International Society for Optics and Photonics, Lund, Sweden, 5–7 February 2002; pp. 1–18. [Google Scholar]
- Uebelhart, S.A. Non-Deterministic Design and Analysis of Parameterized Optical Structures during Conceptual Design. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2006. [Google Scholar]
- Yan, C.; Xu, J.; Peng, Y. Stray light suppression of off-axis triple mirror space optical telescope systems. Opt. Precis. Eng. 2010, 18, 289–293. [Google Scholar]
- Krödel, M.R.; Hofbauer, P. Ultra-lightweighted HB-Cesic one-meter mirror demonstrator. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation, San Diego, CA, USA, 27 June–2 July 2010. [Google Scholar]
- Zhang, X.J.; Li, Z.L.; Zhang, Z.Y. Space telescope aspherical mirror structure design based on SiC material. Infrared Laser Eng. 2007, 36, 577–582. (In Chinese) [Google Scholar]
- Bao, H.; Li, Z. Design of the strip SiC mirror supporting structure and lightweight. Opt. Tech. 2008, 34, 593–596. [Google Scholar]
- Stahl, H.P. Advanced Mirror Technology Development for Very Large Space Telescopes. In Proceedings of the 223rd American Astronomical Society Meeting, National Harbor, MD, USA, 5–9 January 2014. [Google Scholar]
- Egerman, R.; Matthews, G.; Wynn, J.; Kirk, C.; Havey, K. The Current and Future State-of-the-art Glass Optics. In Astro2010: The Astronomy and Astrophysics Decadal Survey; NASA: Washington, DC, USA, 2009. [Google Scholar]
- Stahl, H.P. Advanced Mirror Technology Development (AMTD) Project: Overview and Year Four Accomplishments. In Proceedings of the SPIE Astronomical Telescopes + Instrumentation, Edinburgh, UK, 26 June–1 July 2016. [Google Scholar]
- Bittner, H.; Erdmann, M.; Haberler, P. SOFIA Primary Mirror Assembly: Structural Properties and Optical Performance. In Proceedings of the Astronomical Telescopes and Instrumentation, Waikoloa, HI, USA, 22–23 August 2002; pp. 266–273. [Google Scholar]
- Parks, R.E.; Wortley, R.W.; Cannon, J.E. Engineering with lightweight mirrors. In Proceedings of the SPIE Astronomical Telescopes and Instrumentation for the 21st Century, Tucson, AZ, USA, 11–16 February 1990. [Google Scholar]
- Anderson, D.; Parks, R.E.; Hansen, Q.M.; Melugin, R. Gravity denections of lightweighted mirrors. In Proceedings of the International Conference on Advanced Technology Optical Telescopes, Tucson, AZ, USA, 11–13 March 1982. [Google Scholar]
- Friedman, E. Photonjcs Rules of Thumb; McGraw Hill: New York, NY, USA, 2003. [Google Scholar]
- Xu, H.; Guan, Y.J. Structural design of 1 m diameter space mirror component of space camera. Opt. Precis. Eng. 2013, 21, 1488–1495. [Google Scholar]
- Yang, J.W.; Huang, Q.L. Optimized design of structure parameters for large aperture mirrors. Chin. Space Sci. Technol. 2011, 31, 77–83. (In Chinese) [Google Scholar]
- Li, Z.L.; Xu, H.; Guan, Y.J. Structural design of 1.5 m mirror subassembly for space camera. Opt. Precis. Eng. 2015, 23, 1635–1641. (In Chinese) [Google Scholar]
- Zhang, B.W.; Wang, X.Y.; Zhao, Y. Development of space-based large aperture mirror support technology. Infrared Laser Eng. 2018, 47, 1113001. (In Chinese) [Google Scholar] [CrossRef]
- Wu, Q.; Yang, H.; Yang, J.; Chen, C.; Wang, Z.; Liu, H.; Gao, M. Design and analysis for primary mirror and its support of space camera. Opt. Tech. 2004, 30, 152–156. (In Chinese) [Google Scholar]
- Zhu, N. Research on the Design of the Supporting Structure of Lightweight Mirror. Ph.D. Thesis, University of Chinese Academy of Sciences, Chengdu, China, 2016. (In Chinese). [Google Scholar]
- Wang, K.J.; Dong, J.H. Composite support structure of large aperture mirror of space remote sensor. Opt. Precis. Eng. 2016, 24, 1719–1730. [Google Scholar] [CrossRef]



| Material | Density g/cm3 | Coefficient of Linear Expansion α × 10−6/K | Modulus of Elasticity Gpa |
|---|---|---|---|
| Fused silicon | 2.2 | 0.55 | 67 |
| Zerodur | 2.53 | 0.05 | 91 |
| Be | 1.87 | 11.3 | 287 |
| Sic | 3.12 | 2.24 | 400 |
| ULE | 2.21 | 0.03 | 68 |
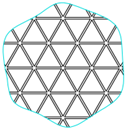
| Triangular rib structure | Weight: 14.1 kg | Fundamental frequency: 1287.5 Hz |
 |  | 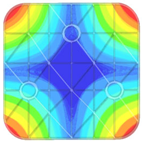 |
| Square rib structure | Weight: 14.5 kg | Fundamental frequency: 1235.6 Hz |
 |  |  |
| Hexagonal rib structure | Weight: 15.7 kg | Fundamental frequency: 1248.8 Hz |
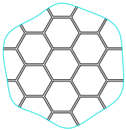 |  |  |
| Triangular rib structure | Maximum displacement change: 1.2 × 10−4 mm | Maximum stress change: 0.09 Mpa |
 | 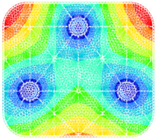 |  |
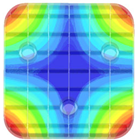
| Square rib structure | Maximum displacement change: 1.8 × 10−4 mm | Maximum stress change: 0.16 Mpa |
 |  |  |
| Hexagonal rib structure | Maximum displacement change: 1.9 × 10−4 mm | Maximum stress change: 0.12 Mpa |
 |  |  |
| Zerodur | Maximum displacement change: 2.3 × 10−4 mm | Maximum stress change: 0.22 Mpa |
 |  |
| Serial Number | Width of Rib (mm) | Mass (kg) | Mirror Mode (Hz) |
|---|---|---|---|
| 1 | 2.5 | 12.8 | 1285.1 |
| 2 | 3 | 13.4 | 1285.9 |
| 3 | 3.5 | 13.8 | 1286.7 |
| 4 | 4 | 14.1 | 1287.5 |
| 5 | 2.5~3 | 13.2 | 1289.2 |
| 6 | 2.5~3.5 | 13.4 | 1292.9 |
| 7 | 2.5~4 | 13.6 | 1316.4 |
| Material | Density g/cm3 | Coefficient of Linear Expansion α × 10−6/K | Modulus of Elasticity Gpa | Poisson |
|---|---|---|---|---|
| ULE | 2.21 | 0.03 | 67.6 | 0.17 |
| TC4R | 4.45 | 9.1 | 110 | 0.34 |
| InvarSteel | 8.18 | 0.05 | 145 | 0.25 |
| AlSiC | 2.9 | 9.8 | 145 | 0.32 |
| Optical cement | 1.7 | 110 | 600 | 0.49 |
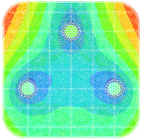
| First-order mode shape | Second-order mode shape |
 | 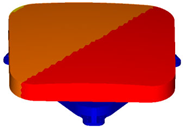 |
| Third-order mode shape | Fourth-order mode shape |
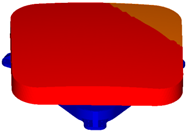 |  |
| Order | Frequency (Hz) | Mode Shape Description |
|---|---|---|
| 1 | 173.3 | The primary mirror rotates around the Z axis |
| 2 | 186.9 | Primary mirror X-direction translation |
| 3 | 204.4 | Primary mirror Y-direction translation |
| 4 | 292.9 | The primary mirror rotates around the Y axis |
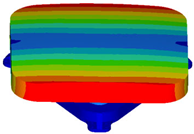
| working condition | Gravity load (1 G) | Forced displacement (5 μm) | |
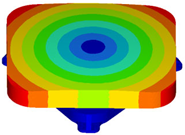
| Surface error RMS/λ (λ = 632.8 nm) |  | 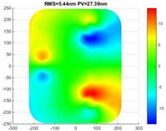 | 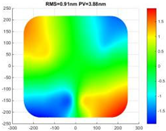 |
| Y: RMS = 6.71 nm (λ/94.3) | X: RMS = 5.44 nm (λ/116.3) | RMS = 0.91 nm (λ/695.4) | |
| working condition | Temperature load (15 °C~25 °C) | Axial temperature gradient load (5 °C) | Radial temperature gradient load (5 °C) |
| Surface error RMS/λ (λ = 632.8 nm) | 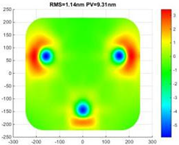 | 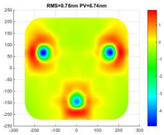 | 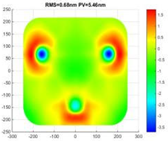 |
| RMS = 1.14 nm (λ/555.1) | RMS = 0.78 nm (λ/811.3) | RMS = 0.68 nm (λ/930.6) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Tian, A.; Liu, B.; Du, X.; Dong, S. Lightweight Design and Evaluation of Square Reflector. Appl. Sci. 2023, 13, 9160. https://doi.org/10.3390/app13169160
Zhu Z, Tian A, Liu B, Du X, Dong S. Lightweight Design and Evaluation of Square Reflector. Applied Sciences. 2023; 13(16):9160. https://doi.org/10.3390/app13169160
Chicago/Turabian StyleZhu, Zhongyao, Ailing Tian, Bingcai Liu, Xin Du, and Suotao Dong. 2023. "Lightweight Design and Evaluation of Square Reflector" Applied Sciences 13, no. 16: 9160. https://doi.org/10.3390/app13169160
APA StyleZhu, Z., Tian, A., Liu, B., Du, X., & Dong, S. (2023). Lightweight Design and Evaluation of Square Reflector. Applied Sciences, 13(16), 9160. https://doi.org/10.3390/app13169160






