Neighborhood Rough Fuzzy Penetration Control Method with Variable Precision Based on GMAW
Abstract
:1. Introduction
2. Materials and Methods
Theory and Method of Variable Precision Neighborhood Rough Sets
- , if and only if ;
- ;
- .
- (1)
- .
- (2)
- .
| Algorithm 1. Reduction based on VPNRS model |
| Input: Decision table |
| Output: Reduction set |
| 1: Initialize |
| 2: , normalize each attribute data separately |
| 3: for each |
| 4: for each |
| 5: Compute the lower approximation according to Definition 4 |
| 6: end for |
| 7: Compute according to Definition 7 |
| 8: Select attribute with maximum values |
| 9: if then |
| 10: |
| 11: |
| 12: else |
| 13: |
| 14: end if |
| 15: end for |
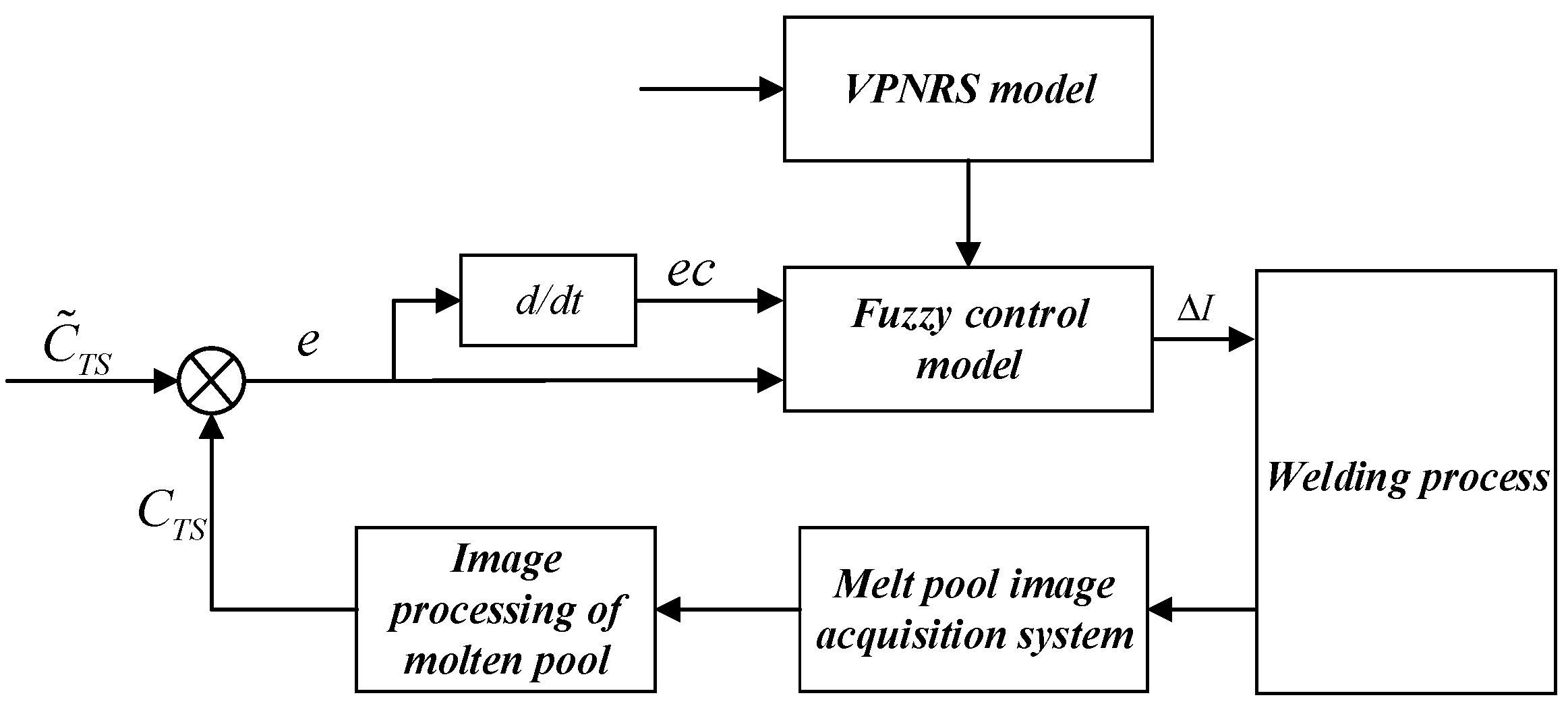
3. Description of Fuzzy Control System
3.1. Establishment of Characterization Information of Weld Pool
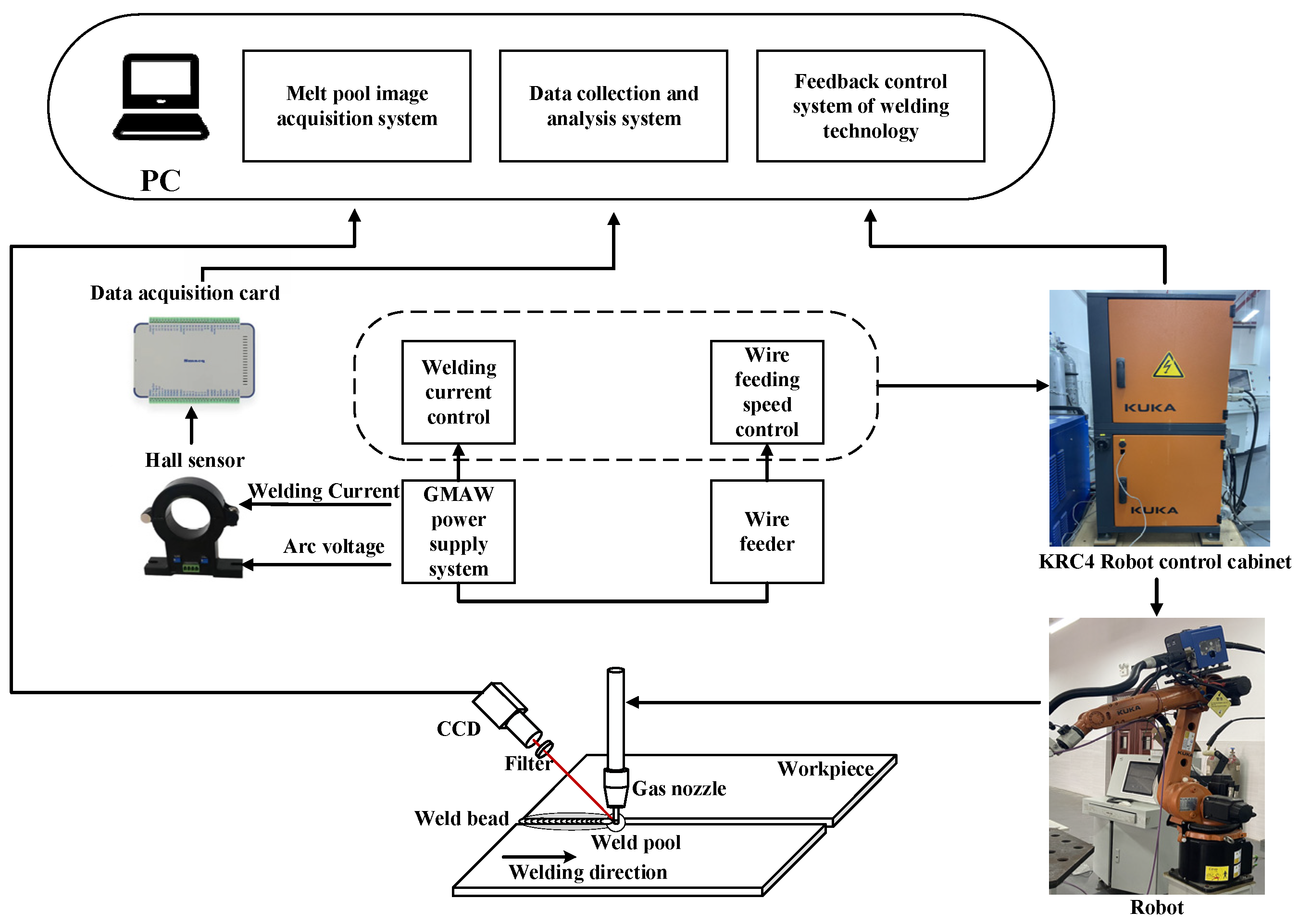
3.1.1. Experimental Data Acquisition System
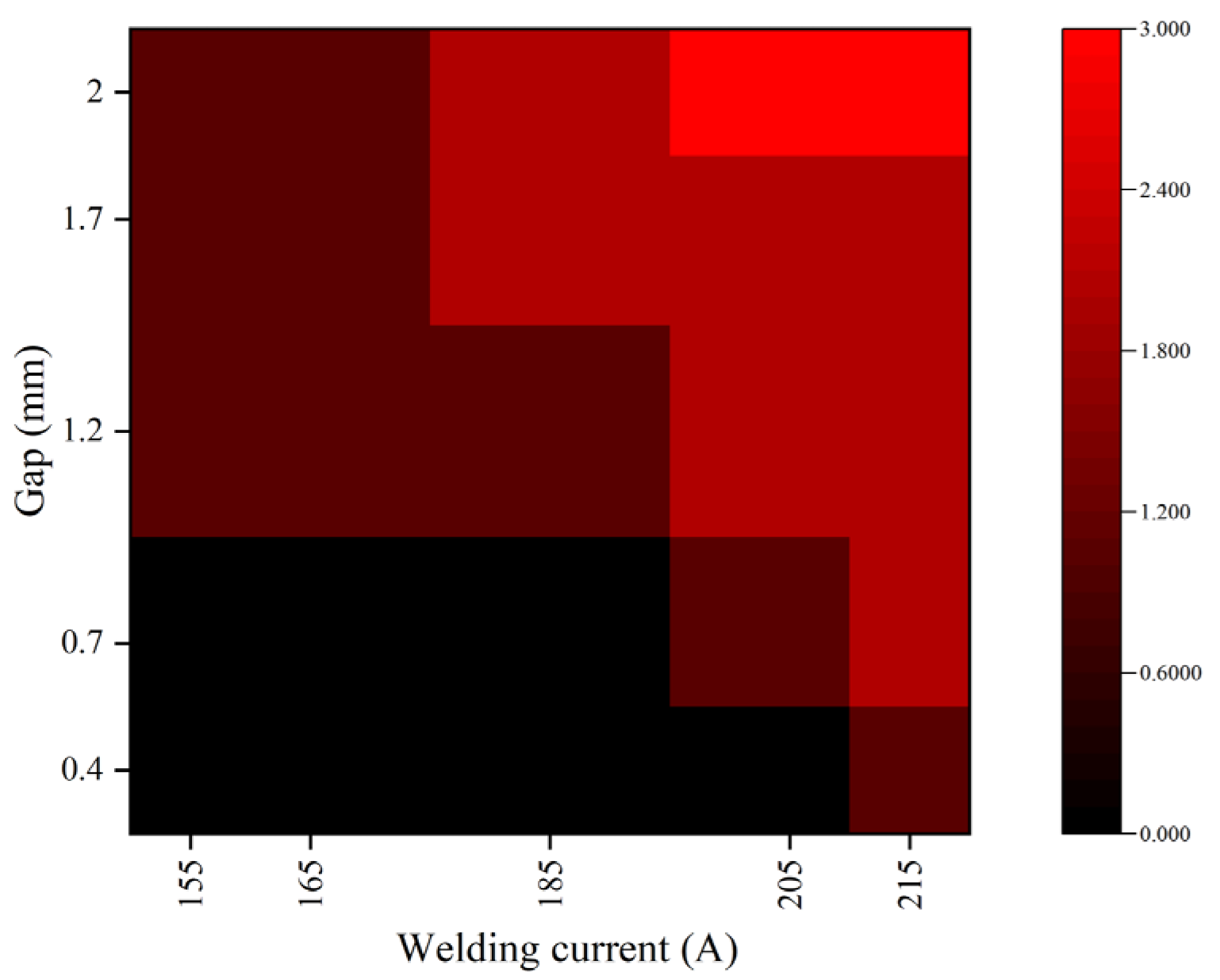
3.1.2. The Experiment of Representation Information Acquisition
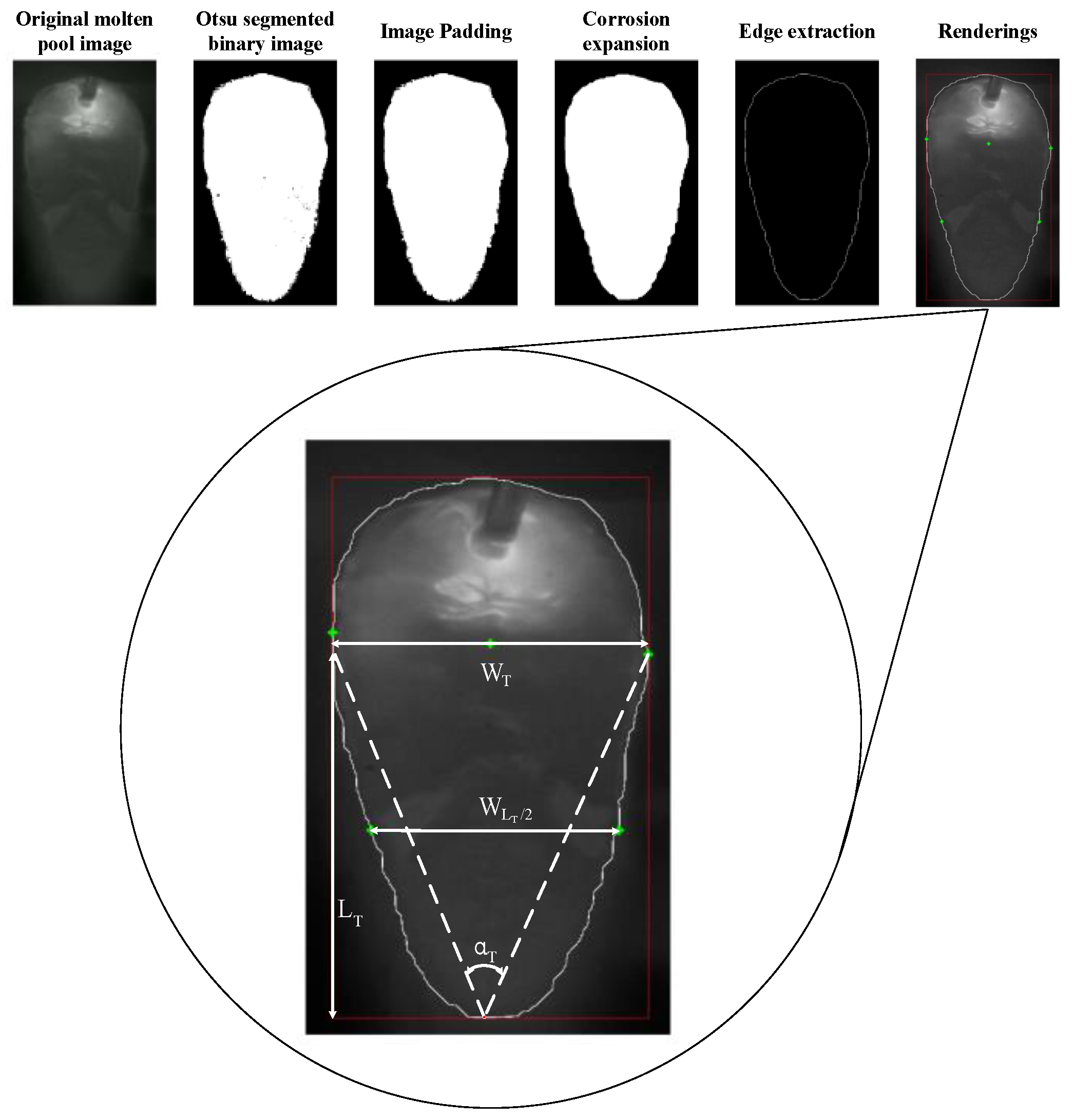
3.1.3. Representation Information Extraction
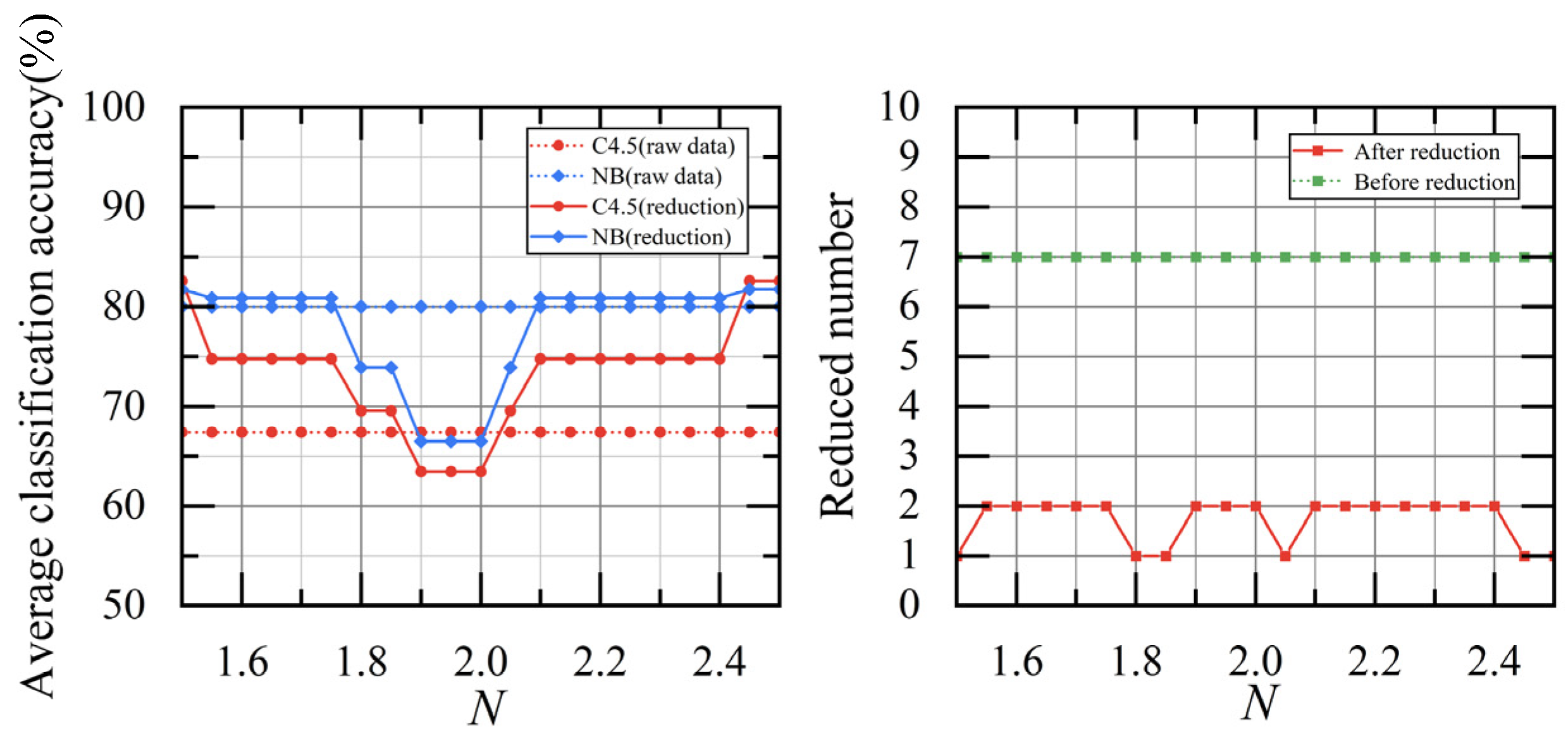
3.2. VPNRS Feature Extraction and Classification Rule Acquisition
- Rule 1.
- The area coefficient of the molten pool tail is large, and the weld is not fully penetrated ().
- Rule 2.
- In the area coefficient of the molten pool tail, the weld is thoroughly penetrated ().
- Rule 3.
- The area coefficient of the molten pool tail is small, and the weld is over-penetrated ().
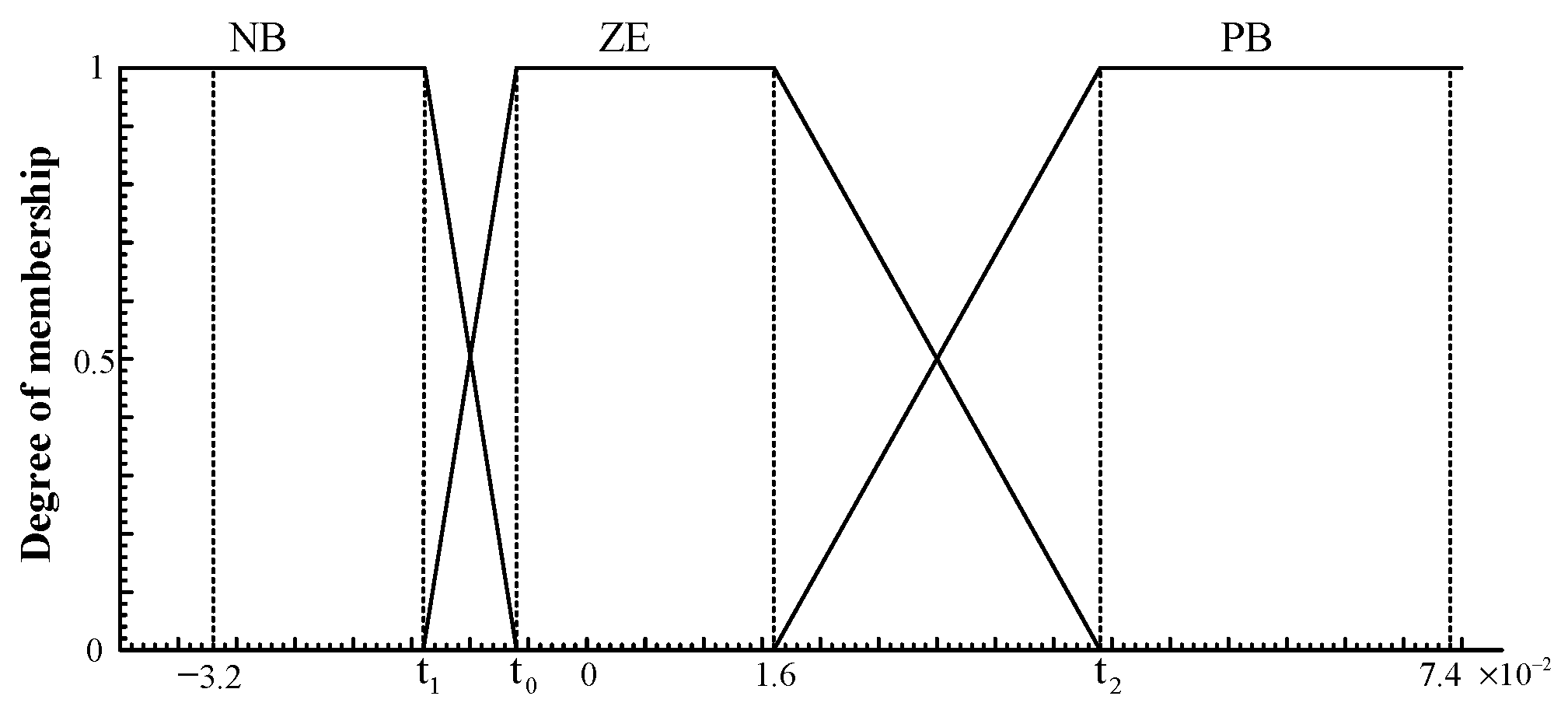
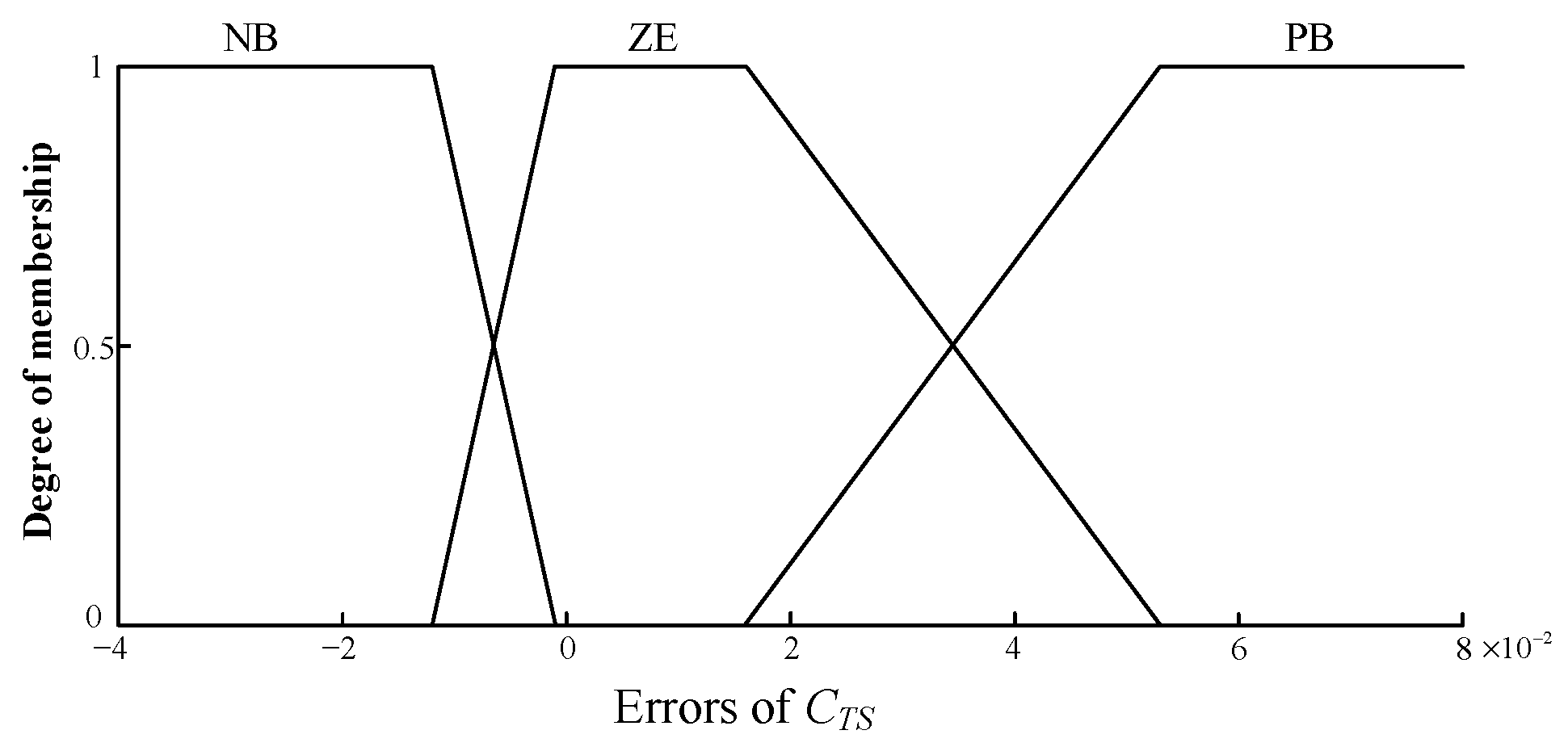
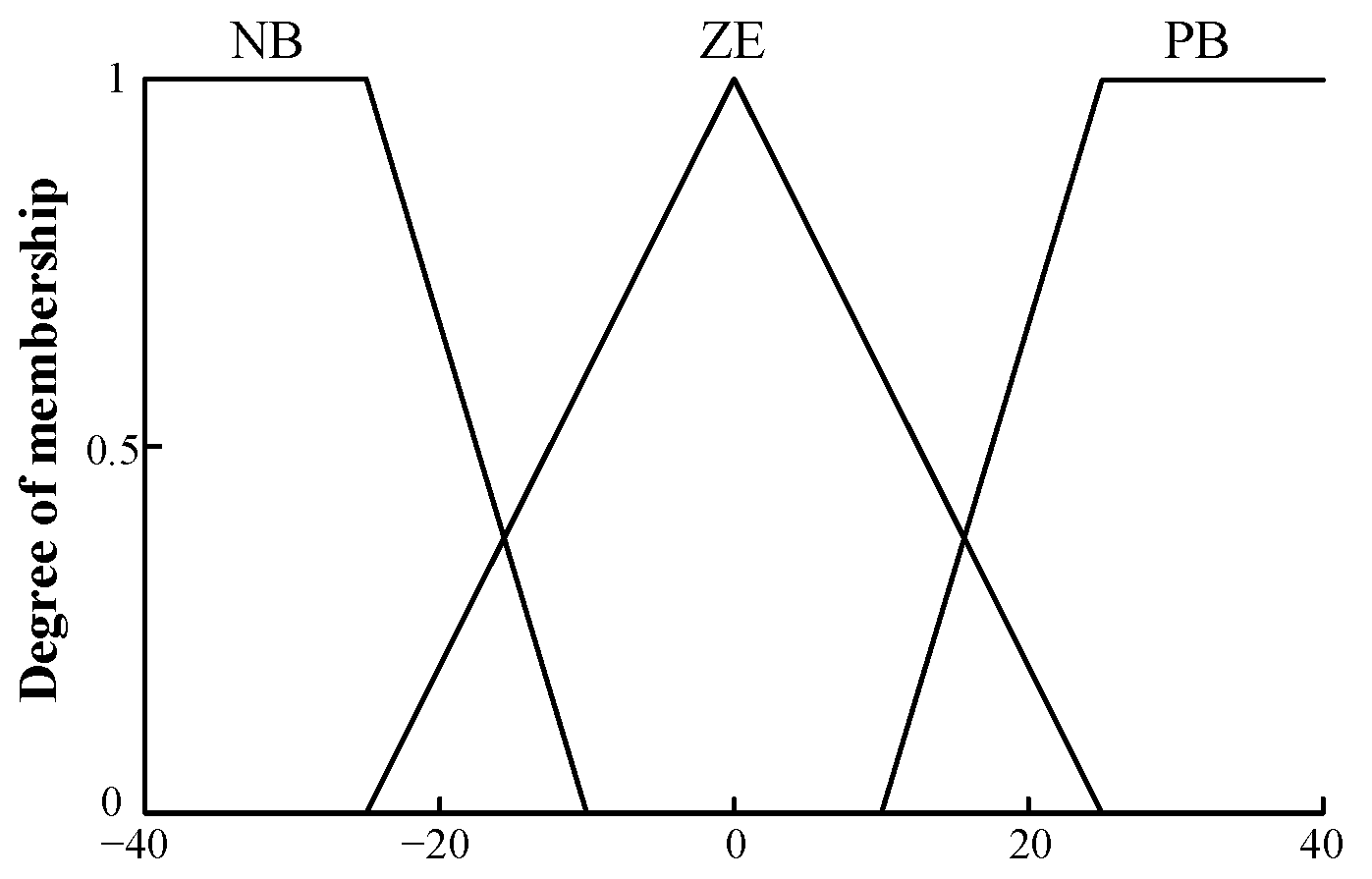
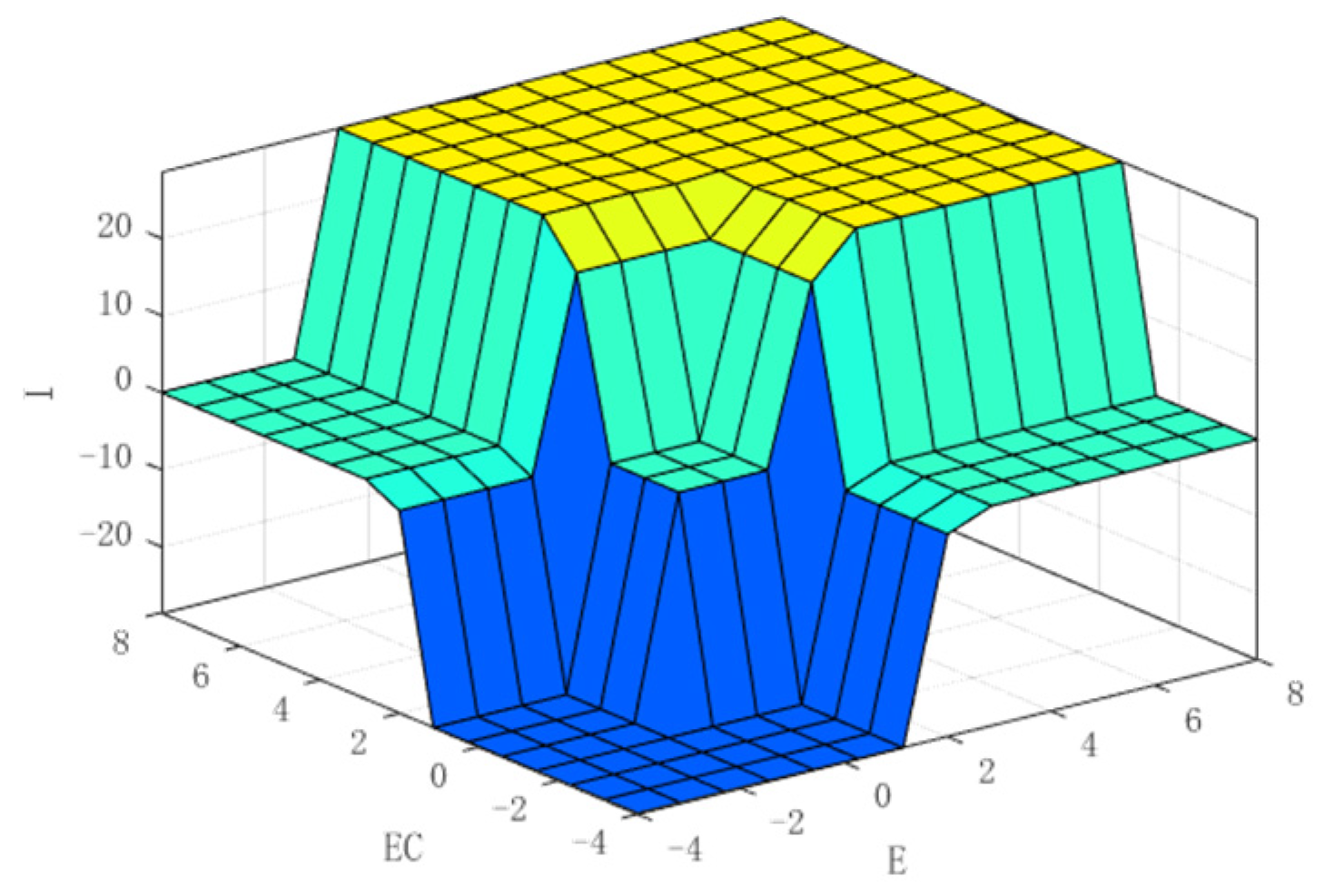
3.3. Establishment of Fuzzy Control System
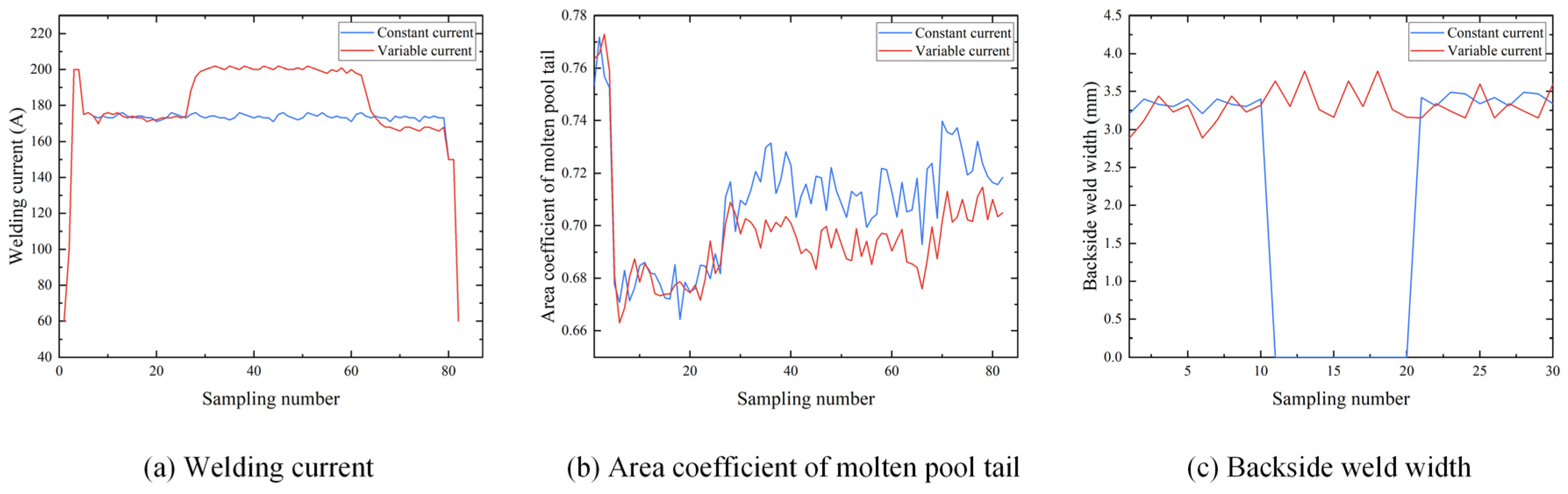
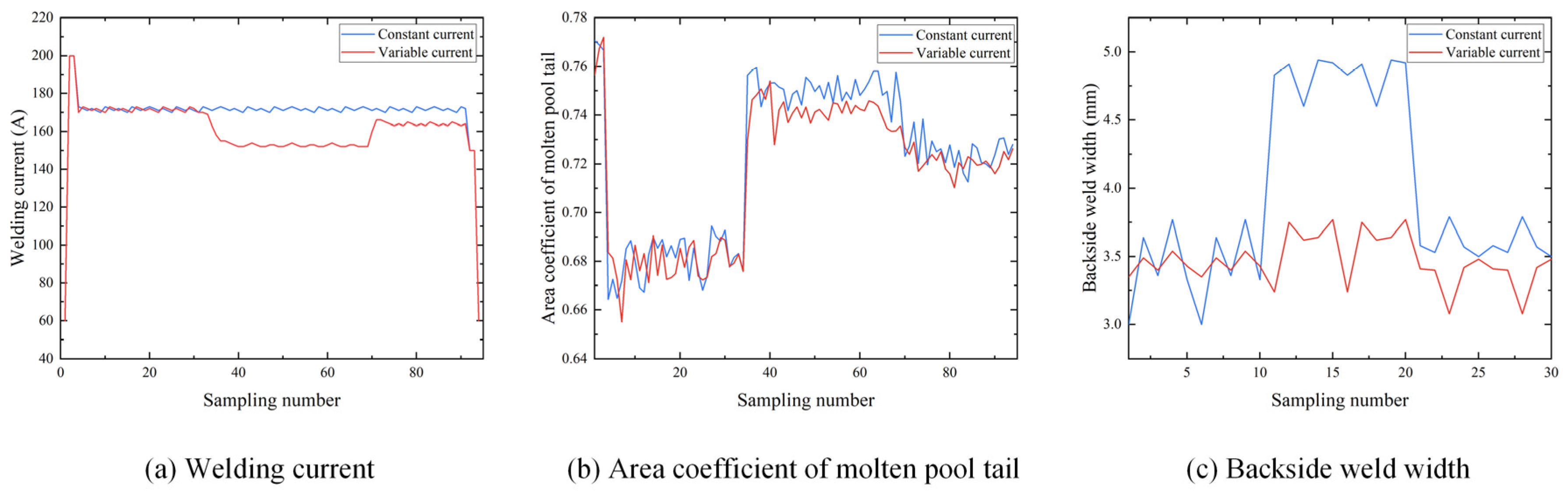
4. Experimental Verification and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tsumoto, S. Rough Sets: Past, Present and Future. J. Jpn. Soc. Fuzzy Theory Syst. 2001, 13, 552–561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Suo, M.; Tao, L.; Zhu, B.; Miao, X.; Liang, Z.; Ding, Y.; Zhang, X.; Zhang, T. Single-parameter decision-theoretic rough set. Inf. Sci. 2020, 539, 49–80. [Google Scholar] [CrossRef]
- Kannan, E.; Ravikumar, S.; Anitha, A.; Kumar, S.A.P.; Vijayasarathy, M. Analyzing uncertainty in cardiotocogram data for the prediction of fetal risks based on machine learning techniques using rough set. J. Ambient Intell. Humaniz. Comput. 2021, 1–13. [Google Scholar] [CrossRef]
- Wang, B.; Chen, S.; Wang, J. Rough set based knowledge modeling for the aluminum alloy pulsed GTAW process. Int. J. Adv. Manuf. Technol. 2005, 25, 902–908. [Google Scholar] [CrossRef]
- Li, W.H.; Chen, S.B.; Wang, B. A variable precision rough set based modeling method for pulsed GTAW. Int. J. Adv. Manuf. Technol. 2008, 36, 1072–1079. [Google Scholar] [CrossRef]
- Feng, Z.-Q.; Liu, C.-G.; Huang, H. Knowledge modeling based on interval-valued fuzzy rough set and similarity inference: Prediction of welding distortion. J. Zhejiang Univ. Sci. C 2014, 15, 636–650. [Google Scholar] [CrossRef]
- Chady, T.; Sikora, R.; Misztal, L.; Grochowalska, B.; Grzywacz, B.; Szydłowski, M.; Waszczuk, P.; Szwagiel, M. The Application of Rough Sets Theory to Design of Weld Defect Classifiers. J. Nondestruct. Eval. 2017, 36, 40. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Devanathan, R.; Wang, J.; Chen, X.; Sun, Z. Vision based neurofuzzy logic control of weld pool geometry. Sci. Technol. Weld. Join. 2002, 7, 321–325. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, R.; Chen, H.; Lv, N.; Chen, S. Arc sound model for pulsed GTAW and recognition of different penetration states. Int. J. Adv. Manuf. Technol. 2020, 108, 3175–3191. [Google Scholar] [CrossRef]
- Lv, N.; Xu, Y.; Li, S.; Yu, X.; Chen, S. Automated control of welding penetration based on audio sensing technology. J. Mater. Process. Technol. 2017, 250, 81–98. [Google Scholar] [CrossRef]
- Baek, D.; Moon, H.S.; Park, S.-H. In-process prediction of weld penetration depth using machine learning-based molten pool extraction technique in tungsten arc welding. J. Intell. Manuf. 2022, 1–17. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, H.; Zhong, Q.; Lin, S.; Wu, J.; Xu, M.; Zhang, Q. Recognition of penetration state in GTAW based on vision transformer using weld pool image. Int. J. Adv. Manuf. Technol. 2022, 119, 5439–5452. [Google Scholar] [CrossRef]
- Yu, R.; Han, J.; Zhao, Z.; Bai, L. Real-Time Prediction of Welding Penetration Mode and Depth Based on Visual Characteristics of Weld Pool in GMAW Process. IEEE Access 2020, 8, 81564–81573. [Google Scholar] [CrossRef]
- Hu, Q.-H.; Yu, D.; Xie, Z. Numerical Attribute Reduction Based on Neighborhood Granulation and Rough Approximation. J. Softw. 2008, 19, 640–649. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Zhou, J. Research of reduct features in the variable precision rough set model. Neurocomputing 2009, 72, 2643–2648. [Google Scholar] [CrossRef]
- Hu, Q.H.; Zhao, H.; Yu, D.R. Efficient symbolic and numerical attribute reduction with neighborhood rough sets. Moshi Shibie yu Rengong Zhineng/Pattern Recognit. Artif. Intell. 2008, 21, 732–738. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.-W.; Wang, P.; Qiu, J.-Q.; Jiang, Y. An improved approach to feature selection. In Proceedings of the 2010 International Conference on Machine Learning and Cybernetics, Qingdao, China, 11–14 July 2010; pp. 488–493. [Google Scholar] [CrossRef]
- An, R.M.; Suo, M.L. Astronautics, Application of attributes reduction and weights calculation through neigh-borhood rough set. Comput. Eng. Appl. 2016, 52, 160–165. [Google Scholar] [CrossRef]
- Deo, M.V. Minimization of bowing distortion in welded stiffeners using differential heating. In Minimization of Welding Distortion and Buckling: Modelling and Implementation; Michaleris, P., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 169–185. [Google Scholar] [CrossRef]
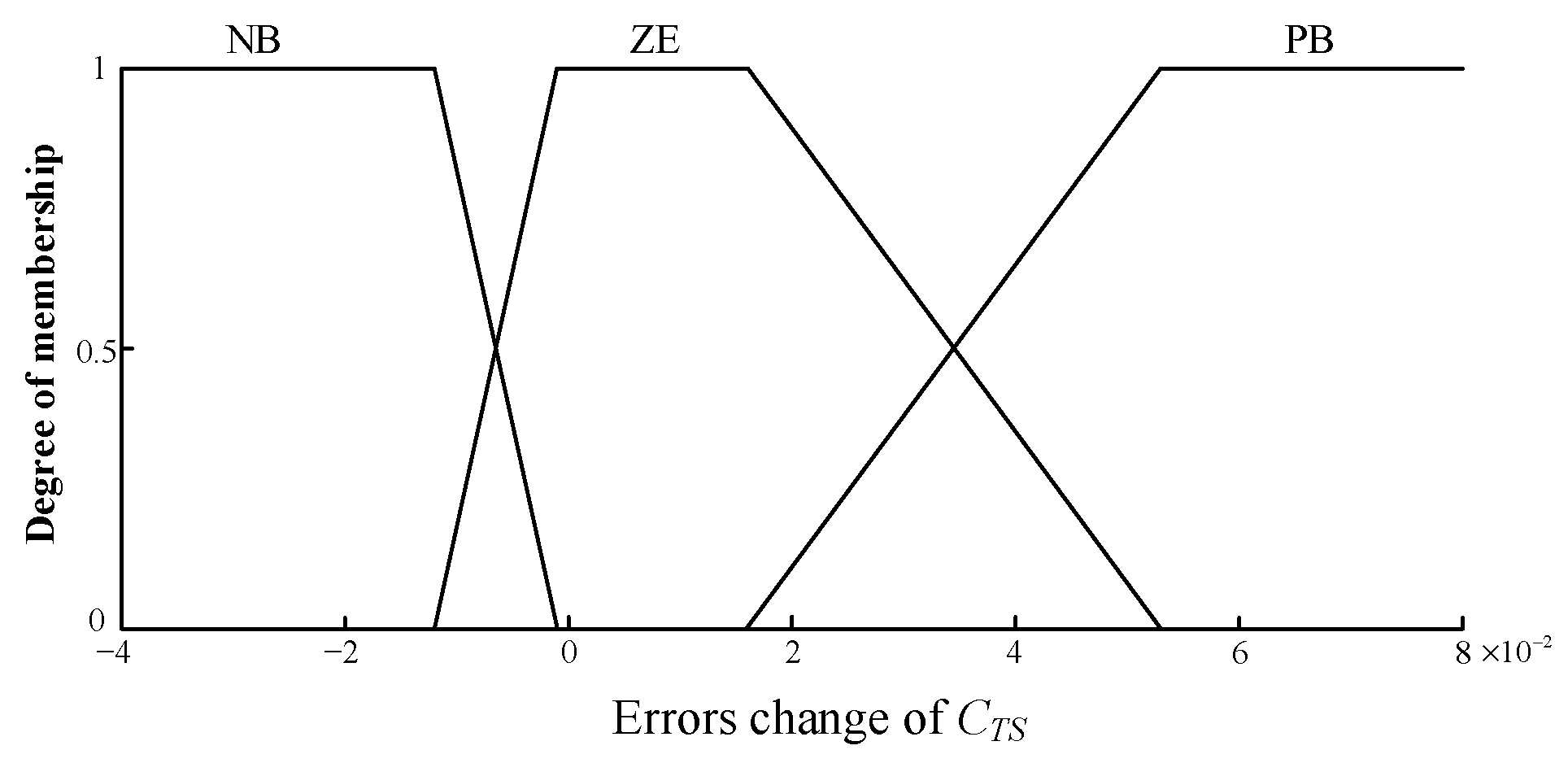
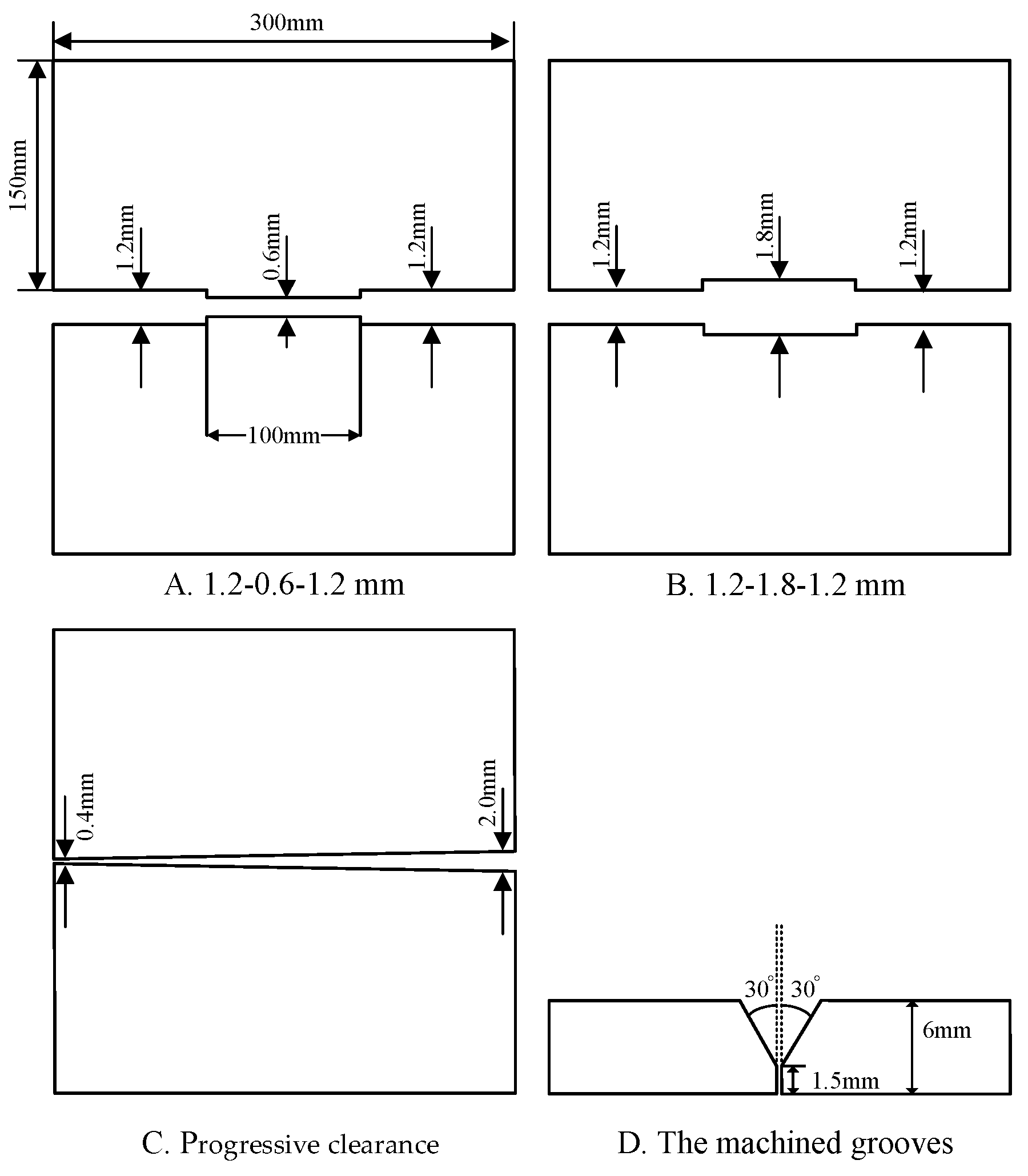




| Specimen Material | Q235 |
|---|---|
| Shielded gas | 85% CO2 + 15% Ar |
| Specimen size (mm3) | |
| Gas flow () | |
| Wire diameter () | 1.2 |
| Welding wire elongation () | 10 |
| Welding speed () | 47 |
| Assembly clearance (mm) | 0.4–2.0 |
| Welding voltage (V) | 20.5 |
| welding current (A) | 155–215 |
| Welding mode | Pulse welding |
| 203.5 | 227.4 | 1.0557 | 34,264.2 | 0.740344 | 58.38582 | 0.817982 | 0 | |
| 227.1 | 246.4 | 1.11908 | 40,220 | 0.718398 | 56.95522 | 0.794792 | 0 | |
| 287.2 | 279 | 1.24302 | 55,542.4 | 0.693106 | 51.83622 | 0.7656 | 0 | |
| 388.2 | 303.2 | 1.28024 | 77,677.8 | 0.65948 | 42.6706 | 0.703328 | 0 | |
| 380.7 | 294.6 | 1.29466 | 70,471.8 | 0.627972 | 42.30562 | 0.66299 | 1 | |
| 209.2 | 230.4 | 0.90887 | 35,064.8 | 0.727834 | 57.69378 | 0.794246 | 0 | |
| 228.2 | 241.6 | 0.94455 | 39,214.6 | 0.711268 | 55.79898 | 0.781472 | 0 | |
| 284.5 | 276.8 | 1.02794 | 54,364 | 0.69035 | 51.8864 | 0.752902 | 0 | |
| 349.9 | 286.6 | 1.22096 | 63,152.8 | 0.629686 | 44.54132 | 0.653802 | 1 | |
| 356.5 | 286.8 | 1.24315 | 61,489.8 | 0.601464 | 43.82376 | 0.639982 | 2 | |
| 198.2 | 195.4 | 1.21924 | 25,912.6 | 0.669246 | 52.5764 | 0.72167 | 1 | |
| 229 | 222.6 | 1.32878 | 33,977 | 0.66655 | 51.84138 | 0.708012 | 1 | |
| 285.1 | 256.2 | 1.38284 | 47,002.4 | 0.643292 | 48.41272 | 0.660664 | 1 | |
| 356.1 | 272.4 | 1.30719 | 58,891.8 | 0.60684 | 41.88194 | 0.620408 | 2 | |
| 393.9 | 264.2 | 1.49169 | 62,363 | 0.599 | 37.07392 | 0.6063 | 2 | |
| 225.5 | 192.2 | 1.17430 | 29,641 | 0.683952 | 46.16006 | 0.700376 | 1 | |
| 264.5 | 207.4 | 1.27540 | 36,261.8 | 0.660962 | 42.82836 | 0.685534 | 1 | |
| 306.1 | 223.2 | 1.37139 | 43,665 | 0.638984 | 40.07414 | 0.656882 | 2 | |
| 397.1 | 240.2 | 1.65288 | 57,250 | 0.599762 | 33.69362 | 0.610434 | 2 | |
| 448.5 | 244.2 | 1.83692 | 64,010 | 0.585122 | 30.5613 | 0.58698 | 2 | |
| 222.7 | 184.4 | 1.45976 | 26,597 | 0.647332 | 45.05956 | 0.677862 | 1 | |
| 250 | 210.8 | 1.52088 | 33,429.4 | 0.633874 | 45.73774 | 0.662322 | 1 | |
| 323.8 | 222.4 | 1.77036 | 35,481.56 | 0.617926 | 37.93956 | 0.621488 | 2 |
| Data Set | Abbreviation | Samples | Numerical Features | Classes | Mean SD | |
|---|---|---|---|---|---|---|
| 1 | Variable gap-current Welding | Welding | 23 | 7 | 3 | 0.284346 |
| Data | N | Red | Significance |
|---|---|---|---|
| Welding | 1.5 | 5 | 0.0435 |
| 1.55 | 5 | 0.0435 | |
| 6 | 0.0435 | ||
| 1.6 | 5 | 0.05 | |
| 6 | 0.05 | ||
| 1.65 | 5 | 0.0435 | |
| 6 | 0.0435 | ||
| 1.7 | 5 | 0.087 | |
| 6 | 0.0435 | ||
| 1.75 | 5 | 0.087 | |
| 6 | 0.0435 | ||
| 1.8 | 5 | 0.087 | |
| 6 | 0.0435 |
| 3 | 0 | |
| 3 | 0 | |
| 3 | 0 | |
| 2 | 0 | |
| 1 | 1 | |
| 3 | 0 | |
| 3 | 0 | |
| 3 | 0 | |
| 1 | 1 | |
| 1 | 2 | |
| 2 | 1 | |
| 2 | 1 | |
| 2 | 1 | |
| 1 | 2 | |
| 1 | 2 | |
| 2 | 1 | |
| 2 | 1 | |
| 2 | 2 | |
| 1 | 2 | |
| 1 | 2 | |
| 2 | 1 | |
| 2 | 1 | |
| 1 | 2 |
| E | ||||
|---|---|---|---|---|
| NB | ZE | PB | ||
| EC | NB | NB | NB | ZE |
| ZE | NB | ZE | PB | |
| PB | ZE | PB | PB | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, X.; Feng, Z.; Yuan, H.; Zeng, X.; Pan, Z.; Li, X.; Li, Q.; Huang, X. Neighborhood Rough Fuzzy Penetration Control Method with Variable Precision Based on GMAW. Appl. Sci. 2023, 13, 9215. https://doi.org/10.3390/app13169215
Xiang X, Feng Z, Yuan H, Zeng X, Pan Z, Li X, Li Q, Huang X. Neighborhood Rough Fuzzy Penetration Control Method with Variable Precision Based on GMAW. Applied Sciences. 2023; 13(16):9215. https://doi.org/10.3390/app13169215
Chicago/Turabian StyleXiang, Xiaohong, Zhiqiang Feng, Hao Yuan, Xianping Zeng, Zufu Pan, Xin Li, Quan Li, and Xiaohu Huang. 2023. "Neighborhood Rough Fuzzy Penetration Control Method with Variable Precision Based on GMAW" Applied Sciences 13, no. 16: 9215. https://doi.org/10.3390/app13169215
APA StyleXiang, X., Feng, Z., Yuan, H., Zeng, X., Pan, Z., Li, X., Li, Q., & Huang, X. (2023). Neighborhood Rough Fuzzy Penetration Control Method with Variable Precision Based on GMAW. Applied Sciences, 13(16), 9215. https://doi.org/10.3390/app13169215






