Abstract
Subspace clustering methods based on the low-rank and sparse model are effective strategies for high-dimensional data clustering. However, most existing low-rank and sparse methods with self-expression can only deal with linear structure data effectively, but they cannot handle data with complex nonlinear structure well. Although kernel subspace clustering methods can efficiently deal with nonlinear structure data, some similarity information between samples may be lost when the original data are reconstructed in the kernel space. Moreover, these kernel subspace clustering methods may not obtain an affinity matrix with an optimal block diagonal structure. In this paper, we propose a novel subspace clustering method termed kernel block diagonal representation subspace clustering with similarity preservation (KBDSP). KBDSP contains three contributions: (1) an affinity matrix with block diagonal structure is generated by introducing a block diagonal representation term; (2) a similarity-preserving regularizer is constructed and embedded into our model by minimizing the discrepancy between inner products of original data and inner products of reconstructed data in the kernel space, which better preserve the similarity information between original data; (3) the KBDSP model is proposed by integrating the block diagonal representation term and similarity-preserving regularizer into the kernel self-expressing frame. The optimization of our proposed model is solved efficiently by utilizing the alternating direction method of multipliers (ADMM). Experimental results on nine datasets demonstrate the effectiveness of the proposed method.
1. Introduction
In real applications, high-dimensional datasets need to be processed [1,2]. In recent years, subspace clustering developed as a hot research topic and was introduced to process high-dimensional data efficiently [3,4,5]. Subspace clustering has been widely applied in many application areas, such as computer vision [6], image representation and compression [7], motion segmentation [8], and face clustering [9]. The existing subspace clustering methods can be divided into five categories: iterative models [10]; statistical models [11]; algebraic models [12]; spectral clustering-based models [1,13,14,15]; and deep learning-based models [15,16]. Notably, the spectral clustering-based subspace clustering approaches have achieved outstanding performance. These methods have two main parts: (1) affinity matrix construction; (2) spectral clustering [17]. Recently, many spectral clustering methods have emerged [13,14,18,19,20,21], and the two most representative models are sparse subspace clustering (SSC) [14] and low-rank representation (LRR) [22]. SSC and LRR have obtained great success in many research areas. These methods based on sparse or low-rank representation techniques can obtain a coefficient matrix by using a self-expression model. The coefficient matrix is named the similarity matrix [23]. The similarity matrix is adaptively calculated and can effectively avoid the drawback that the number of neighbors is difficult to set for a graph in subspace clustering methods. However, all these methods can only process linear subspaces and they cannot handle the nonlinear data; but in fact, most data are nonlinear structures in the real world [24,25]. In addition, although a lot of recent clustering studies based on deep learning are proposed [15,16], the topics of these research studies are not the emphasis of this paper.
To overcome the drawback that the existing linear subspace clustering methods cannot deal with nonlinear data, some kernel self-expression methods [26,27,28,29,30,31] extended linear subspace clustering to nonlinear subspace clustering by employing the “kernel strategy”, where the linear subspace clustering can be carried out. The two typical methods are kernelized SSC (KSSC) [30] and kernelized LRR (KLRR) [14]. KSSC and KLRR have captured nonlinear structure information in the input space and have made the most development in many applications. Although these kernel subspace clustering methods based on kernel self-expression can efficiently process the nonlinear structure data, some similarity information between samples may be lost when reconstructing the original data in the kernel space. In practice, real data with manifold structures present complex structures aside from sparse or low rank [32]. Hence, it is essential to construct a representation that can sufficiently implant the rich structure information of original data.
Many methods discover the underlying structure by exploring data relations [33,34,35]. Some subspace clustering methods based on structure learning have been proposed, such as similarity learning via kernel-preserving embedding (SLKE) [35] and structure learning with similarity preserving (SLSP) [36]. SLKE constructs a model by retaining the similarity information between data, which conveys better performance. SLSP constructs a structure learning framework that contains the similarity information of original data, which overcomes the drawback that the SLKE algorithm might lose some low-order information of original data. In summary, although these methods can obtain good performance, they are subject to the learned similarity matrix that does not have an optimal block diagonal structure. Hence, the construction of the block diagonal similarity matrix is a hot topic that recently emerged in the field of subspace clustering methods.
In the research works of the literature [8,14,15,16,17,18,19,20,21,22], all kinds of norm regularization terms in self-expressive models have been used to learn a block diagonal coefficient matrix, such as norm, norm, and nuclear norm. However, those regularization methods have two drawbacks: one is that the number of blocks in the coefficient matrix cannot be controlled, and another is that the learned coefficient matrix may not be an optimal block diagonal because of the noise in the data. To remedy these drawbacks, the block diagonal representation (BDR) subspace clustering algorithms [13,27,37,38,39,40,41] are proposed to pursue a “good” block diagonal structure of the coefficient matrix, such as implicit block diagonal low-rank representation (IBDLR) [40]. IBDLR constructs a novel model by integrating the block diagonal prior and implicit feature representation into the low-rank representation model. These algorithms based on the block diagonal representation gradually improve clustering performance. However, these subspace clustering methods based on BDR are not introduced into the similarity-preserving mechanism.
To resolve the above problems, this paper first constructs a representation, which can better capture the rich structure information in original data. Second, to promote the affinity matrix from the self-expression learning framework to obey a “good” block diagonal structure for spectral clustering, we introduce the block diagonal representation (BDR) term to our model. Third, the kernel self-expressing framework is introduced into our model, which can efficiently process the nonlinear structure data. By fully considering these issues, we propose a novel robust subspace clustering method termed kernel block diagonal representation subspace clustering with similarity preservation (KBDSP) by embedding the block diagonal representation term and similarity-preserving regularizer into the kernel self-expressing framework. Experiments on nine datasets prove the effectiveness and robustness of our proposed KBDSP method. To sum up, the main contributions of this work can be summarized as follows:
- (1)
- To capture the nonlinear structure of original data, a subspace clustering frame based on kernel self-expressing is introduced into our model.
- (2)
- To better preserve the similarity information between original data, a similarity-preserving regularizer is constructed and introduced to our model by minimizing the difference between inner products of original data and inner products of reconstructed data in the kernel space.
- (3)
- To obtain the similarity matrix with optimal block diagonal structure, a block diagonal representation is introduced to our model. Then, the optimal block diagonal matrix is directly captured by optimizing the objective function, overcoming the drawback that sparse or low-rank-based subspace clustering methods cannot obtain the optimal block diagonal matrix.
- (4)
- Our KBDSP model is proposed by integrating the block diagonal representation term and similarity-preserving regularizer into the kernel self-expressing frame. The proposed optimization model is solved by applying the alternating direction method of multipliers (ADMM).
This paper includes the following five sections. Self-expression-based subspace clustering, kernel-based subspace clustering, and block diagonal representation term are briefly introduced in Section 2. Section 3 describes the proposed KBDSP method in detail. Section 4 presents the experimental results on nine datasets. Section 5 gives the conclusions.
2. Related Works
2.1. Self-Expression-Based Subspace Clustering
The self-expression-based subspace clustering methods aim to express each data point as a linear combination of all other data points in the same subspace [11]. Its general model is defined as:
where R(Z) denotes the regularization term, and denotes a trade-off parameter. Z is delivered by solving the specific model and a balanced affinity matrix is constructed by , which is very important to design a proper regularizer for promoting the clustering performance. are three common regularization terms [39]. To the best desirable outcome, the coefficient matrix Z is an optimal block diagonal matrix. However, the coefficient matrix Z is influenced by noise and is usually not a block diagonal.
2.2. Kernel-Based Subspace Clustering
To complete our framework more generally, we introduce the kernel self-expressing model for subspace clustering. Based on kernel function mapping, Equation (1) can be mapped into higher dimensional kernel space, where nonlinear relational data can be transformed into linear relational data. The optimization model of kernel self-expression subspace clustering is expressed as:
where is a kernel function mapping, K is a kernel matrix whose elements are computed as , and R(Z) is the regularization term.
In Equation (2), the Frobenius norm is used to calculate the representation error. Nevertheless, when there are outliers in data, the Frobenius norm is not robust. To solve the problem of clustering robustness, robust kernel low-rank representation (RKLRR) [14] is put forward, in which a closed-form solution is provided for the challenge problem. Although RKLRR can solve the problem of clustering robustness, the learned affinity matrix is not ensured to be an optimal block diagonal.
2.3. Block Diagonal Regularizer
The BDR algorithm directly pursues the block diagonal matrix by introducing a block diagonal regularization term and obtains better clustering performance [27]. The optimization model of the BDR algorithm can be expressed as:
where X represents a data matrix, Z represents a coefficient matrix, and represents a k-block diagonal regularizer.
3. The Proposed KBDSP Method
3.1. KBDSP Model
To preserve the similarity information between samples and simultaneously obtain a similarity matrix with optimal block diagonal structure, we propose a novel subspace clustering method (KBDSP). Inspired by Kang et al. [39], we preserve the similarity information by minimizing the difference of two inner products: one refers to the inner products between original data in the kernel space, and another refers to the inner products of reconstructed data in the kernel space. Based on this, the optimization problem is expressed as:
After, this can be simplified as
To effectively deal with the nonlinear structure data, we adopt the kernel self-expression subspace clustering framework. In the meantime, we introduce the block diagonal regularization term into the kernel self-expression framework in order to obtain the similarity matrix with block diagonal structure. Thus, our proposed kernel block diagonal representation subspace clustering with similarity preservation (KBDSP) model is
An auxiliary matrix B and a regularization term are drawn into our model for separating the variables. Thus, the optimization problem (6) can be translated to
where and γ are the non-negative trade-off parameters.
3.2. Optimization of KBDSP
To facilitate the solution of the problem (7), we transform it to the following equivalent problem by importing three new auxiliary variables:
The problem (8) is solved by using ADMM.
The corresponding augmented Lagrangian function is
where are Lagrangian multipliers and is a penalty parameter. These variables can be updated alternatively.
- (1)
- Updating J
After deleting the irrelevant terms, the problem (9) is written as:
Let the first derivative be equal to zero, we obtain:
- (2)
- Updating G
Let the first derivative be equal to zero, we have:
- (3)
- Updating H
Let the first derivative be equal to zero, we have:
- (4)
- Updating Z
Let the first derivative equal to zero, we have:
- (5)
- Updating B
For B, the subproblem is:
According to the Ky Fan Theorem [42], problem (18) can be rewritten as:
where , U consists of k eigenvectors associated with the k smallest eigenvalues of Diag (B1) − B. I denotes the identity matrix and 1 denotes a column vector with all elements being 1.
For Equation (19), it is equivalent to:
Let , , then .
Once we obtain the matrix B, we can calculate the similarity matrix by , and then, we can obtain the clustering results by applying the spectral clustering algorithm [20]. The updating process is terminated when the convergence condition is reached, i.e., , where is the stop threshold.
To make the process clear, the complete procedures to solve problem (7) is outlined as follows (Algorithm 1).
| Algorithm 1 The Algorithm of KBDSP |
| Input: Kernel matrix K, parameters , number of cluster k, Initialize: Random matrix Repeat 1. Calculate by using the solution (11); 2. Calculate according to the solution (13); 3. Calculate by using the solution (15); 4. Calculate according to (17); 5. Calculate by solving (20); 6. Update Lagrange multipliers ; Until stopping criterion is met. |
4. Experimental Results and Analysis
To verify the effectiveness of our KBDSP algorithm, we perform our experiments on nine widely used benchmark datasets and compare the results with state-of-the-art methods.
4.1. Datasets
Nine corresponding benchmark datasets are used in our experiments, including five face image datasets (YALE, http://www.cvc.yale.edu/projects/yalefaces/yalefaces.html, accessed on 16 May 2012; JAFFE, http://www.kasrl.org/jaffe.html, accessed on 28 May 2020; ORL, https://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html, accessed on 28 May 2020; AR, http://www2.ece.ohio-state.edu/∼aleix/ARdatabase.html, accessed on 28 May 2020 and COIL20, http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php, accessed on 28 May 2020), a binary alpha digit’s dataset BA, and three text datasets (Tr11, Tr41, and Tr45).
The YALE dataset consists of 165 grayscale face images of 15 people. For each individual, there are 11 images, which were obtained under varying illuminations, and all the images are resized to the size of 32 × 32. The JAFFE dataset consists of 213 face images of seven facial expressions, each of which is resized to 26 × 26 pixels. The ORL dataset is composed of 400 face images from 40 people. For each person, there are 10 images, which were obtained under varying lighting and varying facial expressions, and all the images are resized to 26 × 26. The AR database is composed of more than 4000 frontal images from 126 individuals, 120 of which are used in our experiment [37]. The 120 individuals consist of 65 men and 55 women. The COIL20 dataset consists of 72 images of 20 individuals, and all the images are resized to 32 × 32 pixels. The BA dataset contains 1404 handwritten digits images, including digits “0” to “9” and uppercase letters “A” to “Z”. The sizes of all these images are 20 ×16 pixels. The text datasets include TR11, TR41, and TR45. The detailed information of these datasets is presented in Table 1.

Table 1.
Detailed information of the nine widely used datasets.
4.2. Comparison of the Methods
We compare our KBDSP method with several state-of-the-art methods, including SC [17], KSSC [30], KLRR [14], IBDLR [40], SLKEs [35], SLKEr [35], SLSPs [36], and SLSPr [36]. These state-of-the-art methods can be classified into three types: clustering methods based on similarity preservation, clustering methods based on kernel self-expression, and clustering methods based on block diagonal representation. To show faithful comparison, all parameters of these state-of-the-art methods are manually tuned to be the best. The parameter settings of all experimental methods have been shown in Table 2, in which the recommended parameters are indicated in bold.

Table 2.
Parameter settings.
4.3. Evaluation Metrics
To effectively evaluate the KBDSP algorithm and other advanced algorithms quantitatively, three public evaluation metrics are adopted, which are clustering accuracy (ACC), normalized mutual information (NMI), and Purity [37].
Suppose n is the total number of sample points. We use and to denote the cluster label and the ground truth cluster label, respectively. Then accuracy is defined as follows:
where denotes the Kronecker delta function, and it takes the value 1 if x and y are equal, otherwise it takes the value 0. The is a mapping function by which each cluster label can be mapped to ground truth cluster label according to the Kuhn–Munkers algorithm.
We use S and to denote the set of clustering that generated from a clustering algorithm and the ground truth set of clustering, respectively. Then NIM is defined as:
where and are the marginal probability distribution functions of S and , respectively. denotes the joint probability density functions of S and . represents the entropy function. The larger the value of NMI, the higher similar S and are.
Purity is used to measure the overall precision of the clusters, and it is defined as
The higher these three metrics are, the better the clustering performance.
4.4. Kernel Design
As with the literature [14], we design 12 kernels in this work which include 7 Gaussian kernels, 4 polynomial kernels and a linear kernel. The Gaussian kernel function is defined as , where parameter σ denotes the maximal distance between and , and parameter l takes values in the set {0.01, 0.05, 0.1, 1, 10, 50, 100}. The polynomial kernel function is defined as , where parameter a takes values in the set {0, 1} and parameter b takes values in the set {2, 4}. The linear kernel is defined as .
4.5. Experimental Results and Analysis
We perform the proposed method on the nine datasets including Yale, JAFFE, ORL, AR, COIL20, BA, TR11, TR41, and TR45. We conduct all the experimental methods on the 12 kernels, and the average experimental results over 12 kernels are computed at each run of the experiment. The experiment is repeated ten times for each experimental method, and the average experimental results are displayed in Table 3. The best results are highlighted with boldface. As can be seen in Table 3, the proposed method presents the best performance in comparison with other methods in most cases, which shows the effectiveness of introducing block diagonal representation term and the similarity-preserving term in our model.
Specifically, we obtain the following eight findings from the results listed in Table 3.
- (1)
- SC is a representative clustering approach. Compared to the SC algorithm, our proposed KBDSP obtains better results in terms of three evaluation metrics, namely ACC, NMI, and Purity. From Table 3, we can see the average values of three evaluation metrics of KBDSP are 19%, 18%, and 22%, which are higher than SC, respectively. This is attributed to the advantage that the learned Z is an input of SC instead of the kernel matrix in SC.
- (2)
- KSSC and KLRR methods have made satisfactory results in many fields because they can exploit the nonlinear structure of original data. It is worth mentioning that our method outperforms these two methods in most cases. The superiority of KBDSP derives from our similarity-preserving strategy.
- (3)
- Compared to SLKEs and SLKEr, KBDSP obtains a higher performance. The reasons for performance improvement have two aspects: one is that our kernel self-expression frame can preserve some low-order information of input data, which is lost in SLKEs and SLKEr methods; the other is that we can learn a similarity matrix with block diagonal structure by introducing the block diagonal representation term to our model.
- (4)
- SLSPs and SLSPr can not only handle nonlinear datasets, but also preserve similar information. The experimental results of the two methods are shown in Table 3, from which we can see they have improved performance compared to SC, KSSC, KLRR, SLKEs and SLKEr. However, KBDSP still outperforms them in most instances. For example, from Table 3, we can see the average values of three evaluation metrics of KBDSP are 14%, 15%, and 2%, which are higher than SLSPs, respectively. These results prove that the introduced block diagonal representation term can help boost performance.
- (5)
- IBDLR and KBDSP enable the learning desired affinity matrix with an optimal block diagonal structure by importing block diagonal representation term. From Table 3, it can be seen that KBDSP and IBDLR have better performance than other algorithms except SLSPs on all datasets, which verifies that KBDSP and IBDLR methods with block diagonal representation term are effective. This indicates that the KBDSP and IBDLR are beneficial for datasets that have many classes, and that they can capture the block diagonal structure of data. For COIL20 and BA datasets, which have a greater number of instances, Table 3 shows that our KBDSP achieves nearly 13% higher than other compared methods apart from IBDLR on the COIL20 dataset. In addition, as can be seen in Table 3, we can observe that KBDSP outperforms IBDLR on the COIL20 dataset; this is because our method considers the similarity-preserving strategy, but the IBDLR method does not.
- (6)
- For the TR11, TR41, and TR45 datasets, which have high dimensions of features, SLSPr presents better performance than IBDLR because it introduces a similarity-preserving mechanism. Benefiting from the similarity-preserving strategy and block diagonal representation term, the proposed KBDSP consistently outperforms IBDLR and even SLSPr in most cases on the TR11, TR41, and TR45 datasets. This indicates KBDSP is beneficial, performing well with the amount of information provided by datasets that have rich features, such that KBDSP can exploit the intrinsic structure of data.
- (7)
- From Table 3, it can be seen that our proposed KBDSP method has the smallest standard deviation in almost all cases, which means that KBDSP has good stability.
- (8)
- The one-way ANOVA was used to test the significant difference in the Purity of compared methods. From Figure 1, we can see that the p-values for the Purity metric is less than 0.05, showing significant difference between performance of the proposed and existing methods.
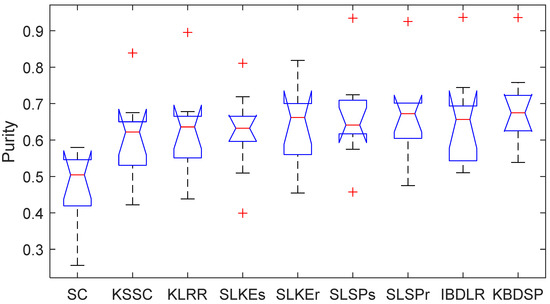 Figure 1. The results of ANOVA for Purity of compared methods (F = 2.65, p = 0.0132).
Figure 1. The results of ANOVA for Purity of compared methods (F = 2.65, p = 0.0132).
In summary, the experimental results demonstrate that our method can beat others in almost all experiments. This is because our method introduces simultaneously the similarity-preserving mechanism, block diagonal representation term, and kernel self-expressing model. Experimental results prove the proposed KBDSP can not only exploit the intrinsic structure and nonlinear structure of original data, but also obtain a coefficient matrix with an optimal block diagonal structure. Therefore, KBDSP can obtain better clustering performance compared to other state-of-the-art methods.


Table 3.
Clustering results (mean ± standard deviation) of the compared methods.
Table 3.
Clustering results (mean ± standard deviation) of the compared methods.
| Data | Metrics | SC [17] | KSSC [30] | KLRR [14] | SLKEs [35] | SLKEr [35] | SLSPs [36] | SLSPr [36] | IBDLR [40] | KBDSP * |
|---|---|---|---|---|---|---|---|---|---|---|
| Yale | ACC | 0.4425 ± 0.042 | 0.4715 ± 0.042 | 0.4569 ± 0.037 | 0.3404 ± 0.043 | 0.4768 ± 0.045 | 0.3768 ± 0.053 | 0.528 ± 0.024 | 0.4727 ± 0.045 | 0.5626 ± 0.020 |
| NMI | 0.4859 ± 0.043 | 0.4761 ± 0.040 | 0.4882 ± 0.034 | 0.3799 ± 0.046 | 0.5047 ± 0.038 | 0.4030 ± 0.058 | 0.5425 ± 0.021 | 0.5122 ± 0.043 | 0.5662 ± 0.018 | |
| Purity | 0.4665 ± 0.041 | 0.5379 ± 0.028 | 0.5862 ± 0.032 | 0.6323 ± 0.042 | 0.5747 ± 0.030 | 0.6313 ± 0.047 | 0.6138 ± 0.019 | 0.5212 ± 0.038 | 0.6394 ± 0.015 | |
| JAFFE | ACC | 0.5563 ± 0.045 | 0.7691 ± 0.039 | 0.7358 ± 0.042 | 0.6625 ± 0.053 | 0.7409 ± 0.054 | 0.7514 ± 0.052 | 0.9031 ± 0.043 | 0.9081 ± 0.022 | 0.9091 ± 0.016 |
| NMI | 0.6069 ± 0.034 | 0.7145 ± 0.037 | 0.7414 ± 0.051 | 0.7847 ± 0.050 | 0.7691 ± 0.058 | 0.7656 ± 0.053 | 0.8991 ± 0.038 | 0.8971 ± 0.029 | 0.9178 ± 0.010 | |
| Purity | 0.5798 ± 0.037 | 0.8389 ± 0.015 | 0.8955 ± 0.039 | 0.8108 ± 0.037 | 0.8187 ± 0.051 | 0.9345 ± 0.018 | 0.9253 ± 0.035 | 0.9369 ± 0.016 | 0.9362 ± 0.011 | |
| ORL | ACC | 0.4948 ± 0.043 | 0.4573 ± 0.033 | 0.4971 ± 0.047 | 0.3696 ± 0.041 | 0.5865 ± 0.044 | 0.3858 ± 0.052 | 0.6075 ± 0.049 | 0.6071 ± 0.042 | 0.6340 ± 0.012 |
| NMI | 0.6981 ± 0.035 | 0.6094 ± 0.030 | 0.5461 ± 0.038 | 0.5614 ± 0.043 | 0.7580 ± 0.039 | 0.5304 ± 0.057 | 0.7758 ± 0.043 | 0.7696 ± 0.037 | 0.7964 ± 0.010 | |
| Purity | 0.5387 ± 0.034 | 0.6372 ± 0.024 | 0.6421 ± 0.033 | 0.6302 ± 0.041 | 0.6812 ± 0.046 | 0.7044 ± 0.024 | 0.7013 ± 0.034 | 0.6765 ± 0.036 | 0.7110 ± 0.009 | |
| AR | ACC | 0.2205 ± 0.017 | 0.4116 ± 0.018 | 0.4888 ± 0.021 | 0.2866 ± 0.012 | 0.2479 ± 0.019 | 0.4247 ± 0.014 | 0.5056 ± 0.022 | 0.5010 ± 0.026 | 0.5083 ± 0.013 |
| NMI | 0.5797 ± 0.012 | 0.6687 ± 0.012 | 0.7131 ± 0.014 | 0.6022 ± 0.010 | 0.5616 ± 0.009 | 0.6750 ± 0.026 | 0.7466 ± 0.020 | 0.7484 ± 0.018 | 0.6954 ± 0.014 | |
| Purity | 0.2558 ± 0.009 | 0.5090 ± 0.016 | 0.5659 ± 0.018 | 0.3992 ± 0.008 | 0.4545 ± 0.024 | 0.5749 ± 0.028 | 0.5870 ± 0.008 | 0.5502 ± 0.025 | 0.5833 ± 0.012 | |
| COIL20 | ACC | 0.4205 ± 0.041 | 0.5744 ± 0.038 | 0.5776 ± 0.039 | 0.4537 ± 0.024 | 0.5237 ± 0.040 | 0.5341 ± 0.038 | 0.5362 ± 0.032 | 0.6922 ± 0.023 | 0.7119 ± 0.006 |
| NMI | 0.5381 ± 0.035 | 0.7050 ± 0.038 | 0.6888 ± 0.036 | 0.6047 ± 0.034 | 0.6657 ± 0.038 | 0.6628 ± 0.052 | 0.6649 ± 0.032 | 0.7877 ± 0.019 | 0.7977 ± 0.006 | |
| Purity | 0.4559 ± 0.029 | 0.6751 ± 0.020 | 0.6611 ± 0.022 | 0.7190 ± 0.018 | 0.7420 ± 0.042 | 0.7241 ± 0.020 | 0.6106 ± 0.016 | 0.7442 ± 0.011 | 0.7578 ± 0.012 | |
| BA | ACC | 0.2785 ± 0.026 | 0.3711 ± 0.028 | 0.3280 ± 0.027 | 0.3533 ± 0.021 | 0.4088 ± 0.033 | 0.4103 ± 0.034 | 0.4128 ± 0.020 | 0.3643 ± 0.029 | 0.4252 ± 0.016 |
| NMI | 0.4387 ± 0.027 | 0.5249 ± 0.021 | 0.4501 ± 0.030 | 0.5278 ± 0.028 | 0.5361 ± 0.038 | 0.5441 ± 0.033 | 0.5461 ± 0.022 | 0.4997 ± 0.033 | 0.5704 ± 0.015 | |
| Purity | 0.3095 ± 0.025 | 0.4219 ± 0.023 | 0.4383 ± 0.034 | 0.5093 ± 0.012 | 0.5163 ± 0.040 | 0.4573 ± 0.034 | 0.4749 ± 0.021 | 0.5102 ± 0.041 | 0.5386 ± 0.017 | |
| TR11 | ACC | 0.4335 ± 0.053 | 0.4443 ± 0.055 | 0.3364 ± 0.049 | 0.4043 ± 0.036 | 0.4986 ± 0.041 | 0.4016 ± 0.033 | 0.5135 ± 0.023 | 0.5183 ± 0.039 | 0.5234 ± 0.025 |
| NMI | 0.3142 ± 0.031 | 0.3863 ± 0.036 | 0.2375 ± 0.026 | 0.2831 ± 0.035 | 0.4408 ± 0.054 | 0.2744 ± 0.041 | 0.4576 ± 0.040 | 0.4372 ± 0.064 | 0.4752 ± 0.030 | |
| Purity | 0.5043 ± 0.029 | 0.6417 ± 0.032 | 0.5064 ± 0.038 | 0.6254 ± 0.032 | 0.6860 ± 0.057 | 0.6409 ± 0.058 | 0.6886 ± 0.020 | 0.6749 ± 0.044 | 0.6747 ± 0.022 | |
| TR41 | ACC | 0.4452 ± 0.021 | 0.5179 ± 0.026 | 0.5344 ± 0.037 | 0.3885 ± 0.026 | 0.4588 ± 0.033 | 0.4192 ± 0.032 | 0.5555 ± 0.028 | 0.4964 ± 0.034 | 0.5558 ± 0.020 |
| NMI | 0.3657 ± 0.032 | 0.4438 ± 0.047 | 0.4642 ± 0.032 | 0.3635 ± 0.054 | 0.3691 ± 0.050 | 0.3170 ± 0.060 | 0.5345 ± 0.040 | 0.4462 ± 0.051 | 0.5453 ± 0.024 | |
| Purity | 0.5672 ± 0.025 | 0.5934 ± 0.028 | 0.6359 ± 0.040 | 0.6472 ± 0.046 | 0.6361 ± 0.048 | 0.6412 ± 0.034 | 0.6724 ± 0.019 | 0.5966 ± 0.048 | 0.6501 ± 0.019 | |
| TR45 | ACC | 0.4561 ± 0.034 | 0.4771 ± 0.038 | 0.4953 ± 0.041 | 0.5594 ± 0.044 | 0.5632 ± 0.044 | 0.5319 ± 0.037 | 0.6025 ± 0.030 | 0.5284 ± 0.044 | 0.6492 ± 0.026 |
| NMI | 0.3310 ± 0.027 | 0.3909 ± 0.050 | 0.4084 ± 0.035 | 0.4773 ± 0.061 | 0.4995 ± 0.056 | 0.4430 ± 0.036 | 0.5394 ± 0.036 | 0.4570 ± 0.060 | 0.6027 ± 0.030 | |
| Purity | 0.5059 ± 0.031 | 0.6221 ± 0.023 | 0.6781 ± 0.029 | 0.6449 ± 0.040 | 0.6617 ± 0.053 | 0.6989 ± 0.025 | 0.7014 ± 0.015 | 0.6563 ± 0.050 | 0.7060 ± 0.024 | |
| Avg | ACC | 0.4164 ± 0.036 | 0.4994 ± 0.037 | 0.4945 ± 0.037 | 0.4243 ± 0.033 | 0.5006 ± 0.039 | 0.4706 ± 0.038 | 0.5739 ± 0.030 | 0.5654 ± 0.034 | 0.6088 ± 0.017 |
| NMI | 0.4843 ± 0.031 | 0.5466 ± 0.035 | 0.5264 ± 0.033 | 0.5094 ± 0.040 | 0.5672 ± 0.042 | 0.5128 ± 0.046 | 0.6341 ± 0.032 | 0.6172 ± 0.039 | 0.6630 ± 0.016 | |
| Purity | 0.4648 ± 0.029 | 0.6086 ± 0.023 | 0.6233 ± 0.031 | 0.6243 ± 0.031 | 0.6412 ± 0.043 | 0.6675 ± 0.032 | 0.6639 ± 0.021 | 0.6519 ± 0.029 | 0.6886 ± 0.016 |
The asterisk (*) in the table represents the proposed algorithm.
4.6. Computational Complexity Analysis
We analyze the computational complexity of our proposed KBDSP method. KBDSP mainly includes two steps. The first step is to construct the kernel matrix, which has complexity. The second step is to implement Algorithm 1. The computational complexity of the second step is mainly determined by complexity of updating J, G, H, A, Z and B. The complexities of updating J, G, H, A and Z are ,, ,, respectively. Updating B requires . Therefore, the total time complexity of KBDSP is , where n is the number of data points and t is the number of iterations in KBDSP.
4.7. Robustness Experiments
In this section, we verify the robustness of our KBDSP. As shown in Figure 2, pixels of a certain percentage in each image of the Yale dataset were corrupted Gaussian noise with a mean 0 and a variance 0.1. The percentage of corrupted pixels in each image varies randomly from 10% to 90% with a step of 20%. To ensure the reliability of the results, we repeat experiments for each method 10 times and report the average results. The ACC metric is used for evaluation. The experiments’ results are shown in Figure 3. As can be seen from Figure 3, the ACC of all methods decreases significantly when more pixels are corrupted by noise. In addition, it can be seen that our KBDSP method obtains the best results. This is mainly because KBDSP uses the similarity-preserving strategy, which can effectively suppress noise.

Figure 2.
Example images of the Yale dataset corrupted by Gaussian noise.
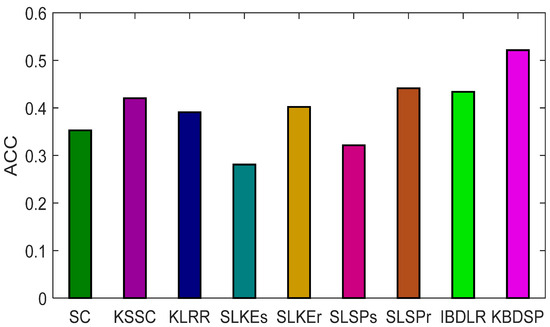
Figure 3.
ACC of Yale dataset with Gaussian noise.
4.8. Parameter Sensitivity Analysis and Convergence Analysis
There are three parameters in the proposed KBDSP, i.e., and γ. The parameter is used to balance the similarity-preserving term , parameter β is used to control the term , and parameter γ is used to control the block diagonal representation term . The Yale and JAFFE datasets are selected for the evaluation of KBDSP. As shown in Figure 4 and Figure 5, the NMI versus different values of parameters and γ are shown. Parameters and γ take values in set , , and , respectively. From Figure 4 and Figure 5, it can be seen that KBDSP performs well for a wide range of and γ on the two datasets, and KBDSP is not very sensitive to these parameters. Moreover, when parameters and γ are set to 0.01, 0.001, and 0.1, respectively, the clustering performance of KBDSP is better than other comparison methods. Therefore, we fix , and γ = 0.1 for KBDSP in all experiments of this paper.
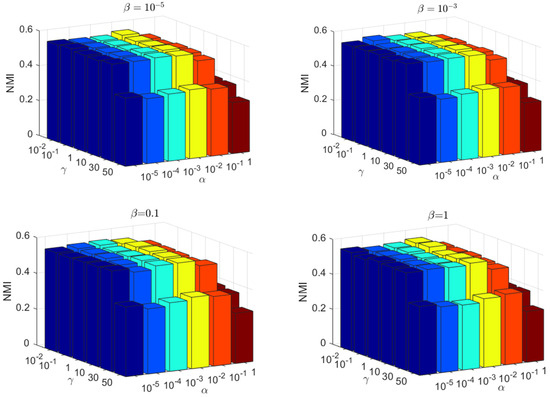
Figure 4.
The NMI versus different values of parameters on the Yale datasets.
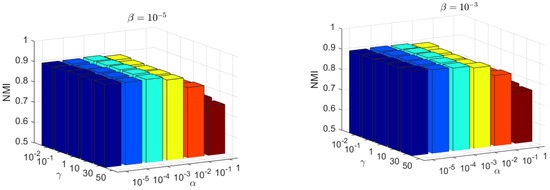
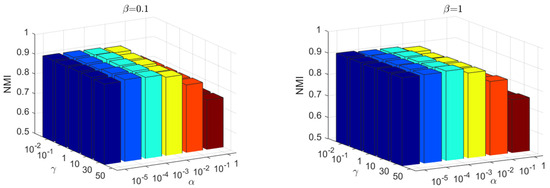
Figure 5.
The NMI versus different values of parameters on the JAFFE datasets.
For convergence analysis, we show the empirical convergence curves of the KBDSP algorithm on four datasets in Figure 6. The four datasets are YALE, ORL, JAFFE, and TR45, respectively. It is observed that our method converges in objective value within a few iterations and reaches a steady state with more iterations, which indicates fast convergence and efficiency of KBDSP.
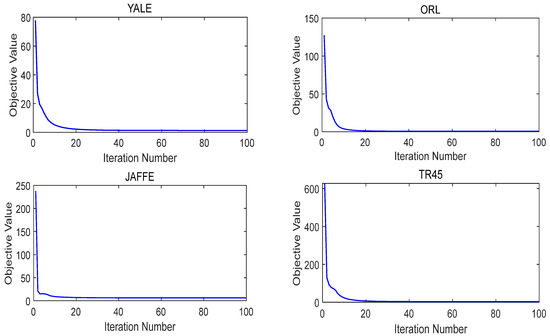
Figure 6.
The convergence curve of KBDSP on four datasets.
5. Conclusions
In this paper, a novel subspace clustering method based on kernel block diagonal representation and similarity-preserving strategy is proposed. The proposed KBDSP method has three steps: (1) capture the nonlinear structure of input data by introducing the kernel self-expressing frame to our model; (2) generate a similarity matrix with block diagonal structure by introducing the block diagonal representation term to our model; (3) capture the pairwise similarity information between data points by introducing the similarity-preserving term to our model. In this study, we conducted experiments on nine benchmark datasets. Experimental results have well demonstrated the effectiveness and superiority of the proposed KBDSP method. In future work, we will consider extending KBDSP to the deep framework to further improve its performance utilizing nonlinear information. In the proposed KBDSP, we only use single kernel methods to conduct the algorithm. Therefore, in the future, we will also research multiple kernel learning methods to improve the KBDSP method.
Author Contributions
Conceptualization, Y.Y.; Methodology, Y.Y.; Formal analysis, F.L.; Writing—original draft, F.L.; Visualization, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Basic Research Plan in Shaanxi Province (No. 2020JM-543), and the Key Research and Development Project of Shaanxi Province (No. 2021GY-083).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The codes and data used in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare that there are no conflicts of interests; we do not have any possible conflicts of interest.
References
- Li, C.G.; You, C.; Vidal, R. Structured Sparse Subspace Clustering: A Joint Affinity Learning and Subspace Clustering Framework. IEEE Trans. Image Process. 2017, 26, 2988–3001. [Google Scholar] [CrossRef]
- Agrawal, R.; Gehrke, J.; Gunopulos, D.; Raghavan, P. Automatic subspace clustering of high dimensional data for data mining applications. ACM 1998, 27, 94–105. [Google Scholar]
- Qin, Y.; Wu, H.; Zhao, J.; Feng, G. Enforced block diagonal subspace clustering with closed form solution. Pattern Recognit. 2022, 130, 108791. [Google Scholar] [CrossRef]
- Jia, H.; Zhu, D.; Huang, L.; Mao, Q.; Wang, L.; Song, H. Global and local structure preserving nonnegative subspace clustering. Pattern Recognit. 2023, 138, 109388. [Google Scholar] [CrossRef]
- Maggu, J.; Majumdar, A. Kernelized transformed subspace clustering with geometric weights for non-linear manifolds. Neurocomputing 2023, 520, 141–151. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, A.Y.; Derksen, H.; Fossum, R. Estimation of subspace arrangements with applications in modeling and segmenting mixed data. SIAM Rev. 2018, 50, 413–458. [Google Scholar] [CrossRef]
- Hong, W.; Wright, J.; Huang, K.; Ma, Y. Multi-scale hybrid linear models for lossy image representation. IEEE Trans. Image Process. 2006, 15, 3655–3671. [Google Scholar] [CrossRef]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef]
- Shi, X.; Guo, Z.; Xing, F.; Cai, J.; Yang, L. Self-learning for face clustering. Pattern Recognit. 2018, 79, 279–289. [Google Scholar] [CrossRef]
- Ho, J.; Yang, M.H.; Lim, J.; Lee, K.C.; Kriegman, D. Clustering appearances of objects under varying illumination conditions. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; Volume 1, pp. 11–18. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Vidal, R.; Ma, Y.; Sastry, S. Generalized principal component analysis (GPCA). IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1945–1959. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Feng, J.; Lin, Z.; Mei, T.; Yan, S. Subspace clustering by block diagonal representation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 487–501. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Tan, M.; Xu, D.; Dong, Z.Y. Robust kernel low-rank representation. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 2268–2281. [Google Scholar] [CrossRef] [PubMed]
- Sekmen, A.; Koku, B.; Parlaktuna, M.; Abdul-Malek, A.; Vanamala, N. Unsupervised deep learning for subspace clustering, in: Big Data (Big Data). In Proceedings of the 2017 IEEE International Conference on IEEE, Boston, MA, USA, 11–14 December 2017; pp. 2089–2094. [Google Scholar]
- Ng, A.Y.; Jordan, M.I.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 9–14 December 2002; pp. 849–856. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 171–184. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Min, H.; Zhao, Z.-Q.; Zhu, L.; Huang, D.-S.; Yan, S. Robust and efficient subspace segmentation via least squares regression. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany. [Google Scholar]
- Luo, D.; Nie, F.; Ding, C.; Huang, H. Multi-subspace representation and discovery. In Proceedings of the Joint European Conference Machine Learning and Knowledge Discovery in Databases, Athens, Greece, 5–9 September 2011; pp. 405–420. [Google Scholar]
- Lu, C.; Feng, J.; Lin, Z.; Yan, S. Correlation adaptive subspace segmentation by trace lasso. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 1345–1352. [Google Scholar]
- Feng, J.; Lin, Z.; Xu, H.; Yan, S. Robust subspace segmentation with block diagonal prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3818–3825. [Google Scholar]
- Chen, S.B.; Ding, C.H.; Luo, B. Similarity learning of manifold data. IEEE Trans. Cybern. 2015, 45, 1744–1756. [Google Scholar] [CrossRef]
- Seung, H.S.; Lee, D.D. The manifold ways of perception. Science 2000, 290, 2268–2269. [Google Scholar] [CrossRef]
- Kang, Z.; Peng, C.; Cheng, Q. Kernel-driven similarity learning. Neurocomputing 2017, 267, 210–219. [Google Scholar] [CrossRef]
- Ji, P.; Reid, I.; Garg, R.; Li, H. Adaptive low-rank kernel subspace clustering. arXiv 2017, arXiv:1707.04974. [Google Scholar]
- Liu, M.; Wang, Y.; Sun, J.; Ji, Z. Adaptive low-rank kernel block diagonal representation subspace clustering. Appl. Intell. 2022, 52, 2301–2316. [Google Scholar] [CrossRef]
- Wang, J.; Saligrama, V.; Castañón, D.A. Structural similarity and distance in learning. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; pp. 744–751. [Google Scholar]
- Patel, V.M.; Van Nguyen, H.; Vidal, R. Latent space sparse subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, NSW, Australia, 1–8 December 2013; pp. 225–232. [Google Scholar]
- Patel, V.M.; Vidal, R. Kernel sparse subspace clustering. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 2849–2853. [Google Scholar]
- Nguyen, H.; Yang, W.; Shen, F.; Sun, C. Kernel low rank representation for face recognition. Neurocomputing 2015, 155, 32–42. [Google Scholar] [CrossRef]
- Haeffele, B.; Young, E.; Vidal, R. Structured low-rank matrix factorization: Optimality, algorithm, and applications to image processing. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 2007–2015. [Google Scholar]
- Kang, Z.; Lu, Y.; Su, Y.; Li, C.; Xu, Z. Similarity Learning via Kernel Preserving Embedding. AAAI 2019, 33, 4057–4064. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Kang, Z.; Xu, H.; Wang, B.; Zhu, H.; Xu, Z. Clustering with similarity preserving. Neurocomputing 2019, 365, 211–218. [Google Scholar] [CrossRef]
- Peng, X.; Feng, J.; Zhou, J.T.; Lei, Y.; Yan, S. Deep Subspace Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5509–5521. [Google Scholar] [CrossRef] [PubMed]
- Kang, Z.; Lu, X.; Lu, Y.; Peng, C.; Chen, W.; Xu, Z. Structure Learning with Similarity Preserving. Neural Netw. 2020, 129, 138–148. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Ren, Z.; Sun, Q.; Wu, M.; Yin, M.; Sun, Y. Joint correntropy metric weighting and block diagonal regularizer for robust multiple kernel subspace clustering. Inf. Sci. 2019, 500, 48–66. [Google Scholar] [CrossRef]
- Zhang, X.; Xue, X.; Sun, H.; Liu, Z.; Guo, L.; Guo, X. Robust multiple kernel subspace clustering with block diagonal representation and low-rank consensus kernel. Knowl.-Based Syst. 2021, 227, 107243. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Shao, L.; Yang, J. Discriminative block diagonal representation learning for image recognition. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3111–3125. [Google Scholar] [CrossRef]
- Xie, X.; Guo, X.; Liu, G.; Wang, J. Implicit block diagonal low-rank representation. IEEE Trans. Image Process. 2018, 27, 477–489. [Google Scholar] [CrossRef]
- Wang, L.; Huang, J.; Yin, M.; Cai, R.; Hao, Z. Block diagonal representation learning for robust subspace clustering. Inf. Sci. 2020, 526, 54–67. [Google Scholar] [CrossRef]
- Fan, K. On a theorem of Wey1 concerning eigenvalues of linear transformations I. Proc. Natl. Acad. Sci. USA 1949, 35, 652–655. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).