Seismic Exploration Methods for Structural Studies and for Active Fault Characterization: A Review
Abstract
:1. Introduction
2. Review of Reflection Seismology
3. Developments in Seismic Imaging
3.1. Dense-Wide Aperture Acquisition
3.2. Seismic Ray Tomography
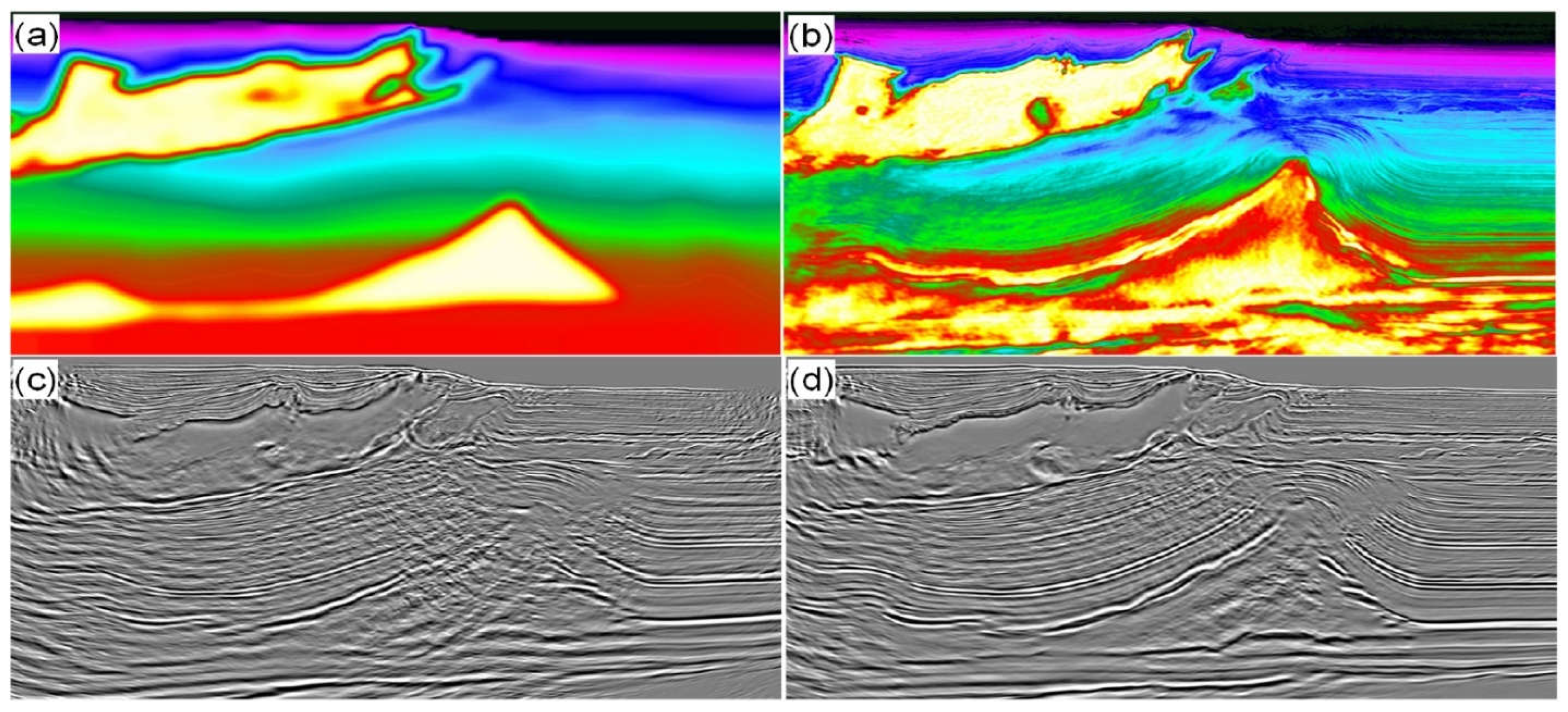
3.3. Full-Waveform Inversion
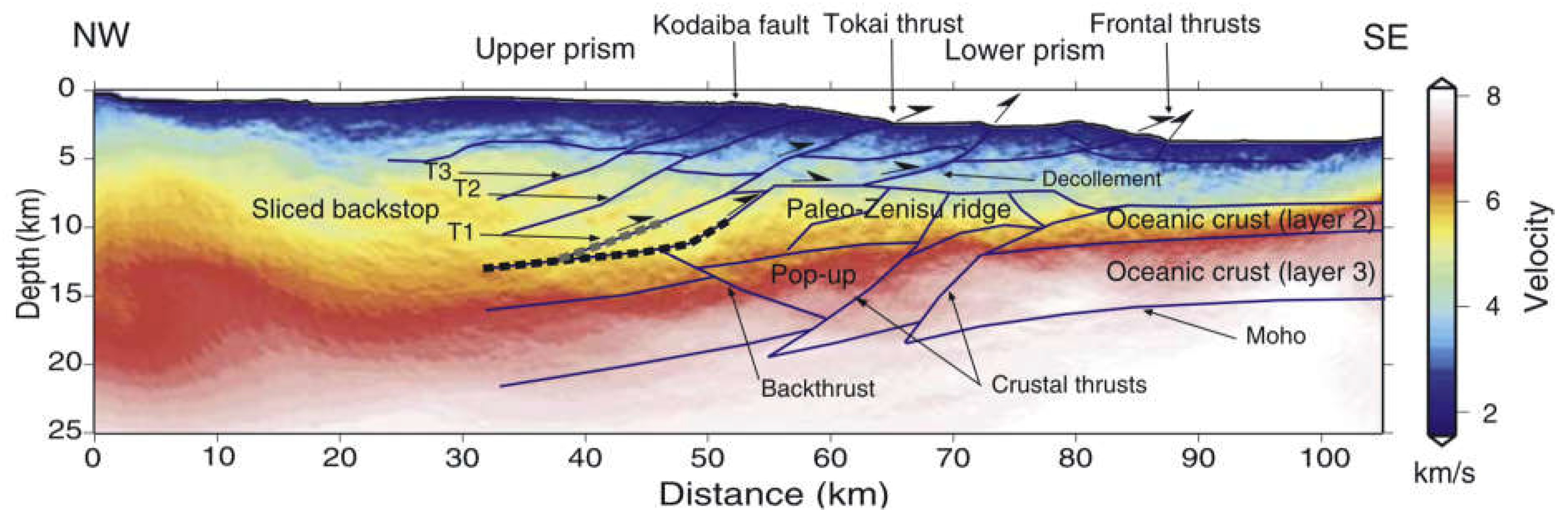
3.4. Pre-Stack Depth Migration
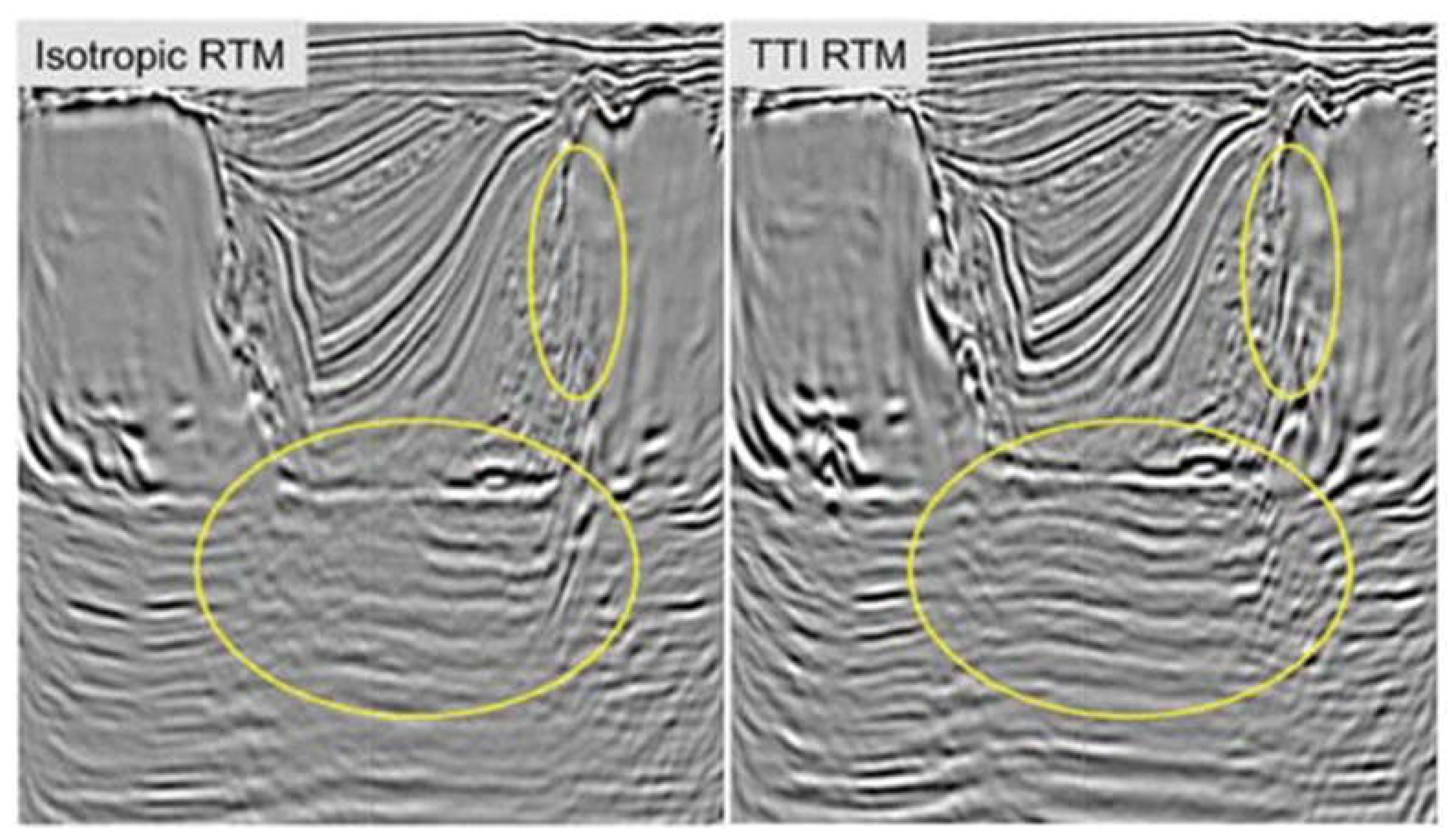
3.5. Seismic Anisotropy
4. Seismic Attributes
4.1. Reflection Strength Attributes
4.2. Instantaneous Frequency
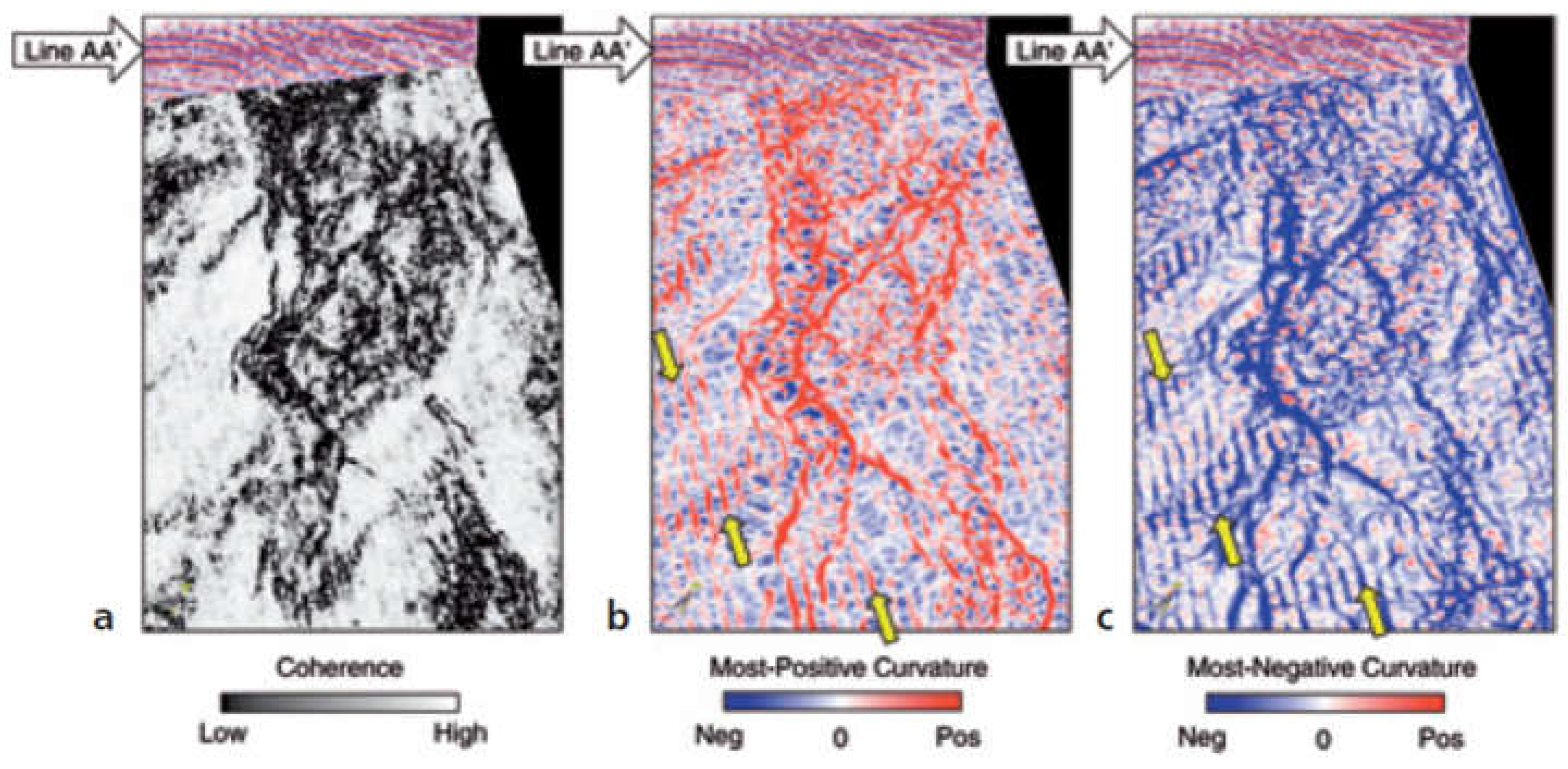
4.3. Coherence
4.4. Curvature
4.5. Polarization
4.6. Amplitude versus Offset Analysis
4.7. Seismic Attributes and Strain
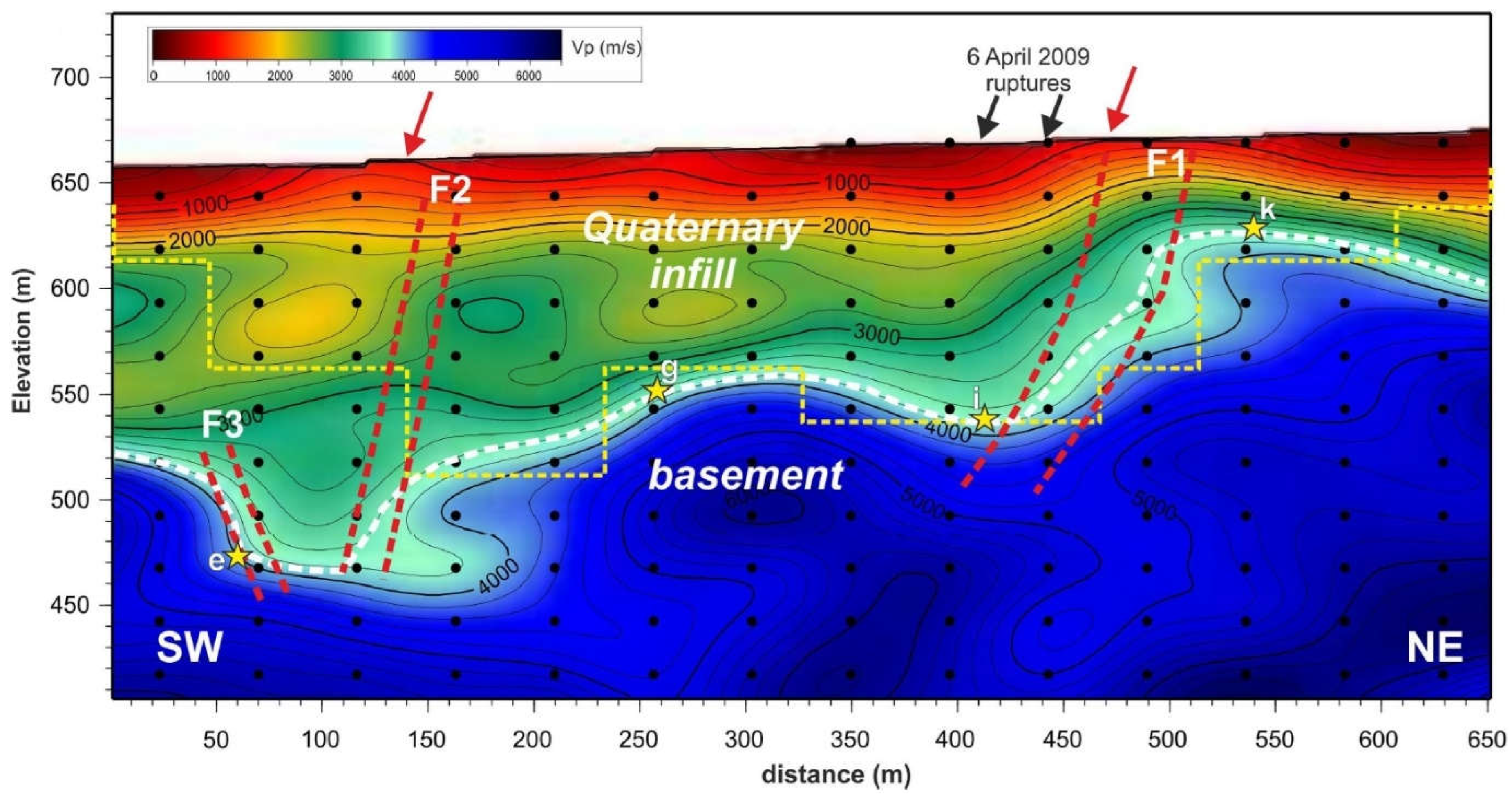
5. Active Fault Characterization
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- O’Brien, P.N.S. Aspects of seismic reflection prospecting for oil and gas. Geophys. J. Int. 1983, 74, 97–127. [Google Scholar] [CrossRef]
- Sheriff, R.; Geldart, L. Exploration Seismology; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wadsworth, G.P.; Robinson, E.A.; Bryan, J.G.; Hurley, P.M. Detection of reflection on seismic records by linear operators. Geophysics 1953, 18, 539–586. [Google Scholar] [CrossRef]
- Robinson, E.A.; Clark, R.D. Reflecting on the digital revolution. Lead. Edge 2005, 24, 1030–1032. [Google Scholar] [CrossRef]
- Robinson, E.A. The MIT Geophysical Analysis Group (GAG) from inception to 1954. Geophysics 2005, 70, 7JA–30JA. [Google Scholar] [CrossRef]
- Treitel, S. The MIT geophysical analysis group (GAG): 1954 and beyond. Geophysics 2005, 70, 31JA–35JA. [Google Scholar] [CrossRef]
- Steeples, D.W.; Schmeissner, C.M.; Macy, B.K. The Evolution of Shallow Seismic Exploration. J. Environ. Eng. Geophys. 1995, 1, 1–66. [Google Scholar] [CrossRef]
- Steeples Don, W. A review of shallow seismic methods. Ann. Geofis. 2000, 43, 1021–1044. [Google Scholar] [CrossRef]
- Tucker, P.M.; Yorston, H.J. Pitfalls in Seismic Interpretation; No. 2; SEG: Tulsa, OK, USA, 1973. [Google Scholar]
- Badley, M.E. Practical Seismic Interpretation; IHRDC Press: Boston, MA, USA, 1985. [Google Scholar]
- Avseth, P.; Mukerji, T.; Mavko, G. Quantitative Seismic Interpretation: Applying Rock Physics Tools to Reduce Interpretation Risk; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Khan, U.; Zhang, B.; Du, J.; Jiang, Z. 3D structural modeling integrated with seismic attribute and petrophysical evaluation for hydrocarbon prospecting at the Dhulian Oilfield, Pakistan. Front. Earth Sci. 2021, 15, 649–675. [Google Scholar] [CrossRef]
- McCalpin, J.P. Paleoseismology; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Yeats, R.S.; Sieh, K.E.; Allen, C.R. Geology of Earthquakes; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Thenhaus, P.C.; Campbell, K.W. Seismic hazard analysis: In Earthquake Engineering Handbook; Chen, W.F., Scawthorn, C., Eds.; CRC Press: Boca Raton, FL, USA, 2003; pp. 1–50. [Google Scholar]
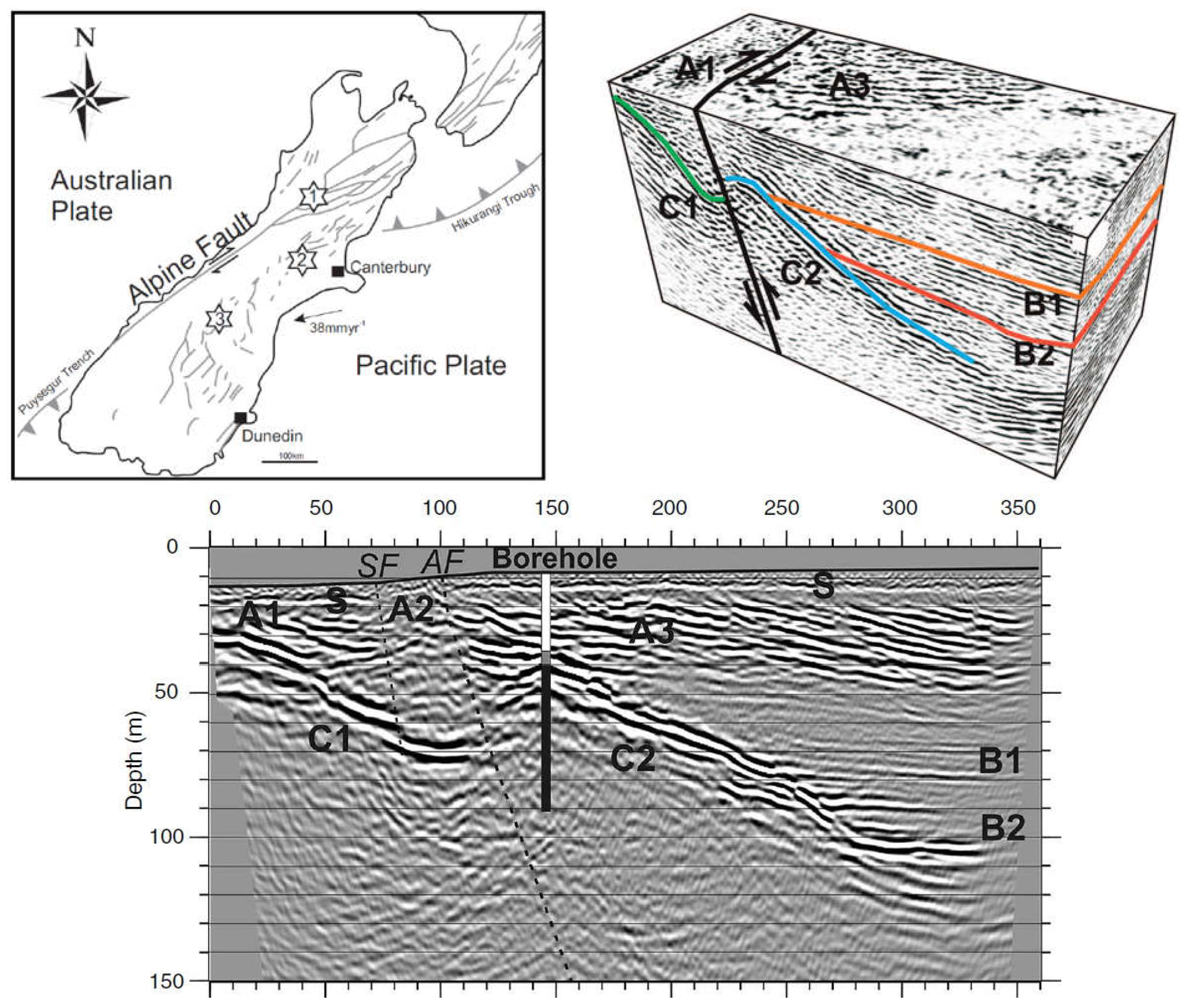
- Kaiser, A.E.; Horstmeyer, H.; Green, A.G.; Campbell, F.M.; Langridge, R.M.; McClymont, A.F. Detailed images of the shallow Alpine Fault Zone, New Zealand, determined from narrow-azimuth 3D seismic reflection data. Geophysics 2011, 76, B19–B32. [Google Scholar] [CrossRef]
- Maraio, S.; Villani, F.; Bruno, P.P.G.; Sapia, V.; Improta, L. Active fault detection and characterization by ultrashallow seismic imaging: A case study from the 2016 Mw 6.5 central Italy earthquake. Tectonophysics 2023, 850, 229733. [Google Scholar] [CrossRef]
- Waters, K.H. Reflection Seismology: A Tool for Energy Resource Exploration; Wiley: New York, NY, USA, 1981; p. 537. [Google Scholar]
- Yilmaz, O. Seismic data analysis (2 volumes). In Investigations in Geophysics; SEG: Tulsa, OK, USA, 2001; Volume 10, p. 1000. [Google Scholar]
- Caldwell, J.; Dragoset, W. A brief overview of seismic air-gun arrays. Lead. Edge 2000, 8, 817–928. [Google Scholar] [CrossRef]
- Stone, C.J.; Tasker, M.L. The effects of seismic airguns on cetaceans in UK waters. J. Cetacean Res. Manag. 2006, 8, 255. [Google Scholar] [CrossRef]
- Neidell, N.S.; Taner, M.T. Semblance and other coherency measures for multichannel data. Geophysics 1971, 36, 482–497. [Google Scholar] [CrossRef]
- Claerbout, J.F. Imaging the Earth’s Interior; Blackwell Scientific Publications: Hoboken, NJ, USA, 1985. [Google Scholar]
- Lailly, P. The seismic inverse problem as a sequence of before stack migrations. In Conference on Inverse Scattering: Theory and Application; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1983; pp. 206–220. [Google Scholar]
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC1–WCC26. [Google Scholar] [CrossRef]
- Biondi, B.; Almomin, A. Tomographic full waveform inversion (TFWI) by combining full waveform inversion with wave-equation migration velocity anaylisis. In SEG Technical Program Expanded Abstracts 2012; Society of Exploration Geophysicists: Houston, TX, USA, 2012; pp. 1–5. [Google Scholar]
- Richardson, A. Seismic full-waveform inversion using deep learning tools and techniques. arXiv 2018, arXiv:1801.07232. [Google Scholar]
- Zhang, Z.; Wu, Z.; Wei, Z.; Mei, J.; Huang, R.; Wang, P. FWI Imaging: Full-Wavefield Imaging through Full-Waveform Inversion: 90th Annual International Meeting, SEG Expanded Abstracts, 656–660. Abstract. 2020. Available online: https://library.seg.org/doi/abs/10.1190/segam2020-3427858.1 (accessed on 16 March 2023).
- Operto, S.; Ravaut, C.; Improta, L.; Virieux, J.; Herrero, A.; Dell’Aversana, P. Quantitative imaging of complex structures from dense wide-aperture seismic data by multiscale traveltime and waveform inversions: A case study. Geophys. Prospect. 2004, 52, 625–651. [Google Scholar] [CrossRef]
- Improta, L.; Bruno, P.P. Combining seismic reflection with multifold wide-aperture profiling: An effective strategy for high-resolution shallow imaging of active faults. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Bruno, P.P.; Castiello, A.; Villani, F.; Improta, L. High-resolution densely spaced wide-aperture seismic profiling as a tool to aid seismic hazard assessment of fault-bounded intramontane basins: Application to Vallo Di Diano, Southern Italy. Bull. Seismol. Soc. Am. 2013, 103, 1969–1980. [Google Scholar] [CrossRef]
- Ravaut, C.; Operto, S.; Improta, L.; Virieux, J.; Herrero, A.; Dell’Aversana, P. Multiscale imaging of complex structures from multifold wide-aperture seismic data by frequency-domain full-waveform tomography: Application to a thrust belt. Geophys. J. Int. 2004, 159, 1032–1056. [Google Scholar] [CrossRef]
- Wei, X.; Ruan, A.; Ding, W.; Wu, Z.; Dong, C.; Zhao, Y.; Niu, X.; Zhang, J.; Wang, C. Crustal structure and variation in the southwest continental margin of the South China Sea: Evidence from a wide-angle seismic profile. J. Asian Earth Sci. 2020, 203, 104557. [Google Scholar] [CrossRef]
- Nolet, G. Seismic Tomography: With Applications in Global Seismology and Exploration Geophysics; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Rawlinson, N.; Sambridge, M. Seismic traveltime tomography of the crust and lithosphere. Adv. Geophys. 2005, 46, 81–139. [Google Scholar]
- Zelt, C.A.; Barton, P.J. Three-dimensional seismic refraction tomography: A comparison of two methods applied to data from the Faeroe Basin. J. Geophys. Res. Solid Earth 1998, 103, 7187–7210. [Google Scholar] [CrossRef]
- Tarantola, A.; Valette, B. Generalized nonlinear inverse problems solved using the least squares criterion. Rev. Geophys. 1982, 20, 219–232. [Google Scholar] [CrossRef]
- Rawlinson, N.; Pozgay, S.; Fishwick, S. Seismic tomography: A window into deep Earth. Phys. Earth Planet. Inter. 2010, 178, 101–135. [Google Scholar] [CrossRef]
- Buddensiek, M.L.; Sheng, J.; Crosby, T.; Schuster, G.T.; Bruhn, R.L.; He, R. Colluvial wedge imaging using traveltime and waveform tomography along the Wasatch Fault near Mapleton, Utah. Geophys. J. Int. 2008, 172, 686–697. [Google Scholar] [CrossRef]
- Improta, L.; Villani, F.; Bruno, P.P.; Castiello, A.; De Rosa, D.; Varriale, F.; Punzo, M.; Brunori, C.A.; Civico, R.; Pierdominici, S.; et al. High-resolution controlled-source seismic tomography across the Middle Aterno basin in the epicentral area of the 2009, Mw 6.3, L’Aquila earthquake (central Apennines, Italy). Ital. J. Geosci. 2012, 131, 373–388. [Google Scholar]
- Villani, F.; Improta, L.; Pucci, S.; Civico, R.; Bruno, P.P.G.; Pantosti, D. Investigating the architecture of the Paganica Fault (2009 Mw 6.1 earthquake, central Italy) by integrating high-resolution multi-scale refraction tomography and detailed geological mapping. Geophys. J. Int. 2016, 208, ggw407. [Google Scholar]
- Bruno, P.P.G.; Villani, F.; Improta, L. High-Resolution Seismic Imaging of Fault-Controlled Basins: A Case Study From the 2009 Mw 6.1 Central Italy Earthquake. Tectonics 2022, 41, e2022TC007207. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Z.; Mei, J.; Lin, F.; Huang, R. Full-waveform inversion for salt: A coming of age. Lead. Edge 2019, 38, 204–213. [Google Scholar] [CrossRef]
- Brossier, R.; Operto, S.; Virieux, J. Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion. Geophysics 2009, 74, WCC105–WCC118. [Google Scholar] [CrossRef]
- Woodward, M.J.; Nichols, D.; Zdraveva, O.; Whitfield, P.; Johns, T. A decade of tomography. Geophysics 2008, 73, VE5–VE11. [Google Scholar] [CrossRef]
- Vantassel, J.P.; Kumar, K.; Cox, B.R. Using convolutional neural networks to develop starting models for near-surface 2-D full waveform inversion. Geophys. J. Int. 2022, 231, 72–90. [Google Scholar] [CrossRef]
- Zhang, Z.; Alkhalifah, T. Regularized elastic full-waveform inversion using deep learning. In Advances in Subsurface Data Analytics; Elsevier: Amsterdam, The Netherlands, 2022; pp. 219–250. [Google Scholar]
- Dessa, J.X.; Operto, S.; Kodaira, S.; Nakanishi, A.; Pascal, G.; Virieux, J.; Kaneda, Y. Multiscale seismic imaging of the eastern Nankai trough by full waveform inversion. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Shen, X.; Ahmed, I.; Brenders, A.; Dellinger, J.; Etgen, J.; Michell, S. Full-waveform inversion: The next leap forward in subsalt imaging. Lead. Edge 2018, 37, b1–b67. [Google Scholar] [CrossRef]
- Adamczyk, A.; Malinowski, M.; Malehmir, A. High-resolution near-surface velocity model building using full-waveform inversion—A case study from southwest Sweden. Geophys. J. Int. 2014, 197, 1693–1704. [Google Scholar] [CrossRef]
- Schneider, W. Integral formulation for migration in two and three dimensions. Geophysics 1978, 43, 49–76. [Google Scholar] [CrossRef]
- Hagedoorn, J. A process of seismic reflection interpretation. Geophys. Prospect. 1954, 2, 85–127. [Google Scholar] [CrossRef]
- Claerbout, J.F.; Doherty, S.M. Downward continuation of moveout-corrected seismo-grams. Geophysics 1972, 37, 741–768. [Google Scholar] [CrossRef]
- Gazdag, J. Wave-equation migration by phase shift. Geophysics 1978, 43, 1342–1351. [Google Scholar] [CrossRef]
- Stolt, R.H. Migration by Fourier transform. Geophysics 1978, 43, 23–48. [Google Scholar] [CrossRef]
- Stolt, R.H.; Benson, A.K. Seismic Migration: Theory and Practice; Geophysical Press: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Sen, M.K.; Stoffa, P.L. Global Optimization Methods in Geophysical Inversion; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- McMechan, G.A. Migration by extrapolation of time-dependent boundary values. Geophys. Prospect. 1983, 31, 413–420. [Google Scholar] [CrossRef]
- Baysal, E.; Kosloff, D.D.; Sherwood, J.W. Reverse time migration. Geophysics 1983, 48, 1514–1524. [Google Scholar] [CrossRef]
- Whitmore, N.D.; Lines, L.R. Vertical seismic profiling depth migration of a salt dome flank. Geophysics 1986, 51, 1087–1109. [Google Scholar] [CrossRef]
- Mora, P. Inversion = migration + tomography. Geophysics 1989, 54, 1575–1586. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; McMechan, G.A. Imaging conditions for prestack reverse-time migration. Geophysics 2008, 73, S81–S89. [Google Scholar] [CrossRef]
- Babuska, V.; Cara, M. Seismic Anisotropy in the Earth; Springer Science and Business Media: Berlin/Heidelberg, Germany, 1991; Volume 10. [Google Scholar]
- Savage, M.K. Seismic anisotropy and mantle deformation: What have we learned from shear wave splitting? Rev. Geophys. 1999, 37, 65–106. [Google Scholar] [CrossRef]
- Helbig, K.; Thomsen, L. 75-plus years of anisotropy in exploration and reservoir seismics: A historical review of concepts and methods. Geophysics 2005, 70, 9ND–23ND. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Wang, W.; Cai, Y.; Fang, L. Seismic anisotropy and implications for lithospheric deformation beneath the Ordos Block and surrounding regions. Geophys. J. Int. 2021, 226, 1885–1896. [Google Scholar] [CrossRef]
- Valcke, S.L.A.; Casey, M.; Lloyd, G.E.; Kendall, J.M.; Fisher, Q.J. Lattice preferred orientation and seismic anisotropy in sedimentary rocks. Geophys. J. Int. 2006, 166, 652–666. [Google Scholar] [CrossRef]
- Crampin, S. A review of wave motion in anisotropic and cracked elastic-media. Wave Motion 1981, 3, 343–391. [Google Scholar] [CrossRef]
- Crampin, S. Evaluation of anisotropy by shear-wave splitting. Geophysics 1985, 50, 142–152. [Google Scholar] [CrossRef]
- Crampin, S. The New Geophysics: Shear-wave splitting provides a window into the crack-critical rock mass. Lead. Edge 2003, 22, 536–549. [Google Scholar] [CrossRef]
- Lynn, H.B.; Thomsen, L. Shear wave exploration along the principal axis. In Proceedings of the 56th Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 2–6 November 1986; pp. 474–476. [Google Scholar]
- Willis, H.; Rethford, G.; Bielanski, E. Azimuthal anisotropy: The occurence and effect on shear wave data quality. In Proceedings of the 56th Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 2–6 November 1986; pp. 479–481. [Google Scholar]
- Martin, M.A.; Davis, T.L. Shear-wave birefringence: A new tool for evaluating fractured reservoirs. Lead. Edge 1987, 6, 22–28. [Google Scholar] [CrossRef]
- Li, Y.G.; Leary, P.C.; Aki, K. Observation and modelling of fault-zone fracture seismic anisotropy—II. P-wave polarization anomalies. Geophys. J. Int. 1987, 91, 485–492. [Google Scholar] [CrossRef]
- Alford, R.M. Shear data in the presence of azimuthal anisotropy. In Proceedings of the 56th Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 2–6 November 1986; pp. 476–479. [Google Scholar]
- Montagner, J.P.; Guillot, L. Seismic anisotropy and global geodynamics. Rev. Mineral. Geochem. 2002, 51, 353–385. [Google Scholar] [CrossRef]
- Long, M.D.; Becker, T.W. Mantle dynamics and seismic anisotropy. Earth Planet. Sci. Lett. 2010, 297, 341–354. [Google Scholar] [CrossRef]
- Schaeffer, A.J.; Lebedev, S.; Becker, T.W. Azimuthal seismic anisotropy in the Earth’s upper mantle and the thickness of tectonic plates. Geophys. Suppl. Mon. Not. R. Astron. Soc. 2016, 207, 901–933. [Google Scholar] [CrossRef]
- Tsvankin, I.; Gaiser, J.; Grechka, V.; Van Der Baan, M.; Thomsen, L. Seismic anisotropy in exploration and reservoir characterization: An overview. Geophysics 2010, 75, A15–A75. [Google Scholar] [CrossRef]
- Thomsen, L. Weak elastic anisotropy. Geophysics 1986, 51, 1954–1966. [Google Scholar] [CrossRef]
- Alkhalifah, T.; Tsvankin, I. Velocity analysis for transversely isotropic media. Geophysics 1995, 60, 1550–1566. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Y.; Zhang, H.; Young, J. Subsalt imaging using TTI reverse time migration. Lead. Edge 2009, 28, 448–452. [Google Scholar] [CrossRef]
- Taner, M.T.; Sheriff, R.E. Application of Amplitude, Frequency, and Other Attributes to Stratigraphic and Hydrocarbon Determination; Society of Exploration Geophysicists: Houston, TX, USA, 1977. [Google Scholar]
- Craven, J.A.; Styles, P. Seismic curvature attributes for fault/fracture detection. Lead. Edge 1999, 18, 342–346. [Google Scholar]
- Chopra, S.; Marfurt, K. Seismic Attributes for Prospect Identification and Reservoir Characterization; SEG: Tulsa, OK, USA, 2007. [Google Scholar]
- Chopra, S.; Marfurt, K.J. Seismic attributes—A historical perspective. Geophysics 2005, 70, 3SO–28SO. [Google Scholar] [CrossRef]
- Chopra, S.; Marfurt, K.J. Volumetric curvature attributes for fault/fracture characterization. First Break 2007, 25. [Google Scholar] [CrossRef]
- Chopra, S.; Marfurt, K.J. Seismic attributes for fault/fracture characterization. In SEG International Exposition and Annual Meeting; SEG: Tulsa, OK, USA, 2007; p. SEG-2007. [Google Scholar]
- Castillo, F. Seismic Attributes for 3-D Fracture Interpretation; Halliburton: Calgary, AB, Canada, 2010. [Google Scholar]
- Bruno, P.P.G.; Berti, C.; Pazzaglia, F.J. Accommodation, slip inversion, and fault segmentation in a province-scale shear zone from high-resolution, densely spaced wide-aperture seismic profiling, Centennial Valley, MT, USA. Sci. Rep. 2019, 9, 9214. [Google Scholar] [CrossRef]
- Barnes, A.E. Instantaneous frequency and amplitude at the envelope peak of a constant-phase wavelet. Geophysics 1991, 56, 1058–1060. [Google Scholar] [CrossRef]
- Barnes, A.E. The calculation of instantaneous frequency and instantaneous bandwidth. Geophysics 1992, 57, 1520–1524. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis; Prentice Hall: Hoboken, NJ, USA, 1995; Volume 778. [Google Scholar]
- Xing, L.; Aarre, V.; Barnes, A.; Theoharis, T.; Salman, N.; Tjåland, E. Instantaneous frequency seismic attribute benchmarking. In SEG Technical Program Expanded Abstracts 2017; Society of Exploration Geophysicists: Houston, TX, USA, 2017; pp. 2086–2090. [Google Scholar]
- Taner, M.T.; Rock Solid Images. Seismic Attributes: CSEG Recorder; Rock Solid Images: Houston, TX, USA, 2001. [Google Scholar]
- Bahorich, M.S.; Farmer, S.L. 3-D seismic discontinuity for faults and stratigraphic features: The coherence cube. Lead. Edge 1995, 14, 1053–1058. [Google Scholar] [CrossRef]
- Marfurt, K.J.; Kirlin, R.L.; Farmer, S.L.; Bahorich, M.S. 3-D seismic attributes using a semblance-based coherency algorithm. Geophysics 1998, 63, 1150–1165. [Google Scholar] [CrossRef]
- Marfurt, K.J.; Sudhaker, V.; Gersztenkorn, A.; Crawford, K.D.; Nissen, S.E. Coherency calculations in the presence of structural dip. Geophysics 1999, 64, 104–111. [Google Scholar] [CrossRef]
- Gersztenkorn, A.; Marfurt, K.J. Eigen structure-based coherence computations as an aid to 3-D structural and stratigraphic mapping. Geophysics 1999, 64, 1468–1479. [Google Scholar] [CrossRef]
- Li, F.; Lu, W. Coherence attribute at different spectral scales. Interpretation 2014, 2, SA99–SA106. [Google Scholar] [CrossRef]
- Roberts, A. Curvature attributes and their application to 3 D interpreted horizons. First Break 2001, 19, 85–100. [Google Scholar] [CrossRef]
- Mai, H.T.; Marfurt, K.J.; Chávez-Pérez, S. Coherence and volumetric curvatures and their spatial relationship to faults and folds, an example from Chicontepec basin, Mexico. In Proceedings of the 2009 SEG Annual Meeting, OnePetro, Houston, TX, USA, 25–30 October 2009. [Google Scholar]
- Sigismondi, E.M.; Soldo, C.J. Curvature attributes and seismic interpretation: Case studies from Argentina basins. Lead. Edge 2003, 22, 1122–1126. [Google Scholar] [CrossRef]
- Lisle, R.J. Detection of zones of abnormal strains in structures using Gaussian curvature analysis. AAPG Bull. 1994, 78, 1811–1819. [Google Scholar]
- Plesinger, A.; Hellweg, M.; Seidl, D. Interactive highresolution polarization analysis of broad-band seismograms. J. Geophys. 1986, 59, 129–139. [Google Scholar]
- Rene, R.M.; Fitter, J.L.; Forsyth, P.M.; Kim, K.Y.; Murray, D.J.; Walters, J.K.; Westerman, J.D. Multicomponent seismic studies using complex trace analysis. Geophysics 1986, 51, 1235–1251. [Google Scholar] [CrossRef]
- Vidale, J.E. Complex polarization analysis of particle motion. Bull. Seismol. Soc. Am. 1986, 76, 1393–1405. [Google Scholar]
- Park, J.; Vernon, F.L., III; Lindberg, S.R. Frequency dependent polarization analysis of high-frequency seismograms. J. Geophys. Res. 1987, 92, 12664–12667. [Google Scholar] [CrossRef]
- Shih, X.R.; Meyer, R.P.; Schneider, J.F. An automated, analytical method to determine shear-wave splitting. Tectonophysics 1989, 165, 271–278. [Google Scholar] [CrossRef]
- Bataille, K.; Chiu, J.M. Polarization analysis of highfrequency, three component seismic data. Bull. Seismol. Soc. Am. 1991, 81, 622–642. [Google Scholar] [CrossRef]
- Li, X.Y.; Crampin, S. Complex component analysis of shear-wave splitting: Theory. Geophys. J. Internat. 1991, 107, 597–604. [Google Scholar] [CrossRef]
- Rutty, M.J.; Greenhalgh, S.A. Multi-component seismic event correlation in coherent noise. Expl. Geophys. 1992, 23, 287–292. [Google Scholar] [CrossRef]
- Diallo, M.S.; Kulesh, M.; Holschneider, M.; Scherbaum, F.; Adler, F. Characterization of polarization attributes of seismic waves using continuous wavelet transforms. Geophysics 2006, 71, V67–V77. [Google Scholar] [CrossRef]
- Morozov, I.B.; Smithson, S.B. Instantaneous polarization attributes and directional filtering. Geophysics 1996, 61, 872–881. [Google Scholar] [CrossRef]
- Feng, H.; Bancroft, J.C. AVO principles, processing and inversion. CREWES Res. Rep. 2006, 18, 1–19. [Google Scholar]
- Rutherford, S.R.; Williams, R.H. Amplitude-versus-offset variations in gas sands. Geophysics 1989, 54, 680–688. [Google Scholar] [CrossRef]
- Knott, C.G. Reflexion and refraction of elastic waves with seismological applications. Phil. Mag. 1899, 48, 64–97. [Google Scholar] [CrossRef]
- Zoeppritz, K. Erdbebenwellen VIIIB, On the reflection and propagation of seismic waves. Gött. Nachr. 1919, I, 66–84. [Google Scholar]
- Koefoed, O. On the effect of Poisson.s ratios of rock strata on the reflection coefficients of plane waves. Geophys. Prosp. 1955, 3, 381–387. [Google Scholar] [CrossRef]
- Ostrander, W.J. Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence. Geophysics 1982, 49, 1637–1648. [Google Scholar] [CrossRef]
- Shuey, R.T. A simplification of the Zoeppritz equations. Geophysics. 1985, 50, 609–614. [Google Scholar] [CrossRef]
- Gray, D. Fracture detection using 3D seismic azimuthal AVO. CSEG Rec. 2008, 33, 38–49. [Google Scholar]
- Reine, C.; Lovric, S. Geophysical insights into completions and production predictability for a shale gas reservoir using fault intensity and AVO inversion. In Unconventional Resources Technology Conference; Society of Exploration Geophysicists, American Association of Petroleum Geologists, Society of Petroleum Engineers: Houston, TX, USA, 2013; pp. 1672–1678. [Google Scholar]
- Nanda, N.C. Analysing seismic attributes. In Seismic Data Interpretation and Evaluation for Hydrocarbon Exploration and Production: A Practitioner’s Guide; Springer International Publishing: Cham, Switzerland, 2021; pp. 205–222. [Google Scholar]
- Pratt, T.L.; Dolan, J.F.; Odum, J.K.; Stephenson, W.J.; Williams, R.A.; Templeton, M.E. Multiscale seismic imaging of active fault zones for hazard assessment; a case study of the Santa Monica fault zone, Los Angeles, California. Geophysics 1998, 63, 479–489. [Google Scholar] [CrossRef]
- Okay, A.İ.; Kaşlılar-Özcan, A.; İmren, C.; Boztepe-Güney, A.; Demirbağ, E.; Kuşçu, İ. Active faults and evolving strike-slip basins in the Marmara Sea, northwest Turkey: A multichannel seismic reflection study. Tectonophysics 2000, 321, 189–218. [Google Scholar] [CrossRef]
- Demanet, D.; Renardy, F.; Vanneste, K.; Jongmans, D.; Camelbeeck, T.; Meghraoui, M. The use of geophysical prospecting for imaging active faults in the Roer Graben, Belgium. Geophysics 2001, 66, 78–89. [Google Scholar] [CrossRef]
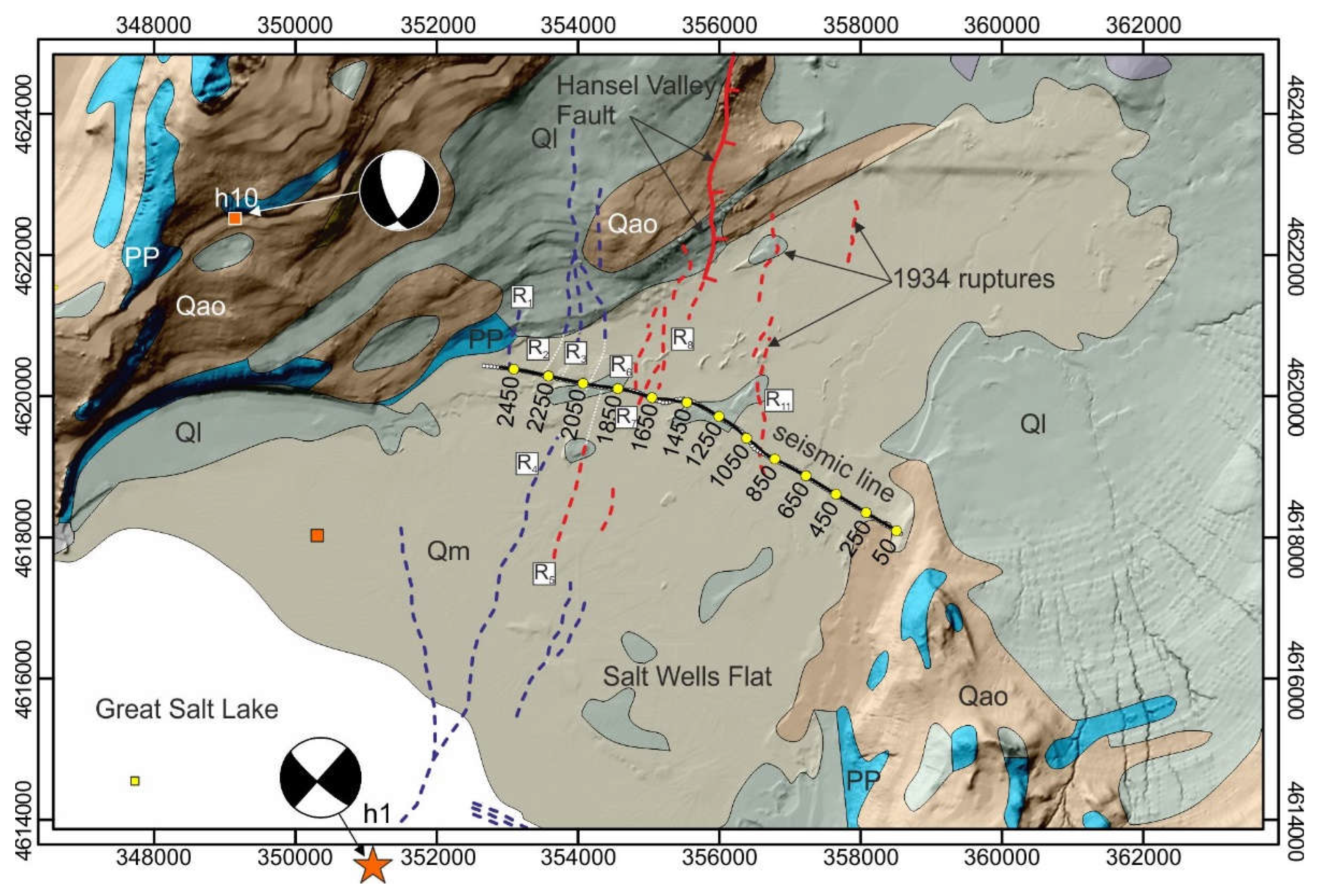
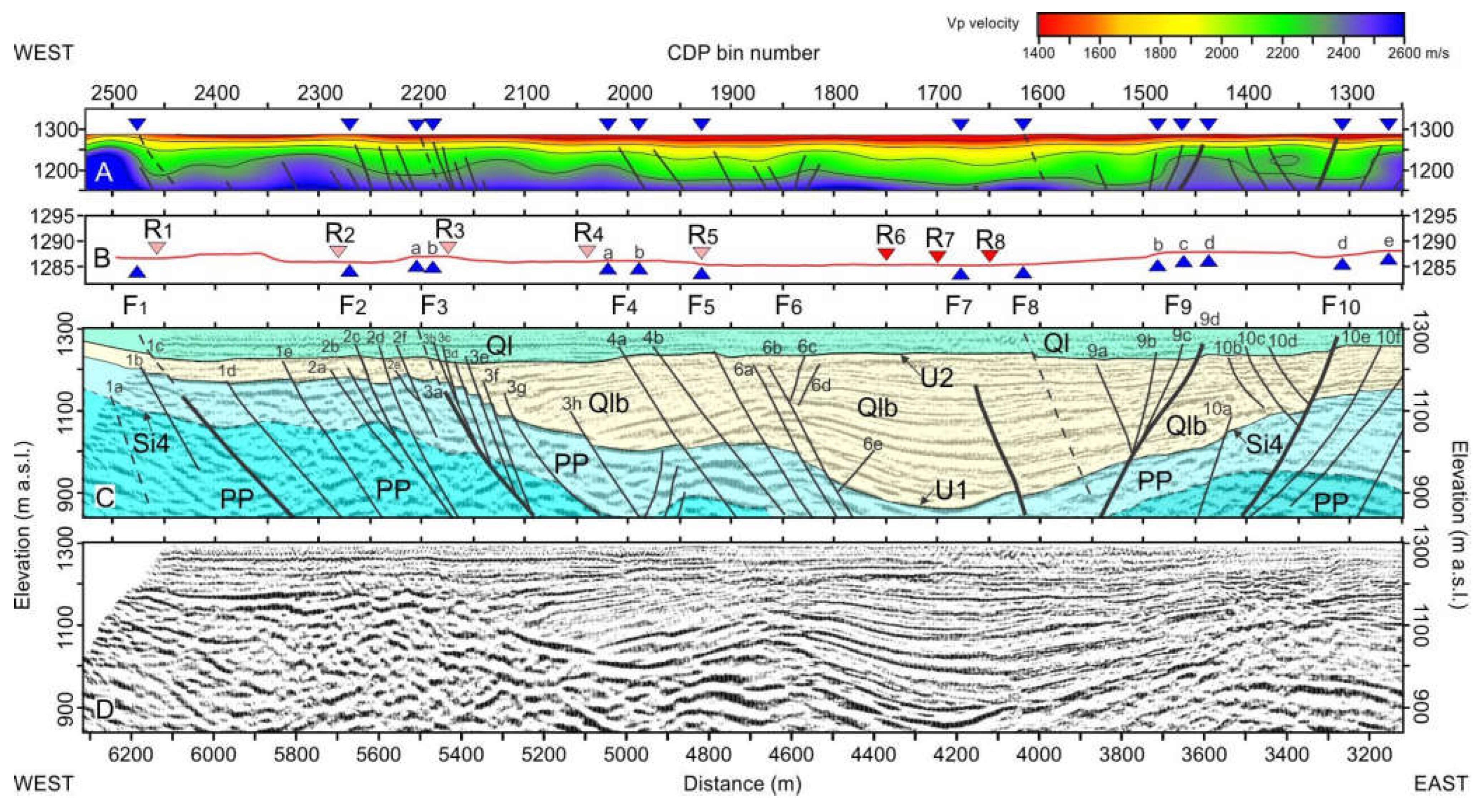
- Bruno, P.P.G.; DuRoss, C.B.; Kokkalas, S. High-resolution seismic profiling reveals faulting associated with the 1934 Ms 6.6 Hansel Valley earthquake (Utah, USA). GSA Bull. 2017, 129, 1227–1240. [Google Scholar] [CrossRef]
- Gracia, E.; Danobeitia, J.; Vergés, J.; Parsifal Team. Mapping active faults offshore Portugal (36 N–38 N): Implications for seismic hazard assessment along the southwest Iberian margin. Geology 2003, 31, 83–86. [Google Scholar] [CrossRef]
- Bruno, P.P.; Castiello, A.; Improta, L. Ultrashallow seismic imaging of the causative fault of the 1980, M6. 9, southern Italy earthquake by pre-stack depth migration of dense wide-aperture data. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Shenon, P.J. The Utah earthquake of March 12, 1934 (extracts from unpublished report). In United States Earthquakes, 1934; Neumann, F., Ed.; Serial 593; United States Coast and Geodetic Survey: Washington, DC, USA, 1936; pp. 43–48. [Google Scholar]
- Adams, T.C. Land subsidence north of Great Salt Lake, Utah. Bull. Seismol. Soc. Am. 1938, 28, 65–70. [Google Scholar] [CrossRef]
- Doser, D.I. Extensional tectonics in northern Utah-southern Idaho, U.S.A., and the 1934 Hansel Valley sequence. Phys. Earth Planet. Inter. 1989, 54, 120–134. [Google Scholar] [CrossRef]
- Smith, R.B.; Arabasz, W.J. Seismicity of the Intermountain seismic belt. In Neotectonics of North America, Boulder Colorado; Slemmons, D.B., Engdahl, I.R., Zoback, M.L., Blackwell, D., Eds.; Decade Map v. 1; Geological Society of America: Boulder, CO, USA, 1991; pp. 185–227. [Google Scholar]
- Hintze, L.; Willis, G.; Laes, D.; Sprinkel, D.; Brown, K. Digital Geologic Map of Utah, scale 1:500,000. Utah Geol. Surv. 2000. [Google Scholar] [CrossRef]
- Sutherland, R.D.; Eberhart-Phillips, R.A.; Harris, T.; Stern, R.J.; Beavan, S.; Ellis, S.; Henrys, S.C.; Cox, R.J.; Norris, K.R.; Berryman, J.; et al. Do great earthquakes occur on the Alpine fault in central South Island, New Zealand? In Acontinental Plate Boundary: Tectonics at South Island, New Zealand; Okaya, D., Stern, T., Davey, F.J., Eds.; American Geophysical Union Geophysical Monographs: Washington, DC, USA, 2007; Volume 175, pp. 235–251. [Google Scholar]
- Stirling, M.W.; Wesnousky, S.G.; Berryman, K.R. Probabilistic seismic hazard analysis of New Zealand. N. Z. J. Geol. Geophys. 1998, 41, 355–375. [Google Scholar] [CrossRef]
- Norris, R.J.; Koons, P.O.; Cooper, A.F. The obliquely-convergent plate boundary in the South Island of New Zealand: Implications for ancient collision zones. J. Struct. Geol. 1990, 12, 715–725. [Google Scholar] [CrossRef]
- Pantosti, D.; Valensise, G. Faulting mechanism and complexity of the November 23, 1980, Campania-Lucania earthquake, inferred from surface observations. J. Geophys. Res. Solid Earth 1990, 95, 15319–15341. [Google Scholar] [CrossRef]
- Pantosti, D.; Schwartz, D.P.; Valensise, G. Paleoseismology along the 1980 surface rupture of the Irpinia fault: Implications for earthquake recurrence in the southern Apennines, Italy. J. Geophys. Res. Solid Earth 1993, 98, 6561–6577. [Google Scholar] [CrossRef]
- Bruno, P.P.G.; Ferrara, G.; Improta, L.; Maraio, S.; Di Fiore, V.; Iacopini, D.; Fusco, M.; Punzo, M.; Paoletti, V.; Cavuoto, G.; et al. High-resolution 3-D geophysical imaging across a seismogenic fault: The TEst Site IRpinia fAult (TESIRA) project (No. EGU23-11176). In Proceedings of the EGU Copernicus Meetings, Vienna, Austria, 24–28 April 2023. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, P.P.G. Seismic Exploration Methods for Structural Studies and for Active Fault Characterization: A Review. Appl. Sci. 2023, 13, 9473. https://doi.org/10.3390/app13169473
Bruno PPG. Seismic Exploration Methods for Structural Studies and for Active Fault Characterization: A Review. Applied Sciences. 2023; 13(16):9473. https://doi.org/10.3390/app13169473
Chicago/Turabian StyleBruno, Pier Paolo G. 2023. "Seismic Exploration Methods for Structural Studies and for Active Fault Characterization: A Review" Applied Sciences 13, no. 16: 9473. https://doi.org/10.3390/app13169473
APA StyleBruno, P. P. G. (2023). Seismic Exploration Methods for Structural Studies and for Active Fault Characterization: A Review. Applied Sciences, 13(16), 9473. https://doi.org/10.3390/app13169473





