Plasma Ion Bombardment Induced Heat Flux on the Wafer Surface in Inductively Coupled Plasma Reactive Ion Etch
Abstract
:1. Introduction
2. Theory
2.1. Heat Flux Calculation Method
2.2. OES Line Ratio Method
3. Experimental Apparatus
3.1. Experimental Equipment and Sensor Used
3.2. Experiment 1: OES Wavelength Selection
3.3. Experiment 2: SLP vs. OES
3.4. Experiment 3: ESTW vs. OES
4. Result and Discussion
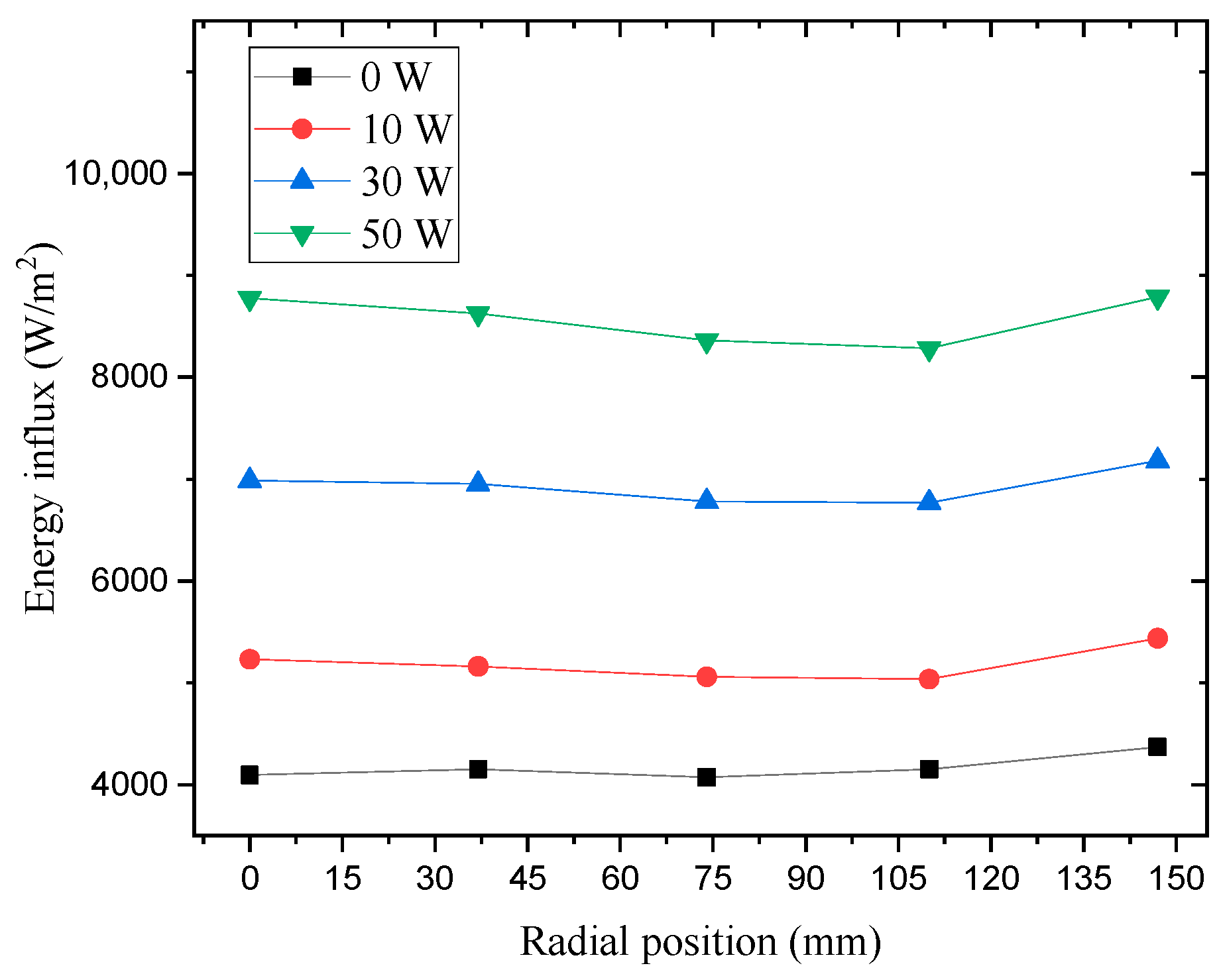
4.1. Experimental Result
4.2. Heat Flux Calculation
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, B.; Kumar, A.; Pamarthy, S. High aspect ratio silicon etch: A review. J. Appl. Phys. 2010, 108, 051101. [Google Scholar] [CrossRef]
- Huang, S.; Shim, S.; Nam, S.K.; Kushner, M.J. Pattern dependent profile distortion during plasma etching of high aspect ratio features in SiO2. J. Vac. Sci. Technol. A 2020, 38, 023001. [Google Scholar] [CrossRef]
- Wang, S.; Wendt, A.E. Control of Ion Energy distribution at substrates during plasma processing. J. Appl. Phys. 2000, 88, 643–646. [Google Scholar] [CrossRef]
- Ishikawa, K.; Karahashi, K.; Ishijima, T.; Cho, S.I.; Elliott, S.; Hausmann, D.; Mocuta, D.; Wilson, A.; Kinoshita, K. Progress in nanoscale dry processes for fabrication of high-aspect-ratio features: How can we control critical dimension uniformity at the bottom? Jpn. J. Appl. Phys. 2018, 57, 06JA01. [Google Scholar] [CrossRef]
- Kim, Y.; Kang, S.K.; Kim, S.D.; Kim, S.E. Wafer warpage analysis of stacked wafers for 3D integration. Microelectron. Eng. 2012, 89, 46–49. [Google Scholar] [CrossRef]
- Shirazi, A.; Varvani-Farahani, A.; Lu, H. An inverse analysis of warpage for trilayer thin-plate under thermal cycles. Mater. Des. 2010, 31, 4219–4228. [Google Scholar] [CrossRef]
- Kanno, S.; Miya, G.; Tanaka, J.; Masuda, T.; Kuwahara, K.; Sakaguchi, M.; Makino, A.; Tsubone, T.; Fujii, T. Controlling gate-CD uniformity by means of a CD prediction model and wafer-temperature distribution control. Thin Solid Films. 2007, 515, 4941–4944. [Google Scholar] [CrossRef]
- Yoon, T.W.; Choi, M.; Hong, S.J. Thermal and electrical analysis of the electrostatic chuck for the etch equipment. IEEE Trans. Semicon. Manuf. 2021, 20, 19–24. [Google Scholar] [CrossRef]
- Hsu, K.C.; Yang, J.Y.; Chen, J.Z.; Yu, Y.H.; Chen, Y.J. Modeling and simulation of heat transfer characteristics of 12-inch wafer on electrostatic chuck. In Proceedings of the 10th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 21–23 October 2015; pp. 304–307. [Google Scholar]
- Olson, K.A.; Kotecki, D.E.; Ricci, A.J.; Lassig, S.E.; Husain, A. Characterization, modeling, and design of an electrostatic chuck with improved wafer temperature uniformity. Rev. Sci. Instrum. 1995, 66, 1108–1114. [Google Scholar] [CrossRef]
- Shan, H.; Pu, B.Y.; Gao, H.; Ke, K.H.; Lewis, J.; Welch, M.; Deshpandey, C. Process kit and wafer temperature effects on dielectric etch rate and uniformity of electrostatic chuck. J. Vac. Sci. Technol. B 1996, 14, 521–526. [Google Scholar] [CrossRef]
- Wright, D.R.; Hartman, D.C.; Sridharan, U.C.; Kent, M.; Jasinski, T.; Kang, S. Low temperature etch chuck: Modeling and experimental results of heat transfer and wafer temperature. J. Vac. Sci. Technol. A 1992, 10, 1065–1070. [Google Scholar] [CrossRef]
- Cui, Y.; Jian, S.; Chen, C.; Lin, Y.; Su, Z.; Zhang, H.; Yuan, R.; Chen, Z.; Dong, Z.; Li, L. Uniformity improvement of deep silicon cavities fabricated by plasma etching with 12-inch wafer level. J. Micromech. Microeng. 2019, 29, 105010. [Google Scholar] [CrossRef]
- Zhao, S.X.; Gao, F.; Wang, Y.N.; Bogaerts, A. Gas ratio effects on the Si etch rate and profile uniformity in an inductively coupled Ar/CF4 plasma. Plasma Sources Sci. Technol. 2012, 22, 015017. [Google Scholar] [CrossRef]
- Burtsev, A.; Li, Y.X.; Zeijl, H.W.; Beenakker, C.I.M. An anisotropic U-shaped SF6-based plasma silicon trench etching investigation. Microelectron. Eng. 1998, 40, 85–97. [Google Scholar] [CrossRef]
- Rosli, S.A.; Aziz, A.A.; Hashim, M.R. ICP-RIE dry etching using Cl2-based on GaN. Sains Malays. 2011, 40, 79–82. [Google Scholar]
- Oehrlein, G.S.; Kurogi, Y. Sidewall surface chemistry in directional etching processes. Mater. Sci. Eng. 1998, 24, 153–183. [Google Scholar] [CrossRef]
- Dixit, P.; Miao, J. Effect of clamping ring materials and chuck temperature on the formation of silicon nanograss in deep RIE. J. Electrochem. Soc. 2006, 153, G771. [Google Scholar] [CrossRef]
- Kim, T.W.; Aydil, E.S. Effects of chamber wall conditions on Cl concentration and Si etch rate uniformity in plasma etching reactors. J. Electrochem. Soc. 2003, 150, G418. [Google Scholar] [CrossRef]
- Durandet, A.; Joubert, O.; Pelletier, J.; Pichot, M. Effects of ion bombardment and chemical reaction on wafer temperature during plasma etching. J. Appl. Phys. 1990, 67, 3862–3866. [Google Scholar] [CrossRef]
- Shinoda, K.; Miyoshi, N.; Kobayashi, H.; Miura, M.; Kurihara, M.; Maeda, K.; Negishi, N.; Sonoda, Y.; Tanaka, M.; Yasui, N. Selective atomic-level etching using two heating procedures, infrared irradiation and ion bombardment, for next-generation semiconductor device manufacturing. J. Phys. D 2017, 50, 194001. [Google Scholar] [CrossRef]
- Kersten, H.; Stoffels, E.; Stoffels, W.W.; Otte, M.; Csambal, C.; Deutsch, H.; Hippler, R. Energy influx from an rf plasma to a substrate during plasma processing. J. Appl. Phys. 2000, 87, 3637–3645. [Google Scholar] [CrossRef]
- Tinck, S.; Boullart, W.; Bogaerts, A. Simulation of an Ar/Cl2 inductively coupled plasma: Study of the effect of bias, power and pressure and comparison with experiments. J. Phys. D 2008, 41, 065207. [Google Scholar] [CrossRef]
- Kim, J.H.; Cho, S.W.; Park, C.J.; Chae, H.; Kim, C.K. Angular dependences of SiO2 etch rates at different bias voltages in CF4, C2F6, and C4F8 plasmas. Thin Solid Films. 2017, 637, 43–48. [Google Scholar] [CrossRef]
- Tandou, T.; Kubo, S.; Negishi, N.; Izawa, M. Improving the etching performance of high-aspect-ratio contacts by wafer temperature control: Uniform temperature design and etching rate enhancement. Precis. Eng. 2016, 44, 87–92. [Google Scholar] [CrossRef]
- Tinck, S.; Tillocher, T.; Dussart, R.; Bogaerts, A. Cryogenic etching of silicon with SF6 inductively coupled plasmas: A combined modelling and experimental study. J. Phys. D 2015, 48, 155204. [Google Scholar] [CrossRef]
- Freed, M.; Kruger, M.V.P.; Poolla, K.; Spanos, C.J. Wafer-grown heat flux sensor arrays for plasma etch processes. IEEE Trans. Semicon. Manuf. 2005, 18, 148–162. [Google Scholar] [CrossRef]
- Lim, Y.M.; Eo, H.; Kim, K.H.; Lee, M.Y.; Chung, C.W. A wafer-like apparatus for two-dimensional measurement of plasma parameters and temperature distribution in low-temperature plasmas. Rev. Sci. Instrum. 2021, 92, 053531. [Google Scholar] [CrossRef]
- Kersten, H.; Snijkers, R.J.M.M.; Schulze, J.; Kroesen, G.M.W.; Deutsch, H.; De Hoog, F.J. Energy transfer from radio frequency sheath accelerated CF3+ and Ar+ ions to a Si wafer. Appl. Phys. Lett. 1994, 64, 1496–1498. [Google Scholar] [CrossRef]
- Shindo, W.; Ohmi, T. Ion energy, ion flux, and ion mass effects on low-temperature silicon epitaxy using low-energy ion bombardment process. J. Appl. Phys. 1996, 79, 2347–2351. [Google Scholar] [CrossRef]
- Lim, Y.D.; Lee, D.Y.; Yoo, W.J.; Ko, H.S.; Lee, S.H. Temperature of a semiconducting substrate exposed to an inductively coupled plasma. J. Korean Phys. Soc. 2011, 59, 262–270. [Google Scholar] [CrossRef]
- Zhu, X.M.; Pu, Y.K. A simple collisional–radiative model for low-pressure argon discharges. J. Phys. D 2007, 40, 2533. [Google Scholar] [CrossRef]
- Zhu, X.M.; Chen, W.C.; Li, J.; Pu, Y.K. Determining the electron temperature and the electron density by a simple collisional–radiative model of argon and xenon in low-pressure discharges. J. Phys. D 2008, 42, 025203. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, S.X.; Li, X.S.; Wang, Y.N. Comparison between experiment and simulation for argon inductively coupled plasma. Phys. Plasmas 2009, 16, 113502. [Google Scholar] [CrossRef]
- Okada, K.; Komatsu, S.; Matsumoto, S. Langmuir probe measurements in a low pressure inductively coupled plasma used for diamond deposition. J. Vac. Sci. Technol. A 1999, 17, 721–725. [Google Scholar] [CrossRef]
- Lee, H.C.; Lee, M.H.; Chung, C.W. Effects of rf-bias power on plasma parameters in a low gas pressure inductively coupled plasma. Appl. Phys. Lett. 2010, 96, 071501. [Google Scholar] [CrossRef]
- Park, H.; Choe, W. Parametric study on excitation temperature and electron temperature in low pressure plasmas. Curr. Appl. Phys. 2010, 10, 1456–1460. [Google Scholar] [CrossRef]
- Wang, S.Q.; Macdonald, P.; Kruger, M. Plasma etch process diagnosis and control by wireless sensor wafer in semiconductor chip manufacturing. In Proceedings of the 8th International Conference Solid-State and Integrated Circuit Technology Proceedings, Shanghai, China, 23–26 October 2006; pp. 2175–2180. [Google Scholar]
- Yue, H.U.A.; Jian, S.O.N.G.; Zeyu, H.A.O.; Zhang, G.; Chunsheng, R.E.N. Effects of direct current discharge on the spatial distribution of cylindrical inductively-coupled plasma at different gas pressures. Plasma Sci. Technol. 2017, 20, 014005. [Google Scholar]
- Collison, W.Z.; Ni, T.Q.; Barnes, M.S. Studies of the low-pressure inductively-coupled plasma etching for a larger area wafer using plasma modeling and Langmuir probe. J. Vac. Sci. Technol. A 1998, 16, 100–107. [Google Scholar] [CrossRef]
- Suzuki, A.; Terasawa, N.; Moriya, T.; Kang, S.Y. Effects of surface conditions of the focus ring on etching uniformity. In Proceedings of the 2010 International Symposium on Semiconductor Manufacturing (ISSM 2010), Tokyo, Japan, 18–20 October 2010; pp. 1–3. [Google Scholar]




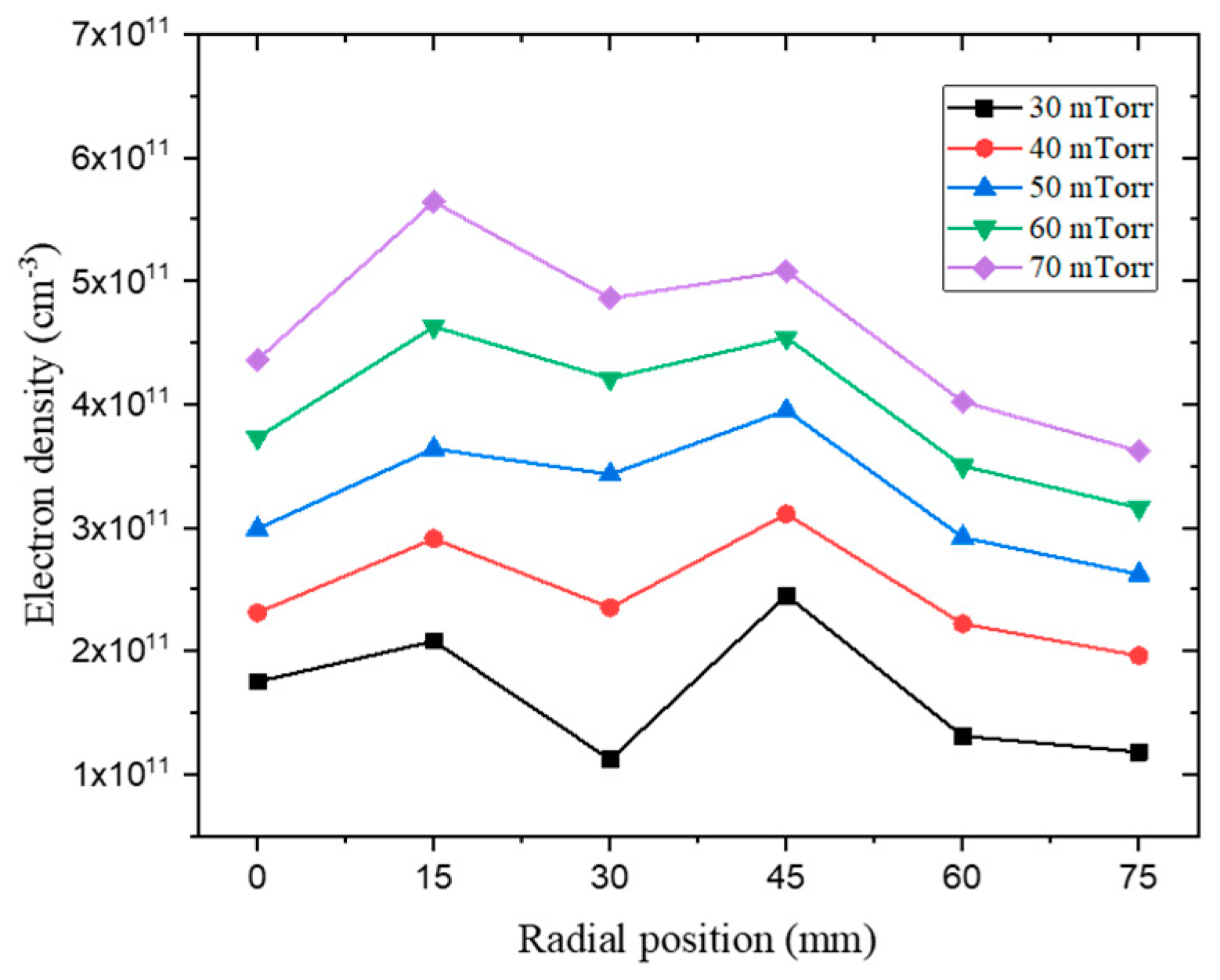

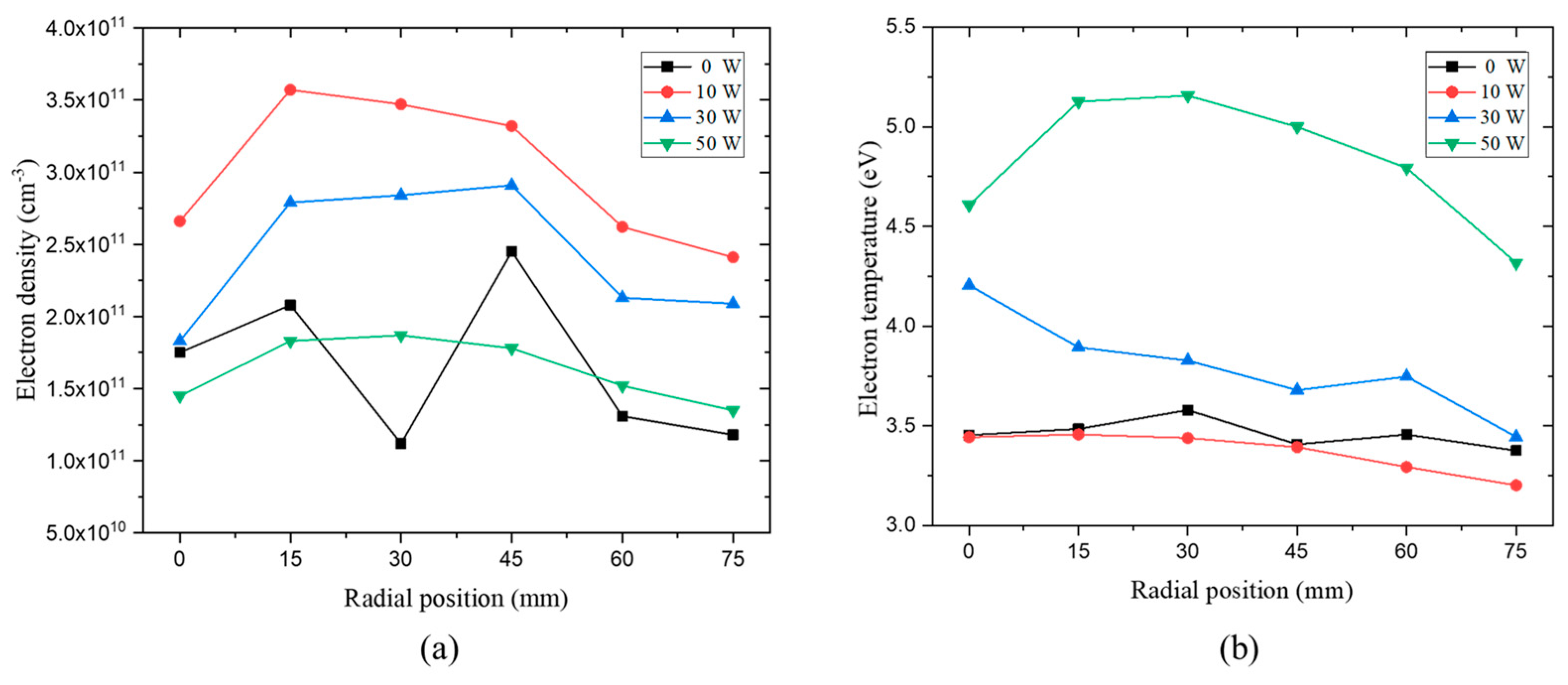
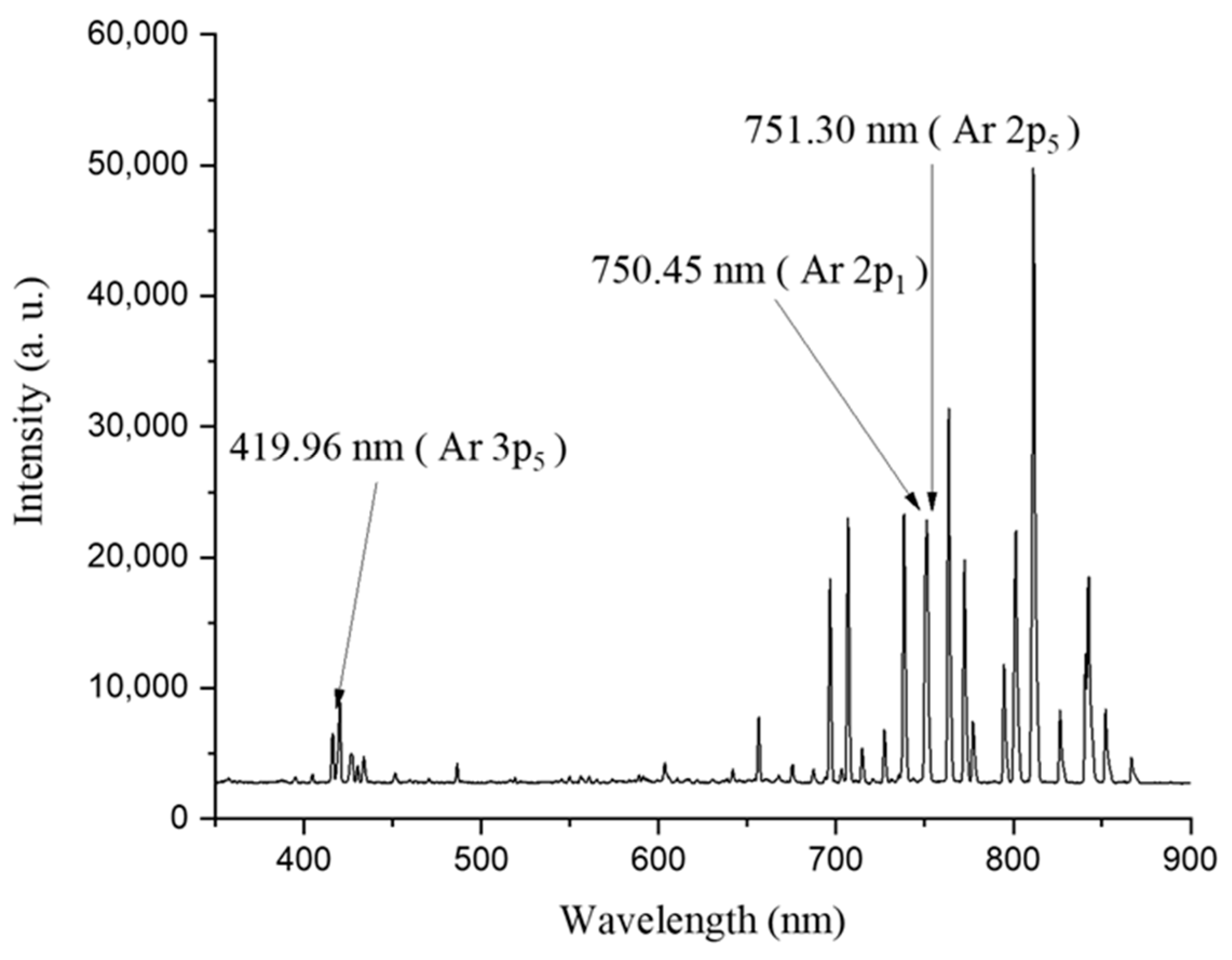
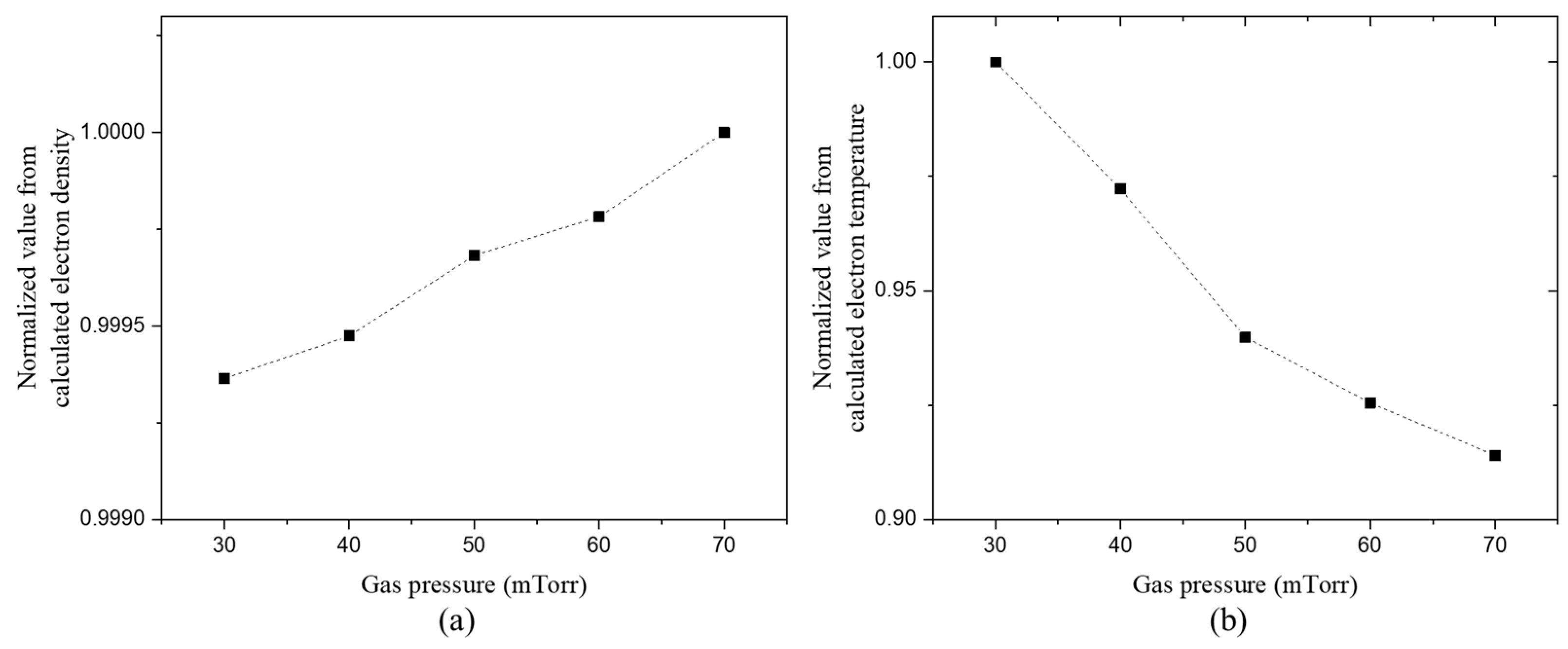

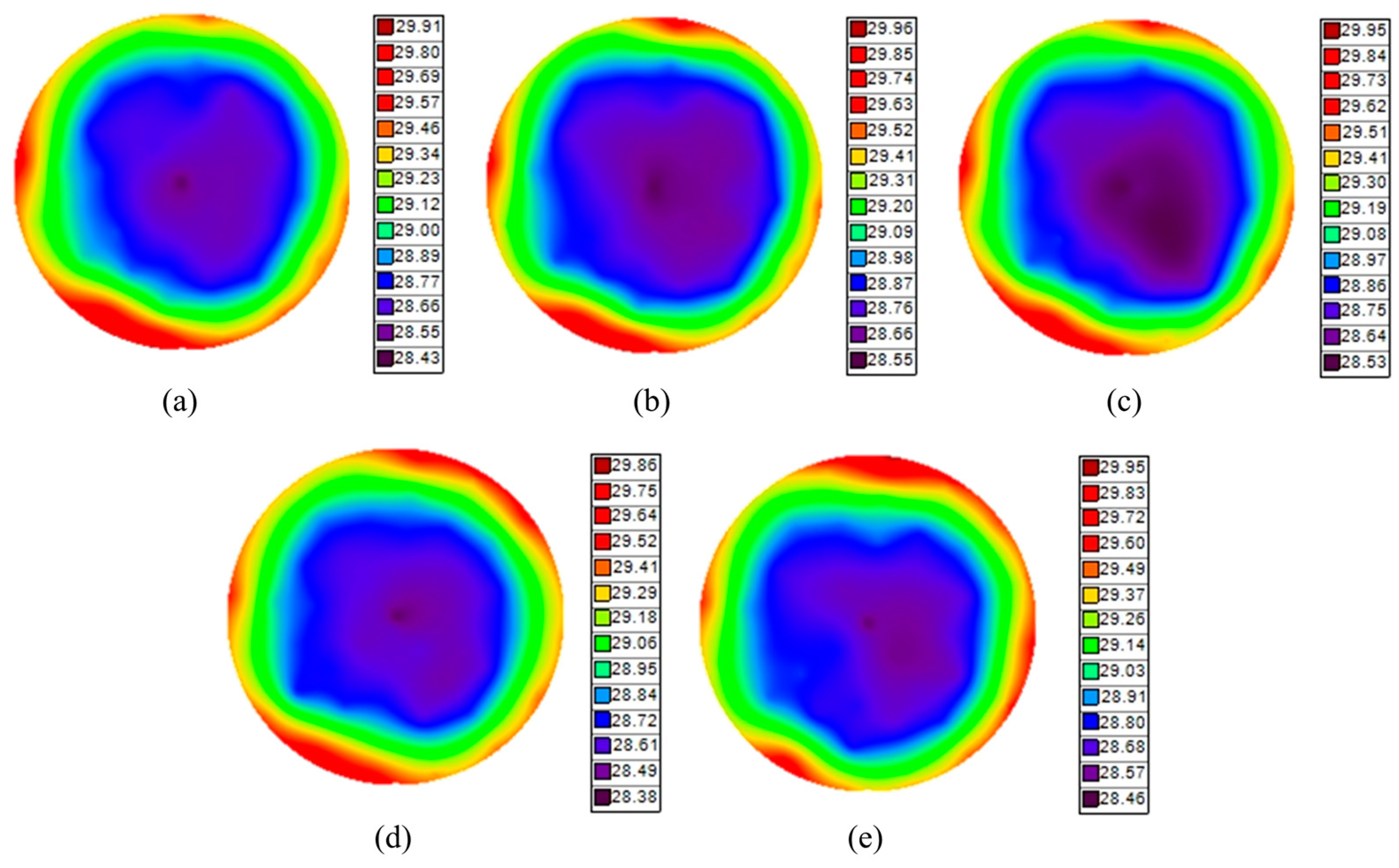
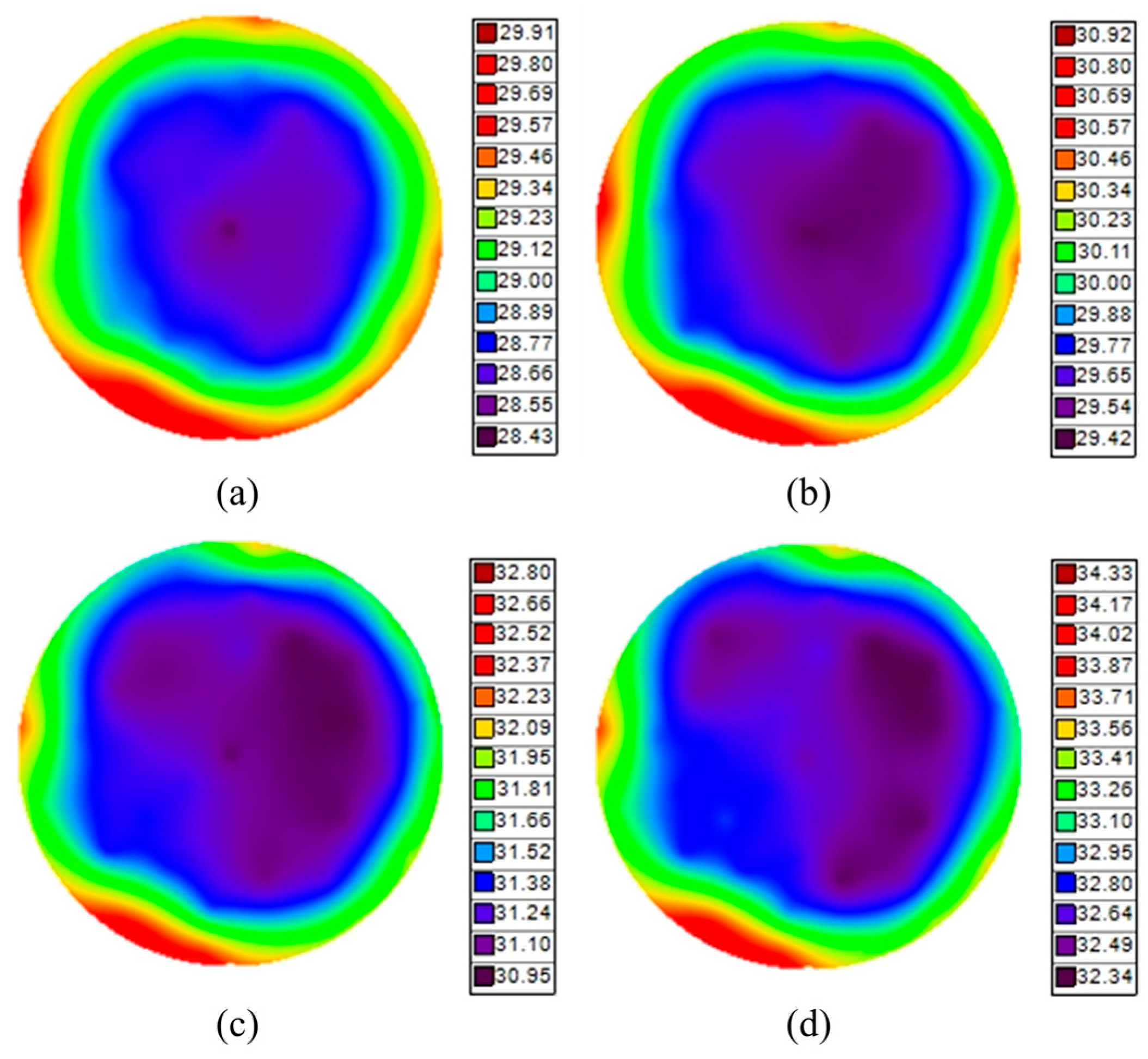
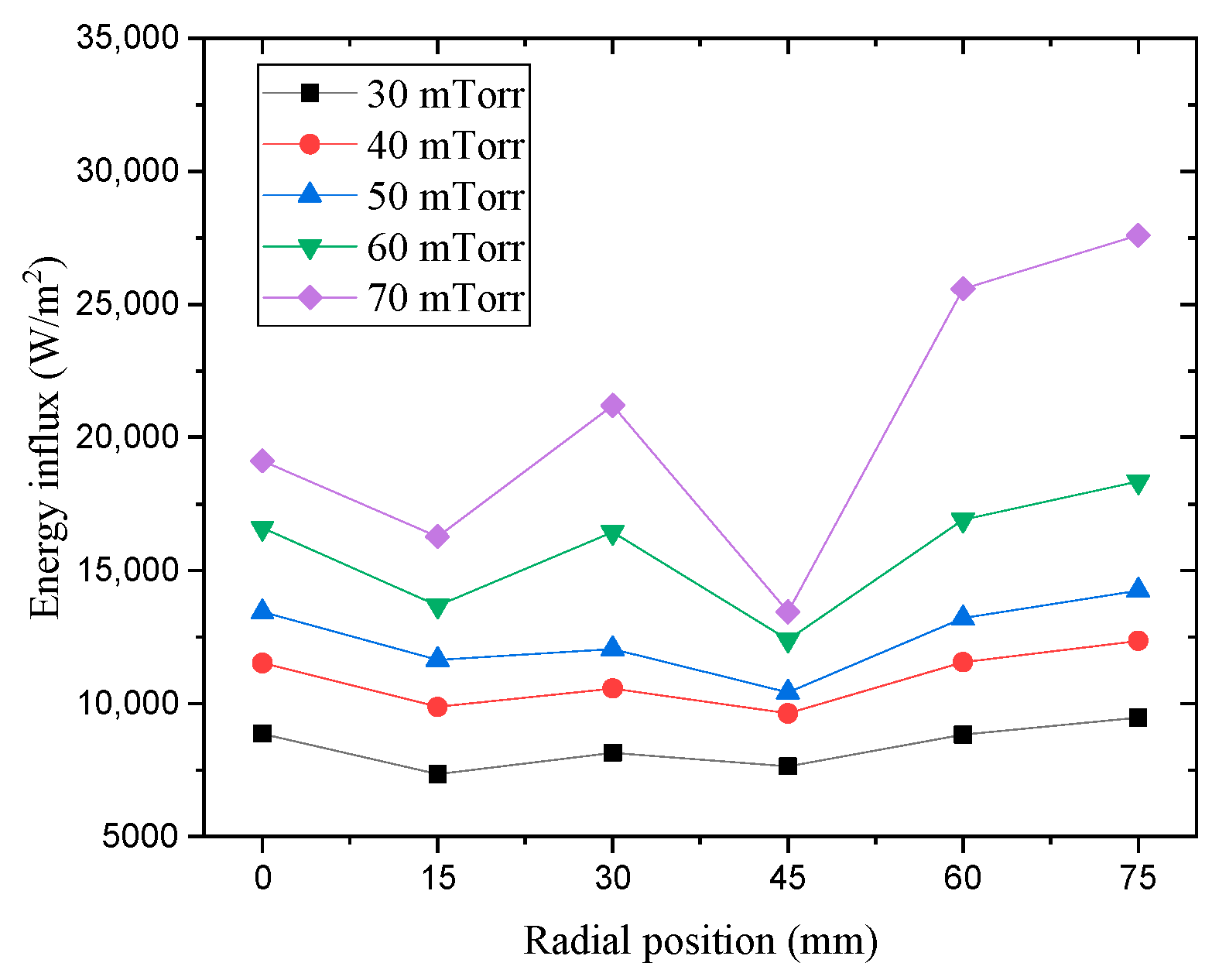
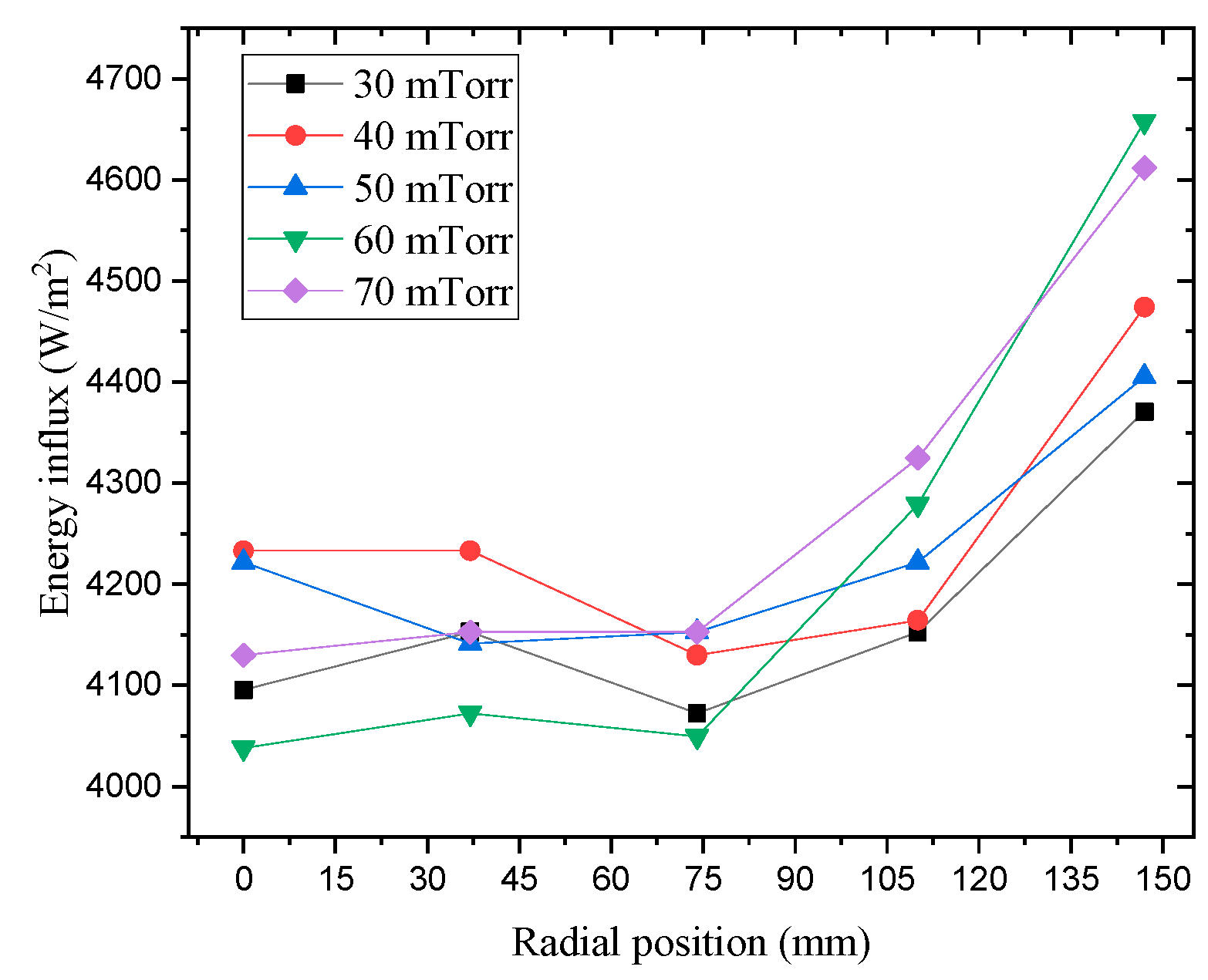
| No. | RF Power [W] | Bias Power [W] | Pressure [mTorr] | Gas [sccm] |
|---|---|---|---|---|
| Ar | ||||
| 1 | 200 | 0 | 30 | 30 |
| 2 | 10 | 30 | ||
| 3 | 30 | 30 | ||
| 4 | 50 | 30 | ||
| 5 | 0 | 40 | ||
| 6 | 0 | 50 | ||
| 7 | 0 | 60 | ||
| 8 | 0 | 70 |
| Radial Position [mm] | Pressure [mTorr] | ||||
|---|---|---|---|---|---|
| 30 | 40 | 50 | 60 | 70 | |
| 0 | 4908.1 | 6335.6 | 8176.4 | 10,388.2 | 12,521.3 |
| 15 | 5888.1 | 8232.9 | 10,399.7 | 13,579.1 | 17,169.1 |
| 30 | 3257.1 | 6487.4 | 9597.5 | 12,069.7 | 14,253.7 |
| 45 | 6779.4 | 8565.2 | 11,013.8 | 12,829.6 | 14,647.5 |
| 60 | 3678.3 | 5977.2 | 7715.7 | 9270.9 | 10,758.5 |
| 75 | 3234.5 | 5094.0 | 6738.0 | 8136.9 | 9402.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, S.I.; Park, H.K.; An, S.; Hong, S.J. Plasma Ion Bombardment Induced Heat Flux on the Wafer Surface in Inductively Coupled Plasma Reactive Ion Etch. Appl. Sci. 2023, 13, 9533. https://doi.org/10.3390/app13179533
Cho SI, Park HK, An S, Hong SJ. Plasma Ion Bombardment Induced Heat Flux on the Wafer Surface in Inductively Coupled Plasma Reactive Ion Etch. Applied Sciences. 2023; 13(17):9533. https://doi.org/10.3390/app13179533
Chicago/Turabian StyleCho, Sung Il, Hyun Keun Park, Surin An, and Sang Jeen Hong. 2023. "Plasma Ion Bombardment Induced Heat Flux on the Wafer Surface in Inductively Coupled Plasma Reactive Ion Etch" Applied Sciences 13, no. 17: 9533. https://doi.org/10.3390/app13179533
APA StyleCho, S. I., Park, H. K., An, S., & Hong, S. J. (2023). Plasma Ion Bombardment Induced Heat Flux on the Wafer Surface in Inductively Coupled Plasma Reactive Ion Etch. Applied Sciences, 13(17), 9533. https://doi.org/10.3390/app13179533









