Synthesis of State/Output Feedback Event-Triggered Controllers for Load Frequency Regulation in Hybrid Wind–Diesel Power Systems

Abstract

Hybrid power systems based on renewable energy sources and diesel generators are efficient solutions for supplying electricity to remote and off-grid locations. One of the most crucial problems in hybrid power systems is frequency regulation, which is established by balancing the supplied power with the load demand using the load frequency control approach. Since most feedback signals are analog and the control setups are digital, the resulting control system is a sampled-data system, which requires careful designs for both the control law and the sampling frequency to guarantee closed-loop stability. This paper is concerned with the state-feedback load frequency regulation for hybrid wind–diesel power systems under event-triggered implementation. It is assumed that the full state measurement is available for feedback and that sensors and controllers communicate over a shared digital network. To mitigate the communication load on the network, an event-triggering mechanism is constructed by emulation, based on the time-regularization principle in the sense that each consecutive triggering instant is speared by a specified minimum dwell time. The closed-loop system is described as a hybrid dynamical system to account for mixed dynamical behaviors naturally arising in networked control systems. By means of appropriate Lyapunov functions, the closed-loop stability is ensured under the proposed triggering rule. Moreover, the enforced dwell time between transmissions ensures that the accumulation of sampling times is prevented, which is crucial for the event-triggering condition to be implementable in practice. The required conditions to apply this technique are derived in terms of a linear matrix inequality. Numerical simulations on an isolated hybrid power system were implemented to demonstrate the efficiency of the proposed method. Comparative simulations with relevant techniques in the literature were carried out, which showed that the proposed approach can produce fewer transmission numbers over the network.

1. Introduction

In an isolated power system known as a hybrid wind–diesel power system (HWDPS), diesel generators are used in conjunction with wind turbine generators to use less fuel and obtain the best energy output possible from the variable wind resources. This consequently lowers operating costs and has a less negative impact on the environment. The HWDPS system is an attractive solution for supplying electric power to isolated areas due to the technical difficulties and economic challenges of providing electric energy to such areas directly from the grid. Since both wind energy and actual energy needs are intermittent, it is essential to have a suitable control approach for upholding the desired frequency by eliminating any offset between the generation and load. In this regard, the load frequency control (LFC) technique has been developed in the literature in order to balance the power supply and keep the system frequency at a desirable level, see [1,2,3] and the references therein.

Different LFC strategies have been proposed to reduce the frequency mismatch between generation and load demands, such as PID control [4,5,6], artificial neural network (ANN) control [7,8], fuzzy control [9,10], optimal control [11,12,13,14], adaptive control [15,16,17], and sliding mode control [18,19,20]. Most existing LFC techniques are carried out in the continuous-time domain. However, in practice, the feedback signal is often analog and the control setup is digital, i.e., the sampled-data control (SDC) [21,22]. Hence, it is important to consider the digital implementation effect when the feedback law is constructed. In particular, the sampling effect needs to be considered in the control design, otherwise, the closed-loop stability can no longer be guaranteed. In this context, some results have been reported in the literature regarding the lowest stabilizing sampling rate in a periodic time-triggered implementation [23,24]. However, since periodic sampling is often based on the worst-case scenario, the derived sampling frequency can be conservative [25]. To overcome this issue, event-triggered control (ETC) has been proposed, such that the sequence of sampling times is produced by state-dependent sampling, as opposed to fixed periodic sampling, such that a new transmission is only generated when it is necessary from the stability/performance perspectives [26]. A critical property of ETC is to ensure the existence of a strictly positive minimum time between the transmission instant to avoid the accumulation of sample intervals over a finite period of time (Zeno phenomenon). This task becomes more difficult to resolve when external disturbances impact the system [27,28] or are subject to communication delays [29,30].

Different ETC approaches have been applied to the FLC problem in the literature [31,32,33,34,35,36,37,38,39]. In [31,32], memory-based ETC techniques were designed for the LFC problem for multi-area power systems [31] and T–S fuzzy wind turbine systems [32]. The developed approach in [31] takes into account possible cyber attacks and network delays and an $H_{\infty }$ stability property has been established. The authors of [32] considered modeling uncertainty and distributed delay. The authors of [33] investigated the LFC problem using an event-triggered sliding mode control (SMC) in the presence of external disturbances and transmission time delays. The plant model in [33] was assumed to be linear time-invariant (LTI) and the analysis was carried out in continuous-time. In [34], an area-based ETC was developed for the LFC of multi-area power systems in an asynchronous fashion. Then, the frequency fluctuation was handled by an SMC. Each area power system was described by an LTI discrete-time model. In [35], an ETC mechanism was developed for the LFC to ensure $H_{\infty }$ stability against cyber attacks, such as denial-of-service and deception attacks. The system was modeled as a linear switched system and stability was performed in continuous-time. The authors of [36] combined an ETC with an observer-based SMC controller to address the problem of LFC for multi-area power systems. The constructed ETC in [36] was adaptive in the sense that the triggering threshold was time-varying and not fixed. The overall system was described as an LTI continuous-time system. The authors of [37] proposed a dynamic ETC technique for a nonlinear multi-area power system to ensure the $H_{\infty }$ stability of the closed-loop system against transmission delays. The stability analysis was carried out in continuous-time using Lyapunov–Krasovskii functions. In [38], new ETC conditions were synthesized based on sampled memory signals of the output feedback for the LFC of power systems. The closed-loop system was described as a T-S fuzzy system with time-varying delay and stability was studied in continuous-time. A perdition-based ETC approach was developed in [39] for the LFC problem with input/output time delay. The communication instants over the sensor-to-controller and the controller-to-plant channels were produced by two independent ETCs. The closed-loop system was described in the discrete-time domain and a uniform ultimate boundedness stability was guaranteed. We should note that all the aforementioned results were either performed in continuous-time [31,32,33,35,36,37,38] or in discrete-time [34,39]. However, SDC systems involve the two dynamical behaviors and, hence, it is more natural to model such systems as a hybrid dynamical system (HDS).

The objective of this paper is to synthesize the stabilizing state-feedback ETCs for the LFC control problem in isolated hybrid power systems. The control design problem is solved sequentially in two steps, following the emulation approach. In other words, first, the sampling effect is neglected and a state-feedback law is designed in continuous-time to stabilize the closed-loop system. Then, an event-triggering rule is derived to maintain the closed-loop stability while ensuring that the Zeno behavior is ruled out. The latter characteristic is attained through the time regularization technique, such that the minimum dwell time is enforced between each triggering instant. The entire system is formulated as a hybrid dynamical system to deal with both continuous-time dynamics and discrete changes [40]. A linear matrix inequality (LMI) condition is used to present the required conditions, which allows systematic design methodology. The presented method guarantees that the closed-loop system is ${\mathcal{L}}_2$-gain-stable. Note that a similar ETC mechanism was constructed in [41] by switching between periodic sampling and event-triggering for output feedback linear systems. However, the approach of [41] was developed for static output feedback control, which, in practice, is restrictive to impose since such a static controller may not be feasible, even if the plant model is controllable and observable [42]. In contrast to [41], the developed approach in this study is focused on dynamic output feedback control, which is more general and ensures the existence of a stabilizing feedback law for any controllable and observable system. In addition, the enforced minimum time in our ETM is designed as the maximally allowable transmission interval (MATI) for time-triggered implementation based on [23], which is not the case in [41]. Moreover, the modeling framework and the stability in this study are different from those in [41] since we investigate the closed-loop stability in the framework of a hybrid dynamical system, as opposed to the time-delay approach in [41].

A simulation comparison with [43] was made to emphasize the effectiveness of the approach. The comparison results show that the approach [43] can ensure a larger periodic sampling time than what we guarantee. On the other hand, our proposed technique generates fewer triggering instant numbers than [43]. In other words, the approach of [43] outperforms the proposed technique in the periodic time-triggered control; the proposed approach is superior to [43] under event-triggered implementation.

The key contributions of this paper are as follows:

• A new event-triggering mechanism for the FLC problem is proposed based on time-regularization. By using such a technique, the closed-loop stability is preserved in the presence of sampling while the Zeno behavior is prevented. The structure of the developed ETC mechanism is different from the proposed techniques in [31,32,33,34,35,36,37,38,39].
• A hybrid dynamical model is developed to account for the mixed dynamics that naturally arise in networked control and sampled-data systems, in contrast to the continuous-time analysis, as in [31,32,33,35,36,37,38], or discrete-time, as in [34,39].
• Better performance than time-triggering is guaranteed thanks to the structure of the developed ETC mechanism, which ensures that the generated triggering instants are less than or, at worst, equal to periodic sampling times. Such a performance guarantee is an attractive feature compared to existing ETC mechanisms.
• A less conservative ETC performance is achieved, in terms of the generated number of triggering times, compared with the approach of [43].

The rest of this article is structured as follows. Section 2 presents the introduction, while Section 3 formulates the problem. Then, in Section 4, a summary of the stabilizing feedback controller and the ETC is provided. In Section 5, the hybrid dynamical model is presented and the stability results are formally stated. Section 7 provides the simulation, while Section 9 concludes the paper.

2. Preliminaries

Let ${\mathbb{R}}_{}^{}:=(-\infty ,\infty )$ denote the set of real numbers, ${\mathbb{R}}_{\ge 0}^{}:=[0,\infty )$ the set of real positive numbers, and $\mathbb{N}:=\{0,1,2,\dots \}$ the set of integer numbers. For a real symmetric matrix A, we denote by ${\lambda }_{min}\left(A\right)$ the minimum eigenvalue and by ${\lambda }_{max}\left(A\right)$ the maximum eigenvalue. The transpose of A is written as $A^T$ and the identity matrix of dimension n is denoted by ${\mathbb{I}}_n$. We write $(x,y)\in {\mathbb{R}}_{}^{n_x+n_y}$ to express the vector ${[x^T,y^T]}^T$ for $x\in {\mathbb{R}}_{}^{n_x}$ and $y\in {\mathbb{R}}_{}^{n_y}$. The Euclidean norm of a vector $x\in {\mathbb{R}}_{}^{n_x}$ is defined as $\left|x\right|:=\sqrt{x^{T}x}$, and if a matrix $A\in {\mathbb{R}}_{}^{n\times m}$, we define $\left|A\right|:=\sqrt{{\lambda }_{max}\left(A^{T}A\right)}$.

Based on the framework of [40], we consider the following hybrid systems:

$$\begin{array}{c}\hfill \dot{x}=F(x,w)x\in \mathcal{C},x^{+}\in G\left(x\right)x\in \mathcal{D},\end{array}$$

(1)

where $x\in {\mathbb{R}}_{}^{n_x}$ is the state, $w\in {\mathbb{R}}_{}^{n_w}$ is the external disturbance, $\mathcal{C}$ is the flow set, F is the flow map, $\mathcal{D}$ is the jump set, and G is the jump map.

Definition 1

([44]). System (1) is said to achieve ${\mathcal{L}}_2$-gain stability from the input w to an output $y=f(x,w)$ if the following holds:

$$\begin{array}{c}\hfill {\left|\right|y\left|\right|}_2\le \alpha \left(\right|x(0,0)\left|\right)+{\eta \left|\right|w\left|\right|}_2,\end{array}$$

(2)

where $\alpha \in {\mathcal{K}}_{\infty }$ and $\eta \ge 0$, and in this case, the achieved ${\mathcal{L}}_2$-gain is less than or equal to η.

3. Problem Formulation

The considered hybrid wind–diesel power system is schematically shown in Figure 1. The system comprises a diesel generator with a speed regulator, a wind turbine generator with a pitch angle controller, and battery energy storage. The electric power is produced by wind turbines, which are complemented by diesel generators and battery storage to compensate for variations in the active power. For the purposes of this analysis, first-order dynamical models for the wind turbine generator and battery energy storage are sufficient.

The system under consideration has the following linearized model:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =Ax\left(t\right)+Bu\left(t\right)+Ew\left(t\right)\hfill \\ \hfill u\left(t\right)& =-Kx\left(t\right),\hfill \end{array}$$

(3)

where $x\left(t\right)\in {\mathbb{R}}_{}^{n_{11}}$ is the state, $u\left(t\right)\in {\mathbb{R}}_{}^2$ is the control input, $w\left(t\right)\in {\mathbb{R}}_{}^2$ is the external disturbance, $x\left(t\right):=(x_1,x_2,\dots ,x_{11})$ with $x_1\left(t\right)=\Delta f\left(t\right)$, $x_2\left(t\right)=\Delta P_g\left(t\right)$, $x_3\left(t\right)=\Delta \nu \left(t\right)$, $x_5\left(t\right)=\Delta f_w\left(t\right)$, $x_6\left(t\right)=\Delta P_w\left(t\right)$, $x_7\left(t\right)=\Delta \beta \left(t\right)$, $x_9\left(t\right)=\Delta P_b\left(t\right)$, $x_4\left(t\right), x_8\left(t\right)$ are dummy states, and $x_{10}\left(t\right), x_{11}\left(t\right)$ are augmented states for stability. The matrix K is the controller gain matrix to be designed, and plant matrices $A, B$ are constant and have the following structure:

$$\begin{array}{ccc}\hfill A& =\hfill & \left[\begin{array}{ccccccccccc}\frac{-(1+K_{pt}{K}_{ig})}{T_{pt}}& \frac{K_{pt}}{T_{pt}}& 0& 0& \frac{K_{pt}{K}_{ig}}{T_{pt}}& 0& 0& 0& -\frac{K_{pt}}{T_{pt}}& 0& 0\\ 0& \frac{-1}{T_{d4}}& \frac{1}{T_{d4}}& 0& 0& 0& 0& 0& 0& 0& 0\\ \frac{-K_{d1}{T}_{d1}}{R_d{T}_{d2}{T}_{d3}}& 0& \frac{-1}{T_{d3}}& \frac{-Kd1(T_{d1}-T_{d2})}{T_{d2}{T}_{d3}}& 0& 0& 0& 0& 0& 0& 0\\ \frac{-1}{R_d{T}_{d2}}& 0& 0& \frac{-1}{T_{d2}}& 0& 0& 0& 0& 0& 0& 0\\ \frac{K_g}{T_w}& 0& 0& 0& \frac{(K_{tp}-K_{ig}-1)}{T_w}& \frac{1}{T_w}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& \frac{-1}{T_{p3}}& \frac{K_{pc}{K}_{p3}}{T_{p3}}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{-1}{T_{p2}}& \frac{K_{p1}{K}_{p2}(1-T_{p2})}{T_{p2}}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -1& 0& 0& 0\\ \frac{1}{T_b}& 0& 0& 0& 0& 0& 0& 0& \frac{-1}{T_b}& 0& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\end{array}\right]\hfill \\ \hfill B& =\hfill & \left[\begin{array}{ccccccccccc}0& 0& \frac{K_{d1}{T}_{d1}}{T_{d2}{T}_{d3}}& \frac{1}{T_{d2}}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& \frac{K_{p1}{K}_{p2}{T}_{p1}}{T_{p2}}& 1& 0& 0& 0\end{array}\right]\hfill \\ \hfill E& =\hfill & \left[\begin{array}{ccccccccccc}\frac{-Kpt}{T_{pt}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{1}{T_w}& 0& 0& 0& 0& 0& 0\end{array}\right]\hfill \end{array}$$

(4)

Since the feedback information is sent to the controller over a digital channel, the controller can only access the value of $x\left(t\right)$ at discrete-time instants $t_k,k\in \mathbb{N}$. Hence, considering the effect of the network, the plant model (3) is modified to

$$\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =\hfill & Ax\left(t\right)+Bu\left(t\right)+Ew\left(t\right)\hfill \\ \hfill u\left(t\right)& =\hfill & -Kx\left(t_k\right)\forall t\in (t_k,t_{k+1}],\hfill \end{array}$$

(5)

where the received state information $x\left(t_k\right)$ at the controller is kept constant between two transmissions, i.e., $\forall t\in (t_k,t_{k+1}]$, by means of the zero-order hold (ZOH) implementation. As such, we need to design both the feedback law and the triggering rule to generate the sequence of sampling times $t_k,k\in \mathbb{N}$. The latter will be designed using the event-triggered approach to reduce the amount of transmissions between the sensors and the controller. A major challenge in this context is to prevent the occurrence of Zeno phenomena while preserving the closed-loop stability. The networked control architecture of the hybrid power system is depicted in Figure 2. The full state measurement $x\left(t\right)$ is received by the ETC mechanism to release the discrete-time value $x\left(t_k\right)$ at the next transmission instant $t_k,k\in \mathbb{N}$. Accordingly, the control input $u\left(t_k\right)$ is updated and it remains constant until the next update by means of ZOH implementation. We assume that the communication channel is noiseless and delay-free.

• Problem statement. Design the feedback gain matrix K and the event-triggering rule for sampling times $t_k,k\in \mathbb{N}$, such that:

• The closed-loop stability is guaranteed in the presence of external disturbances;
• Zeno behavior is ruled out.

The problem is solved using the emulation technique, such that the controller is synthesized first in continuous-time, the sampling issue is considered, and an event-triggering mechanism is derived to keep the closed-loop system stable. In the following section, we explain how to design the feedback law in continuous-time.

4. State-Feedback Control

4.1. Feedback Law

In this section, we ignore the effect of sampling and we explain how to design the controller in continuous-time. In view of (3), if the pair $(A,B)$ is controllable, one can design K, such that the closed-loop eigenvalues are located at any desirable locations using the eigenstructure assignment. Alternatively, the linear quadratic regulator (LQR) approach can be used to compute the gain matrix K in an optimal sense according to the desired state/input response, based on the solution of the algebraic Riccati equation (ARE), to find a symmetric positive definite matrix $P\in {\mathbb{R}}_{}^{11}\times {\mathbb{R}}_{}^{11}$ that satisfies

$$\begin{array}{ccc}\hfill A^{T}P+PA+Q-PB{R}^{-1}{B}^{T}P& =\hfill & 0,\hfill \end{array}$$

(6)

where the matrix $Q\in {\mathbb{R}}_{}^{11}\times {\mathbb{R}}_{}^{11}$ is symmetric and positive semi-definite and $R\in {\mathbb{R}}_{}^2\times {\mathbb{R}}_{}^2$ is symmetric and positive semi-definite. The matrices $Q,R$ are constructed based on the desired state/input, such that the following objective function is minimized by the controller $J={\int }_0^{\infty }(x^{T}Qx+u^{T}Ru)dt$. Then, by solving the algebraic Riccati equation, the optimal state-feedback law K that minimizes the cost function J is given by $K=R^{-1}{B}^{T}P$. Note that the solution of the ARE (6) is always guaranteed if $(A,B)$ is controllable. However, due to the large sizes of matrices $A,B$, and since the state vector $x\left(t\right)$ involves dummy states $x_4,x_8$ and augmented states $x_{10},x_{11}$, the requirement that $(A,B)$ be controllable can be conservative. Hence, to relax such a requirement, we assume that the pair $(A,B)$ is only sterilizable, which implies that the uncontrollable modes of $A-BK$ are naturally stable. To that end, we need to check which of the closed-loop eigenvalues are controllable and design the controller accordingly. For this purpose, we use the Popov–Belevitch–Hautus (PBH) test or PBH for stabilizability, which states that the pair $A,B$ is stabilizable if and only if the following condition holds

$$\begin{array}{c}\hfill rank[\lambda I_n-AB]=n\forall \lambda \in {\mathbb{C}}^{+},\end{array}$$

(7)

where n is the dimension of the state vector x, and $I_n$ is an identity matrix of dimension n, i.e., the rank conditions hold for all unstable eigenvalues $\lambda$ of the closed-loop system $A-BK$.

4.2. Event-Triggering Rule

After designing the gain matrix K, we consider the effect of sampling and we synthesize an event-triggering mechanism to generate the transmission times. The sampling error is defined as follows:

$$\begin{array}{ccc}\hfill e\left(t\right)& =\hfill & x\left(t_k\right)-x\left(t\right)\forall t\in [t_k,t_{k+1}).\hfill \end{array}$$

(8)

It should be noted that $e\left(t\right)$ is reset to zero at each $t_k$ by updating the last sent value $x\left(t_k\right)$ to the current value $x\left(t\right)$. Hence, we have

$$\begin{array}{ccc}\hfill \dot{e}\left(t\right)& =\hfill & -\dot{x}\left(t\right)\hfill \\ \hfill e\left(t_k^{+}\right)& =\hfill & 0.\hfill \end{array}$$

(9)

From (8) and (19), we obtain

$$\begin{array}{ccc}\dot{x}\left(t\right)\hfill & =\hfill & (A-BK)x\left(t\right)-BKe\left(t\right)+Ew\left(t\right)\hfill \\ \hfill & =:\hfill & {\mathcal{A}}_{1}x\left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_{1}w\left(t\right).\hfill \end{array}$$

(10)

Consequently, the dynamics of the sampling error $e\left(t\right)$ are

$$\begin{array}{ccc}\dot{e}\left(t\right)\hfill & =\hfill & -(A-BK)x\left(t\right)+BKe\left(t\right)-Ew\left(t\right)\hfill \\ \hfill & =:\hfill & {\mathcal{A}}_{2}x\left(t\right)+{\mathcal{B}}_{2}e\left(t\right)+{\mathcal{E}}_{2}w\left(t\right).\hfill \end{array}$$

(11)

An intuitive design of the ETC will be $t_{k+1}=inf\{t\ge t_k:\left|e\left(t\right)\right|\ge \sigma \left|x\left(t\right)\right|\}$, where $\sigma >0$ is a design parameter to be specified later. However, in this case, an infinite number of transmissions can possibly occur within a finite time, leading to Zeno sampling, particularly since the plant is affected by external disturbances, which is not implementable in practice due to hardware constraints. By employing the time-regularization technique, one efficient way to solve this problem is to impose a strictly positive minimum duration T on the inter-transmission intervals; see, e.g., [26,28,45]. In this way, the ETC condition is modified to

$$\begin{array}{c}\hfill t_{k+1}=inf\{t\ge t_k+T:\left|e\left(t\right)\right|\ge \sigma \left|x\left(t\right)\right|\},\end{array}$$

(12)

where $T>0$ is a design parameter. Hence, according to (12), an updated transmission $t_{k+1}$ is only permitted when a certain amount of time T has passed since the last triggering instant $t_k$, and such that $\left|e\right(t\left)\right|\ge \sigma \left|x\right(t\left)\right|$ is satisfied. The enforced dwell time T is designed as the maximal allowable transmission interval (MATI) in the time-triggered control [23]. To that end, based on [23], the following conditions are required to derive the MATI bound.

Assumption 1.

Consider the system (10), (11). There exist $\epsilon ,\gamma ,\eta >0$, and a real matrix $P=P^T>0$, such that the following condition holds:

$$\begin{array}{c}\left[\begin{array}{ccc}{\mathcal{A}}_1^T\mathit{P}+\mathit{P}{\mathcal{A}}_1+{\mathcal{A}}_2^T{\mathcal{A}}_2+(1+\epsilon ){\mathbb{I}}_{n_x}& ★& ★\\ {\mathcal{B}}_1^T\mathit{P}& -{\gamma }^2{\mathbb{I}}_{n_x}& ★\\ {\mathcal{E}}_1^T\mathit{P}+{\mathcal{E}}_2^T{\mathcal{A}}_2& 0& {\mathcal{E}}_2^T{\mathcal{E}}_2-\mathit{\eta }{\mathbb{I}}_{n_w}\end{array}\right]<0.\hfill \end{array}$$

(13)

Condition (13) imposes an ${\mathcal{L}}_2$-gain stability from $(e,w)$ to x with an ${\mathcal{L}}_2$-gain equal to $\sqrt{\eta }$. In other words, by defining $W\left(e\right):=\left|e\right|$ and $V\left(x\right):=x^{T}Px$, it holds that

$$\begin{array}{ccc}\langle \nabla W\left(e\right),{\mathcal{A}}_{2}x\left(t\right)+{\mathcal{B}}_{2}e\left(t\right)+{\mathcal{E}}_{2}w\left(t\right)\rangle \hfill & \le \hfill & H(x,w)+L\left|e\right|,\hfill \end{array}$$

(14)

where $H(x,w):=|{\mathcal{A}}_{2}x+{\mathcal{E}}_{2}w|$ and $L:=|{\mathcal{B}}_2|$. Consequently, by post- and pre-multiplying (13) by $(x,e,w)$ and its transpose, the feasibility of (13) implies that

$$\begin{array}{c}\hfill \langle \nabla V\left(x\right),{\mathcal{A}}_{1}x\left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_{1}w\left(t\right)\rangle \le -{(1+\epsilon )\left|x\right|}^2-H^2(x,w)+{\gamma }^2{W}^2\left(e\right)+\eta {\left|w\right|}^2.\end{array}$$

(15)

Then, according to [23], the stability of the closed-loop system $(x,e)$ is maintained under time-triggered control if the time T is taken, such that $T\in \mathcal{T}(\gamma ,L)$, where $\mathcal{T}(\gamma ,L)$, and is given by

$$\mathcal{T}(\gamma ,L):=\left\{\begin{array}{cc}\frac{1}{Lr}arctan\left(r\right)\hfill & \gamma >L\hfill \\ \frac{1}{L}\hfill & \gamma =L\hfill \\ \frac{1}{Lr}arctan\left(r\right)\hfill & \gamma <L\hfill \end{array}\right.$$

(16)

with $r:=\sqrt{\left|{\left(\frac{\gamma }{L}\right)}^2-1\right|}$ and $\gamma ,L$ from Assumption 1. To provide some insight into how this time $\mathcal{T}(\gamma ,L)$ is computed in [23], let us define the variable $\varphi \in {\mathbb{R}}_{\ge 0}^{}$ with the following dynamics:

$$\dot{\varphi }=-2L\varphi -{\tilde{\gamma }}^2({\varphi }^2+1)\varphi \left(0\right)={\lambda }^{-1},$$

(17)

where $\lambda \in (0,1)$, $\tilde{\gamma }=\sqrt{\gamma +\nu }$ with $\gamma$ comes from Assumption 1, with any small $\nu >0$ and L, as defined in (14). Hence, the time $\mathcal{T}(\gamma ,L)$ corresponds to the time it takes for $\varphi$ to decrease from ${\lambda }^{-1}$ to $\lambda$.

We note that, in view of (15), if we enforce ${\gamma }^2{W}^2\left(e\right)\le \epsilon {\left|x\right|}^2$, then it holds that

$$\begin{array}{c}\hfill \langle \nabla V\left(x\right),{\mathcal{A}}_{1}x\left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_{1}w\left(t\right)\rangle \le -{\left|x\right|}^2+\eta {\left|w\right|}^2\end{array}$$

(18)

which ensures that the closed-loop system is ${\mathcal{L}}_2$-stable. Hence, the triggering threshold $\sigma$ in (12) is defined as $\sigma =\frac{\sqrt{\epsilon }}{\gamma }$.

To summarize, the ETC (12) is designed as follows. We

• Stabilize the plant model (3) in continuous-time;
• Check the feasibility of Assumption (12) and determine the value of $\gamma ,L$.
• Compute the MATI bound $\mathcal{T}(\gamma ,L)$ from (16) and take $T\in \mathcal{T}(\gamma ,L)$.
• Determine the value of the ETC threshold $\sigma$, as will be specified later.

5. Stability Analysis

From the developments in Section 4.2, it is clear that the overall system involves interactions between continuous- and discrete-time dynamics. Hence, it would be realistic to model the closed-loop system as a hybrid dynamical system. In view of (8)–(11) and since ZOH is employed, we obtain the following impulsive model:

$$\begin{array}{cc}\left.\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =\hfill & {\mathcal{A}}_{1}x\left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_{1}w\left(t\right)\hfill \\ \hfill \dot{e}\left(t\right)& =\hfill & {\mathcal{A}}_{2}x\left(t\right)+{\mathcal{B}}_{2}e\left(t\right)+{\mathcal{E}}_{2}w\left(t\right)\hfill \end{array}\right\}\hfill & \forall t\in {\mathbb{R}}_{}^{}\hfill \\ \left.\begin{array}{ccc}\hfill u\left(t\right)& =\hfill & -Kx\left(t_k\right)\hfill \\ \hfill \dot{e}\left(t_k\right)& =\hfill & 0\hfill \end{array}\right\}\hfill & \forall t\in [t_k,t_{k+1}).\hfill \end{array}$$

(19)

Additionally, a time variable with the following dynamics needs to be included as an auxiliary variable

$$\begin{array}{ccccc}\hfill \dot{\tau }\left(t\right)& =\hfill & 1\forall t\in [t_k,t_{k+1}),\tau \left(t_k^{+}\right)\hfill & =\hfill & 0.\hfill \end{array}$$

(20)

The variable $\tau$ is used to track the elapsed time from the transmission instant $t_k,k\in \mathbb{N}$ until the next sampling time $t_{k+1}$, where $\tau$ is reset to zero, as described in (20).

We employ the framework [40] to define the closed-loop system as a hybrid dynamical system, where the jump dynamics refer to the discrete-time changes and the flow dynamics refer to continuous-time behavior. Additionally, the flow set and the jump set are used to indicate whether the system is operating in continuous or discrete time, respectively. The reader may refer to [40] for more information on these terms. Let $\xi :=(x,e,\tau )\in {\mathbb{R}}_{}^{n_x}\times {\mathbb{R}}_{}^{n_x}\times {\mathbb{R}}_{}^{}$. Then, the hybrid dynamical system is

$$\begin{array}{cccc}\hfill \dot{\xi }\left(t\right)& \in \hfill & \left[\begin{array}{c}{\mathcal{A}}_{1}x\left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_{1}w\left(t\right)\\ {\mathcal{A}}_{2}x\left(t\right)+{\mathcal{B}}_{2}e\left(t\right)+{\mathcal{E}}_{2}w\left(t\right)\\ 1\end{array}\right],\hfill & \xi \left(t\right)\in \mathcal{C}\hfill \\ \hfill \xi \left(t_k^{+}\right)& \in \hfill & \left[\begin{array}{c}x\\ 0\\ 0\end{array}\right],\hfill & \xi \left(t\right)\in \mathcal{D},\hfill \end{array}$$

(21)

where the flow set $\mathcal{C}$ and the jump set $\mathcal{D}$ are constructed based on the ETC (12) as follows:

$$\begin{array}{ccc}\hfill \mathcal{C}& =\hfill & \left\{\xi \left(t\right):\left|e\right(t\left)\right|\le \sigma \left|x\right(t\left)\right|\mathrm{or}\tau \in [0,T]\right\}\hfill \\ \hfill \mathcal{D}& =\hfill & \left\{\xi \left(t\right):\left|e\right(t\left)\right|\ge \sigma \left|x\right(t\left)\right|\mathrm{and}\tau \ge T\right\}.\hfill \end{array}$$

(22)

Note that the flow and jump sets $C,D$ are closed and the flow and jump maps in (21) are continuous, which ensures that the hybrid model (21) is well-posed; see [40] for more details.

Now, we present the main results.

Theorem 1.

Consider systems (21) and (22) with Assumption 1. Take $\sigma =\frac{\sqrt{\epsilon }}{\gamma }$ and $T\in (0,\mathcal{T}(\gamma ,L\left)\right)$ in (22). Then, systems (21), (22) are ${\mathcal{L}}_2$-gain-stable from w to x with an ${\mathcal{L}}_2$-gain that is less than or equal to $\sqrt{\eta }$.

Proof of Theorem 1.

Recall that $\xi =(x,e,\tau )$, as defined in (21). For all $\xi \in C\cup D$, we define $R\left(\xi \right):=V\left(x\right)+max\{0,\tilde{\gamma }\varphi \left(\tau \right)W^2\left(e\right)\}$ with $V\left(x\right)$ and $W\left(e\right)$, as defined in (15) and (14). We study the dynamics of $R\left(\xi \right)$ during the flow and jump phases.

Let $\xi \in D$, we obtain, in view of (21), and the fact that $W\left(0\right)=0$

$$\begin{array}{ccc}\hfill R\left(G\right(\xi \left)\right)& =\hfill & V\left(x\right)+max\{0,\tilde{\gamma }\varphi \left(0\right)W^2\left(0\right)\}\hfill \\ \hfill & \le \hfill & R\left(\xi \right),\hfill \end{array}$$

(23)

where $G\left(\xi \right):=(x,0,0)$.

Let $\xi \in C$, and suppose that $\varphi \left(\tau \right)<0$, which implies that $\tau >T$. Hence, ${\gamma }^2{W}^2\left(e\right)\le \epsilon {\left|x\right|}^2$ in view of (22) since $\xi \in C$. Consequently,

$$\begin{array}{ccc}\hfill \dot{R}(\xi ;F(\xi ,w))& \le \hfill & -{\left|x\right|}^2+\eta {\left|w\right|}^2,\hfill \end{array}$$

(24)

where $F(\xi ,w):=({\mathcal{A}}_{1}x\left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_{1}w\left(t\right),{\mathcal{A}}_{2}x\left(t\right)+{\mathcal{E}}_{2}w\left(t\right),1)$.

When $\xi \in C$ and $\varphi \left(\tau \right)>0$, we have $R\left(\xi \right)=V\left(x\right)+\tilde{\gamma }\varphi \left(\tau \right)W^2\left(e\right)$. As with Assumptions 1 and (17), we obtain

$$\begin{array}{ccc}\hfill \dot{R}(\xi ;F(\xi ,w))& \le \hfill & -{(1+\epsilon )\left|x\right|}^2-H^2(x,w)+{\gamma }^2{W}^2\left(e\right)+\eta {\left|w\right|}^2+2\lambda \varphi \left(\tau \right)W\left(e\right)H(x,w)\hfill \\ \hfill & \hfill & -{\tilde{\gamma }}^2{\varphi }^2\left(\tau \right)W^2\left(e\right)-{\tilde{\gamma }}^2{W}^2\left(e\right)\hfill \end{array}$$

(25)

Using the fact that $2{\tilde{\gamma }}^2\varphi \left(\tau \right)W\left(e\right)H(x,w)\le {\tilde{\gamma }}^2{\varphi }^2\left(\tau \right)W^2\left(e\right)+H^2(x,w)$, we obtain

$$\begin{array}{ccc}\hfill \dot{R}(\xi ;F(\xi ,w))& \le \hfill & -{(1+\epsilon )\left|x\right|}^2+{\gamma }^2{W}^2\left(e\right)+\eta {\left|w\right|}^2-{\tilde{\gamma }}^2{W}^2\left(e\right)\hfill \end{array}$$

(26)

Recall that ${\tilde{\gamma }}^2={\gamma }^2+\nu$, it holds that

$$\begin{array}{ccc}\hfill \dot{R}(\xi ;F(\xi ,w))& \le \hfill & -{(1+\epsilon )\left|x\right|}^2+{\eta \left|w\right|}^2-\nu W^2\left(e\right)-{\epsilon \left|x\right|}^2+\eta {\left|w\right|}^2.\hfill \end{array}$$

(27)

As a result, in view of (24) and (27), for all $\xi \in \mathcal{C}$, it holds that

$$\dot{R}(\xi ;F(\xi ,w))\le -{\epsilon \left|x\right|}^2+\eta {\left|w\right|}^2,$$

(28)

which implies ${\mathcal{L}}_2$-gain stability. □

The developed ETC strategy in this study is based on the following assumptions:

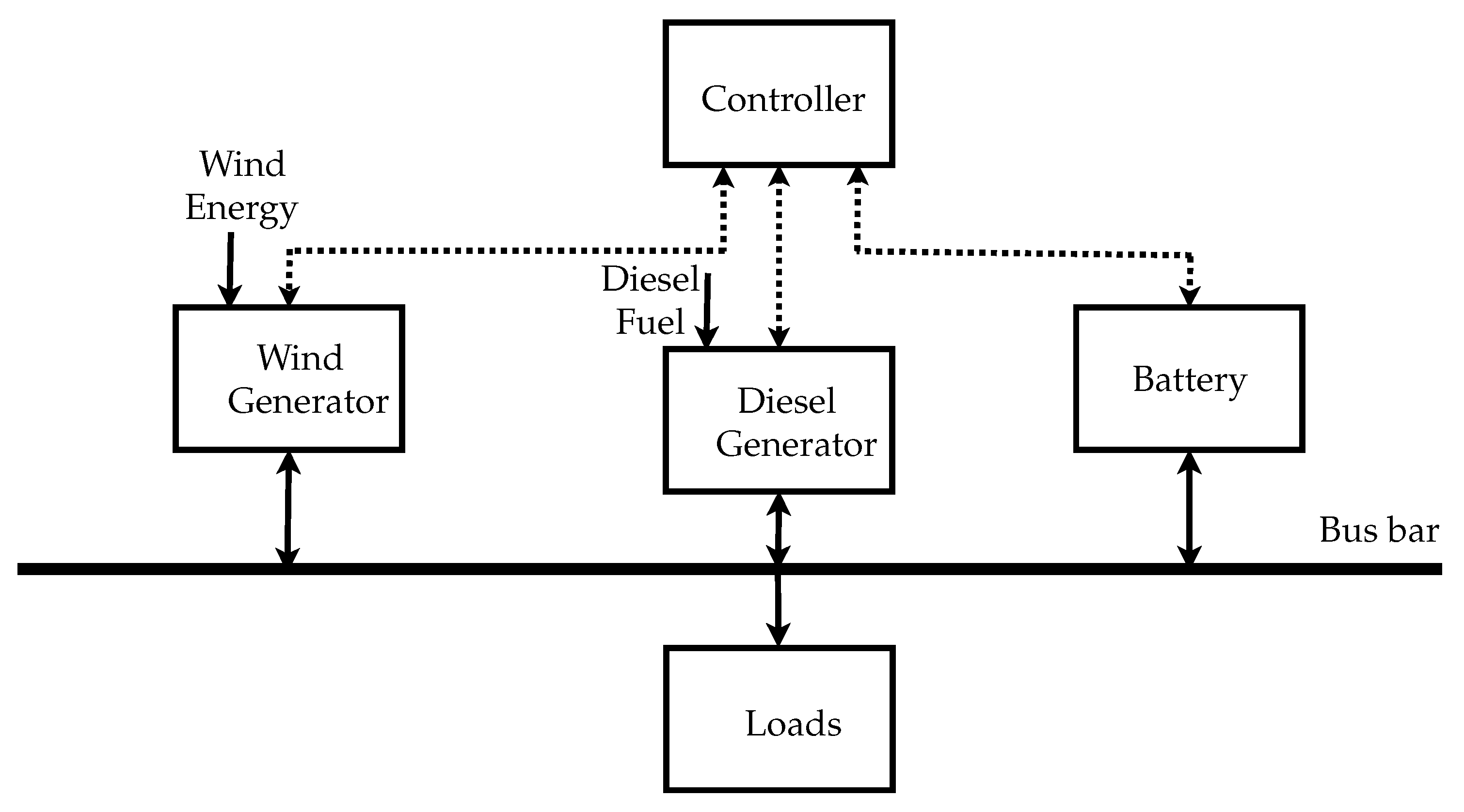
• The hybrid wind–diesel system is described by the linearized model (3).
• The full state vector $x\left(t\right)$ is available for feedback.
• Plant matrices $A,B$ are controllable/stabilizable.
• The communication network is noiseless and delay-free.
• The event-triggering rule $\left|e\right|\le \sigma \left|x\right|$ can be continuously verified by the ETC.

The first assumption is valid when the HWDPS system operates around the equilibrium point or when a small signal analysis is used to derive the dynamic model of the HWDPS [46].

The second statement is used to simplify the design of the feedback law. In practice, this requirement might be difficult to meet, and in this case, output feedback methods can be employed, such as the observer-based control and the ETC approach, which can be adapted by modifying the closed-loop matrices ${\mathcal{A}}_1,{\mathcal{B}}_1,{\mathcal{E}}_1,{\mathcal{A}}_2,{\mathcal{B}}_2,{\mathcal{E}}_2$ in the hybrid model (21), as shown in the next section.

The third assumption is standard in order to design state-feedback controllers of the form $u=-Kx$, as in (3). This assumption practically implies that sufficient actuators are available in the HWDPS system to control the required state variables, which, in practice, is often the case.

The fourth assumption is introduced to facilitate the analysis since the presence of communication delays can significantly affect the ETC performance. In particular, if the communication delays are larger than the sampling intervals, then all the control updates will be outdated, which can destabilize the closed-loop system. In this context, it is often assumed that communication delays are small compared to sampling intervals, and the concept of the maximal allowable delay (MAD) is employed, see, e.g., [44]. Addressing such an issue is far from being trivial and requires separate analysis to derive the MAD bound.

The fifth assumption means that the sensors are equipped with some special circuits (smart sensors) to continuously verify the event-triggering rule and it decides when a new measurement should be transmitted to the controller. This requirement is feasible when the feedback signal is analog and the sensor can be equipped with such a circuit. If the sensors are digital devices, periodic event-triggering conditions can be used alternatively, in which the triggering rule is only checked at periodic time instants, as in [47,48]. However, the application of the developed ETC method in this study cannot be directly applied to this scenario and a complete new analysis is required to ensure the closed-loop stability.

6. Robustness of the Developed Event-Triggered Controller

In this section, we study the robustness of the developed ETC mechanism against external disturbances, measurement noises, and computational errors. Consider the following system:

$$\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =\hfill & Ax\left(t\right)+Bu\left(t\right)+Ew\left(t\right)\hfill \\ \hfill y\left(t\right)& =\hfill & Cx\left(t\right)+\nu \left(t\right),\hfill \end{array}$$

(29)

where $x\in {\mathbb{R}}_{}^{n_x}$ is the state, $u\in {\mathbb{R}}_{}^{n_u}$ is the control input, $y\in {\mathbb{R}}_{}^{n_y}$ is the measured output, $w\in {\mathbb{R}}_{}^{n_w}$ is the external disturbance, and $\nu \in {\mathbb{R}}_{}^{n_{\nu }}$ is the measurement noise, which is assumed to be differentiable. Here, we assume that only some parts of the state can be measured, not the full state, as considered in Section 3, which is more challenging. Matrices $A,B,E$ are given in (4) and the matrix C is given by

$$\begin{array}{ccc}\hfill C& =\hfill & \left[\begin{array}{ccccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0,\end{array}\right]\hfill \end{array}$$

(30)

which implies that only the system frequency $x_1=f\left(t\right)$ and wind generation frequency $x_5=f_w\left(t\right)$ can be measured. The plant (29) is stabilized by the following observer-based controller

$$\begin{array}{ccc}\hfill \dot{\zeta }\left(t\right)& =\hfill & A\zeta \left(t\right)+Bu\left(t\right)+F(y\left(t_k\right)-C\zeta \left(t\right))\hfill \\ \hfill u\left(t\right)& =\hfill & -K\zeta \left(t\right)+\upsilon \left(t\right),\hfill \end{array}$$

(31)

where $\zeta \in {\mathbb{R}}_{}^{n_{\zeta }}$ is the estimated state, $\upsilon \in {\mathbb{R}}_{}^{n_{\upsilon }}$ is the computational error, such as glitch or controller disturbances, and F is the gain matrix of the observer. Note that the plant output $y\left(t\right)$ is only sent to the controller at triggering instants $t_k$, as indicated by the term $y\left(t_k\right)$ in (31). Now, we define the sampling error of the output measurement $y\left(t\right)$ as follows:

$$\begin{array}{ccc}\hfill e\left(t\right)& =\hfill & y\left(t_k\right)-y\left(t\right)\forall t\in [t_k,t_{k+1}).\hfill \end{array}$$

(32)

Then, systems (29) and (31) become

$$\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =\hfill & Ax\left(t\right)-BK\zeta \left(t\right)+B\upsilon \left(t\right)+Ew\left(t\right)\hfill \\ \hfill \dot{\zeta }\left(t\right)& =\hfill & A\zeta \left(t\right)-BK\zeta \left(t\right)+B\upsilon \left(t\right)+F\left(y\right(t)+e(t\left)\right)-FC\zeta \left(t\right)\hfill \\ \hfill & =\hfill & (A-BK-FC)\zeta +FCx\left(t\right)+F\nu \left(t\right)+Fe\left(t\right)+B\upsilon \left(t\right).\hfill \end{array}$$

(33)

Consequently, the dynamics of $e\left(t\right)$ become

$$\begin{array}{ccc}\dot{e}\left(t\right)\hfill & =\hfill & -C\dot{x}+\dot{\nu }\left(t\right)\hfill \\ \hfill & =\hfill & -CAx\left(t\right)+CBK\zeta \left(t\right)-CB\upsilon \left(t\right)-CEw\left(t\right)+\dot{\nu }\left(t\right).\hfill \end{array}$$

(34)

Let $\chi \left(t\right):=\left(x\right(t),\zeta (t\left)\right)$, $\omega \left(t\right):=(w\left(t\right),\upsilon \left(t\right),\nu \left(t\right),\dot{\nu }\left(t\right))$. Then, closed-loop systems (33) and (34) can be written as

$$\begin{array}{ccc}\hfill \dot{\chi }\left(t\right)& =\hfill & \left[\begin{array}{cc}A& -BK\\ FC& A-BK-FC\end{array}\right]\chi \left(t\right)+\left[\begin{array}{c}0\\ F\end{array}\right]e\left(t\right)+\left[\begin{array}{cccc}E& B& 0& 0\\ 0& B& F& 0\end{array}\right]\omega \left(t\right)\hfill \\ \hfill & =:\hfill & {\mathcal{A}}_1\chi \left(t\right)+{\mathcal{B}}_{1}e\left(t\right)+{\mathcal{E}}_1\omega \left(t\right),\hfill \end{array}$$

(35)

and

$$\begin{array}{ccc}\hfill \dot{e}\left(t\right)& =\hfill & \left[\begin{array}{cc}-CA& CBK\end{array}\right]\chi \left(t\right)+\left[\begin{array}{c}-CE0-CB1\end{array}\right]\omega \left(t\right)\hfill \\ \hfill & =:\hfill & {\mathcal{A}}_2\chi \left(t\right)+{\mathcal{E}}_1\omega \left(t\right).\hfill \end{array}$$

(36)

Then, if we define $\xi =(\chi ,e,\tau )$, we obtain the hybrid model (21) with ${\mathcal{B}}_2=0$ and ${\mathcal{A}}_1,{\mathcal{B}}_1,{\mathcal{E}}_1,{\mathcal{A}}_2,{\mathcal{E}}_2$, and the flow and jump sets are modified as follows:

$$\begin{array}{ccc}\hfill \mathcal{C}& =\hfill & \left\{\xi \left(t\right):\left|e\right(t\left)\right|\le \sigma \left|y\right(t\left)\right|\mathrm{or}\tau \in [0,T]\right\}\hfill \\ \hfill \mathcal{D}& =\hfill & \left\{\xi \left(t\right):\left|e\right(t\left)\right|\ge \sigma \left|y\right(t\left)\right|\mathrm{and}\tau \ge T\right\},\hfill \end{array}$$

(37)

where the triggering threshold is now a function of the measured output y rather than the full state, as in (22). Then, the obtained result in Theorem 1 applies. Indeed, in this case, the obtained ETC parameters and the guaranteed ${\mathcal{L}}_2$-gain will be different, according to the existing disturbances.

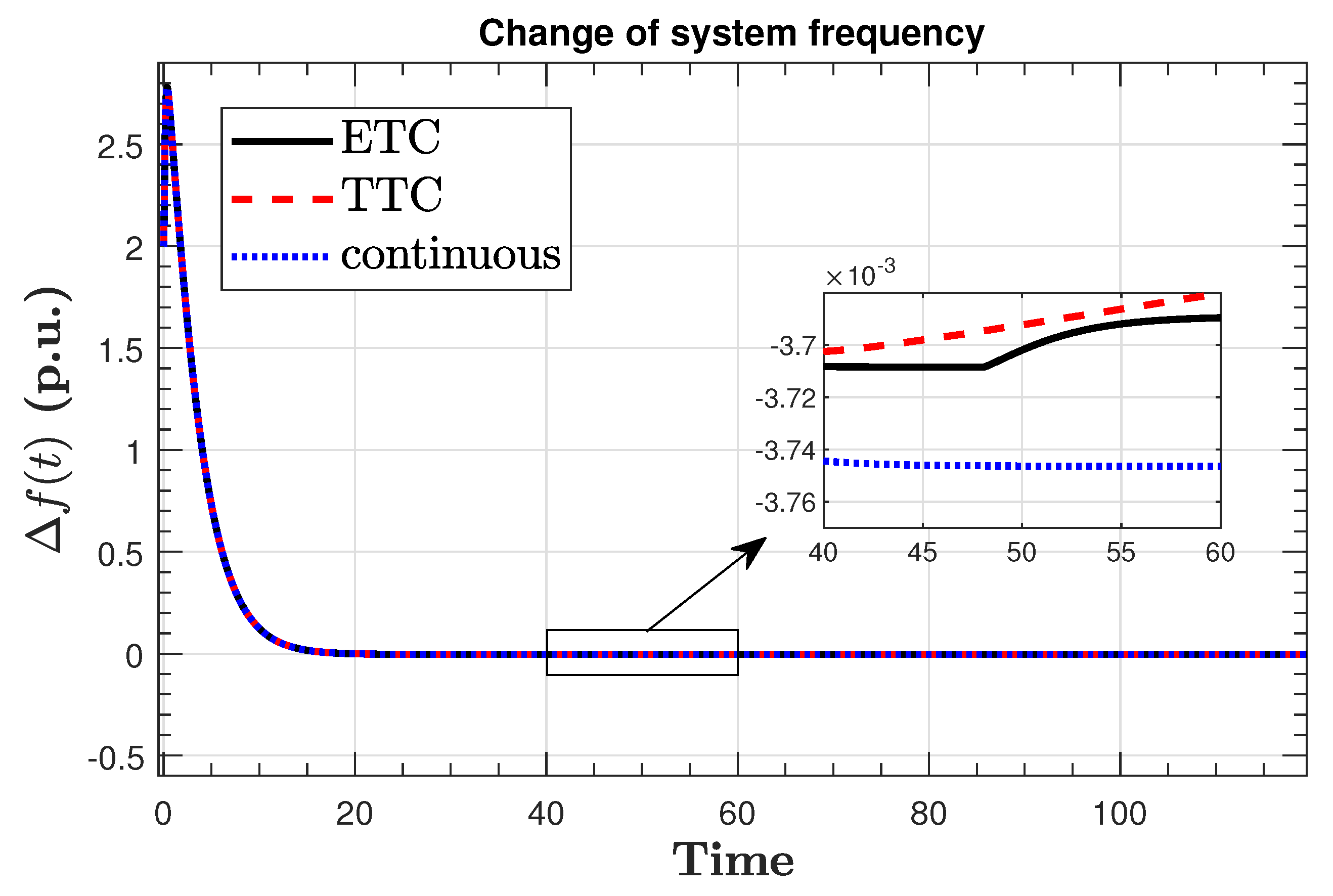
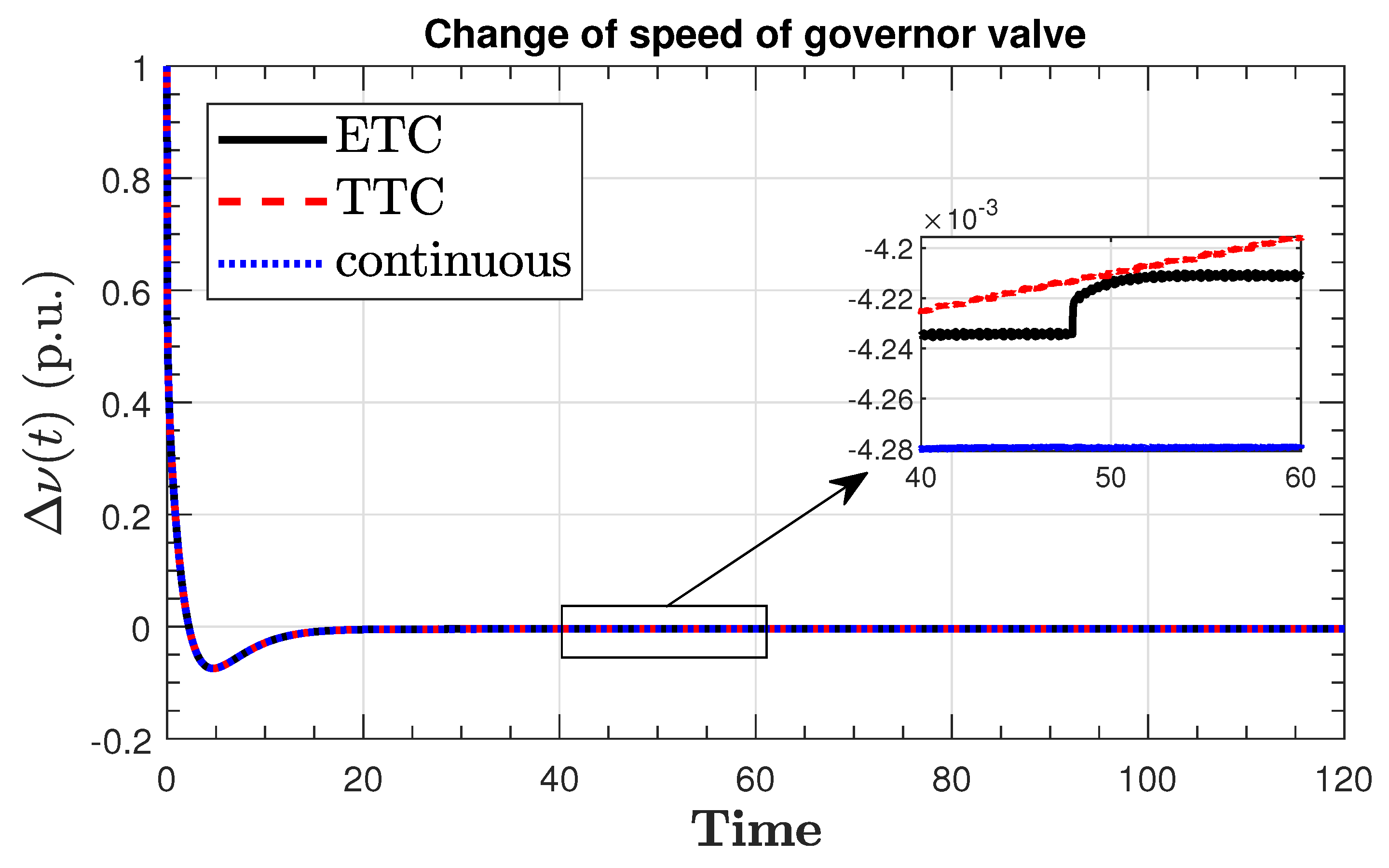
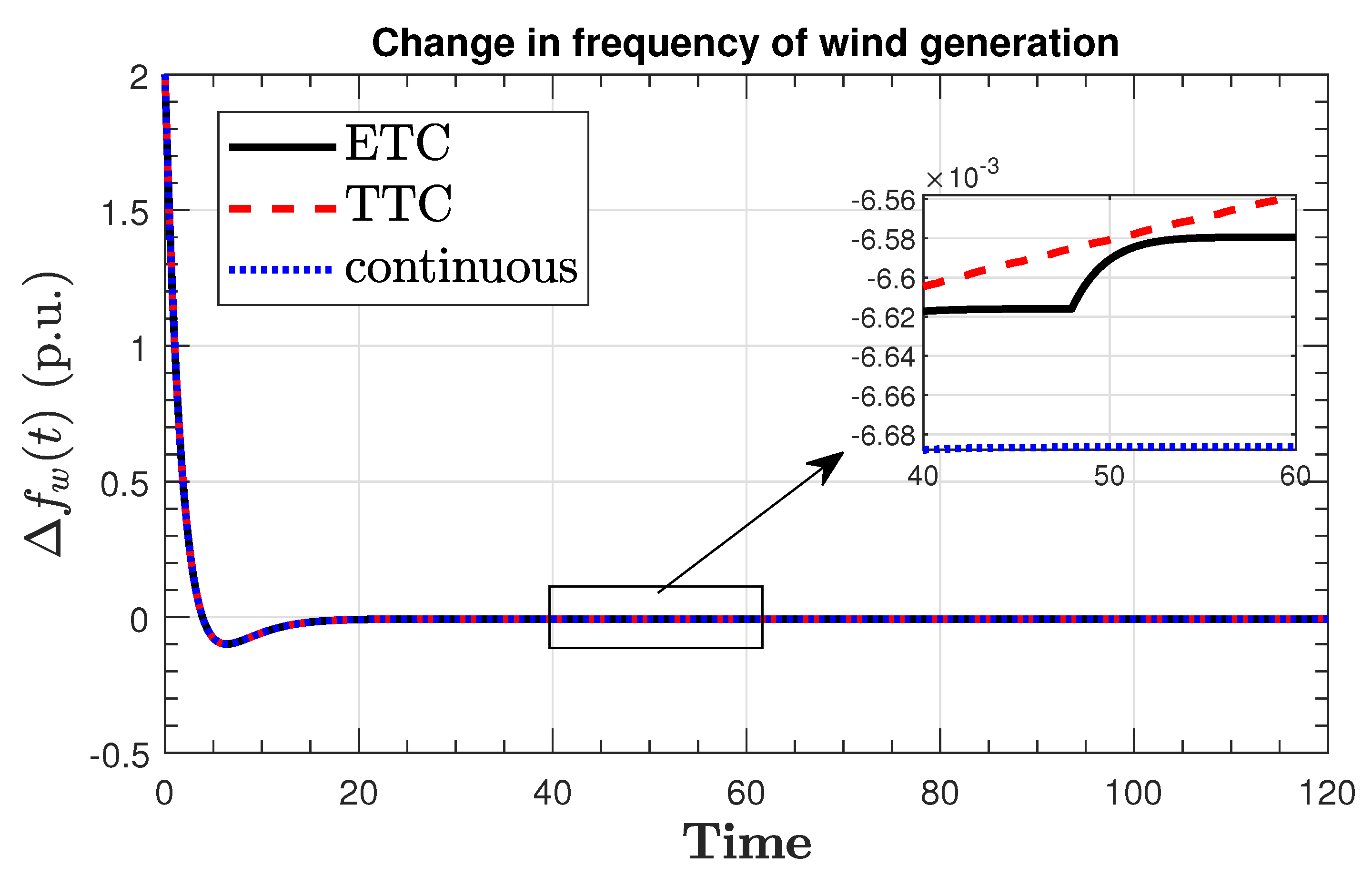
7. Results and Discussion

The obtained results in the previous section are verified by simulation using the parameters given in [43], which leads to the following state space matrices.

$$\begin{array}{ccc}\hfill A& =\hfill & \left[\begin{array}{ccccccccccc}-1.4202& 4.9957& 0& 0& 1.3588& 0& 0& 0& -4.9957& 0& 0\\ 0& -0.3333& 0.3333& 0& 0& 0& 0& 0& 0& 0& 0\\ -2.560& 0& -40.0& 12.80& 0& 0& 0& 0& 0& 0& 0\\ -0.10& 0& 0& -0.50& 0& 0& 0& 0& 0& 0& 0\\ 0.0680& 0& 0& 0& -0.3176& 0.250& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -1.0& 0.1120& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -24.3902& 12.1951& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -1.0& 0& 0& 0\\ 20.0& 0& 0& 0& 0& 0& 0& 0& -20.0& 0& 0\\ 1.0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1.0& 0& 0& 0& 0& 0& 0\end{array}\right]\hfill \\ \hfill B& =\hfill & {\left[\begin{array}{ccccccccccc}0& 0& 12.80& 0.50& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 18.2927& 1.0& 0& 0& 0\end{array}\right]}^T\hfill \\ \hfill E& =\hfill & {\left[\begin{array}{ccccccccccc}-4.9957& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0.25& 0& 0& 0& 0& 0& 0\end{array}\right]}^T.\hfill \end{array}$$

(38)

We design the controller, as described in Section 4, where we set the control input matrix $R=\mathrm{diag}\{3,3\}\times {10}^4$ and the state matrix $Q=\mathrm{diag}\{0.01,0,0,0,0.03,0,0,0,0,0.01,0.03\}$ by manual tuning, and we obtain

$$\begin{array}{c}\hfill K=\left[\begin{array}{ccccccccccc}0.1& 1.4& 0& 0.3& 1.1& 3& 0& 0& 0& 0.6& 0.2\\ 0& 0.2& 0& 0& 3.1& 0.8& 0& 0& 0& -0.1& 1\end{array}\right]\times {10}^{-3}.\end{array}$$

Then, by using the MATLAB environment with the YALMIP toolbox and the SeDuMi solver [49], the following values are obtained from the solution of the LMI condition (13): $\epsilon =2.0835\times -5$, $\gamma =1.0001$, $\eta =31.6228$, $\sigma =0.0046$ and $\mathcal{T}(\gamma ,\beta )=1.51$ s. Thus, all of the ETC parameters were established. Then, by using the hybrid dynamical systems MATLAB toolbox HyEQ [50], simulations of system (21) were executed with the arbitrary initial values $x\left(t_0\right)=(2,3,1,2,3,5,4,5,3,-2,-4)$, $e\left(t_0\right)={\left[0\right]}_{11\times 1}$ and $\tau \left(t_0\right)=0$ for 120 s with random disturbances w. The resulting average and lowest inter-transmission intervals are ${\tau }_{avg}=6.1684,{\tau }_{min}=T=1.51$ s, respectively. The closed-loop response is shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 for the continuous-time, time-triggered, and event-triggered controls. The simulation results show that the system frequency $f\left(t\right)$, the active power of the diesel generator $P_g\left(t\right)$, the active power of wind generation $P_w\left(t\right)$, the speed of governor valve $\nu \left(t\right)$, the frequency response of wind generation $f_w\left(t\right)$, the output response of the hydraulic pitch actuator $\beta \left(t\right)$, and the active power of the battery all converge to the origin in a short time. Figure 10 shows the sampling-induced errors of the system states, where the sampling errors are reset to zero at each transmission instant $t_k,k\in \mathbb{N}$, according to (9). The generated transmission instants $t_k,k\in \mathbb{N}$ by the proposed ETC (12) are depicted in Figure 11, where the ETC generates inter-transmission times that are much larger than (more than 10 times) the sampling period $T=1.51$ s, demonstrating the effectiveness of the ETC in reducing the feedback transmission amount. Moreover, the state response shows that the event-triggered controller provides almost the same response as the continuous-time and triggered implementations while the transmission amounts are reduced.

In Figure 3, we see that the system frequency $f\left(t\right)$ starts at an initial value of $f\left(0\right)=2$ (Hz), increases to about $2.8$ Hz, and then converges rapidly to the origin at around 15 s.

The active power of the diesel generator $P_g\left(t\right)$ starts at the initial value of $P_g\left(0\right)=3$ (KW) and converges to the origin in less than 15 s, while no overshoot is exhibited in the response, as shown in Figure 4.

Figure 5 shows the active power of wind generation $P_w\left(t\right)$, which starts at $P_g\left(0\right)=5$ (KW) and converges to the origin at a short time, about 7 s, while no overshoot is observed.

The speed response of the governor valve $\nu \left(t\right)$ is depicted in Figure 6, where it starts from the initial value $\nu \left(0\right)=1$ (m/s) and converges to the origin with an observed overshoot that is less than $10\%$.

In Figure 7, the frequency response of the wind generation $f_w\left(t\right)$ is depicted, where it starts from the initial value $f_w\left(0\right)=3$ (Hz), slightly increases, and then converges to the origin without overshoot.

The output response of the hydraulic pitch actuator $\beta \left(t\right)$ is shown in Figure 8, where it starts from the initial value of $\beta \left(0\right)=4$ (KW) and approaches the origin in a short time without overshoot.

Figure 9 presents the trajectory of the active power of the battery $P_b\left(t\right)$, which starts from $P_b\left(0\right)=3$ (KW) and converges to the origin in a short time, without overshoot.

Figure 10 shows the sampling-induced errors for all considered states, with a zoom-in on the first 10 s for readability. All sampling errors are reset to zero at each triggering instant $t_k,k\in \mathbb{N}$, as discussed in (9).

Figure 11 presents the generated sampling times by the proposed ETC mechanism (37). We observe that the first series of sampling times are typically produced by the periodic sampling rule with $T=1.51$ s while the remaining transmission instants are much larger than T. This behavior reflects the fact that, at the first stage of response, i.e., the transient response, more information needs to be submitted to the controller to update the control signal, such that the closed-loop stability can be ensured. Then, during the second stage, i.e., the steady-state stage, fewer control updates are needed, as all the states have already stabilized at the origin, as required. We can observe that the last transmission interval number is about 15 s as opposed to the periodic sampling period, $T=1.51$ s, i.e., the transmission intervals by the ETC mechanism are 10 times larger than the sampling period T during the steady-state stage, demonstrating the efficiency of the ETC control in reducing the communication load over the network.

To further illustrate the advantage of the approach, the obtained results are compared with [43] for sampling periods $T=2$ s and $T=4$ s, as shown in

Table 1. Comparison with [43], with a sampling period of $T=2$ s.

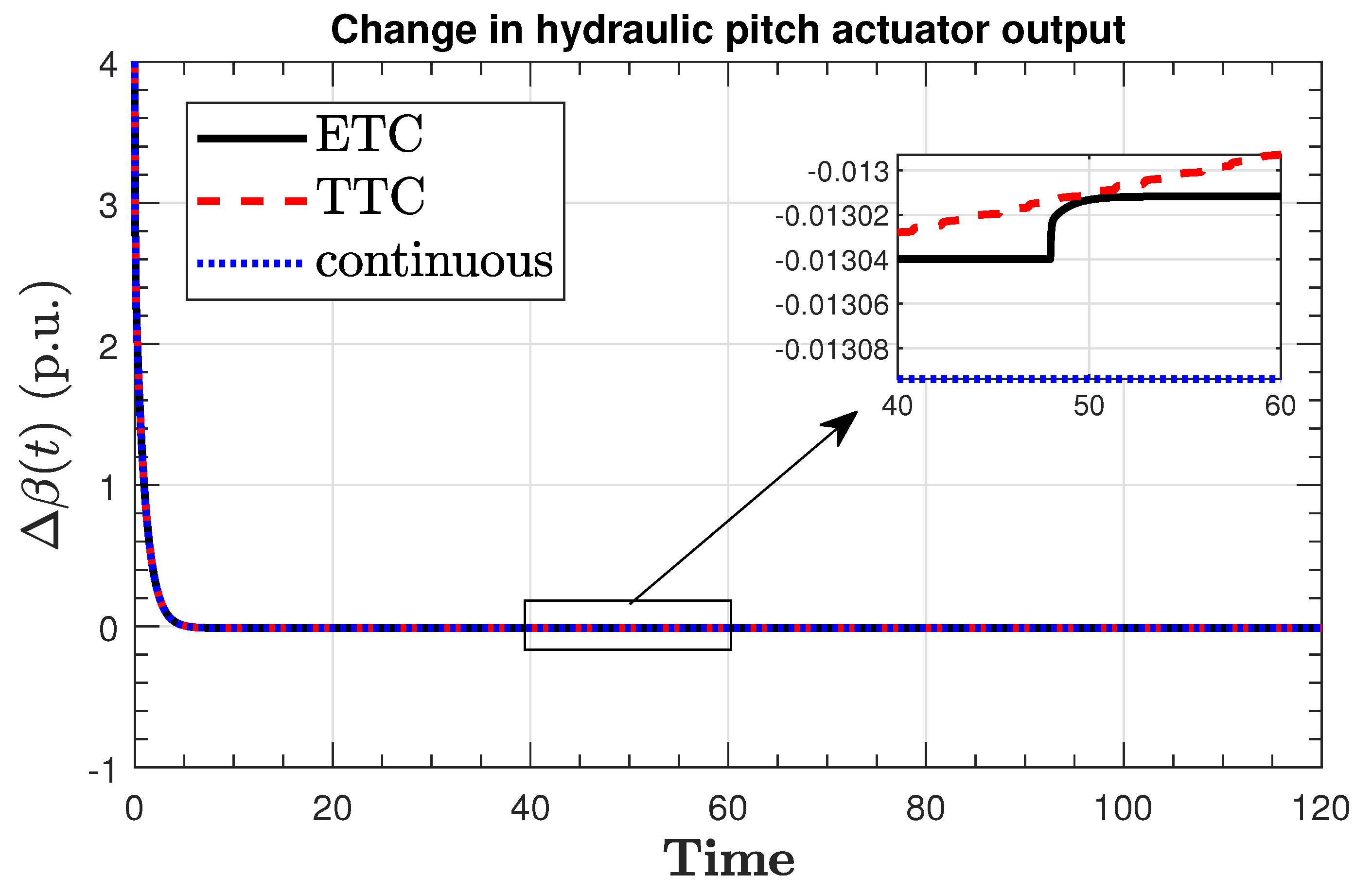
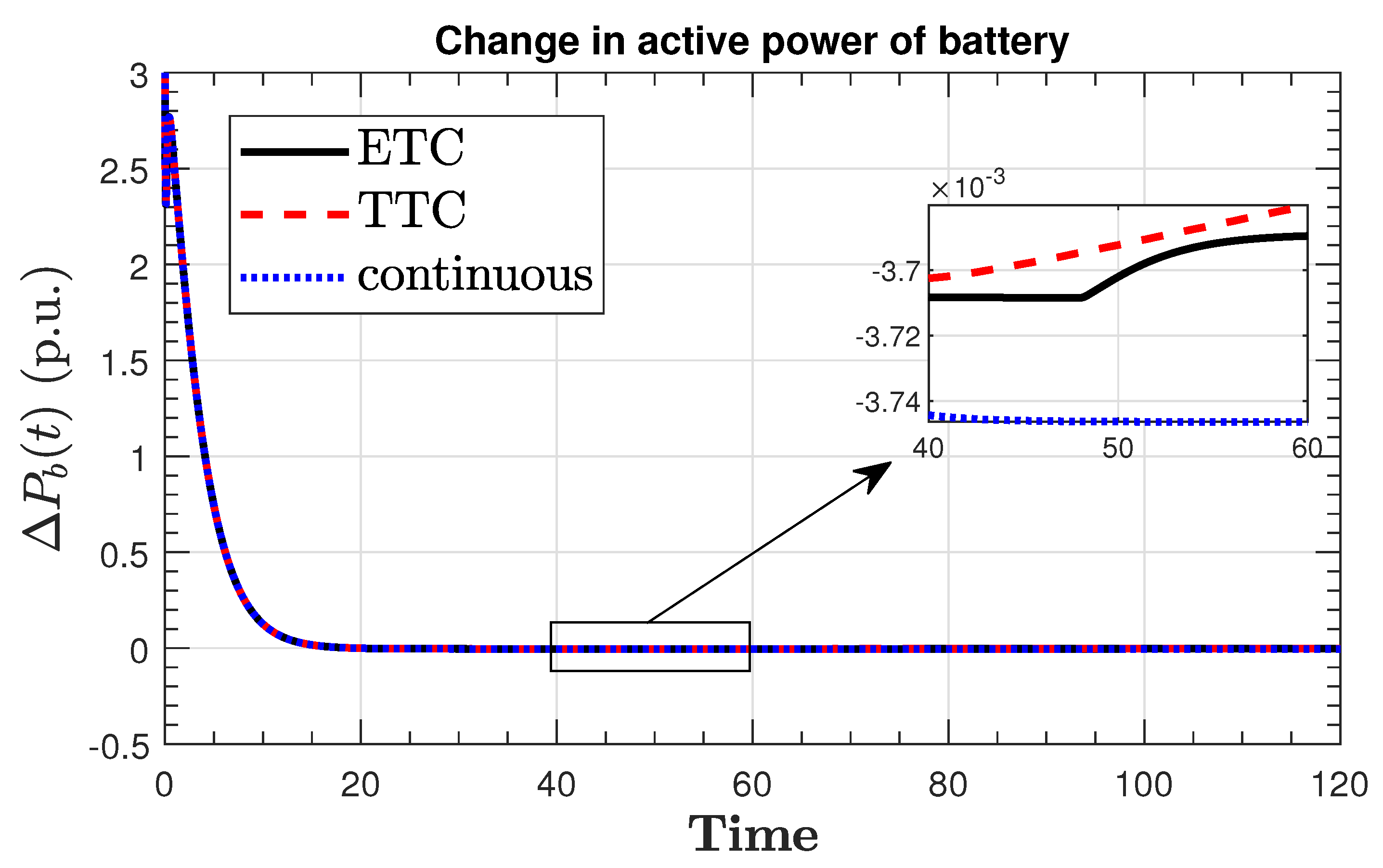
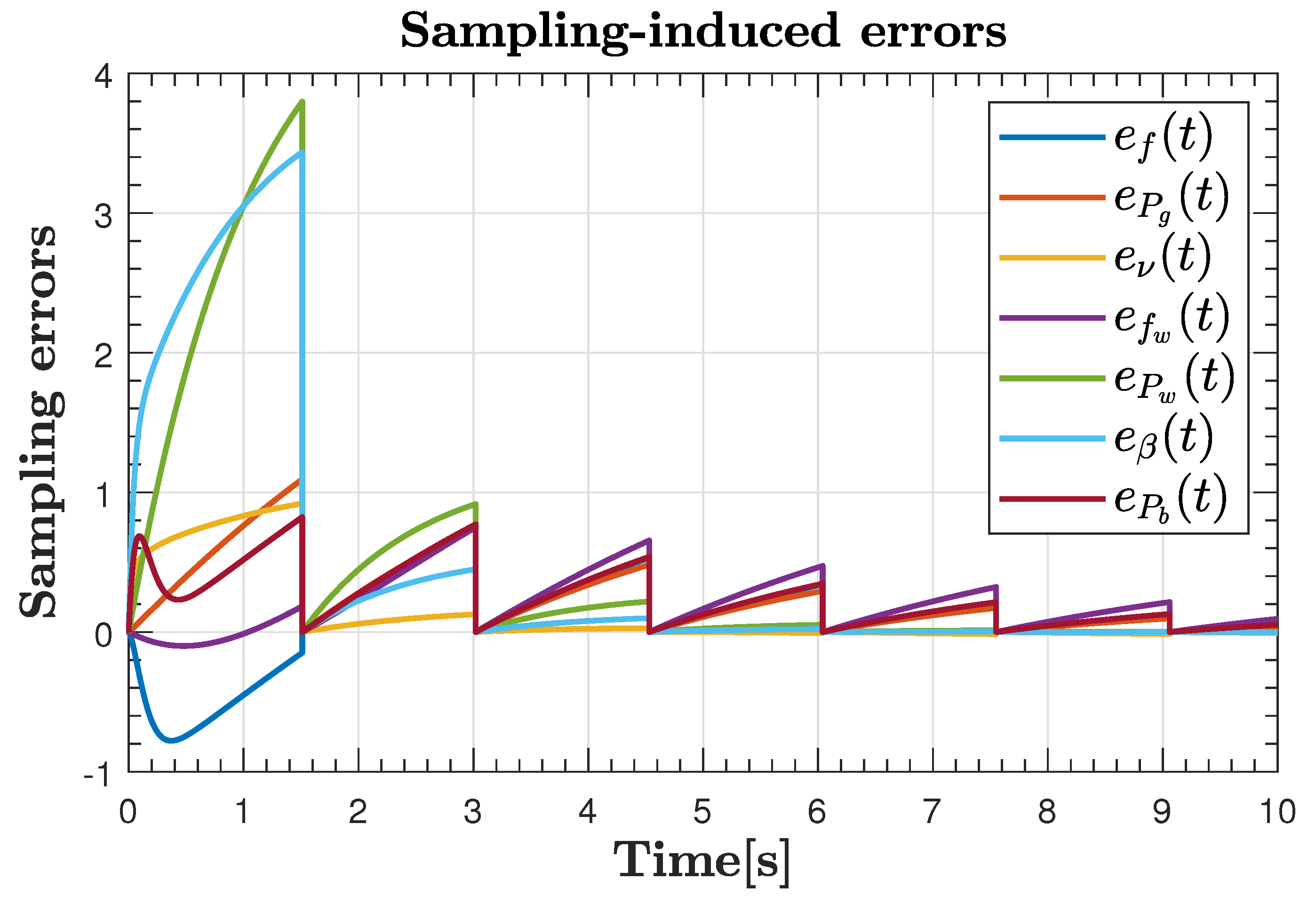
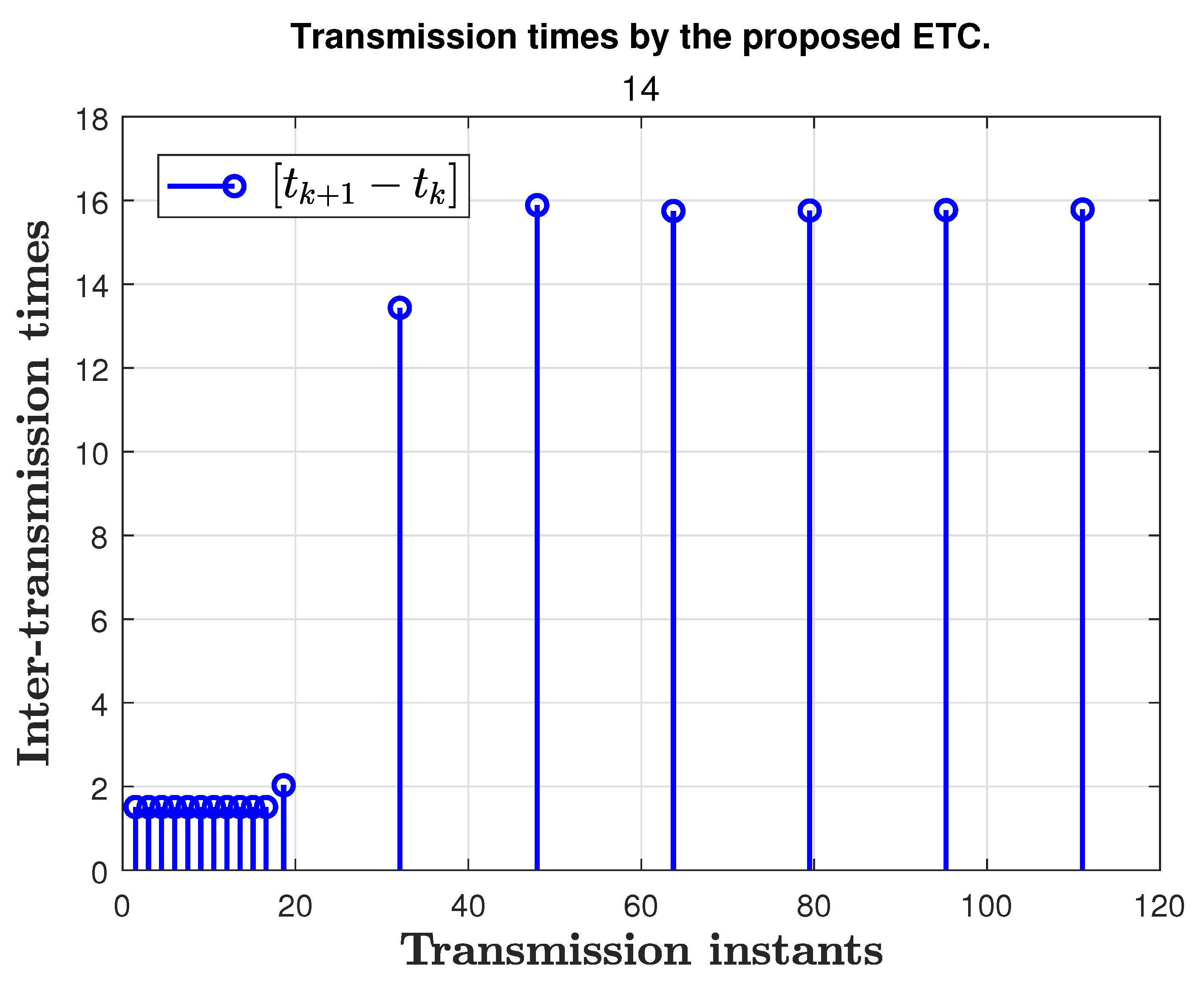
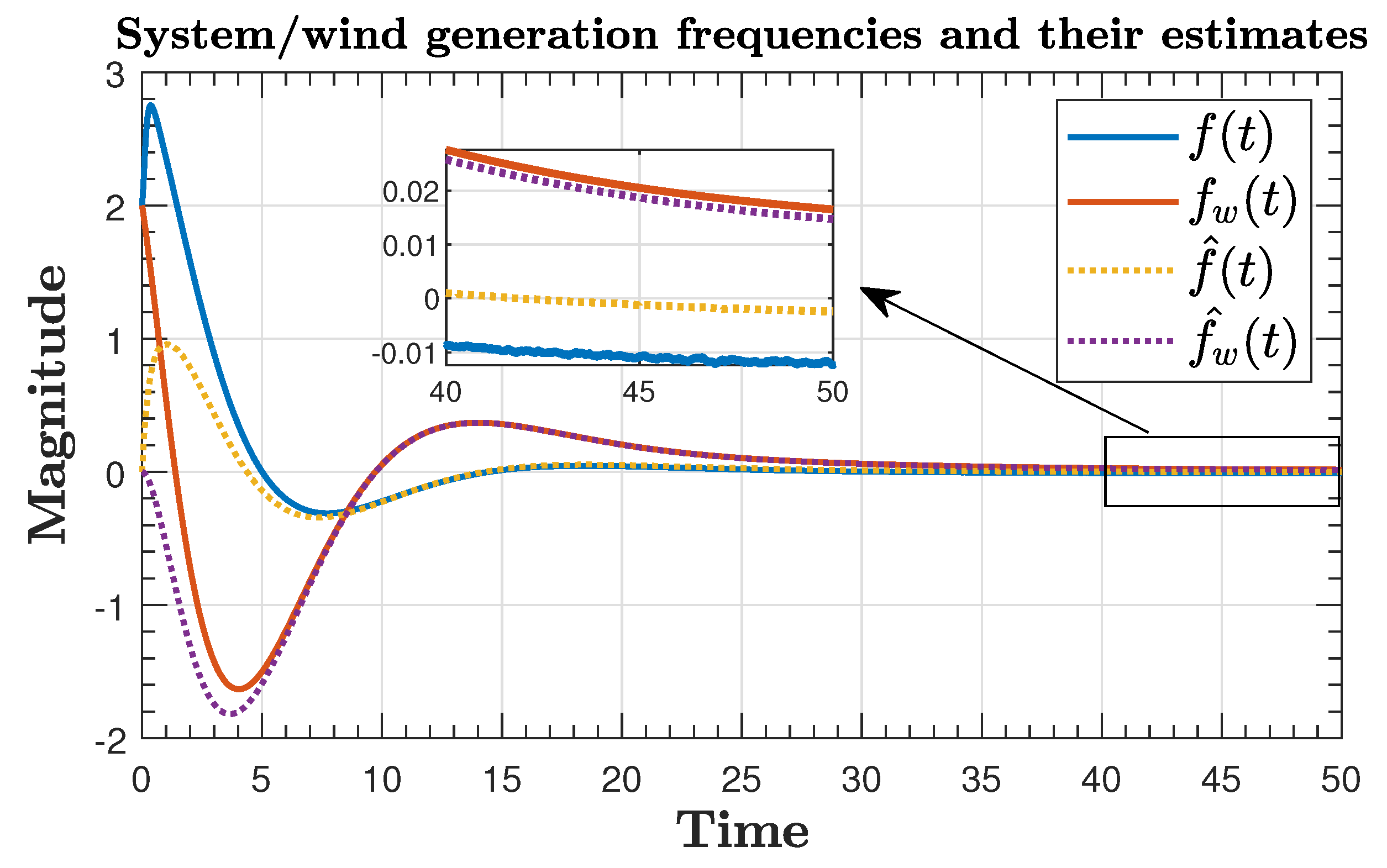
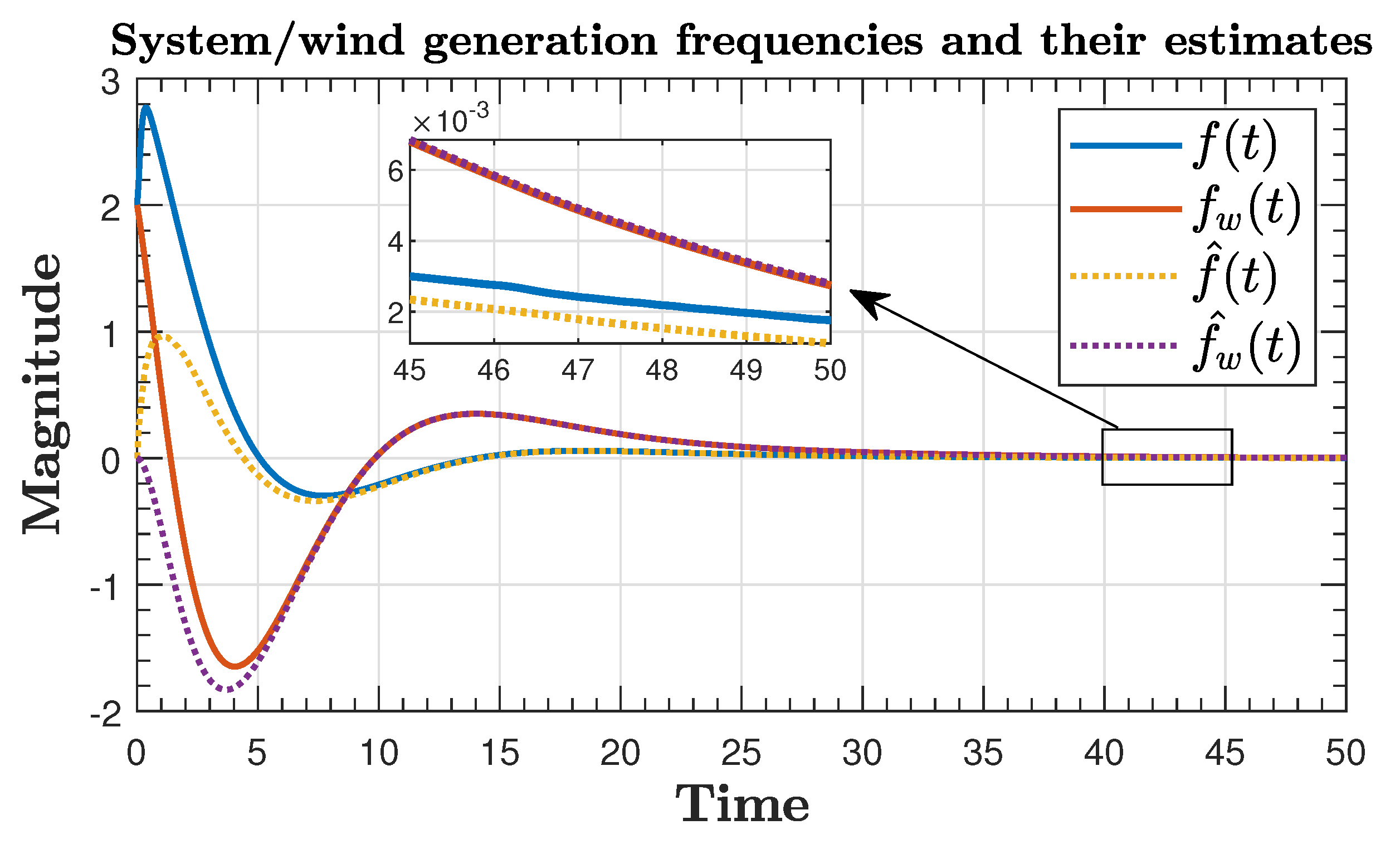
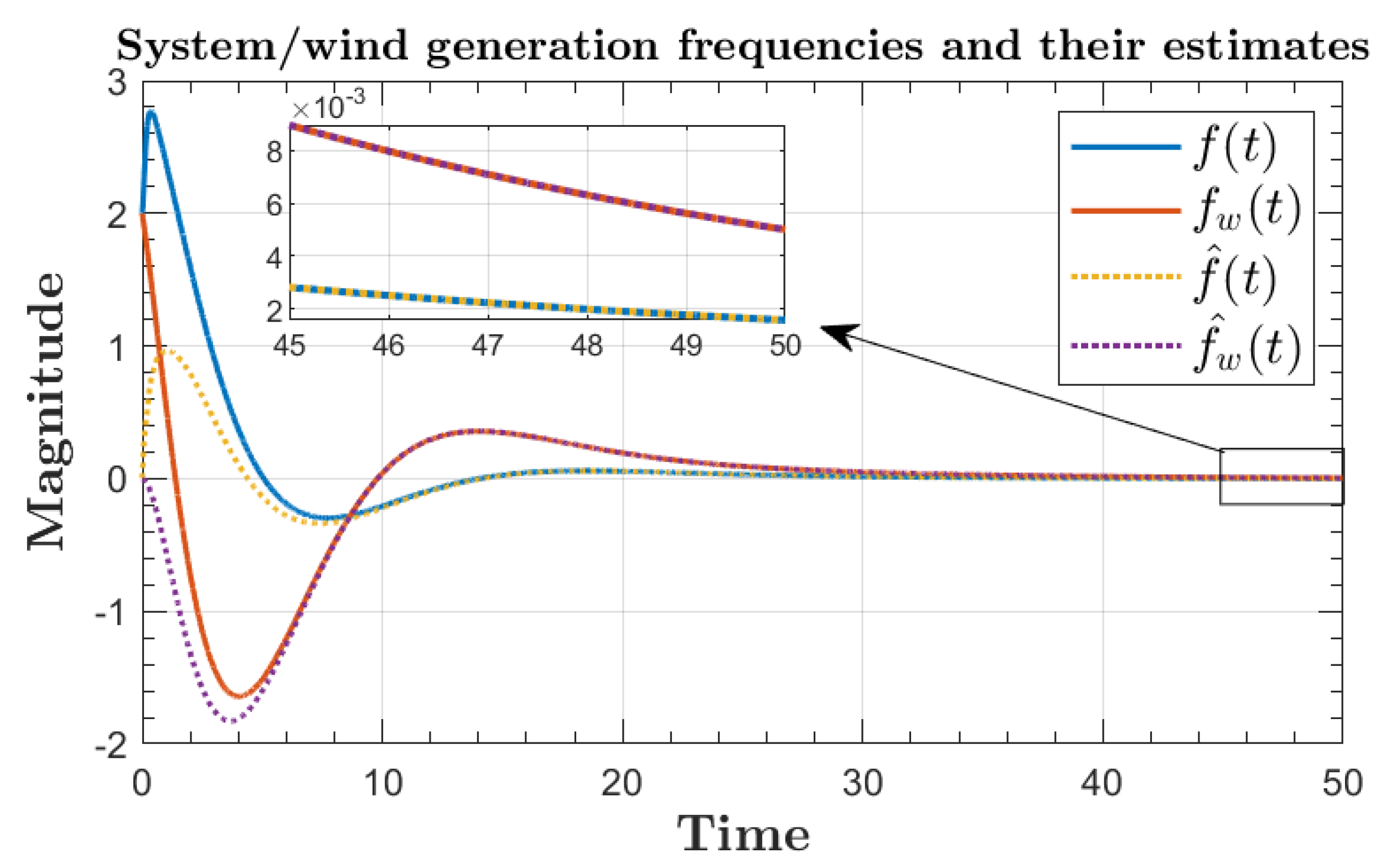
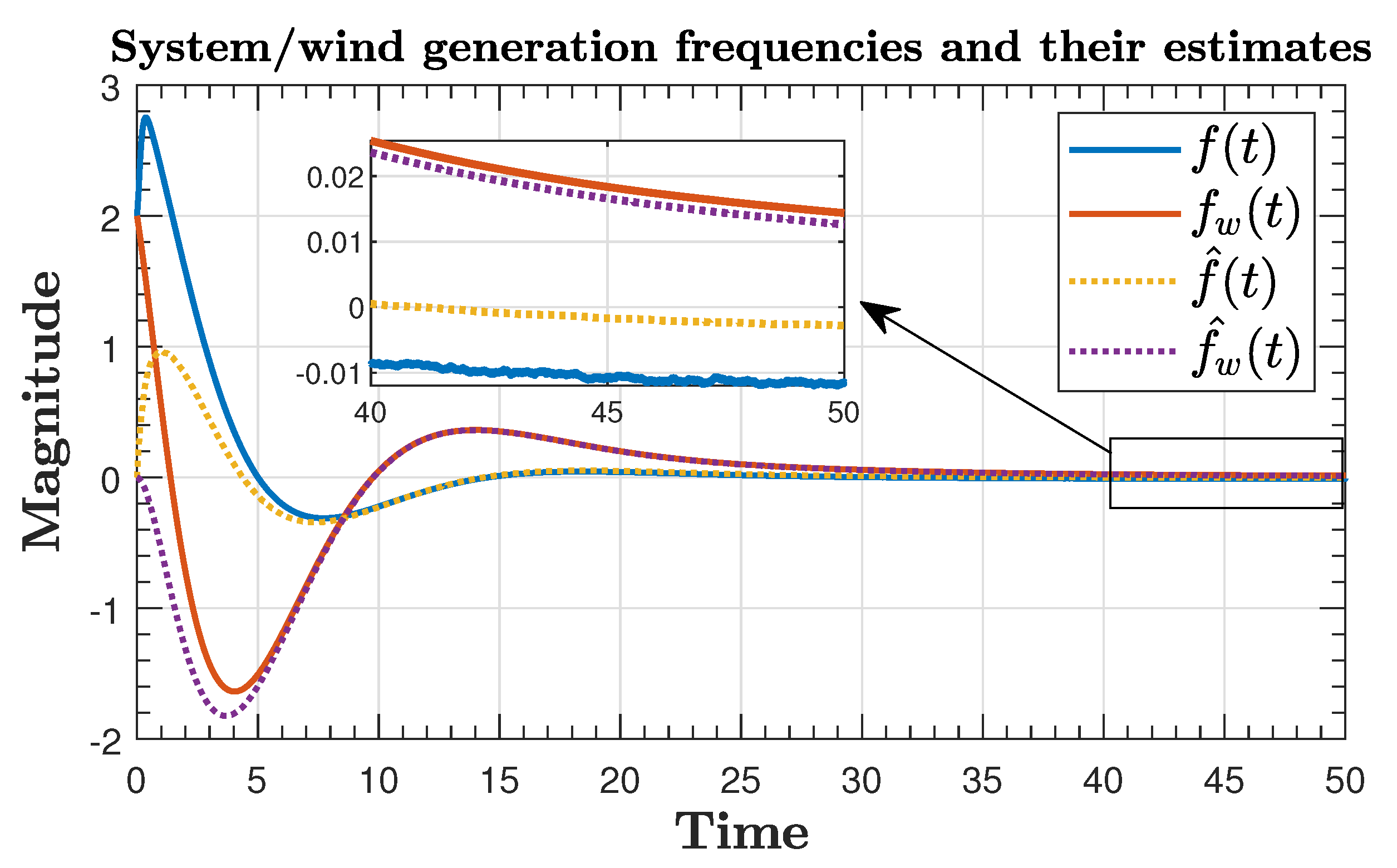
Result	Guaranteed Min Sampling Time	Number of ETC Transmissions
[43]	2 s	31
Proposed ETC technique	$1.51$ s	18

and

Table 2. Comparison with [43], with a sampling period of $T=4$ s.

Result	Periodic Sampling Time	Number of ETC Transmissions
[43]	4 s	21
Proposed ETC technique	$1.51$ s	18

. From the obtained results, we see that the approach in [43] ensures a larger periodic sampling time than what we can produce. However, the number of transmission times with our proposed ETC is fewer than those generated by the ETC in [43]; this reduction in transmission times is the primary objective for integrating the ETC into the feedback loop.

Robustness Analysis

In this section, we examine the robustness of the developed method against different types of exogenous inputs, including external disturbance measurement noises and computational errors, as explained in Section 6. By solving the LMI condition (13), the obtained MATI bound in this case is $T=0.2103$ and the guaranteed ${\mathcal{L}}_2$-gain is $\eta =4.1729$. Figure 12, Figure 13, Figure 14 and Figure 15 show that the closed-loop system is robust against exogenous inputs, such as external disturbances, measurement noise computational errors with a slight degradation of state response, as depicted in the zoomed-in boxes in Figure 12, Figure 13, Figure 14 and Figure 15.

8. Sensitivity Analysis

In this section, we investigate the sensitivity of the proposed approach against parameter variations. To that end, we will assume that all system parameters in are uncertain within a $\pm 10\%$ bound; we check the robustness of the ETC mechanism in this case by using the MATLAB Robust Control Toolbox. The analysis results show that the obtained closed-loop stability can tolerate up to 320% of the modeled uncertainty, which indicates that the designed controller exhibits high robustness against parameter variations. The nominal parameter values and the minimum stabilizing values are presented in

Table 3. Nominal and minimum stabilizing parameter values.

Parameter	Nominal Value	Min Stabilizing Value	Parameter	Nominal Value	Min Stabilizing Value
$K_{ig}$	$0.272$	$0.0406$	$T_{p1}$	$0.6$	$1.0912$
$K_{tp}$	$0.0014$	$5.7271\times {10}^{-4}$	$T_{p2}$	$0.04$	$0.0074$
$K_{pt}$	$81.43$	$30.1212$	$T_{p3}$	$1.0$	$0.1650$
$K_{pc}$	$0.08$	$0.0972$	$T_{pt}$	$16.3$	$2.4306$
$K_{p1}$	$1.25$	$0.6071$	$T_w$	$4.0$	$0.8755$
$K_{p2}$	$1.0$	$1.1106$	$T_{d1}$	$1.0$	$1.8509$
$K_{p3}$	$1.40$	$0.9991$	$T_{d2}$	$2.0$	$0.2982$
$K_{d1}$	$0.64$	$1.1846$	$T_{d3}$	$0.025$	$0.0463$
$R_d$	$5.0$	$0.7456$	$T_{d4}$	$3.0$	$0.4474$
$T_b$	$0.05$	$0.0925$

.

Figure 16 shows the state response when subject to $\pm 50\%$ parameter uncertainties. We see that all the system states converge to the origin, which supports the obtained robustness results.

9. Conclusions

The robust control architecture for event-triggered implementations in a wind–diesel hybrid power system has been explored in this study. The proposed method uses state-feedback for stabilization and prevents the appearance of Zeno behavior. To account for both continuous-time dynamics and discrete transitions, the entire system is described as a hybrid dynamical system. Numerical simulations were conducted to prove the effectiveness of the technique. The simulation outcomes demonstrate that the ETC mechanism outperforms the time-triggered control by significantly lowering the number of transmissions.

The developed ETC in this study is based on the continuous-time verification of the triggering rule, which is relevant when the feedback signal is analog and the sensor is equipped with some computational capabilities to decide the next transmission instant. When employing digital sensors, the proposed approach is not feasible, and periodic ETC is needed, which is an interesting and challenging research direction. Moreover, the analysis in this paper focused on the stabilization of the control system using state-feedback control. In practice, several control applications require set-point reference tracking of the system state/output using popular techniques, such as PID control, which is an interesting research direction to consider. Furthermore, the robustness of the proposed approach has been established in this study against exogenous inputs. Communication delays and parameter variations are important aspects that should be considered for practical implementations, and may be studied in future work. Other network-induced constraints, such as quantization, packet dropout, and malicious attacks, are relevant problems in practice.