Physically-Data Driven Approach for Predicting Formation Leakage Pressure: A Dual-Drive Method
Abstract
:1. Introduction
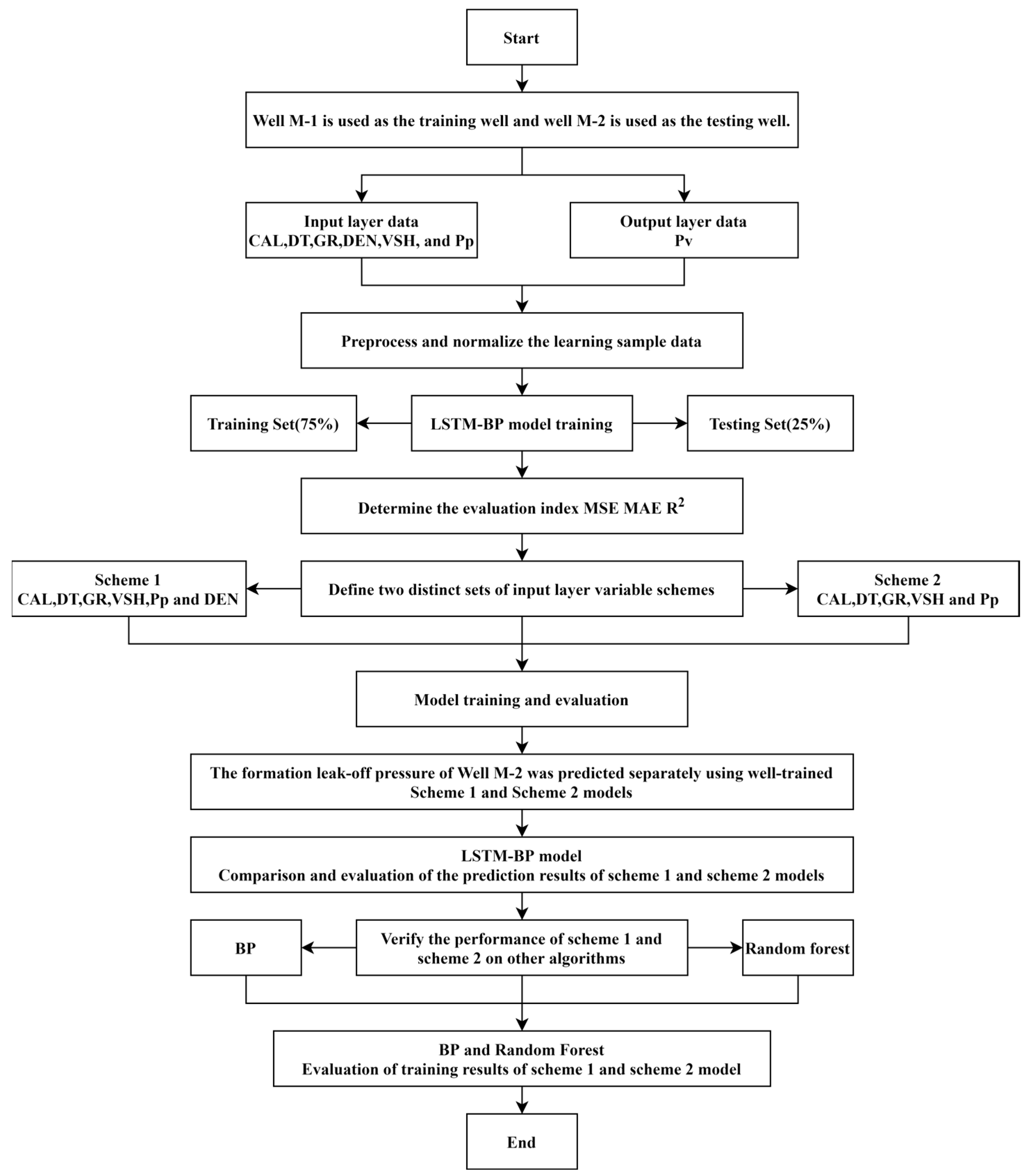
2. Theory and Methods
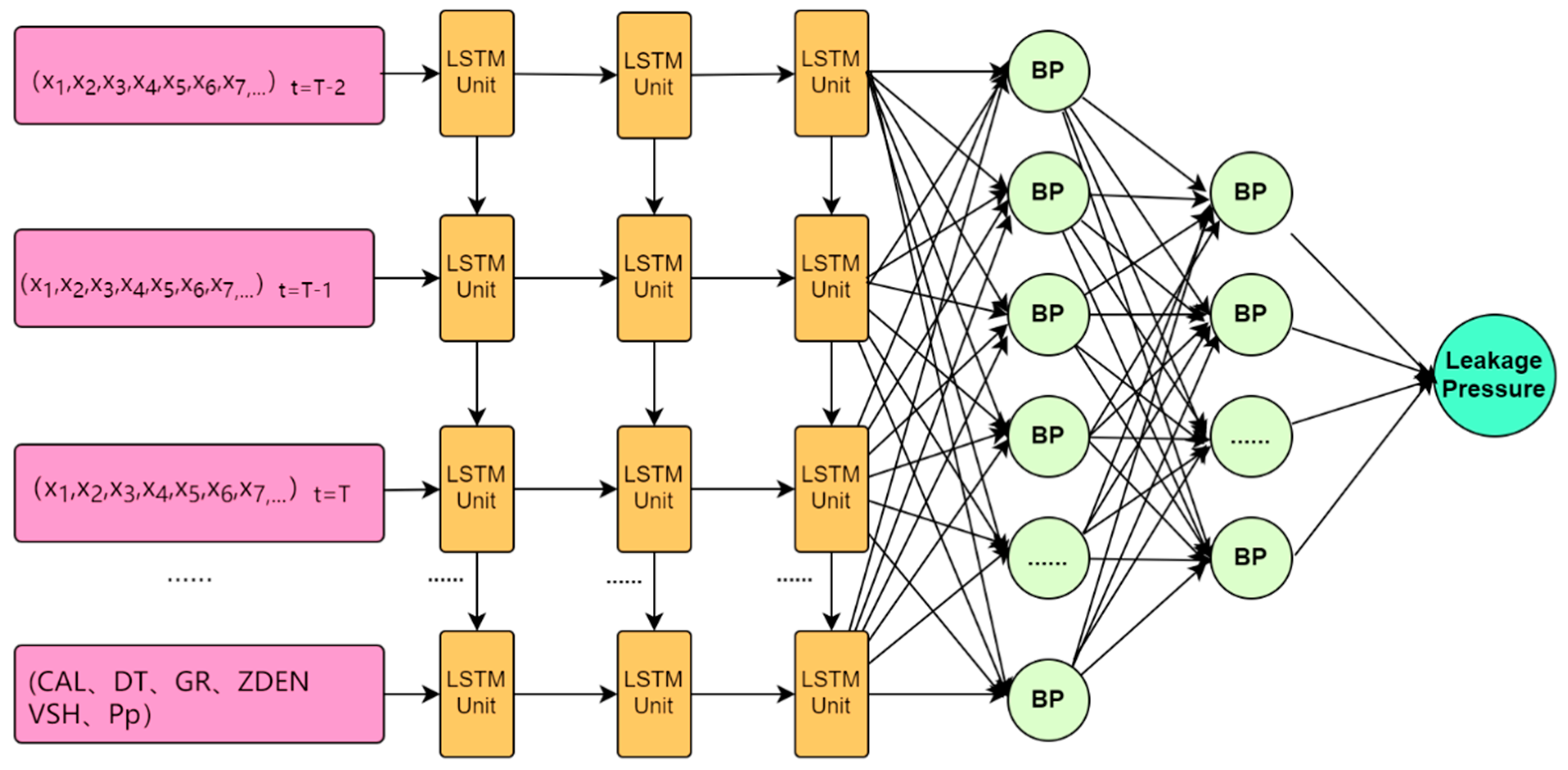
2.1. LSTM Algorithm Theory
- (1)
- Long-term dependencies: Traditional RNNs encounter challenges in managing long sequence dependencies, whereas LSTM can preserve long-term dependencies by regulating the flow of information.
- (2)
- Avoiding gradient vanishing or exploding: Traditional RNNs are susceptible to the issues of gradient vanishing or exploding, whereas LSTM incorporates gate mechanisms to regulate the flow of information, effectively mitigating these problems.
- (3)
- Enhanced memory capacity: LSTM can selectively retain or discard past information through the control of the forget gate and input gate, thereby exhibiting improved memory capabilities.
- (4)
- Learning patterns in long sequences: LSTM can acquire patterns in long sequences by regulating the flow of information, facilitating superior processing of long sequence data.
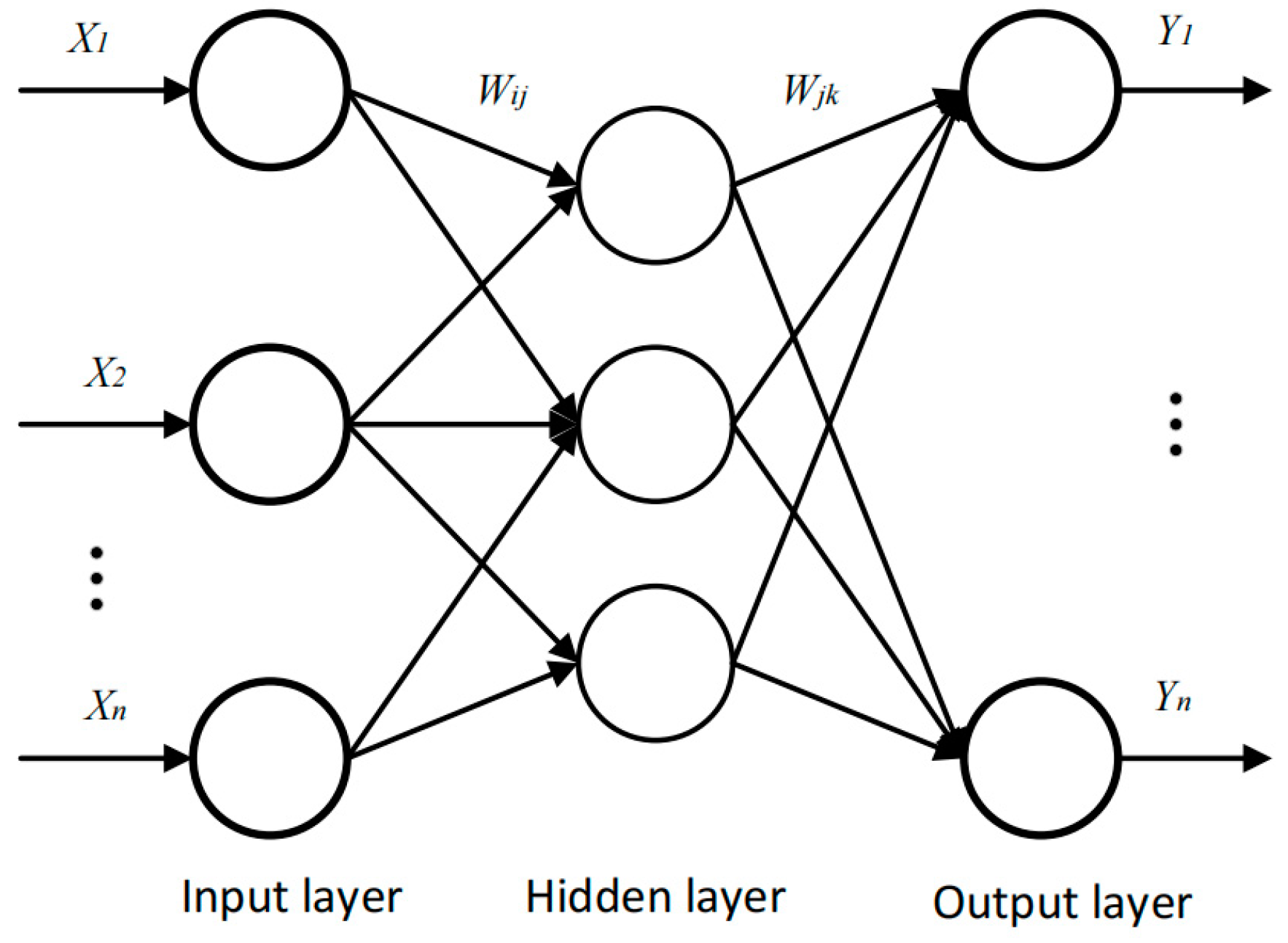
2.2. Backpropagation Neural Network Algorithm
3. Selection, Processing, and Correlation Analysis of Training Samples
3.1. Overview of Data Sources
3.2. Selection of Input Layer Data
3.3. Data Preprocessing
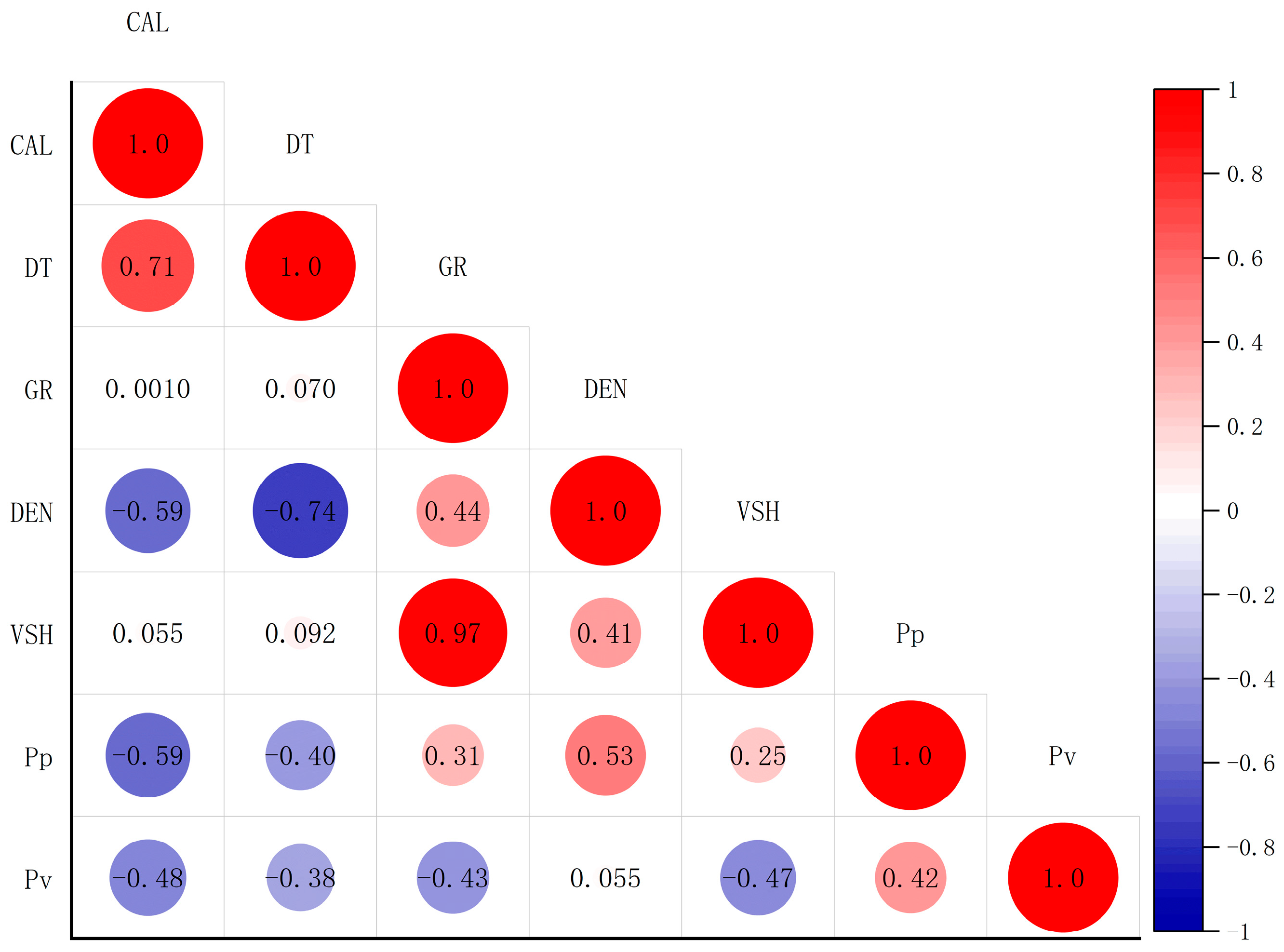
3.4. Data Correlation Analysis and the Setting of Two Models
4. Construction, Evaluation, and Application of Intelligent Prediction Models for Formation Pressure Loss
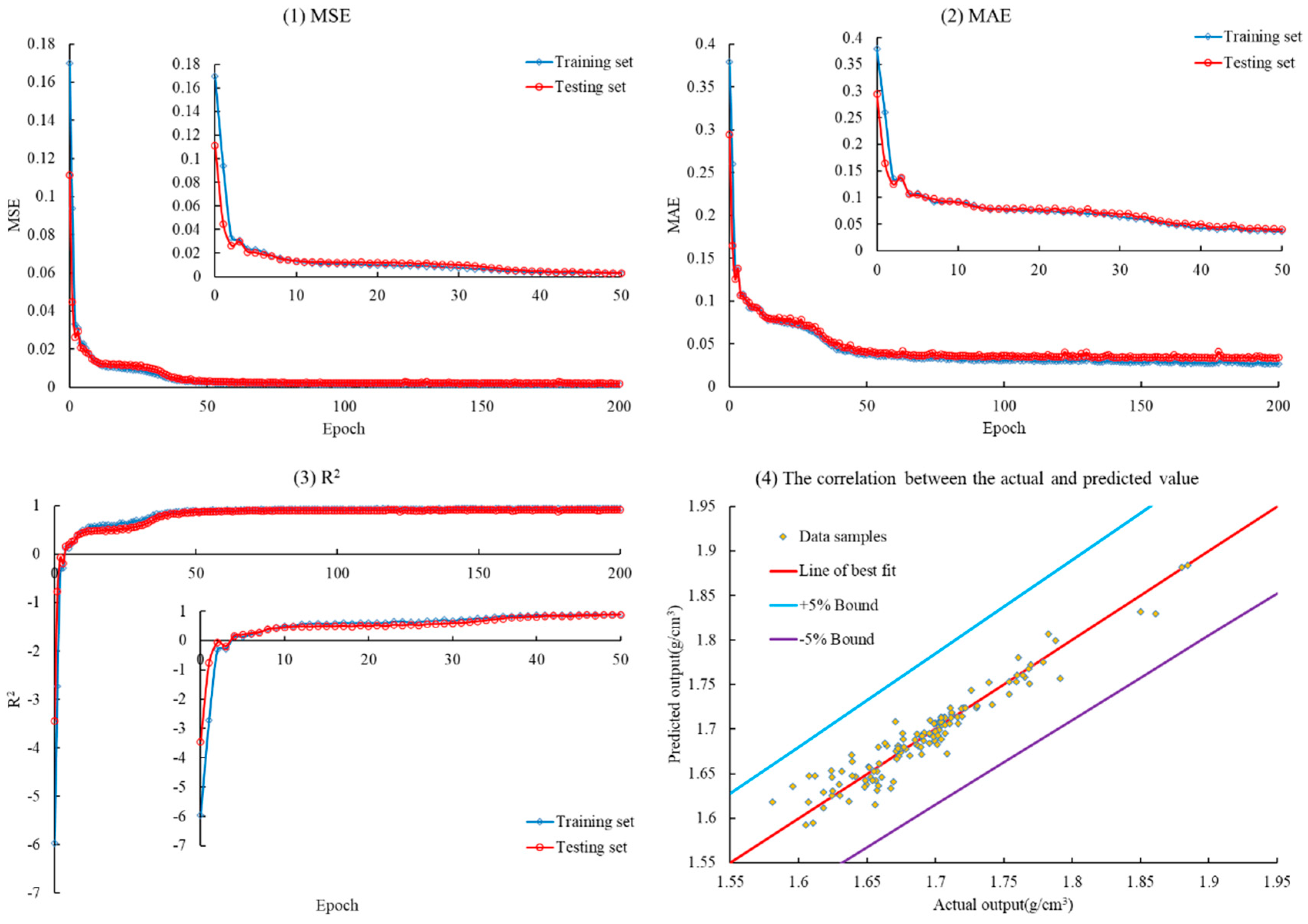
4.1. Model Parameter and Evaluation Metric Settings
4.2. Construction, Evaluation, Comparison, and Application of the Two Approaches
5. Conclusions
- (1)
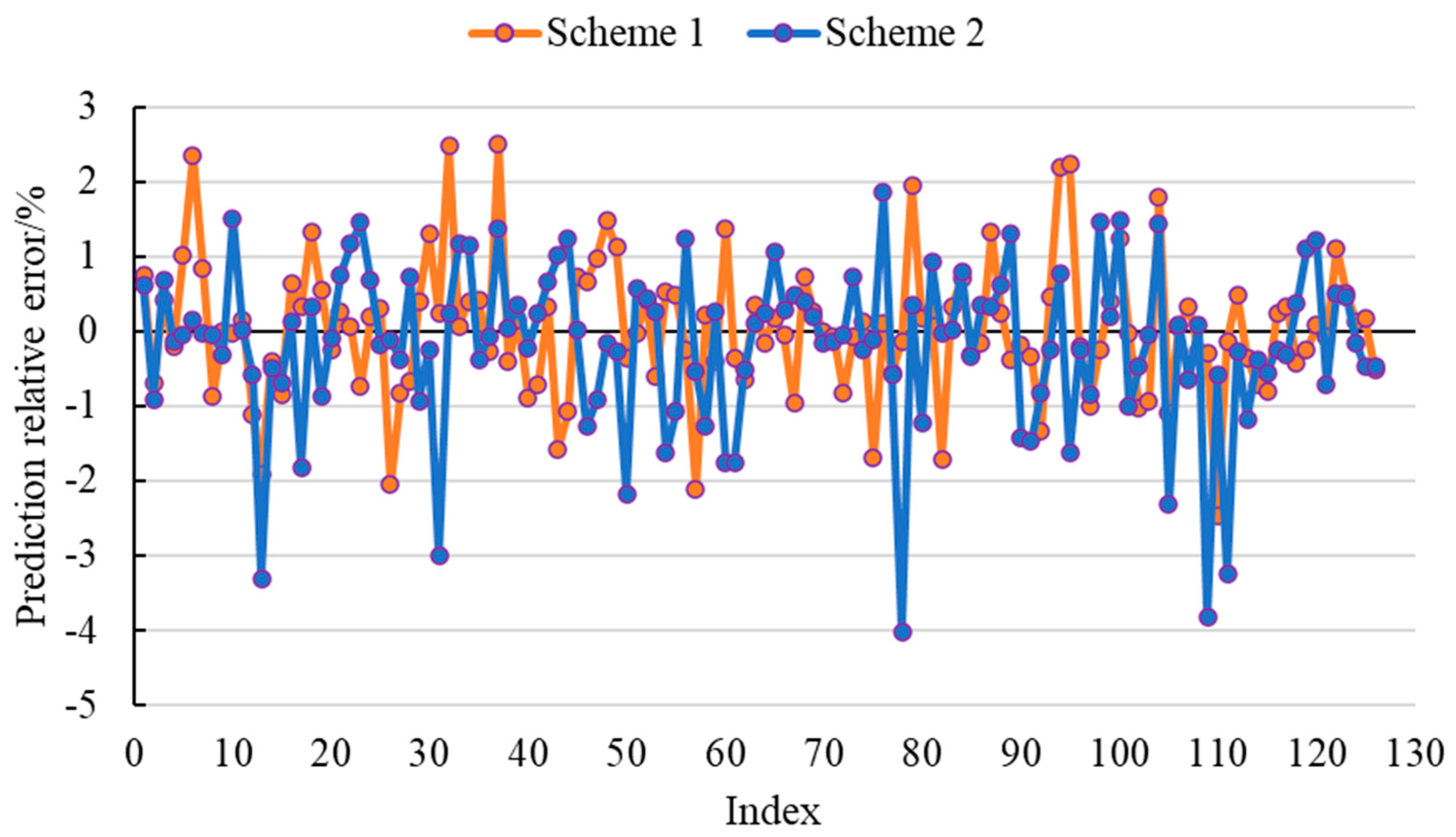
- In this study, an LSTM-BP intelligent prediction model was developed to estimate formation leak-off pressure, and both Scheme 1 and Scheme 2 were employed for evaluation. The results demonstrated a significant disparity in the performance of the three evaluation metrics between the Scheme 1 and Scheme 2 models throughout the training process. Notably, the Scheme 1 model exhibited commendable performance on both the training and testing sets, whereas the Scheme 2 model displayed inadequate performance. The Scheme 1 model achieved a remarkable reduction of 992.393% and 240.674% in MSE and MAE on the testing set, respectively, in comparison to the Scheme 2 model. Furthermore, it achieved a notable increase of 66.920% in R2. The Scheme 1 model demonstrated a relative error range of (−2.467%, 2.510%) and (−6.141%, 5.201%) on the testing set, confirming the high prediction accuracy of the LSTM-BP model developed in this study. Moreover, incorporating formation density as an input variable, despite lacking a direct singular correlation with leak-off pressure, did not diminish the predictive accuracy of the model. In fact, it contributed to a narrower range of relative errors.
- (2)
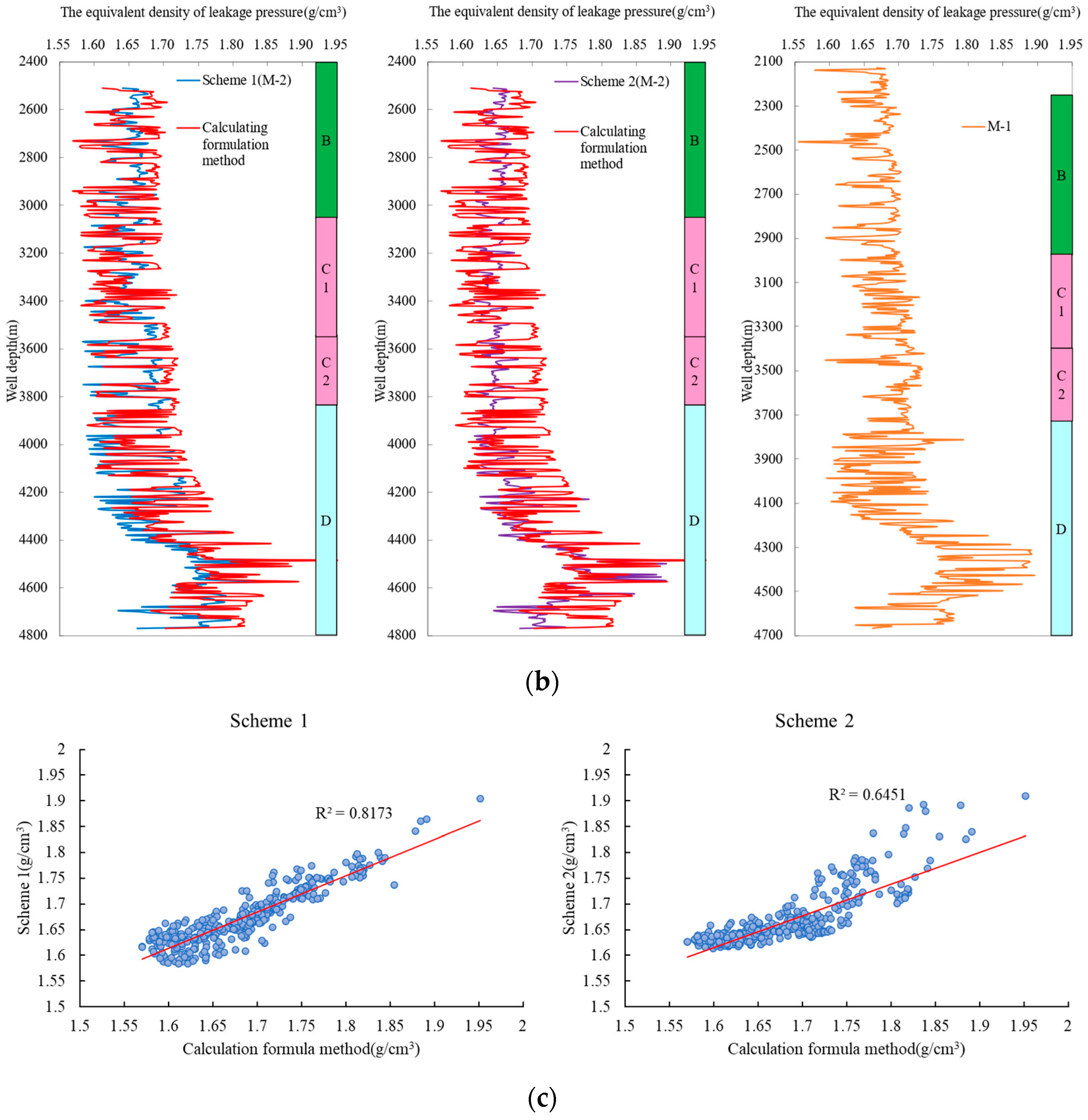
- The LSTM-BP models, trained using Scheme 1 and Scheme 2, were employed to predict the formation leak-off pressure in the adjacent M-2 well. The outcomes demonstrated that the predicted values from both model schemes displayed comparable overall trends. Nevertheless, the majority of predicted outcomes from the Scheme 2 model fell within the prediction range of the Scheme 1 model, implying that the Scheme 1 model exhibited greater volatility in its predictions. Additionally, it was observed that the predicted outcomes of the Scheme 1 model closely aligned with the results derived from the formula method, whereas the Scheme 2 model exhibited noticeably inferior performance compared to the Scheme 1 model.
- (3)
- The models were trained using the BP and random forest algorithms based on Scheme 1 and Scheme 2. The findings revealed that, irrespective of BP or random forest, the Scheme 1 models outperformed the Scheme 2 models on the testing set. These results suggest the generalizability of the conclusions drawn in this study to other algorithms. Additionally, it was noted that both the BP and random forest models exhibited inferior performance compared to the LSTM-BP model developed in this study, highlighting the superiority of the LSTM-BP model.
- (4)
- The prevention of wellbore losses poses a challenging problem in the field of oil and gas exploration and development. Wellbore losses involve intricate mechanisms, and controlling them requires consideration of multiple factors. Precisely predicting formation leak-off pressure plays a crucial role in effective control measures. The development of the LSTM-BP intelligent prediction model for formation leak-off pressure, which incorporates physical data and is driven by dual factors, represents a valuable contribution to the study of formation leak-off pressure and serves to advance the progress of intelligent drilling technology. Nevertheless, this study possesses certain deficiencies and constraints. For instance, the model’s input layer solely incorporates well logging data. Subsequently, the inclusion of rock mechanical parameters like Young’s modulus and Poisson’s ratio, along with engineering logs such as drilling speed and pump pressure, into the input layer variables could be contemplated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CAL | Borehole diameter (in) |
| DEN | Formation density logging (g/cm3) |
| DT | Delta t (μs/ft) |
| GR | Gamma logging (API) |
| VSH | Mud content (dimensionless quantity) |
| Pp | The equivalent density of pore pressure (g/cm3) |
| Pv | The equivalent density of leakage pressure (g/cm3) |
| A | A Formation |
| B | B Formation |
| C | C Formation |
| C1 | Strata of the upper section of C Formation |
| C2 | Strata of the lower section of C Formation |
| D | D Formation |
| Scheme 1 | The first set of input layer variable scheme for the model, including six variables: CAL, DT, GR, VSH, Pp, and DEN |
| Scheme 2 | The second set of input layer variable scheme for the model, including five variables: CAL, DT, GR, VSH, and Pp |
References
- Arshad, U.; Jain, B.; Ramzan, M.; Alward, W.; Diaz, L.; Hasan, I.; Aliyev, A.; Riji, C. Engineered solution to reduce the impact of lost circulation during drilling and cementing in Rumaila Field. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 6 December 2015. [Google Scholar]
- Mehrabian, A.; Jamison, D.E.; Teodorescu, G. Geomechanics of Lost-Circulation Events and Wellbore-Strengthening Operations. SPE J. 2015, 20, 1305–1316. [Google Scholar] [CrossRef]
- Sun, J.S.; Bai, Y.R.; Cheng, R.C.; Lyu, K.H.; Liu, F.; Feng, J.; Lei, S.F.; Zhang, J.; Hao, H.J. Research progress and prospect of plugging technologies for fractured formation with severe lost circulation. Pet. Explor. Dev. 2021, 48, 732–743. [Google Scholar] [CrossRef]
- Kang, Y.L.; Xu, C.Y.; You, L.J.; Yu, H.F.; Zhang, D.J. Temporary sealing technology to control formation damage induced by drill-in fluid loss in fractured tight gas reservoir. J. Nat. Gas Sci. Eng. 2014, 20, 67–73. [Google Scholar] [CrossRef]
- Zhai, X.P.; Chen, H.; Lou, Y.S.; Wu, H.M. Prediction and control model of shale induced fracture leakage pressure. J. Pet. Sci. Eng. 2021, 198, 108186. [Google Scholar] [CrossRef]
- Morita, N.; Black, A.D.; Guh, G.F. Theory of lost circulation pressure. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, 23 September 1990. [Google Scholar]
- Lavrov, A.; Tronvoll, J. Modeling mud loss in fractured formation. In Proceedings of the Abu Dhabi International Conference and Exhibition, Abu Dhabi, United Arab Emirates, 10 October 2004. [Google Scholar]
- Majidi, R.; Miska, S.Z.; Yu, M.; Thompson, L.G.; Zhang, J. Quantitative Analysis of Mud Losses in Naturally Fractured Reservoirs: The Effect of Rheology. SPE Drill. Complet. 2010, 25, 509–517. [Google Scholar] [CrossRef]
- Lei, Q.; Xiong, W.; Yuan, J.; Cui, Y.; Wu, Y.S. Analysis of stress sensitivity and its influence on oil production from tight reservoirs. In Proceedings of the Eastern Regional Meeting, Lexington, KY, USA, 17 October 2007. [Google Scholar]
- Lan, H.T.; Moore, I.D. New design equation for maximum allowable mud pressure in sand during horizontal Directional drilling. Tunn. Undergr. Space Technol. 2022, 126, 104543. [Google Scholar] [CrossRef]
- Yang, M.; Yang, L.C.; Wang, T.; Chen, Y.H.; Yang, C.; Li, L.X. Estimating formation leakage pressure using a coupled model of circulating temperature-pressure in an eccentric annulus. J. Pet. Sci. Eng. 2020, 189, 106918. [Google Scholar] [CrossRef]
- Aadnoy, B.S.; Belayneh, M. Elasto-plastic fracturing model for wellbore stability using non-penetrating fluids. J. Pet. Sci. Eng. 2004, 45, 179–192. [Google Scholar] [CrossRef]
- Feng, Y.C.; Gray, K.E. Modeling Lost Circulation Through Drilling-Induced Fractures. SPE J. 2018, 23, 205–223. [Google Scholar] [CrossRef]
- Wang, R.; Chen, G.; Liu, Y. A Dynamic Model of Machine Learning and Deep Learning in Shield Tunneling Parameters Prediction. In Proceedings of the 17th East Asian-Pacific Conference on Structural Engineering and Construction, 2022: EASEC-17, Singapore, 27–30 June 2022; Springer Nature Singapore: Singapore, 2023; pp. 1241–1254. [Google Scholar]
- Chen, G.; Li, Q.Y.; Li, D.Q.; Wu, Z.Y.; Liu, Y. Main frequency band of blast vibration signal based on wavelet packet transform. Appl. Math. Model. 2019, 74, 569–585. [Google Scholar] [CrossRef]
- Kokkinos, N.C.; Nkagbu, D.C.; Marmanis, D.; Dermentzis, K.; Maliaris, G. Evolution of Unconventional Hydrocarbons: Past, Present, Future and Environmental FootPrint. J. Eng. Sci. Technol. Rev. 2022, 15, 15–24. [Google Scholar] [CrossRef]
- Krishna, S.; Ridha, S.; Vasant, P.; Ilyas, S.U.; Sophian, A. Conventional and intelligent models for detection and prediction of fluid loss events during drilling operations: A comprehensive review. J. Pet. Sci. Eng. 2020, 195, 107818. [Google Scholar] [CrossRef]
- Sabah, M.; Talebkeikhah, M.; Agin, F.; Talebkeikhah, F.; Hasheminasab, E. Application of decision tree, artificial neural networks, and adaptive neuro-fuzzy inference system on predicting lost circulation: A case study from Marun oil field. J. Pet. Sci. Eng. 2019, 177, 236–249. [Google Scholar] [CrossRef]
- Geng, Z.; Wang, H.Q.; Fan, M.; Lu, Y.H.; Nie, Z.; Ding, Y.H.; Chen, M. Predicting seismic-based risk of lost circulation using machine learning. J. Pet. Sci. Eng. 2019, 176, 679–688. [Google Scholar] [CrossRef]
- Pang, H.W.; Meng, H.; Wang, H.Q.; Fan, Y.D.; Nie, Z.; Jin, Y. Lost circulation prediction based on machine learning. J. Pet. Sci. Eng. 2022, 208, 109364. [Google Scholar] [CrossRef]
- Li, Z.; Chen, M.; Jin, Y.; Lu, Y.; Wang, H.; Geng, Z.; Wei, S. Study on intelligent prediction for risk level of lost circulation while drilling based on machine learning. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17 June 2018. [Google Scholar]
- Jahanbakhshi, R.; Keshavarzi, R.; Jalili, S. Artificial neural network-based prediction and geomechanical analysis of lost circulation in naturally fractured reservoirs: A case study. Eur. J. Environ. Civ. Eng. 2014, 18, 320–335. [Google Scholar] [CrossRef]
- Hou, X.X.; Yang, J.; Yin, Q.S.; Liu, H.; Chen, H.; Zheng, J.; Wang, J.; Cao, B.; Zhao, X.; Hao, M.; et al. Lost circulation prediction in South China Sea using machine learning and big data technology. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4 May 2020. [Google Scholar]
- Unrau, S.; Torrione, P. Adaptive real-time machine learning-based alarm system for influx and loss detection. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9 October 2017. [Google Scholar]
- Andia, P.; Sant, R.V.; Whiteley, N. A comprehensive real-time data analysis tool for fluid gains and losses. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, Fort Worth, TX, USA, 6 March 2018. [Google Scholar]
- Li, C.; Wang, Z.R.; Rao, M.Y.; Belkin, D.; Song, W.H.; Jiang, H.; Yan, P.; Li, Y.N.; Lin, P.; Hu, M.; et al. Long short-term memory networks in memristor crossbar arrays. Nat. Mach. Intell. 2019, 1, 49–57. [Google Scholar] [CrossRef]
- Graves, A.; Jaitly, N. Towards end-to-end speech recognition with recurrent neural networks. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 21–26 June 2014; JMLR.org: Beijing, China, 2014; Volume 32, pp. 1764–1772. [Google Scholar]
- Cortez, B.; Carrera, B.; Kim, Y.J.; Jung, J.Y. An architecture for emergency event prediction using LSTM recurrent neural networks. Expert Syst. Appl. 2018, 97, 315–324. [Google Scholar] [CrossRef]
- Habler, E.; Shabtai, A. Using LSTM encoder-decoder algorithm for detecting anomalous ADS-B messages. Comput. Secur. 2018, 78, 155–173. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ma, T.S.; Zhang, Y.; Qiu, Y.; Liu, Y.; Li, Z.L. Effect of parameter correlation on risk analysis of wellbore instability in deep igneous formations. J. Pet. Sci. Eng. 2022, 208, 109521. [Google Scholar] [CrossRef]
- Zhao, G.; Ding, W.L.; Tian, J.; Liu, J.S.; Gu, Y.; Shi, S.Y.; Wang, R.Y.; Sun, N. Spearman rank correlations analysis of the elemental, mineral concentrations, and mechanical parameters of the Lower Cambrian Niutitang shale: A case study in the Fenggang block, Northeast Guizhou Province, South China. J. Pet. Sci. Eng. 2022, 208, 109550. [Google Scholar] [CrossRef]







| NO | Parameters | Value |
|---|---|---|
| 1 | Model layers | 3 |
| 2 | Number of neurons per layer | 30 |
| 3 | Activation function | LeakyRelu |
| 4 | Loss function | MSE |
| 5 | Maximum number of iterations (epoch) | 300 |
| 6 | Batch size | 50 |
| 7 | Data partitioning | Randomly select 75% of the data as the training set and 25% of the data as the test set. |
| Name | Input Variables | MSE | Difference (%) | MAE | Difference (%) | R2 | Difference (%) |
|---|---|---|---|---|---|---|---|
| Option 1 | CAL, DT, GR, VSH, Pp, and DEN | 0.000229935 | 992.393 | 0.011198329 | 240.674 | 0.92178272 | 66.920 |
| Option 2 | CAL, DT, GR, VSH, and Pp | 0.0025118 | 0.038149745 | 0.552230669 |
| Formation | Well Depth (m) | Predicted Value of Equivalent Density of Leakage Pressure (g/cm3) | |||||
|---|---|---|---|---|---|---|---|
| Scheme 1 | Scheme 2 | Calculation Formula Method | |||||
| Minimum | Maximum | Minimum | Maximum | Minimum | Maximum | ||
| B | 2510~3014 | 1.587 | 1.689 | 1.618 | 1.679 | 1.570 | 1.705 |
| C1 | 3014~3569 | 1.584 | 1.700 | 1.612 | 1.675 | 1.582 | 1.718 |
| C2 | 3569–3854 | 1.584 | 1.711 | 1.619 | 1.680 | 1.593 | 1.722 |
| D | 3854~4790 | 1.589 | 1.905 | 1.617 | 1.909 | 1.590 | 1.952 |
| Top Depth (m) | Bottom Depth (m) | Drilling Fluid Density (g/cm3) | Formation |
|---|---|---|---|
| 2325 | 3765 | 1.18 | B and C1 |
| 3765 | 4172 | 1.25 | C1, C2, and D |
| 4172 | 4658 | 1.3 | D |
| 4658 | 4790 | 1.45 | D |
| ML Models | Name | Evaluation Index | |||||
|---|---|---|---|---|---|---|---|
| MAE | Difference (%) | MSE | Difference (%) | R2 | Difference (%) | ||
| Random forest | Scheme 1 | 0.012151 | 8.172 | 0.000435 | 15.825 | 0.833446 | 3.266 |
| Scheme 2 | 0.013233 | 0.000504 | 0.807089 | ||||
| BP | Scheme 1 | 0.027050 | 2.324 | 0.00151 | 15.636 | 0.405156 | 16.454 |
| Scheme 2 | 0.027678 | 0.001746 | 0.347911 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Tan, Q.; Li, B.; Feng, Y.; Dong, B.; Yan, K.; Ding, J.; Zhang, S.; Guo, J.; Deng, J.; et al. Physically-Data Driven Approach for Predicting Formation Leakage Pressure: A Dual-Drive Method. Appl. Sci. 2023, 13, 10147. https://doi.org/10.3390/app131810147
Li H, Tan Q, Li B, Feng Y, Dong B, Yan K, Ding J, Zhang S, Guo J, Deng J, et al. Physically-Data Driven Approach for Predicting Formation Leakage Pressure: A Dual-Drive Method. Applied Sciences. 2023; 13(18):10147. https://doi.org/10.3390/app131810147
Chicago/Turabian StyleLi, Huayang, Qiang Tan, Bojia Li, Yongcun Feng, Baohong Dong, Ke Yan, Jianqi Ding, Shuiliang Zhang, Jinlong Guo, Jingen Deng, and et al. 2023. "Physically-Data Driven Approach for Predicting Formation Leakage Pressure: A Dual-Drive Method" Applied Sciences 13, no. 18: 10147. https://doi.org/10.3390/app131810147
APA StyleLi, H., Tan, Q., Li, B., Feng, Y., Dong, B., Yan, K., Ding, J., Zhang, S., Guo, J., Deng, J., & Chen, J. (2023). Physically-Data Driven Approach for Predicting Formation Leakage Pressure: A Dual-Drive Method. Applied Sciences, 13(18), 10147. https://doi.org/10.3390/app131810147






