High-Precision Ranging Method of 5G NR Co-Band PRS in Industrial Internet Scenarios
Abstract
:1. Introduction
1.1. Related Work
1.2. Our Contributions
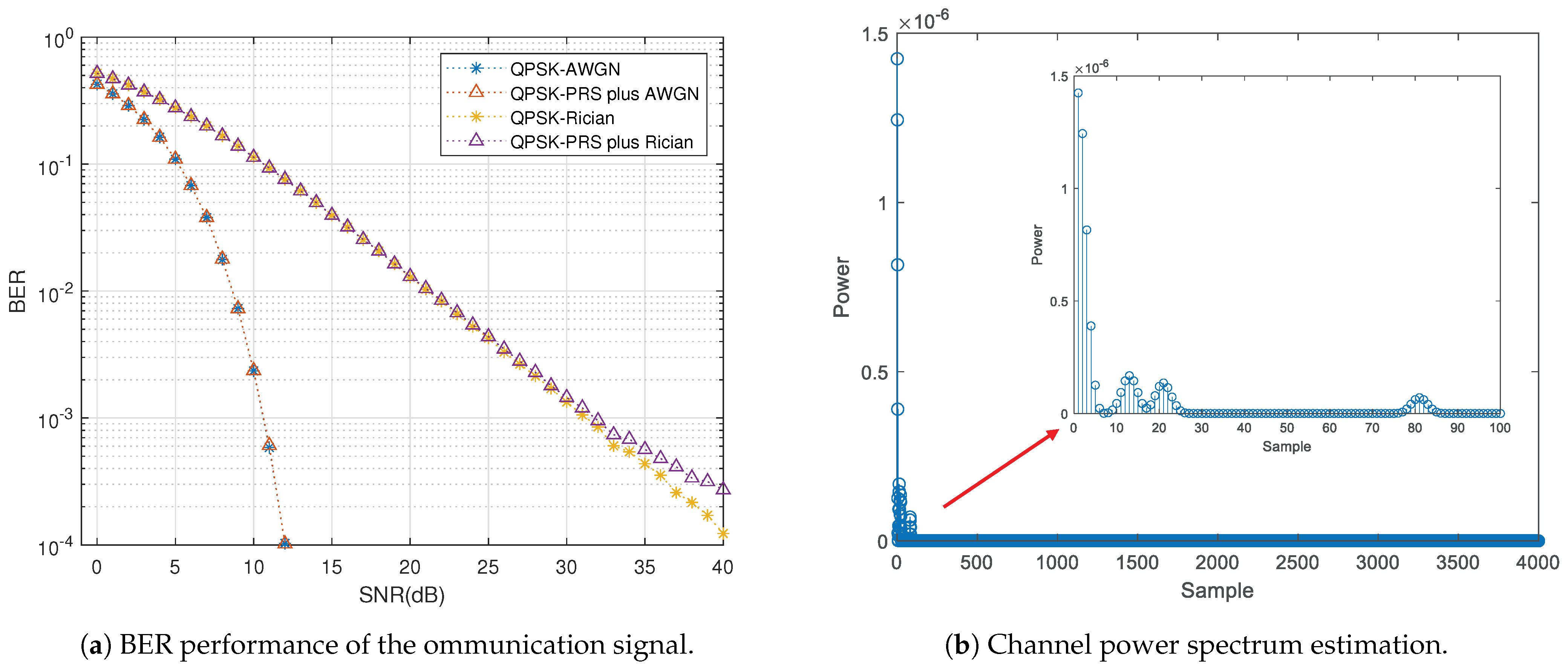
- Unlike the conventional PRS signal, which occupies resources in the time-frequency domain, we propose and analyze a novel low-power PRS signal called the Co-Band PRS signal. This signal does not occupy additional communication sub-carriers or resources and causes minimal interference to communication signals.
- For Co-Band PRS, we propose a high-precision ranging scheme that first captures the communication signal and then tracks the positioning signal. This approach effectively improves signal capture efficiency and tracking accuracy.
- We propose an innovative weighted window coarse synchronization method that offers improved performance at low signal-to-noise ratio (SNR) compared to conventional maximum likelihood (ML)-based symbol timing offset (STO) estimation algorithms.
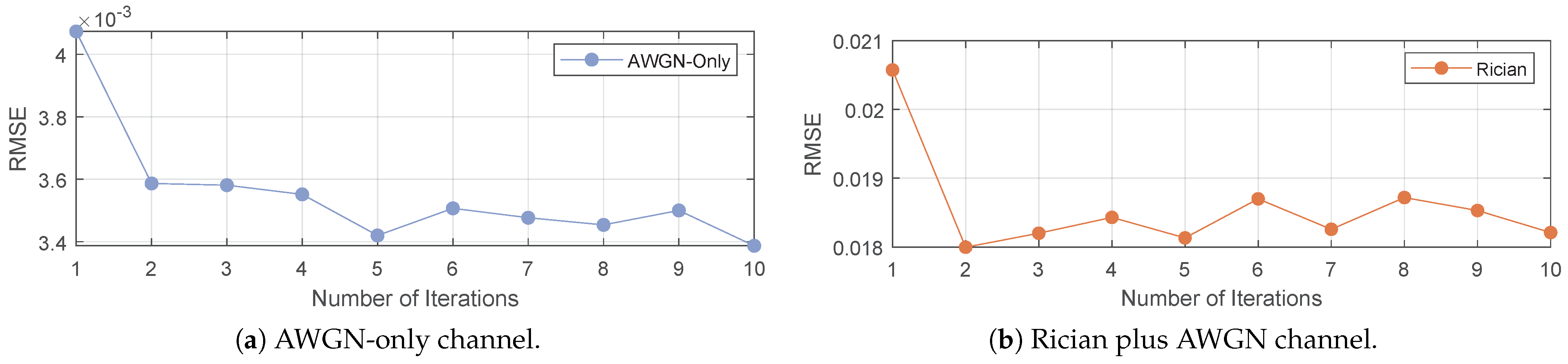
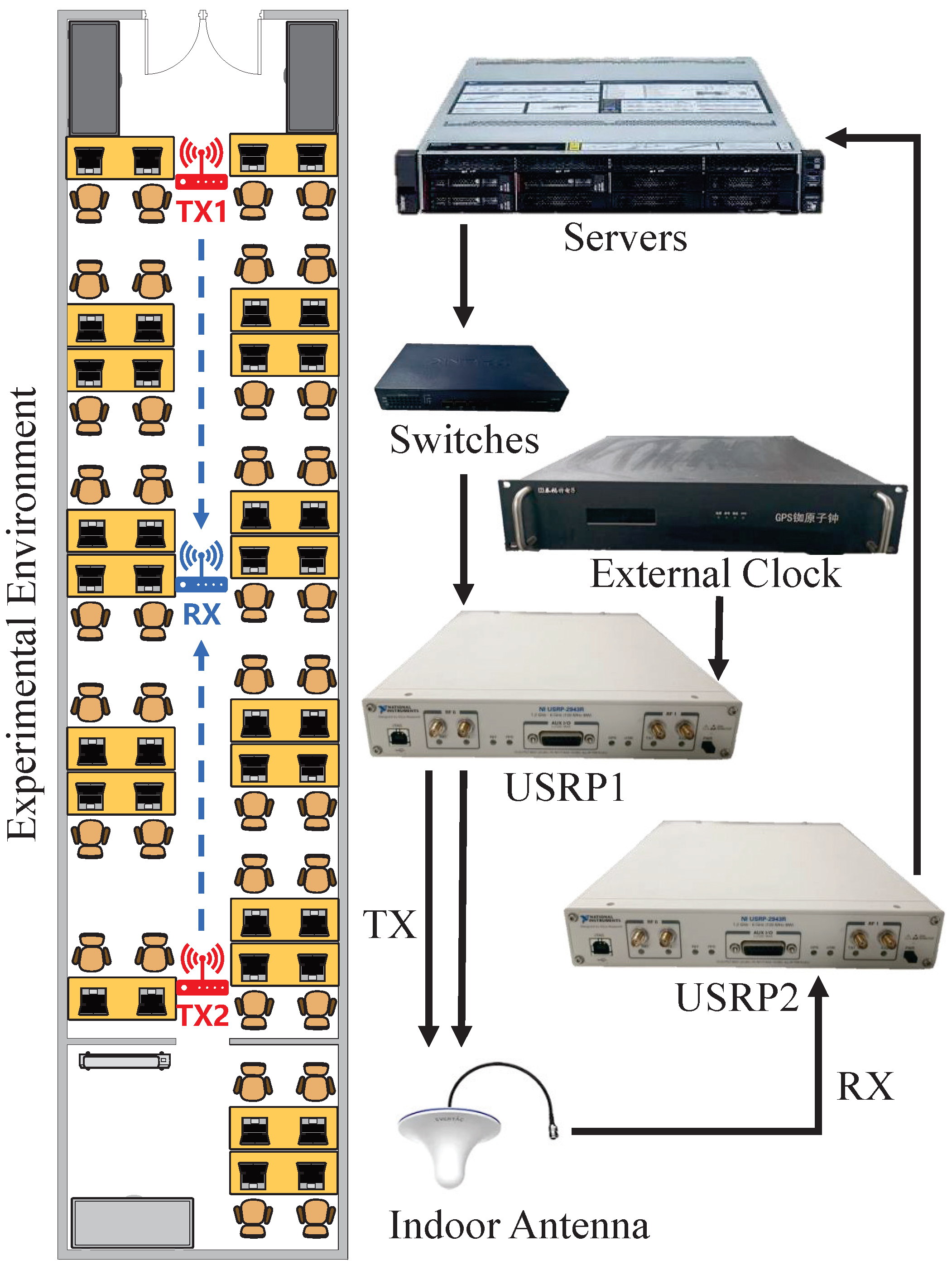
- The iterative DLL algorithm is used to track the positioning signals, and achieves a code tracking accuracy of samples in simulation. The USRPs are used to create a realistic testing environment, and achieve a final ranging accuracy of 0.16 m@90%.
2. System Model
2.1. Framework Structure
2.2. 5G NR Co-Band PRS Signal Model
2.3. Co-Band PRS Receive Signal Model
3. Proposed Timing Recovery Scheme
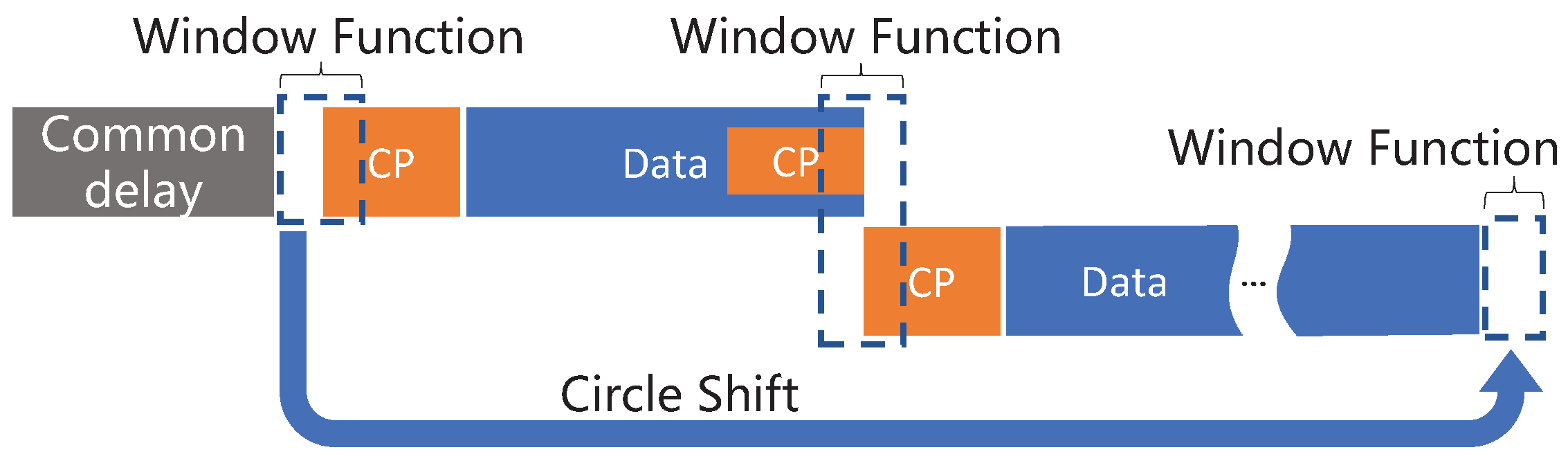
3.1. Coarse Synchronization Solution
3.2. Multi-Path Delay Estimation
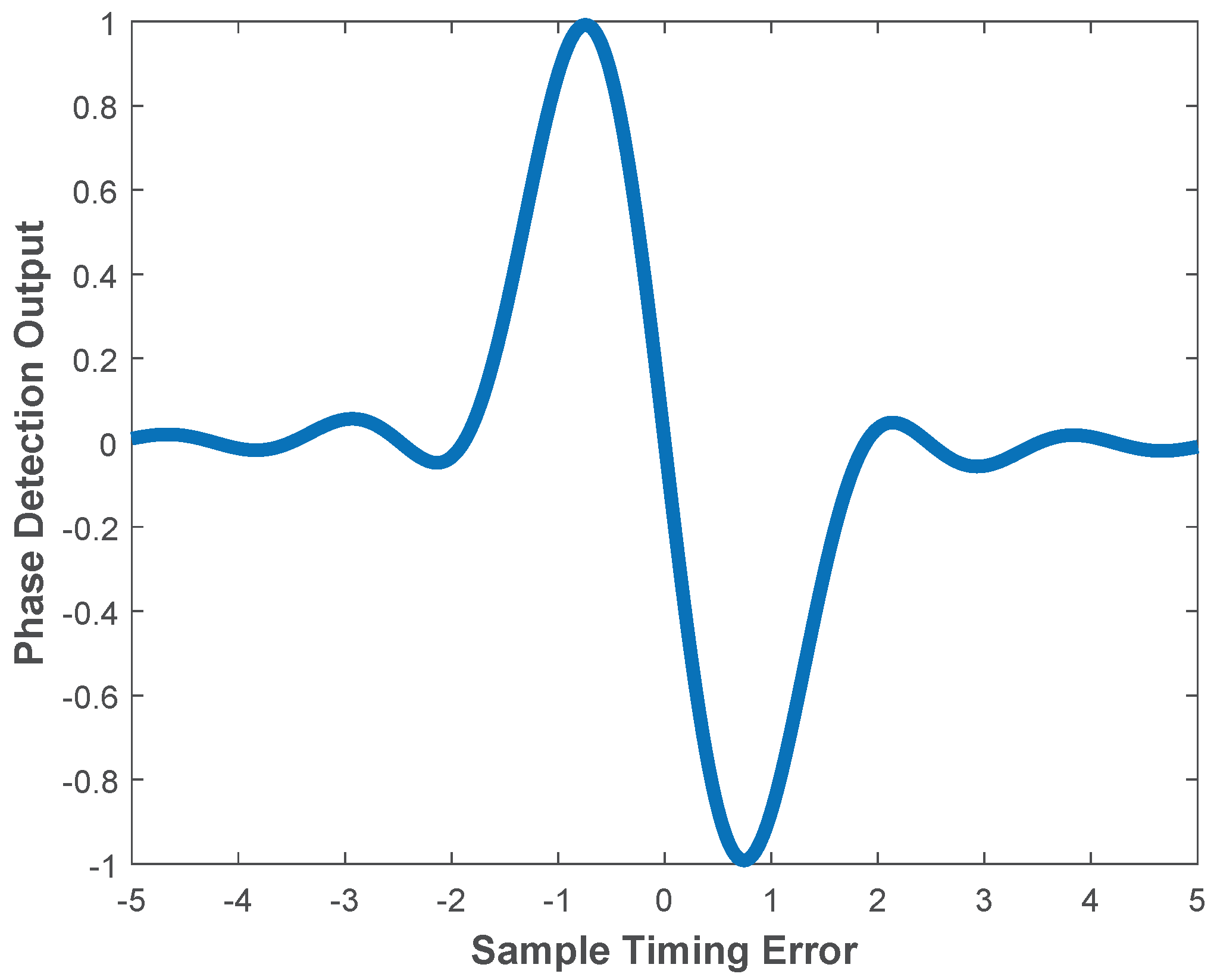
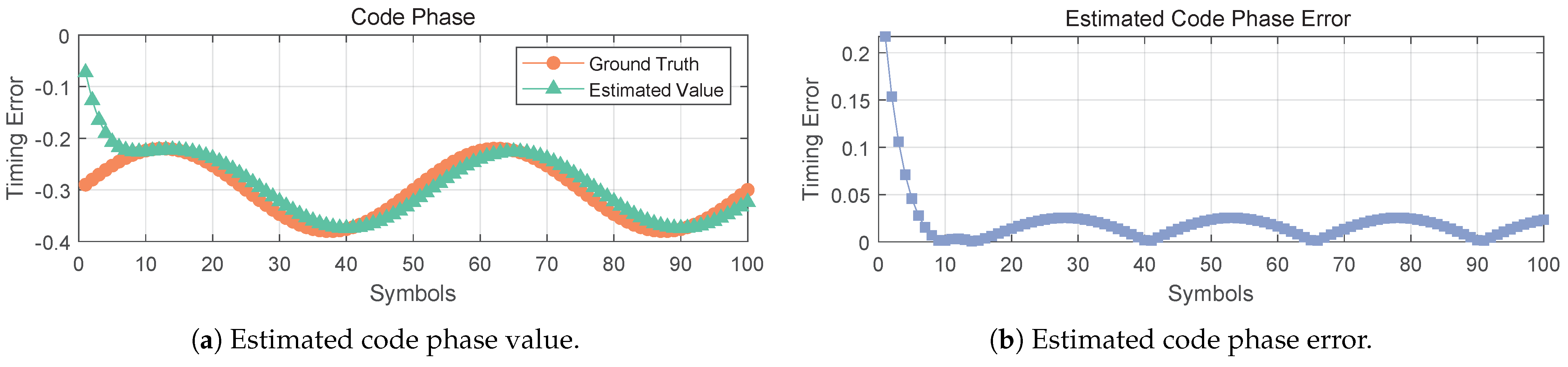
3.3. Delay-Locked Loop Design
| Algorithm 1 Iterative DLL algorithm |
Input: , , Output:
|
4. Simulation Results and Errors Analysis
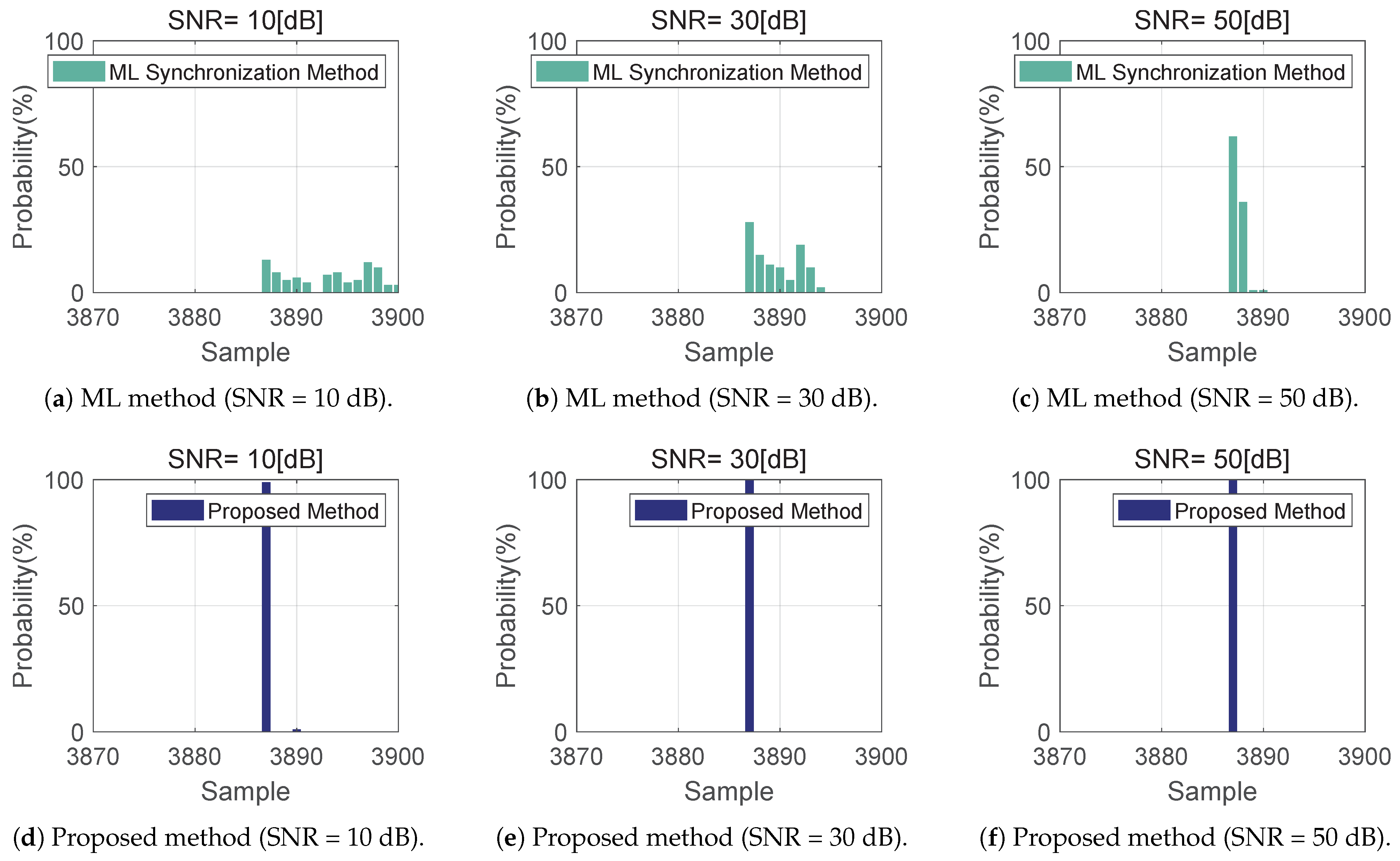
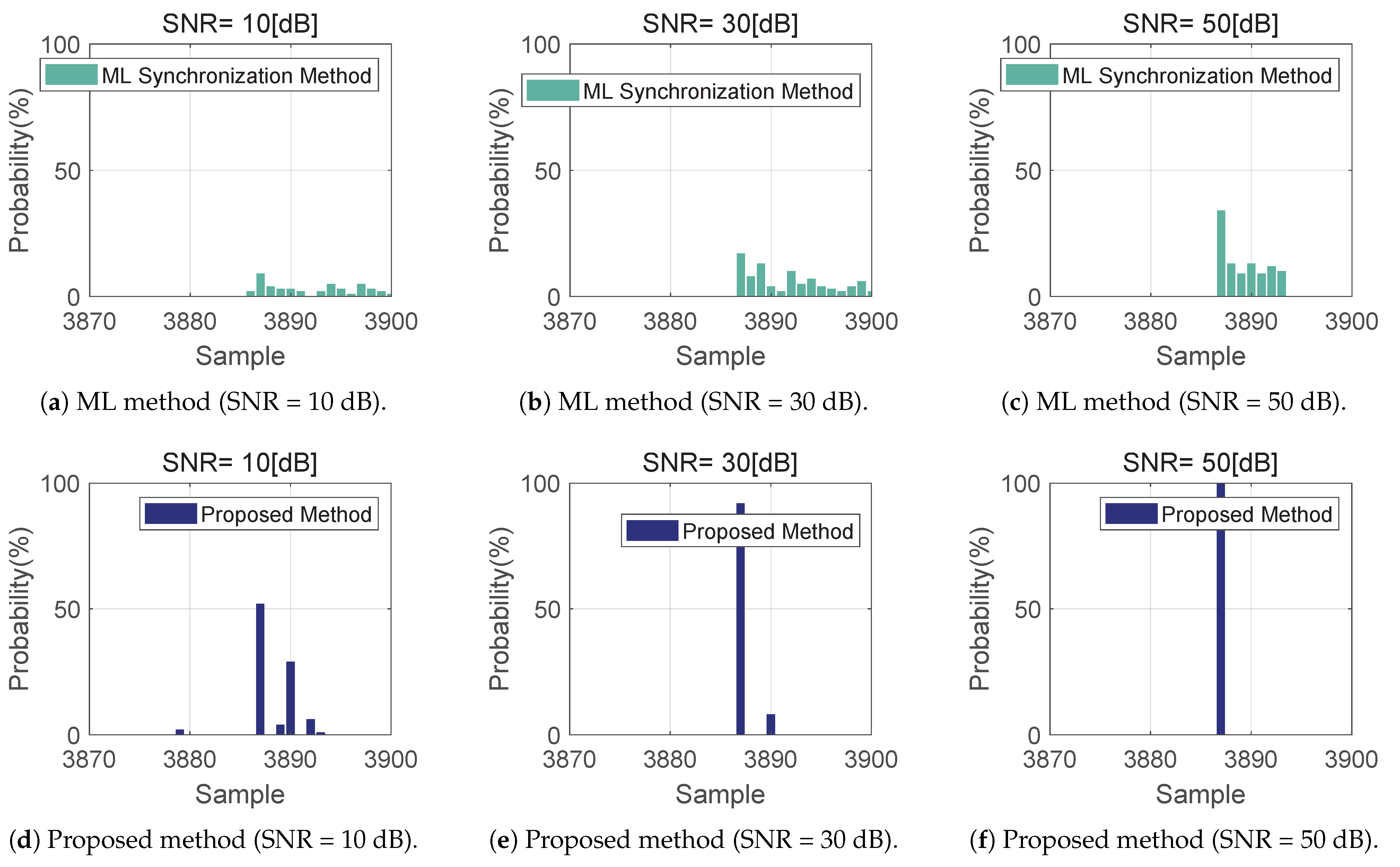
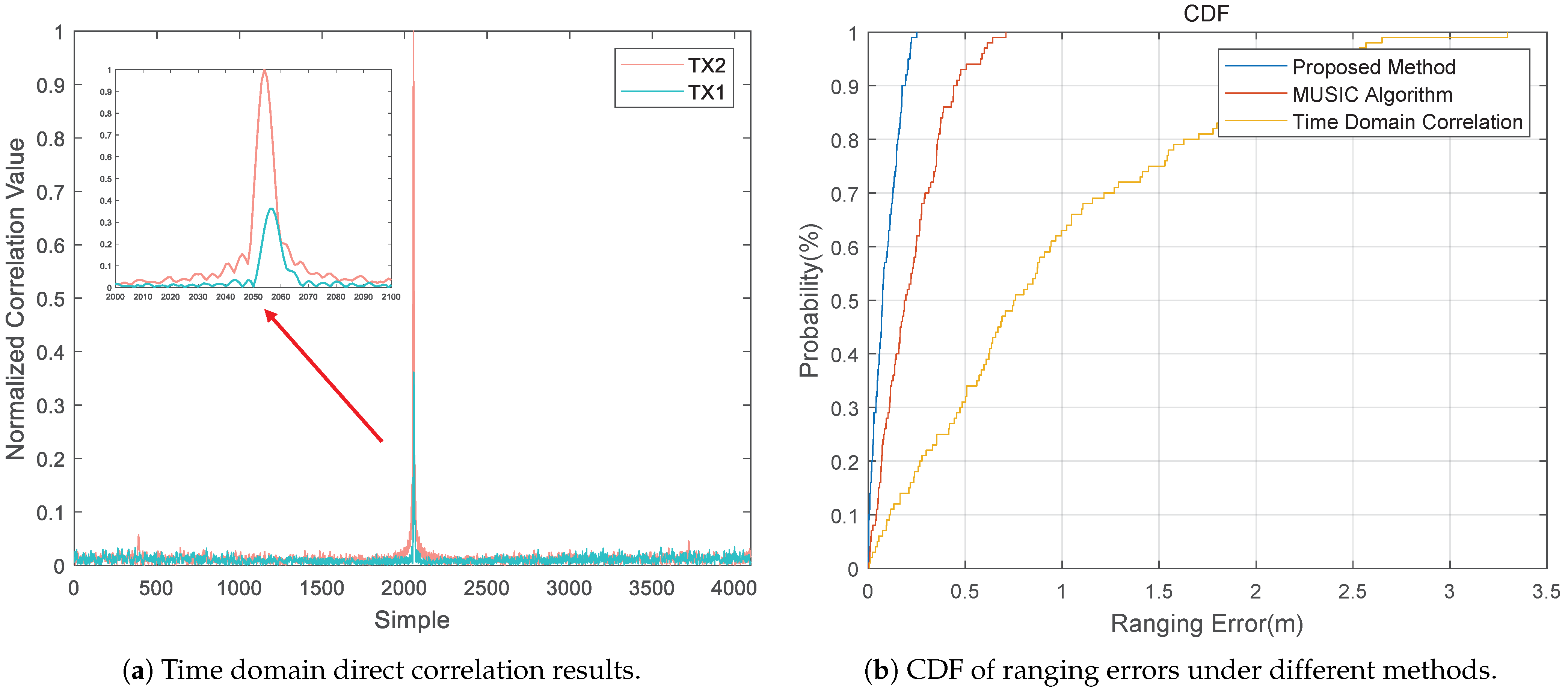
4.1. Simulation and Analysis
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bencak, P.; Hercog, D.; Lerher, T. Indoor positioning system based on bluetooth low energy technology and a nature-inspired optimization algorithm. Electronics 2022, 11, 308. [Google Scholar] [CrossRef]
- Shang, S.; Wang, L. Overview of wifi fingerprinting-based indoor positioning. IET Commun. 2022, 16, 725–733. [Google Scholar] [CrossRef]
- Wang, F.; Tang, H.; Chen, J. Survey on nlos identification and error mitigation for uwb indoor positioning. Electronics 2023, 12, 1678. [Google Scholar] [CrossRef]
- Zhu, N.; Marais, J.; Bétaille, D.; Berbineau, M. Gnss position integrity in urban environments: A review of literature. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2762–2778. [Google Scholar] [CrossRef]
- Wang, C.-X.; Haider, F.; Gao, X.; You, X.-H.; Yang, Y.; Yuan, D.; Aggoune, H.M.; Haas, H.; Fletcher, S.; Hepsaydir, E. Cellular architecture and key technologies for 5g wireless communication networks. IEEE Commun. Mag. 2014, 52, 122–130. [Google Scholar] [CrossRef]
- del Peral-Rosado, J.A.; Raulefs, R.; López-Salcedo, J.A.; Seco-Granados, G. Survey of cellular mobile radio localization methods: From 1 g to 5 g. IEEE Commun. Surv. Tutor. 2017, 20, 1124–1148. [Google Scholar] [CrossRef]
- Müürsepp, I.; Kulmar, M.; Elghary, O.; Alam, M.M.; Chen, T.; Horsmanheimo, S.; Scholliers, J. Performance evaluation of 5g-nr positioning accuracy using time difference of arrival method. In Proceedings of the 2021 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Athens, Greece, 7–10 September 2021; pp. 494–499. [Google Scholar]
- Mendrzik, R.; Wymeersch, H.; Bauch, G.; Abu-Shaban, Z. Harnessing nlos components for position and orientation estimation in 5 g millimeter wave mimo. IEEE Trans. Wirel. Commun. 2018, 18, 93–107. [Google Scholar] [CrossRef]
- Huo, Y.; Lin, X.; Di, B.; Zhang, H.; Hernando, F.J.L.; Tan, A.S.; Mumtaz, S.; Demir, T.; Chen-Hu, K. Technology trends for massive mimo towards 6 G. Sensors 2023, 23, 6062. [Google Scholar] [CrossRef]
- Mazloum, T.; Santamaria, L.; Munoz, F.; Clemente, A.; Gros, J.-B.; Nasser, Y.; Odit, M.; Lerosey, G.; D’Errico, R. Impact of multiple ris on channel characteristics: An experimental validation in ka band. In Proceedings of the 2023 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Gothenburg, Sweden, 6–9 June 2023; IEEE: New York, NY, USA, 2023; pp. 13–18. [Google Scholar]
- Luan, M.; Wang, B.; Zhao, Y.; Feng, Z.; Hu, F. Phase design and near-field target localization for ris-assisted regional localization system. IEEE Trans. Veh. Technol. 2021, 71, 1766–1777. [Google Scholar] [CrossRef]
- Leitinger, E.; Meissner, P.; Rüdisser, C.; Dumphart, G.; Witrisal, K. Evaluation of position-related information in multipath components for indoor positioning. IEEE J. Sel. Areas Commun. 2015, 33, 2313–2328. [Google Scholar] [CrossRef]
- Li, X.; Pahlavan, K. Super-resolution toa estimation with diversity for indoor geolocation. IEEE Trans. Wirel. Commun. 2004, 3, 224–2344. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. Esprit-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Driusso, M.; Babich, F.; Knutti, F.; Sabathy, M.; Marshall, C. Estimation and tracking of lte signals time of arrival in a mobile multipath environment. In Proceedings of the 2015 9th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 7–9 September 2015; pp. 276–281. [Google Scholar]
- Wang, Y.; Li, C.; Yu, Y.; Huang, S. Enabling low-power high-accuracy positioning (lphap) in 3gpp nr standards. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021; pp. 1–7. [Google Scholar]
- Yang, B.; Letaief, K.B.; Cheng, R.S.; Cao, Z. Timing recovery for ofdm transmission. IEEE J. Sel. Areas Commun. 2000, 18, 2278–2291. [Google Scholar] [CrossRef]
- Thevenon, P.; Julien, O.; Macabiau, C.; Serant, D.; Corazza, S.; Bousquet, M.; Ries, L.; Grelier, T. Pseudo-range measurements using ofdm channel estimation. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 481–493. [Google Scholar]
- Shamaei, K.; Kassas, Z.M. Lte receiver design and multipath analysis for navigation in urban environments. Navigation 2018, 65, 655–675. [Google Scholar] [CrossRef]
- Jin, C.; Bajaj, I.; Zhao, K.; Tay, W.P.; Ling, K.V. 5g positioning using code-phase timing recovery. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–7. [Google Scholar]
- Yin, L.; Cao, J.; Lin, K.; Deng, Z.; Ni, Q. A novel positioning-communication integrated signal in wireless communication systems. IEEE Wirel. Commun. Lett. 2019, 8, 1353–1356. [Google Scholar] [CrossRef]
- Sharifi-Tehrani, O.; Sabahi, M.F.; Danaee, M.R. Efficient gnss jamming mitigation using the marcenkopastur law and karhunen-loeve decomposition. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2291–2303. [Google Scholar] [CrossRef]
- Lee, J.-H.; Han, J.C.; Kim, S.-C. Joint carrier frequency synchronization and channel estimation for ofdm systems via the em algorithm. IEEE Trans. Veh. Technol. 2006, 55, 167–172. [Google Scholar] [CrossRef]
- Morelli, M.; Moretti, M. Fine carrier and sampling frequency synchronization in ofdm systems. IEEE Trans. Wirel. Commun. 2010, 9, 1514–1524. [Google Scholar] [CrossRef]
- Gul, M.M.U.; Ma, X.; Lee, S. Timing and frequency synchronization for ofdm downlink transmissions using zadoff-chu sequences. IEEE Trans. Wirel. Commun. 2014, 14, 1716–1729. [Google Scholar] [CrossRef]
- de Beek, J.-J.V.; Sandell, M.; Borjesson, P.O. Ml estimation of time and frequency offset in ofdm systems. IEEE Trans. Signal Process. 1997, 45, 1800–1805. [Google Scholar] [CrossRef]
- Beek, J.-J.V.D.; Sandell, M.; Isaksson, M.; Borjesson, P.O. Low-complex frame synchronization in ofdm systems. In Proceedings of the ICUPC’95-4th IEEE International Conference on Universal Personal Communications, Tokyo, Japan, 6–10 November 1995; pp. 982–986. [Google Scholar]
- Ren, X.; Chen, W.; Tao, M. Position-based compressed channel estimation and pilot design for high-mobility ofdm systems. IEEE Trans. Veh. Technol. 2014, 64, 1918–1929. [Google Scholar] [CrossRef]
- Tao, L.; Yu, J.; Zhang, J.; Shao, Y.; Chi, N. Reduction of intercarrier interference based on window shaping in ofdm rof systems. IEEE Photonics Technol. Lett. 2013, 25, 851–854. [Google Scholar] [CrossRef]
- Rinder, P.; Bertelsen, N. Design of a Single Frequency GPS Software Receiver; Aalborg Universitet, Institute of Electronic Systems: Nordjylland, Denmark, 2004. [Google Scholar]
- Kaplan, E.D.; Hegarty, C. Understanding GPS/GNSS: Principles and Applications; Artech House: Norwood, MA, USA, 2017. [Google Scholar]




| Parameters | Value |
|---|---|
| Carrier Frequency | 3.4 GHz |
| Subcarrier Spacing | 30 kHz |
| FFT Points N | 4096 |
| Cyclic Prefix | Normal |
| Number of RB | 200 |
| PRS Resource Set Period | 4 |
| PRS Resource Repetition | 4 |
| Number of PRS Symbols | 12 |
| Comb Size | 2 |
| Factor | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, K.; Deng, Z.; Guo, X.; Ma, Z.; Liu, J. High-Precision Ranging Method of 5G NR Co-Band PRS in Industrial Internet Scenarios. Appl. Sci. 2023, 13, 10302. https://doi.org/10.3390/app131810302
Luo K, Deng Z, Guo X, Ma Z, Liu J. High-Precision Ranging Method of 5G NR Co-Band PRS in Industrial Internet Scenarios. Applied Sciences. 2023; 13(18):10302. https://doi.org/10.3390/app131810302
Chicago/Turabian StyleLuo, Kai, Zhongliang Deng, Xiaobin Guo, Ziyao Ma, and Jingrong Liu. 2023. "High-Precision Ranging Method of 5G NR Co-Band PRS in Industrial Internet Scenarios" Applied Sciences 13, no. 18: 10302. https://doi.org/10.3390/app131810302
APA StyleLuo, K., Deng, Z., Guo, X., Ma, Z., & Liu, J. (2023). High-Precision Ranging Method of 5G NR Co-Band PRS in Industrial Internet Scenarios. Applied Sciences, 13(18), 10302. https://doi.org/10.3390/app131810302







