High-Speed Vehicles in Low-Pressure Tunnels—Influence of Choked Flows
Abstract
:1. Introduction
- Will high vehicle speeds cause sonic airspeeds and hence choked flow conditions?
- Will the low ambient pressures ensure relatively low maximum pressures?
- Will the low ambient pressures ensure relatively low maximum temperatures?
- Will the low ambient pressures have a strong influence on heat flows?
- How will multiple vehicles interact aerodynamically?
- How beneficial will it be to link tunnels with vehicles travelling in opposite directions?
1.1. Theoretical Methodology
1.2. Terminology
1.3. Outline of Paper
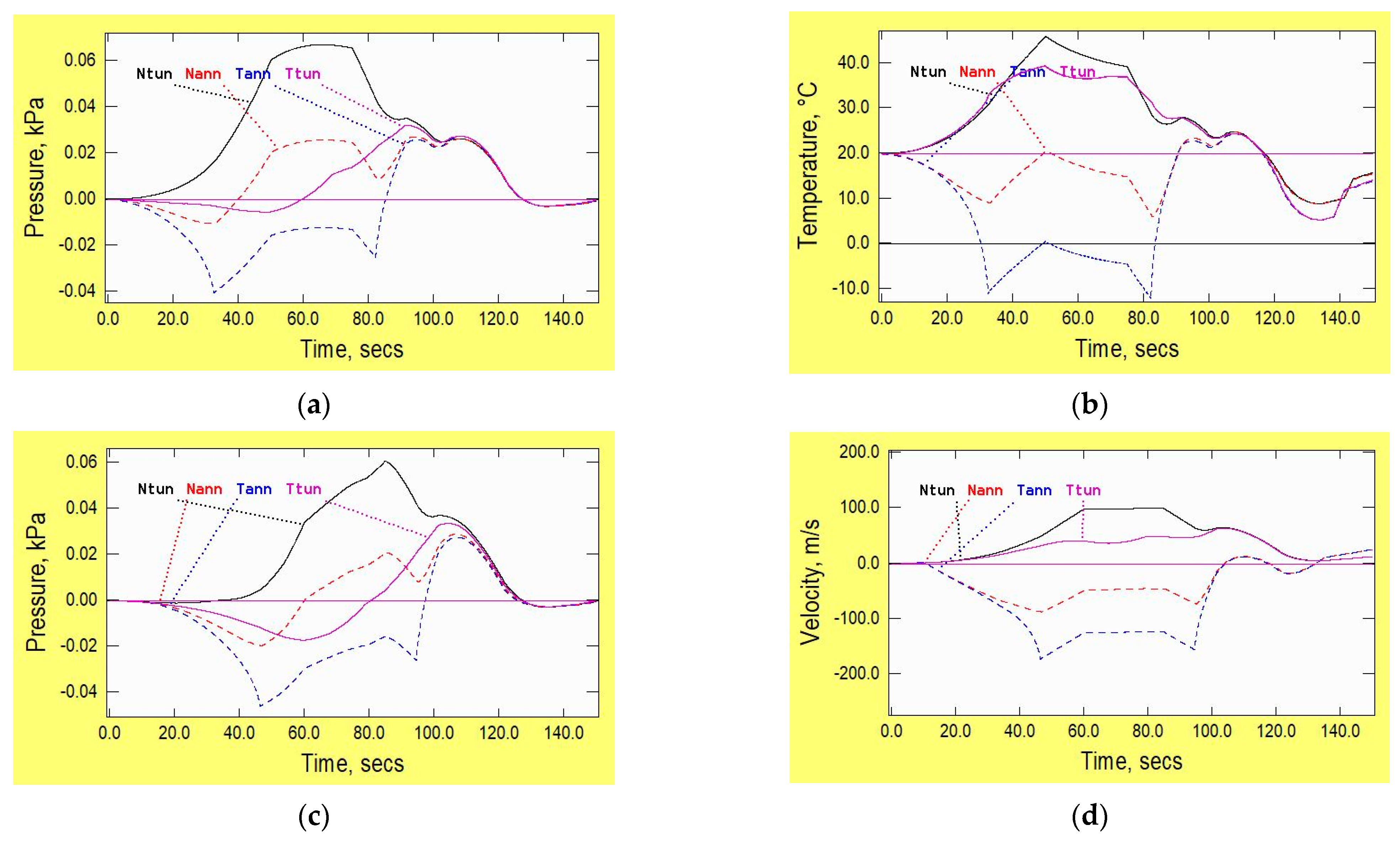
2. Base Case
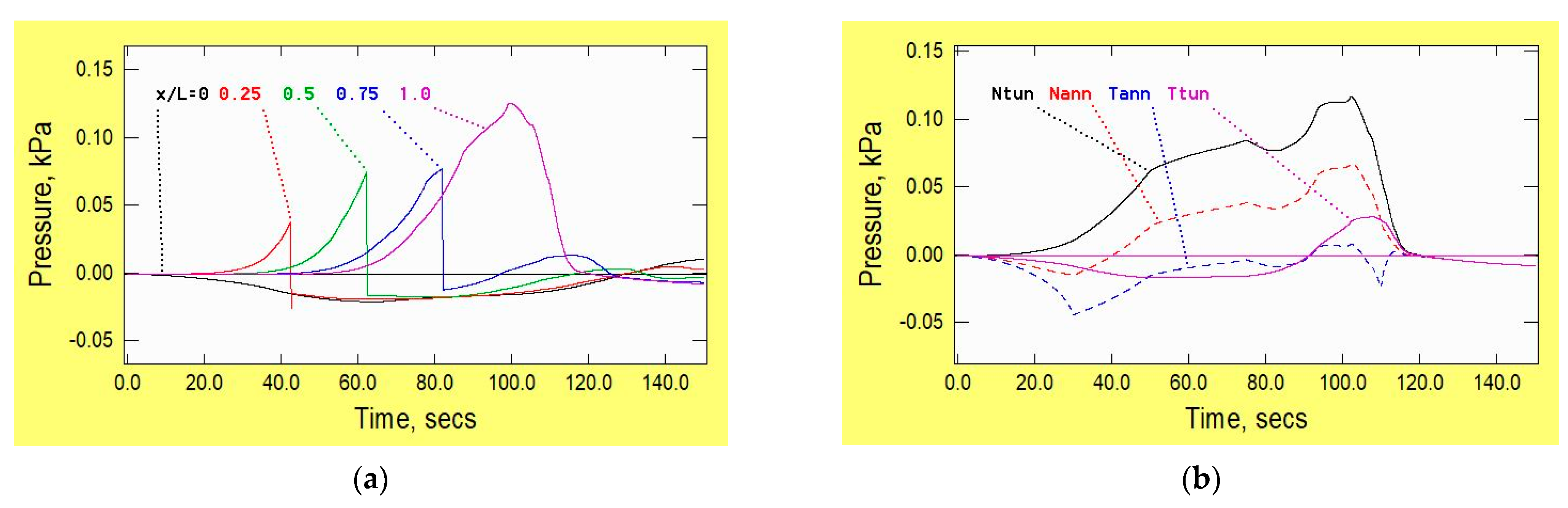
2.1. Pressure
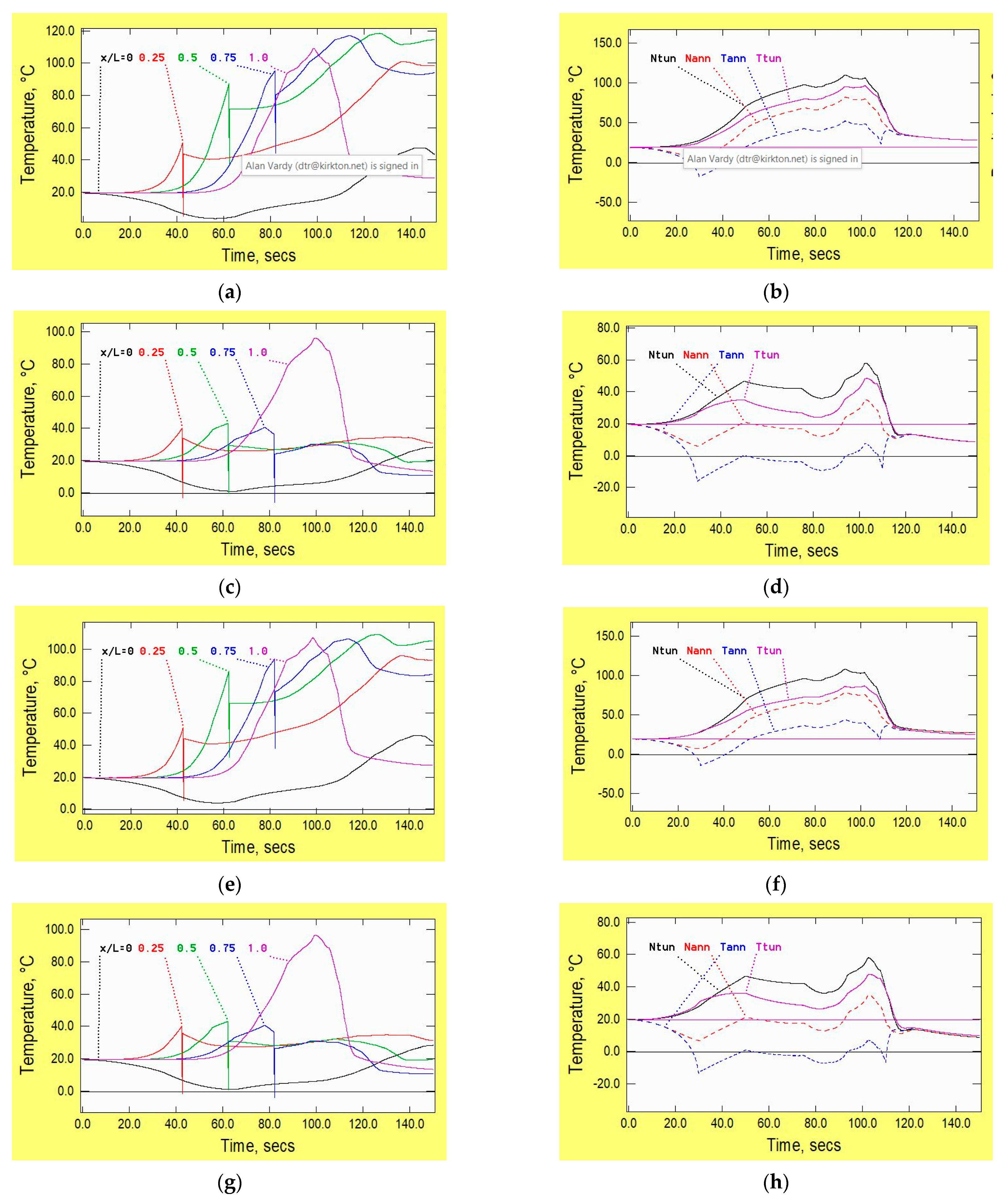
2.2. Temperature
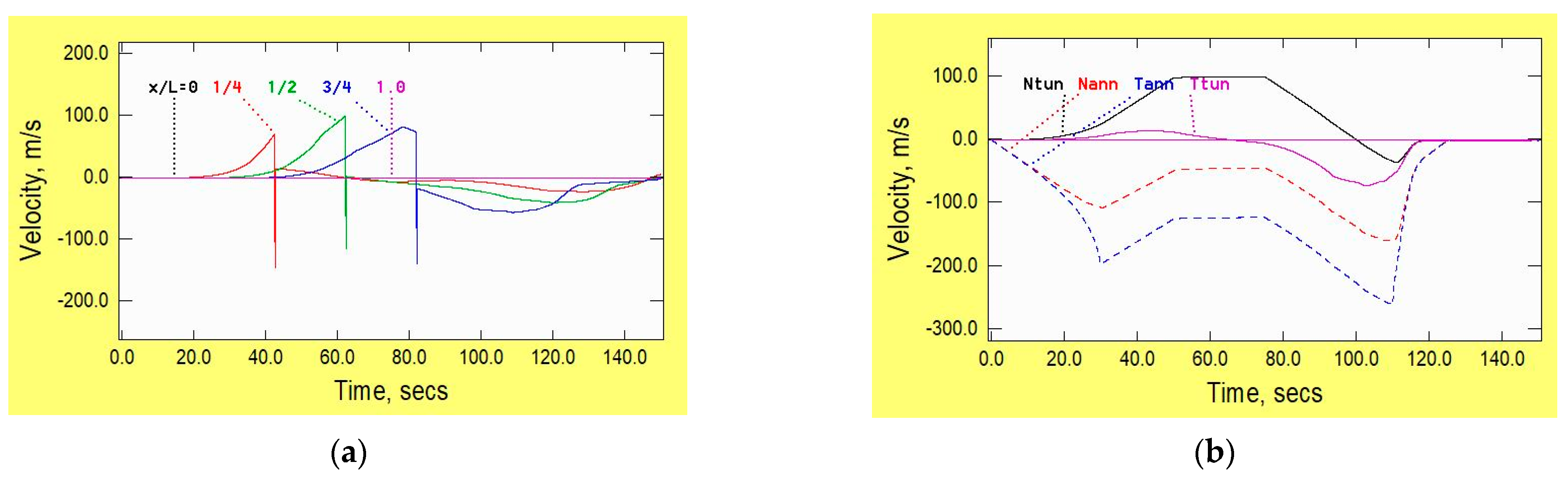
2.3. Velocity
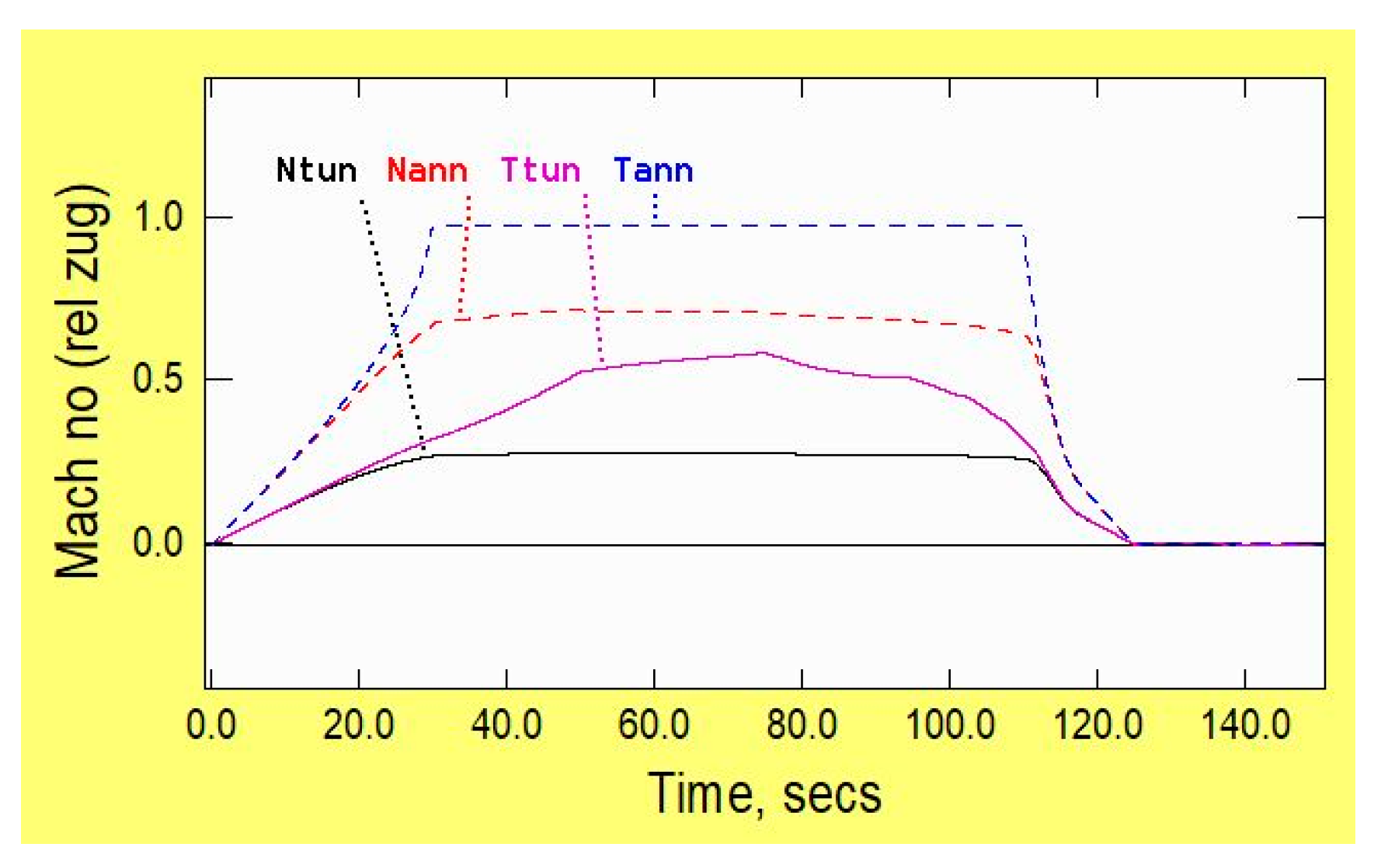
2.4. Mach Number
- (Ntun, Ttun = small distances ahead of the nose and behind the tail.
- Nann, Tann = in the annulus, small distances from the nose and tail).
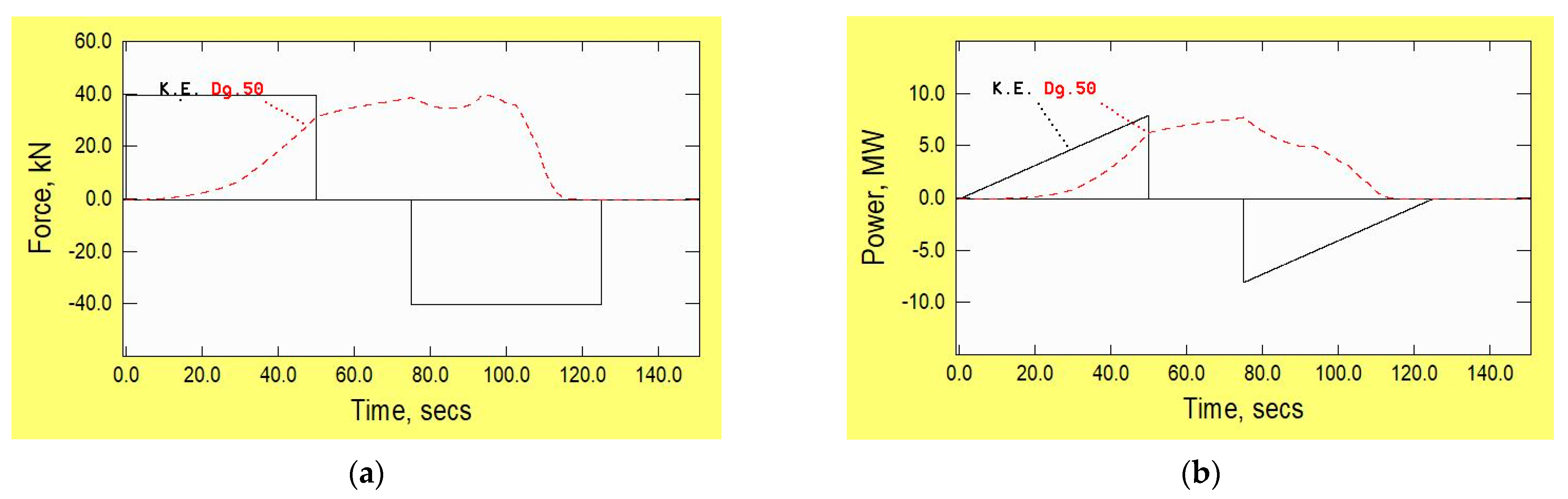
2.5. Drag and Power
- Inefficiencies in the propulsion and braking systems;
- Sensible heat from passengers;
- On-board systems such as lighting and air management.
2.6. Numerical Accuracy
2.6.1. Analytical Equations
2.6.2. Numerical Equations
2.6.3. Numerical Discretisation (Grid Size)
2.6.4. Convergence Tolerances
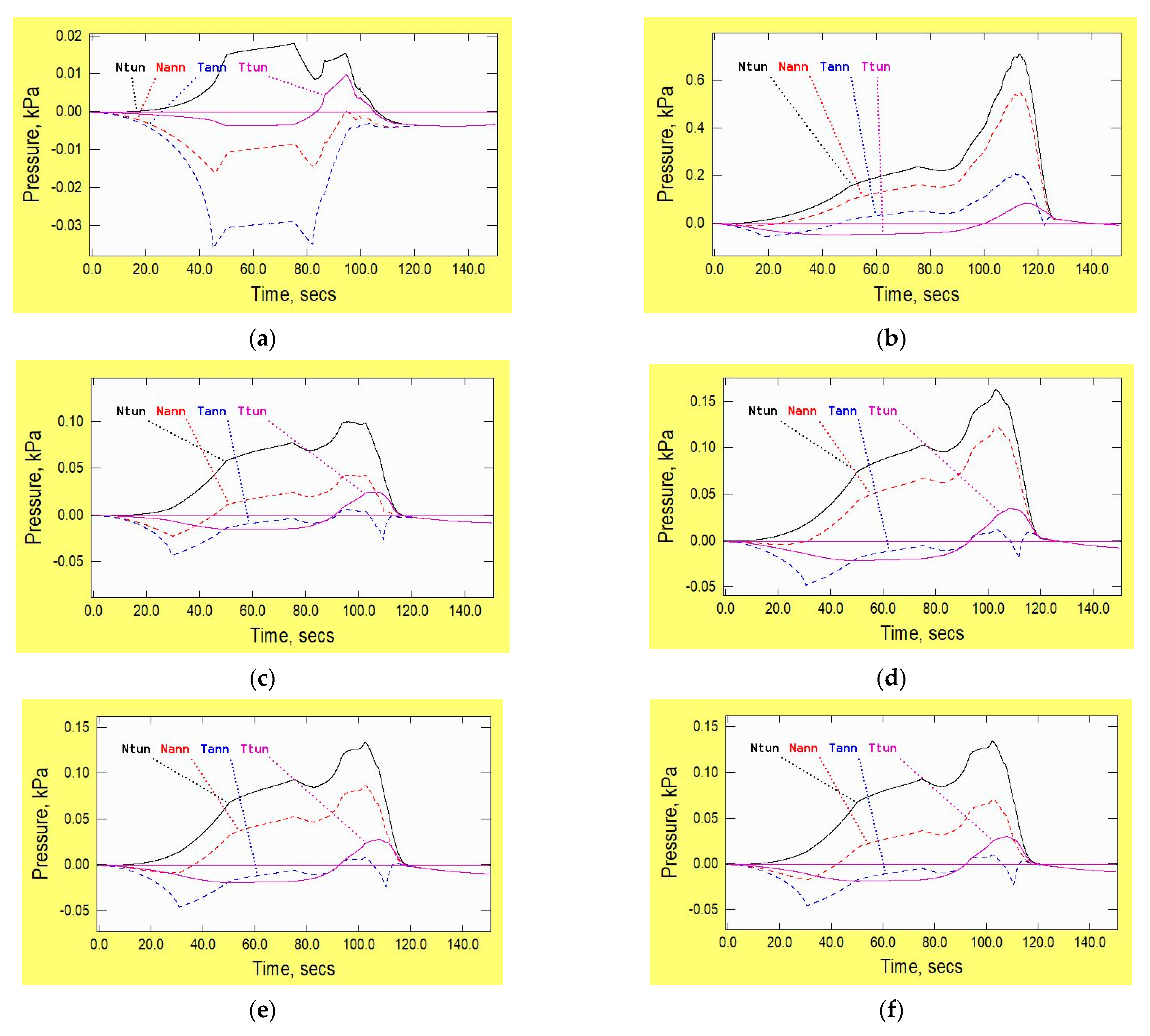
3. Sensitivity to Key Parameters
3.1. Vehicle Parameters
3.1.1. Cross-Sectional Area
3.1.2. Length
3.1.3. Skin Friction
3.1.4. Nose Loss Coefficient
3.1.5. Tail Loss Coefficient
3.2. Thermodynamic Influences
3.2.1. Heat Transfers at Tunnel and Vehicle Surfaces
3.2.2. Other Causes of Heat Transfers
3.3. Operational Considerations
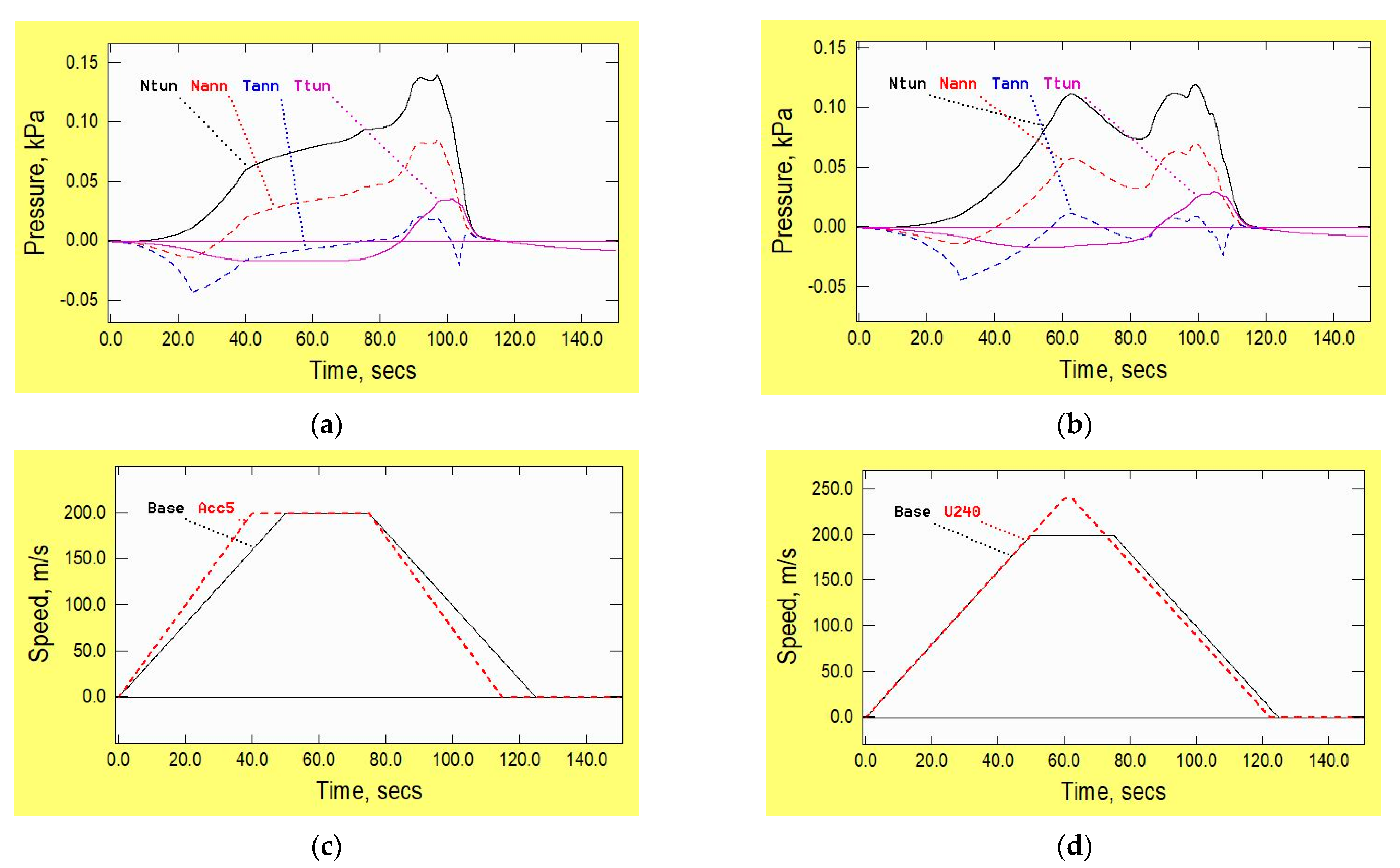
3.3.1. Ambient Pressure
3.3.2. Vehicle Speed History
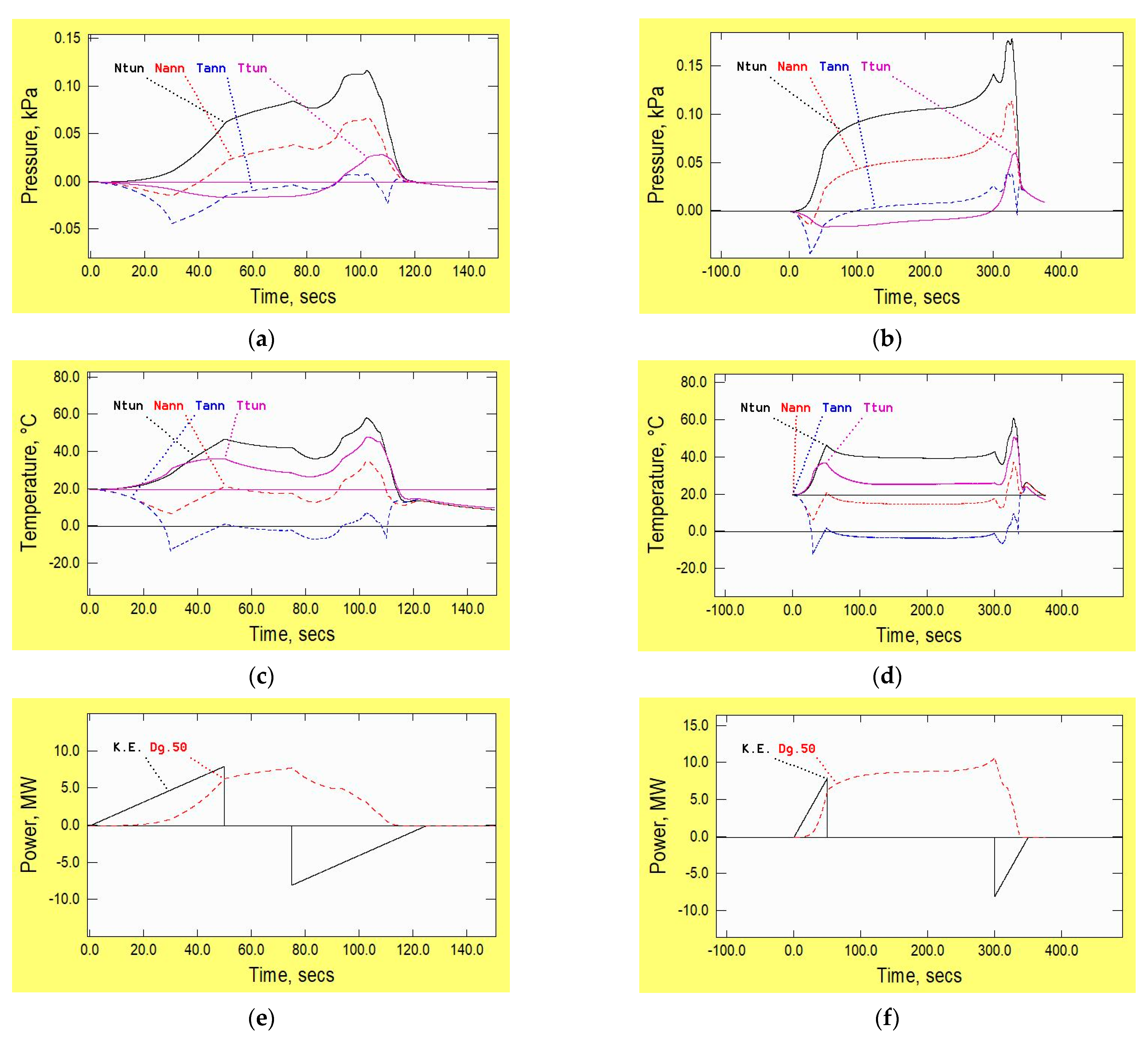
3.3.3. Number of Vehicles
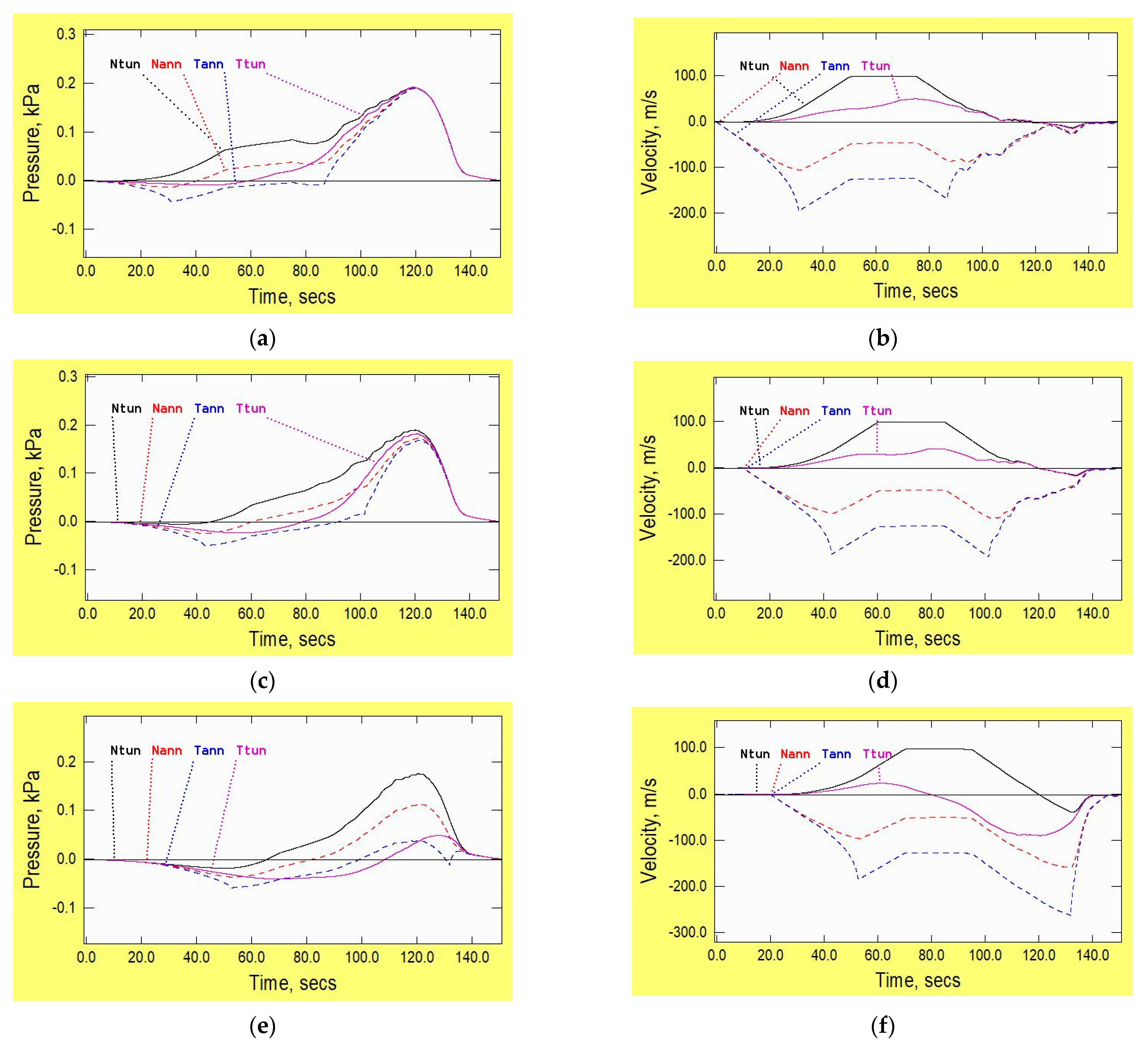
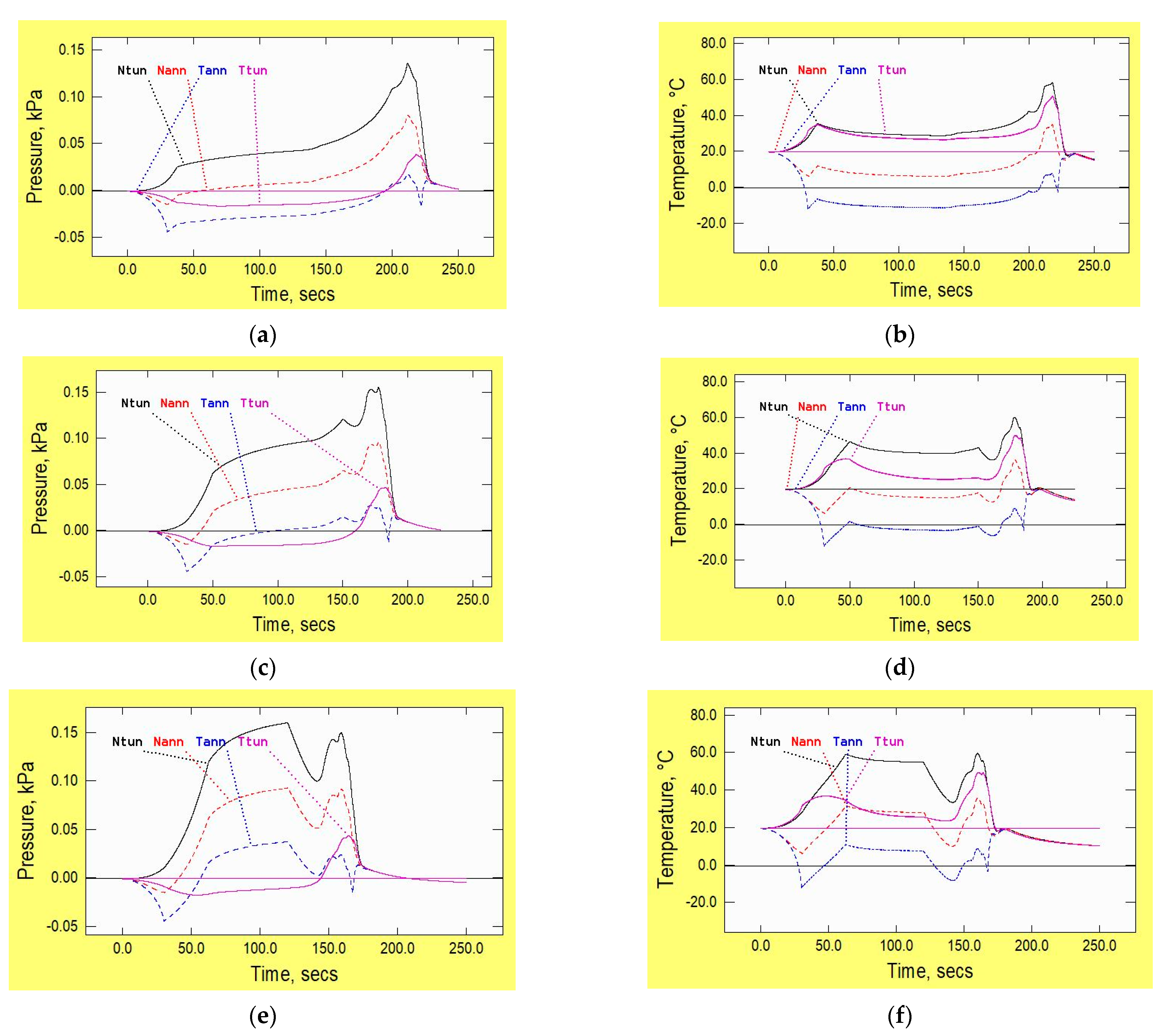
4. Longer Tunnels
Influence of Vehicle Speed
5. Alternative Tunnel Configuration
6. Other Aerodynamic Considerations
6.1. Response to System Power Failure
6.2. Loss of Vehicle Sealing
6.3. Tunnel Wall Temperatures
6.4. Open Connections between Tunnels
6.5. Stations
6.6. Other Factors
7. Summary and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Theoretical Basis
References
- Niu, J.; Sui, Y.; Yu, Q.; Cao, X.; Yuan, Y. Aerodynamics of railway train/tunnel system: A review of recent research. Energy Built Environ. 2020, 1, 351–375. [Google Scholar] [CrossRef]
- Kauzinyte, G.; Vezza, M.; Alizadeh, S.; Eckford, D. Hyperloop: Simulation and assessment of high-speed vehicle transport in evacuated tubes. In Proceedings of the 18th International Symposium on the Aerodynamics, Ventilation and fire in Vehicle Tunnels, Athens, Greece, 25–27 September 2019; Aini, E., Ed.; BHR Group: Bedfordshire, UK, 2019; pp. 61–76. [Google Scholar]
- Bizzozero, M.; Sato, Y.; Sayed, M.A. Aerodynamic study of a Hyperloop pod equipped with compressor to overcome the Kantrowitz limit. J Wind. Eng. Ind. Aero. 2021, 218, 104784. [Google Scholar] [CrossRef]
- Museros, P.; Lázaro, C.; Pinazo, B.; Monleόn, S. Key aspects in the analysis and design of Hyperloop infrastructure under static, dynamic and thermal loads. Engrg. Struct. 2021, 239, 112177. [Google Scholar] [CrossRef]
- Nick, N.; Sato, Y. Computational fluid dynamics simulation of Hyperloop pod predicting laminar-turbulent transition. Rail. Eng. Sci. 2020, 28, 97–111. [Google Scholar] [CrossRef]
- Tudor, D.; Paolone, M. Operational-driven optimal-design of a hyperloop system. Transp. Eng. 2021, 5, 100079. [Google Scholar] [CrossRef]
- Braun, J.; Sousa, J.; Pekardan, C. Aerodynamic Design and Analysis of the Hyperloop. AIAA J. 2017, 55, 4053–4060. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, L.; Ma, J.; Liu, Y. Aerodynamic simulation of evacuated tube maglev trains with different streamlined designs. J. Mod. Transp. 2012, 20, 115–120. [Google Scholar] [CrossRef]
- Opgenoord, M.M.J.; Caplan, P.C. Aerodynamic design of the hyperloop concept. AIAA J. 2018, 56, 4261–4270. [Google Scholar] [CrossRef]
- Zhang, Y. Numerical simulation and analysis of aerodynamic drag on a subsonic train in evacuated tube transportation. J. Mod. Transp. 2012, 20, 44–48. [Google Scholar] [CrossRef]
- Swissmetro. Swissmetro Main-Study-1994–1998. 1999. Available online: https://swissmetro-ng.org/wp-content/uploads/Swissmetro-Main-Study-1994-1998-Level-A.pdf (accessed on 9 June 2023).
- ThermoTun. 2022. Available online: www.ThermoTun.com (accessed on 9 June 2023).
- Vardy, A.E. On the method of characteristics in highly compressible flows. In Proceedings of the 14th International Conference on Pressure Surges, Eindhoven, The Netherlands, 12–14 April 2023; Jones, S., Ed.; Tech Univ Eindhoven: Eindhoven, The Netherlands, 2023; pp. 443–457. [Google Scholar]
- Oh, J.-S.; Kang, T.; Ham, S.; Lee, K.-S.; Jang, Y.J.; Ryou, H.-S.; Ryu, J. Numerical analysis of aerodynamic characteristics of hyperloop system. Energies 2019, 12, 518. [Google Scholar] [CrossRef]
- Gorji, S.; Seddighi, M.; Ariyaratne, C.; Vardy, A.E.; O’Donoghue, T.; Pokrajac, D.; He, S. A Comparative Study of Turbulence Models in a Transient Channel Flow. Comput. Fluids 2014, 89, 111–123. [Google Scholar] [CrossRef]
- Shapiro, A.H. The Dynamics and Thermodynamics of Compressible Fluid Flow; Wiley: Hoboken, NJ, USA, 1953. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients in Systems; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- NUMSTA. 2019. Available online: https://www.alexander-rudolf.de/NUMSTA/ (accessed on 9 June 2023).
- Vardy, A.E.; Rudolf, A.; Gloth, O. Thermal, Mach-number and inertial compressibility in railway tunnels. In Proceedings of the 13th International Symposium on the Aerodynamics and Ventilation of Vehicle Tunnels, New Brunswick, NJ, USA, 13–15 May 2009; Sweetland, I.A., Ed.; BHR Group: Bedfordshire, UK, 2009; pp. 505–520. [Google Scholar]





| Category | Parameter | Base Case Value |
|---|---|---|
| Tunnel | Length | 15.4 km |
| Cross-sectional area | 10 m2 | |
| Skin friction coefficient | ftun = 0.0025; λtun = 0.01 | |
| Vehicle | Length | 50 m |
| Cross-sectional area | 5 m2 | |
| Skin friction coefficient | fveh = 0.002; λveh = 0.008 | |
| Nose loss coefficient | zero | |
| Tail loss coefficient | 0.4 βveh2 | |
| Mass per unit length (loaded) | 0.2 tonnes/m | |
| Rolling resistance | zero | |
| Maximum speed | 200 m/s (720 km/h) | |
| Acceleration/deceleration | 0.4 m/s2 (≈0.4 g) | |
| Ambient conditions | Air pressure | 100 Pa |
| Air temperature | 20 °C | |
| All surface temperatures | 20 °C | |
| Efficiencies | Power supply to vehicle | 100% |
| Regenerative braking | 100% | |
| Stipulations | Surface heat transfers | (see Section 3.2) |
| Numerical | Grid length | 5 m |
| Blockage Ratio | Bizzozero et al. (2021) [3] | Present 1-D Analysis | |||
|---|---|---|---|---|---|
| Ma = 0.5 | Ma = 0.6 | Ma = 0.5825 | at t = 50 s | at t = 75 s | |
| 0.2 | 0.21 | 1.29 | 1.20 | 1.21 | 1.36 |
| 0.3 | 1.50 | 3.01 | 2.89 | 2.72 | 3.16 |
| 0.4 | 3.87 | 4.51 | 4.46 | 3.97 | 4.78 |
| 0.5 | 6.33 | 6.07 | 6.09 | 5.32 | 6.57 |
| 0.6 | 9.38 | 8.29 | 8.38 | 6.95 | 8.82 |
| 0.7 | 14.5 | 12.24 | 12.43 | 9.02 | 11.94 |
| 0.8 | 23.02 | 19.43 | 19.73 | 11.82 | 16.62 |
| 0.9 | 49.18 | 40.60 | 41.31 | 15.74 | 24.21 |
| Vehicle | Length | Max Drag | Max Power | Total Energy |
|---|---|---|---|---|
| m | kN | kW | MJ | |
| 1st of 3 | 50 | 0.592 | 11.8 | 5.25 |
| 2nd of 3 | 50 | 0.567 | 11.3 | 5.23 |
| 3rd of 3 | 50 | 1.133 | 16.0 | 8.14 |
| Single | 150 | 1.069 | 19.5 | 10.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vardy, A.E. High-Speed Vehicles in Low-Pressure Tunnels—Influence of Choked Flows. Appl. Sci. 2023, 13, 10314. https://doi.org/10.3390/app131810314
Vardy AE. High-Speed Vehicles in Low-Pressure Tunnels—Influence of Choked Flows. Applied Sciences. 2023; 13(18):10314. https://doi.org/10.3390/app131810314
Chicago/Turabian StyleVardy, Alan E. 2023. "High-Speed Vehicles in Low-Pressure Tunnels—Influence of Choked Flows" Applied Sciences 13, no. 18: 10314. https://doi.org/10.3390/app131810314




