Genetic-Algorithm-Driven Parameter Optimization of Three Representative DAB Controllers for Voltage Stability
Abstract
:1. Introduction
2. Mathematical Model of DAB Converter
3. Controller Design and Genetic Algorithm Optimization Approach
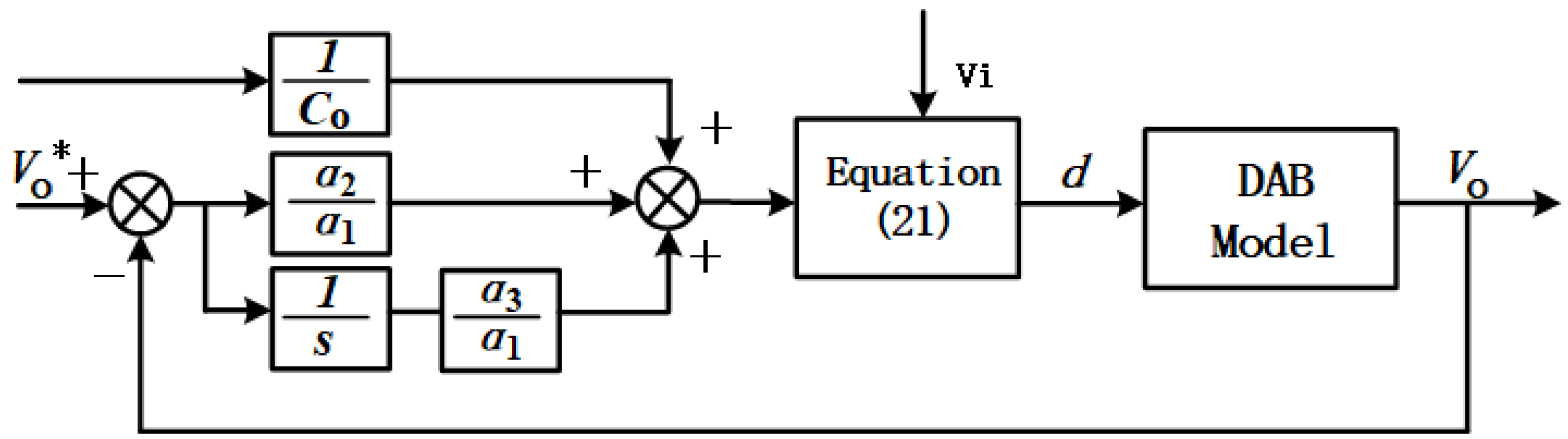
3.1. PI Control Based on Pole Placement Method
3.2. Sliding Mode Control
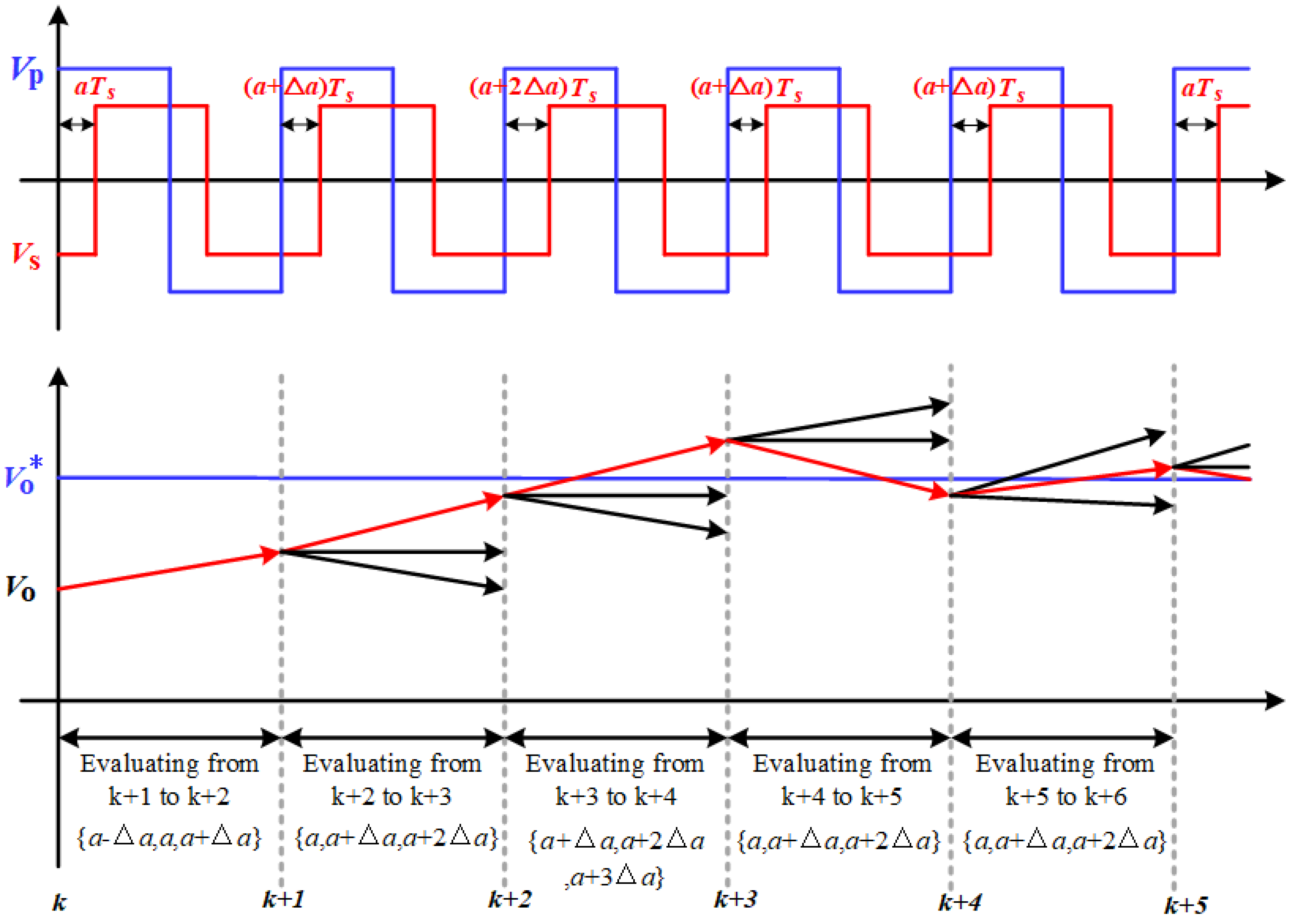
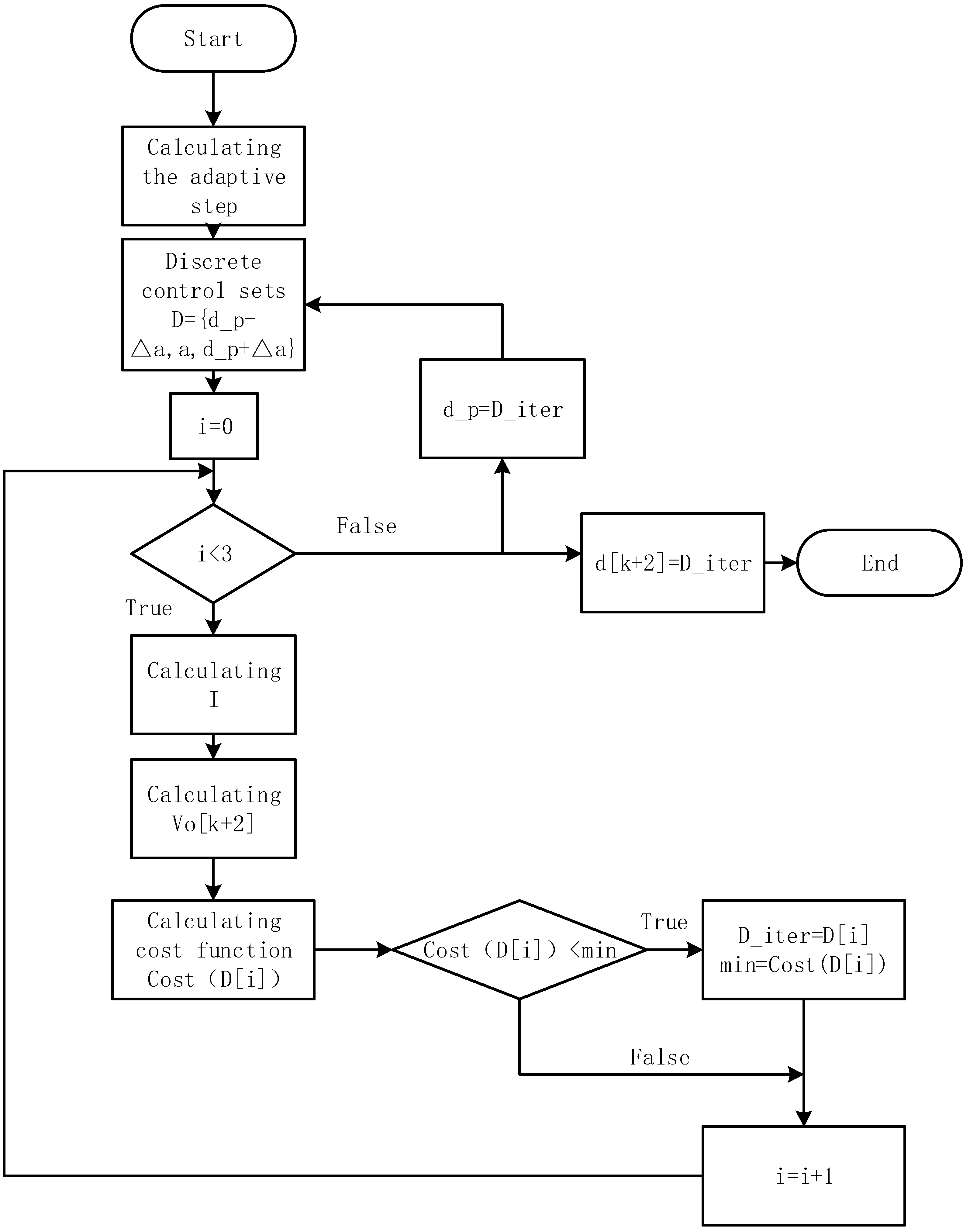
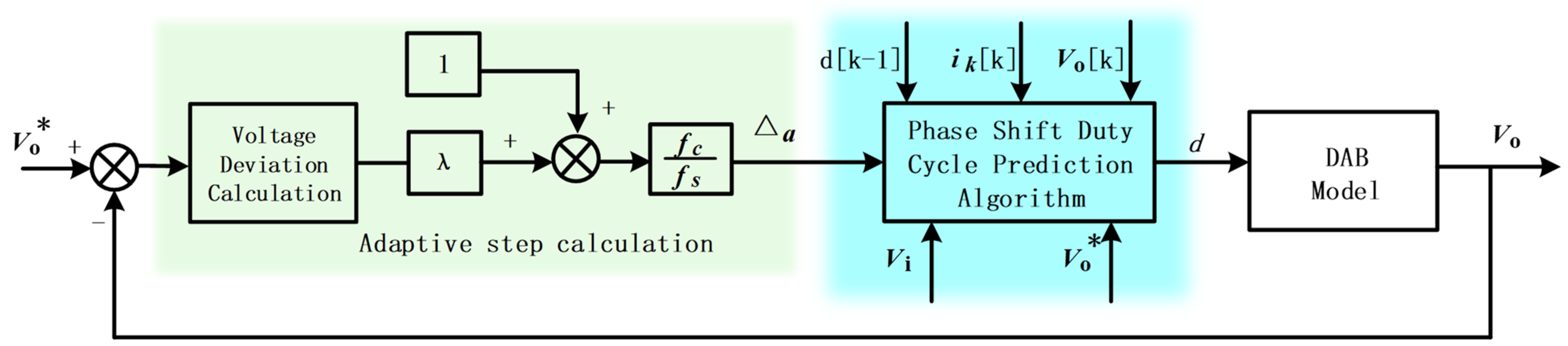
3.3. Model Preedictive Control
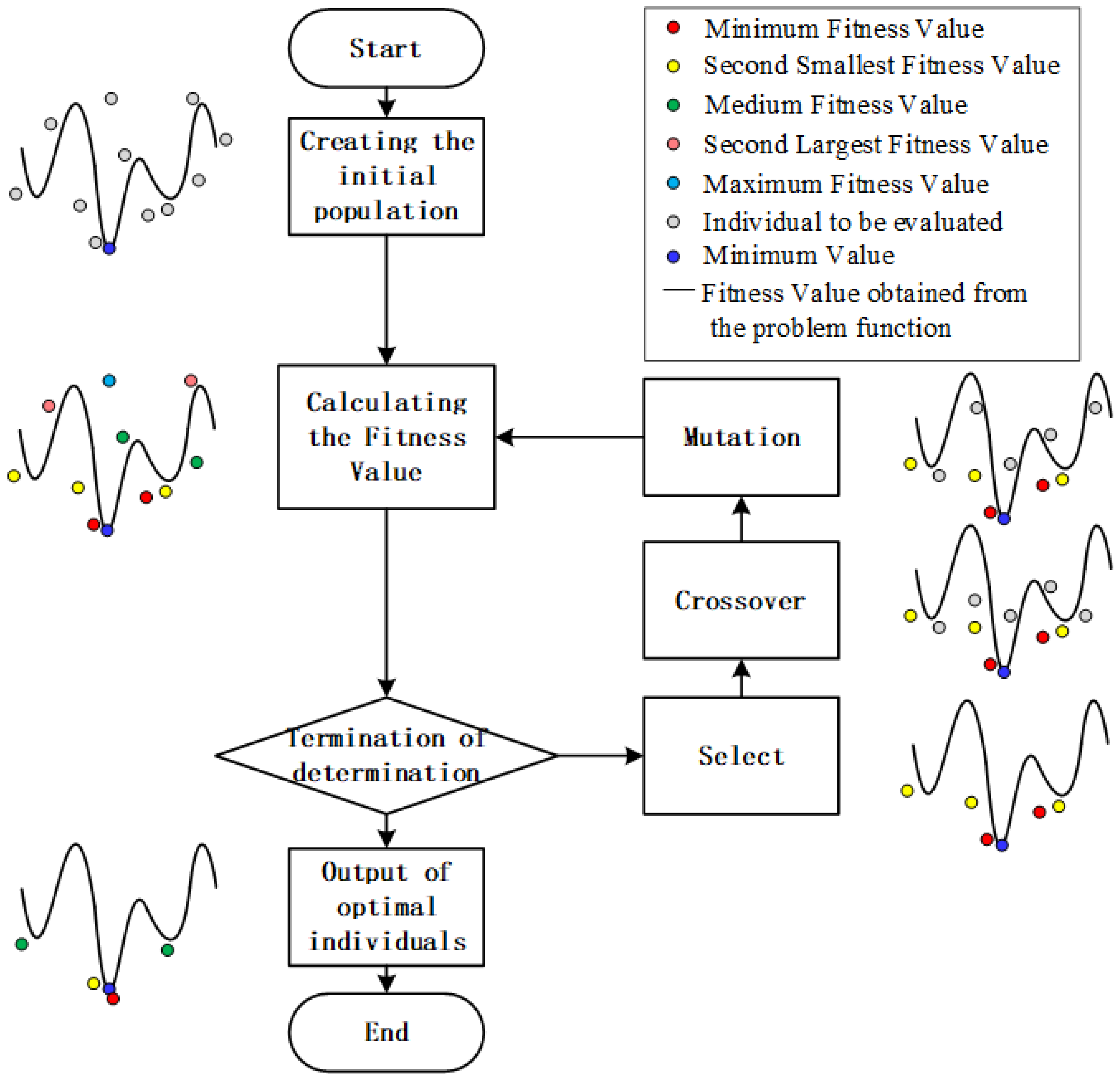
3.4. Genetic Algorithm
- 1.
- Population Initialization—Create an initial random population consisting of multiple individuals, with each individual corresponding to a potential solution. For the method of encoding the initial population, this paper defines the optimized variable range within lb and ub, and adopts real number encoding to encode the variables. Real number encoding is a common GA encoding method that transforms real-valued variables to gene values in the chromosome, where each gene represents a real-valued solution. In real number encoding, floating-point numbers are commonly used to represent gene values since the optimized variable range is usually a continuous real-valued range. Assuming the length of the chromosome is LC, each individual can be represented as an -length binary string or floating-point string. For real number encoding, the representation can be done using floating-point strings instead of binary strings. In real number encoding, it is necessary to perform the conversion between gene values and actual variable values to ensure that the optimized solutions fall within the variable range [29]. The detailed process of real-valued encoding is as follows:
- (1)
- Determine Chromosome Length—Initially, the length of the chromosome (number of genes) is established, which governs the encoding precision. Typically, this length depends on the number of problem variables and the required accuracy. Let us denote the chromosome length as ;
- (2)
- Initialize Individuals—For each individual, a random array of floating-point numbers is generated, with a length of . The range of each element (upper and lower limits) is set to ;
- (3)
- Mapping Gene Values to Actual Variable Values—Transform each gene value into the range of the actual variable. Assuming the range of the variables to be optimized is , the following formula is used to map the gene value genevalue to the actual variable value :. Specifically, for each gene value genevalue, it is mapped to an actual variable value x, where x lies within the range ;
- 2.
- Evaluation of Fitness—Evaluate each individual in the population based on the problem’s objective function to obtain its fitness value, which measures the quality of the solution. In GA, the fitness function plays a crucial role in assessing the superiority of each individual. In this paper, the fitness function is defined as . Selecting this expression as the fitness function aims to choose control parameters with smaller voltage mutations during transient processes when operating conditions change, to better control the voltage stability of the DC bus;
- 3.
- Selection—Based on the fitness values, select some individuals as “parents”, with the selection probability proportional to their fitness. In the selection operation, this paper adopts the elitism strategy. Elitism is a strategy that preserves the best individuals, passing the most excellent ones directly to the next generation in each population, ensuring the retention of excellent solutions [30]. This prevents the GA from losing the optimal solution during the optimization process. The individuals in the population are sorted from high to low based on the fitness values obtained in the previous step. The top few individuals with the highest fitness are selected as elite individuals and directly passed on to the next generation population;
- 4.
- Crossover—Perform crossover operations on the selected parent individuals to generate new individuals (offspring) in the hope of obtaining better characteristics. This paper uses a random discrete crossover algorithm called crossoverscattered. It randomly selects two parent individuals and randomly chooses some gene positions for crossover. Then, it exchanges the selected genes at those positions between the two parent individuals, resulting in two offspring individuals [31];
- 5.
- Mutation—Perform mutation operations on the offspring individuals, introducing random perturbations to maintain population diversity and explore new solution spaces [31]. This paper uses a uniform mutation algorithm called mutationuniform, which evaluates each gene in the individual based on the specified mutation probability. If the mutation probability requirement is met, the value of that gene is randomly perturbed within its range;
- 6.
- Update Population—Combine the generated offspring individuals with the parent individuals to form a new population;
- 7.
- Termination Criteria—Repeat the above steps until the predetermined termination criteria are met, such as reaching the maximum number of iterations or finding satisfactory solutions.
| Algorithm 1: Genetic Algorithm |
| Input: DAB parameters GA parameters GA options Output: the best control parameters of DAB |
| // Initialize population using the “initializePopulation” function with population size “options.populationSize”. 1 population = initializePopulation(options.populationSize, numVars, lb, ub) // Evaluate fitness for each individual in the population using the “evaluateFitness” function. 2 evaluateFitness(population) // Sort the population based on fitness values. 3 sortPopulationByFitness(population) // Iterate over each generation. 4 FOR generation = 1 TO options.numGenerations // Initialize a new population to store the next generation. 5 newPopulation = [] // Iterate over each individual. 6 FOR i = 1 TO options.populationSize // Select parents using the “selectParent” function from the current popu lation. 7 parent1 = selectParent(population) 8 parent2 = selectParent(population) // Generate offspring through crossover and mutation using the “crossover AndMutate” function, based on parents’ genes and within the bounds defined by “lb” and “ub”. 9 child = crossoverAndMutate(parent1, parent2, lb, ub) // Append the offspring to the new population. 10 newPopulation.append(child) 11 END FOR // Update the population. 12 population = newPopulation // Reevaluate fitness and sort the population based on the updated fitness values. 13 evaluateFitness(population) 14 sortPopulationByFitness(population) // Retrieve the best individual. 15 bestIndividual = population [1] 16 END FOR 17 RETURN bestIndividual |
4. Simulation Results and Performance Evaluation
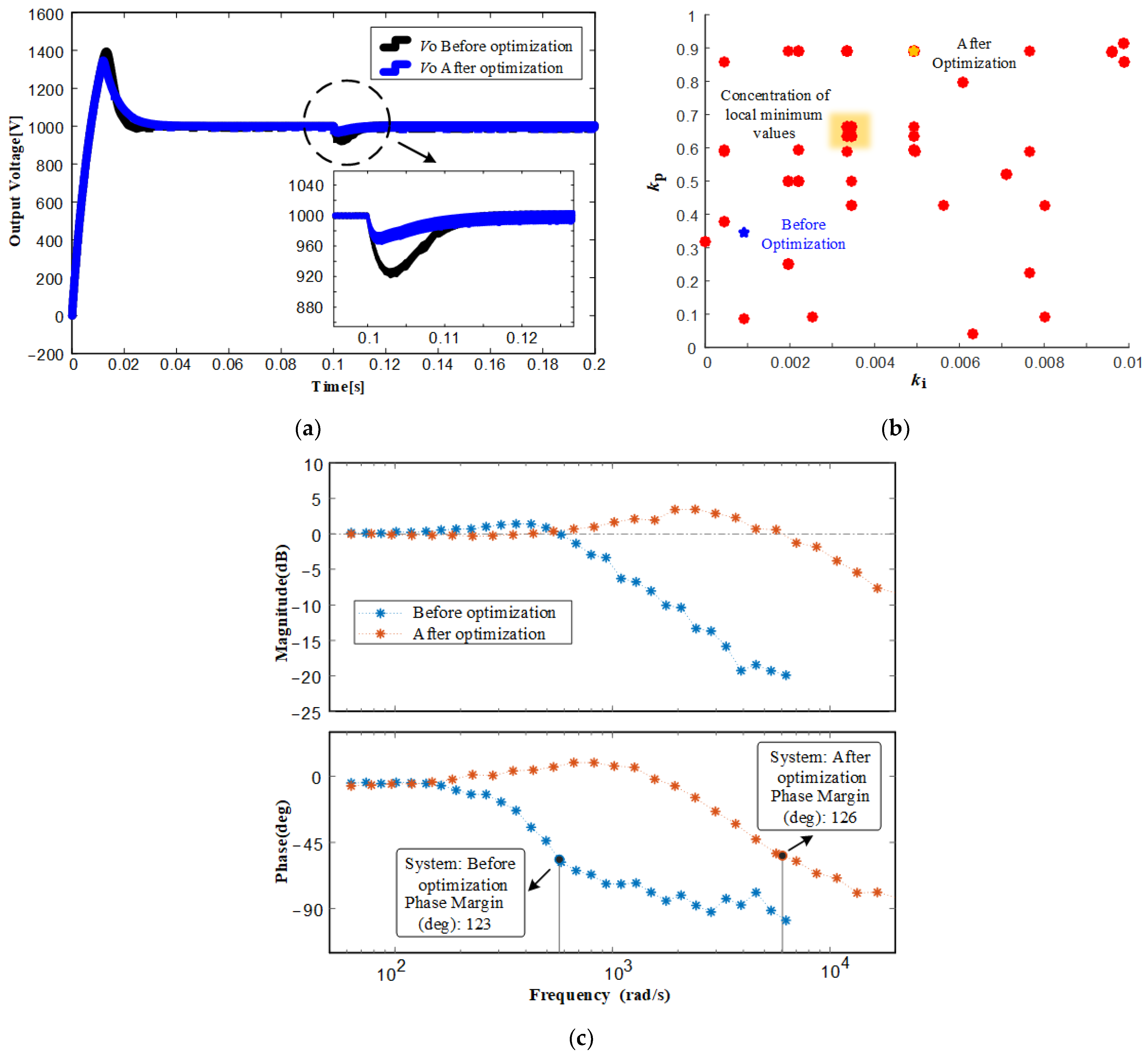
4.1. The Optimization Results of the Control Parameters for PI Control
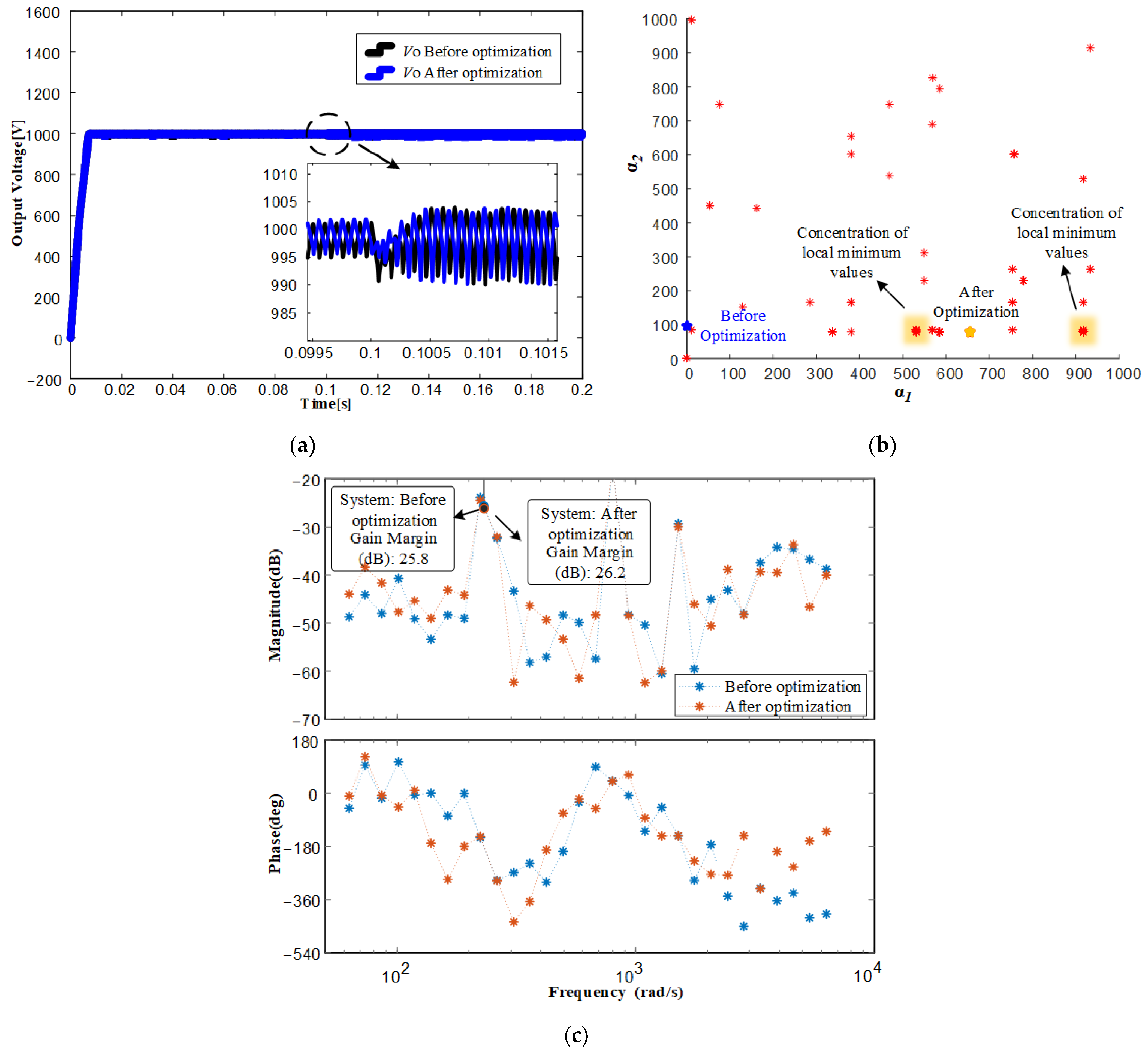
4.2. The Optimization Results of the Control Parameters for SMC Control
4.3. The Optimization Results of the Control Parameters for MPC Control
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, S.; Gautam, A.R.; Fulwani, D. Constant power loads and their effects in DC distributed power systems: A review. Renew. Sustain. Energy Rev. 2017, 72, 407–421. [Google Scholar] [CrossRef]
- Lucas-Marcillo, K.E.; Guingla, D.A.P.; Barra, W.; De Medeiros, R.L.P.; Rocha, E.M.; Vaca-Benavides, D.A.; Orellana, S.J.R.; Muentes, E.V.H. Novel robust methodology for controller design aiming to ensure DC microgrid stability under CPL power variation. IEEE Access 2019, 7, 64206–64222. [Google Scholar] [CrossRef]
- Lucas, K.E.; Pagano, D.J.; Medeiros, R.L.P. Single Phase-Shift Control of DAB Converter using Robust Parametric Approach. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; pp. 1–6. [Google Scholar]
- Jing, G.; Zhang, A.; Zhang, H. Review on DC Distribution Network Protection Technology with Distributed Power Supply. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 3583–3586. [Google Scholar]
- Shao, S.; Chen, H.; Wu, X.; Zhang, J.; Sheng, K. Circulating Current and ZVS-on of a Dual Active Bridge DC-DC Converter: A Review. IEEE Access 2019, 7, 50561–50572. [Google Scholar] [CrossRef]
- Xia, P.; Shi, H.; Wen, H.; Bu, Q.; Hu, Y.; Yang, Y. Robust LMI-LQR Control for Dual-Active-Bridge DC–DC Converters With High Parameter Uncertainties. IEEE Trans. Transp. Electrif. 2020, 6, 131–145. [Google Scholar] [CrossRef]
- Li, K.; Yang, Y.; Tan, S.-C.; Hui, R.S.-Y. Sliding-mode-based direct power control of dual-active-bridge DC-DC converters. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 188–192. [Google Scholar]
- Zhang, L.; Wang, Y.; Cheng, L.; Kang, W. A Three-Parameter Adaptive Virtual DC Motor Control Strategy for a Dual Active Bridge DC–DC Converter. Electronics 2023, 12, 1412. [Google Scholar] [CrossRef]
- Shao, S.; Jiang, M.; Ye, W.; Li, Y.; Zhang, J.; Sheng, K. Optimal Phase-Shift Control to Minimize Reactive Power for a Dual Active Bridge DC–DC Converter. IEEE Trans. Power Electron. 2019, 34, 10193–10205. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Hebala, O.M.; Aboushady, A.A.; Ahmed, K.H.; Abdelsalam, I. Generic Closed-Loop Controller for Power Regulation in Dual Active Bridge DC–DC Converter With Current Stress Minimization. IEEE Trans. Ind. Electron. 2019, 66, 4468–4478. [Google Scholar] [CrossRef]
- Jeung, Y.C.; Lee, D.C. Voltage and Current Regulations of Bidirectional Isolated Dual-Active-Bridge DC–DC Converters Based on a Double-Integral Sliding Mode Control. IEEE Trans. Power Electron. 2019, 34, 6937–6946. [Google Scholar] [CrossRef]
- An, F.; Song, W.; Yu, B.; Yang, K. Model Predictive Control With Power Self-Balancing of the Output Parallel DAB DC–DC Converters in Power Electronic Traction Transformer. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1806–1818. [Google Scholar] [CrossRef]
- Chen, L.; Shao, S.; Xiao, Q.; Tarisciotti, L.; Wheeler, P.W.; Dragičević, T. Model predictive control for dual-active-bridge converters supplying pulsed power loads in naval DC micro-grids. IEEE Trans. Power Electron. 2019, 35, 1957–1966. [Google Scholar] [CrossRef]
- Michalewicz, Z.; Schoenauer, M. Evolutionary algorithms for constrained parameter optimization problems. Evol. Comput. 1996, 4, 1–32. [Google Scholar] [CrossRef]
- Fleming, P.J.; Fonseca, C.M. Genetic Algorithms in Control Systems Engineering. IFAC Proc. Vol. 1993, 26, 605–612. [Google Scholar] [CrossRef]
- Meng, X.; Song, B. Fast Genetic Algorithms Used for PID Parameter Optimization. In Proceedings of the 2007 IEEE International Conference on Automation and Logistics, Jinan, China, 18–21 August 2007; pp. 2144–2148. [Google Scholar]
- Chahar, V.; Chhabra, J.; Kumar, D. Parameter Adaptive Harmony Search Algorithm for Unimodal and Multimodal Optimization Problems. J. Comput. Sci. 2013, 5, 144–155. [Google Scholar] [CrossRef]
- Richter, J.N.; Peak, D. Fuzzy evolutionary cellular automata. In Proceedings of the International Conference on Artificial Neural Networks in Engineering, Madrid, Spain, 28–30 August 2002; p. 185. [Google Scholar]
- Pilat, M.; White, T. Using Genetic Algorithms to Optimize ACS-TSP. In Ant Algorithms, Proceedings of the Third International Workshop, ANTS 2002, Belgium, Brussels, 12–14 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2463, pp. 282–287. [Google Scholar]
- Azab, M.; Serrano-Fontova, A. Optimal Tuning of Fractional Order Controllers for Dual Active Bridge-Based DC Microgrid Including Voltage Stability Assessment. Electronics 2021, 10, 1109. [Google Scholar] [CrossRef]
- Jeung, Y.-C.; Choi, I.-C.; Lee, D.-C. Robust voltage control of dual active bridge DC-DC converters using sliding mode control. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 629–634. [Google Scholar]
- Qin, H.; Kimball, J.W. Generalized average modeling of dual active bridge DC–DC converter. IEEE Trans. Power Electron. 2011, 27, 2078–2084. [Google Scholar]
- You, W.; Zedong, Z.; Yongdong, L. DAB-based PET in MVDC traction and shipboard applications with distribution and redundant control. J. Eng. 2019, 2019, 3209–3213. [Google Scholar] [CrossRef]
- Tan, S.-C.; Lai, Y.-M.; Tse, C.-K. Sliding Mode Control of Switching Power Converters: Techniques and Implementation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Martinez-Salamero, L.; Calvente, J.; Giral, R.; Poveda, A.; Fossas, E. Analysis of a bidirectional coupled-inductor Cuk converter operating in sliding mode. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 355–363. [Google Scholar] [CrossRef]
- Chen, L.; Gao, F.; Shen, K.; Wang, Z.; Tarisciotti, L.; Wheeler, P.; Dragičević, T. Predictive control based DC microgrid stabilization with the dual active bridge converter. IEEE Trans. Ind. Electron. 2020, 67, 8944–8956. [Google Scholar] [CrossRef]
- Nardoto, A.; Amorim, A.; Santana, N.; Bueno, E.; Encarnação, L.; Santos, W. Adaptive Model Predictive Control for DAB Converter Switching Losses Reduction. Energies 2022, 15, 6628. [Google Scholar] [CrossRef]
- Chang, W.-D. Nonlinear system identification and control using a real-coded genetic algorithm. Appl. Math. Model. 2007, 31, 541–550. [Google Scholar] [CrossRef]
- Costa, L.; Oliveira, P. An Elitist Genetic Algorithm for Multiobjective Optimization. In Metaheuristics: Computer Decision-Making. Applied Optimization; Springer: Boston, MA, USA, 2003; Volume 86. [Google Scholar]
- Zainuddin, F.; Abd Samad, M.F. A Review of Crossover Methods and Problem Representation of Genetic Algorithm in Recent Engineering Applications. Int. J. Adv. Sci. Technol. 2020, 29, 759–769. [Google Scholar]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Vi | 2500 V | Vo | 1000 V |
| P | 50 kW | fS | 10 kHz |
| o | 20 Ω | N | 2.5 |
| L | 8 × 10−4 H | Co | 5 × 10−4 F |
| Ci | 5 × 10−5 F | tmax * | 2 × 10−6 s |
| Parameter | Value |
|---|---|
| Population size | 20 |
| The maximum number of generations | 50 |
| Crossover probability | 0.8 |
| Mutation probability | 0.01 |
| The Number of elite individuals | 2 |
| PI Control parameter optimization boundary | ; |
| SMC Control parameter optimization boundary | ; |
| MPC Control parameter optimization boundary | ; |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.; Chen, W. Genetic-Algorithm-Driven Parameter Optimization of Three Representative DAB Controllers for Voltage Stability. Appl. Sci. 2023, 13, 10374. https://doi.org/10.3390/app131810374
Du W, Chen W. Genetic-Algorithm-Driven Parameter Optimization of Three Representative DAB Controllers for Voltage Stability. Applied Sciences. 2023; 13(18):10374. https://doi.org/10.3390/app131810374
Chicago/Turabian StyleDu, Wenjie, and Wenjie Chen. 2023. "Genetic-Algorithm-Driven Parameter Optimization of Three Representative DAB Controllers for Voltage Stability" Applied Sciences 13, no. 18: 10374. https://doi.org/10.3390/app131810374
APA StyleDu, W., & Chen, W. (2023). Genetic-Algorithm-Driven Parameter Optimization of Three Representative DAB Controllers for Voltage Stability. Applied Sciences, 13(18), 10374. https://doi.org/10.3390/app131810374






