Performance Analysis of the Maximum Likelihood Estimation of Signal Period Length and Its Application in Heart Rate Estimation with Reduced Respiratory Influence

Featured Application

A radar-based heart rate estimation method is presented and analyzed. It is also applicable to other signal period length estimations.

Abstract

The remote and non-contact monitoring of human respiration and heartbeat based on radars is a safe and convenient practice. However, how to accurately estimate the heart rate is still an open issue, because the heartbeat information in radar signals is affected by respiratory harmonics. In this paper, a maximum likelihood estimation was introduced to extract the heart rate from high-pass-filtered radar heartbeat waveforms where the low-frequency respiratory and heartbeat components were attenuated. The closed-form asymptotic estimation variance of the maximum likelihood estimator was derived to describe its performance in white Gaussian noise with a high signal-to-noise ratio (SNR). The proposed method was verified using two publicly available datasets and demonstrated superior performance compared to other methods. The estimation method and the asymptotic estimation variance here described are also applicable for signal period estimation in other settings with similar conditions.

1. Introduction

The remote monitoring of human vital signals based on radars, including respiratory and heartbeat rate, is cost-effective and can provide a large amount of health information [1,2,3,4]. The methods proposed in previous studies were able to provide good respiratory rate estimations, while the heartbeat rate estimation was always variable [5]. This is because radars mainly measure the micro-Doppler effect caused by the motion of the human body resulting from a variety of activities, among which, respiration is the main one when the heartbeat is relatively weak [6,7].

1.1. Background

Numerous approaches have been proposed to separate the heartbeat waveform from respiration and estimate the heart rate [8,9]. Park et al. used arctangent demodulation to process the quadrature signals and recover the body movement, reducing the influence of respiration on heartbeat [10]. Arctangent demodulation regards a human subject as a single scatter point, which is not appropriate and can lead to variable results. Edanami et al. recovered the heartbeat signal by direct high-pass filtering of the sampled radar signal, with a passband frequency of 0.85 Hz, and estimated the heart rate by fast Fourier transform (FFT) [11]. It is also a feasible solution, but the human Doppler signal collected by the radar has rich harmonics, which results in the mixing of the respiratory harmonics and the heartbeat component in the frequency domain, especially for the mm-wave radars with high carrier frequencies [12]. It invalids the common band-pass filters with a cut-off frequency of about 1 Hz [13], thus seriously hindering the extraction of the heartbeat and the estimation of the heartbeat rate [14,15].

In recent years, Zheng et al. proposed using high-order heartbeat harmonics for heart rate estimation, which are at high frequencies and almost unaffected by respiration [16]. Although the strongest fundamental frequency is completely abandoned in this way, its effective suppression of the respiratory interference is still beneficial for the heart rate estimation. A similar idea was adopted by Rong et al. for wall vital signal monitoring [17]. However, how to estimate the heartbeat rate from the numerous and weak high-order harmonics is still a problem. Finding a single second- or third-order harmonic in the spectrum is obviously not enough to make full use of the signal; so the performance is poor in the case of a low signal-to-noise ratio [18]. On the other hand, a period length estimation method of an unknown waveform signal in the time domain based on the maximum likelihood theory originally designed for pitch period estimation by Wise et al. in [19] was introduced in radar-based monitoring by Conte et al. [20]. The estimator makes no assumption about the signal waveform in the time domain, which is suitable for the heartbeat signal [21].

1.2. Contributions of This Paper

Noting that the maximum likelihood estimation is sensitive to interference, we propose to use it to recover the heart rate from high-pass filtered heartbeat high-order harmonics. In addition, the signal period estimation described in [19] is biased and irregular; so, it is impossible to evaluate the performance of maximum likelihood estimation using the Cramer–Rao bound. Therefore, an approximate periodic signal model is further proposed. The closed form asymptotic estimation variance of signal period length estimation was derived and could accurately describe the performance of the maximum likelihood estimation of an arbitrary waveform signal in white noise. The main contributions of this paper are reported below.

(1)

A heart rate estimation method is proposed.

(2)

A regularized estimation model is proposed, and the asymptotic estimation variance of the estimator was derived accordingly.

(3)

The proposed method was further validated by experimental data.

2. Method

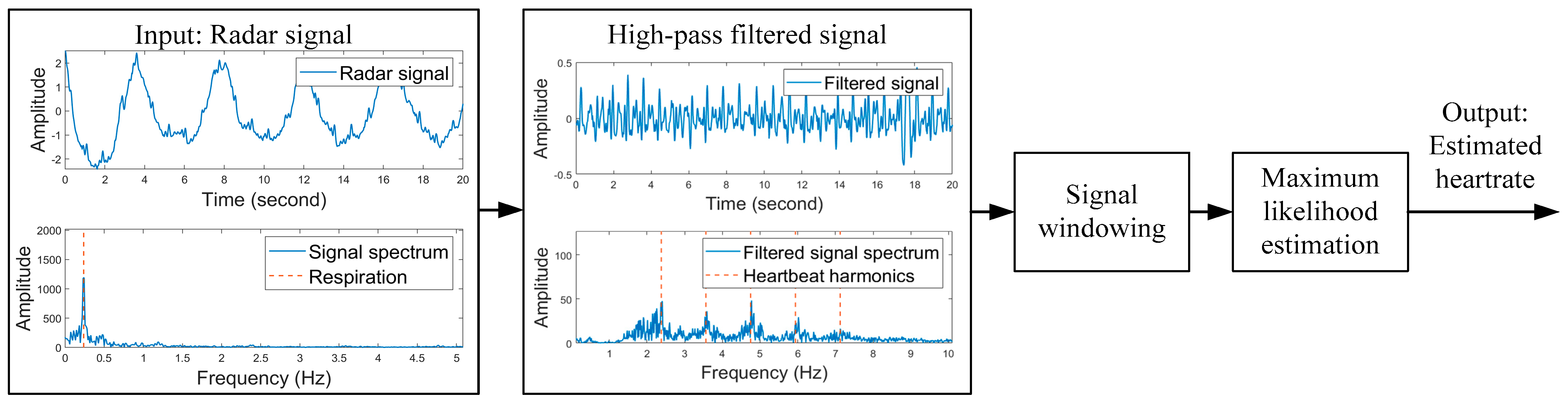
2.1. Radar-Based Heartbeat Rate Estimation

A Doppler radar mainly measures the fluctuation of the human chest; the sampled radar signal $\mathrm{r}=\left[r[0],r[1],r[2],\dots ,r[K-1]\right]$ is modeled according to

$$r[k]={\displaystyle \sum _{n=1}^{N_s}{\sigma }_n{e}^{\left(\frac{4\pi j}{\lambda }{d}_n[k]\right)}},$$

(1)

where $N_s$ is the number of scatters on the human body, ${\sigma }_n$ is the amplitude of the signal from the $n$th scatter, and $d_n[k]$ is the displacement of the $n$th scatter in the $k$th sample [22]. Though the sampled signal is a very complex mixture of respiratory and heartbeat-induced phase changes, it was demonstrated that the heartbeat information is distinguishable in the frequency domain, where multiple respiratory and heartbeat harmonics can be observed [18]. The respiratory rate is commonly between 0.1 and 0.3 Hz, and its second-, third- and higher-order harmonic spectral lines may appear at around 1 Hz. The heartbeat frequency is also about 1 Hz, and its fundamental frequency is hard to distinguish from the respiratory harmonics, while its harmonic frequencies may be more than 2 Hz and hardly affected by respiration.

Therefore, we propose to use a high-pass filter to simultaneously attenuate the respiratory components and the heartbeat fundamental frequency, while maintaining the high-order harmonics of the heartbeat. The filtered radar signal $\mathrm{x}=\left[x[0],x[1],x[2],\dots ,x[K-1]\right]$ is periodic with unknown waveform and modeled as

$$x[k]=s[k\mathrm{mod}{P}_s],$$

(2)

where $P_s$ is the period length of the signal, and $\mathrm{s}=\left[s[0],s[1],s[2],\dots ,x[P_s-1]\right]$ is the waveform in one period.

The maximum likelihood estimation of $P_s$ with the signal model (2) in white Gaussian noise is [20]

$${\hat{P}}_s=\underset{P}{\arg \max }\left\{\frac{1}{\lfloor \frac{K}{P}\rfloor -1}{\displaystyle \sum _{k=0}^{P-1}{\left|{\displaystyle \sum _{l=0}^{\lfloor \frac{K}{P}\rfloor -1}x\left[k+lP\right]}\right|}^2}\right\},$$

(3)

where ${\hat{P}}_s$ is the estimated signal period, and the heartbeat rate was output as $60 f_s/{\hat{P}}_s$ beats per minute, with $f_s$ being the sampling rate. The symbol $\lfloor \rfloor$ means rounding down and returns the maximum integer not greater than the number inside. The flowchart of the proposed heartbeat estimation method is shown in Figure 1.

2.2. Asymptotic Performance of the Maximum Likelihood Estimation

The periodic signal model (2) includes $P_s+1$ unknown parameters, where $P_s$ is unknown itself. Therefore, it constitutes an irregular estimation problem, whose maximum likelihood estimator is biased, and the classical Cramer–Rao bound does not exist [21]. To accurately describe the performance of the estimator, we established a regularized model similar to that of Equation (2) with a fixed number of unknown parameters:

$$x[k]=\tilde{s}[k\mathrm{mod}{P}_s]$$

(4)

where $P_s$ is the unknown signal period, and the array $\tilde{\mathrm{s}}=\left[\tilde{s}[0],\tilde{s}[1],\dots ,\tilde{s}[{\tilde{P}}_s-1],0,..0\right]$ including $P_s$ samples is the waveform in one period, with ${\tilde{P}}_s<P_s$ being known. Although $P_s$ is unknown, we assumed that the number of non-zero waveform samples within each period was known and the rest of the signal was 0. The number of observed periods $\tilde{N}$ was also considered a known constant integer, while it was ignored that an incomplete period might exist, and the total number of samples was $K=\tilde{N}{P}_s$. There are ${\tilde{P}}_s+1$ unknown parameters in total in Equation (4), and the corresponding Cramer–Rao bound of Equation (4) in white Gaussian noise can be derived.

Consider only real signals and the Fisher matrix $\mathrm{I}$

$$\mathrm{I}=\left[\begin{array}{llll}{\mathrm{I}}_{0,0}& {\mathrm{I}}_{0,1}& \cdots & {\mathrm{I}}_{0,{\tilde{P}}_s}\\ {\mathrm{I}}_{1,0}& {\mathrm{I}}_{1,1}& 0& 0\\ ⋮& 0& \ddots & 0\\ {\mathrm{I}}_{{\tilde{P}}_s,0}& 0& 0& {\mathrm{I}}_{{\tilde{P}}_s,{\tilde{P}}_s}\end{array}\right],$$

(5)

where

$$\begin{array}{ll}{\mathrm{I}}_{0,0}& =\frac{1}{{\sigma }^2}{\left[\frac{\partial \left[\tilde{s}(0),\tilde{s}(\Delta )\dots \tilde{s}\left(\left(\tilde{N}{P}_s-1\right)\Delta \right)\right]}{\partial \left(\Delta P_s\right)}\right]}^T\left[\frac{\partial \left[\tilde{s}(0),\tilde{s}(\Delta )\dots \tilde{s}\left(\left(\tilde{N}{P}_s-1\right)\Delta \right)\right]}{\partial \left(\Delta P_s\right)}\right]\\ & =\frac{1}{{\sigma }^2}{{\displaystyle \sum _{p=0}^{P_s-1}{\displaystyle \sum _{l=1}^{\tilde{N}-1}\left(\frac{\partial \tilde{s}\left(\left(l{P}_s+p\right)\Delta \right)}{\partial \left(\Delta P_s\right)}\right)}}}^2\\ & =\frac{1}{{\sigma }^2}{{\displaystyle \sum _{p=0}^{{\tilde{P}}_s-1}{\displaystyle \sum _{l=1}^{\tilde{N}-1}\left({l\frac{\partial \tilde{s}(t)}{\partial t}|}_{t=p\Delta }\right)}}}^2\\ & =\frac{1}{{\sigma }^2}\left[{\displaystyle \sum _{l=1}^{\tilde{N}-1}{l}^2}\right]\left[{{\displaystyle \sum _{p=0}^{{\tilde{P}}_s-1}\left({\frac{\partial \tilde{s}(t)}{\partial t}|}_{t=p\Delta }\right)}}^2\right],\end{array}$$

(6)

where $\Delta =1/f_s$ is the sampling interval. The derivative is for $\Delta P_s$ rather than for $P_s$ in order to obtain the CRB of the period length in analog time; $s(t)$ is the analog signal waveform of the periodic signal which satisfies the equations $\tilde{s}(p\Delta )=\tilde{s}[p]$ and $\tilde{s}\left(p\Delta \right)=\tilde{s}\left(p\Delta +P_s\Delta \right)$.

The 2nd of the $\tilde{P}$ elements in the first row and the 2nd of the $\tilde{P}$ elements in the first column of the matrix $\mathrm{I}$ are

$$\begin{array}{ll}{\mathrm{I}}_{0,(p+1)}& ={\mathrm{I}}_{(p+1),0}\\ & =\frac{1}{{\sigma }^2}{\left[\frac{\partial \left[\tilde{s}(0),\tilde{s}(\Delta )\dots ,\tilde{s}\left(\left(\tilde{N}{P}_s-1\right)\Delta \right)\right]}{\partial \left(\Delta P_s\right)}\right]}^T\left[\frac{\partial \left[\tilde{s}(0),\tilde{s}(\Delta )\dots ,\tilde{s}\left(\left(\tilde{N}{P}_s-1\right)\Delta \right)\right]}{\partial \left(\tilde{s}\left(p\Delta \right)\right)}\right]\\ & =\frac{1}{{\sigma }^2}{\displaystyle \sum _{l=1}^{\tilde{N}-1}\left(l{\frac{\partial \tilde{s}(t)}{\partial t}|}_{t=p\Delta }\right)}\\ & =\frac{1}{{\sigma }^2}\left({\displaystyle \sum _{l=1}^{\tilde{N}-1}l}\right)\left({\frac{\partial \tilde{s}(t)}{\partial t}|}_{t=p\Delta }\right),\end{array}$$

(7)

where $p=0,1\dots {\tilde{P}}_s-1$.

The elements on the diagonal of the matrix other than ${\mathrm{I}}_{0,0}$ are

$$\begin{array}{ll}{\mathrm{I}}_{(p+1),(p+1)}& =\frac{1}{{\sigma }^2}{\left[\frac{\partial \left[\tilde{s}(0),\tilde{s}(\Delta )\dots ,\tilde{s}\left(\left(\tilde{N}{P}_s-1\right)\Delta \right)\right]}{\partial \left(\tilde{s}\left(k\Delta \right)\right)}\right]}^T\left[\frac{\partial \left[\tilde{s}(0),\tilde{s}(\Delta )\dots ,\tilde{s}\left(\left(\tilde{N}{P}_s-1\right)\Delta \right)\right]}{\partial \left(\tilde{s}\left(k\Delta \right)\right)}\right]\\ & =\frac{1}{{\sigma }^2}\tilde{N}.\end{array}$$

(8)

Focus only on the estimated variance of the period length ${\left[{\mathrm{I}}^{-1}\right]}_{0,0}$, which is the upper left corner element of the inverse matrix of $\mathrm{I}$

$$\begin{array}{ll}{\left[{\mathrm{I}}^{-1}\right]}_{0,0}& ={\sigma }^2{\left\{{\mathrm{I}}_{0,0}-\frac{1}{\tilde{N}}\left[{\mathrm{I}}_{0,1},{\mathrm{I}}_{0,2},\dots {\mathrm{I}}_{0,{\tilde{P}}_s}\right]\cdot {\left[{\mathrm{I}}_{1,0},{\mathrm{I}}_{2,0},\dots {\mathrm{I}}_{{\tilde{P}}_s,0}\right]}^T\right\}}^{-1}\\ & ={\sigma }^2{\left\{{\mathrm{I}}_{0,0}-\frac{1}{\tilde{N}}{\displaystyle \sum _{p=1}^{{\tilde{P}}_s}{\mathrm{I}}_{0,p}^2}\right\}}^{-1}\\ & ={\sigma }^2{\left\{\left[{\displaystyle \sum _{l=1}^{\tilde{N}-1}{l}^2}-\frac{1}{\tilde{N}}{\left({\displaystyle \sum _{l=1}^{\tilde{N}-1}l}\right)}^2\right]\left[{\displaystyle \sum _{p=0}^{{\tilde{P}}_s-1}{\left(\frac{\partial \tilde{s}(t)}{\partial t}|{}_{t=p\Delta }\right)}^2}\right]\right\}}^{-1}\\ & ={\sigma }^2\frac{12}{{\tilde{N}}^3-\tilde{N}}{\left\{{\displaystyle \sum _{p=0}^{{\tilde{P}}_s-1}{\left(\frac{\partial \tilde{s}(t)}{\partial t}|{}_{t=p\Delta }\right)}^2}\right\}}^{-1},\end{array}$$

(9)

which can be reorganized with

$${\sigma }^2{\left\{{\displaystyle \sum _{p=0}^{{\tilde{P}}_s-1}{\left(\frac{\partial \tilde{s}(t)}{\partial t}|{}_{t=p\Delta }\right)}^2}\right\}}^{-1}={\sigma }^2\left(\frac{N_0/2}{\epsilon {\overline{F}}^2}\right).$$

(10)

where $N_0$ is the noise power spectrum density, ε is the energy of $\tilde{\mathrm{s}}$, and ${\overline{F}}^2$ is a measurement of the bandwidth of $\tilde{\mathrm{s}}$, defined as

$${\overline{F}}^2=\frac{{\displaystyle {\int }_{-\infty }^{\infty }{(2\pi f)}^2{\left|\tilde{S}(f)\right|}^{2}df}}{{\displaystyle {\int }_{-\infty }^{\infty }{\left|\tilde{S}(f)\right|}^{2}df}},$$

(11)

where $\tilde{S}(f)$ is the Fourier transform of $\tilde{\mathrm{s}}$ [23]. Equation (10) is exactly the Cramer–Rao bound of the signal delay estimation with the known waveform $\tilde{\mathrm{s}}$ [24].

The estimated variance of the maximum likelihood estimator of the model (4) should be asymptotic to the Cramer–Rao bound in Equation (9) [25], and the asymptotic variance of the estimator in Equation (2) can be approximated as

$${\sigma }^2\frac{12}{N^3-N}{\left\{{\displaystyle \sum _{p=0}^{{\tilde{P}}_s-1}{\left(\frac{\partial s(t)}{\partial t}|{}_{t=p\Delta }\right)}^2}\right\}}^{-1}={\sigma }^2\left(\frac{12}{N^3-N}\right)\frac{N_0/2}{\epsilon \frac{{\displaystyle {\int }_{-\infty }^{\infty }{(2\pi f)}^2{\left|S(f)\right|}^{2}df}}{{\displaystyle {\int }_{-\infty }^{\infty }{\left|S(f)\right|}^{2}df}}}$$

(12)

where $N=\lfloor K/P_s\rfloor$, and $S(f)$ is the Fourier transform of $\mathrm{s}$. This can be easily extended to the case of complex signal.

3. Experiments

3.1. Simulation

A simulation was used to analyze the performance of the maximum likelihood estimator and verify the derived asymptotic variance in Equation (12). The simulation used a signal with a bandwidth of 50 Hz and a period length of 1 s. In total, 10,000 Monte Carlo simulations with Gaussian white noise were performed to obtain the mean square errors (MSE) under different SNRs and observation lengths of 2 s, 4 s, and 6 s, where $N=2$, $4$, and $6$.

The results are presented in Figure 2, together with the asymptotic estimation variance, which fitted well the simulated MSEs at high SNR. This demonstrated that the proposed asymptotic estimation variance could be used to describe the performance of the maximum likelihood estimator with adequate accuracy. In addition, the asymptotic variance of the signals with longer length decreased significantly. Under the same SNR, the variance of the 4 s signal was 1/10 of that of the 2 s signal, and the variance of the 6 s signal was only 1/35 of that of the 2 s signal.

3.2. Verification with Measured Data

Two publicly available datasets [11,26] were used for performance evaluation and comparison. One was constructed by Edanami et al. from nine subject using 10 GHz and 24 GHz Doppler radars with a sampling rate of 1000 Hz. The other was compiled by Schellenberger et al. from 30 subjects using a 24 GHz Doppler radar with a sampling rate of 2000 Hz, and only data acquired while the subjects were resting were used for the heart rate estimation. Both datasets provide synchronized reference electrocardiogram signals.

The radar data from the two datasets were first down-sampled to 20 Hz to speed up the processing. The proposed method adopts a high-pass filter with a passband frequency of 1.8 Hz, which filters out the fundamental frequency of the heartbeat and other respiratory components. The signals from each subject in the two datasets were recorded over about 600 s, and the filtered data were compartmentalized into 60 10 s windows. The heartbeat rate ranges between 45 to 90 beats per minute (0.75 to 1.5 Hz). The estimation root-mean-square error (RMSE) is defined as

$$\mathrm{RMSE}=\frac{1}{N_w}\sqrt{{\displaystyle \sum _n^{N_w}{\left({\hat{f}}_{HR}\left(n\right)-f_{REF}(n)\right)}^2}}.$$

(13)

where $N_w$ is the number of windows in each dataset, and ${\hat{f}}_{HR}\left(n\right)$ and $f_{REF}(n)$ are the estimated heartbeat rate and reference heart rate in each window, respectively. The results for the two datasets are presented in

Table 1. Estimation RMSE for the two measured datasets. Methods used in previous studies were implemented for comparison, and the proposed method yielded the minimum error.

	Dataset 1 [11], 10 Ghz	Dataset 1 [11], 24 Ghz	Dataset 2 [26], 24 Ghz
Proposed	3.88 1	4.47	6.30
Park [10]	13.47	16.48	8.18
Edanami [11]	13.22	15.29	9.46
Rong [18]	8.35	8.94	12.70
Conte [20]	10.64	13.00	8.40
He [27]	9.97	7.85	9.12
Zhu [28]	6.27	8.74	8.78

¹ Measured in beats per minute.

, where the estimation RMSEs of six methods used in previous studies are listed for comparison.

4. Discussion

In Table 1, the proposed method, lacking the respiratory components, yielded the smallest RMSE in all scenarios. Differently from the other six methods, it uses all high-order heartbeat harmonics that are not affected by respiration; so, its performance is better and more stable.

The previously described arctangent demodulation [10] yielded larger RMSEs, especially for dataset 1 where the background clutter and non-orthogonal channels degraded the demodulation performance. Although it performed better for dataset 2, its performance was still not as good as that of the proposed method.

The performances of the two spectral analyses reported in [11,18] were also inferior and unstable. The method based on second-order harmonic, described in [18], performed better for dataset 1, while the method based on fundamental frequency, employed in [11], performed better for dataset 2. This is because the dataset 1 has a higher SNR and allows the extraction of second-order harmonic, while the strong noise in dataset 2 masks the harmonics and renders the respiratory interference less important. Compared with maximum likelihood, these methods based on a single spectral line are not suitable for heart rate estimation, because the heartbeat information scattered in many harmonics is not fully utilized. Instead of digital filtering, [27,28] extracted the heartbeat signal using the wavelet transform and an empirical model decomposition, respectively. A narrow band signal with the most significant heartbeat signal was selected for heart rate estimation, which is similar to band-pass filtering. These methods not only eliminated the low-frequency respiratory component, but also attenuated the high-frequency noise; so, their results may be slightly better than those obtained in [11] but not essentially different.

On the other hand, also the method described in [20] that carried out a maximum likelihood estimation directly on raw radar signals had an inferior performance, especially for dataset 1. The maximum likelihood estimation derived from the signal model (2) did not consider any interferences and was subjected to them. The unfiltered respiratory harmonics mixed with the heartbeat, resulting in an error that was particularly significant for dataset 1. Different from [20], the proposed method ignores the fundamental frequency of heartbeat to ensure the purity of the signal used for maximum likelihood estimation, thus obtaining better results.

5. Conclusions

A maximum likelihood estimation-based method is proposed to extract the heart rate from high-pass-filtered radar waveforms where the low-frequency respiratory and heartbeat fundamental frequencies are attenuated. The closed-form asymptotic estimation variance of the maximum likelihood estimator was derived according to a regularized signal model to describe the estimator’s performance. The proposed method was verified using two publicly available datasets and yielded the smallest RMSE when compared with state-of-art methods. The estimation method and the asymptotic estimation variance are also applicable for signal period estimation in other settings.