The Accuracy Assessment of Lithospheric Density Models
Abstract
:1. Introduction
2. Numerical Model
2.1. Geoid
2.2. Sub-Lithospheric Mantle Geoid
2.2.1. Bouguer Disturbing Potential
2.2.2. Crust-Stripped Disturbing Potential
2.2.3. Mantle Disturbing Potential
2.2.4. Lithosphere-Stripped Disturbing Potential
2.2.5. Sub-Lithospheric Mantle Disturbing Potential
3. Model Uncertainties
3.1. Errors Due to Lithospheric Thickness Uncertainties
3.2. Errors Due to Lithospheric Mantle Density Uncertainties
4. Results
5. Error Analysis
6. Summary and Concluding Remarks
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Forsberg, R.; Tscherning, C.C. Topographic effects in gravity field modelling for BVP. In Geodetic Boundary Value Problems in View of the One Centimeter Geoid; Springer: Berlin/Heidelberg, Germany, 1997; pp. 239–272. [Google Scholar]
- Hwang, C.; Wang, C.-G.; Hsiao, Y.-S. Terrain correction computation using Gaussian quadrature. Comput. Geosci. 2003, 29, 1259–1268. [Google Scholar] [CrossRef]
- Agren, J. Regional Geoid Determination Methods for the Era of Satellite Gravimetry: Numerical Investigations Using Synthetic Earth Gravity Models. Ph.D. Thesis, Royal Institute of Technology (KTH), Department of Infrastructure, Stockholm, Sweden, 2004. [Google Scholar]
- Hwang, C.; Hsiao, Y.-S.; Shih, H.-C.; Yang, M.; Chen, K.-H.; Forsberg, R.; Olesen, A.V. Geodetic and geophysical results from a Taiwan airborne gravity survey: Data reduction and accuracy assessment. J. Geophys. Res. Solid Earth 2007, 112, B04407. [Google Scholar] [CrossRef]
- Makhloof, A.A.E. The Use of Topographic-Isostatic Mass Information in Geodetic Applications. Ph.D. Thesis, Universitäts-und Landesbibliothek Bonn, Bonn, Germany, 2007. [Google Scholar]
- Makhloof, A.A.; Ilk, K.-H. Effects of topographic–isostatic masses on gravitational functionals at the Earth’s surface and at airborne and satellite altitudes. J. Geod. 2008, 82, 93–111. [Google Scholar] [CrossRef]
- Tsoulis, D.; Novák, P.; Kadlec, M. Evaluation of precise terrain effects using high-resolution digital elevation models. J. Geophys. Res. Atmos. 2009, 114, B02404. [Google Scholar] [CrossRef]
- Flury, J.; Rummel, R. On the geoid–quasigeoid separation in mountain areas. J. Geod. 2009, 83, 829–847. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Sideris, M.G. Topographic Reductions in Gravity and Geoid Modeling. In Geoid Determination; Springer: Berlin/Heidelberg, Germany, 2013; pp. 337–400. [Google Scholar] [CrossRef]
- Jiang, T.; Dang, Y.; Zhang, C. Gravimetric geoid modeling from the combination of satellite gravity model, terrestrial and airborne gravity data: A case study in the mountainous area, Colorado. Earth Planets Space 2020, 72, 189. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W.; Rathnayake, S.; Pitoňák, M. The effect of anomalous global lateral topographic density on the geoid-to-quasigeoid separation. J. Geod. 2021, 95, 12. [Google Scholar] [CrossRef]
- Tenzer, R.; Hirt, C.; Novák, P.; Pitoňák, M.; Šprlák, M. Contribution of mass density heterogeneities to the quasigeoid-to-geoid separation. J. Geod. 2016, 90, 65–80. [Google Scholar] [CrossRef]
- Artemieva, I.M.; Mooney, W.D. Thermal thickness and evolution of Precambrian lithosphere: A global study. J. Geophys. Res. Atmos. 2001, 106, 16387–16414. [Google Scholar] [CrossRef]
- Kaban, M.K.; Schwintzer, P.; Artemieva, I.M.; Mooney, W.D. Density of the continental roots: Compositional and thermal contributions. Earth Planet. Sci. Lett. 2003, 209, 53–69. [Google Scholar] [CrossRef]
- Artemieva, I.M. Global 1 × 1 thermal model TC1 for the continental lithosphere: Implications for lithosphere secular evolution. Tectonophysics 2006, 416, 245–277. [Google Scholar] [CrossRef]
- Tenzer, R.; Vajda, P. Global map of the gravity anomaly corrected for complete effects of the topography, and of density contrasts of global ocean, ice, and sediments. Contrib. Geophys. Geod. 2008, 38, 357–370. [Google Scholar]
- Mooney, W.D.; Kaban, M.K. The North American upper mantle: Density, composition, and evolution. J. Geophys. Res. Atmos. 2010, 115, B12424. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W. Mantle and sub-lithosphere mantle gravity maps from the LITHO1.0 global lithospheric model. Earth-Sci. Rev. 2019, 194, 38–56. [Google Scholar] [CrossRef]
- Wieczorek, M.A. Gravity and topography of the terrestrial planets. Treatise Geophys. 2007, 10, 165–206. [Google Scholar]
- Uieda, L.; Barbosa, V.C.F.; Braitenberg, C.; Marotta, A.M.; Barzaghi, R.; Zhang, Y.; Chen, C. Tesseroids: Forward-modeling gravitational fields in spherical coordinates. Geophysics 2016, 81, F41–F48. [Google Scholar] [CrossRef]
- Yang, M.; Hirt, C.; Pail, R. TGF: A New MATLAB-based Software for Terrain-related Gravity Field Calculations. Remote Sens. 2020, 12, 1063. [Google Scholar] [CrossRef]
- Nagy, D. The Gravitational Attraction of a Right Rectangular Prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
- Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. J. Geod. 2000, 74, 552–560. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. The use of height data in gravity field approximation by collocation. J. Geophys. Res. Solid Earth 1981, 86, 7843–7854. [Google Scholar] [CrossRef]
- Götze, H.; Lahmeyer, B. Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 1988, 53, 1096–1108. [Google Scholar] [CrossRef]
- Denker, H. Regional gravity field modeling: Theory and Practical Results. In Sciences of Geodesy-II; Springer: Berlin/Heidelberg, Germany, 2003; pp. 185–291. [Google Scholar]
- Tsoulis, D. Terrain modeling in forward gravimetric problems: A case study on local terrain effects. J. Appl. Geophys. 2003, 54, 145–160. [Google Scholar] [CrossRef]
- Novák, P.; Grafarend, E.W. The effect of topographical and atmospheric masses on spaceborne gravimetric and gradiometric data. Stud. Geophys. Geod. 2006, 50, 549–582. [Google Scholar] [CrossRef]
- Asgharzadeh, M.F.; von Frese, R.R.B.; Kim, H.R.; Leftwich, T.E.; Kim, J.W.; Paulatto, M.; Minshull, T.A.; Baptie, B.; Dean, S.; Hammond, J.O.S.; et al. Spherical prism gravity effects by Gauss-Legendre quadrature integration. Geophys. J. Int. 2007, 169, 1–11. [Google Scholar] [CrossRef]
- Heck, B.; Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. J. Geod. 2006, 81, 121–136. [Google Scholar] [CrossRef]
- D’urso, M.G. On the evaluation of the gravity effects of polyhedral bodies and a consistent treatment of related singularities. J. Geod. 2012, 87, 239–252. [Google Scholar] [CrossRef]
- Grombein, T.; Seitz, K.; Heck, B. Optimized formulas for the gravitational field of a tesseroid. J. Geod. 2013, 87, 645–660. [Google Scholar] [CrossRef]
- Parker, R.L. The Rapid Calculation of Potential Anomalies. Geophys. J. Int. 1972, 31, 447–455. [Google Scholar] [CrossRef]
- Colombo, O.L. Numerical Methods for Harmonic Analysis on the Sphere; OSU Report No. 310; Department of Geodetic Science and Surveying, Ohio State University: Columbus, OH, USA, 1981. [Google Scholar]
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Report 355; Department of Geodetic Science and Surveying, Ohio State University: Columbus, OH, USA, 1984. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Phillips, R.J. Potential anomalies on a sphere: Applications to the thickness of the lunar crust. J. Geophys. Res. Planets 1998, 103, 1715–1724. [Google Scholar] [CrossRef]
- Chambat, F.; Valette, B. Earth gravity up to second order in topography and density. Phys. Earth Planet. Inter. 2005, 151, 89–106. [Google Scholar] [CrossRef]
- Eshagh, M. Comparison of two approaches for considering laterally varying density in topographic effect on satellite gravity gradiometric data. Acta Geophys. 2009, 58, 661–686. [Google Scholar] [CrossRef]
- Tenzer, R.; Novák, P.; Vajda, P. Uniform spectral representation of the Earth’s inner density structures and their gravitational field. Contrib. Geophys. Geod. 2011, 41, 191–209. [Google Scholar] [CrossRef]
- Balmino, G.; Vales, N.; Bonvalot, S.; Briais, A. Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies. J. Geod. 2011, 86, 499–520. [Google Scholar] [CrossRef]
- Hirt, C.; Kuhn, M. Evaluation of high-degree series expansions of the topographic potential to higher-order powers. J. Geophys. Res. Solid Earth 2012, 117, B12407. [Google Scholar] [CrossRef]
- Novák, P.; Tenzer, R.; Eshagh, M.; Bagherbandi, M. Evaluation of gravitational gradients generated by Earth’s crustal structures. Comput. Geosci. 2013, 51, 22–33. [Google Scholar] [CrossRef]
- Haagmans, R. A synthetic Earth for use in geodesy. J. Geod. 2000, 74, 503–511. [Google Scholar] [CrossRef]
- Kuhn, M.; Featherstone, W.E. Construction of a synthetic Earth gravity model by forward gravity modelling. In A Window on the Future of Geodesy, Proceedings of the International Association of Geodesy IAG General Assembly, Sapporo, Japan, 30 June–11 July 2003; Springer: Berlin/Heidelberg, Germany, 2005; pp. 350–355. [Google Scholar]
- Baran, I.; Kuhn, M.; Claessens, S.J.; Featherstone, W.E.; Holmes, S.A.; Vaníček, P. A synthetic Earth Gravity Model Designed Specifically for Testing Regional Gravimetric Geoid Determination Algorithms. J. Geod. 2006, 80, 1–16. [Google Scholar] [CrossRef]
- Kitterød, N.O.; Leblois, É. Modelling Bedrock Topography. In Earth Surface Dynamics Discussions; Copernicus GmbH: Göttingen, Germany, 2019; pp. 1–36. [Google Scholar]
- Tenzer, R.; Bagherbandi, M.; Gladkikh, V. Signature of the upper mantle density structure in the refined gravity data. Comput. Geosci. 2012, 16, 975–986. [Google Scholar] [CrossRef]
- Tenzer, R.; Hamayun, K.; Vajda, P. Global maps of the CRUST2.0 crustal components stripped gravity disturbances. J. Geophys. Res. 2009, 114, B05408. [Google Scholar] [CrossRef]
- Tenzer, R.; Vajda, P. Global maps of the step-wise topography corrected and crustal components stripped geoids using the CRUST 2.0 model. Contrib. Geophys. Geod. 2009, 39, 1–17. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W.; Jin, S. Effect of Upper Mantle Density Structure on Moho Geometry. Pure Appl. Geophys. 2015, 172, 1563–1583. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W.; Baranov, A.; Bagherbandi, M. Gravity Maps of Antarctic Lithospheric Structure from Remote-Sensing and Seismic Data. Pure Appl. Geophys. 2018, 175, 2181–2203. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Majid, A. The uncertainty of CRUST1.0: Moho depth and density contrast models. J. Appl. Geod. 2021, 15, 143–152. [Google Scholar] [CrossRef]
- Steinberger, B. Effects of latent heat release at phase boundaries on flow in the Earth’s mantle, phase boundary topography and dynamic topography at the Earth’s surface. Phys. Earth Planet. Int. 2007, 164, 2–20. [Google Scholar] [CrossRef]
- Müller, R.D.; Flament, N.; Matthews, K.J.; Williams, S.E.; Gurnis, M. Formation of Australian continental margin highlands driven by plate–mantle interaction. Earth Planet. Sci. Lett. 2016, 441, 60–70. [Google Scholar] [CrossRef]
- Rubey, M.; Brune, S.; Heine, C.; Davies, D.R.; Williams, S.E.; Müller, R.D. Global patterns in Earth’s dynamic topography since the Jurassic: The role of subducted slabs. Solid Earth 2017, 8, 899–919. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W.; Tsoulis, D.; Bagherbandi, M.; Sjöberg, L.E.; Novák, P.; Jin, S. Analysis of the Refined CRUST1.0 Crustal Model and its Gravity Field. Surv. Geophys. 2015, 36, 139–165. [Google Scholar] [CrossRef]
- Dziewonski, A.; Hales, A.; Lapwood, E. Parametrically simple earth models consistent with geophysical data. Phys. Earth Planet. Inter. 1975, 10, 12–48. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Kennett, B.L.N.; Engdahl, E.R. Traveltimes for global earthquake location and phase identification. Geophys. J. Int. 1991, 105, 429–465. [Google Scholar] [CrossRef]
- Kennett, B.L.N.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
- Montagner, J.-P.; Kennett, B.L.N. How to reconcile body-wave and normal-mode reference earth models. Geophys. J. Int. 1996, 125, 229–248. [Google Scholar] [CrossRef]
- Van der Lee, S.; Nolet, G. Upper mantle S velocity structure of North America. J. Geophys. Res. Solid Earth 1997, 102, 22815–22838. [Google Scholar] [CrossRef]
- Kustowski, B.; Ekström, G.; Dziewoński, A.M. Anisotropic shear-wave velocity structure of the Earth’s mantle: A global model. J. Geophys. Res. Solid Earth 2008, 113, B06306. [Google Scholar] [CrossRef]
- Simmons, N.A.; Forte, A.M.; Boschi, L.; Grand, S.P. GyPSuM: A joint tomographic model of mantle density and seismic wave speeds. J. Geophys. Res. Solid Earth 2010, 115, B123. [Google Scholar] [CrossRef]
- Trabant, C.; Hutko, A.R.; Bahavar, M.; Karstens, R.; Ahern, T.; Aster, R. Data Products at the IRIS DMC: Stepping Stones for Research and Other Applications. Seism. Res. Lett. 2012, 83, 846–854. [Google Scholar] [CrossRef]
- Nataf, H.-C.; Ricard, Y. 3SMAC: An a priori tomographic model of the upper mantle based on geophysical modeling. Phys. Earth Planet. Inter. 1996, 95, 101–122. [Google Scholar] [CrossRef]
- Mooney, W.D.; Laske, G.; Masters, T.G. CRUST 5.1: A global crustal model at 5×. J. Geophys. Res. Solid Earth 1998, 103, 727–747. [Google Scholar] [CrossRef]
- Bassin, C. The current limits of resolution for surface wave tomography in North America. Eos Trans. AGU 2000, 81, F897. [Google Scholar]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0-A 1-degree global model of Earth’s crust. In Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2013; Volume 15, p. 2658. [Google Scholar]
- Pasyanos, M.E.; Masters, T.G.; Laske, G.; Ma, Z. LITHO1.0: An updated crust and lithospheric model of the Earth. J. Geophys. Res. Solid Earth 2014, 119, 2153–2173. [Google Scholar] [CrossRef]
- Simmons, N.A.; Myers, S.C.; Johannesson, G.; Matzel, E. LLNL-G3Dv3: Global P wave tomography model for improved regional and teleseismic travel time prediction. J. Geophys. Res. Solid Earth 2012, 117, B10302. [Google Scholar] [CrossRef]
- Hirt, C.; Rexer, M. Earth2014: 1 arc-min shape, topography, bedrock and ice-sheet models—Available as gridded data and degree-10,800 spherical harmonics. Int. J. Appl. Earth. Obs. Geoinf. 2015, 39, 103–112. [Google Scholar] [CrossRef]
- Chen, W.; Tenzer, R. Harmonic coefficients of the Earth’s spectral crustal model 180–ESCM180. Earth Sci. Inform. 2015, 8, 147–159. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical Geodesy; WH Freeman: New York, NY, USA, 1967. [Google Scholar]
- Pizzetti, P. Sopra il calcolo teorico delle deviazioni del geoide dall’ ellissoide. Atti. R. Accad. Sci. Torino 1911, 46, 331–350. [Google Scholar]
- Somigliana, C. Teoria generale del campo gravitazionale dell’ellissoide di rotazione. Mem. Soc. Astron. Ital. 1929, 4, 425. [Google Scholar]
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
- Wieczorek, M. Gravity and Topography of the Terrestrial Planets. Treatise Geophys. 2015, 10, 153–193. [Google Scholar] [CrossRef]
- Tenzer, R.; Foroughi, I.; Sjöberg, L.E.; Bagherbandi, M.; Hirt, C.; Pitoňák, M. Definition of Physical Height Systems for Telluric Planets and Moons. Surv. Geophys. 2018, 39, 313–335. [Google Scholar] [CrossRef]
- Tenzer, R.; Vajda, P.; Hamayun, K. Global atmospheric corrections to the gravity field quantities. Contr. Geophys. Geod. 2009, 39, 221–236. [Google Scholar] [CrossRef]
- Tenzer, R.; Chen, W. Comparison of gravimetric, isostatic, and spectral decomposition methods for a possible enhancement of the mantle signature in the long-wavelength geoidal geometry. Remote Sens. 2023. accepted. [Google Scholar]
- Tenzer, R.; Novák, P.; Vajda, P.; Gladkikh, V.; Hamayun, K. Spectral harmonic analysis and synthesis of Earth’s crust gravity field. Comput. Geosci. 2011, 16, 193–207. [Google Scholar] [CrossRef]
- Tenzer, R.; Gladkikh, V.; Novák, P.; Vajda, P. Spatial and Spectral Analysis of Refined Gravity Data for Modelling the Crust–Mantle Interface and Mantle-Lithosphere Structure. Surv. Geophys. 2012, 33, 817–839. [Google Scholar] [CrossRef]
- Gladkikh, V.; Tenzer, R. A Mathematical Model of the Global Ocean Saltwater Density Distribution. Pure Appl. Geophys. 2011, 169, 249–257. [Google Scholar] [CrossRef]
- Foroughi, I.; Tenzer, R. Comparison of different methods for estimating the geoid-to-quasigeoid separation. Geophys. J. Int. 2017, 210, 1001–1020. [Google Scholar] [CrossRef]
- Förste, C.; Bruinsma, S.; Flechtner, F.; Abrykosov, O.; Dahle, C.; Marty, J.; König, R. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. In AGU Fall Meeting Abstracts; Tapley, B.D., Bettadpur, S., Watkins, M., Eds.; GFZ Data Services: Potsdam, Germany, 2014. [Google Scholar]
- Sheng, M.; Shaw, C.; Vaníček, P.; Kingdon, R.; Santos, M.; Foroughi, I. Formulation and validation of a global laterally varying topographical density model. Tectonophysics 2019, 762, 45–60. [Google Scholar] [CrossRef]
- Divins, D.L. Total Sediment Thickness of the World’s Oceans & Marginal Seas; NOAA National Geophysical Data Center: Boulder, CO, USA, 2003. [Google Scholar]
- Baranov, A.; Tenzer, R.; Bagherbandi, M. Combined Gravimetric–Seismic Crustal Model for Antarctica. Surv. Geophys. 2018, 39, 23–56. [Google Scholar] [CrossRef]
- Hinze, W.J. Bouguer reduction density, why 2.67? Geophysics 2003, 68, 1559–1560. [Google Scholar] [CrossRef]
- Artemjev, M.; Kaban, M.; Kucherinenko, V.; Demyanov, G.; Taranov, V. Subcrustal density inhomogeneities of Northern Eurasia as derived from the gravity data and isostatic models of the lithosphere. Tectonophysics 1994, 240, 248–280. [Google Scholar] [CrossRef]
- Tenzer, R.; Gladkikh, V. Assessment of Density Variations of Marine Sediments with Ocean and Sediment Depths. Sci. World J. 2014, 2014, 823296. [Google Scholar] [CrossRef]
- Hager, B.H. Subducted slabs and the geoid: Constraints on mantle rheology and flow. J. Geophys. Res. Solid Earth 1984, 89, 6003–6015. [Google Scholar] [CrossRef]
- Panasyuk, S.V.; Hager, B.H. Models of isostatic and dynamic topography, geoid anomalies, and their uncertainties. J. Geophys. Res. Solid Earth 2000, 105, 28199–28209. [Google Scholar] [CrossRef]
- Barnett-Moore, N.; Hassan, R.; Müller, R.D.; Williams, S.E.; Flament, N. Dynamic topography and eustasy controlled the paleogeographic evolution of northern Africa since the mid-Cretaceous. Tectonics 2017, 36, 929–944. [Google Scholar] [CrossRef]
- Flament, N.; Gurnis, M.; Williams, S.; Seton, M.; Skogseid, J.; Heine, C.; Müller, R.D. Topographic asymmetry of the South Atlantic from global models of mantle flow and lithospheric stretching. Earth Planet. Sci. Lett. 2014, 387, 107–119. [Google Scholar] [CrossRef]
- Flament, N.; Gurnis, M.; Müller, R.D.; Bower, D.J.; Husson, L. Influence of subduction history on South American topography. Earth Planet. Sci. Lett. 2015, 430, 9–18. [Google Scholar] [CrossRef]
- Cao, W.; Flament, N.; Zahirovic, S.; Williams, S.; Müller, R.D. The interplay of dynamic topography and eustasy on continental flooding in the late Paleozoic. Tectonophysics 2019, 761, 108–121. [Google Scholar] [CrossRef]
- Lithgow-Bertelloni, C.; Silver, P.G. Dynamic topography, plate driving forces and the African superswell. Nature 1998, 395, 269–272. [Google Scholar] [CrossRef]
- Self, S.; Rampino, M. The Crust and Lithosphere; Geological Society of London: London, UK, 2012. [Google Scholar]
- Turcotte, D.L.; Schubert, G. Geodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002; p. 472. [Google Scholar]
- Conrad, C.P.; Lithgow-Bertelloni, C. Influence of continental roots and asthenosphere on plate-mantle coupling. Geophys. Res. Lett. 2006, 33, L05312. [Google Scholar] [CrossRef]
- Hoggard, M.J.; Czarnota, K.; Richards, F.D.; Huston, D.L.; Jaques, A.L.; Ghelichkhan, S. Global distribution of sediment-hosted metals controlled by craton edge stability. Nat. Geosci. 2020, 13, 504–510. [Google Scholar] [CrossRef]
- Schaeffer, A.J.; Lebedev, S. Global shear speed structure of the upper mantle and transition zone. Geophys. J. Int. 2013, 194, 417–449. [Google Scholar] [CrossRef]
- Ho, T.; Priestley, K.; Debayle, E. A global horizontal shear velocity model of the upper mantle from multimode Love wave measurements. Geophys. J. Int. 2016, 207, 542–561. [Google Scholar] [CrossRef]
- Priestley, K.; McKenzie, D.; Ho, T. A lithosphere–asthenosphere boundary—A global model derived from multimode surface-wave tomography and petrology. In Lithospheric Discontinuities; Wiley Online Library: Toronto, ON, Canada, 2018; pp. 111–123. [Google Scholar]
- Debayle, E.; Dubuffet, F.; Durand, S. An automatically updated S-wave model of the upper mantle and the depth extent of azimuthal anisotropy. Geophys. Res. Lett. 2016, 43, 674–682. [Google Scholar] [CrossRef]
- Schaeffer, A.; Lebedev, S. Imaging the North American continent using waveform inversion of global and USArray data. Earth Planet. Sci. Lett. 2014, 402, 26–41. [Google Scholar] [CrossRef]
- Celli, N.L.; Lebedev, S.; Schaeffer, A.J.; Gaina, C. African cratonic lithosphere carved by mantle plumes. Nat. Commun. 2020, 11, 92. [Google Scholar] [CrossRef] [PubMed]
- Celli, N.; Lebedev, S.; Schaeffer, A.; Ravenna, M.; Gaina, C. The upper mantle beneath the South Atlantic Ocean, South America and Africa from waveform tomography with massive data sets. Geophys. J. Int. 2020, 221, 178–204. [Google Scholar] [CrossRef]
- Christensen, N.I.; Mooney, W.D. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. Solid Earth 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Hager, B.H.; Richards, M.A. Long-wavelength variations in Earth’s geoid: Physical models and dynamical implications. Phil. Trans. R. Soc. Lond. Ser. A 1989, 328, 309–327. [Google Scholar] [CrossRef]
- Simmons, A.J.; Willett, K.M.; Jones, P.D.; Thorne, P.W.; Dee, D.P. Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets. J. Geophys. Res. Atmos. 2010, 115, D01110. [Google Scholar] [CrossRef]
- Jordan, T.H. The continental tectosphere. Rev. Geophys. 1975, 13, 1–12. [Google Scholar] [CrossRef]
- Gung, Y.C.; Panning, M.; Romanowicz, B. Global anisotropy and the thickness of continents. Nature 2003, 422, 707–711. [Google Scholar] [CrossRef]
- Artemieva, I.M. Dynamic topography of the East European craton: Shedding light upon lithospheric structure, composition and mantle dynamics. Glob. Planet. Chang. 2007, 58, 411–434. [Google Scholar] [CrossRef]
- Sjöberg, L.E.; Bagherbandi, M. A method of estimating the Moho density contrast with a tentative application by EGM08 and CRUST2.0. Acta Geophys. 2011, 59, 502–525. [Google Scholar] [CrossRef]
- Rogers, N.; Blake, S.; Burton, K. An Introduction to Our Dynamic Planet; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Carlson, R.L.; Raskin, G.S. Density of the ocean crust. Nature 1984, 311, 555–558. [Google Scholar] [CrossRef]
- Hoggard, M.J.; White, N.; Al-Attar, D. Global dynamic topography observations reveal limited influence of large-scale mantle flow. Nat. Geosci. 2016, 9, 456–463. [Google Scholar] [CrossRef]
- Simmons, N.A.; Gurrola, H. Multiple seismic discontinuities near the base of the transition zone in the Earth’s mantle. Nature 2000, 405, 559–562. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, J.F.; Shearer, P.M. Constraining seismic velocity and density for the mantle transition zone with reflected and transmitted waveforms. Geochem. Geophys. Geosyst. 2006, 7, Q10012. [Google Scholar] [CrossRef]
- Griffin, W.L.; O’Reilly, S.Y.; Afonso, J.C.; Begg, G.C. The Composition and Evolution of Lithospheric Mantle: A Re-evaluation and its Tectonic Implications. J. Pet. 2009, 50, 1185–1204. [Google Scholar] [CrossRef]
- Ishii, M.; Tromp, J. Normal-mode and free-air gravity constraints on lateral variations in velocity and density of Earth’s mantle. Science 1999, 285, 1231–1236. [Google Scholar] [CrossRef]
- Kuo, C.; Romanowicz, B. Density and seismic velocity variations determined from normal mode spectra. EOS Trans. Am. Geophys. 1999, 80, S14. [Google Scholar]
- Panasyuk, S.; Ishii, M.; O’Connell, R.; Tromp, J. Constraints on the density and viscosity structure of the earth. EOS Trans. Am. Geophys. 1999, 80, F28. [Google Scholar]
- Resovsky, J.S.; Ritzwoller, M.H. Regularization uncertainty in density models estimated from normal mode data. Geophys. Res. Lett. 1999, 26, 2319–2322. [Google Scholar] [CrossRef]
- Romanowicz, B. Can we resolve 3-D density heterogeneity in the lower mantle? Geophys. Res. Lett. 2001, 28, 1107–1110. [Google Scholar] [CrossRef]
- Kuo, C.; Romanowicz, B. On the resolution of density anomalies in the Earth’s mantle using spectral fitting of normal-mode data. Geophys. J. Int. 2002, 150, 162–179. [Google Scholar] [CrossRef]
- Dziewonski, A.M. Mapping the lower mantle: Determination of lateral heterogeneity in p velocity up to degree and order 6. J. Geophys. Res. Solid Earth 1984, 89, 5929–5952. [Google Scholar] [CrossRef]
- Euler, G.G.; Wysession, M.E. Geographic variations in lowermost mantle structure from the ray parameters and decay constants of core-diffracted waves. J. Geophys. Res. Solid Earth 2017, 122, 5369–5394. [Google Scholar] [CrossRef]
- Fisher, J.L.; Wysession, M.E.; Fischer, K.M. Small-scale lateral variations in D″ attenuation and velocity structure. Geophys. Res. Lett. 2003, 30, 8. [Google Scholar] [CrossRef]
- French, S.W.; Romanowicz, B.A. Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography. Geophys. J. Int. 2014, 199, 1303–1327. [Google Scholar] [CrossRef]
- French, S.W.; Romanowicz, B. Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 2015, 525, 95–99. [Google Scholar] [CrossRef]
- Garnero, E.J.; McNamara, A.K.; Shim, S.-H. Continent-sized anomalous zones with low seismic velocity at the base of Earth’s mantle. Nat. Geosci. 2016, 9, 481–489. [Google Scholar] [CrossRef]
- Grand, S.P. Mantle shear–wave tomography and the fate of subducted slabs. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 2475–2491. [Google Scholar] [CrossRef]
- Hansen, S.E.; Nyblade, A.A.; Benoit, M.H. Mantle structure beneath Africa and Arabia from adaptively parameterized P-wave tomography: Implications for the origin of Cenozoic Afro-Arabian tectonism. Earth Planet. Sci. Lett. 2012, 319–320, 23–34. [Google Scholar] [CrossRef]
- Houser, C.; Masters, G.; Shearer, P.; Laske, G. Shear and compressional velocity models of the mantle from cluster analysis of long-period waveforms. Geophys. J. Int. 2008, 174, 195–212. [Google Scholar] [CrossRef]
- Hung, S.-H.; Shen, Y.; Chiao, L.-Y. Imaging seismic velocity structure beneath the Iceland hot spot: A finite frequency approach. J. Geophys. Res. Solid Earth 2004, 109, B08305. [Google Scholar] [CrossRef]
- Hung, S.-H.; Garnero, E.J.; Chiao, L.; Kuo, B.; Lay, T. Finite frequency tomography of D″ shear velocity heterogeneity beneath the Caribbean. J. Geophys. Res. Solid Earth 2005, 110, B07305. [Google Scholar] [CrossRef]
- Hutko, A.; Lay, T.; Garnero, E.; Revenaugh, J. Seismic detection of folded, subducted lithosphere at the core-mantle boundary. Nature 2006, 441, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Kàrason, H.; Van der Hilst, R. Tomographic imaging of the lowermost mantle with differential times of refracted and diffracted core phases (PKP, Pdiff). J. Geophys. Res. 2001, 106, 6569–6587. [Google Scholar] [CrossRef]
- Kito, T.; Rost, S.; Thomas, C.; Garnero, E.J. New insights into the p-and s-wave velocity structure of the D” discontinuity beneath the cocos plate. Geophys. J. Int. 2007, 169, 631–645. [Google Scholar]
- Koelemeijer, P.; Ritsema, J.; Deuss, A.; van Heijst, H.-J. SP12RTS: A degree-12 model of shear- and compressional-wave velocity for Earth’s mantle. Geophys. J. Int. 2016, 204, 1024–1039. [Google Scholar] [CrossRef]
- Lei, J.; Zhao, D. Global P-wave tomography: On the effect of various mantle and core phases. Phys. Earth Planet. Inter. 2006, 154, 44–69. [Google Scholar] [CrossRef]
- Li, C.; van der Hilst, R.D.; Engdahl, E.R.; Burdick, S. A new global model for P wave speed variations in Earth’s mantle. Geochem. Geophys. Geosyst. 2008, 9, 5. [Google Scholar] [CrossRef]
- Lu, C.; Grand, S.P. The effect of subducting slabs in global shear wave tomography. Geophys. J. Int. 2016, 205, 1074–1085. [Google Scholar] [CrossRef]
- Masters, G.; Laske, G.; Bolton, H.; Dziewonski, A. The relative behavior of shear velocity, bulk sound speed, and compressional velocity in the mantle: Implications for chemical and thermal structure. Earth’s Deep. Inter. Miner. Phys. Tomogr. Glob. Scale 2000, 117, 63–87. [Google Scholar] [CrossRef]
- Mégnin, C.; Romanowicz, B. The three-dimensional shear velocity structure of the mantle from the inversion of body, surface and higher-mode waveforms. Geophys. J. Int. 2000, 143, 709–728. [Google Scholar] [CrossRef]
- Montelli, R.; Nolet, G.; Dahlen, F.A.; Masters, G.; Engdahl, E.R.; Hung, S.-H. Finite-Frequency Tomography Reveals a Variety of Plumes in the Mantle. Science 2004, 303, 338–343. [Google Scholar] [CrossRef] [PubMed]
- Montelli, R.; Nolet, G.; Masters, G.; Dahlen, F.; Hung, S.-H. Global P and PP traveltime tomography: Rays versus waves. Geophys. J. Int. 2004, 158, 637–654. [Google Scholar] [CrossRef]
- Montelli, R.; Nolet, G.; Dahlen, F.A.; Masters, G. A catalogue of deep mantle plumes: New results from finite-frequency tomography. Geochem. Geophys. Geosyst. 2006, 7, 11. [Google Scholar] [CrossRef]
- Moulik, P.; Ekström, G. An anisotropic shear velocity model of the earth’s mantle using normal modes, body waves, surface waves and long-period waveforms. Geophys. J. Int. 2014, 199, 1713–1738. [Google Scholar] [CrossRef]
- Obayashi, M.; Fukao, Y. P and PCP travel time tomography for the core-mantle boundary. J. Geophys. Res. Solid Earth 1997, 102, 17825–17841. [Google Scholar] [CrossRef]
- Obayashi, M.; Yoshimitsu, J.; Nolet, G.; Fukao, Y.; Shiobara, H.; Sugioka, H.; Miyamachi, H.; Gao, Y. Finite frequency whole mantle p wave tomography: Improvement of subducted slab images. Geophys. Res. Lett. 2013, 40, 5652–5657. [Google Scholar] [CrossRef]
- Obayashi, M.; Yoshimitsu, J.; Sugioka, H.; Ito, A.; Isse, T.; Shiobara, H.; Reymond, D.; Suetsugu, D. Mantle plumes beneath the South Pacific superswell revealed by finite frequency P tomography using regional seafloor and island data. Geophys. Res. Lett. 2016, 43, 11628–11634. [Google Scholar] [CrossRef]
- Panning, M.; Romanowicz, B. A three-dimensional radially anisotropic model of shear velocity in the whole mantle. Geophys. J. Int. 2006, 167, 361–379. [Google Scholar] [CrossRef]
- Ren, Y.; Stutzmann, E.; van der Hilst, R.D.; Besse, J. Understanding seismic heterogeneities in the lower mantle beneath the Americas from seismic tomography and plate tectonic history. J. Geophys. Res. Solid Earth 2007, 112, B1. [Google Scholar] [CrossRef]
- Rickers, F.; Fichtner, A.; Trampert, J. The Iceland–Jan Mayen plume system and its impact on mantle dynamics in the North Atlantic region: Evidence from full-waveform inversion. Earth Planet. Sci. Lett. 2013, 367, 39–51. [Google Scholar] [CrossRef]
- Ritsema, J.; van Heijst, H.J.; Woodhouse, J.H. Complex Shear Wave Velocity Structure Imaged Beneath Africa and Iceland. Science 1999, 286, 1925–1928. [Google Scholar] [CrossRef] [PubMed]
- Ritsema, J.; van Heijst, H.J.; Woodhouse, J.H. Global transition zone tomography. J. Geophys. Res. Solid Earth 2004, 109, B2. [Google Scholar] [CrossRef]
- Ritsema, J.; Deuss, A.; van Heijst, H.J.; Woodhouse, J.H. S40RTS: A degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 2011, 184, 1223–1236. [Google Scholar] [CrossRef]
- Sambridge, M.; Guđmundsson, Ó. Tomographic systems of equations with irregular cells. J. Geophys. Res. Solid Earth 1998, 103, 773–781. [Google Scholar] [CrossRef]
- Shephard, G.E.; Matthews, K.J.; Hosseini, K.; Domeier, M. On the consistency of seismically imaged lower mantle slabs. Sci. Rep. 2017, 7, 10976. [Google Scholar] [CrossRef]
- Sigloch, K. Mantle provinces under North America from multifrequency p wave tomography. Geochem. Geophys. Geosyst. 2011, 12, 2. [Google Scholar] [CrossRef]
- Tesoniero, A.; Auer, L.; Boschi, L.; Cammarano, F. Hydration of marginal basins and compositional variations within the continental lithospheric mantle inferred from a new global model of shear and compressional velocity. J. Geophys. Res. Solid Earth 2015, 120, 7789–7813. [Google Scholar] [CrossRef]
- Thomas, C.; Garnero, E.J.; Lay, T. High-resolution imaging of lowermost mantle structure under the Cocos plate. J. Geophys. Res. Solid Earth 2004, 109, B08307. [Google Scholar] [CrossRef]
- van der Hilst, R.D.; Widiyantoro, S.; Engdahl, E.R. Evidence for deep mantle circulation from global tomography. Nature 1997, 386, 578–584. [Google Scholar] [CrossRef]
- van der Hilst, R.D.; de Hoop, M.V.; Wang, P.; Shim, S.-H.; Ma, P.; Tenorio, L. Seismostratigraphy and Thermal Structure of Earth’s Core-Mantle Boundary Region. Science 2007, 315, 1813–1817. [Google Scholar] [CrossRef] [PubMed]
- van der Meer, D.G.; van Hinsbergen, D.J.; Spakman, W. Atlas of the underworld: Slab remnants in the mantle, their sinking history, and a new outlook on lower mantle viscosity. Tectonophysics 2018, 723, 309–448. [Google Scholar] [CrossRef]
- Van der Voo, R.; Spakman, W.; Bijwaard, H. Tethyan subducted slabs under India. Earth Planet. Sci. Lett. 1999, 171, 7–20. [Google Scholar] [CrossRef]
- Wolfe, C.J.; Solomon, S.C.; Laske, G.; Collins, J.A.; Detrick, R.S.; Orcutt, J.A.; Bercovici, D.; Hauri, E.H. Mantle Shear-Wave Velocity Structure Beneath the Hawaiian Hot Spot. Science 2009, 326, 1388–1390. [Google Scholar] [CrossRef] [PubMed]
- Woodhouse, J.H.; Dziewonski, A.M. Seismic modelling of the Earth’s large-scale three-dimensional structure. Phil. Trans. R. Soc. A Math. Phys. Eng. Sci. 1989, 328, 291–308. [Google Scholar] [CrossRef]
- Wysession, M.E. Large-scale structure at the core–mantle boundary from diffracted waves. Nature 1996, 382, 244–248. [Google Scholar] [CrossRef]
- Wysession, M.E.; Bartkó, L.; Wilson, J.B. Mapping the lowermost mantle using core-reflected shear waves. J. Geophys. Res. Solid Earth 1994, 99, 13667–13684. [Google Scholar] [CrossRef]
- Zhao, D. Global tomographic images of mantle plumes and subducting slabs: Insight into deep Earth dynamics. Phys. Earth Planet. Inter. 2004, 146, 3–34. [Google Scholar] [CrossRef]
- Zhou, H.-W. A high-resolution p wave model for the top 1200 km of the mantle. J. Geophys. Res. Solid Earth 1996, 101, 27791–27810. [Google Scholar] [CrossRef]
- Zhu, A.; Wysession, M.E. Mapping global d” p velocities from isc pcp-p differential travel times. Phys. Earth Planet. Inter. 1997, 99, 69–82. [Google Scholar] [CrossRef]
- Zhu, H.; Bozdağ, E.; Peter, D.; Tromp, J. Structure of the European upper mantle revealed by adjoint tomography. Nat. Geosci. 2012, 5, 493–498. [Google Scholar] [CrossRef]
- Zielhuis, A.; Nolet, G. Shear-wave velocity variations in the upper mantle beneath central Europe. Geophys. J. Int. 1994, 117, 695–715. [Google Scholar] [CrossRef]
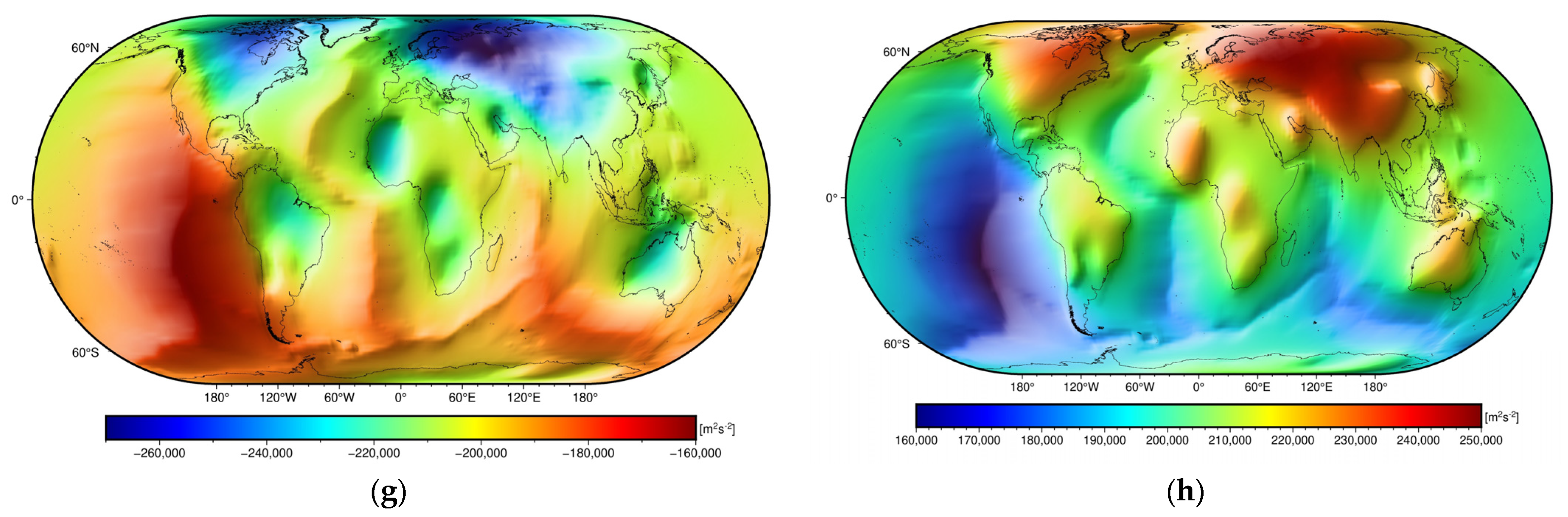


| Gravitational Potential | Min [m2·s−2] | Max [m2·s−2] | Mean [m2·s−2] | STD [m2·s−2] |
|---|---|---|---|---|
| 2226 | 8494 | 3589 | 1114 | |
| −3472 | −312 | −731 | 729 | |
| −28,533 | −16,402 | −22,386 | 3185 | |
| −3862 | −1937 | −2719 | 444 | |
| 11,529 | 25,075 | 15,661 | 2741 | |
| −69,885 | −46,423 | −55,734 | 5832 | |
| −262,661 | −17,4276 | −213,366 | 17,795 | |
| 168,987 | 244,558 | 203,311 | 16,194 |
| Refined Geoid | Min [m] | Max [m] | Mean [m] | STD [m] |
|---|---|---|---|---|
| −106 | 85 | −1 | 29 | |
| 1198 | 2946 | 2269 | 356 | |
| −1358 | 1743 | 671 | 630 | |
| 5772 | 6617 | 6358 | 128 | |
| 24,009 | 33,222 | 28,130 | 1835 | |
| 6445 | 8388 | 7384 | 372 |
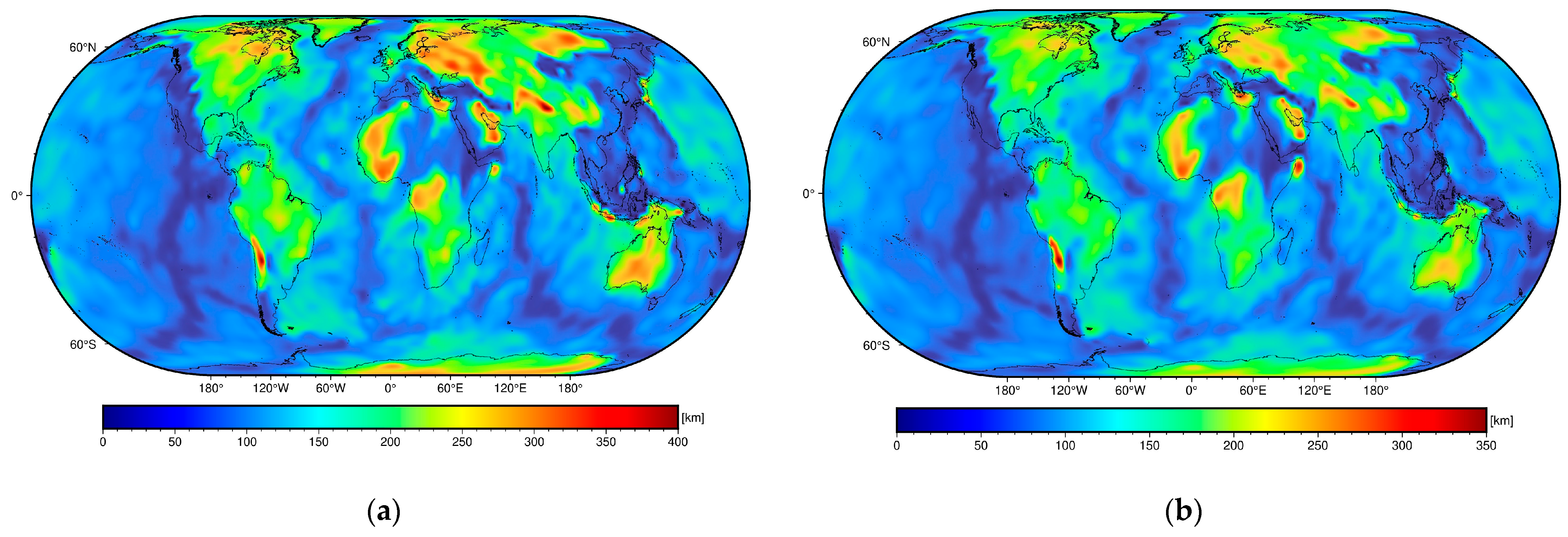
| Lithospheric Thickness Model | Min [km] | Max [km] | Mean [km] | STD [km] |
|---|---|---|---|---|
| SLNAAFSA | 38 | 364 | 115 | 57 |
| SL2013sv | 40 | 350 | 112 | 52 |
| LITHO1.0 | 7 | 271 | 114 | 55 |
| CAM2016 | 38 | 241 | 111 | 46 |
| 3D2015-07Sv | 36 | 703 | 110 | 51 |
| Differences | Min [km] | Max [km] | Mean [km] | RMS [km] |
|---|---|---|---|---|
| SLNAAFSA–SL2013sv | −237 | 303 | 3 | 11 |
| SLNAAFSA–LITHO1.0 | −196 | 289 | 1 | 77 |
| SLNAAFSA–CAM2016 | −160 | 307 | 4 | 26 |
| SLNAAFSA–3D2015-07Sv | −638 | 309 | 5 | 26 |
| SL2013sv–LITHO1.0 | −195 | 298 | −1 | 74 |
| SL2013sv–CAM2016 | −160 | 306 | 1 | 22 |
| SL2013sv–3D2015-07Sv | −637 | 303 | 3 | 24 |
| LITHO1.0–CAM2016 | −184 | 206 | 2 | 71 |
| LITHO1.0–3D2015-07Sv | −603 | 206 | 4 | 74 |
| CAM2016–3D2015-07Sv | −561 | 195 | 2 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tenzer, R.; Chen, W. The Accuracy Assessment of Lithospheric Density Models. Appl. Sci. 2023, 13, 10432. https://doi.org/10.3390/app131810432
Tenzer R, Chen W. The Accuracy Assessment of Lithospheric Density Models. Applied Sciences. 2023; 13(18):10432. https://doi.org/10.3390/app131810432
Chicago/Turabian StyleTenzer, Robert, and Wenjin Chen. 2023. "The Accuracy Assessment of Lithospheric Density Models" Applied Sciences 13, no. 18: 10432. https://doi.org/10.3390/app131810432
APA StyleTenzer, R., & Chen, W. (2023). The Accuracy Assessment of Lithospheric Density Models. Applied Sciences, 13(18), 10432. https://doi.org/10.3390/app131810432






