Speed Control of PMSM Based on Fuzzy Active Disturbance Rejection Control under Small Disturbances
Abstract
:1. Introduction
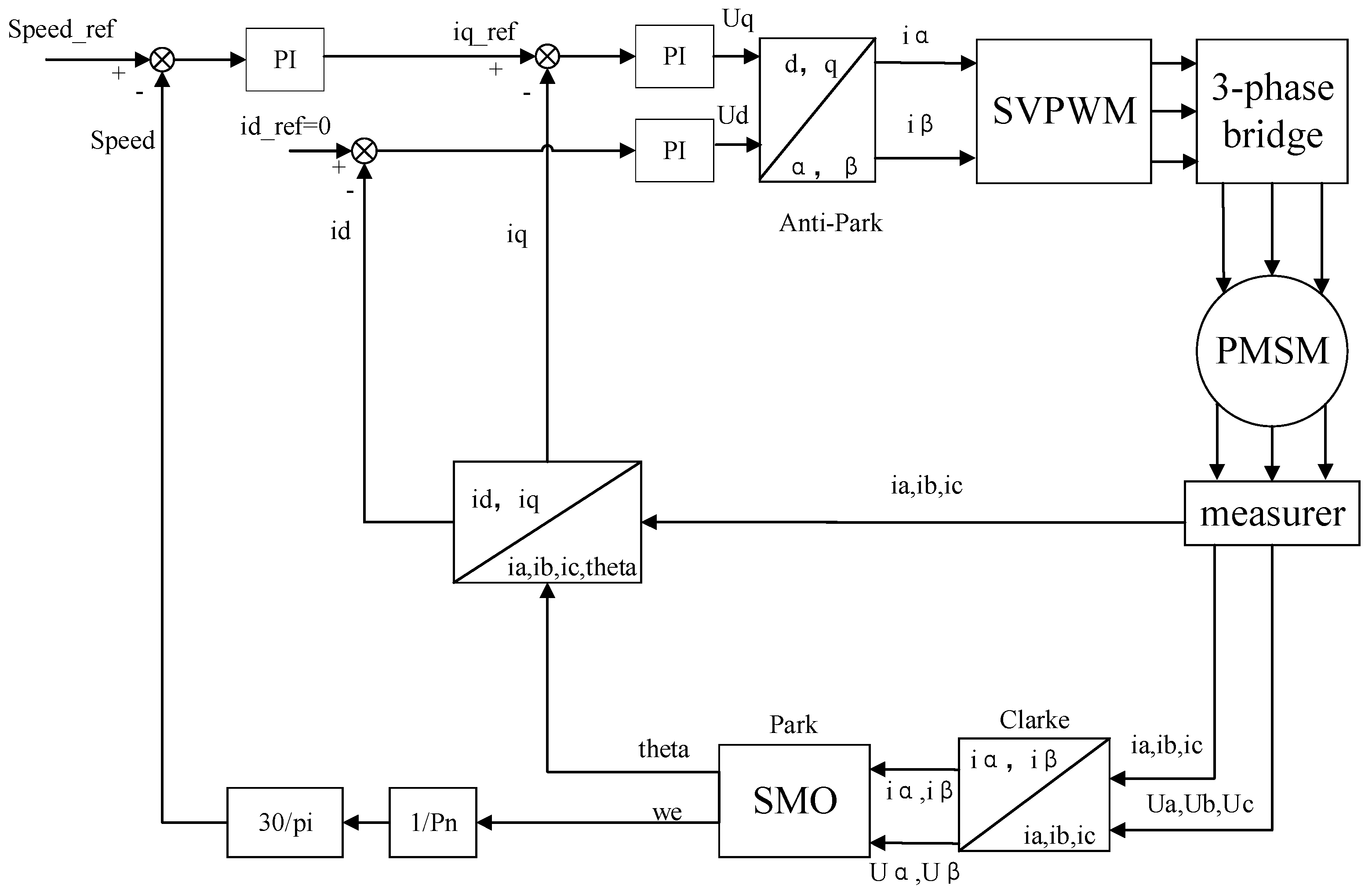
2. SMO-Based PMSM Simulation Modeling
2.1. Motor Modeling
2.2. SMO Establishment
2.3. Setting Up the PI Controller with Parameters
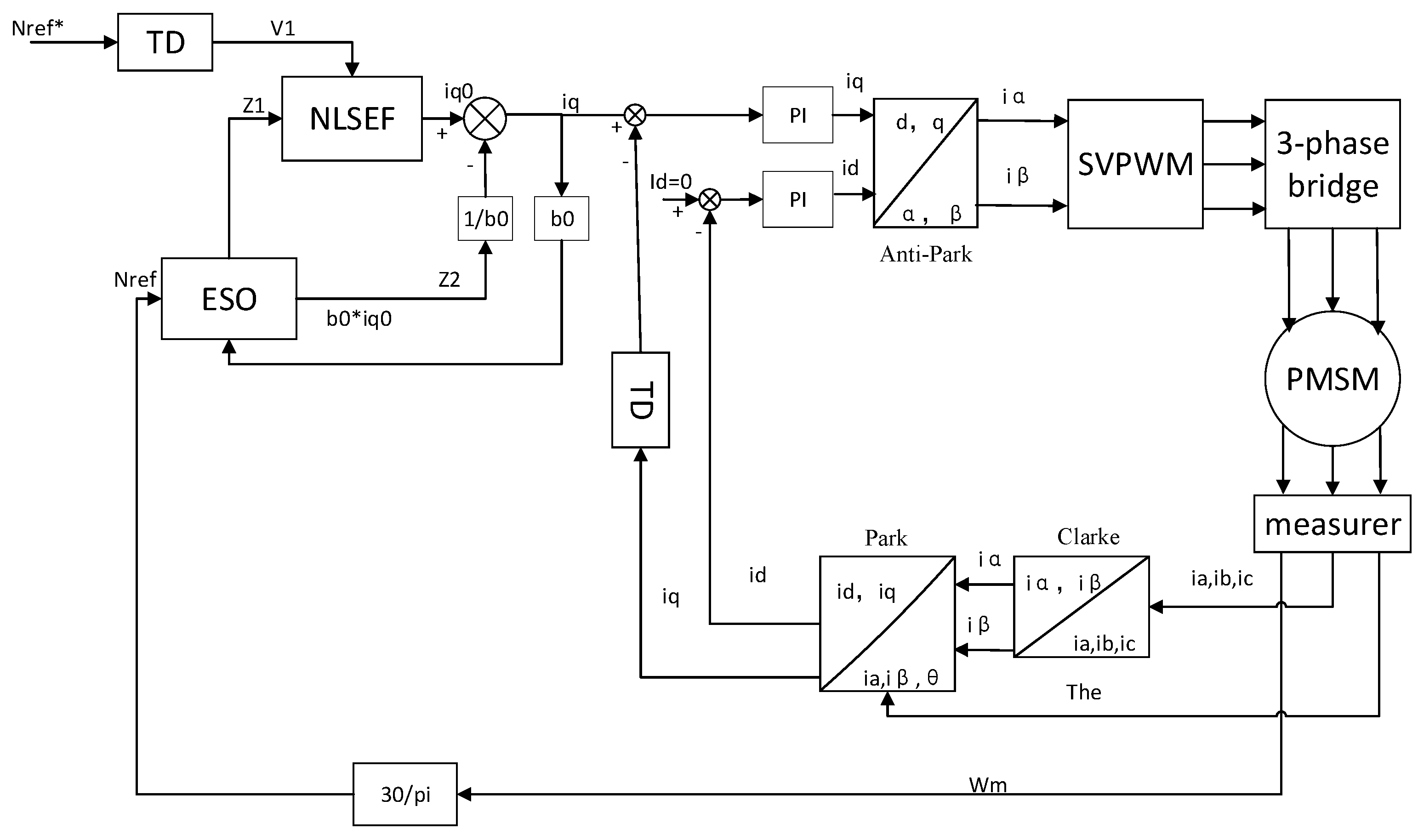
3. ADRC Design and Parameterization
3.1. TD Design
3.2. ESO Design
3.2.1. α and β Parameterization
3.2.2. ESO Gain Adjustment
3.3. NLSEF Design
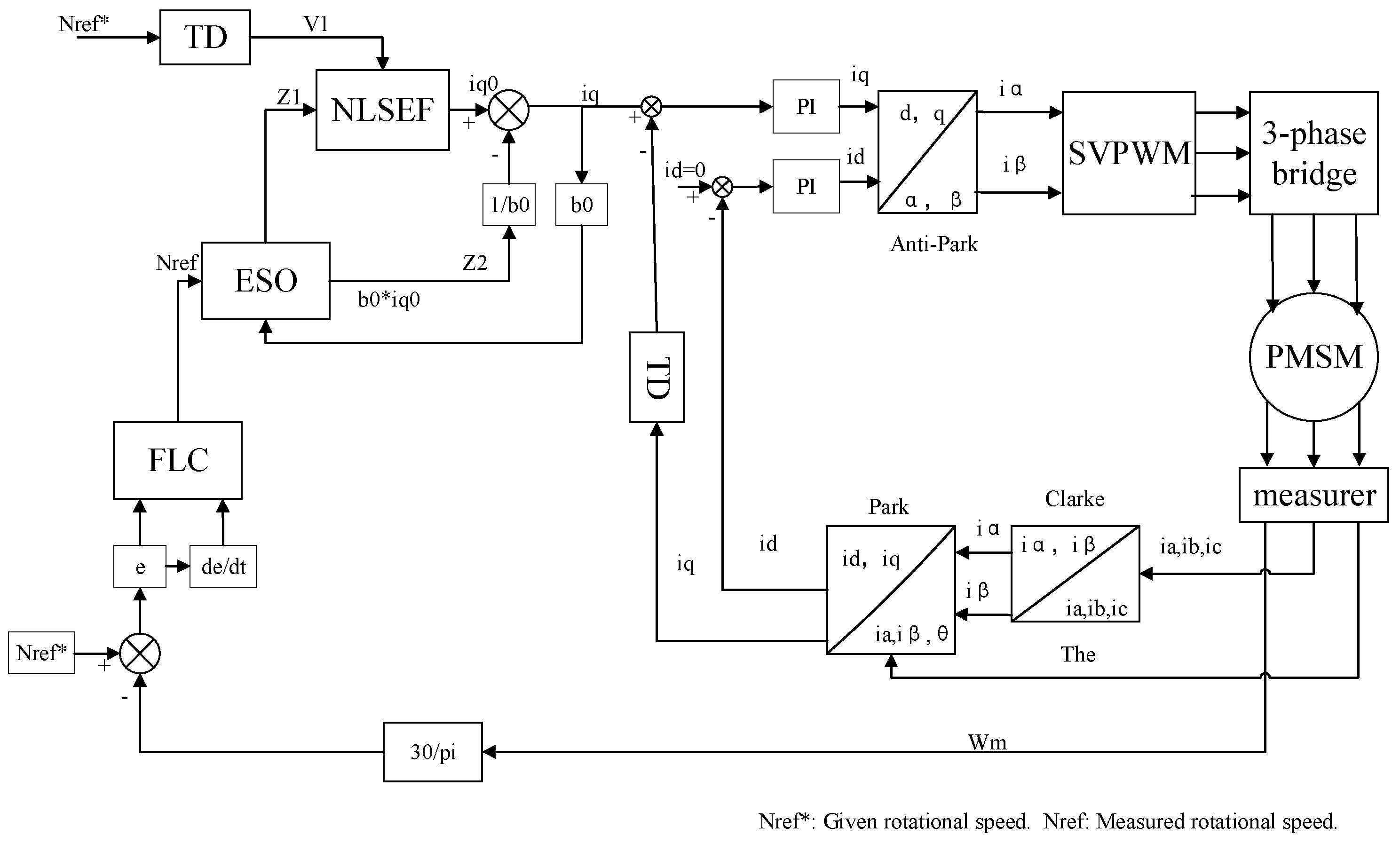
3.4. Fuzzy-ADRC Design
4. Analysis of Simulation Findings
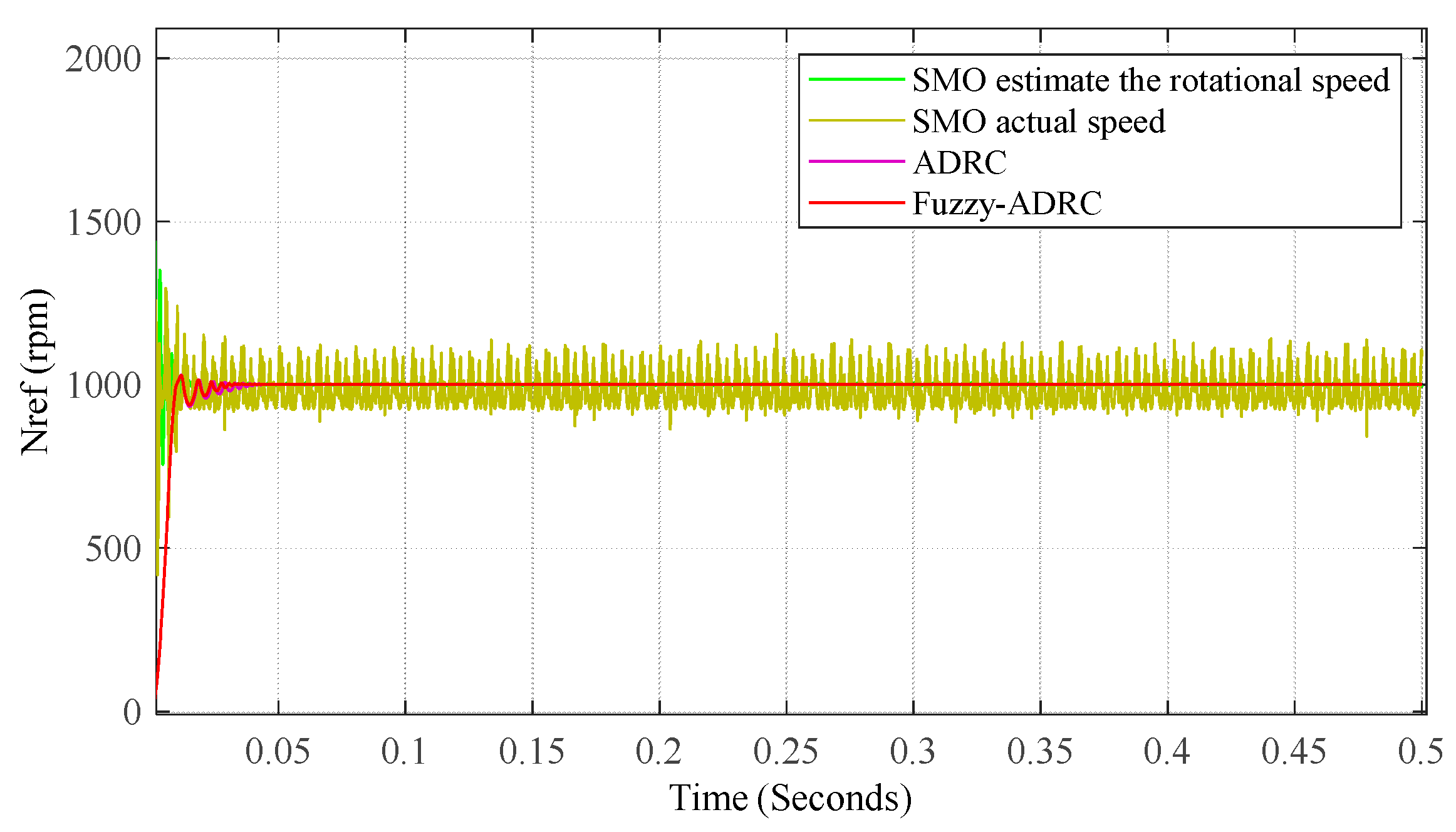
4.1. Analysis of Simulation Findings
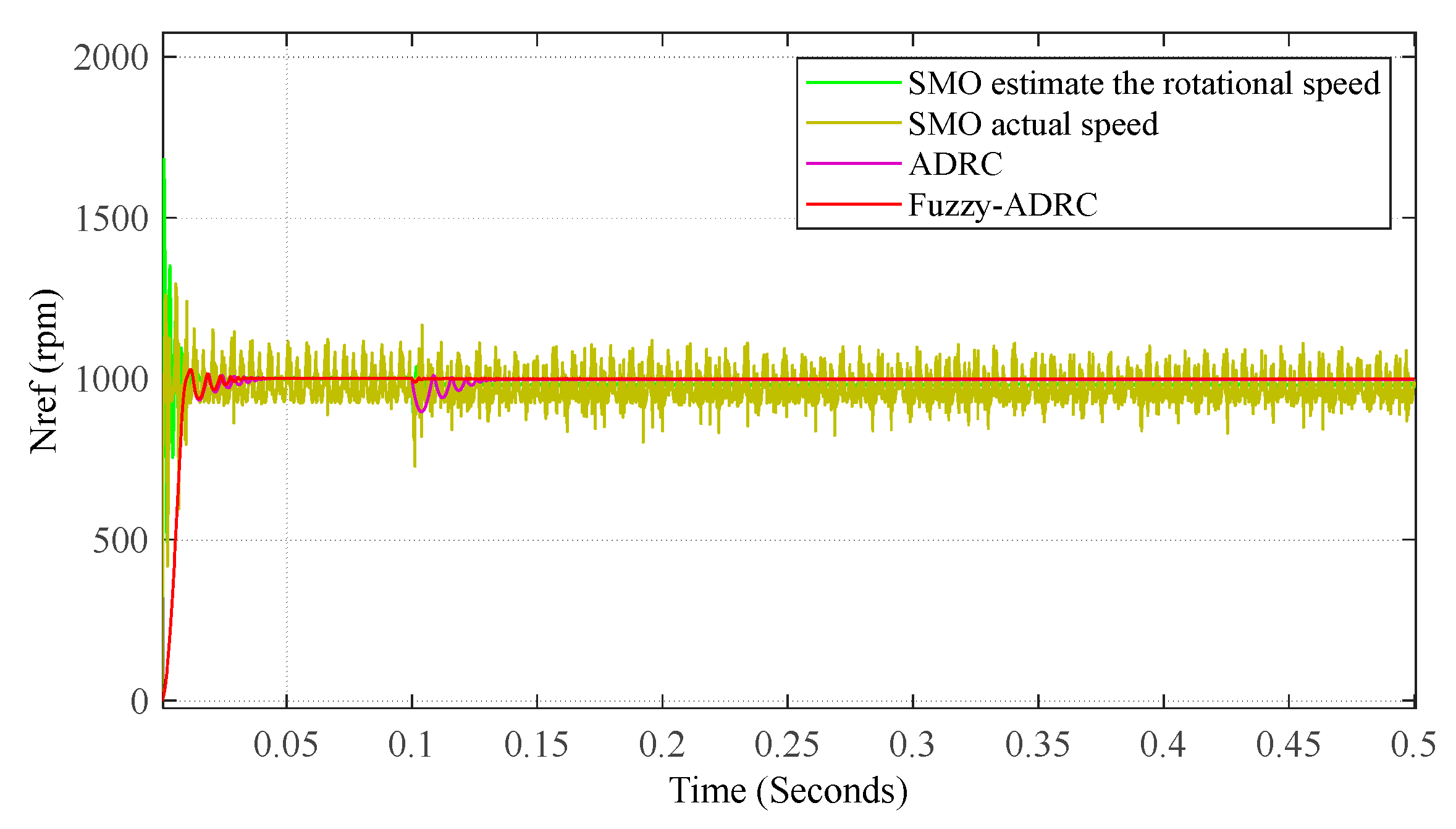
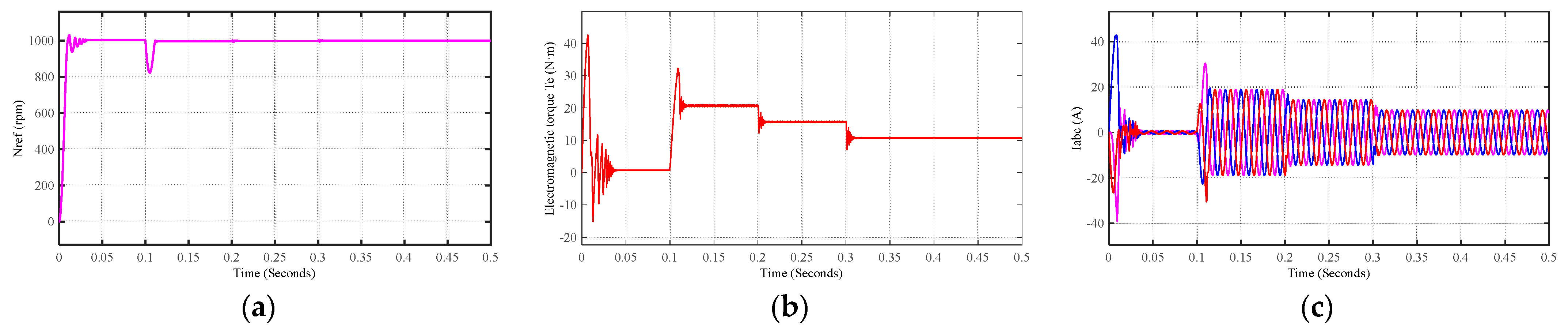
4.2. Introduction of Small Load Experimental Simulation Analysis
4.3. Simulation Analysis under Variable Speed Conditions
4.4. Simulation Analysis with the Introduction of Variable Loads
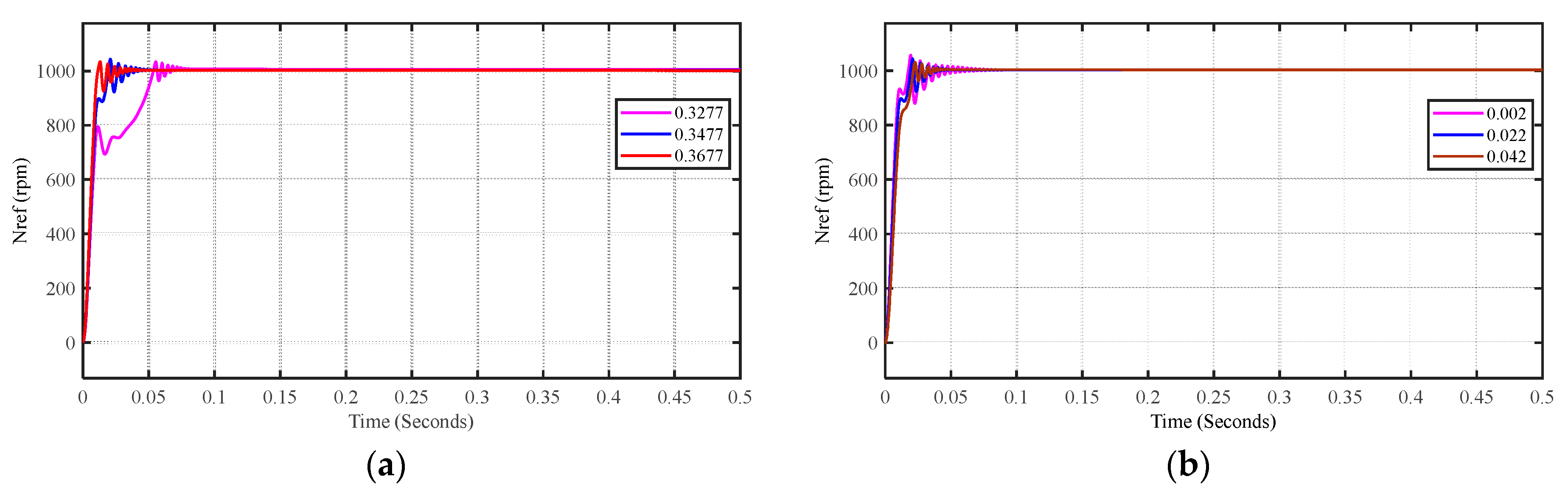
4.5. Simulation Analysis of Internal Parameter Variations in Motors
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, G.; Wei, T.; Ding, X. Multi-objective optimal design of PMSM for high efficiency and high dynamic performance. IEEE Access 2018, 6, 23568–23581. [Google Scholar] [CrossRef]
- Sarsembayev, B.; Suleimenov, K.; Do, T.D. High order disturbance observer based PI-PI control system with tracking anti-windup technique for improvement of transient performance of PMSM. IEEE Access 2021, 9, 66323–66334. [Google Scholar] [CrossRef]
- Gu, D.; Yao, Y.; Zhang, D.M.; Cui, Y.B.; Zeng, F.Q. Matlab/simulink based modeling and simulation of fuzzy PI control for PMSM. Procedia Comput. Sci. 2020, 166, 195–199. [Google Scholar] [CrossRef]
- Kashif, M.; Singh, B. Modified Active-Power MRAS Based Adaptive Control with Reduced Sensors for PMSM Operated Solar Water Pump. IEEE Trans. Energy Convers. 2022, 38, 38–52. [Google Scholar] [CrossRef]
- Anwer AM, O.; Omar, F.A.; Kulaksiz, A.A. Design of a fuzzy logic-based MPPT controller for a PV system employing sensorless control of MRAS-based PMSM. Int. J. Control. Autom. Syst. 2020, 18, 2788–2797. [Google Scholar] [CrossRef]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using SMC—A review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Application of fractional order sliding mode control for speed control of PMSM. IEEE Access 2019, 7, 101765–101774. [Google Scholar] [CrossRef]
- Vadivel, R.; Joo, Y.H. Reliable fuzzy H∞ control for PMSM against stochastic actuator faults. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2232–2245. [Google Scholar] [CrossRef]
- Li, L.; Pei, G.; Liu, J.; Du, P.; Pei, L.; Zhong, C. 2-DOF Robust H∞ Control for PMSM with Disturbance Observer. IEEE Trans. Power Electron. 2020, 36, 3462–3472. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.; Chen, D.; Qi, J. Model reference adaptive control of marine permanent magnet propulsion motor based on parameter identification. Electronics 2022, 11, 1012. [Google Scholar] [CrossRef]
- Abba, A.; Abbate, N.; Abdi, E.; Kadir, A.; Abdulla, W.; Abidi, K.; Abou-Alfotouh, A.M.; Abu Qahouq, J.A.; Abu-Rub, H.; Aceiton, R.; et al. Multiparameter identification of PMSM based on model reference adaptive system—Simulated annealing particle swarm optimization algorithm. Electronics 2022, 11, 159. [Google Scholar]
- Zhou, C.; Shen, Y.; Wang, Z. Research on vibration suppression of transmission chain in wind power generation system with gear clearance based on IMC. Int. J. Innov. Comput. Inf. Control. 2022, 18, 1247–1263. [Google Scholar]
- Yuan, T.; Zhang, Y.; Wang, D. Performance improvement for PMSM control system based on composite controller used adaptive IMC. Energy Rep. 2022, 8, 11078–11087. [Google Scholar] [CrossRef]
- Han, J. From PID to ADRC. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Sun, D. Comments on ADRC. IEEE Trans. Ind. Electron. 2007, 54, 3428–3429. [Google Scholar]
- Zhou, K.; Ai, M.; Sun, Y.; Wu, X.; Li, R. PMSM vector control strategy based on active disturbance rejection controller. Energies 2019, 12, 3827. [Google Scholar] [CrossRef]
- Du, C.; Yin, Z.; Zhang, Y.; Liu, J.; Sun, X.; Zhong, Y. Research on ADRC with parameter autotune mechanism for induction motors based on adaptive particle swarm optimization algorithm with dynamic inertia weight. IEEE Trans. Power Electron. 2018, 34, 2841–2855. [Google Scholar] [CrossRef]
- Aole, S.; Elamvazuthi, I.; Waghmare, L.; Patre, B.; Bhaskarwar, T.; Meriaudeau, F.; Su, S. ADRC based sinusoidal trajectory tracking for an upper limb robotic rehabilitation exoskeleton. Appl. Sci. 2022, 12, 1287. [Google Scholar] [CrossRef]
- Liu, C.; Luo, G.; Chen, Z.; Tu, W. Measurement delay compensated LADRC based current controller design for PMSM drives with a simple parameter tuning method. ISA Trans. 2020, 101, 482–492. [Google Scholar] [CrossRef]
- Sui, S.; Zhao, T. ADRC for optoelectronic stabilized platform based on adaptive fuzzy SMC. ISA Trans. 2022, 125, 85–98. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, H.; Zhao, B.; Zhao, L. A GA-based parameters tuning method for an ADRC controller of ISP for aerial remote sensing applications. ISA Trans. 2018, 81, 318–328. [Google Scholar] [CrossRef]
- Gao, P.; Su, X.; Pan, Z.; Xiao, M.; Zhang, W.; Liu, R. ADRC for Speed Control of PMSM Based on Auxiliary Model and Supervisory RBF. Appl. Sci. 2022, 12, 10880. [Google Scholar] [CrossRef]
- Lu, W.; Li, Q.; Lu, K.; Lu, Y.; Guo, L.; Yan, W.; Xu, F. Load adaptive PMSM drive system based on an improved ADRC for manipulator joint. IEEE Access 2021, 9, 33369–33384. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, H. ADRC of Bearingless PMSM Based on GA and Neural Network Parameters Dynamic Adjustment Method. Electronics 2023, 12, 1455. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Z.; Xu, B. Simulation of Non-inductive Vector Control of PMSM Based on SMO. arXiv 2023, arXiv:2305.04046. [Google Scholar]




| Technical Term | Acronyms |
|---|---|
| Internal Model Control | IMC |
| Sliding Mode Control | SMC |
| Genetic Algorithm | GA |
| Backpropagation Neural Network | BPNN |
| Fuzzy Controller | FC |
| Sliding Mode Observer | SMO |
| Feedforward Control | FFC |
| r/rc | n3 | n2 | n1 | O | p1 | p2 | p3 |
|---|---|---|---|---|---|---|---|
| n1 | O | O | O | n1 | n2 | n2 | n3 |
| n2 | O | n1 | n1 | n1 | n2 | n3 | n3 |
| n1 | n1 | n1 | n2 | n2 | n3 | n3 | p2 |
| O | n2 | n2 | p3 | p3 | p3 | p2 | p2 |
| p1 | n2 | p3 | p3 | p2 | p2 | p1 | p1 |
| p2 | p3 | p3 | p2 | p1 | p1 | p1 | O |
| p3 | p3 | p2 | p1 | p1 | O | O | O |
| Parameters | Numerical Value | Parameters | Numerical Value |
|---|---|---|---|
| 500 | 100,000 | ||
| 0.004 | 0.01 | ||
| 2 | 0.95 | ||
| 120.54 | 55,000 | ||
| 120.54 | 36,000 | ||
| 70,440 | 53,000 | ||
| 70,440 | 5000 | ||
| 4 |
| Parameters | Numerical Value |
|---|---|
| Rated voltage U/V | 220 |
| Rated power P/W | 200 |
| Rated speed n/(r/min) | 3000 |
| Rated torque Te/(N∙M) | 10 |
| Rated current I/A | 1.5 |
| Rotor inertia J/(kg∙m2) | |
| Permanent magnet flux | 0.3477 |
| Stator resistance (between lines) Rs/ | 11.6 |
| Stator inductance (between lines) Ls/H | 0.022 |
| Switching frequency | |
| Polar logarithm P | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, C. Speed Control of PMSM Based on Fuzzy Active Disturbance Rejection Control under Small Disturbances. Appl. Sci. 2023, 13, 10775. https://doi.org/10.3390/app131910775
Zhang Q, Zhang C. Speed Control of PMSM Based on Fuzzy Active Disturbance Rejection Control under Small Disturbances. Applied Sciences. 2023; 13(19):10775. https://doi.org/10.3390/app131910775
Chicago/Turabian StyleZhang, Qi, and Caiyue Zhang. 2023. "Speed Control of PMSM Based on Fuzzy Active Disturbance Rejection Control under Small Disturbances" Applied Sciences 13, no. 19: 10775. https://doi.org/10.3390/app131910775
APA StyleZhang, Q., & Zhang, C. (2023). Speed Control of PMSM Based on Fuzzy Active Disturbance Rejection Control under Small Disturbances. Applied Sciences, 13(19), 10775. https://doi.org/10.3390/app131910775





