Study on the Frontal Collision Safety of Trains Based on Collision Dynamics
Abstract
:1. Introduction
2. Three-Dimensional Train Collision Dynamic Model
3. The Nonlinear Factors and Their Mathematical Models in a Multibody System
3.1. Mathematical Model for Wheel–Rail Contact
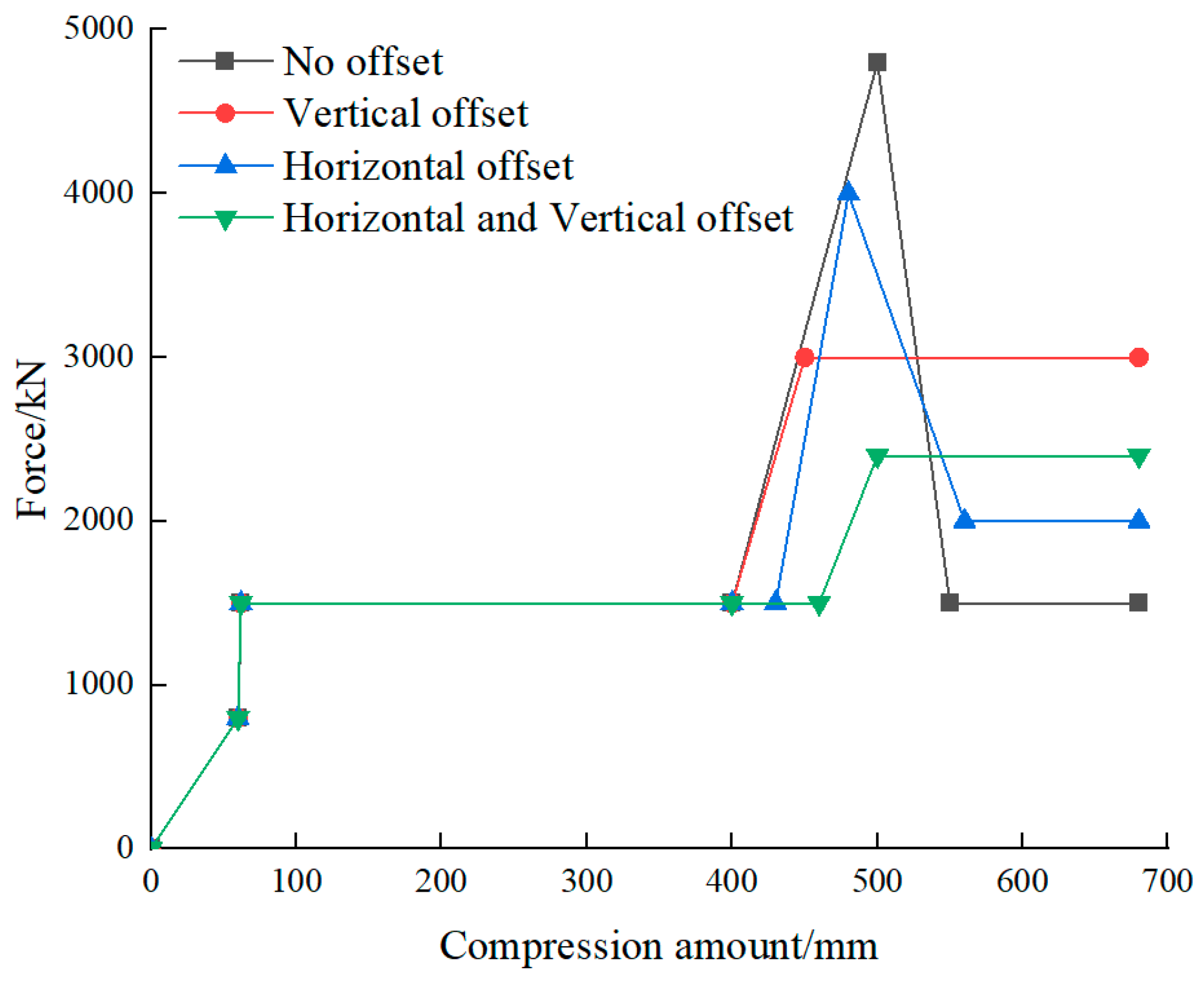
3.2. Mathematical Model for Car–End Contact
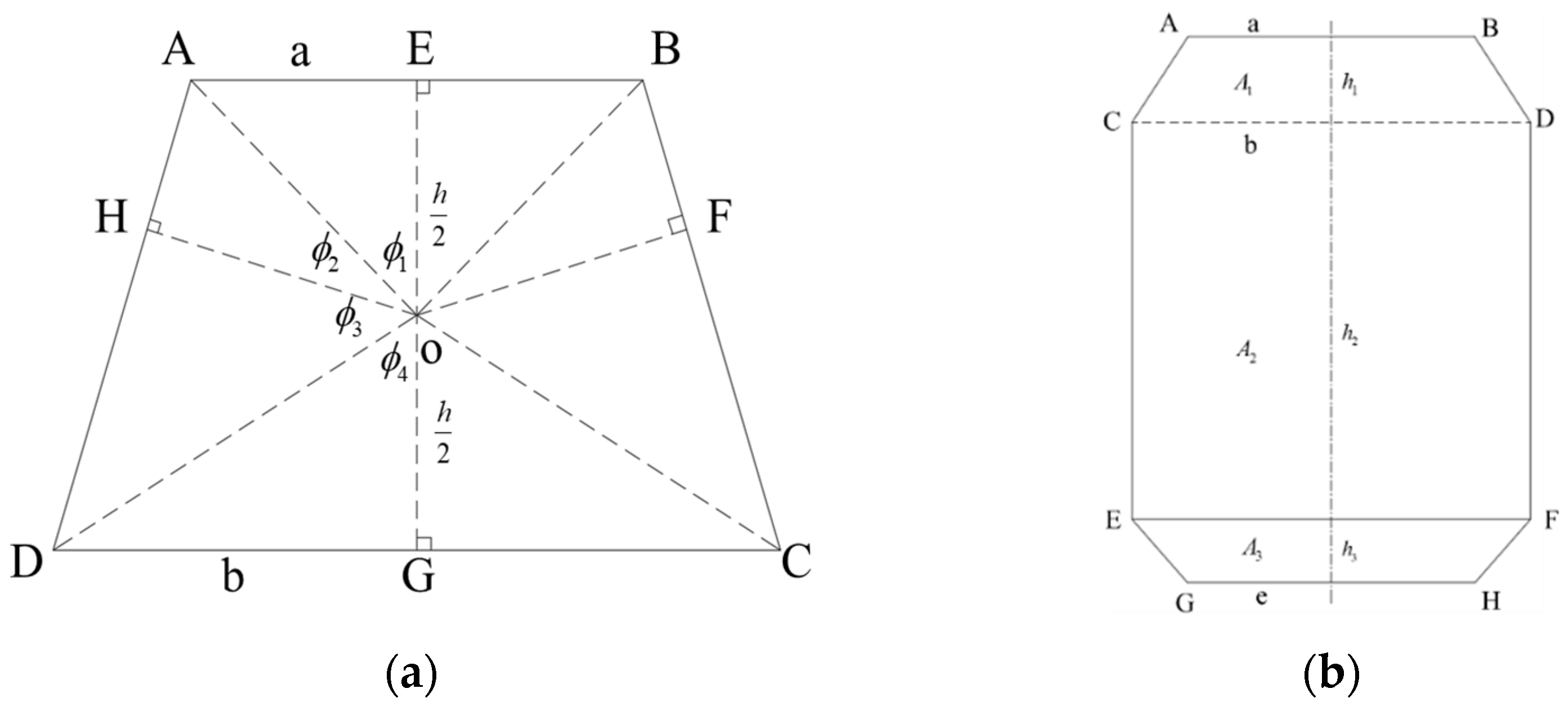
3.2.1. Shape Coefficient
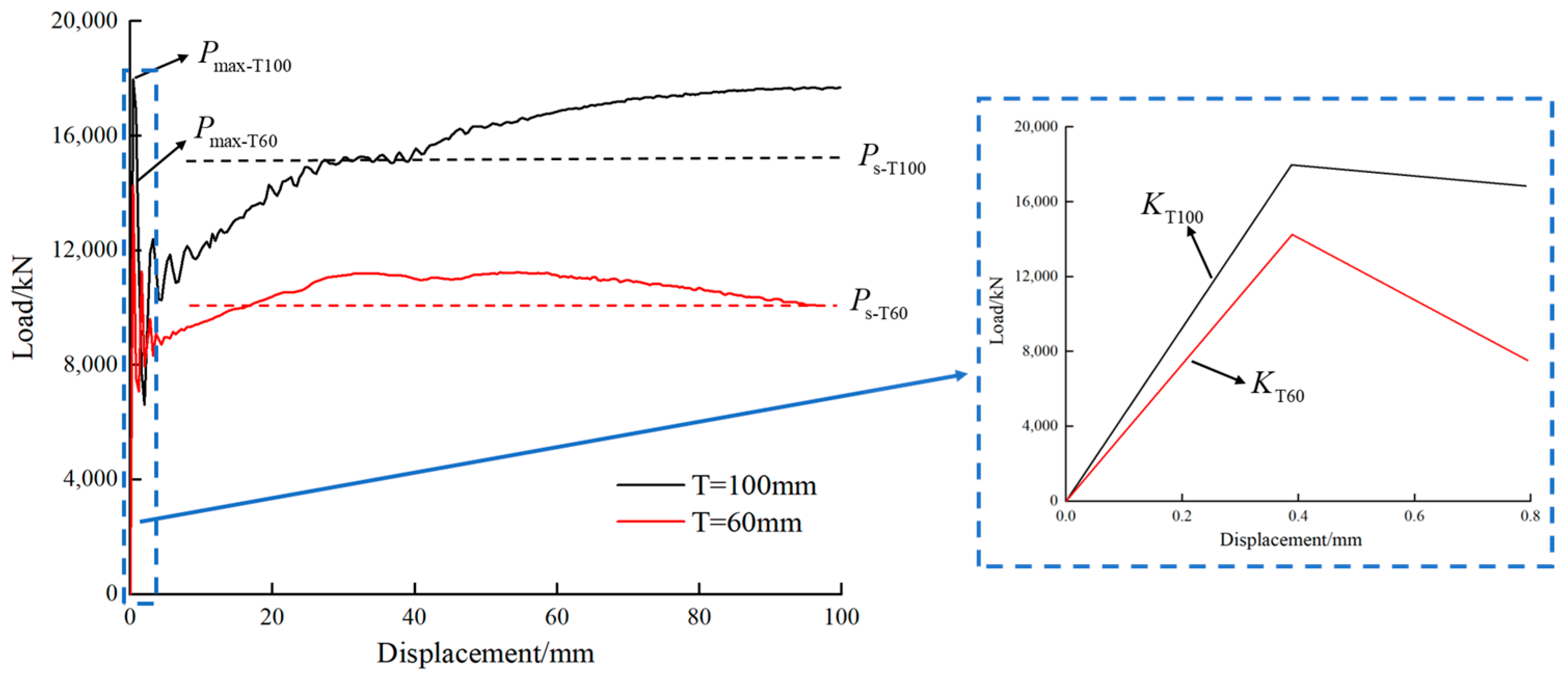
3.2.2. Stiffness Weakening Coefficient and Steady-State Coefficient
3.3. Mathematical Model for Coupler
3.4. Mathematical Model for Other Nonlinear Factors
4. Research on High-Speed Collision Safety of Trains and Results Analysis
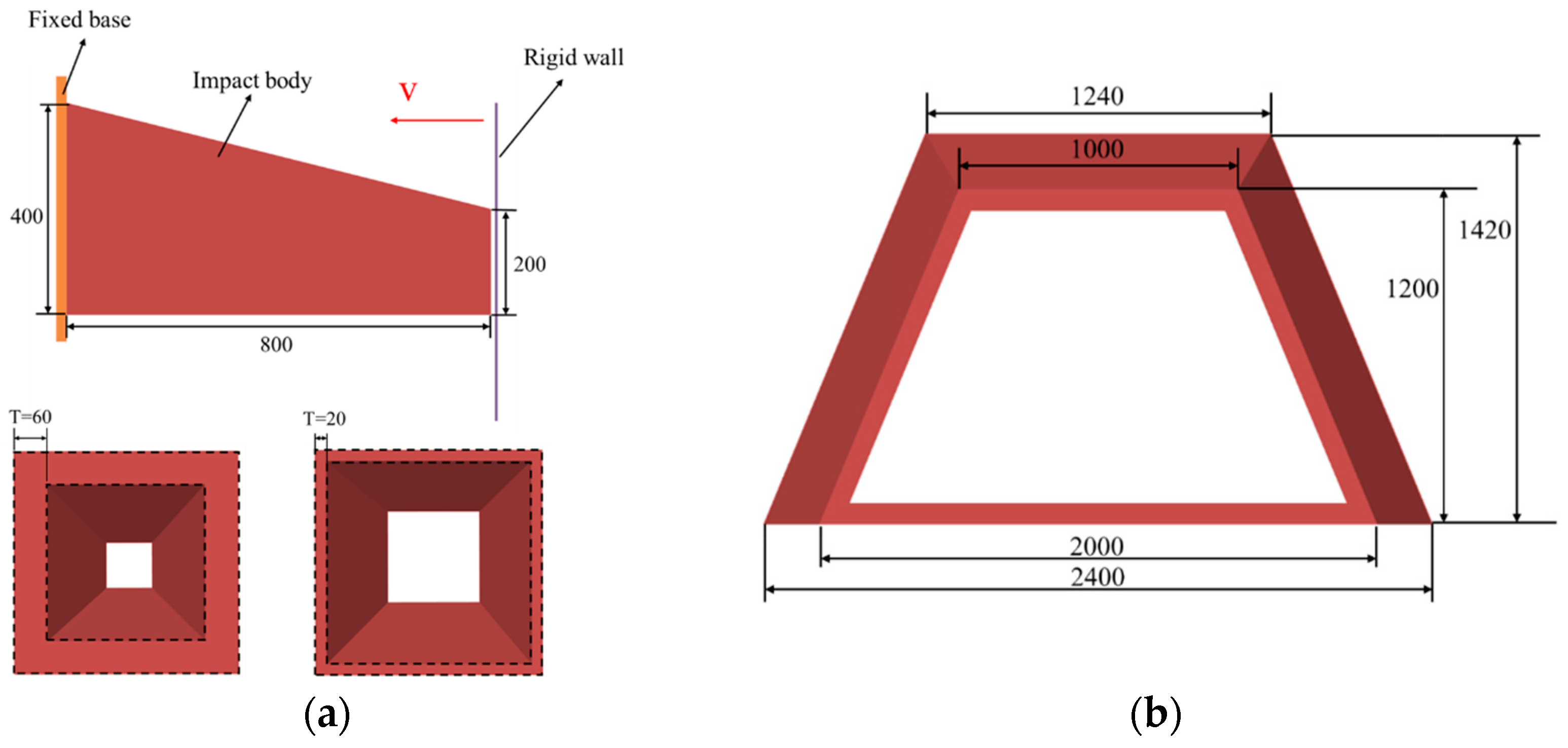
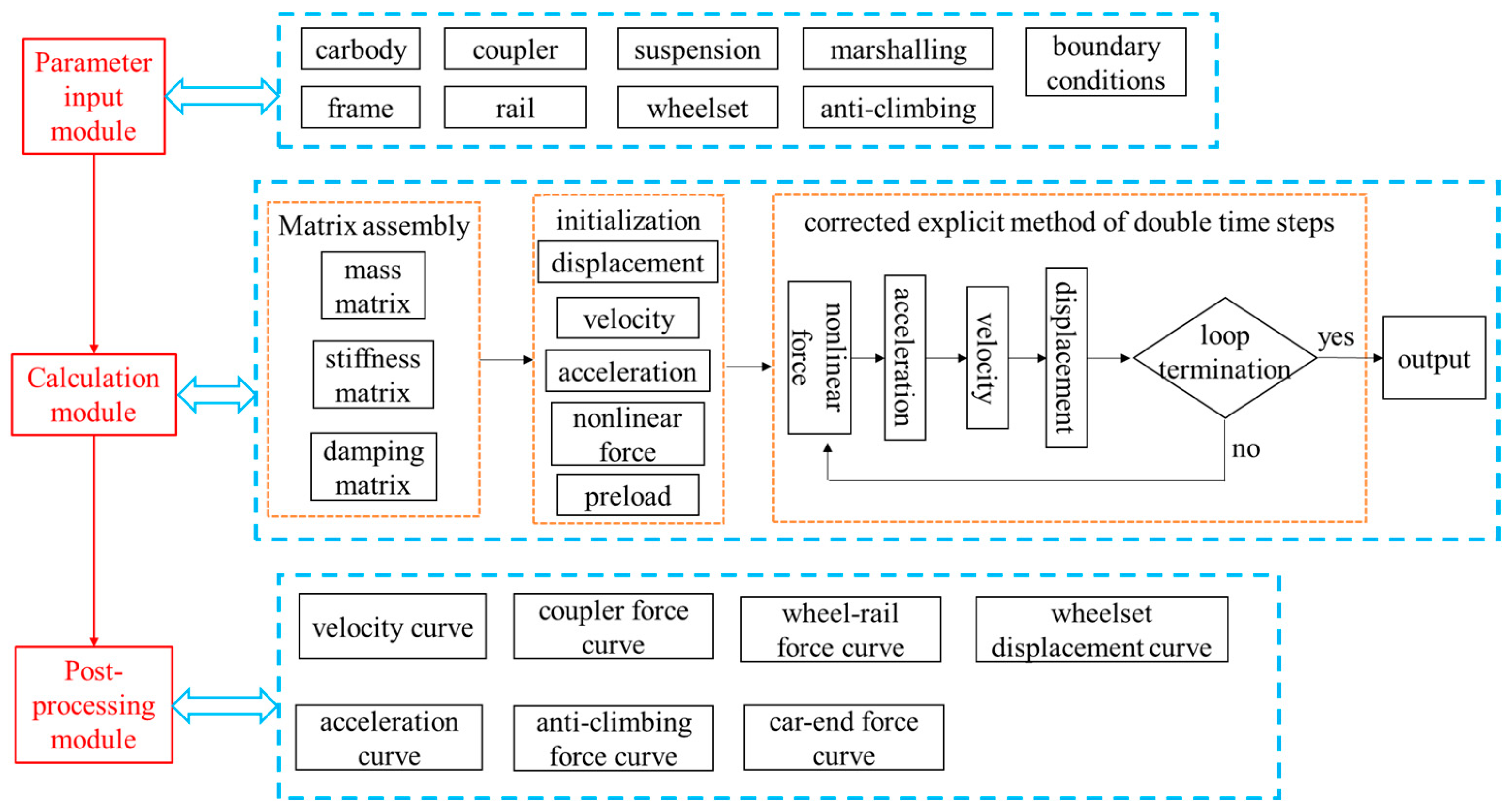
4.1. Dynamic Calculation Program and Collision Scenarios
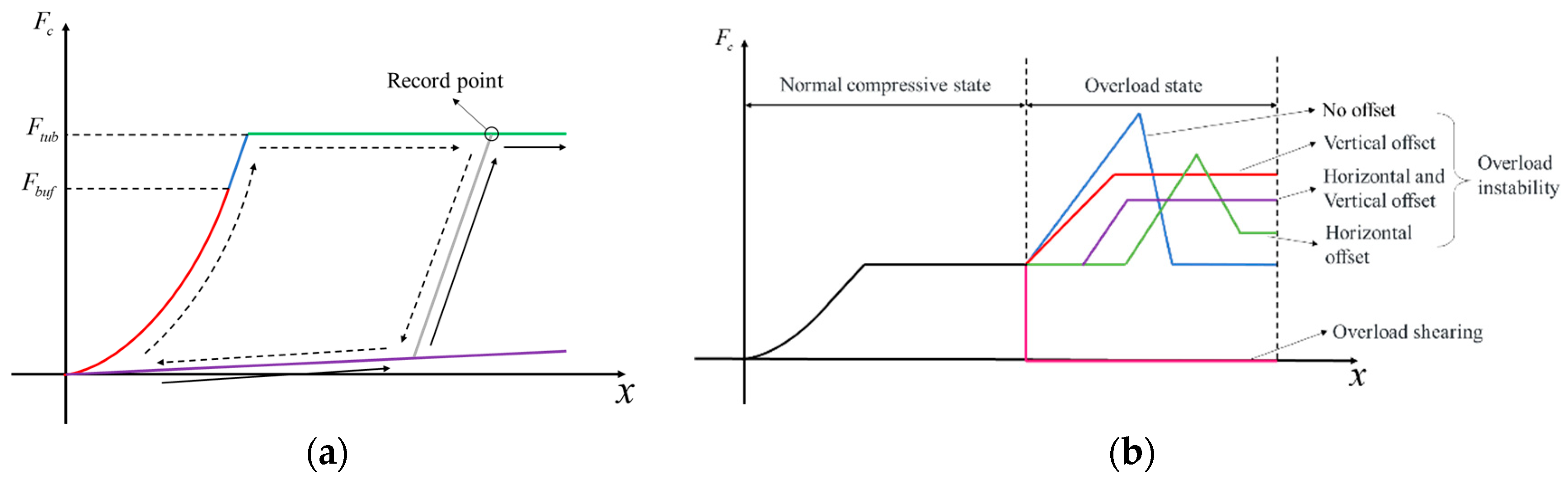
4.2. Assessment of Train Collision States
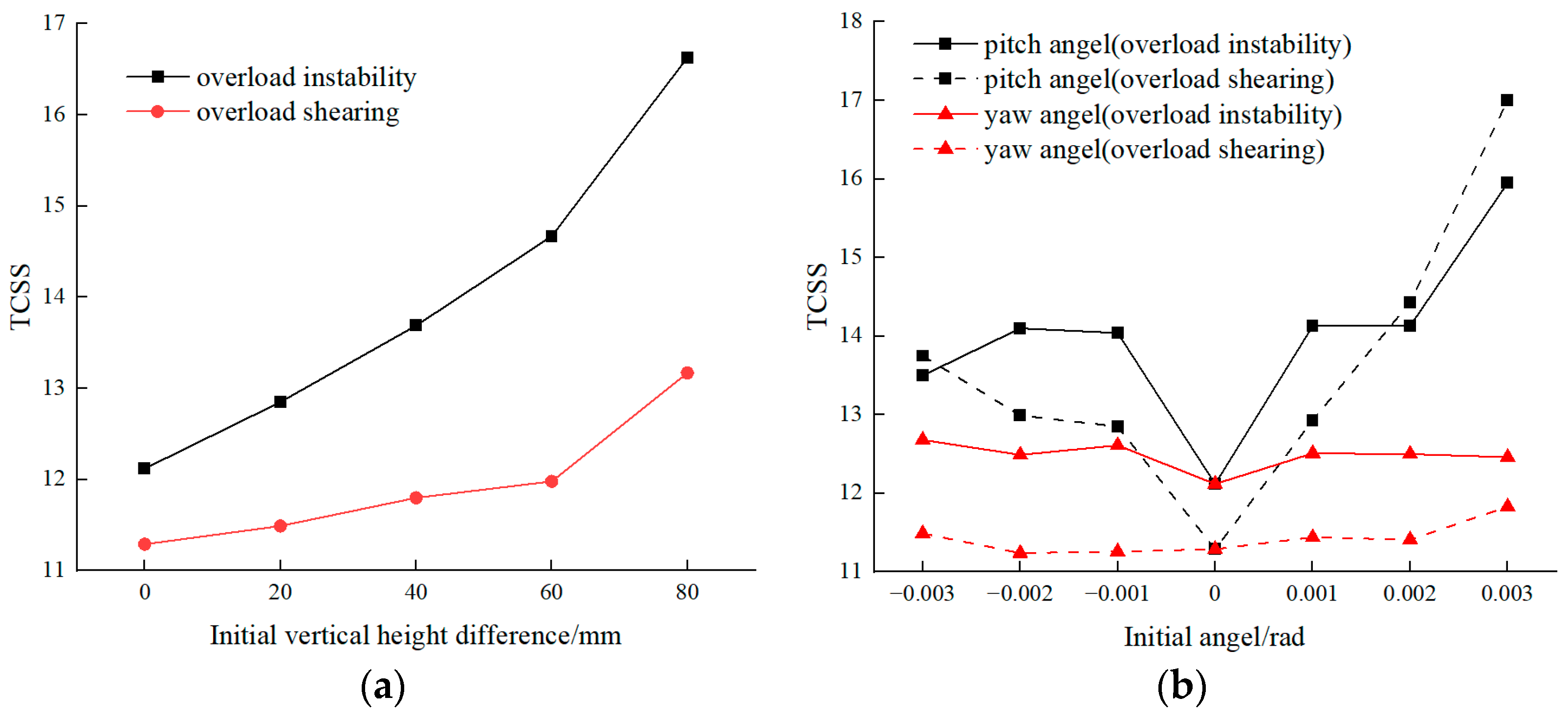
4.3. The Influence of Initial Attitude on Collisions
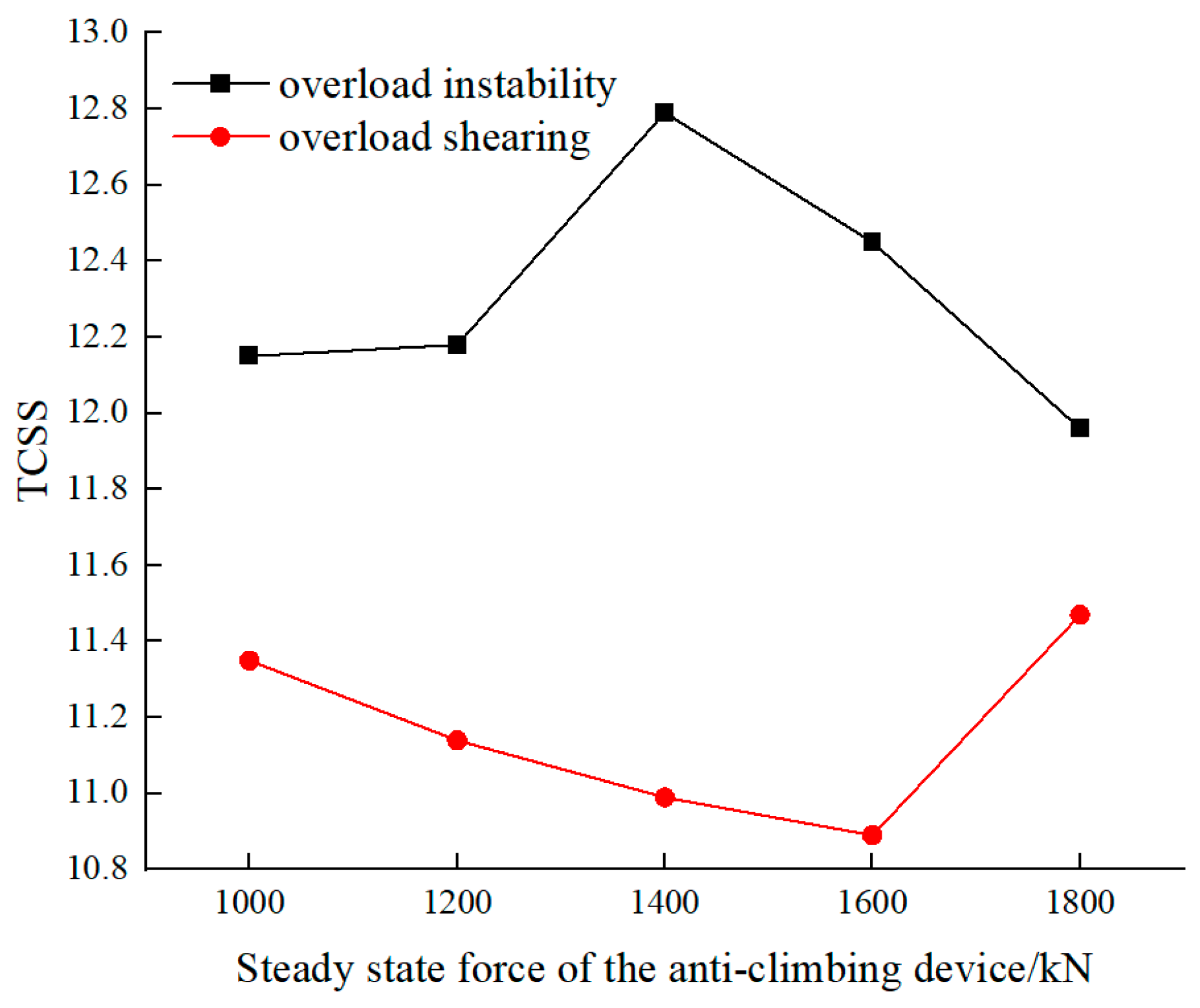
4.4. The Influence of Leading Car Energy-Absorbing Device Parameters on Collisions
5. Conclusions
- (1)
- The collision dynamic model considers the wheel–rail contact, car–end contact, and coupler overload issues in high-speed collisions. Based on mathematical models, simulation programs are developed to effectively simulate and calculate the problem of high-speed frontal train collisions;
- (2)
- A calculation method for car–end contact is established based on a typical compliant contact model, which can be used in the collision dynamic model. An engineering determination method for the coefficients in the calculation method is studied through finite element numerical simulations, enabling rapid calculation of the car–end contact force;
- (3)
- A collision dynamic simulation is conducted on a specific model of a high-speed train to investigate the impact of the initial attitude and parameters of the leading energy-absorption device on collision safety. The results indicate that an initial height difference and yaw angle will increase TCSS, making the train more dangerous after the collision;
- (4)
- Different overload states of the intermediate coupler lead to different effects of parameter variations in the leading energy-absorption device on TCSS. For trains with overload instability, TCSS shows a trend of initially increasing and then decreasing with the increase in force level of the energy-absorption device after the collision. On the other hand, trains with overload shearing exhibit the opposite trend. Therefore, it is necessary to select appropriate force levels for the energy-absorption device based on the actual situation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Location | Value | Location | Value |
|---|---|---|---|
| (1,1) | (1,2) (1,3) (2,1) (3,1) | ||
| (2,8) (8,2) | (2,2) (3,3) | ||
| (2,4) (2,5) (3,6) (3,7) (4,2) (5,2) (6,3) (7,3) | (3,8) (8,3) | ||
| (4,4) (5,5) (6,6) (7,7) | (4,9) (6,10) (9,4) (10,6) | ||
| (5,9) (7,10) (9,5) (10,7) | (8,8) | ||
| (8,9) (8,10) | (8,11) | ||
| (8,12) (8,13) | (9,8) (10,8) | ||
| (9,9) (10,10) | (9,11) (10,11) | ||
| (9,12) (10,13) | (9,14) (9,15) (10,16) (10,17) | ||
| (9,25) (10,25) | (9,26) (10,27) | ||
| (11,8) | (11,9) (11,10) | ||
| (11,11) | (11,12) (11,13) | ||
| (12,8) (13,8) | (12,9) (13,10) | ||
| (12,11) (13,11) | (12,12) (13,13) | ||
| (12,14) (12,15) (13,16) (13,17) (14,12) (15,12) (16,13) (17,13) | (14,9) (15,9) (16,10) (17,10) | ||
| (18,18) | (14,14) (15,15) (16,16) (17,17) | ||
| (18,25) (25,18) | (18,19) (18,20) (19,18) (20,18) | ||
| (19,21) (19,22) (20,23) (20,24) (21,19) (22,19) (23,20) (24,20) | (18,26) (18,27) | ||
| (19,26) (20,27) | (19,25) (20,25) (20,32) (25,19) (25,20) | ||
| (19,19) (20,20) | (19,32) | ||
| (21,26) (22,26) (23,27) (24,27) | (21,21) (22,22) (23,23) (24,24) | ||
| (22,33) (24,34) | (21,33) (23,34) | ||
| (25,26) (25,27) | (25,25) | ||
| (26,19) | (26,18) | ||
| (26,20) (26,21) (27,22) (27,23) | (26,26) (27,27) | ||
| (26,32) (32,26) | (26,25) (27,25) | ||
| (27,18) | (26,28) (26,29) (27,30) (27,31) (28,26) (29,26) (30,27) (31,27) | ||
| (27,32) (32,27) | (27,20) | ||
| (32,19) | (28,28) (29,29) (30,30) (31,31) | ||
| (32,32) | (32,20) | ||
| (35,33) (36,33) (37,34) (38,34) | (33,33) (34,34) | ||
| (35,35) (36,36) (37,37) (38,38) |
| Component | Mass/ kg | X-Axis Moment of Inertia/ | Y-Axis Moment of Inertia/ | Z-Axis Moment of Inertia/ |
|---|---|---|---|---|
| A1 carbody | 35,542 | 82,867 | 1.68 × 106 | 1.69 × 106 |
| A2 carbody | 33,937 | 86,337 | 1.95 × 106 | 1.95 × 106 |
| A3 carbody | 33,937 | 86,337 | 1.95 × 106 | 1.95 × 106 |
| A4 carbody | 35,542 | 82,867 | 1.68 × 106 | 1.69 × 106 |
| frame of power bogie | 3671 | 2895 | 1838 | 4582 |
| wheelset of power bogie | 2177 | 1581 | — | 1607 |
| frame of trailer bogie | 2724 | 2148 | 1364 | 3399 |
| wheelset of trailer bogie | 1642 | 1192 | — | 1212 |
| Component | Stiffness | Damping | |||
|---|---|---|---|---|---|
| Vertical | Longitudinal | Lateral | Vertical | Lateral | |
| primary suspension | 1.25 × 106 | 1.10 × 108 | 5.70 × 106 | 9.80 × 103 | 9.80 × 103 |
| secondary suspension | 3.85 × 105 | 9.00 × 105 | 5.70 × 106 | 3.60 × 104 | 3.60 × 104 |
| traction rod | - | 1.58 × 108 | - | - | - |
References
- Evans, A.W. Fatal train accidents on Europe’s railways: An update to 2019. Accid. Anal. Prev. 2021, 158, 106182. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.-Y.; Rapik Saat, M.; Barkan, C.P. Quantitative causal analysis of mainline passenger train accidents in the United States. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 869–884. [Google Scholar] [CrossRef]
- Xu, T.; Xu, P.; Zhao, H.; Yang, C.; Peng, Y. Vehicle running attitude prediction model based on Artificial Neural Network-Parallel Connected (ANN-PL) in the single-vehicle collision. Adv. Eng. Softw. 2023, 175, 103356. [Google Scholar] [CrossRef]
- Severson, K.J.; Parent, D.P.; Tyrell, D.C. (Eds.) Two-Car Impact Test of Crash-Energy Management Passenger Rail Cars: Analysis of Occupant Protection Measurements. In Proceedings of the ASME 2004 International Mechanical Engineering Congress and Exposition, Anaheim, CA, USA, 13 November 2004. [Google Scholar]
- Tyrell, D.; Jacobsen, K.; Martinez, E. (Eds.) Train-to-Train Impact Test of Crash Energy Management Passenger Rail Equipment: Structural Results. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006. [Google Scholar]
- Tyrell, D.; Severson, K.; Perlman, A.B. (Eds.) Rail Passenger Equipment Crashworthiness Testing Requirements and Implementation. In Proceedings of the ASME 2000 International Mechanical Engineering Congress and Exposition, Cambridge, MA, USA, 6 November 2000. [Google Scholar]
- Sutton, A. The development of rail vehicle crashworthiness. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2002, 216, 97–108. [Google Scholar] [CrossRef]
- Yao, S.; Yan, K.; Lu, S.; Xu, P. Energy-absorption optimisation of locomotives and scaled equivalent model validation. Int. J. Crashworth. 2017, 22, 1–12. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, G.; Guan, W.; Liu, R. Scale similitude rules with acceleration consistency for trains collision. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 2466–2480. [Google Scholar] [CrossRef]
- Li, J.; Gao, G.; Yu, Y.; Li, J. Similitude scaled method for three-dimensional train collision. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 237, 1–12. [Google Scholar] [CrossRef]
- Lu, S.; Wang, P.; Ni, W.; Yan, K.; Chen, Z. A mechanical equivalence similitude method for dynamic responses of high-speed train middle vehicles in a collision. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 237, 1–12. [Google Scholar] [CrossRef]
- Meran, A.P.; Baykasoglu, C.; Mugan, A.; Toprak, T. Development of a design for a crash energy management system for use in a railway passenger car. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 206–219. [Google Scholar] [CrossRef]
- Yao, S.; Zhu, H.; Yan, K.; Liu, M.; Xu, P. The derailment behaviour and mechanism of a subway train under frontal oblique collisions. Int. J. Crashworth. 2021, 26, 133–146. [Google Scholar] [CrossRef]
- Baykasoglu, C.; Mugan, A.; Sunbuloglu, E.; Bozdag, S.E.; Aruk, F.; Toprak, T. Rollover crashworthiness analysis of a railroad passenger car. Int. J. Crashworth. 2013, 18, 492–501. [Google Scholar] [CrossRef]
- Bae, H.-U.; Yun, K.-M.; Lim, N.-H. Containment capacity and estimation of crashworthiness of derailment containment walls against high-speed trains. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 680–696. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, L.; Tong, X.; Cui, K. Crashworthiness study of a subway vehicle collision accident based on finite-element methods. Int. J. Crashworth. 2021, 26, 159–170. [Google Scholar] [CrossRef]
- Song, Z.; Ming, S.; Li, T.; Du, K.; Zhou, C.; Wang, B. Improving the energy absorption capacity of square CFRP tubes with cutout by introducing chamfer. Int. J. Mech. Sci. 2021, 189, 105994. [Google Scholar] [CrossRef]
- Yang, H.; Lei, H.; Lu, G. Crashworthiness of circular fiber reinforced plastic tubes filled with composite skeletons/aluminum foam under drop-weight impact loading. Thin-Walled Struct. 2020, 160, 107380. [Google Scholar] [CrossRef]
- Baroutaji, A.; Arjunan, A.; Stanford, M.; Robinson, J.; Olabi, A.G. Deformation and energy absorption of additively manufactured functionally graded thickness thin-walled circular tubes under lateral crushing. Eng. Struct. 2021, 226, 111324. [Google Scholar] [CrossRef]
- Tang, Z.; Liu, F.J.; Guo, S.H.; Chang, J.; Zhang, J.J. Evaluation of coupled finite element/meshfree method for a robust full-scale crashworthiness simulation of railway vehicles. Adv. Mech. Eng. 2016, 8, 2071833383. [Google Scholar] [CrossRef]
- Xie, S.; Yang, W.; Ping, X. Simulation Analysis of a Multiple-Vehicle, High-Speed Train Collision Using a Simplified Model. Shock Vib. 2018, 2018, 9504141. [Google Scholar] [CrossRef]
- Yuan, C.B. Study on Longitudinal Impact Modeling and Energy Management Based on Train Collision Dynamics. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2018. [Google Scholar]
- Dias, J.; Pereira, M.S. Analysis and design for train crashworthiness using multibody models. Veh. Syst. Dyn. 2004, 40, 107–120. [Google Scholar]
- Ling, L.; Guan, Q.; Dhanasekar, M.; Thambiratnam, D.P. Dynamic simulation of train–truck collision at level crossings. Veh. Syst. Dyn. 2017, 55, 1–22. [Google Scholar] [CrossRef]
- Hou, L.; Peng, Y.; Sun, D. Dynamic analysis of railway vehicle derailment mechanism in train-to-train collision accidents. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2021, 235, 1022–1034. [Google Scholar] [CrossRef]
- Zhou, H.; Zhan, J.; Zhang, C. Simulation of the city tram collision at the level crossing. J. Mech. Eng. 2018, 54, 35–40. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, W.; Hecht, M. Three-dimensional derailment analysis of a crashed city tram. Veh. Syst. Dyn. 2013, 51, 1200–1215. [Google Scholar] [CrossRef]
- Yang, C. Research on Key Issues of Train Collision Dynamics. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Wang, K.W. Calculation of the wheel contact trajectory and wheel-rail contact geometric parameters. J. Southwest Jiaotong Univ. 1984, 1, 89–99. [Google Scholar]
- Luo, L.; Nahon, M. Development and Validation of Geometry-Based Compliant Contact Models. J. Comput. Nonlinear Dyn. 2010, 6, 011004. [Google Scholar] [CrossRef]
- Luo, L. Development and validation of a geometry-based contact force model. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 2010. [Google Scholar]
- Zhang, J.; Zhu, T.; Yang, B.; Wang, X.; Xiao, S.; Yang, G.; Liu, Y. Collision characteristics of the intermediate coupler of a rail vehicle. Veh. Syst. Dyn. 2022, 1–22. [Google Scholar] [CrossRef]


| Fitting Formula Value | Numerical Simulation Value | Relative Error | |
|---|---|---|---|
| stiffness weakening coefficient | 0.166 | 0.175 | 5.14% |
| steady state coefficient | 0.673 | 0.714 | 5.74% |
| Device Name | Buffer | Collapse Tube | Shearing Force/ N | Contact Stiffness/ | ||
|---|---|---|---|---|---|---|
| Stiffness/ | Stroke/ m | Stiffness/ | Stroke/ m | |||
| heading coupler | 1.00 × 107 | 0.10 | 1.50 × 106 | 1.30 | 1.55 × 106 | - |
| intermediate coupler | 1.33 × 107 | 0.06 | 1.50 × 106 | 0.34 | 1.55 × 106 | - |
| anti-climbing | - | - | 1.00 × 106 | 0.50 | - | 5.00 × 107 |
| stop | - | - | - | - | - | 1.00 × 107 |
| Notation | Value | Notation | Value | ||
|---|---|---|---|---|---|
| cab end front section/ m | a1 | 0.57 | intermediate end section/ m | a | 1.08 |
| b1 | 0.96 | b | 1.58 | ||
| h1 | 0.91 | e | 1.15 | ||
| cab end rear section/ m | a2 | 1.23 | h1 | 0.81 | |
| b2 | 1.62 | h2 | 1.15 | ||
| h2 | 2.54 | h3 | 0.91 | ||
| Scheme | Stroke/ mm | Force/ kN | TCSS | |
|---|---|---|---|---|
| Overload Instability | Overload Shearing | |||
| Scheme 1 | 1620 | 1200 | 12.21 | 11.50 |
| Scheme 2 | 1500 | 1300 | 12.22 | 11.27 |
| Scheme 3 | 1390 | 1400 | 12.33 | 11.35 |
| Scheme 4 | 1300 | 1500 | 12.15 | 11.35 |
| Scheme 5 | 1220 | 1600 | 12.20 | 11.50 |
| Scheme 6 | 1150 | 1700 | 12.16 | 11.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhu, T.; Xiao, S. Study on the Frontal Collision Safety of Trains Based on Collision Dynamics. Appl. Sci. 2023, 13, 10805. https://doi.org/10.3390/app131910805
Li Z, Zhu T, Xiao S. Study on the Frontal Collision Safety of Trains Based on Collision Dynamics. Applied Sciences. 2023; 13(19):10805. https://doi.org/10.3390/app131910805
Chicago/Turabian StyleLi, Zongzhi, Tao Zhu, and Shoune Xiao. 2023. "Study on the Frontal Collision Safety of Trains Based on Collision Dynamics" Applied Sciences 13, no. 19: 10805. https://doi.org/10.3390/app131910805
APA StyleLi, Z., Zhu, T., & Xiao, S. (2023). Study on the Frontal Collision Safety of Trains Based on Collision Dynamics. Applied Sciences, 13(19), 10805. https://doi.org/10.3390/app131910805





