Analysis of Low-Frequency Communication of Hypersonic Vehicles in Thermodynamic and Chemical Non-Equilibrium State
Abstract
:1. Introduction
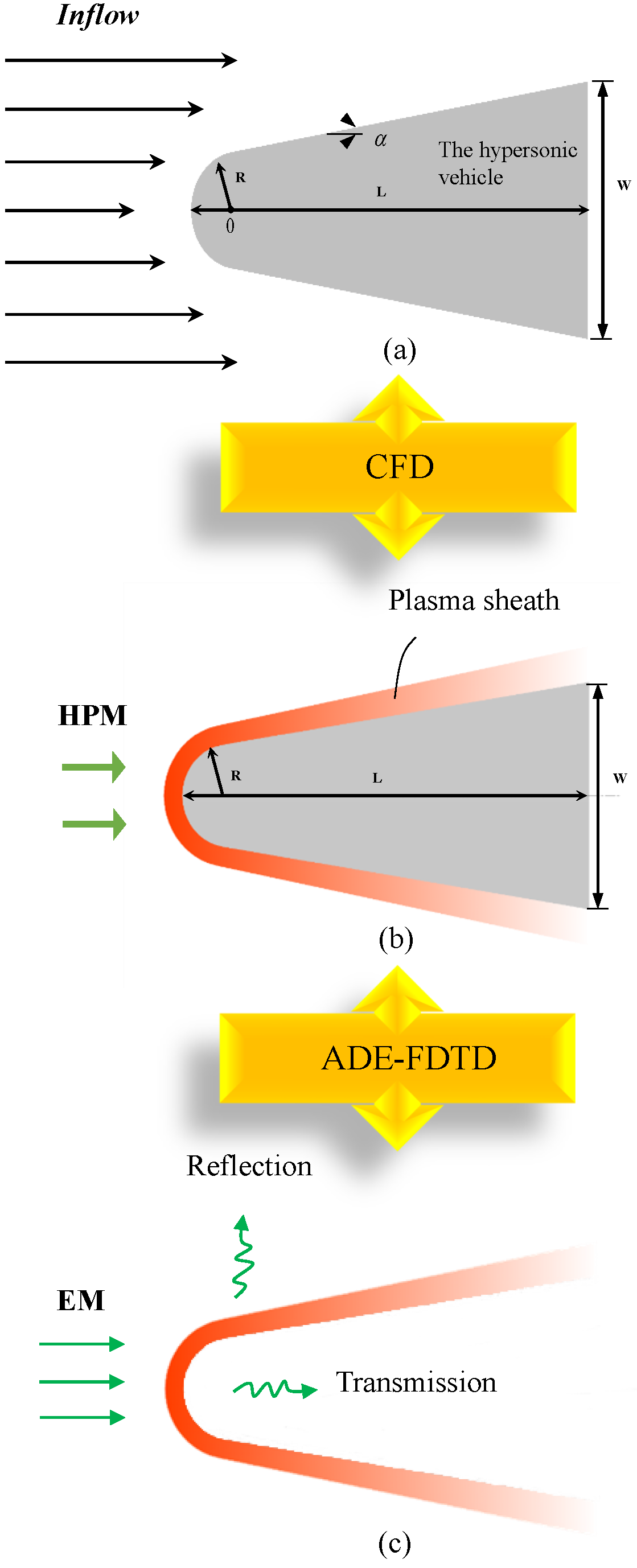
2. Simulation of Plasma Sheath Fluid Model
2.1. Fluid Dynamics Model
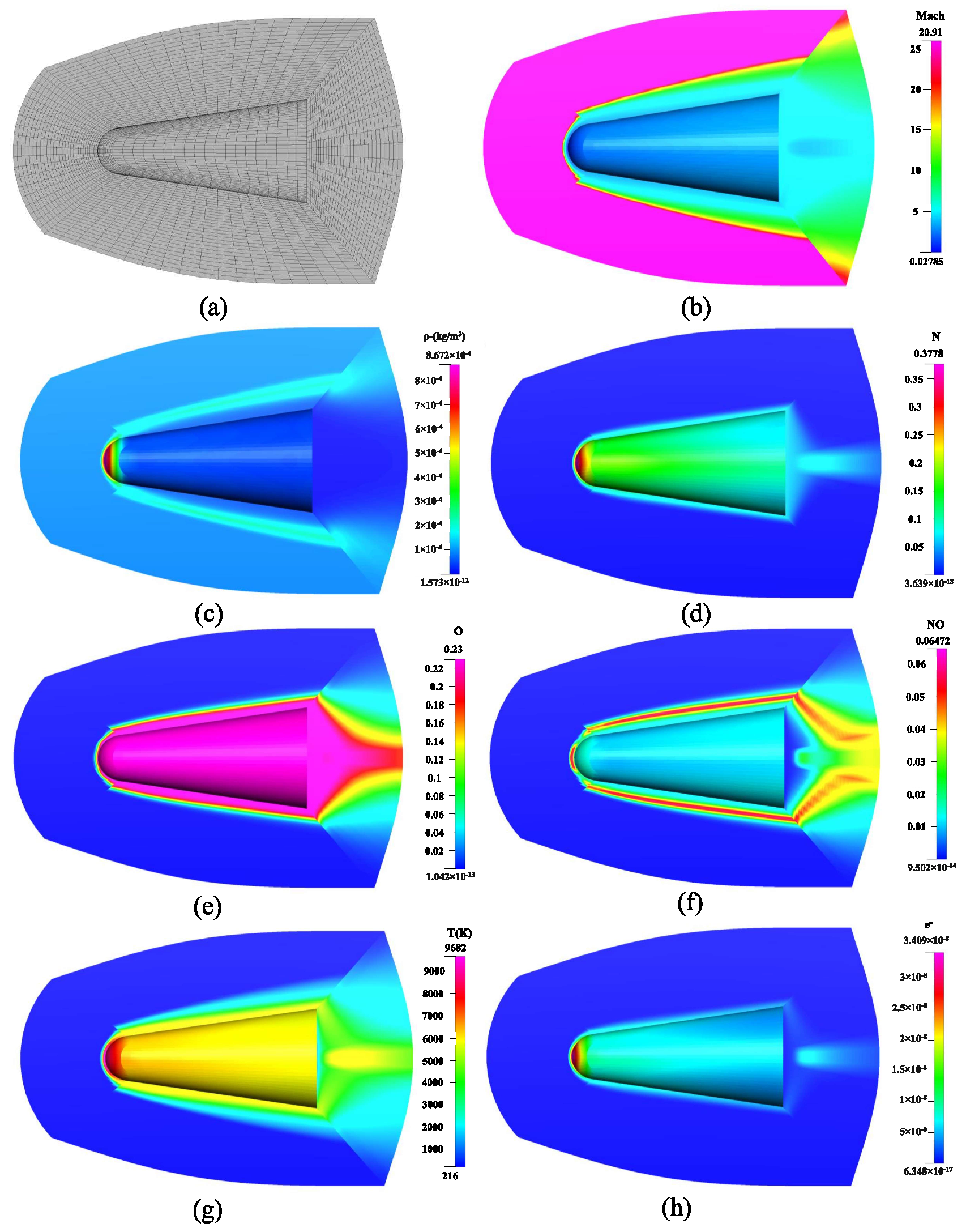
2.2. Numerical Simulation Results
3. Interaction between Plasma Sheath and HPM
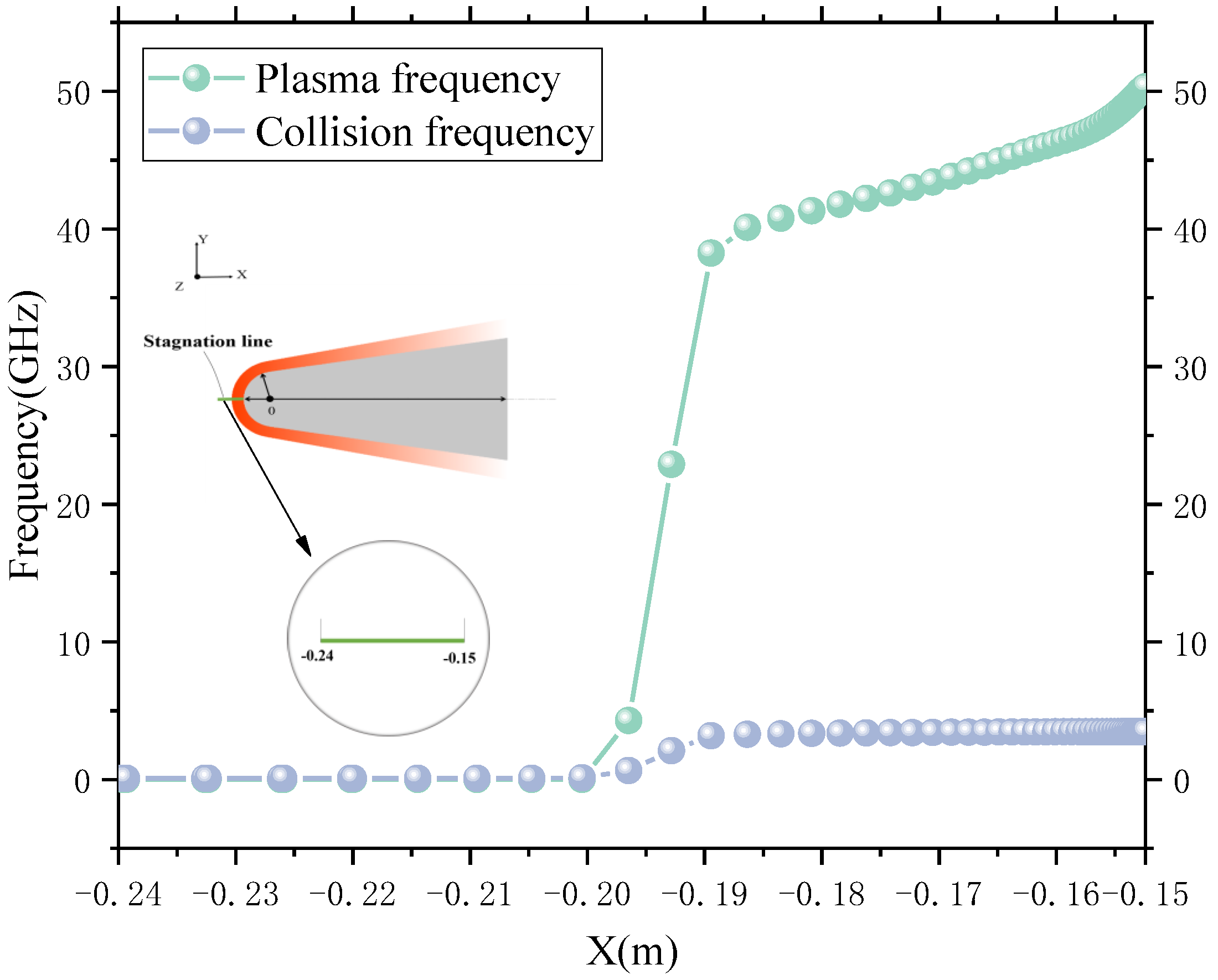
3.1. The EM Properties of Plasma Sheath
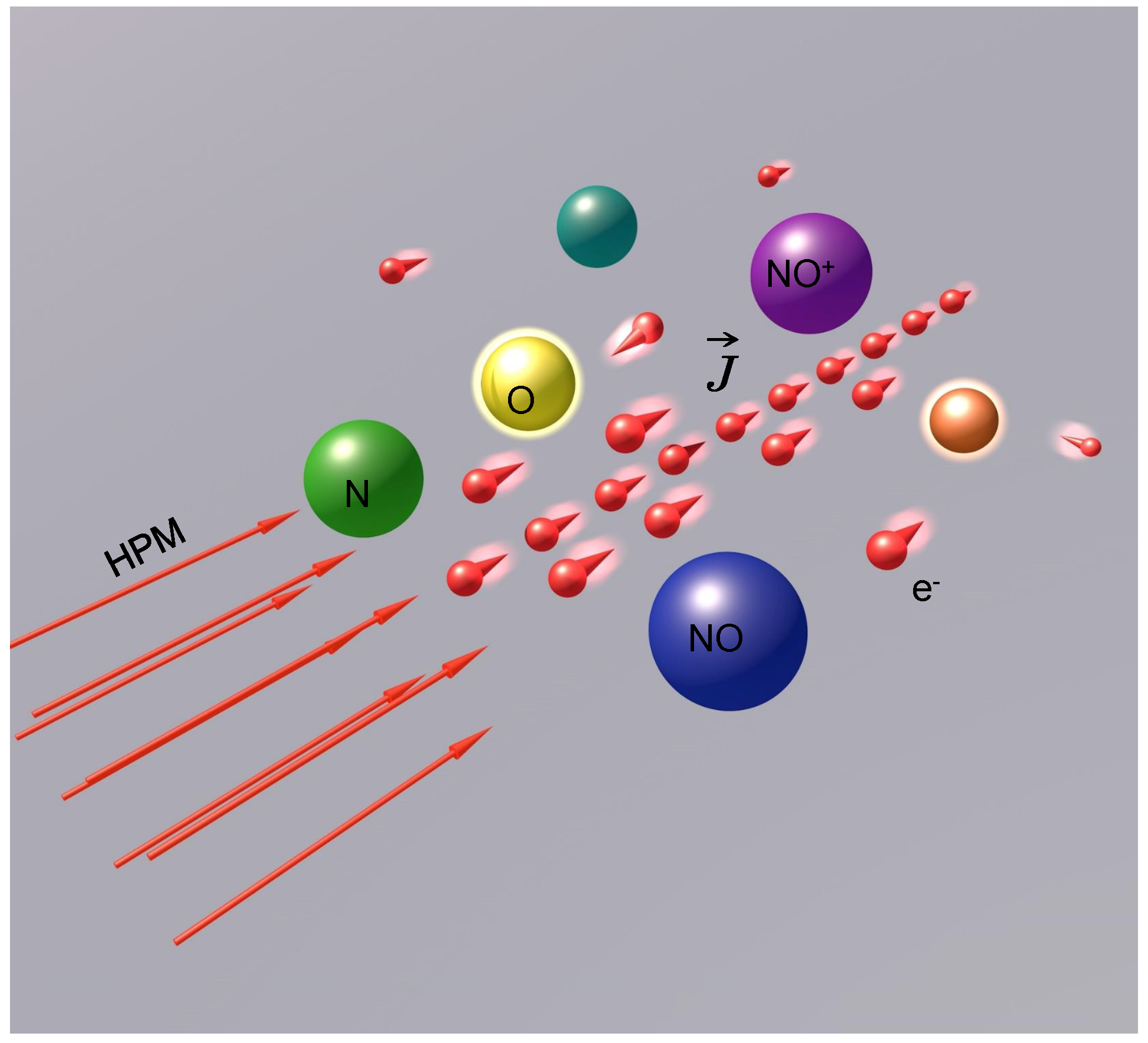
3.2. Particle Model in Thermodynamic Non-Equilibrium State
4. Simulation of Low-Frequency Communication in Plasma Sheath
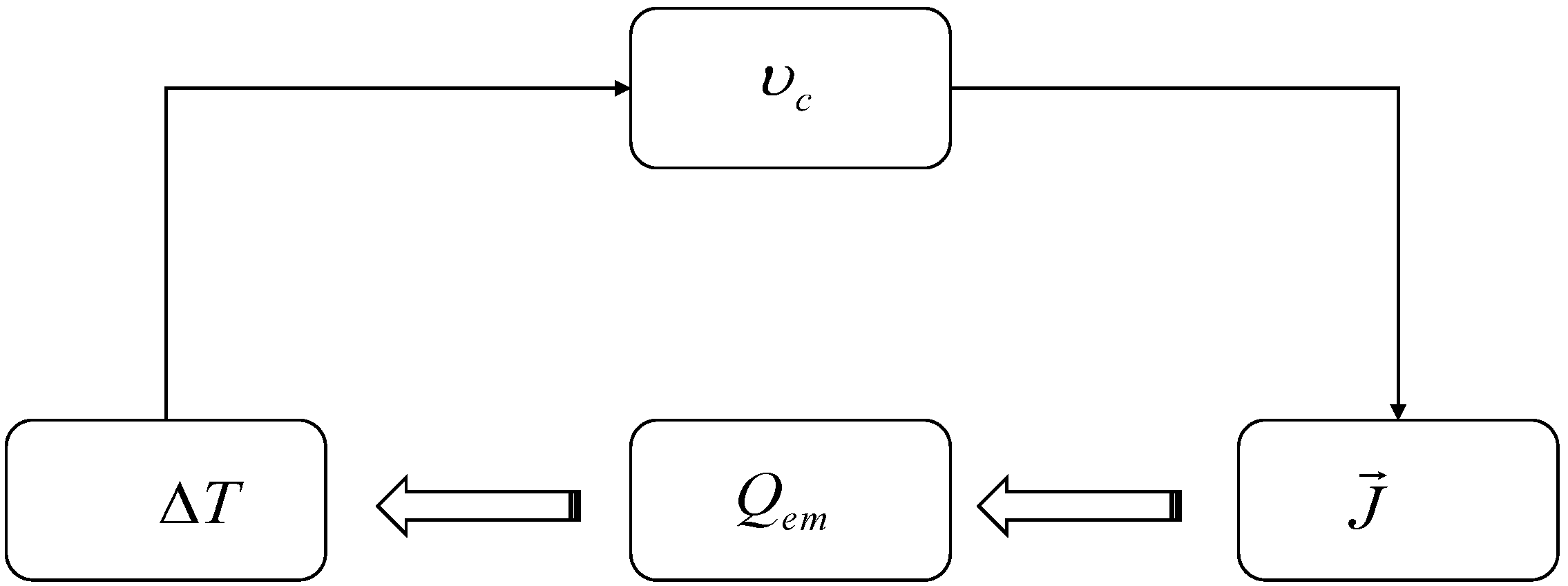
4.1. Temperature Increment Model
4.2. Propagation Characteristics of Low-Frequency EM Waves in Plasma Sheath
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, J.D. Hypersonic and High Temperature Gas Dynamics; AIAA: San Diego, CA, USA, 2000. [Google Scholar]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Bai, B.; Zhao, Z.; Yuan, K.; Tang, R.; Deng, X.; Mao, M.; Xiong, J.; Wang, K. Characteristics of EHF Wave Propagation in Hypersonic Plasma Sheaths Magnetized by Dipole Magnetic Fields. Appl. Sci. 2022, 12, 3105. [Google Scholar] [CrossRef]
- NASA. The Entry Plasma Sheath and its Effect on Space Vehicle Electromagnetic Systems; NASA Special Publication; NASA: Washington, DC, USA, 1971; Volume 252. [Google Scholar]
- Albano, M.; Micheli, D.; Gradoni, G.; Morles, R.B.; Marchetti, M.; Moglie, F.; Primiani, V.M. Electromagnetic shielding of thermal protection system for hypersonic vehicles. Acta Astronaut. 2013, 87, 30–39. [Google Scholar] [CrossRef]
- Hansen, C.; Heims, S.P. A Review of the Thermodynamic, Transport, and Chemical Reaction Rate Properties of High-Temperature Air; Technical Report Archive and Image Library; Ames Aeronautical Laboratory: Moffett Field, CA, USA, 1958. [Google Scholar]
- Tam, L.T.; Li, C.P. Three-dimensional thermochemical nonequilibrium flow modeling for hypersonic flows. AIAA J. 1989, 1860. [Google Scholar]
- Dobrov, Y.; Karpenko, A.; Malkovsky, S.; Sorokin, A.; Volkov, K. Simulation of high-temperature flowfield around hypersonic waverider using graphics processor units. Acta Astronaut. 2022, 204, 745–760. [Google Scholar] [CrossRef]
- Zuo, F.Y.; Mölder, S.; Hu, S.L. Thermochemical non-equilibrium effects on hypersonic wavecatcher intake at Mach 12. Acta Astronaut. 2022, 198, 56–68. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, J.; Luo, S.; Huang, W.; Wang, J.; Liu, M. Thermochemical non-equilibrium effects on hypersonic shock wave/turbulent boundary-layer interaction. Acta Astronaut. 2022, 192, 1–14. [Google Scholar] [CrossRef]
- Dobrov, Y.; Gimadiev, V.; Karpenko, A.; Volkov, K. Numerical simulation of hypersonic flow with non-equilibrium chemical reactions around sphere. Acta Astronaut. 2022, 194, 468–479. [Google Scholar] [CrossRef]
- Mohammadi Estakhri, N.; Edwards, B.; Engheta, N. Inverse-designed metastructures that solve equations. Science 2019, 363, 1333–1338. [Google Scholar] [CrossRef]
- Akbari, M.; Shahbazzadeh, M.J.; La Spada, L.; Khajehzadeh, A. The graphene field effect transistor modeling based on an optimized ambipolar virtual source model for DNA detection. Appl. Sci. 2021, 11, 8114. [Google Scholar] [CrossRef]
- Lalegani, Z.; Ebrahimi, S.S.; Hamawandi, B.; La Spada, L.; Batili, H.; Toprak, M. Targeted dielectric coating of silver nanoparticles with silica to manipulate optical properties for metasurface applications. Mater. Chem. Phys. 2022, 287, 126250. [Google Scholar] [CrossRef]
- Lincoln, R.L.; Scarpa, F.; Ting, V.P.; Trask, R.S. Multifunctional composites: A metamaterial perspective. Multifunct. Mater. 2019, 2, 043001. [Google Scholar] [CrossRef]
- Pacheco-Peña, V.; Beruete, M.; Rodríguez-Ulibarri, P.; Engheta, N. On the performance of an ENZ-based sensor using transmission line theory and effective medium approach. New J. Phys. 2019, 21, 043056. [Google Scholar] [CrossRef]
- Greybush, N.J.; Pacheco-Peña, V.; Engheta, N.; Murray, C.B.; Kagan, C.R. Plasmonic optical and chiroptical response of self-assembled Au nanorod equilateral trimers. ACS Nano 2019, 13, 1617–1624. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; He, M.; Li, X.; Zhang, C. Multiphysics modeling of electromagnetic wave-hypersonic vehicle interactions under high-power microwave illumination: 2-D case. IEEE Trans. Antennas Propag. 2018, 66, 3653–3664. [Google Scholar] [CrossRef]
- Yan, S.; Greenwood, A.; Jin, J.M. Modeling of Plasma Formation During High-Power Microwave Breakdown in Air Using the Discontinuous Galerkin Time-Domain Method. IEEE J. Multiscale Multiphysics Comput. Tech. 2017, 1, 2–13. [Google Scholar] [CrossRef]
- Wang, K.; Li, J. Analyses of Multiphysical Model of Electromagnetic and Fluid in Thermodynamic Equilibrium and Chemical Nonequilibrium State. IEEE Trans. Microw. Theory Tech. 2021, 69, 5228–5240. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications. Comput. Fluid Dyn. Princ. Appl. 2001, 55, 5–22. [Google Scholar]
- Prabhu, R.K.; Stewart, J.R.; Thareja, R.R. A Navier–Stokes solver for high speed equilibrium flows and application to blunt bodies. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989; p. 668. [Google Scholar]
- Taflove, A.; Hagness, S.C.; Piket-May, M. Computational electromagnetics: The finite-difference time-domain method. In The Electrical Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2005; Volume 3. [Google Scholar]
- Takayama, Y.; Klaus, W. Reinterpretation of the auxiliary differential equation method for FDTD. IEEE Microw. Wirel. Components Lett. 2002, 12, 102–104. [Google Scholar] [CrossRef]
- Duan, X.; Hong, W.Y.; Han, L.; Li, A. Auxiliary Differential Equation FDTD Method of Plasma in Parallel Environment. J. Infrared Millim. Terahertz Waves 2009, 30, 860–867. [Google Scholar] [CrossRef]
- Gupta, R.N.; Yos, J.M.; Thompson, R.A. A Review of Reaction Rates and Thermodynamic and Transport Properties for the 11-Species Air Model for Chemical and Thermal Nonequilibrium Calculations to 30,000 K; NASA: Washington, DC, USA, 1989. [Google Scholar]
- Mitcheltree, R.A.; Gnoffo, P.A. Thermochemical nonequilibrium issues for earth reentry of Mars mission vehicles. J. Spacecr. Rocket. 1990, 28, 552–559. [Google Scholar] [CrossRef]
- Shuen, J.S.; Chen, K.H.; Choi, Y. A coupled implicit method for chemical non-equilibrium flows at all speeds. J. Comput. Phys. 1993, 106, 306–318. [Google Scholar] [CrossRef]
- Shuen, J.S.; Liou, M.S.; Leer, B.V. Inviscid flux-splitting algorithms for real gases with non-equilibrium chemistry. J. Comput. Phys. 1990, 90, 371–395. [Google Scholar] [CrossRef]
- Jones, W.L., Jr.; Cross, A.E. Electrostatic-Probe Measurements of Plasma Parameters for Two Reentry Flight Experiments at 25,000 Feet per Second; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1972. [Google Scholar]
- Nagaraj, N.; Lombard, C.K.; Bardina, J. Navier–Stokes simulation of 3-D hypersonic equilibrium air flow. In Proceedings of the 23rd Thermophysics, Plasmadynamics and Lasers Conference, San Antonio, CA, USA, 27–29 June 1988; p. 2695. [Google Scholar]
- Sha, Y.X.; Zhang, H.L.; Guo, X.Y.; Xia, M.Y. Analyses of electromagnetic properties of a hypersonic object with plasma sheath. IEEE Trans. Antennas Propag. 2019, 67, 2470–2481. [Google Scholar] [CrossRef]
- Yuan, Z.C.; Shi, J.M. Electron collision frequency of the non-magnetized plasma. Hejubian Dengliziti Wuli/Nuclear Fusion Plasma Phys. 2004, 24, 157–160. [Google Scholar]
- Cummer, S.A. An analysis of new and existing FDTD methods for isotropic cold plasma and a method for improving their accuracy. Antennas Propag. IEEE Trans. 1997, 45, 392–400. [Google Scholar] [CrossRef]
- Chen, Q.; Katsurai, M.; Aoyagi, P.H. An FDTD formulation for dispersive media using a current density. IEEE Trans. Antennas Propag. 1998, 46, 1739–1746. [Google Scholar] [CrossRef]
- Kelley, D.F.; Luebbers, R.J. Piecewise linear recursive convolution for dispersive media using FDTD. IEEE Trans. Antennas Propag. 1996, 44, 792–797. [Google Scholar] [CrossRef]
- Luebbers, R.; Steich, D. FDTD calculation of scattering from frequency-dependent materials. IEEE Trans. Antennas Propag. 1993, 41, 1249–1257. [Google Scholar] [CrossRef]
- Qian, Z.; Chen, R.; Yang, H.; Leung, K. FDTD analysis of microstrip patch antenna covered by plasma sheath. Prog. Electromagn. Res. 2004, 52, 173–183. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, N.; Mo, J. A novel FDTD formulation for dispersive media. IEEE Microw. Wirel. Components Lett. 2003, 13, 187–189. [Google Scholar]
- Xu, L.; Yuan, N. PLJERC-ADI-FDTD method for isotropic plasma. IEEE Microw. Wirel. Components Lett. 2005, 15, 277–279. [Google Scholar]
- Nickisch, L.J.; Franke, P.M. Finite-difference time-domain solution of Maxwell’s equations for the dispersive ionosphere. IEEE Antennas Propag. Mag. 1992, 34, 33–39. [Google Scholar] [CrossRef]
- Gandhi, O.P.; Gao, B.-Q. A frequency-dependent finite-difference time-domain formulation for general dispersive media. IEEE Trans. Microw. Theory Tech. 1993, 41, 658–665. [Google Scholar] [CrossRef]
- Park, C. Assessment of two-temperature kinetic model for ionizing air. J. Thermophys. Heat Transf. 1989, 3, 233–244. [Google Scholar] [CrossRef]
- Park, C. A review of reaction rates in high temperature air. In Proceedings of the 24th Thermophysics Conference, Buffalo, NY, USA, 12–14 June 1989; p. 1740. [Google Scholar]
- Shengtao, Y.U.; Hsieh, K.; Shuen, J.; Mcbride, B. Numerical simulation of hypersonic inlet flows with equilibrium or finite rate chemistry. In Proceedings of the 26th Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1988. [Google Scholar]
- Gnoffo, P.A.; Gupta, R.N.; Shinn, J.L. Conservation Equations and Physical Models for Hypersonic Air Flows in Thermal and Chemical Nonequilibrium; National Aeronautics and Space Administration, Office of Management, Scientific and Technical Information Division: Washington, DC, USA, 1989.
- Min, Y.; Li, X.; Kai, X.; Liu, Y. Parasitic modulation of electromagnetic signals caused by time-varying plasma. Phys. Plasmas 2015, 22, 022120. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Chen, X.; Wen, Z. Analysis of Low-Frequency Communication of Hypersonic Vehicles in Thermodynamic and Chemical Non-Equilibrium State. Appl. Sci. 2023, 13, 10815. https://doi.org/10.3390/app131910815
Wang K, Chen X, Wen Z. Analysis of Low-Frequency Communication of Hypersonic Vehicles in Thermodynamic and Chemical Non-Equilibrium State. Applied Sciences. 2023; 13(19):10815. https://doi.org/10.3390/app131910815
Chicago/Turabian StyleWang, Kaijie, Xuequan Chen, and Zhongkai Wen. 2023. "Analysis of Low-Frequency Communication of Hypersonic Vehicles in Thermodynamic and Chemical Non-Equilibrium State" Applied Sciences 13, no. 19: 10815. https://doi.org/10.3390/app131910815



