Node2Node: Self-Supervised Cardiac Diffusion Tensor Image Denoising Method
Abstract
:1. Introduction
2. Methods
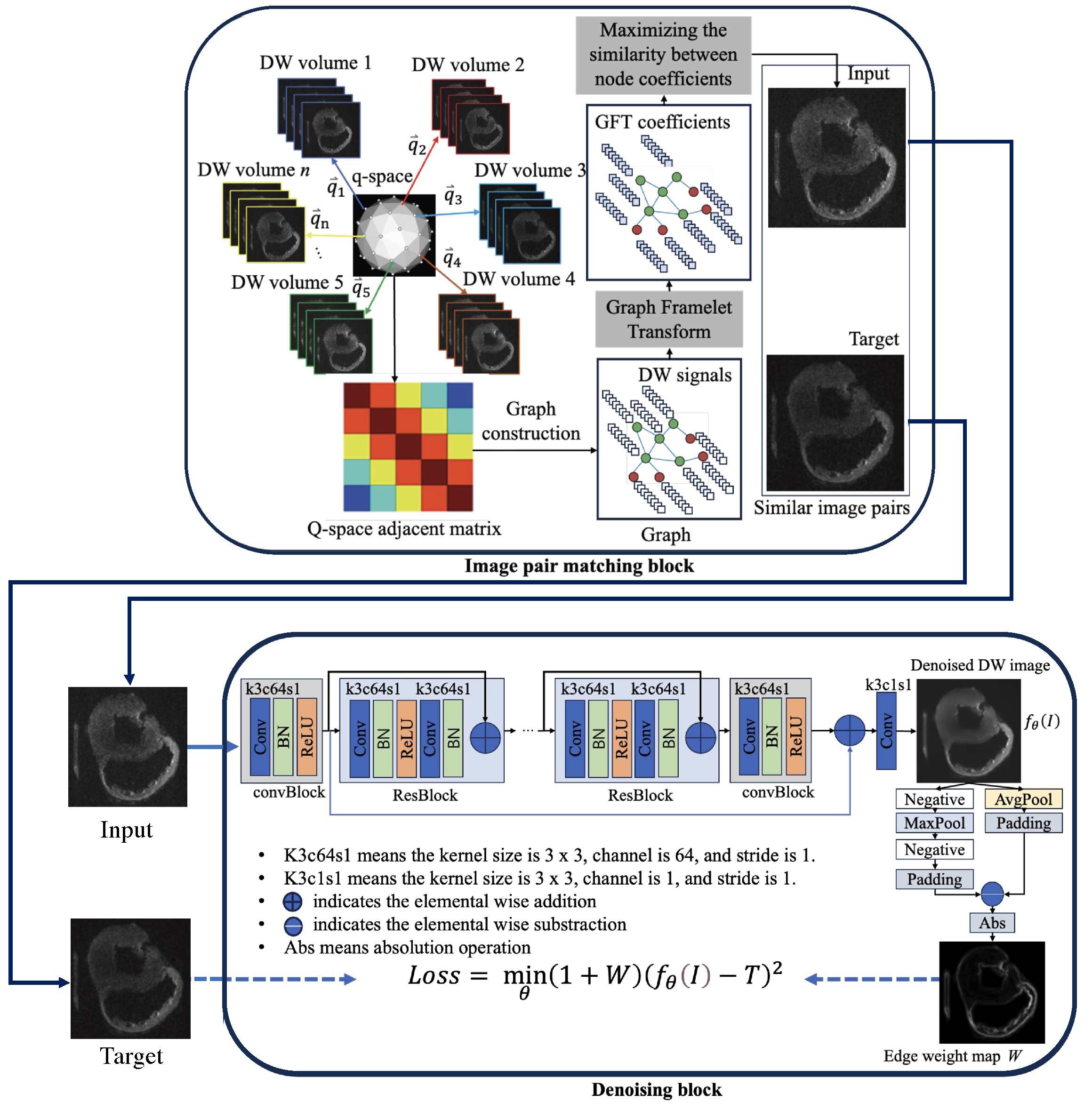
2.1. The Overall Structure of the Node2Node Network
| Algorithm 1 DW noisy image pair matching algorithm |
| Require: : the ith diffusion gradient direction, , n is the number of directions. : the DW image along ith diffusion direction , , : the hand-crafted hyper-parameters
|
2.2. Loss Functions
3. Experiments
3.1. Datasets
- (1)
- Synthetic data: To quantitatively evaluate the performance of the proposed denoising method, we synthesized noise-free DW images using Phantoms (http://www.emmanuelcaruyer.com/phantomas.php, accessed on 12 December 2021). with a b-value of 1000 s/mm and six diffusion gradient directions. The fiber structure setting is the same as that used in the ISBI 2013 HARDI challenge. The DW image size is , and the spatial resolution is mm. To obtain the noisy images, random Gaussian noise with level of 10% was added to the clean image five times, resulting in a total of 1650 noisy DW images.
- (2)
- Ex vivo porcine cardiac DTI data: This dataset was provided by the cardiac MRI research (CMR) group at Stanford University (https://med.stanford.edu/cmrgroup/data/ex_vivo_dt_mri.html, accessed on 22 November 2022). It comprises seven ex vivo porcine hearts that were imaged using a SIEMENS Prisma_fit scanner with a diffusion sequence, TE = 58 ms, TR = 16,670 ms, and 30 diffusion gradient directions with b-value of 1000 s/mm, conducted five times. The image spatial resolution is mm, and the image size is . That means that there are a total of 126,000 DW images in this dataset.
- (3)
- In vivo human cardiac DTI data at multiple cardiac phases: This in vivo human cardiac DTI dataset was also provided by Standord University (https://med.stanford.edu/cmrgroup/data/myofiber_data.html, accessed on 30 June 2023). It contains the cardiac DW images of nine healthy volunteers acquired using a 3T MRI scanner (Prisma, Siemens) and a single-shot spin EPI sequence incorporated with second-order (M1–M2) motion-compensated gradient. For each subject, only one mid-ventricular short-axis slice was imaged at early systole, end systole, and end diastole phases, respectively. The acquisition parameters are: TE = 61 ms, matrix size = 128 × 104, in-plane resolution = mm, slice thickness = 8 mm, b-value = 350 s/mm, and number of diffusion gradient directions = 12. Each subject was scanned eight times, meaning a total of 96 DW images were acquired per cardiac phase. In total, there are 864 images in this dataset.
3.2. Experimental Implementations
3.3. Evaluation Metrics
4. Results
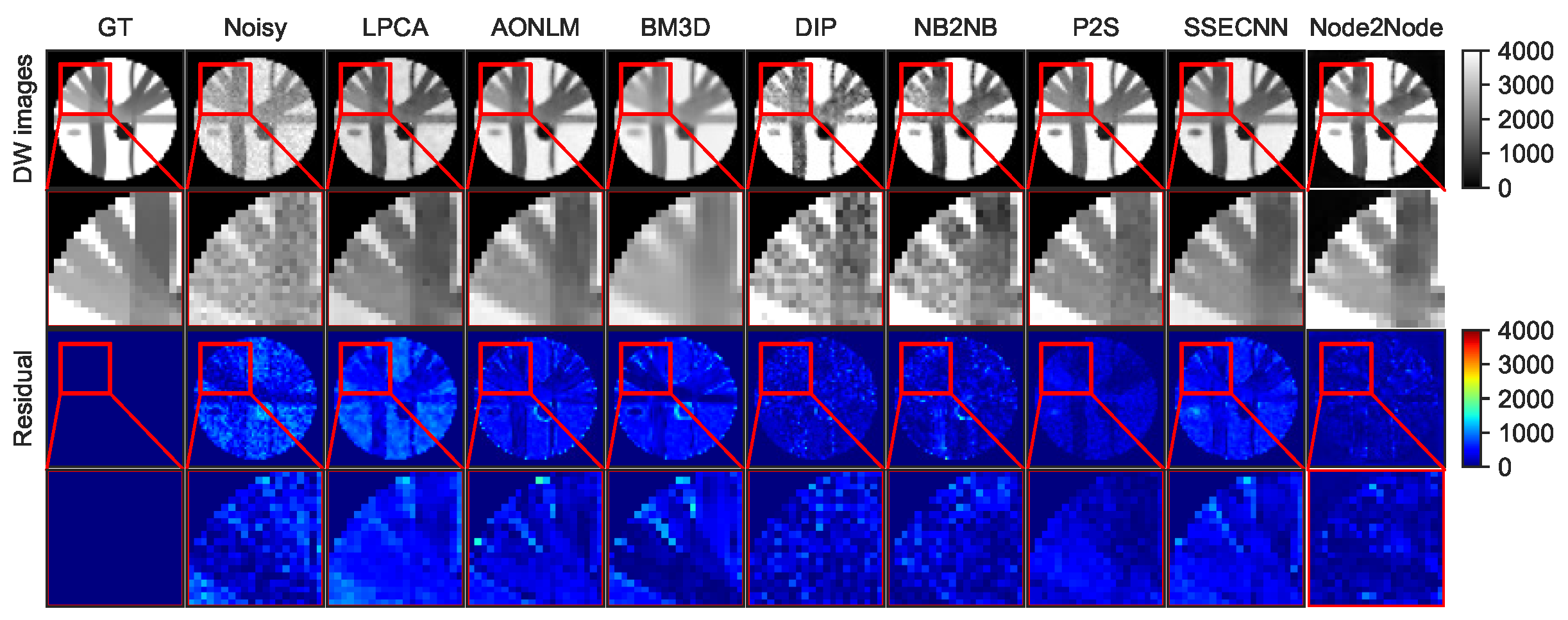
4.1. Denoising Results for Synthetic Dataset
4.2. Denoising Results for Real Data
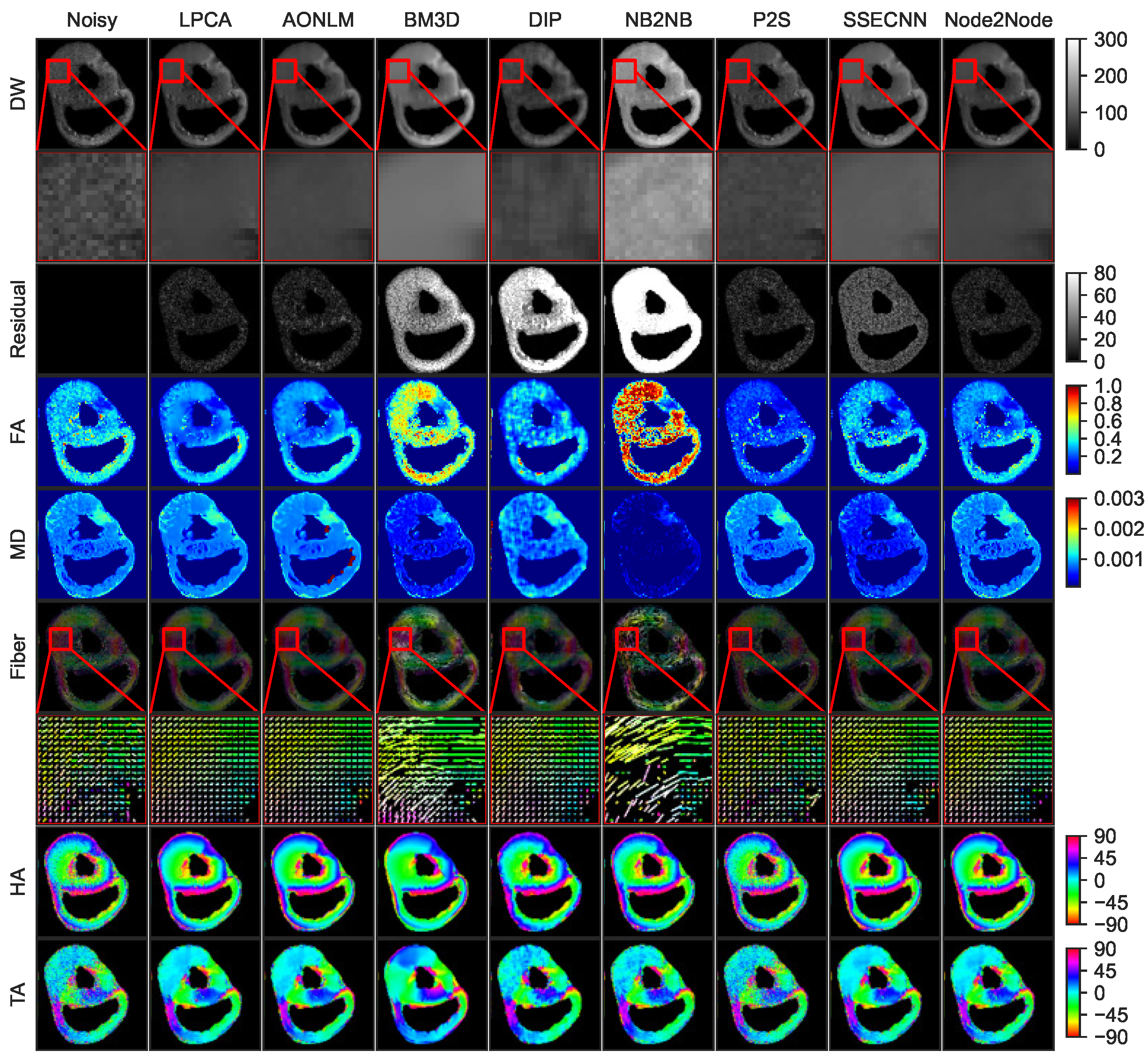
4.2.1. Denoising Results for Ex Vivo Porcine Cardiac DTI
4.2.2. Denoising Results for In Vivo Human Cardiac DTI
4.2.3. Quantitative Comparisons with SOTA Methods on Real Datasets
4.3. Ablation Results
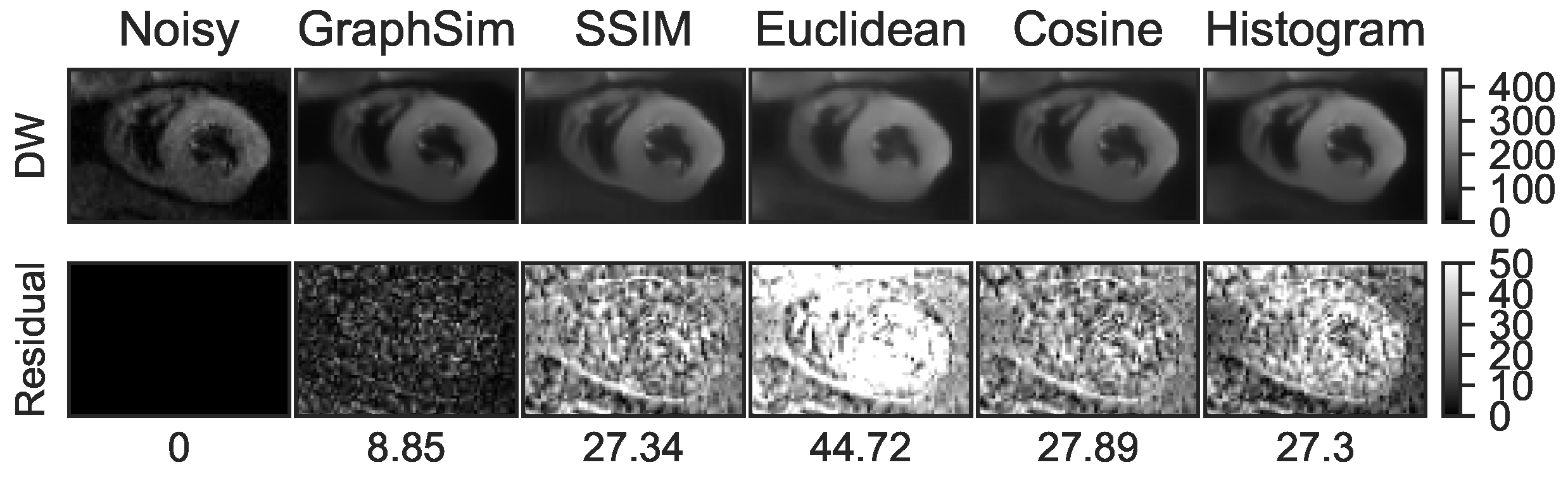
4.3.1. Comparisons in Image Pair Matching Strategies
4.3.2. Effects of the Edge-Weighted Loss
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mozaffarian, D.; Benjamin, E.; Go, A.; Arnett, D.; Blaha, M.; Cushman, M.; Das, S.; de Ferranti, S.; Després, J.; Fullerton, H.; et al. Executive Summary: Heart Disease and Stroke Statistics—2016 Update: A Report From the American Heart Association. Circulation 2016, 133, 447. [Google Scholar] [CrossRef] [PubMed]
- Münzel, T.; Gori, T.; Keaney, J.F., Jr.; Maack, C.; Daiber, A. Pathophysiological role of oxidative stress in systolic and diastolic heart failure and its therapeutic implications. Eur. Heart J. 2015, 36, 2555–2564. [Google Scholar] [CrossRef] [PubMed]
- Jorge, E.; Amorós-Figueras, G.; García-Sánchez, T.; Bragós, R.; Rosell-Ferrer, J.; Cinca, J. Early detection of acute transmural myocardial ischemia by the phasic systolic-diastolic changes of local tissue electrical impedance. Am. J. Physiol. Heart Circ. Physiol. 2016, 310, H436–H443. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Canadilla, P.; Cook, A.C.; Mohun, T.J.; Oji, O.; Schlossarek, S.; Carrier, L.; McKenna, W.J.; Moon, J.C.; Captur, G. Myoarchitectural disarray of hypertrophic cardiomyopathy begins pre-birth. J. Anat. 2019, 235, 962–976. [Google Scholar] [CrossRef] [PubMed]
- Wiest-Daesslé, N.; Prima, S.; Coupé, P.; Morrissey, S.P.; Barillot, C. Non-local means variants for denoising of diffusion-weighted and diffusion tensor MRI. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Brisbane, Australia, 29 October–2 November 2007; pp. 344–351. [Google Scholar]
- Coupé, P.; Manjón, J.V.; Robles, M.; Collins, D.L. Adaptive multiresolution non-local means filter for three-dimensional magnetic resonance image denoising. IET Image Process. 2012, 6, 558–568. [Google Scholar] [CrossRef]
- Lam, F.; Babacan, S.D.; Haldar, J.P.; Weiner, M.W.; Schuff, N.; Liang, Z.P. Denoising diffusion-weighted magnitude MR images using rank and edge constraints. Magn. Reson. Med. 2014, 71, 1272–1284. [Google Scholar] [CrossRef] [PubMed]
- Lam, F.; Liu, D.; Song, Z.; Schuff, N.; Liang, Z.P. A fast algorithm for denoising magnitude diffusion-weighted images with rank and edge constraints. Magn. Reson. Med. 2016, 75, 433–440. [Google Scholar] [CrossRef] [PubMed]
- Gramfort, A.; Poupon, C.; Descoteaux, M. Denoising and fast diffusion imaging with physically constrained sparse dictionary learning. Med. Image Anal. 2014, 18, 36–49. [Google Scholar] [CrossRef]
- Kong, Y.; Li, Y.; Wu, J.; Shu, H. Noise reduction of diffusion tensor images by sparse representation and dictionary learning. Biomed. Eng. Online 2016, 15, 5. [Google Scholar] [CrossRef]
- Awate, S.P.; Whitaker, R.T. Feature-preserving MRI denoising: A nonparametric empirical Bayes approach. IEEE Trans. Med. Imaging 2007, 26, 1242–1255. [Google Scholar] [CrossRef]
- Gonzalez, J.E.I.; Thompson, P.M.; Zhao, A.; Tu, Z. Modeling diffusion-weighted MRI as a spatially variant Gaussian mixture: Application to image denoising. Med. Phys. 2011, 38, 4350–4364. [Google Scholar] [CrossRef] [PubMed]
- Raj, A.; Hess, C.; Mukherjee, P. Spatial HARDI: Improved visualization of complex white matter architecture with Bayesian spatial regularization. NeuroImage 2011, 54, 396–409. [Google Scholar] [CrossRef] [PubMed]
- Manjón, J.V.; Coupé, P.; Martí-Bonmatí, L.; Collins, D.L.; Robles, M. Adaptive non-local means denoising of MR images with spatially varying noise levels. J. Magn. Reson. Imaging 2010, 31, 192–203. [Google Scholar] [CrossRef] [PubMed]
- Manjón, J.V.; Coupé, P.; Concha, L.; Buades, A.; Collins, D.L.; Robles, M. Diffusion weighted image denoising using overcomplete local PCA. PLoS ONE 2013, 8, e73021. [Google Scholar] [CrossRef] [PubMed]
- Fadnavis, S.; Batson, J.; Garyfallidis, E. Patch2Self: Denoising Diffusion MRI with Self Supervised Learning. Adv. Neural Inf. Process. Syst. 2020, 33, 16293–16303. [Google Scholar]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Du, Q.; Tang, Y.; Wang, J.; Hou, X.; Wu, Z.; Li, M.; Yang, X.; Zheng, J. X-ray CT image denoising with MINF: A modularized iterative network framework for data from multiple dose levels. Comput. Biol. Med. 2023, 152, 106419. [Google Scholar] [CrossRef]
- Spuhler, K.; Serrano-Sosa, M.; Cattell, R.; DeLorenzo, C.; Huang, C. Full-count PET recovery from low-count image using a dilated convolutional neural network. Med. Phys. 2020, 47, 4928–4938. [Google Scholar] [CrossRef]
- Fu, M.; Wang, M.; Wu, Y.; Zhang, N.; Yang, Y.; Wang, H.; Zhou, Y.; Shang, Y.; Wu, F.X.; Zheng, H.; et al. A Two-Branch Neural Network for Short-Axis PET Image Quality Enhancement. IEEE J. Biomed. Health Inform. 2023, 27, 2864–2875. [Google Scholar] [CrossRef]
- Zhang, J.; Shangguan, Z.; Gong, W.; Cheng, Y. A novel denoising method for low-dose CT images based on transformer and CNN. Comput. Biol. Med. 2023, 163, 107162. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Li, R.; Li, S.; Wang, T.; Cheng, Y.; Zhang, S.; Wu, W.; Zhao, J.; Qiang, Y.; Wang, L. Unpaired low-dose computed tomography image denoising using a progressive cyclical convolutional neural network. Med. Phys. 2023. [CrossRef] [PubMed]
- Yang, H.; Zhang, S.; Han, X.; Zhao, B.; Ren, Y.; Sheng, Y.; Zhang, X.Y. Denoising of 3D MR images using a voxel-wise hybrid residual MLP-CNN model to improve small lesion diagnostic confidence. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, 18–22 September 2022; pp. 292–302. [Google Scholar]
- Wang, H.; Zheng, R.; Dai, F.; Wang, Q.; Wang, C. High-field mr diffusion-weighted image denoising using a joint denoising convolutional neural network. J. Magn. Reson. Imaging 2019, 50, 1937–1947. [Google Scholar] [CrossRef] [PubMed]
- Tian, Q.; Bilgic, B.; Fan, Q.; Liao, C.; Ngamsombat, C.; Hu, Y.; Witzel, T.; Setsompop, K.; Polimeni, J.R.; Huang, S.Y. DeepDTI: High-fidelity six-direction diffusion tensor imaging using deep learning. NeuroImage 2020, 219, 117017. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.C.; Huang, H.M. Denoising of multi b-value diffusion-weighted MR images using deep image prior. Phys. Med. Biol. 2020, 65, 105003. [Google Scholar] [CrossRef] [PubMed]
- Tian, Q.; Li, Z.; Fan, Q.; Polimeni, J.R.; Bilgic, B.; Salat, D.H.; Huang, S.Y. SDnDTI: Self-supervised deep learning-based denoising for diffusion tensor MRI. NeuroImage 2022, 253, 119033. [Google Scholar] [CrossRef] [PubMed]
- Calvarons, A.F. Improved Noise2Noise denoising with limited data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 796–805. [Google Scholar]
- Huang, T.; Li, S.; Jia, X.; Lu, H.; Liu, J. Neighbor2neighbor: Self-supervised denoising from single noisy images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14781–14790. [Google Scholar]
- Krull, A.; Buchholz, T.O.; Jug, F. Noise2void-learning denoising from single noisy images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2129–2137. [Google Scholar]
- Batson, J.; Royer, L. Noise2self: Blind denoising by self-supervision. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 524–533. [Google Scholar]
- Quan, Y.; Chen, M.; Pang, T.; Ji, H. Self2self with dropout: Learning self-supervised denoising from single image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1890–1898. [Google Scholar]
- Yuan, N.; Wang, L.; Ye, C.; Deng, Z.; Zhang, J.; Zhu, Y. Self-supervised Structural Similarity-based Convolutional Neural Network for Cardiac Diffusion Tensor Image Denoising. Med. Phys. 2023. [CrossRef] [PubMed]
- Wang, Y.G.; Zhuang, X. Tight framelets on graphs for multiscale data analysis. In Proceedings of the Wavelets and Sparsity XVIII, San Diego, CA, USA, 13–15 August 2019; Volume 11138, pp. 100–111. [Google Scholar]
- Garyfallidis, E.; Brett, M.; Amirbekian, B.; Rokem, A.; Van Der Walt, S.; Descoteaux, M.; Nimmo-Smith, I.; Contributors, D. Dipy, a library for the analysis of diffusion MRI data. Front. Neuroinform. 2014, 8, 8. [Google Scholar] [CrossRef]
- Teh, I.; Burton, R.A.; McClymont, D.; Capel, R.A.; Aston, D.; Kohl, P.; Schneider, J.E. Mapping cardiac microstructure of rabbit heart in different mechanical states by high resolution diffusion tensor imaging: A proof-of-principle study. Prog. Biophys. Mol. Biol. 2016, 121, 85–96. [Google Scholar] [CrossRef]




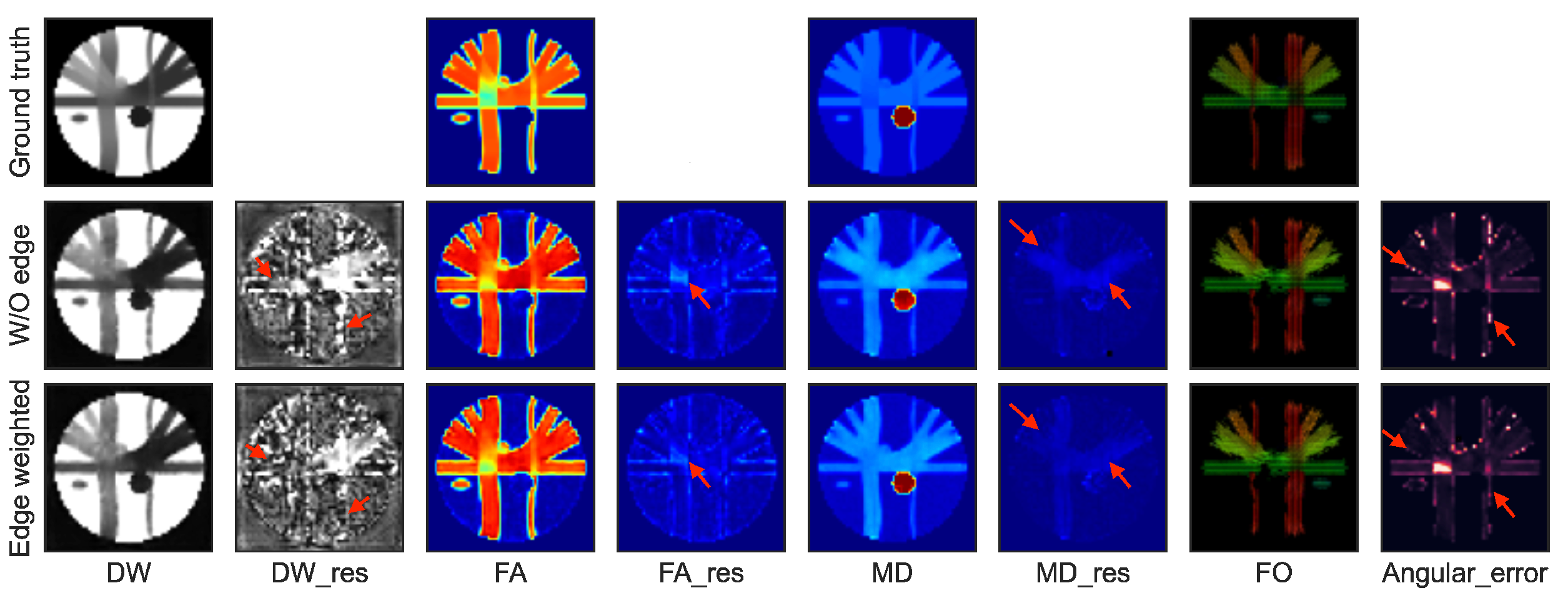
| Method | RMSE | PSNR | SSIM | AAE |
|---|---|---|---|---|
| Noisy | 482.63 | 19.56 | 0.88 | 7.87 |
| LPCA | 499.82 | 19.25 | 0.93 | 3.42 |
| AONLM | 346.70 | 22.43 | 0.94 | 3.84 |
| BM3D | 360.52 | 22.09 | 0.92 | 3.76 |
| DIP | 273.21 | 24.50 | 0.93 | 7.12 |
| NB2NB | 251.69 | 25.21 | 0.95 | 5.78 |
| P2S | 164.29 | 28.92 | 0.97 | 3.25 |
| SSECNN | 358.37 | 22.14 | 0.95 | 4.50 |
| Node2Node | 86.29 | 34.51 | 0.97 | 2.48 |
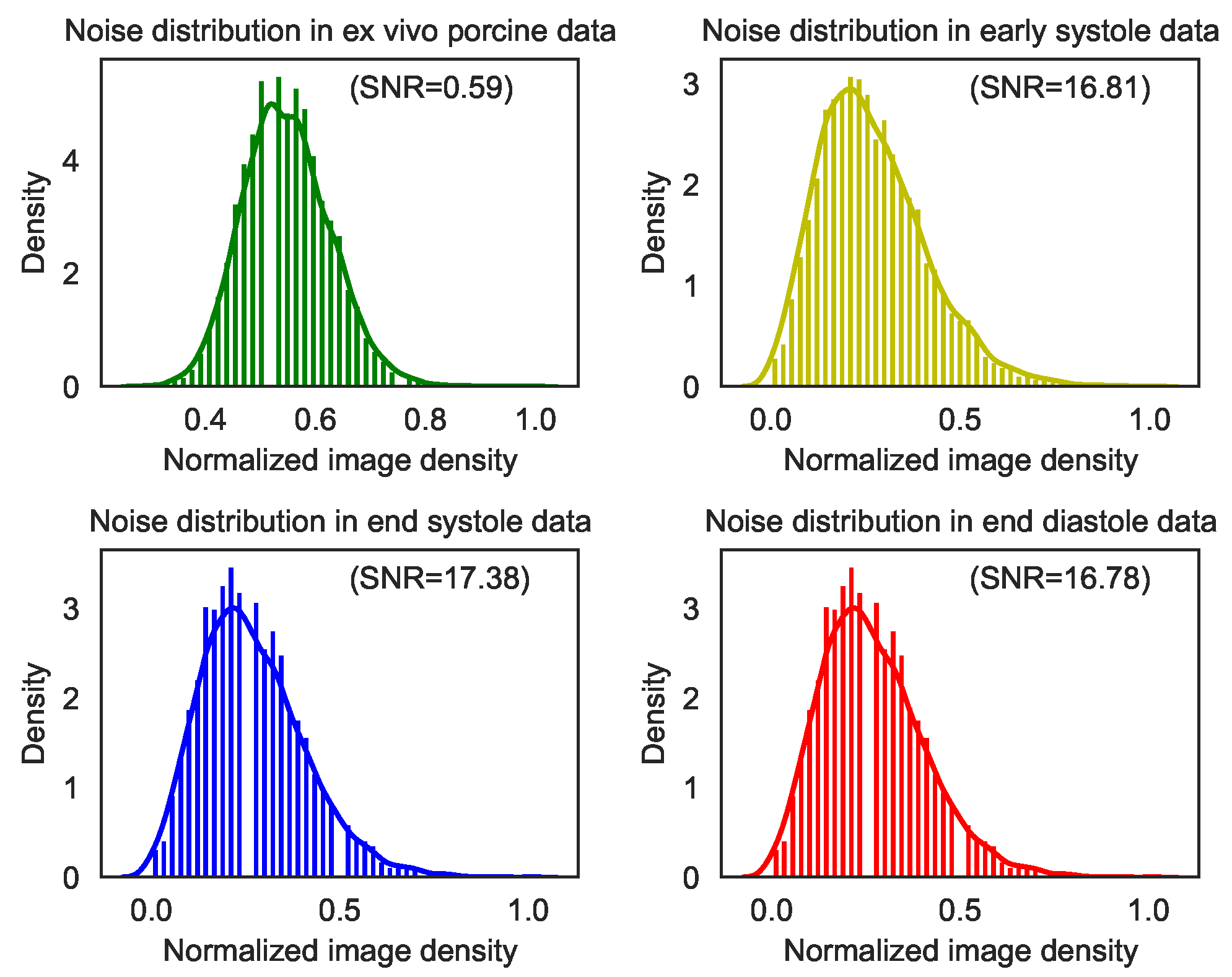
| Method | Porcine Hearts | Early Systole | End Systole | End Diastole | ||||
|---|---|---|---|---|---|---|---|---|
| SNR | CNR | SNR | CNR | SNR | CNR | SNR | CNR | |
| Noisy | 0.59 | 76.20 | 16.81 | 137.48 | 17.38 | 133.63 | 16.78 | 158.94 |
| LPCA | 4.71 | 179.65 | 43.74 | 301.06 | 46.10 | 314.66 | 42.50 | 361.03 |
| AONLM | 3.62 | 168.07 | 16.77 | 137.48 | 17.38 | 16.31 | 16.81 | 158.94 |
| BM3D | 1.39 | 79.79 | 75.70 | 469.04 | 80.56 | 464.33 | 77.05 | 603.10 |
| DIP | 0.72 | 31.83 | 27.11 | 195.25 | 30.90 | 187.01 | 32.46 | 236.86 |
| NB2NB | 2.31 | 59.28 | 40.58 | 200.50 | 42.49 | 215.58 | 37.59 | 241.08 |
| P2S | 1.79 | 120.46 | 30.12 | 184.71 | 32.21 | 196.76 | 29.82 | 220.70 |
| SSECNN | 4.34 | 134.85 | 48.90 | 293.19 | 52.24 | 278.21 | 47.12 | 334.24 |
| Node2Node | 6.50 | 203.58 | 71.29 | 477.57 | 75.60 | 465.23 | 67.52 | 540.70 |
| Method | RMSE | PSNR | SSIM | AAE | |
|---|---|---|---|---|---|
| W/O edge | DW images | 99.24 | 33.30 | 0.97 | – |
| FA maps | 0.033 | 28.44 | 0.83 | – | |
| MD maps | 3.25 × 10 | 39.68 | 0.99 | – | |
| Fiber orientations | – | – | – | 2.68 | |
| Edge-weighted | DW images | 86.29 | 34.51 | 0.97 | – |
| FA maps | 0.029 | 29.38 | 0.85 | – | |
| MD maps | 2.95 × 10 | 4 0.52 | 0.99 | – | |
| Fiber orientations | – | – | – | 2.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, H.; Yuan, N.; Wang, L. Node2Node: Self-Supervised Cardiac Diffusion Tensor Image Denoising Method. Appl. Sci. 2023, 13, 10829. https://doi.org/10.3390/app131910829
Du H, Yuan N, Wang L. Node2Node: Self-Supervised Cardiac Diffusion Tensor Image Denoising Method. Applied Sciences. 2023; 13(19):10829. https://doi.org/10.3390/app131910829
Chicago/Turabian StyleDu, Hongbo, Nannan Yuan, and Lihui Wang. 2023. "Node2Node: Self-Supervised Cardiac Diffusion Tensor Image Denoising Method" Applied Sciences 13, no. 19: 10829. https://doi.org/10.3390/app131910829
APA StyleDu, H., Yuan, N., & Wang, L. (2023). Node2Node: Self-Supervised Cardiac Diffusion Tensor Image Denoising Method. Applied Sciences, 13(19), 10829. https://doi.org/10.3390/app131910829





