1. Introduction
The need for new 3D orthotropic damage models is primarily due to their use in simulating 3D connections in composite structures [
1,
2,
3]. To predict the behavior of exterior profiles in hybrid beams and novel carbon-reinforced fiber aluminum laminates, a number of 2D orthotropic damage models have occasionally been used in conjunction with shell elements [
4,
5]. Other authors, however, discovered limitations in the accuracy of numerically simulating 3D GFRP connections using the classical 2D formulation with continuum shell elements [
6], related to either pilling, shear-out, or bearing due to the incorrect stress distribution in the thickness in shell formulation for non-linear analysis.
Since the start of the 2000s [
7], a more comprehensive 3D orthotropic damage formulation has been sought after due to the engineering industry’s rapid adoption of composite structures. The need for structural design has also grown among structural engineers in the field of composites [
8]. In all circumstances, the problem must be described in 3D, and the accuracy of the computed stress level relies on whether the problem is being examined at the micro, meso, or macro scale [
9].
For the structural designer, applying a complete 3D orthotropic damage model still poses significant issues such as (i) full 3D formulation with explicit material parameters and (ii) simple and clear guidelines for direct application. The scientific community mostly uses these damage orthotropic damage models to confirm experimental campaigns and adopted material properties, therefore these two factors are crucial for the structural designer [
10]. Unfortunately, academic researchers are not using composite orthotropic damage models without a current experimental campaign to arrive at better design solutions, despite the fact that this is a fundamental requirement for engineering in the composites industry given the absence of structural codes for these materials.
There are two main goals for this project. The first is to analyze a novel 3D orthotropic damage model’s numerical effectiveness using the Hashin failure criterion, using classical MTL damage progression [
11] with energy regularization [
12]. Experimental data are compared and used to validate this orthotropic damage model. The second study looks at the new ITE-UMAT algorithm, which speeds up the convergence of the UMAT subroutine when the secant matrix rather than the traditional tangent matrix is employed in the predictor-corrector. The algorithm is compared with fully implicit and explicit numerical results.
According to the authors’ best knowledge, the use of a 3D orthotropic damage model with residual stresses using viscous regularization and the secant matrix for the predictor-corrector algorithm has not been fully studied and validated. This work plans to fill this gap in knowledge.
2. Recent Advances in 3D Orthotropic Damage Models
Since the 2000s, several 3D orthotropic damage models have been proposed, which is primarily due to the scientific community’s availability of commercial finite element software used for implementing new material constitutive relations [
13,
14].
Due to the composite material’s ply-by-ply behavior and the formulation’s simplification, basic 2D orthotropic damage models were employed for shell elements prior to the widespread adoption of 3D orthotropic damage models [
15]. These 2D orthotropic damage models were sufficient to simulate beams [
4], columns [
16], and composite sandwich panels [
17], however, with significant constraints when modelling 3D beam-to-column connections [
6].
The difficulty in evolving from a 2D to a 3D failure model is primarily related to the first being assembled and tested using only plane analysis [
18], as this leads to different results when a formulation is then extended into the third dimension [
19]. In addition, the 3D failure criterion and damage evolution may be significantly influenced by the kind of orthotropic composite material being researched. The use of the 3D Hashin failure criterion is not novel and has been suggested for shell elements [
20] and solid elements [
21,
22], in any case, without any application for the interlaminar failure. An established 3D method based on the combination of several elliptic surfaces for the adoption of separated failure criteria [
23] presented encouraging results in simulating the connection of three bolt joints for T300/5228A composite material, with discontinuous damage evolution. For the stochastic analysis of peek laminates, a few different iterations of these elliptic surfaces were used [
24]. For composite fiber metals, the fiber and matrix 3D failure criteria are based on a square root sum of the total strain [
25], but with a cohesive interlaminar failure criterion. A variation of this last method was applied in FRP composites [
26,
27], but with restrictions on the failure criterion for material orientation. One of the first successful applications for a full 3D analysis with Larc05 was presented in the early work of [
28], with variation proposed by [
29]. Due to its simplicity of implementation, some 3D failure criteria with simple degradation models [
30] in terms of elastic parameters have also been successful and continue to be popular among structural engineers. One of the best examples of a fully 3D Hashin failure criterion using simplified degradation models was suggested by [
31] for bolted connections. Recently, the Hou criteria were successfully used to simulate drilling damage, based on an improved 3D elliptic failure surface [
32]. The NU failure criterion was proposed and implemented in a three-point bending load to improve the matrix damage evolution due to increased shear [
33]. Recently, using an invariant-based concept to study the bearing in composite connections showed excellent findings [
34,
35].
3. 3D Orthotropic Stiffness Formulation
The orthotropic formulation is described using ABAQUS standard notation for both stress and strain tensors [
36]. The compliance and stiffness matrices are used to calculate the elastic constitutive relation for stress and strain (1).
with:
To present a 3D orthotropic stiffness that is both coherent and thermodynamically acceptable, it is necessary to assemble the damage compliance matrix
exclusively using the diagonal term (8) to account for the damage behavior [
29,
37]. It is then possible to assemble the damaged stiffness matrix
, by inverting the previous compliance matrix (10). It is important to state the relevance of
(13), because this term ensures that no transversal stress occurs when subjected to uniform longitudinal stress. Just as in the previous 2D Hashin formulation [
15], the tension and compression damage
are activated using the corresponding effective stress space (3). For this work, damage variables are associated with the fiber
, the matrix
, and the interlaminar
.
where:
The main advantage is that, by design, this matrix verifies thermodynamic admissibility principles when using Gibbs free energy (14) [
38,
39].
with:
with:
where:
When calculating thermodynamic forces with this orthotropic damaged stiffness, these are always positive (16), validating the second principle of thermodynamics (17) and demonstrating the damage model is thermodynamically admissible.
4. Adopted 3D Hashin-Based Damage Model
It is important to note that there is no scientific consensus regarding the true formulation of the 3D Hashin failure criterion. This is because the true cross-failure criterion between intralaminar and interlaminar is still heavily debated in the scientific community [
24,
31]. When the damage evolution laws are studied [
29,
40], this uncertainty becomes even more pronounced, and several assumptions must be admitted to fully verify the thermodynamic admissibility criteria.
Contrary to popular belief, the Hashin failure criterion began as a 3D failure criterion for shell elements and was later simplified for 2D plane elements, though it lacked an interlaminar failure criterion. Another limitation of this failure model is that it was designed for unidirectional composites, but many authors continue to apply it to general lamina composites [
41,
42].
4.1. Hashin 3D Failure Criterion
The Hashin 3D failure criterion in this work is based on the fusion of formulations published by several academics [
21,
30,
43]. These continue to acknowledge a primary plane behavior that is consistent with the material’s primary resistance stress [
6], in which its failure criteria are assembled.
Since it is challenging to accurately describe the real behavior of composites in the 3D space, the original failure criteria make various material and tensor field simplifications. In this work, to extend to a fully 3D Hashin damage model, these simplifications will also be applied and explained throughout the manuscript.
The first simplification admits that all unidirectional fibers are transversely isotropic, in which the failure criterion depends on effective stresses (18), with the plane 2-3 rotating around axis 1 [
43]. Consequently, the failure criteria for fiber breaking are established
in axis-1 and matrix cracking
for plane 2-3, using their respective tensorial plane stresses (18). For this work, all the tensors are expressed in terms of effective stresses because these failure criteria are later employed in damage models.
Despite the fact that the Hashin criterion is always positioned in the material principal directions, it is preferable to rewrite the failure criterion functions in terms of stress invariants using the envelope quadratic Equation (19), in order to support a more reliable failure formulation similar to Von-Mises.
with:
It is possible to simplify in the case of pure shear stress
, for each of the respective shear directions, and compute the values of
,
, and
(21), for which
and
are the longitudinal and shear stress, respectively.
The second simplification is that the tensile and compressive failure criteria may present different failure modes for both the fiber and the matrix, resulting in different failure surface functions.
For the third simplification, it concedes that for the fiber buckling in compression (22), there is no influence of shear stresses. Other authors have used the fiber kinking mode to contest this last fiber simplification for 3D model compression [
28]. Previous studies have observed the deterioration of matrix shear modulus in fiber cycle compression [
44,
45], but with small influence and still some uncertainties. For this reason, simplification is still applied in this work.
For the third simplification, only quadratic terms are admitted in the fiber failure criterion to preserve the envelope ecliptic surface
. In any case, the possibility of a fully closed surface is eliminated by the simplification of the compressive fiber failure criterion. (23).
and
are the fiber tensile and compressive strength, respectively.
The fourth simplification is acknowledging that the tensile matrix failure criterion only depends on quadratic terms (19), which is in accordance with some cohesive models [
46], and promotes a closed failure surface function (24), (25).
and
are the matrix tensile and compressive strength, respectively.
The fifth simplification pertains to the matrix’s resistance to compression, in which the collapse during biaxial behavior is linked to crushing when
. However, it must verify the collapse during uniform compression when
. In these conditions, if the shear stress components are null, and we are on the onset of matrix compressive failure, the following systems of Equation (26) are assembled.
Since the system of equations has three unknowns and only two equations, these cannot be solved directly but rather by using the assumption that in biaxial compression
, the following limit (27) can be admitted. It is possible to determine the remaining unknown matrix compressive parameters for a closed-envelope surface using this limit, as long as
. As a result, the compressive matrix failure criterion can be put together (28).
The condition of matrix tensile and compressive behavior is demonstrated in the work of [
43], and it uses proof by contradiction, in which it is the only condition that does not violate the principal of
in al quadrants of the space
.
In the case of the interlaminar failure criterion, a cohesive model (29) is used for the tensile interlaminar failure criterion with the influence of the shear stresses in the interlaminar plane (30), which is based on the initial work of [
21]. For the interlaminar compressive failure, the influence of the shear is minor, therefore, in this case, only the pressure stresses are not taken into account for the failure criterion (30).
and
are the out-of-plane damage tensile and compressive thresholds, respectively.
4.2. Damage Evolution
For this work, the same formulation of equivalent strains and stresses used in previous 2D Hashin damage models is used [
15]. Then, using the same MLT principles [
11], the equivalent stresses and strains are assembled for the 3D space, with different equivalent stresses and strains for the fiber, matrix, and interlaminar in tensile and compressive damage evolution [
47].
The equivalent strain is calculated using equivalent principal virtual work [
48], written in the form of (31). For the particular cases of the fiber and matrix directions, these equations are rewritten into (32) and (33). The adopted stresses and strains used to compute the equivalent ones are associated with the effective stresses present in the respective failure criterion.
A characteristic length
is added to the formulation to represent the constitutive law as a stress-equivalent displacement relation, which reduces the mesh dependency that may result from material softening [
12]. The characteristic length is calculated in this study as the square root of the numerically calculated surface area. The definitions of equivalent displacement (34) are identical to those first discovered in the study of [
49], which are independent of the direction of the fracture. This last point is crucial in orthotropic damage models since the damage progression will always be influenced by either the behavior of the fibers or the matrix. It has been demonstrated in various publications that some element dependency/sensitivity is predictable as a result of FEM with softening if the mesh is irregular and the stress field distribution is non-uniform [
12,
50].
The evolution law is then revised, finally taking the form embodied in
Figure 1, in which the area
under the curve is linked to the fracture energy
. At the moment, new experimental methodologies are emerging to calculate fracture energy [
51], but for orthotropic materials, the classical Compact Tension test is still suggested.
The initial values and are calculated in the onset of damage, by analytically solving Equations (23), (25), (28), and (30). To verify the Kuhn–Tucker equations, at the beginning of each incremental process, the evolution law is updated to curve .
In [
11], it was shown that the tensile and compressive damage variables are estimated using Equation (35) for a linear softening evolution depending on the fiber or matrix evolution.
In this work, the possibility of the equivalent stresses presenting residual stress is also adopted, which is important primarily when compression is high and very present in the structural response. In addition, to promote some numerical stability, it is recommended to use tensile residual stress that may vary from 1% to 10% of its initial peak value. The adopted residual equivalent stress formulation is presented in
Figure 2. A new damage function is assembled during the residual equivalent stress segment after point D (37).
4.3. Viscous Regularization
Even when only the energy regularization described in the previous section is used, some issues may arise: (i) Loss of positive definiteness of the tangent stiffness; (ii) some damage localization; and (iii) some numerical convergence issues. To overcome these issues, a simple/efficient procedure is to implement viscous regularization.
Damage localizes in a narrow band when the tangent stiffness tensor is not positive definite, and the numerical solution depends on the numerical discretization (decreasing the element size in the localized zone decreases the computed energy dissipated). Therefore, the structural response is not objective because it does not converge to a single solution with mesh refinement. Standard Newton–Rapshon approaches also have convergence issues when the tangent stiffness is not positively definite [
52].
As mentioned above, the viscous regularization approach can help to solve some of these convergence problems. This algorithm is built on an artificial Duvaut–Lions viscosity model [
53]. More details on the theoretical background of this method can be found in the initial published work of [
54]. This algorithm improves convergence by making the tangent stiffness matrix of the softening material positive definite for small enough time increments. In this regularization procedure, the incremental Equation (38) provides a definition for the viscous damage variable.
where
is the damage variable determined as previously explained,
is the regularized viscous damage variable, and
is the viscosity stabilization factor. The viscous and non-viscous stresses are written as (39) and (40), respectively.
The damaged elastic matrix,
, is computed using the viscous damage variables for each failure mode. The rate of convergence of the model in the softening regime is typically improved by using viscous regularization with a small value for the viscosity parameter (small compared to the characteristic time increment), without degrading the quality of the numerical solution. The fundamental notion is that the viscous system’s solution relaxes to that of the inviscid case as
, where
represents time. For the time integration of the internal variables, an algorithm must be implemented. The internal variables can be updated using a backward-Euler approach [
55], resulting in the viscous damage variable (41), by merging it with the preceding expression (38).
Now, it is possible to calculate the viscous damage while keeping the implicit time integration (42), utilizing data from the past viscous damage and the current non-viscous damage.
It is important to guarantee that the level of viscosity is not that high, which is performed indirectly by comparing the level of elastic damaged energy (43) and the viscous energy dissipation (44), in which the first must always override the second. If the time step
if very small, it is possible that the first term of the sum in (44) dominates the second, providing an increase in viscous energy dissipation, which might compromise the accuracy of the results.
5. Proposed Predictor-Corrector Implicit to Explicit
Many authors have used UMAT user-subroutines to implement new materials in ABAQUS without resourcing a fully Jacobi stiffness matrix (aka tangent matrix), using only a secant matrix for the ABAQUS predictor-corrector, with viscous regularization.
As referenced before, viscous regularization has only been demonstrated to be a fully implicit method when a tangent matrix is applied to the predictor-corrector algorithm [
54,
56]. The use of a secant matrix with viscous regularization lacks the theoretical background to prove its implicit convergence. It can be depicted in expression (42) that the if the time step is larger than the viscosity parameter
, then the level of regularization is low enough, and the implicit standard convergence can be admitted since the viscous damage is always related to the current time step as the non-viscous damage. However, if the time step is lower than the viscosity parameter
, then the viscous damage will always be related to the previous time step, therefore prompting an explicit time step integration.
Conflicts may arise in this last scenario because the strain increment corresponds to a full implicit integration strategy (45). These inconsistencies happen when damage follows an explicit time step update
, and the strain increment follows a full implicit integration scheme. This can cause some convergence problems, especially if the time step is very small
. Furthermore, when the time step is very small since the viscous damage solution overrides the non-viscous damage solution, the viscous damage energy tends to grow (44), indirectly providing extra energy that is not real.
To solve this problem, a new implicit-to-explicit algorithm is proposed. The fundamental basis guarantees that when the time step is large, the damage evolution follows an implicit time step integration, but when the time step is smaller than the viscosity parameter, the damage evolution switches to an explicit time step integration. This is an optimization of the predictor-corrector of ABAQUS, which states that when the time step is large a full implicit formulation is used, but when the predictor-corrector algorithm of ABAQUS presents complications in converging or reducing the time step, then an explicit formulation is used to suppress the converging difficulty. The basis of this formulation is using the increment correction parameter
linked to the portion of the non-viscous damage variable
in expression (46).
in which:
It is important to point out that when the material stiffness and stress update during the time integration in the UMAT follows a full implicit formulation; in contrast, when , it follows a full explicit time integration for the material stiffness and stress update.
Using this algorithm, it is guaranteed that when performing the viscous regularization, if the predictor-corrector uses large time steps, then both the viscous and non-viscous solution portion of expression (42) will contribute to the implicit time step integration. However, when the time step is small enough, then the increment correction parameter tends to be small, close to an explicit integration, and the influence of the non-viscous solution overrides the viscous solution, therefore using only the previous damage variable. This way there is no mixed implicit time step integration, with previous step damage variables, as suggested before, perhaps compromising the convergence and accuracy of the numerical solution.
To better understand the variation of
with
for a fixed
, it is depicted in
Figure 3a, in which it is possible to see that even for small times steps from
to
, the value of
, therefore garanting some influence of the
in the final strain increment
. This is close to an implicit behavior but does not guarantee it. As depicted in
Figure 3b using the logarithmic scale, only when
is the value of
, being close to an explicit form, but still with some influence of
in the final strain increment
.
In conclusion, the algorithm tends to be more implicit when , and on the other hand, more explicit when . In any case, this last situation is non-problematic, since for very small time steps , an explicit solution may still provide good and accurate numerical results. It is important to state that this algorithm admits the damage variable from the current time step is always saved for the next time step, otherwise viscous damage and non-viscous damage would never be updated during the incremental processes.
It is important to point out that expression (46) is only used to update the damage variables; however, for the stress update, expression (45) is permanently used even for explicit integration (if not, the internal forces would not be in equilibrium).
6. Numerical Investigation and Validation
In this section, the results from the experimental campaign of [
57,
58,
59] with GFRP specimens, beams, and connections are tested and compared with the proposed damage model and the stabilization algorithm. Since most material parameters, including fracture energy, are included in these experimental results, it is essential to validate numerical models in order to accurately simulate the post-peak behavior in materials with softening. Most of these experimental campaigns have also been verified with previous numerical tests in the works of [
60,
61].
For numerical tests, a total time analysis of 1.0 s was admitted, due to the non-linear analysis being static, and a maximum time step increment of 0.001 s, which is 100 times larger than the chosen viscosity parameter.
6.1. Compact Tension Test
The compact tension test is a traditional test to assess fracture energy, usually in isotropic materials [
62], and was recently extended to also estimate the fracture energy in orthotropic GFRP specimens [
58]. The full details of the experimental campaign for the tensile compact test can be found in [
58], including the test setup and description of the imposed displacement.
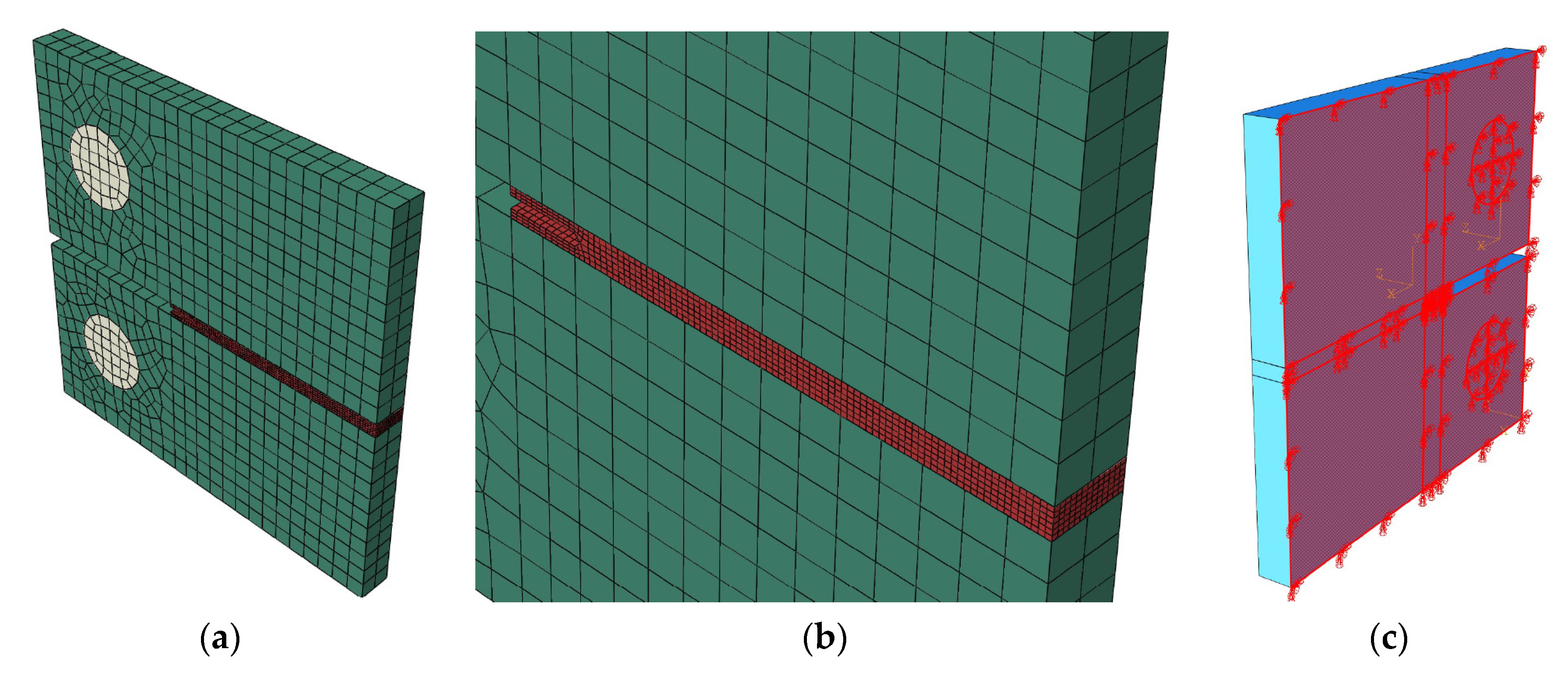
The specimen geometry, test setup, and supporting conditions are all depicted in
Figure 4. For the adopted mesh, to reduce the computational cost, the zone outside the notch was simulated with linear orthotropic GFRP behavior that already existed in the ABAQUS material library. The extra part of the notch was simulated with the proposed UMAT, in which the fracture will take place. These two used different meshes, since the zone in the notch needs an extra refinement, and later were connected using tie constraints. The circular supports were modelled with linear isotropic steel also presented in the ABAQUS material library (
). The interaction between the supports and the GFRP specimen was simulated with hard contact formulation, and with a friction coefficient of 0.2.
To even further reduce the computational cost, only half of the thickness was simulated, therefore transversal symmetry conditions were implemented in
Figure 5. When the mesh was generated, it imposed near-cubic shapes for all solid finite elements, and several meshes were tested to prevent any mesh dependency.
A full 3D non-linear analysis was performed using the ABAQUS standard with C3D8 solid finite elements using full integration. As a result of the structural response presenting softening during the last experimental campaign, displacement control was used when applying a vertical load. All the material properties in plane 1-2 of the GFRP are in
Table 1 and
Table 2, and these were obtained in the experimental campaign of [
58]. For the interlaminar material properties, it was admitted these were the same as the matrix properties, due to some isotropic behavior in the transverse direction.
Three different tests were performed to evaluate the numerical accuracy of the new proposed algorithm: The first test consists of a full implicit material integration with correction parameter ; the second test consists of a full explicit material integration considering ; the third test uses ITE with the correction parameter of expression (47). It is important to point out that the UMAT was used for the GFRP using the ABAQUS standard, so the governing system was solved using the implicit predictor-correct algorithm for the three tests.
By observing
Figure 6, it is important to realize that all three tests provided the same structural response, even during the softening branch. The stiffness is the same in all three tests, but the maximum force is slightly higher in the second test (explicit) as expected. All numerical models present a higher maximum force than the experimental campaign, but this was also observed by other authors [
63]. Interlaminar properties are supposed to be the same as the matrix properties, and this assumption can create slight gaps between numerical and experimental results. Moreover, boundary conditions of simulations may contain minor discrepancies compared to the experimental test, generating small differences in the structural response. The final matrix damage field distribution for all three numerical tests is also presented in
Figure 7a, in which it is not possible to determine the differences between each of the material time integration methods.
Figure 7b also shows the vertical stress distribution and matrix damage for a specific vertical strain. Finally,
Figure 8 compares the final matrix damage field distribution using full implicit material integration, explicit and the ITE algorithm. For the matrix damage evolution, all three tests present the same evolution with the vertical strain, but for the vertical stress evolution during the peak, there is a clear difference between the implicit and explicit material integration (first and third tests, respectively). However, for the evolution of the vertical stress and vertical strain, there is almost no visible difference between the implicit and ITE material integration, concluding that the ITE promotes the same accuracy as the full implicit formulation. Nevertheless, explicit integration generates noticeable discrepancies in the vertical load distribution and stress behavior compared to implicit and ITE analyses. Consequently, the ITE algorithm is the most cost-effective while maintaining great numerical accuracy.
6.2. Three-Point Bending Beam
The three-point bending beam is an experimental study commonly used to extract fracture properties from materials. The experimental setup details are presented in [
59], in which a bilinear softening relation describes the mechanical behavior of damaged pultruded glass fiber-reinforced polymer (GFRP) composites. Based on the work of [
61], the material properties adopted for the numerical test are listed in
Table 3.
Table 4 contains the fracture energies adopted in this framework. For the sake of clarity, tensile and compressive values of fracture energies for the fiber are estimated, while an average value of bilinear behavior is taken into consideration for the matrix. Moreover, interlaminar fracture energy is assumed to be the same as the matrix property.
The computational cost is reduced by considering only one-quarter of the beam, thus requiring symmetry conditions, as illustrated in
Figure 9. Regarding the boundary conditions, the beam is simply supported, and the vertical displacement is applied through isotropic steel support (
), according to [
61]. The part of the beam far from the notch proposes a coarse discretization, and it is modelled with linear orthotropic behavior, in contrast to the region of the notch where the damage occurs, which is modelled using almost cubic C3D8R solid finite elements with reduced integration and hourglass control, as shown in
Figure 10. Tie constraints allow the connection between all parts of the beam.
A full 3D non-linear analysis was performed using the ABAQUS standard, without considering residual stress and with the same time step restrictions as the previous numerical model. This framework proposes a full implicit material integration as the first analysis, followed by an ITE test with the correction parameters defined in (47) as the second test.
The response of the structure in terms of the reaction force vs. CMOD (crack mouth opening displacement) is compared with the experimental data included in [
59], as illustrated in
Figure 11. By considering both full implicit and ITE tests,
Figure 12b exhibits the evolution of principal stress over two different integration points, identified in
Figure 12a, in the band where the damage propagates. A detailed view of damage propagation is provided in
Figure 13; specifically, the matrix is shown in
Figure 13a, the fiber in
Figure 13c, and tensile damages can be recognized, while
Figure 13b shows shear 1-2 damage progression. Finally,
Figure 14 compares the final distribution of tensile matrix damage using full implicit material integration and the ITE algorithm. The numerical assessment correctly simulates the experimental campaign, even though some differences in the softening region can be detected. In particular, the numerical model contains an average value of matrix fracture energy in contrast to the bilinear behavior. Furthermore, the reduced integration results in a smaller characteristic length. In addition, small inconsistencies between experimental and numerical boundary conditions could induce some variabilities. The principal stress and strain obtained from the full implicit case and ITE are coincident, as shown in
Figure 12b. Therefore, the ITE algorithm simulates the mechanical response of the beam with the same accuracy as the full implicit analysis, with the advantage of requiring significantly less computation time. The matrix damage over integration point 2 evolves more rapidly than point 1. However, by looking at
Figure 13c, there is an increase in fiber damage that causes the shear damage at point 1 to exceed that at point 2 from the cross point, as highlighted in
Figure 13b.
6.3. Double-Lap Test
The double-lap test is a standard experiment used to assess the bolt connection between structural elements. The full details of the experimental campaign and test setup are fully described in the work of [
57], in which it is possible to determine the applied load using impose displacements. Some of the material properties adopted for the numerical test are shown in
Table 5, and these were obtained in the previously referenced work while others were estimated. Due to some findings’ fluctuations, the fracture energy was calculated using the same values as in the earlier example in
Table 2. For this numerical test, the bolt edge distances (cover) of 15 mm and 70 mm were simulated since these clearly show a difference between a shear-out and bearing collapse, respectively, as shown in
Figure 15.
A full 3D non-linear analysis was performed using the ABAQUS standard with C3D8 and C3D8R solid finite elements using full and reduced integration and hourglass control to evaluate any mesh sensitivity due to the high variability of the stress field. The time step restrictions are the same as the previous numerical models.
For the GFRP plate, in order to reduce the computational cost, part of the plate near the opening was modelled with the UMAT, but for the other part, an elastic orthotropic material from the ABAQUS library was used. For the steel bolt, an isotropic elastoplastic material from the ABAQUS library was used (
). Again, to reduce the computational cost, only one-quarter of the structure was simulated, which represents one-half of the GFRP plate and one steel plate, as shown in
Figure 16, in which the imposed vertical displacement is inserted into the bottom of the steel plate. Only the ITE algorithm was employed in this example, with the primary goal of numerically evaluating the simulation of the bearing collapse in the contact between the steel bolt and the GFRP plate.
To correctly simulate the bearing, the residual compressive stress after the maximum peak must also be simulated. Two values of compressive residual stress were considered, namely, 15%, as estimated from the work of [
60], and 80%, which is approximately the relation between the bearing resistance and compressive resistance according to [
64], when using the experimental values form [
57]. In addition, to improve convergence, the tensile residual stress was 1% and 10%, respectively. A sensitivity test showed that residual tensile stress below 15% had no influence on the maximum numerical resistance and its softening branch.
The structural response of the numerical models and its comparison with the experimental campaign is exhibited in
Figure 17 for both 15 mm and 70 mm cover, with 15% and 80% residual compressive strength, for both reduced (RED) and full (FULL) integration. The vertical force was measured in the steel plate, and the vertical displacement is the relative movement between the steel plate and the GFRP plate (AB distance
Figure 15). As expected, due to the extra flexibility of the experimental test setup, the numerical model is less flexible than the experimental one. This is a common problem when comparing numerical vs. experimental structural responses [
65]. The magnitude of the stiffness in the numerical model was dependent on the adopted final geometry and support conditions, therefore due to its unknown variability, it is not expected to reach the same value as the one obtained in the experimental campaign. For the 15 mm cover, there is a clear overestimation of the maximum reaction for both reduced and full integration, which is associated with the tensile matrix resistance and longitudinal 1-2 shear resistance being overestimated. Furthermore, the adopted value of the fracture energy was estimated, not measured, in an experimental campaign. However, for the 70 mm cover, the maximum reaction is near the average experimental one, since the bearing is in the collapse mode, and this is associated with the compressive resistance, which was not estimated. It is observed that for the 15 mm cover, there is no clear difference between adopting a residual stress of 15% or 80% since the collapse mode is shear-out. However, for the 70 mm cover, clearly, the 80% residual compressive stress produces better results when compared with the post-peak values of the experimental campaign.
The final shear 1-2 damage field for all numerical models with reduced and full integration is portrayed in
Figure 18, in which it is possible to perceive that for the 15 mm cover, it is clearly a full shear-out collapse, but for the 70 mm cover, there is a bearing collapse followed by a partial shear-out mode that is not finalized. This is in accordance with the findings from the experimental campaign up to a 5 mm relative displacement.
Furthermore, only for the 70 mm cover can it be seen in
Figure 18 that some differences exist in the final shear damage field distribution for 15% and 80% residual compressive stress. Similar to the structural response in
Figure 19, there are some differences in the final shear damage field distribution for reduced and full integration with 80% residual compressive stresses.
In
Figure 20a, the shear stress and shear damage evolution are presented in the Gauss point nearest the circular opening perimeter at 30° of the symmetry axis in the GFRP plate. The findings are shown for both 15 mm and 70 mm covers, with residual compressive stress levels of 15% and 80%. These findings are significant because they show that increasing the residual compressive stress has almost no effect on the residual shear stress and that this is more related to the level of cover, which influences the stress field indirectly. This is also the case for the shear damage evolution displayed in
Figure 20b.
Finally, to better understand that the proposed ITE algorithm does not overestimate the viscous energy and consequently the viscous damage, the elastic damaged energy (ESE) and the viscous dissipation energy (VSE) are exhibited in
Figure 21. As expected for the RED_15%_15, there is a big reduction of force after 0.4 s, as shown in
Figure 17, and as expected in this case, both the value of ESE and VSE increase, but after a given time step, VSE stabilizes and ESE increases, demonstrating that the VSE does not dominate the structural response. For RED_80%_70, this does not occur due to the small force reduction during the structural response, in which VSE is always very small.