Influence of Normal Stiffness and Shear Rate on the Shear Behaviors and Acoustic Emissions Characteristics of Artificial Rock Joints
Abstract
:1. Introduction
2. Methodology
2.1. Specimen Preparation
2.2. Experimental System and Procedure
2.3. Experimental Design
3. Shear Behaviors
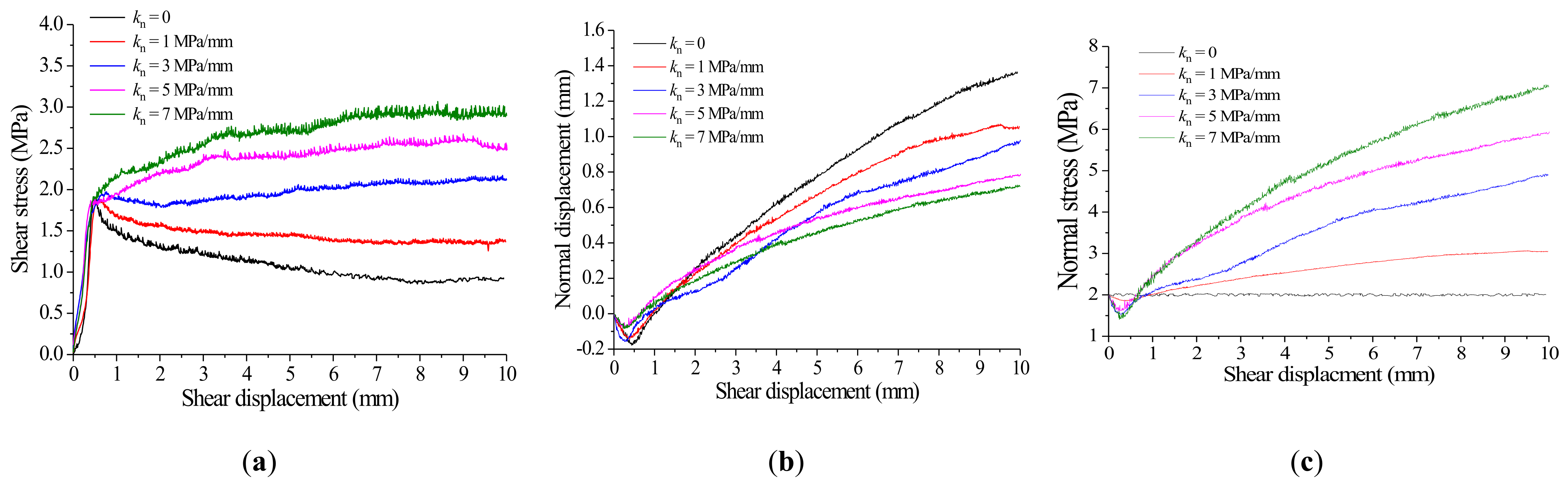
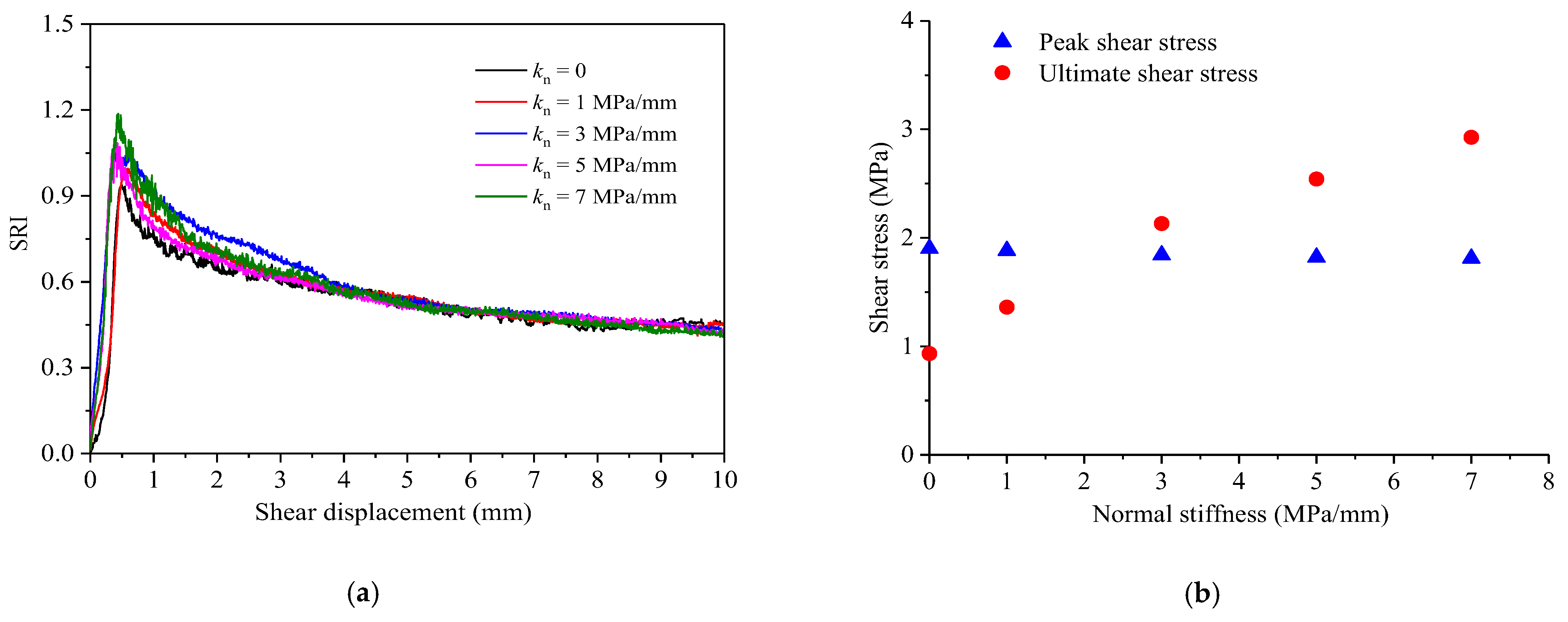
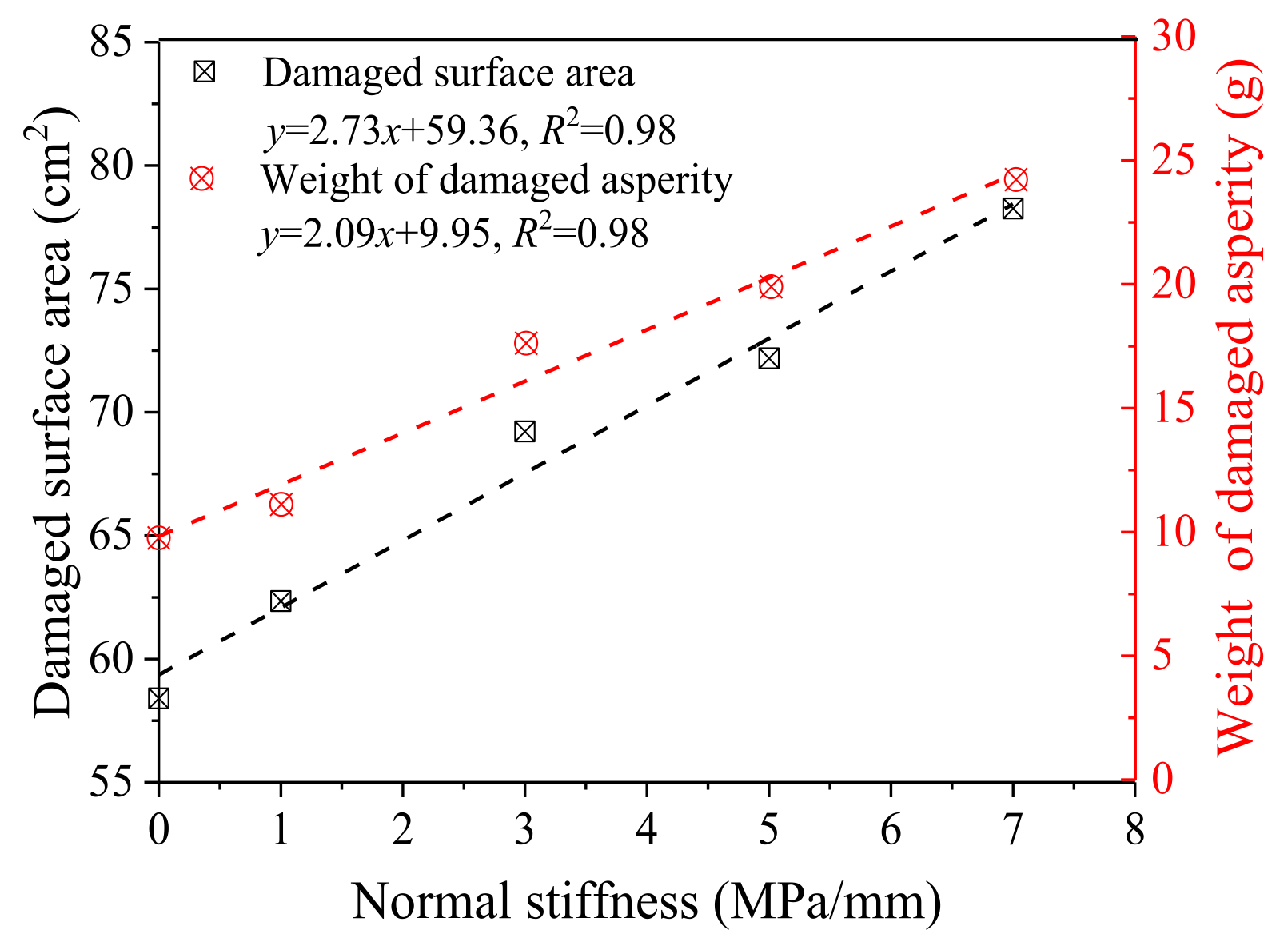
3.1. Effect of Normal Stiffness
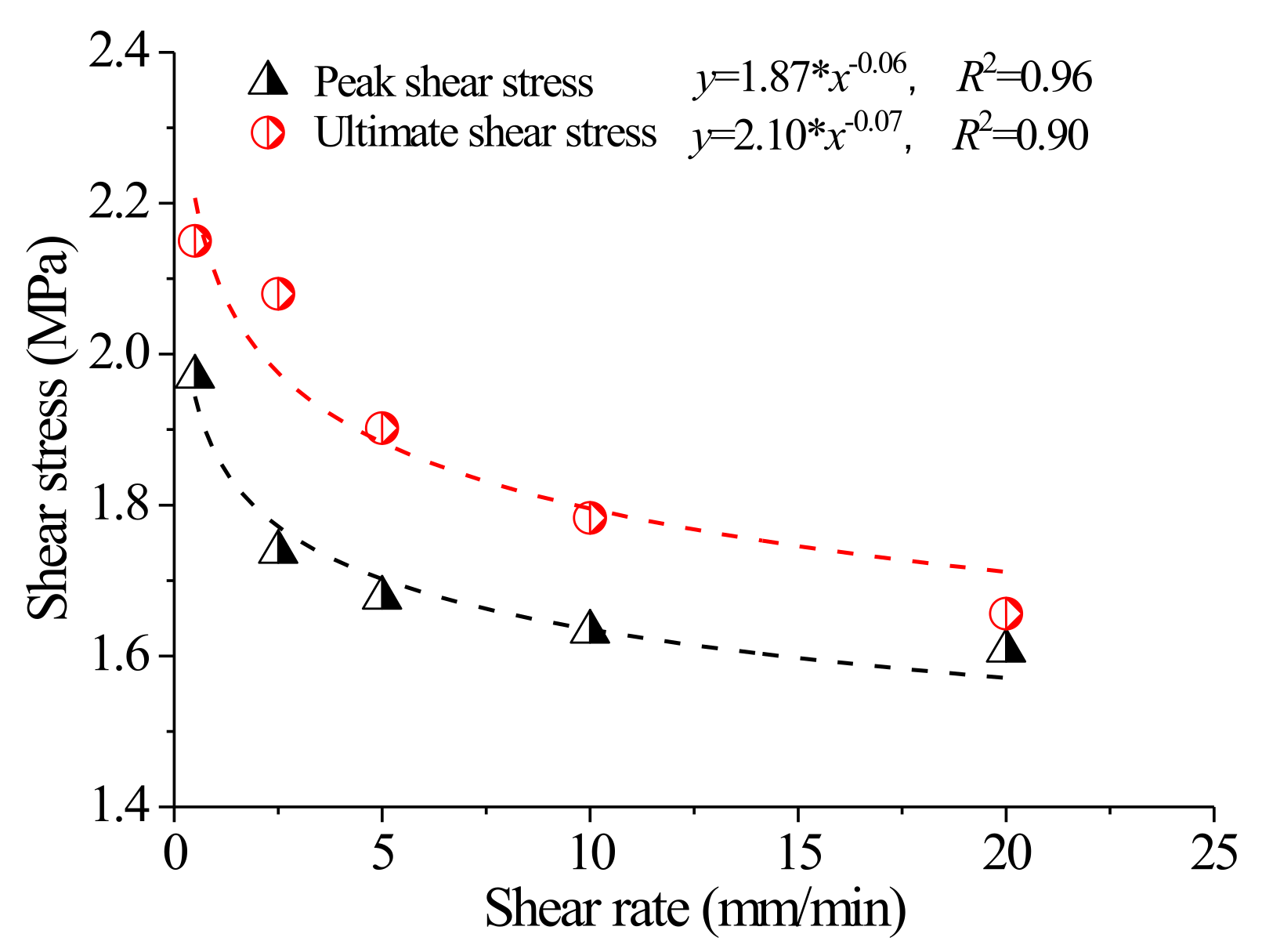
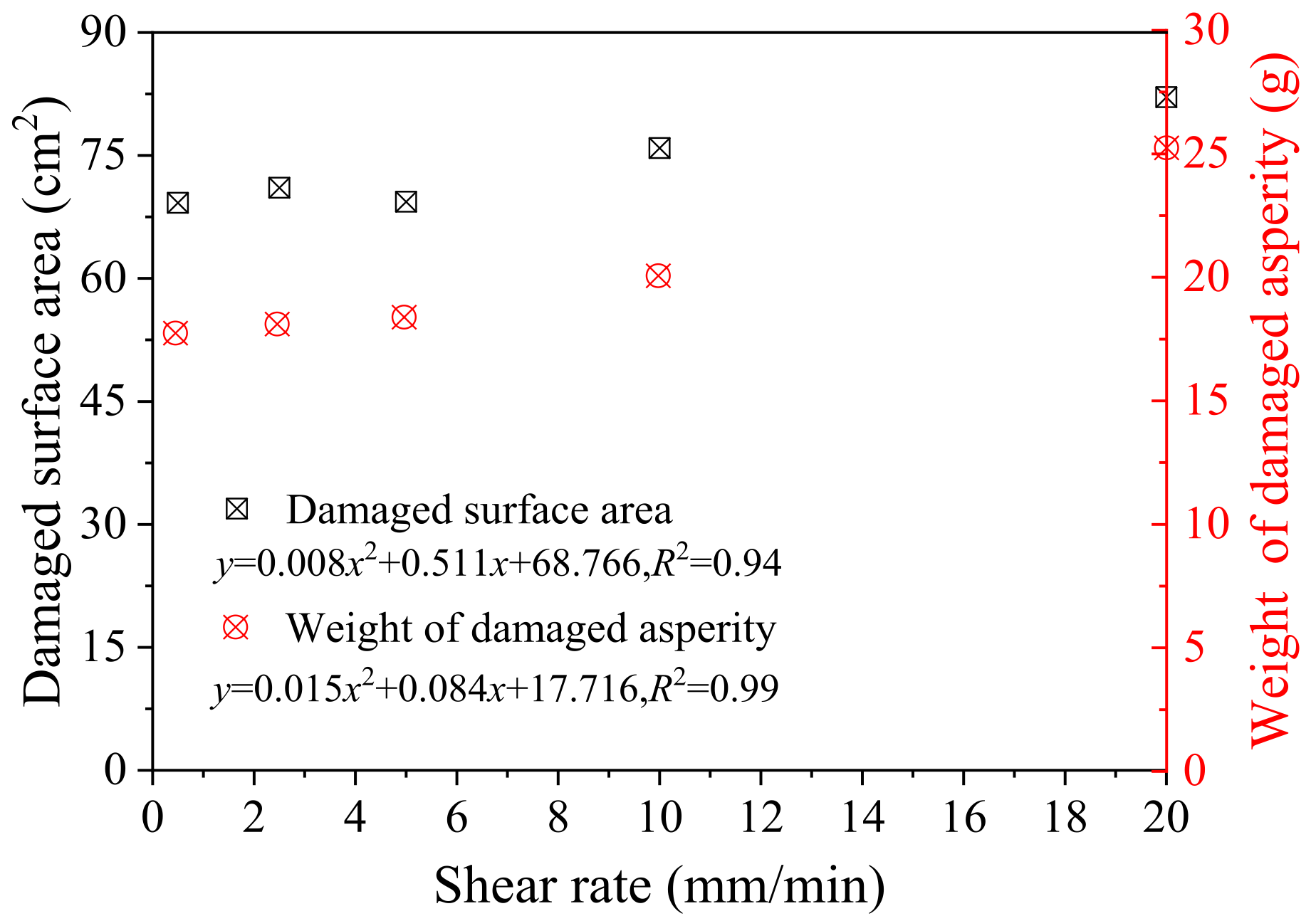
3.2. Effect of Shear Rate
4. AE Characteristics
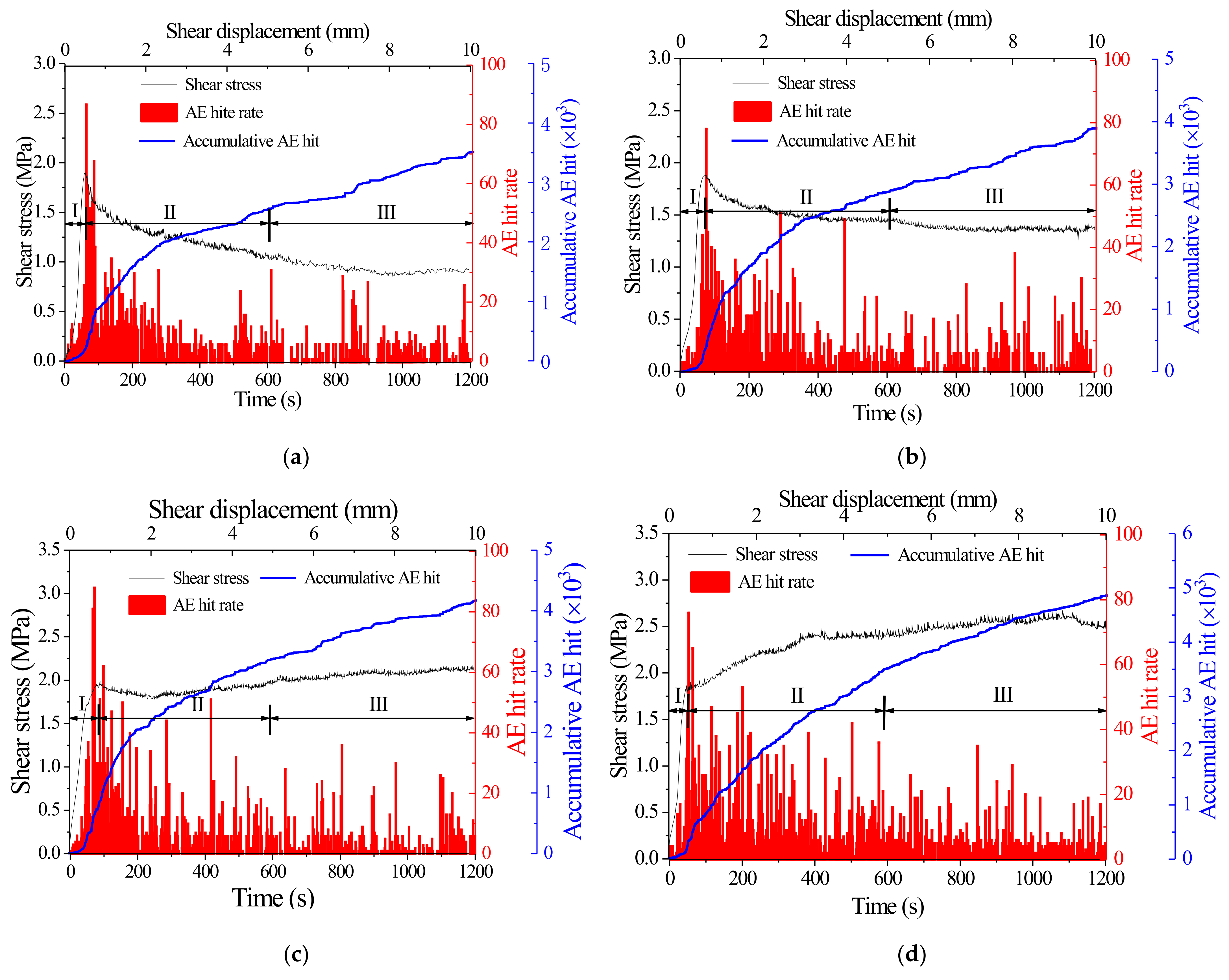
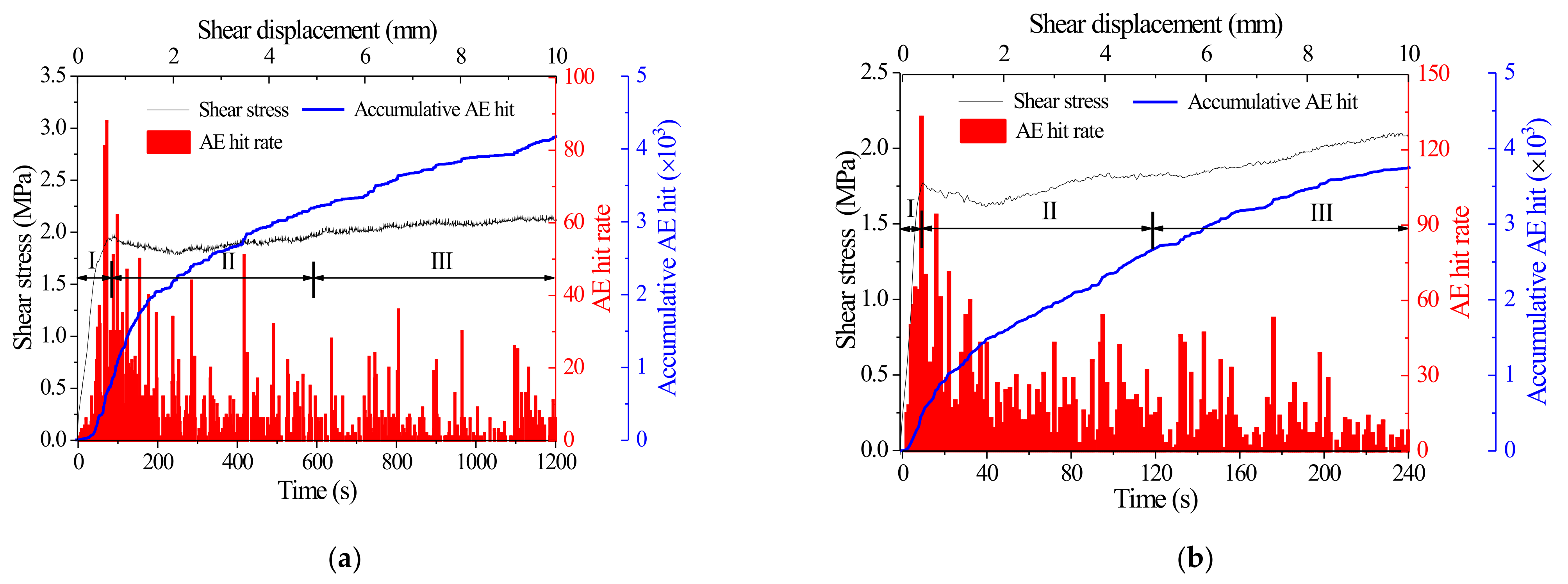
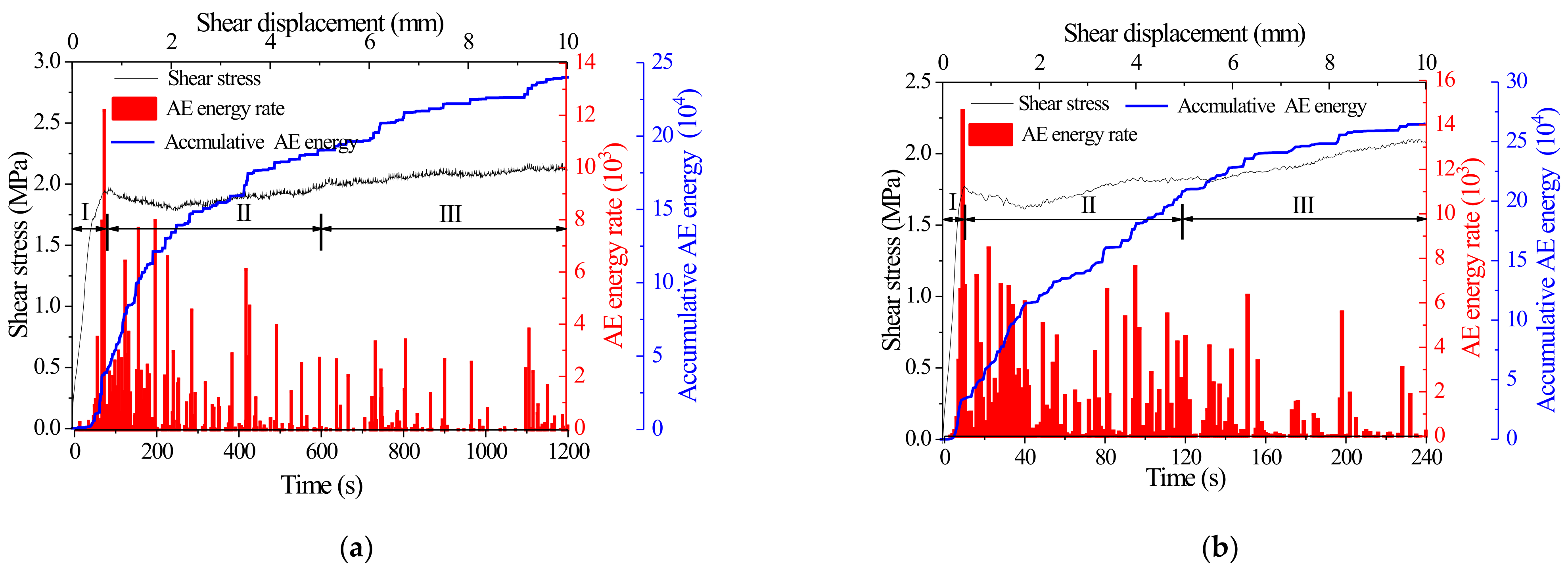
4.1. Effect of Normal Stiffness on AE Characteristics of the Sheared Joints
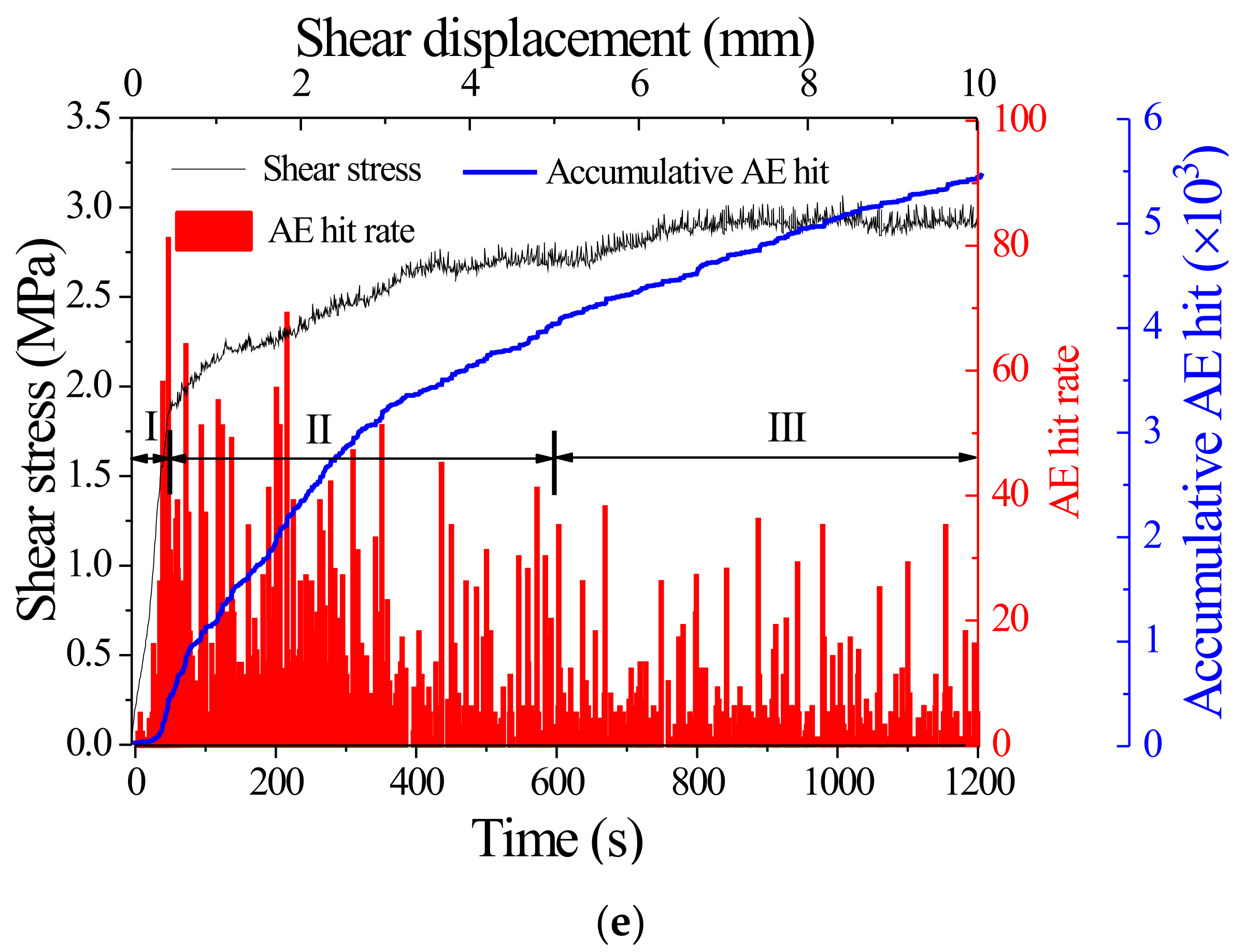
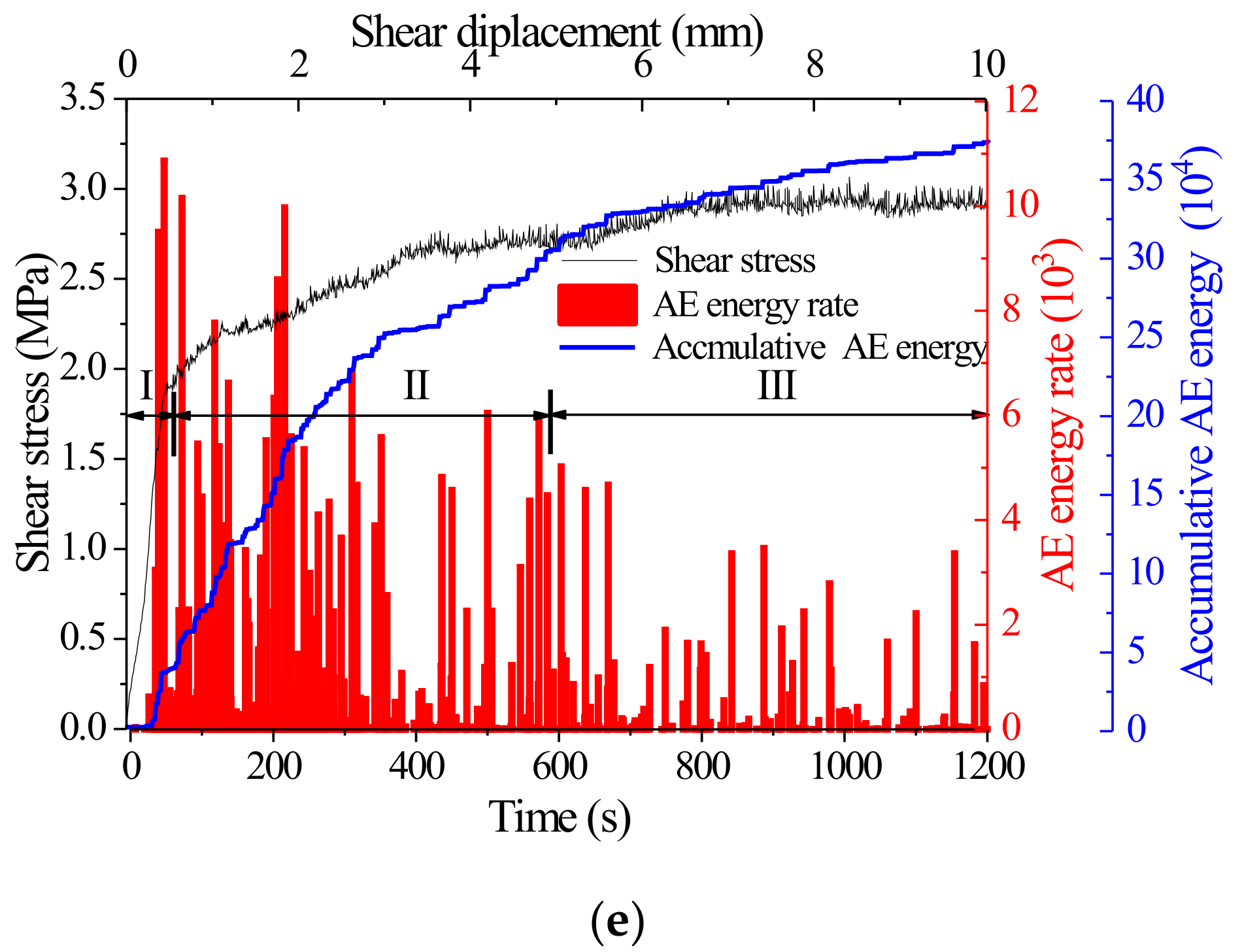
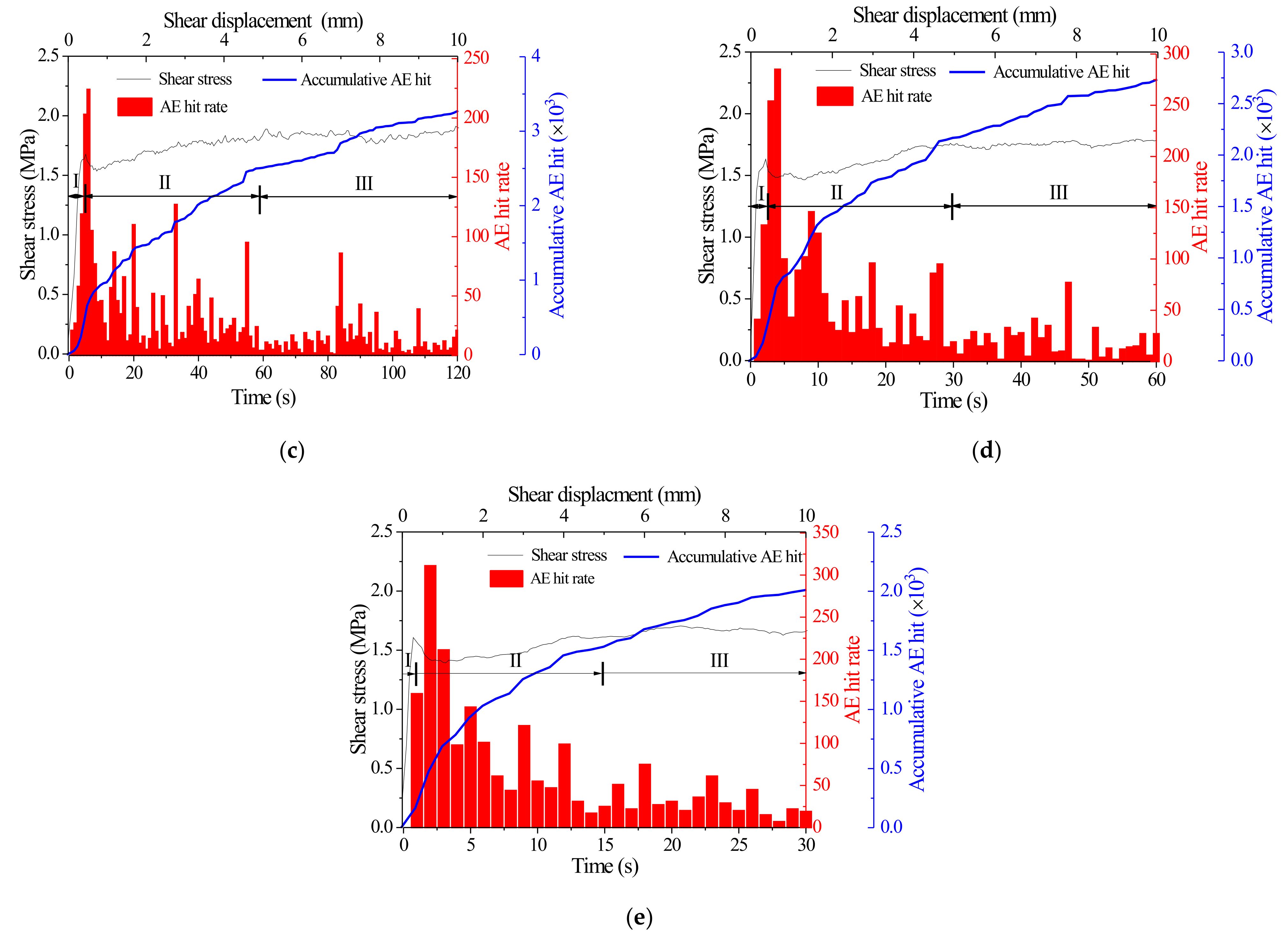
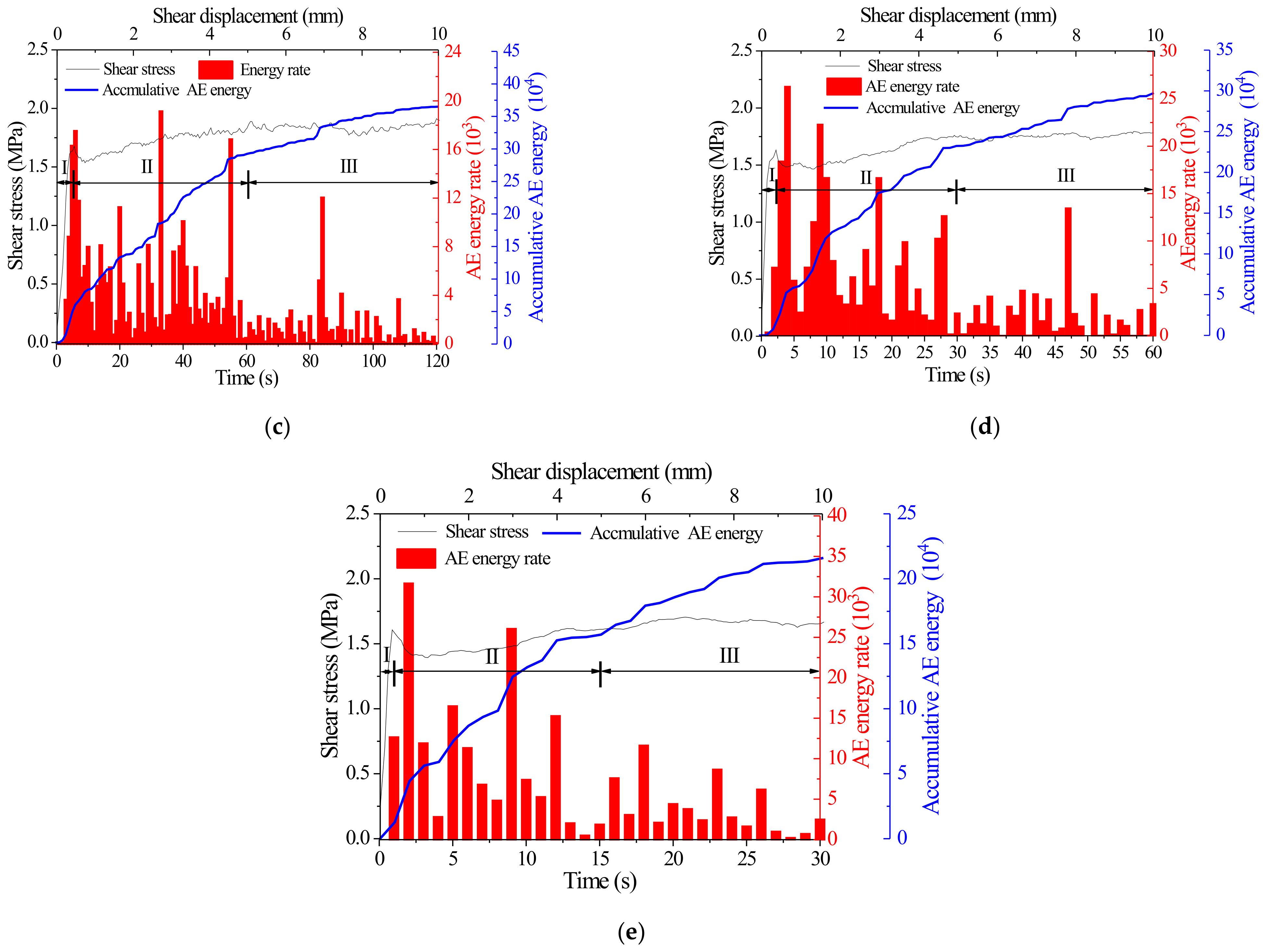
4.2. Effect of Shear Rate on AE Characteristics of Joints
5. Conclusions
- (1)
- With the increase of normal stiffness, the peak shear stress of the joint decreases slightly, but the final shear stress increases linearly. With the increase of normal stiffness, the joint dilatancy decreases significantly, and normal stress increases significantly. The normal stiffness has little influence on the joint surface resistance index.
- (2)
- With the increase of normal stiffness, both the failure area and the failure roughness weight of the joint surface show a linear increase trend, which indicates that under the condition of high normal stress, more failure occurs to the roughness of the joint surface, which is the main reason for the significant increase of final shear stress.
- (3)
- With the increase in shear rate, both the peak shear stress and the final shear stress decrease, and both have a nonlinear relationship with shear rate. When the shear rate is 0.5–5 mm/min, the decline rate of the curve is much higher than that of the curve when the shear rate is 5–20 mm/min. The shear rate has little effect on joint dilatancy, and with the increase of shear rate, the joint dilatancy decreases slightly.
- (4)
- When the shear rate is between 0.5 mm/min and 5 mm/min, the joint failure area and the weight of the damaged, rough body have little difference, but when the shear rate is between 5 mm/min and 20 mm/min, the joint failure area and the weight of the damaged, rough body increase obviously.
- (5)
- In the shearing process, AE signals are mainly generated in the post-peak stage. Generally speaking, the cumulative number of AE impacts and cumulative energy rise with the increase of normal stiffness, which demonstrates that the greater the normal stiffness is, the more serious the failure of the rough surface of the joint.
- (6)
- When the shear rate is low (0.5~5 mm/min), the accumulated AE energy increases from 239,235 to 362,421 with the increase of shear rate; when the shear rate is high (5~20 mm/min), the accumulated AE energy decreases from 362,421 to 241,423 with the increase of shear rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ban, L.R.; Qi, C.Z.; Dan, R.L.; Tao, Z.G.; Xia, C.; Jiang, K. Softening model of shear stiffness before joint peak and analysis of its influencing factors. J. China Coal Soc. 2018, 43, 2765–2772. [Google Scholar]
- Hu, S.Y.; Liu, Q.S.; Li, S.H.; Sang, H.M.; Kang, Y.S. Advance and review on grouting critical problems in fractured mass. Coal Sci. Technol. 2022, 50, 112–126. [Google Scholar]
- Zhao, K. Numerical simulation of shear mechanical properties of coal structural plane. Coal Sci. Technol. 2021, 49, 89–95. [Google Scholar]
- Jiang, Y.J.; Zhang, S.H.; Luan, H.J.; Chen, L.; Zhang, G.; Wang, C. Effects of cyclic loading on rock joints Simulation study of the effect of cyclic loading on the macroscopic shear properties of rock joints. J. China Coal Soc. 2022. [Google Scholar] [CrossRef]
- Jing, H.W.; Zhu, T.T.; Su, H.J.; Yin, Q.; Zhao, H.H.; Han, G.S. Experimental study on anchoring force evolution characteristics of mortar anchor in joint rock mass. Coal Sci. Technol. 2017, 45, 16–21. [Google Scholar]
- Zhao, Z.; Peng, H.; Wu, W.; Chen, Y.-F. Characteristics of shear-induced asperity degradation of rock fractures and implications for solute retardation. Int. J. Rock Mech. Min. Sci. 2018, 105, 53–61. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Zhang, S.H.; Luan, H.J.; Wang, C.S.; Wang, D.; Han, W. Numerical simulation of dynamic contact characteristics of rock mass structural planes under shear load. J. China Coal Soc. 2022, 47, 233–245. [Google Scholar]
- Yin, Q.; Jing, H.W.; Meng, B.; Liu, R.C.; Wu, Y.J. Shear mechanical properties of 3D rough rock fracture surfaces under constant normal stiffness conditions. Chin. J. Rock Mech. Eng. 2020, 39, 2213–2225. [Google Scholar]
- Liu, R.C.; Yin, Q.; Yang, H.Q.; Jing, H.; Yu, L. Cyclic shear mechanical properties of 3D rough joint surfaces under constant normal stiffness boundary conditions. Chin. J. Rock Mech. Eng. 2021, 40, 1092–1109. [Google Scholar]
- Zhou, G.-L.; Xu, T.; Konietzky, H.; Zhu, W.; Heng, Z.; Yu, X.-Y.; Zhao, Y. An improved grain-based numerical manifold method to simulate deformation, damage and fracturing of rocks at the grain size level. Eng. Anal. Bound. Elements 2021, 134, 107–116. [Google Scholar] [CrossRef]
- Zhao, Z.; Dou, Z.; Xu, H.; Liu, Z. Shear behavior of Beishan granite fractures after thermal treatment. Eng. Fract. Mech. 2019, 213, 223–240. [Google Scholar] [CrossRef]
- Meng, F.; Zhou, H.; Wang, Z.; Zhang, C.; Li, S.; Zhang, L.; Kong, L. Characteristics of Asperity Damage and Its Influence on the Shear Behavior of Granite Joints. Rock Mech. Rock Eng. 2017, 51, 429–449. [Google Scholar] [CrossRef]
- Moradian, Z.; Ballivy, G.; Rivard, P. Correlating acoustic emission sources with damaged zones during direct shear test of rock joints. Can. Geotech. J. 2012, 49, 710–718. [Google Scholar] [CrossRef]
- Meng, F.; Zhou, H.; Li, S.; Zhang, C.; Wang, Z.; Kong, L.; Zhang, L. Shear Behaviour and Acoustic Emission Characteristics of Different Joints Under Various Stress Levels. Rock Mech. Rock Eng. 2016, 49, 4919–4928. [Google Scholar] [CrossRef]
- Chai, M.; Hou, X.; Zhang, Z.; Duan, Q. Identification and prediction of fatigue crack growth under different stress ratios using acoustic emission data. Int. J. Fatigue 2022, 160, 106860. [Google Scholar] [CrossRef]
- Muir, C.; Swaminathan, B.; Almansour, A.S.; Sevener, K.; Smith, C.; Presby, M.; Kiser, J.D.; Pollock, T.M.; Daly, S. Damage mechanism identification in composites via machine learning and acoustic emission. Npj Comput. Mater. 2021, 7, 1–15. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Gong, B.; Zhang, Y.J.; Yang, X.Y.; Tang, C.A. Progressive fracturebehavior and acoustic emission release of CJBs affected by joint distance ratio. Mathematics 2022, 10, 4149. [Google Scholar] [CrossRef]
- Gong, B.; Wang, Y.; Zhao, T.; Tang, C.; Yang, X.; Chen, T. AE energy evolution during CJB fracture affected by rock heterogeneity and column irregularity under lateral pressure. Geomat. Nat. Hazards Risk 2022, 13, 877–907. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, B.; Tang, C. Numerical Investigation on Anisotropy and Shape Effect of Mechanical Properties of Columnar Jointed Basalts Containing Transverse Joints. Rock Mech. Rock Eng. 2022, 55, 7191–7222. [Google Scholar] [CrossRef]
- Jiang, Q.; Liu, C.; Feng, G.L.; Yang, Y. Evolution of Natural Joints’ Mesoscopic Failure Modes under Shear Tests: Acoustic Emission Investigation. Int. J. Geomech. 2021, 21, 04021205. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, Q.; Xin, J.; Wu, S.; Liu, J.; Gong, F. Shearing Damage Evolution of Natural Rock Joints with Different Wall Strengths. Rock Mech. Rock Eng. 2022, 55, 1599–1617. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiao, J.; Tanabashi, Y.; Mizokami, T. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition. Int. J. Rock Mech. Min. Sci. 2003, 41, 275–286. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, B.; Tanabashi, Y. Estimating the relation between surface roughness and mechanical properties of rock joints. Int. J. Rock Mech. Min. Sci. 2006, 43, 837–846. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, Y.; Luan, H.; Sugimoto, S. Effect of shearing on hydraulic properties of rough-walled fractures under different boundary conditions. Energy Sci. Eng. 2019, 8, 865–879. [Google Scholar] [CrossRef] [Green Version]
- Song, J.-J.; Son, B.-K.; Lee, C.-I.; Rim, H.-R.; Choi, H.-J. Experimental study for shear behavior of pseudo rock joint under constant normal stiffness condition. In Proceedings of the 31st ITAAITES World Tunnel Congress on Underground Space Use, Istanbul, Turkey, 7–12 May 2005. [Google Scholar] [CrossRef]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Yin, Q.; Ma, G.; Jing, H.; Wang, H.; Su, H.; Wang, Y.; Liu, R. Hydraulic properties of 3D rough-walled fractures during shearing: An experimental study. J. Hydrol. 2017, 555, 169–184. [Google Scholar] [CrossRef]
- Guo, W.; Gu, Q.; Tan, Y.; Hu, S. Case Studies of Rock Bursts in Tectonic Areas with Facies Change. Energies 2019, 12, 1330. [Google Scholar] [CrossRef] [Green Version]
- Ahola, M.P.; Hsiung, S.-M.; Kana, D.D. Experimental study on dynamic behavior of rock joints. Dev. Geotech. Eng. 1996, 79, 467–494. [Google Scholar] [CrossRef]
- Cui, G.J.; Zhang, C.Q.; Liu, L.P.; Zhou, H.; Cheng, G.T. Study on Shear Rate Effect on Mechanical Properties of Bolt Body-Mortar Interface. Rock Soil Mech. 2018, 7. [Google Scholar]
- Atapour, H.; Moosavi, M. The Influence of Shearing Velocity on Shear Behavior of Artificial Joints. Rock Mech. Rock Eng. 2013, 47, 1745–1761. [Google Scholar] [CrossRef]
- Tang, Z.C.; Wong, L.N.Y. Influences of Normal Loading Rate and Shear Velocity on the Shear Behavior of Artificial Rock Joints. Rock Mech. Rock Eng. 2015, 49, 2165–2172. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.P.; Jiang, Y.K.; Wu, X.; Wang, S. Rate-dependent mechanical behavior of rough rock joints. Int. J. Rock Mech. Min. Sci. 2016, 83, 231–240. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.P.; Jiang, Y.J.; Zhang, Y.Z. A Shear Strength Criterion for Rough Structures Considering Shear Rate. Chin. J. Geotech. Eng. 2015, 37, 1399–1404. [Google Scholar]
- Zhang, Y.; Jiang, Y.; Asahina, D.; Wang, C. Experimental and Numerical Investigation on Shear Failure Behavior of Rock-like Samples Containing Multiple Non-Persistent Joints. Rock Mech. Rock Eng. 2020, 53, 4717–4744. [Google Scholar] [CrossRef]
- Tse, R.; Cruden, D.M. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 303–307. [Google Scholar] [CrossRef]
- Jiang, Y.J.; Zhang, S.H.; Luan, H.J.; Wang, C.S.; Wen, Z.J.; Dong, W.; Han, W. Experimental study on shear characteristics of anchored-jointed rock mass under constant normal stiffness boundary conditions. Chin. J. Rock Mech. Eng. 2021, 40, 663–675. [Google Scholar]
- Yong, K.L.; Jung, W.P.; Jae, J.S. Model for the shear behavior of rock joints under CNL and CNS conditions. Int. J. Rock Mech. Min. Sci. 2014, 70, 252–263. [Google Scholar]
- Yuan, W.; Li, J.C. Effect of Shear Rate on Friction Behavior of Straight Joints and Its Mechanism. Chin. J. Rock Mech. Eng. 2021, 40, 3241–3252. [Google Scholar]
- Meng, F.Z.; Wong, L.N.; Zhou, H.; Yu, J.; Cheng, G. Shear Rate Effects on the Post-peak Shear Behaviour and Acoustic Emission Characteristics of Artificially Split Granite Joints. Rock Mech. Rock Eng. 2019, 52, 2155–2174. [Google Scholar] [CrossRef]







| Physico-Mechanical Properties | Index | Unit | Value |
|---|---|---|---|
| Density | ρ | g/cm3 | 2.066 |
| Compressive strength | σc | MPa | 47.4 |
| Modulus of elasticity | Es | MPa | 28.7 |
| Poisson’s ratio | v | – | 0.23 |
| Tensile strength | σt | MPa | 2.5 |
| Cohesion | c | MPa | 5.3 |
| Internal friction angle | φ | ° | 63.3 |
| Number | Initial Normal Stress (MPa) | Normal Stiffness (MPa/mm) | Shear Rate (mm/min) |
|---|---|---|---|
| 1 | 2 | 0 | 0.5 |
| 2 | 1 | ||
| 3 | 3 | ||
| 4 | 5 | ||
| 5 | 7 | ||
| 6 | 3 | 2.5 | |
| 7 | 3 | 5 | |
| 8 | 3 | 10 | |
| 9 | 3 | 20 |
| σn (MPa) | kn (MPa/mm) | v (mm/min) | Nph | Nth | Nh1/Nth | Nh2/Nth | Nh3/Nth | Npe | Nte | Ne1/Nte | Ne2/Nte | Ne3/Nte | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 0.5 | 87 | 3509 | 9.9% | 63.1% | 27% | 10,332 | 143,609 | 12.8% | 68.9% | 18.3% |
| 2 | 1 | 78 | 3893 | 10.5% | 63.3% | 26.2% | 9079 | 178,553 | 9.2% | 71.9% | 18.9% | ||
| 3 | 3 | 88 | 4290 | 12.2% | 61.5% | 26.3% | 12242 | 239,235 | 9.7% | 69.5% | 20.8% | ||
| 4 | 5 | 76 | 4842 | 4.9% | 67.3% | 27.8% | 10380 | 317,610 | 5.3% | 77.1% | 17.6% | ||
| 5 | 7 | 81 | 5417 | 6.1% | 68% | 25.9% | 10865 | 371,112 | 6.3% | 75.4% | 18.3% | ||
| 6 | 3 | 2.5 | 133 | 3749 | 8.4% | 63.1% | 28.5% | 14653 | 264,765 | 4.2% | 74.4% | 21.4% | |
| 7 | 3 | 5 | 224 | 3264 | 6.9% | 69.8% | 23.3% | 17506 | 362,421 | 3.5% | 76.1% | 20.4% | |
| 8 | 3 | 10 | 285 | 2731 | 6.4% | 73% | 20.6% | 26295 | 310,441 | 2.4% | 74.4% | 23.2% | |
| 9 | 3 | 20 | 311 | 2003 | 7.9% | 68.1% | 24% | 31670 | 241,423 | 5.2% | 70.4% | 24.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Li, X.; Wang, C.; Luan, H.; Zhang, S.; Wang, G.; Wang, P. Influence of Normal Stiffness and Shear Rate on the Shear Behaviors and Acoustic Emissions Characteristics of Artificial Rock Joints. Appl. Sci. 2023, 13, 1189. https://doi.org/10.3390/app13021189
Jiang Y, Li X, Wang C, Luan H, Zhang S, Wang G, Wang P. Influence of Normal Stiffness and Shear Rate on the Shear Behaviors and Acoustic Emissions Characteristics of Artificial Rock Joints. Applied Sciences. 2023; 13(2):1189. https://doi.org/10.3390/app13021189
Chicago/Turabian StyleJiang, Yujing, Xinpeng Li, Changsheng Wang, Hengjie Luan, Sunhao Zhang, Gang Wang, and Pu Wang. 2023. "Influence of Normal Stiffness and Shear Rate on the Shear Behaviors and Acoustic Emissions Characteristics of Artificial Rock Joints" Applied Sciences 13, no. 2: 1189. https://doi.org/10.3390/app13021189
APA StyleJiang, Y., Li, X., Wang, C., Luan, H., Zhang, S., Wang, G., & Wang, P. (2023). Influence of Normal Stiffness and Shear Rate on the Shear Behaviors and Acoustic Emissions Characteristics of Artificial Rock Joints. Applied Sciences, 13(2), 1189. https://doi.org/10.3390/app13021189








