Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
- 4% longitudinal direction during stacking/retrieving with load at maximum lift height and actual capacity less than 5000 kg;
- 3.5% longitudinal direction during stacking/retrieving with load at maximum lift height and actual capacity, not less than 5000 kg;
- 18% longitudinal direction during travelling with load at lift height for travelling (maximum 500 mm);
- 6% lateral direction during stacking/retrieving with load at maximum lift height.
2.1. Longitudinal Stability
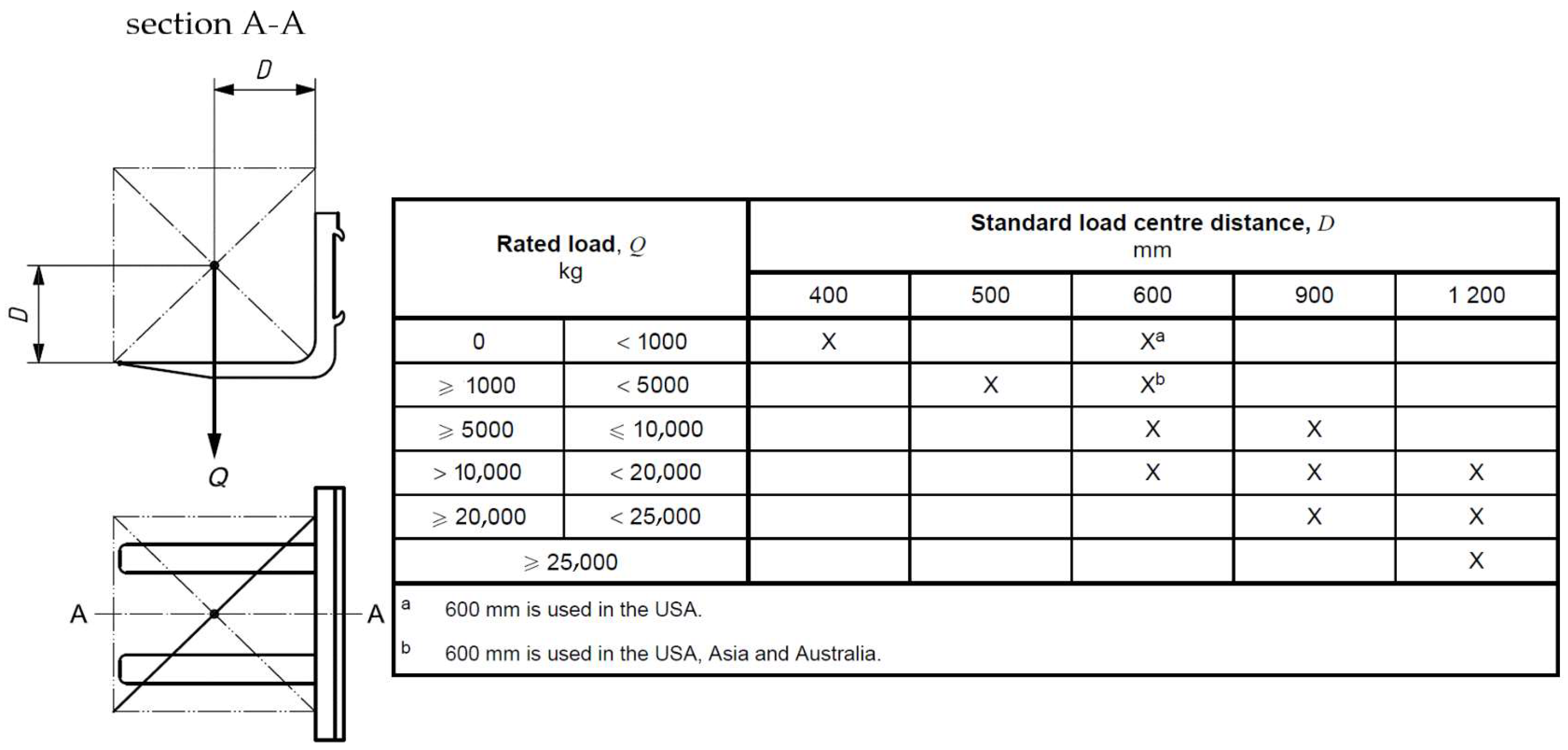
- The rated capacity (Qij) with forks according to EN ISO 3691-1 [16]. It can also be defined by means of a load chart depending on the specified height at a specified load centre distance;
- The type of tyres the load chart refers to (if any);
- The fork arm blade thickness(s).
- Similarly, the following data concerning the interchangeable equipment should be acquired in the instruction handbook:
- The total mass of the interchangeable equipment (PCA);
- The distance (L) measured horizontally from the fork carrier to the centre of gravity for the unladen interchangeable equipment;
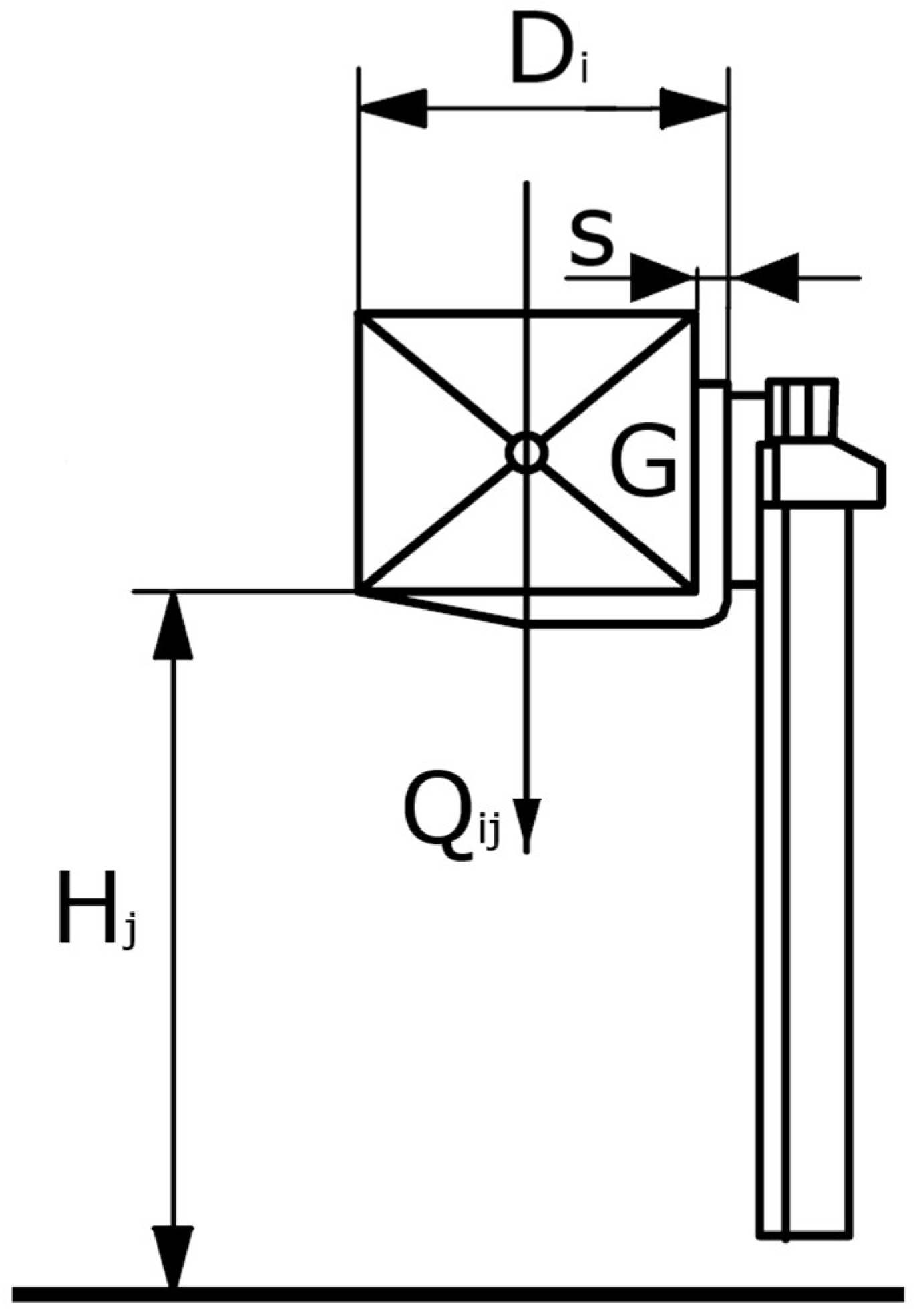
- The distance (Dai) measured horizontally from the fork carrier to the centre of gravity of the load;
- The maximum load permitted by the manufacturer (Qi).
- The maximum load at the fork carrier (CI) as the sum of the maximum load permitted by the manufacturer (Qi) and the total mass of the interchangeable equipment (PCA);
- The overall longitudinal moment at the fork carrier (MLA) according to Equation (2) and nomenclature in Figure 3.
2.2. Lateral Stability
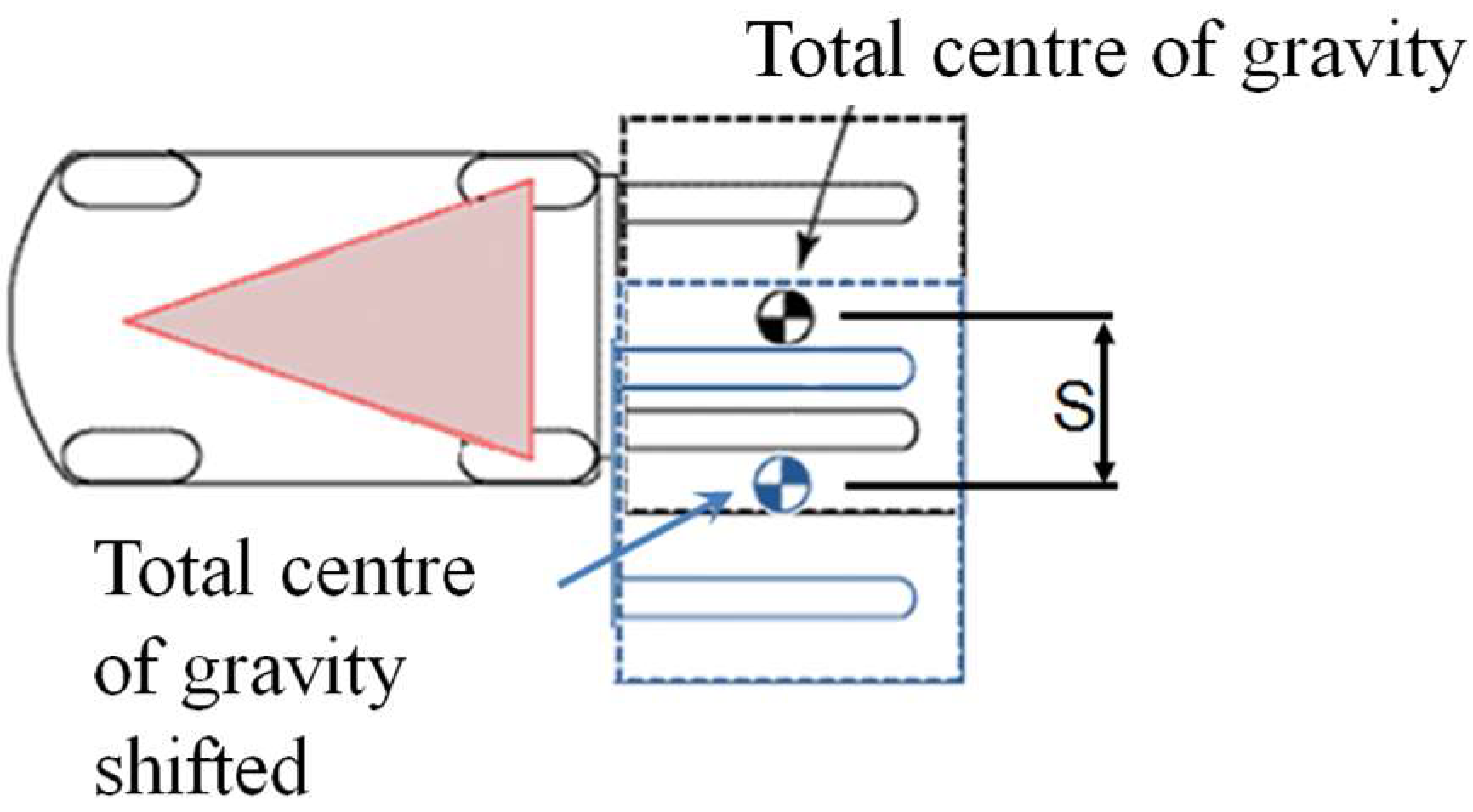
- The maximum lateral displacement S [mm];
- The total mass (PCAS) of the elements FOR the interchangeable equipment which takes part in the lateral displacement [kg].
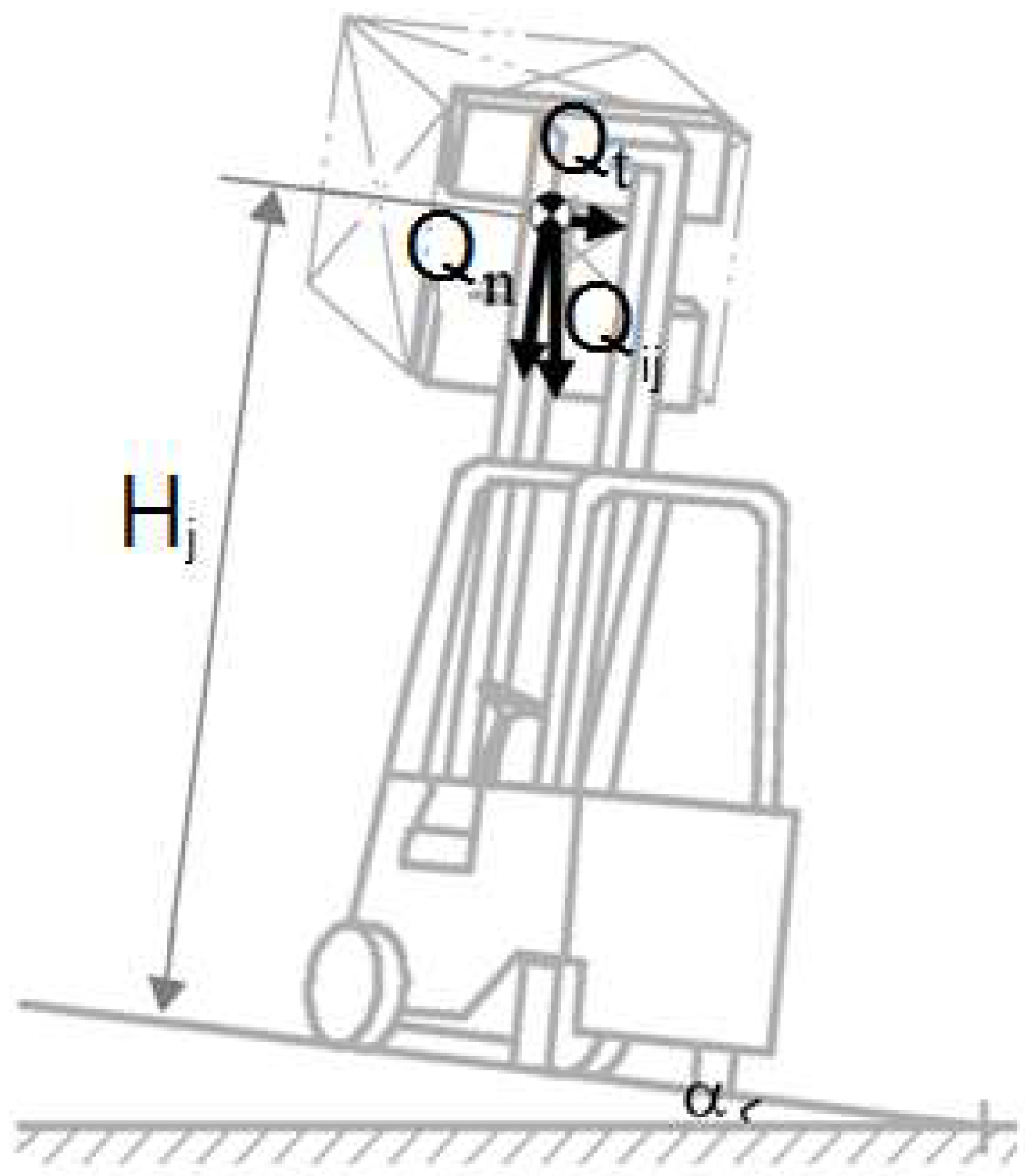
- Evaluate the maximum operating transversal moment (OTM) of the truck as per Equation (5) according to the lift height (Hj in Figure 2). With reference to Figure 4, the load is supposed to be on the fork arm of the FLT and is positioned according to the test condition for lateral stability (Test 3) required by ISO 22915-2 at a slope of 6% (α = 3.4°).
- It is important to evaluate the total transversal moment of the interchangeable equipment (MTA) according to the lift height (Hj) as per Equation (6). The FLT is supposed to be positioned according to the test condition for lateral stability required by ISO 22915-2 (Test 3) at a slope of 6% (α = 3.4°). The value of lateral displacement should be the maximum allowed by the interchangeable equipment by the nature of the load being handled or by the load handle device employed. The total load at the interface (CIL) should be evaluated as the sum of the maximum load permitted by the manufacturer (Qi in Figure 3) and the total mass of the elements of the interchangeable equipment which take part in the lateral displacement (PCAS).
2.3. Lateral Displacement
- -
- At 100 mm for FLT with a rated capacity of <5000 kg;
- -
- At 150 mm for FLT with a rated capacity of ≥5000 kg and ≤10,000 kg;
- -
- At 250 mm for FLT with a rated capacity of >10,000 kg and <20,000 kg;
- -
- At 350 mm for FLT with a rated capacity of ≥20,000 kg.
2.4. Rated Capacity of the Assembly
3. Results
- The lateral displacement—is used for the lateral displacement of the fork arms of a predetermined length. It has a rated capacity of 2500 kg, a horizontal distance of the load centre of gravity from the fork carrier of 600 mm, a weight of 55 kg, a horizontal distance of the interchangeable equipment centre of gravity from the fork carrier of 37 mm, and a lateral displacement of 100 mm.
- The clamp with parallel arms—it is used for handling cardboard bales, wool, garbage, reels of cellulose, foam blocks, concrete blocks, kegs, reels, etc. It allows the clamp to load by means of the parallel motion of its forks/arms. It has a rated capacity of 1900 kg, a horizontal distance of the load centre of gravity from the fork carrier of 637 mm, a weight of 448 kg, a horizontal distance of the interchangeable equipment centre of gravity from the fork carrier of 249 mm, and a lateral displacement of 313 mm.
- The clamp for reels—it is used for handling paper reels of a different nature. This attachment can also continuously rotate the load. It has a rated capacity of 2000 kg, a horizontal distance of the load centre of gravity from the fork carrier of 852 mm, a weight of 620 kg, a horizontal distance of the interchangeable equipment centre of gravity from the fork carrier of 235 mm, and a lateral displacement of 425 mm.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Swartz, G. Forklift tipover: A detailed analysis. Prof. Saf. 1998, 43, 20. [Google Scholar]
- Larsson, T.J.; Oldertz, C. Hazardous Exposures and injury types associated with the use of industrial lift trucks in Sweden 2005–2007. Saf. Sci. Monit. 2011, 15, 237–242. [Google Scholar]
- Saric, S.; Bab-Hadiashar, A.; Hoseinnezhad, R.; Hocking, I. Analysis of forklift accident trends within Victorian industry (Australia). Saf. Sci. 2013, 60, 176–184. [Google Scholar] [CrossRef]
- Rebelle, J.; Mistrot, P.; Poirot, R. Development and validation of a numerical model for predicting forklift truck tip-over. Veh. Syst. Dyn. 2009, 47, 771–804. [Google Scholar] [CrossRef]
- Górny, A. Identification of occupational accident causes by use the Ishikawa diagram and Pareto principles. Econ. Manag. 2017, 1, 384–388. [Google Scholar]
- Kozińska, M.; Radek, N.; Rozlach, A.; Mazur, M. Risk estimation with the application of the matrix method during the operation of the forklift. Syst. Saf. Hum.-Tech. Facil.-Environ. 2021, 3, 337–346. [Google Scholar]
- Duarte, J.; Marques, A.T.; Santos Baptista, J. Occupational accidents related to heavy machinery: A systematic review. Safety 2021, 7, 21. [Google Scholar] [CrossRef]
- Kim, J.B.; Shin, W.; Park, J.H. Stability analysis of counterbalanced forklift trucks. J. Korean Soc. Saf. 2015, 30, 1–8. [Google Scholar]
- Gardella, M.; Martini, A. Multibody models and simulations to assess the stability of counterbalance forklift trucks. In European Congress on Computational Methods in Applied Sciences and Engineering; Springer: Cham, Switzerland, 2019; pp. 526–533. [Google Scholar]
- Xia, G.; Xia, Y.; Tang, X.; Zhao, L.; Hu, J. Anti-rollover control based on stable zone partition of counterbalanced forklift trucks. Int. J. Automot. Technol. 2021, 22, 1529–1543. [Google Scholar] [CrossRef]
- Lee, S.-H.; Bae, Y.-C. Design of simulator for rollover prevention of forklift truck. J. Korea Inst. Electron. Commun. Sci. 2021, 16, 571–576. [Google Scholar]
- Sunday, B.A.K.O. Stability analysis of a semi-trailer articulated vehicle: A review. Int. J. Automot. Sci. Technol. 2021, 5, 131–140. [Google Scholar]
- Lemerle, P.; Höppner, O.; Rebelle, J. Dynamic stability of forklift trucks in cornering situations: Parametrical analysis using a driving simulator. Veh. Syst. Dyn. 2011, 49, 1673–1693. [Google Scholar] [CrossRef]
- Berdiev, A.; Bahadirov, G.; Zhang, D.; Wang, X.; Li, Q. Analysis of the design of lifting and transporting vehicles with a variable center of gravity—A literature and patent overview. Int. J. Eng. Trends Technol. 2021, 69, 56–65. [Google Scholar] [CrossRef]
- ISO 22915-2; Industrial Trucks—Verification of Stability—Part 2: Counterbalanced Trucks with Mast. International Organization for Standardization: Geneva, Switzerland, 2018.
- EN ISO 3691-1; Industrial Trucks—Safety Requirements and Verification—Part 1: Self-Propelled Industrial Trucks, Other than Driverless Trucks, Variable-Reach Trucks and Burden-Carrier Trucks. European Committee for Standardization: Brussels, Belgium, 2020.
- Troyanovskaya, I.; Grebenshchikova, O.; Erofeev, V. Static stability of articulated front loader. AIP Conf. Proc. 2022, 2503, 050033. [Google Scholar]
- Troyanovskaya, I.; Shepelev, S.D. Design of Agricultural Loader with Articulated Frame. In Proceedings of the 6th International Conference on Industrial Engineering (ICIE 2020), Sochi, Russia, 18–22 May 2020. [Google Scholar]
- Robertson, L.S.; Maloney, A. Motor vehicle rollover and static stability: An exposure study. Am. J. Public Health 1997, 87, 839–841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huston, R.L.; Kelly, F.A. Another look at the static stability factor (SSF) in predicting vehicle rollover. Int. J. Crashworthiness 2014, 19, 567–575. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, Y.; Xie, Y.; Zhang, X. Analysis on anti-overturning stability of a truck crane based on zero moment point theory. DYNA 2022, 97, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Kasahara, M.; Mori, Y. Relation between overturn and the center of gravity of a forklift truck. In Proceedings of the 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017; pp. 135–140. [Google Scholar]
- Puder, R.W.; Bogar, W.H.; Jay, R.D. Fork-truck stability—A study in moments. Trans. ASME 1957, 79, 1591–1596. [Google Scholar] [CrossRef]
- FEM European Materials Handling Federation. Guidance on the Classification of Attachments for Industrial Trucks According to Machinery Directive 2006/42/EC, 1st ed.; FEM 4.107; FEM: Brussels, Belgium, 2021. [Google Scholar]



| FLT | Experimental Test [kg] | Analytical Method [kg] | Delta [%] |
|---|---|---|---|
| 1 | 2300 | 2195 | −4.5 |
| 2 | 2400 | 2195 | −8.5 |
| 3 | 1740 | 1785 | +2.5 |
| 4 | 1790 | 1785 | −0.3 |
| 5 | 1840 | 1785 | −3.0 |
| 6 | 2310 | 2235 | −3.2 |
| FLT | Experimental Test [kg] | Analytical Method [kg] | Delta [%] |
|---|---|---|---|
| 1 | 1840 | 1802 | −2.1 |
| 2 | 1900 | 1802 | −5.4 |
| 3 | 1510 | 1502 | −0.5 |
| 4 | 1580 | 1502 | −4.9 |
| 5 | 1610 | 1517 | −5.8 |
| 6 | 1900 | 1942 | +2.2 |
| FLT | Experimental Test [kg] | Analytical Method [kg] | Delta [%] |
|---|---|---|---|
| 1 | 1440 | 1515 | +5.2 |
| 2 | 1630 | 1515 | −7.0 |
| 3 | 1170 | 1080 | −7.7 |
| 4 | 1170 | 1080 | −7.7 |
| 5 | 1240 | 1095 | −11.7 |
| 6 | 1630 | 1410 | −13.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vita, L.; Gattamelata, D. Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment. Appl. Sci. 2023, 13, 1206. https://doi.org/10.3390/app13021206
Vita L, Gattamelata D. Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment. Applied Sciences. 2023; 13(2):1206. https://doi.org/10.3390/app13021206
Chicago/Turabian StyleVita, Leonardo, and Davide Gattamelata. 2023. "Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment" Applied Sciences 13, no. 2: 1206. https://doi.org/10.3390/app13021206
APA StyleVita, L., & Gattamelata, D. (2023). Analytical Method for Assessing Stability of a Counterbalanced Forklift Truck Assembled with Interchangeable Equipment. Applied Sciences, 13(2), 1206. https://doi.org/10.3390/app13021206






