ANN Prediction Model of Concrete Fatigue Life Based on GRW-DBA Data Augmentation
Abstract
:1. Introduction
- (1)
- This paper proposes an optimized GRW-DBA data augmentation algorithm based on group computing and random weight mechanism. Compared with other algorithms such as classic DBA, the GRW-DBA algorithm has a simpler operation process, is not easily affected by outliers, and can obtain generated data that are more in line with the distribution of source data.
- (2)
- We construct a prediction model based on a GRW-DBA data augmentation algorithm and ANN and develop a graphical user interface. Compared with classical mechanical methods, the model can significantly improve the prediction accuracy and at the same time facilitate engineering applications.
2. Methods
2.1. Group Random Weight DBA Algorithm
2.2. Artificial Neural Networks
3. Fatigue Life Prediction Modeling
3.1. Datasets
3.2. Evaluation Indexes
3.3. Modeling Process
3.3.1. Determine the Data Augmentation Factor
3.3.2. Determine the Hyperparameters of the ANN Model
- Iteration times:
- 2.
- Hidden layers:
- 3.
- Learning rate:
4. Experimental Verification
4.1. Validation of Data Augmentation Effects
4.2. Validation of Predictive Models
4.3. Verification of Generalization
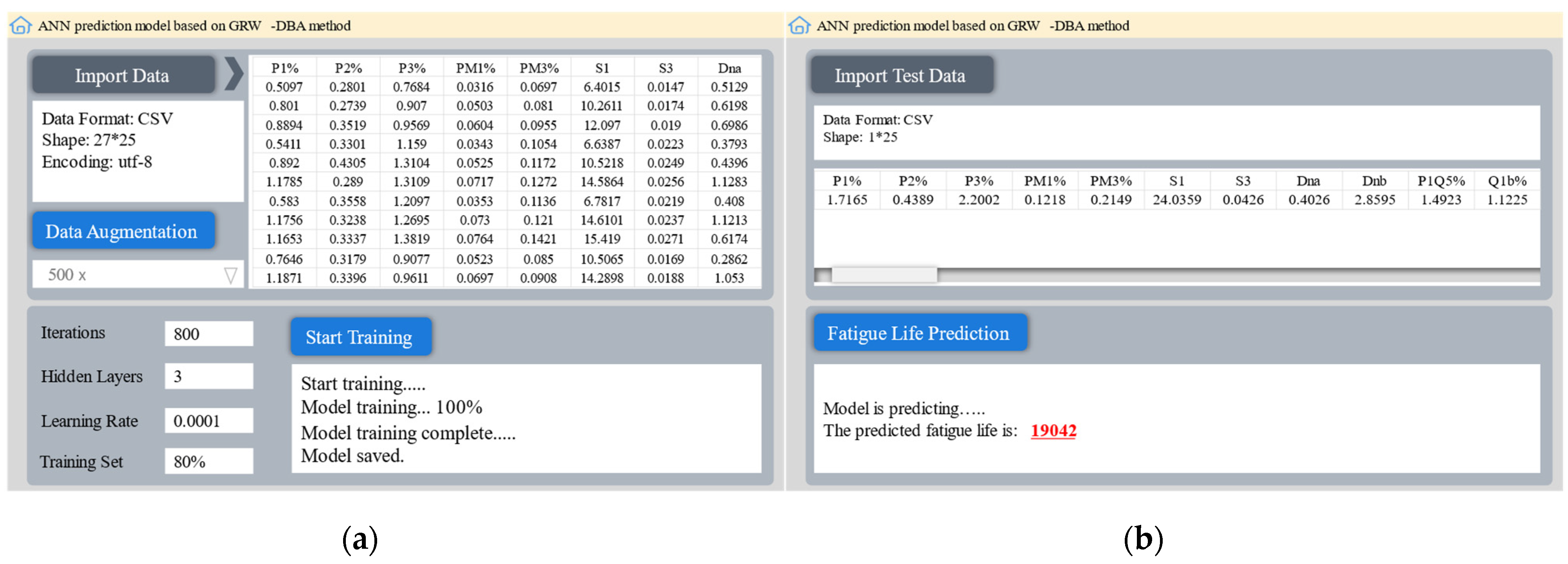
4.4. Graphical User Interface Development
5. Discussion
6. Conclusions
- (1)
- The GRW-DBA data augmentation method proposed in this study can conveniently and effectively augment small datasets while reducing the impact of abnormal sequences on the results. Compared with GAN and classic DBA methods, the GRW-DBA can better improve the prediction accuracy of the ANN model.
- (2)
- The ANN fatigue life prediction model was trained based on the GRW-DBA augmented dataset, under the same conditions. Its prediction accuracy R2 evaluation index increased by 24%, 10.4%, and 7.8% compared with LR, SVM, and AdaBoost. It also shows good generalization in datasets with different distributions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hansen, M. Determination and assessment of fatigue stresses on concrete bridges. Struct. Concr. 2020, 21, 1286–1297. [Google Scholar] [CrossRef]
- Xu, X.Q.; Yang, X.; Yang, W.; Guo, X.F. New damage evolution law for modeling fatigue life of asphalt concrete surfacing of long-span steel bridge. Constr. Build. Mater. 2020, 259, 119795. [Google Scholar] [CrossRef]
- Yuan, M.; Liu, Y.; Yan, D.; Liu, Y. Probabilistic fatigue life prediction for concrete bridges using Bayesian inference. Adv. Civ. Eng. 2019, 22, 765–778. [Google Scholar] [CrossRef]
- Choriev, J.; Muratov, A.; Yangiev, A.; Muratov, O.; Karshiev, R. Design method for reinforced concrete structure durability with the use of safety coefficient by service life period. IOP Conf. Ser. Mater. Sci. Eng. 2020, 883, 012024. [Google Scholar] [CrossRef]
- Fan, Z.; Sun, Y. A study on fatigue behaviors of concrete under uniaxial compression: Testing, analysis, and simulation. J. Test. Eval. 2020, 49, 160–175. [Google Scholar] [CrossRef]
- Zheng, M.; Li, P.; Yang, J.; Li, H.; Qiu, Y.; Zhang, Z. Fatigue life prediction of high modulus asphalt concrete based on the local stress-strain method. Appl. Sci. 2017, 7, 305. [Google Scholar] [CrossRef] [Green Version]
- Lei, D.; Zhang, P.; He, J.; Bai, P.; Zhu, F. Fatigue life prediction method of concrete based on energy dissipation. Constr. Build. Mater. 2017, 145, 419–425. [Google Scholar] [CrossRef]
- Sankar, M.R.; Saxena, S.; Banik, S.R.; Iqbal, I.M.; Nath, R.; Bora, L.J.; Gajrani, K.K. Experimental study and artificial neural network modeling of machining with minimum quantity cutting fluid. Mater. Today Proc. 2019, 18, 4921–4931. [Google Scholar] [CrossRef]
- Roshani, G.H.; Hanus, R.; Khazaei, A.; Zych, M.; Nazemi, E.; Mosorov, V. Density and velocity determination for single-phase flow based on radiotracer technique and neural networks. Flow. Meas. Instrum. 2018, 61, 9–14. [Google Scholar] [CrossRef]
- Mozaffari, H.; Houmansadr, A. Heterogeneous private information retrieval. In Network and Distributed Systems Security (NDSS) Symposium; The National Science Foundation: Alexandria, WV, USA, 2020; pp. 1–18. [Google Scholar]
- Zhou, Z.; Davoudi, E.; Vaferi, B. Monitoring the effect of surface functionalization on the CO2 capture by graphene oxide/methyl diethanolamine nanofluids. J. Environ. Chem. Eng. 2021, 9, 106202. [Google Scholar] [CrossRef]
- Alanazi, A.K.; Alizadeh, S.M.; Nurgalieva, K.S.; Nesic, S.; Grimaldo Guerrero, J.W.; Abo-Dief, H.M.; Eftekhari-Zadeh, E.; Nazemi, E.; Narozhnyy, I.M. Application of neural network and time-domain feature extraction techniques for determining volumetric percentages and the type of two phase flow regimes independent of scale layer thickness. Appl. Sci. 2022, 12, 1336. [Google Scholar] [CrossRef]
- Mozaffari, H.; Houmansadr, A. E2FL: Equal and equitable federated learning. arXiv 2022, arXiv:2205.10454. [Google Scholar]
- Belić, M.; Bobić, V.; Badža, M.; Šolaja, N.; Đurić-Jovičić, M.; Kostić, V.S. Artificial intelligence for assisting diagnostics and assessment of Parkinson’s disease-A review. Clin. Neurol. Neurosur. 2019, 184, 105442. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.X.; Thambiratnam, D.P.; Chan, T.H.T.; Gordan, M.; Razak, H.A. Damage detection in steel-concrete composite bridge using vibration characteristics and artificial neural network. Struct. Infrastruct. E. 2019, 16, 1247–1261. [Google Scholar] [CrossRef]
- Chen, N.; Zhao, S.; Gao, Z.; Wang, D.; Liu, P.; Oeser, M.; Hou, Y.; Wang, L. Virtual mix design: Prediction of compressive strength of concrete with industrial wastes using deep data augmentation. Constr. Build. Mater. 2022, 323, 126580. [Google Scholar] [CrossRef]
- Shang, M.; Li, H.; Ahmad, A.; Ahmad, W.; Ostrowski, K.; Aslam, F.; Majka, T. Predicting the mechanical properties of RCA-based concrete using supervised machine learning algorithms. Materials 2022, 15, 647. [Google Scholar] [CrossRef]
- Deng, F.; He, Y.; Zhou, S.; Yu, Y.; Cheng, H.; Wu, X. Compressive strength prediction of recycled concrete based on deep learning. Constr. Build. Mater. 2018, 175, 562–569. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad, W.; Chaiyasarn, K.; Ostrowski, K.; Aslam, F.; Zajdel, P.; Joyklad, P. Prediction of geopolymer concrete compressive strength using novel machine learning algorithms. Polymers 2021, 13, 3389. [Google Scholar] [CrossRef]
- Zachariah, J.P.; Sarkar, P.P.; Pal, M. Fatigue life of polypropylene-modified crushed brick asphalt mix: Analysis and prediction. P. I. Civil. Eng-Transp. 2021, 174, 110–129. [Google Scholar] [CrossRef]
- Xiao, F.; Amirkhanian, S.; Juang, C.H. Prediction of fatigue life of rubberized asphalt concrete mixtures containing reclaimed asphalt pavement using artificial neural networks. J. Mater. Civ. Eng. 2009, 21, 253–261. [Google Scholar] [CrossRef]
- Yan, C.; Gao, R.; Huang, W. Asphalt mixture fatigue life prediction model based on neural network. In Proceedings of the CICTP 2017: Transportation Reform and Change—Equity, Inclusiveness, Sharing, and Innovation, Shanghai, China, 7–9 July 2017; pp. 1292–1299. [Google Scholar]
- Wu, Q.; Din, K.; Huang, B. Approach for fault prognosis using recurrent neural network. J. Intell. Manuf. 2020, 31, 1621–1633. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Z.W.; Yang, Z.H.; Jiang, J.Y. Interactive effect of mechanical fatigue load and the fatigue effect of freeze-thaw on combined damage of concrete. J. Mater. Civ. Eng. 2015, 27, 04014230. [Google Scholar] [CrossRef]
- Bandara, K.; Hewamalage, H.; Liu, Y.H.; Kang, Y.F.; Bergmeir, C. Improving the accuracy of global forecasting models using time series data augmentation. Pattern Recognit 2021, 120, 108148. [Google Scholar] [CrossRef]
- Terry, T.U.; Pfister, F.M.J.; Pichler, D.; Endo, S.; Lang, M.; Hirche, S. Data augmentation of wearable sensor data for Parkinson’s disease monitoring using convolutional neural networks. In Proceedings of the 19th ACM International Conference on Multimodal Interaction 2017, Glasgow UK, 13–17 November 2017; pp. 216–220. [Google Scholar]
- Kang, Y.F.; Hyndman, R.J.; Li, F. GRA TIS: Generating time series with diverse and controllable characteristics. Stat. Anal. Data. Min. 2020, 13, 354–376. [Google Scholar] [CrossRef]
- Yoon, J.; Jarrett, D.; Schaar, M.V.D. Time-series generative adversarial networks. In Proceedings of the Advances in neural information processing systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 5508–5518. [Google Scholar]
- Amyar, A.; Ruan, S.; Vera, P.; Decazes, P.; Modzelewski, R. RADIOGAN: Deep convolutional conditional generative adversarial network to generate PET images. In Proceedings of the 2020 7th International Conference on Bioinformatics Research and Applications, Berlin, Germany, 13–15 September 2020; pp. 28–33. [Google Scholar]
- Cheung, T.H.; Yeung, D.Y. MODALS: Modality-agnostic automated data augmentation in the latent space. In Proceedings of the International Conference on Learning Representations 2020, Addis Ababa, Ethiopia, 26–30 April 2021; pp. 1–14. [Google Scholar]
- Liu, Y.; Zhou, Y.; Liu, X.; Dong, F.; Wang, C.; Wang, Z. Wasserstein GAN-based small-sample augmentation for new-generation artificial intelligence: A case study of cancer-staging data in biology. Engineering 2019, 5, 156–163. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, M.; Chen, C. A deep-learning intelligent system incorporating data augmentation for short-term voltage stability assessment of power systems. Appl. Energy 2022, 308, 118347. [Google Scholar] [CrossRef]
- Zhao, J.; Ltti, L. shapeDTW: Shape dynamic time warping. Pattern. Recognit. 2017, 74, 171–184. [Google Scholar] [CrossRef] [Green Version]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Data augmentation using synthetic data for time series classification with deep residual networks. arXiv 2018, arXiv:1808.02455. [Google Scholar]
- Yu, G.L.; Bian, Y.Y.; Gamalo, M. Power priors with entropy balancing weights in data augmentation of partially controlled randomized trials. J. Biopharm. Stat. 2022, 32, 4–20. [Google Scholar] [CrossRef]
- Harase, S. Conversion of Mersenne Twister to double-precision floating-point numbers. Math. Comput. Simulat. 2019, 161, 76–83. [Google Scholar] [CrossRef] [Green Version]
- Ramachandra, S.; Durodola, J.F.; Fellows, N.A.; Gerguri, S.; Thite, A. Experimental validation of an ANN model for random loading fatigue analysis. Int. J. Fatigue. 2019, 126, 112–121. [Google Scholar] [CrossRef]
- Li, X.B.; Wang, W.Q. Learning discriminative features via weights-biased softmax loss. Pattern. Recognit. 2020, 107, 107405. [Google Scholar] [CrossRef]
- Shi, J.N.; Zhao, Y.R.; Zeng, B. Relationship between pore structure and bending strength of concrete under a high-low temperature cycle based on grey system theory. J. Grey. Syst. 2020, 32, 101–118. [Google Scholar]
- Zhang, W.; Lee, D.; Lee, J.; Lee, C. Residual strength of concrete subjected to fatigue based on machine learning technique. Struct. Concr. 2021, 23, 2274–2287. [Google Scholar] [CrossRef]
- Ke, Z.H.; Liu, X.N.; Chen, Y.N.; Shi, H.F.; Deng, Z.G. Prediction models establishment and comparison for guiding force of high-temperature superconducting maglev based on deep learning algorithms. Supercond. Sci. Tech. 2022, 35, 024005. [Google Scholar] [CrossRef]
- Dai, X.; Yin, H.; Jha, N.K. Grow and prune compact, fast, and accurate LSTMs. IEEE Trans. Comput. 2020, 69, 441–452. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Qi, X.; Ma, H. LLR: Learning learning rates by LSTM for training neural networks. Neurocomputing 2020, 394, 41–50. [Google Scholar] [CrossRef]
- Klepeis, N.E.; Nelson, W.C.; Ott, W.R.; Robinson, J.P.; Tsang, A.M.; Switzer, P. The national human activity pattern survey (NHAPS): A resource for assessing exposure to environmental pollutants. J. Expo. Anal. Environ. Epidemiol. 2011, 11, 231–252. [Google Scholar] [CrossRef] [Green Version]
- Dubey, S.R.; Chakraborty, S.; Roy, S.K. DiffGrad: An optimization method for convolutional neural networks. IEEE Trans. Neural. Netw. Learn. Syst. 2019, 31, 4500–4511. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Sun, T.; Dou, Y. An adaptive learning rate schedule for SIGNSGD optimizer in neural networks. Neural. Process. Lett. 2022, 54, 803–816. [Google Scholar] [CrossRef]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time series data augmentation for deep learning: A survey. arXiv 2021, arXiv:2002.12478. [Google Scholar]
- Khademi, F.; Akbari, M.; Jamal, S.M.; Nikoo, M. Multiple linear regression, artificial neural network, and fuzzy logic prediction of 28 days compressive strength of concrete. Front. Struct. Civ. Eng. 2017, 11, 90–99. [Google Scholar] [CrossRef]
- Amyar, A.; Guo, R.; Cai, X.; Assana, S.; Chow, K.; Rodriguez, J.; Yankama, T.; Cirillo, J.; Pierce, P.; Goddu, B.; et al. Impact of deep learning architectures on accelerated cardiac T1 mapping using MyoMapNet. NMR Biomed. 2022, 35, e4794. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Wei, H.; Nian, D. Integrated ANN-Bayes-based travel time prediction modeling for signalized corridors with probe data acquisition paradigm. Expert Syst. Appl. 2022, 209, 118319. [Google Scholar] [CrossRef]
- Amyar, A.; Modzelewski, R.; Vera, P.; Morard, V.; Ruan, S. Weakly supervised tumor detection in PET using class response for treatment outcome prediction. J. Imaging 2022, 8, 130. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, J.; Kong, J.; Su, T.; Bai, Y. A reversible automatic selection normalization (RASN) deep network for predicting in the smart agriculture system. Agronomy 2022, 12, 591. [Google Scholar] [CrossRef]
- Amyar, A.; Modzelewski, R.; Vera, P.; Morard, V.; Ruan, S. Multi-task multi-scale learning for outcome prediction in 3D PET images. Comput. Biol. Med. 2022, 151, 106208. [Google Scholar] [CrossRef]











| Datasets | Number | Input Variables | Explanation |
|---|---|---|---|
| Dataset 1 | 1 | P1% | Pore size of 0.1–27.98 nm |
| 2 | P2% | Pore size 27.98–524.26 nm | |
| 3 | P3% | Pore size 524.26–6463.30 nm | |
| 4 | PM1% | Porosity of pore size corresponding to highest peak of P1 part of the curve | |
| 5 | PM3% | Porosity of pore size corresponding to highest peak of P3 part of the curve | |
| 6 | S1 | Rate of change of P1 pore size | |
| 7 | S3 | P3 rate of pore size change | |
| 8 | Dna | P1 pore fractal dimension | |
| 9 | Dnb | P3 pore fractal dimension | |
| 10 | P1Q% | P1 part of the 0.1–7.5 nm pore size porosity | |
| 11 | P1b% | P1 part less than 5 nm pore size porosity | |
| 12 | P1h | P1 part 5–27.98 nm pore size porosity | |
| 13 | Sz | Pore size integrated change rate | |
| 14 | Cz | Pore structure complexity factor | |
| 15 | Large capillaries | Pore size of 50–10,000 nm | |
| 16 | Small capillaries | Pore size 10–50 nm | |
| 17 | Inter-colloidal pores | Pore size 2.5–10 nm | |
| 18 | Micropores | Pore size 0.5–2.5 nm | |
| 19 | Interlayer pores | Aperture size is less than 0.5 nm | |
| 20 | Non-harmful pores | Pore size is less than 20 nm | |
| 21 | Less harmful pores | Pore size is 20–100 nm | |
| 22 | Harmful pores | Pore size is 100–200 nm | |
| 23 | Multi-harmful holes | Pore size is greater than 200 nm | |
| 24 | Ptotal | Total pore size | |
| Dataset 2 | 1 | fc | Compressive strength of concrete |
| 2 | h/w | Height-to-width ratio | |
| 3 | Shape | Shape of the test specimens | |
| 4 | Smax | Maximum stress level | |
| 5 | R | Minimum stress to maximum stress ratio | |
| 6 | f(HZ) | Loading frequency |
| Hyperparameters | Values |
|---|---|
| Number of neurons in the input layer | 24 |
| Hidden layers | 80, 40 |
| Learning rate | 0.001 |
| Activation function | tanh |
| Iteration times | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhang, W.; Zhao, Y. ANN Prediction Model of Concrete Fatigue Life Based on GRW-DBA Data Augmentation. Appl. Sci. 2023, 13, 1227. https://doi.org/10.3390/app13021227
Shi J, Zhang W, Zhao Y. ANN Prediction Model of Concrete Fatigue Life Based on GRW-DBA Data Augmentation. Applied Sciences. 2023; 13(2):1227. https://doi.org/10.3390/app13021227
Chicago/Turabian StyleShi, Jinna, Wenxiu Zhang, and Yanru Zhao. 2023. "ANN Prediction Model of Concrete Fatigue Life Based on GRW-DBA Data Augmentation" Applied Sciences 13, no. 2: 1227. https://doi.org/10.3390/app13021227
APA StyleShi, J., Zhang, W., & Zhao, Y. (2023). ANN Prediction Model of Concrete Fatigue Life Based on GRW-DBA Data Augmentation. Applied Sciences, 13(2), 1227. https://doi.org/10.3390/app13021227






