A Study on Longitudinal Motion Scenario Design for Verification of Advanced Driver Assistance Systems and Autonomous Driving Systems
Abstract
:1. Introduction
2. Simplified Vehicle Model
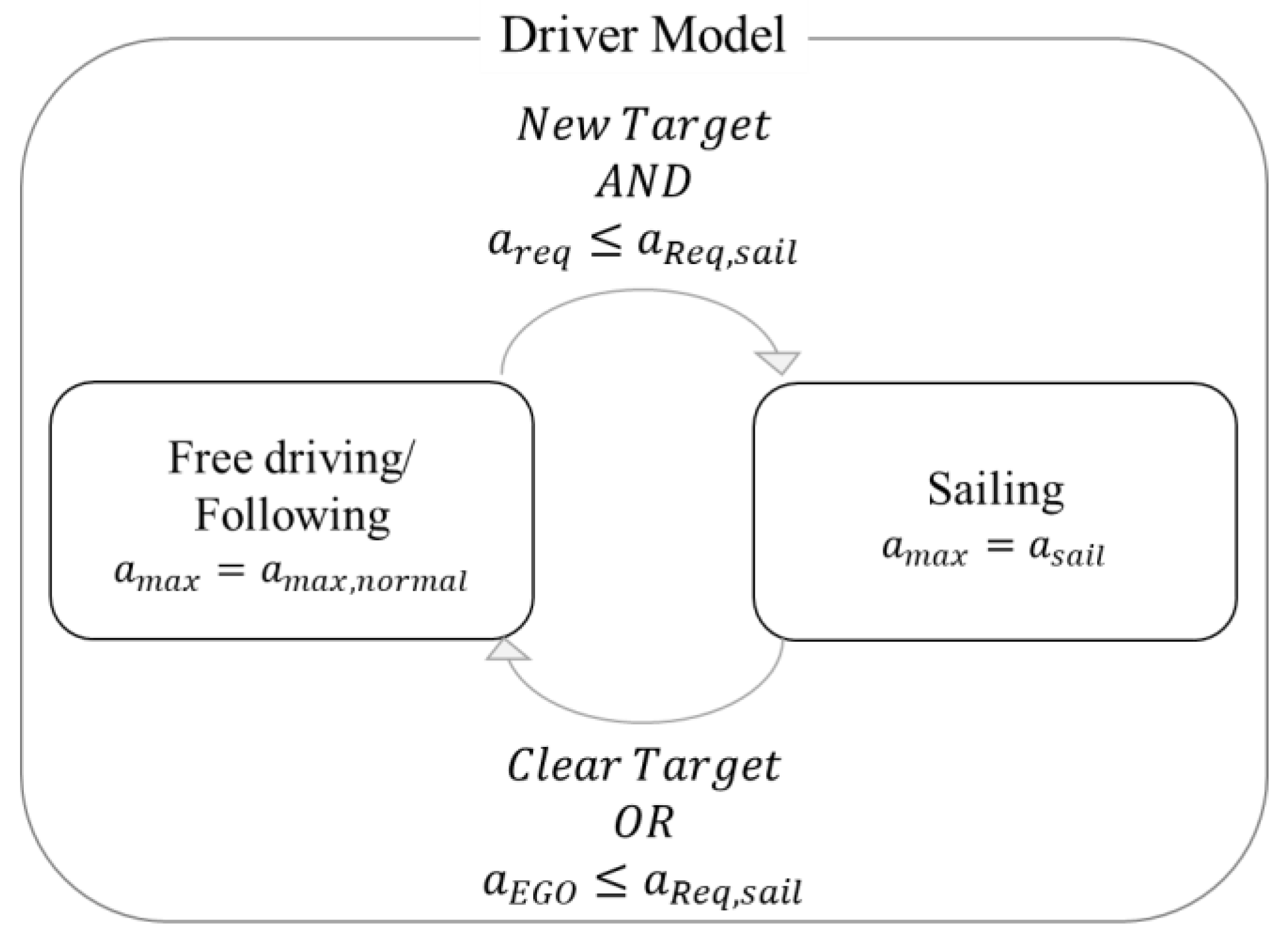
3. Longitudinal Driver Model
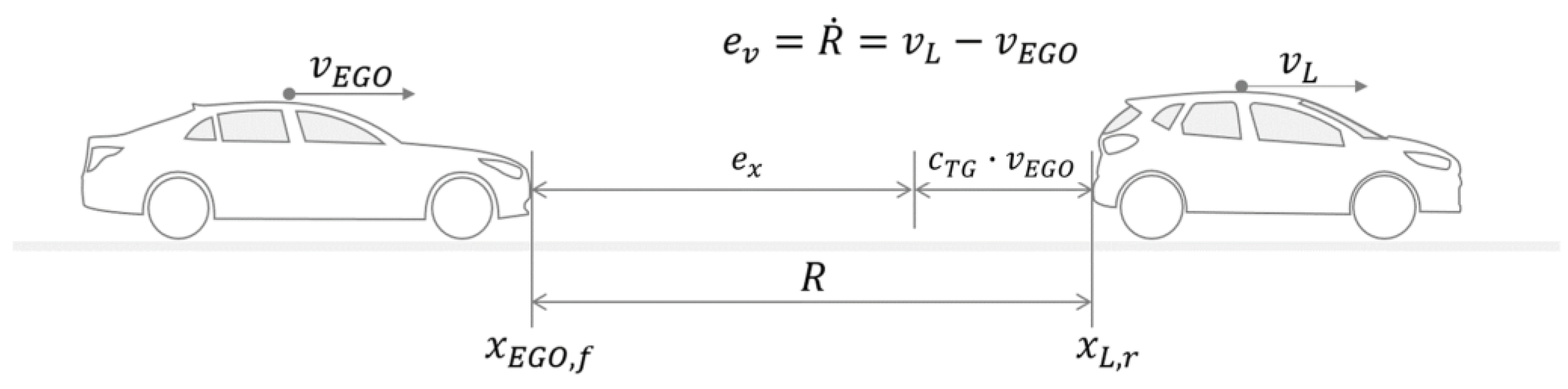
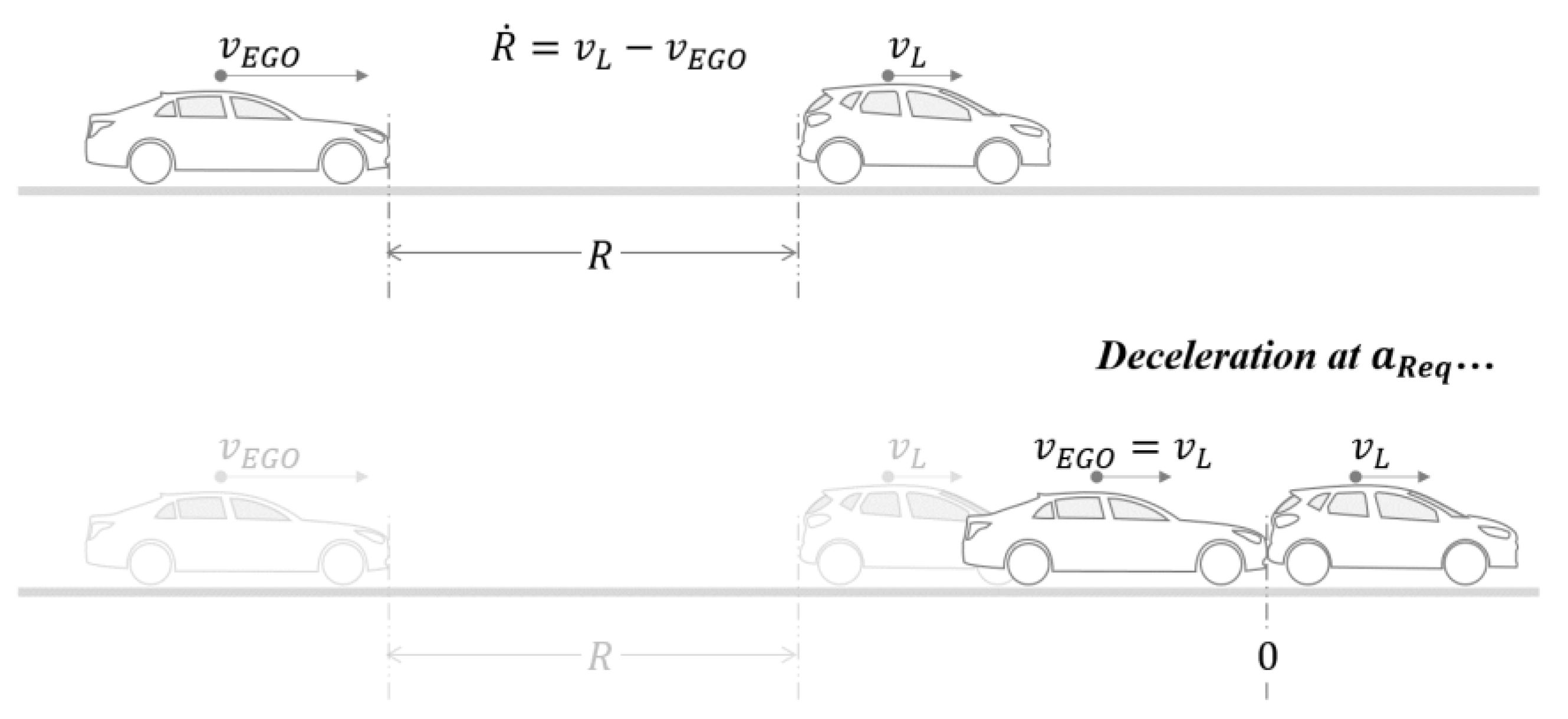
3.1. Error Dynamics for the Car-Following Model
3.2. MPC-Based Driver Model Design
4. Naturalistic Driving Data-Based Longitudinal Driver Model Parameter Design
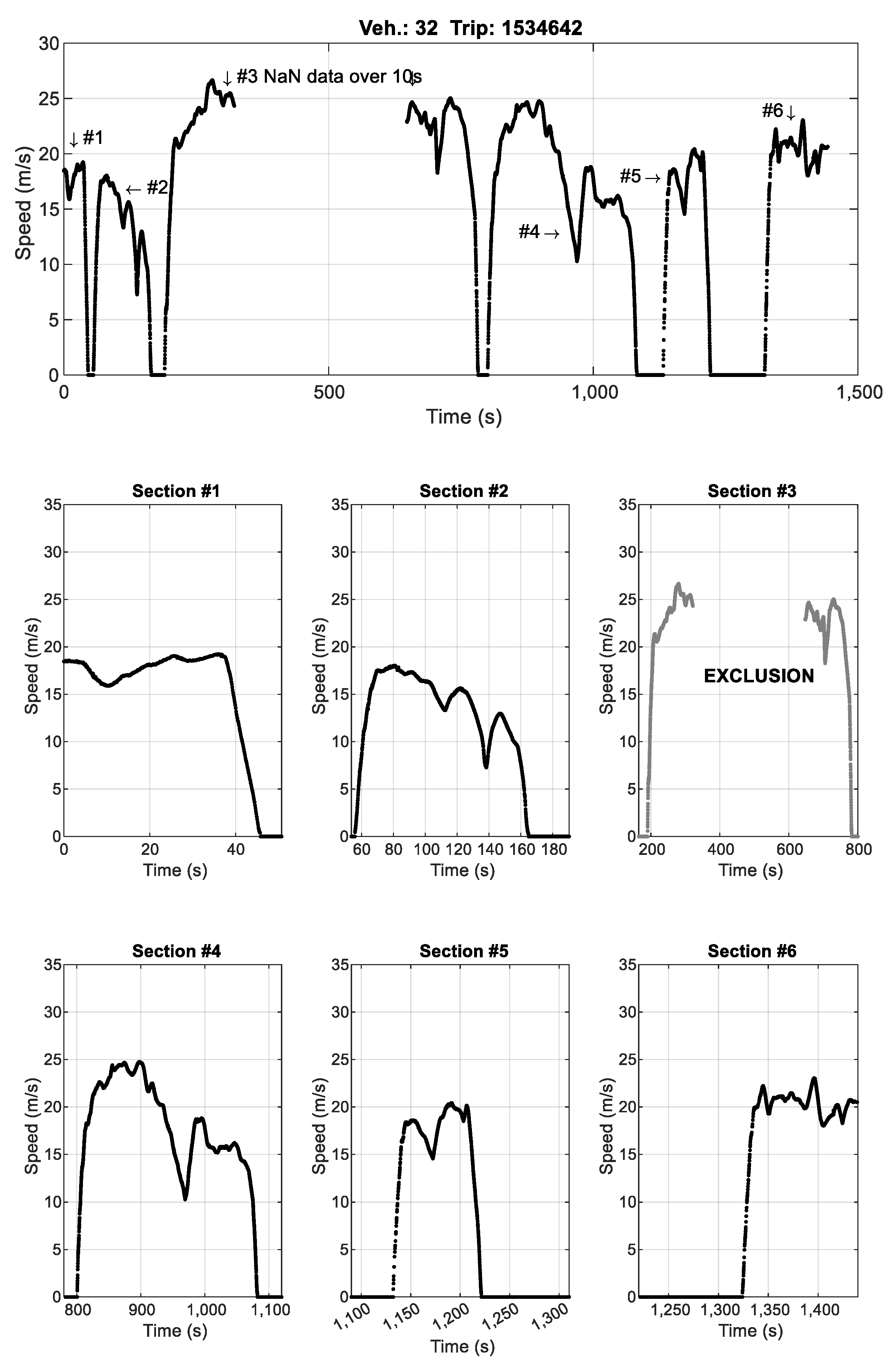
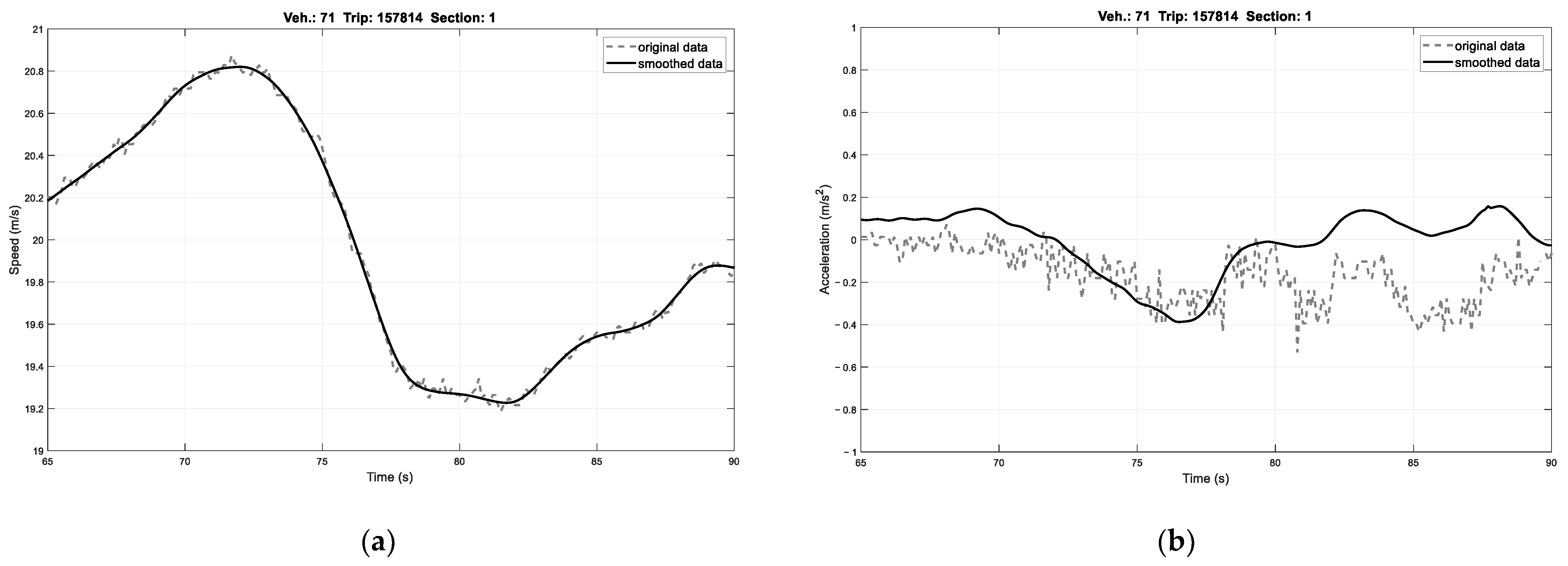
4.1. Driving Data Pre-Processing
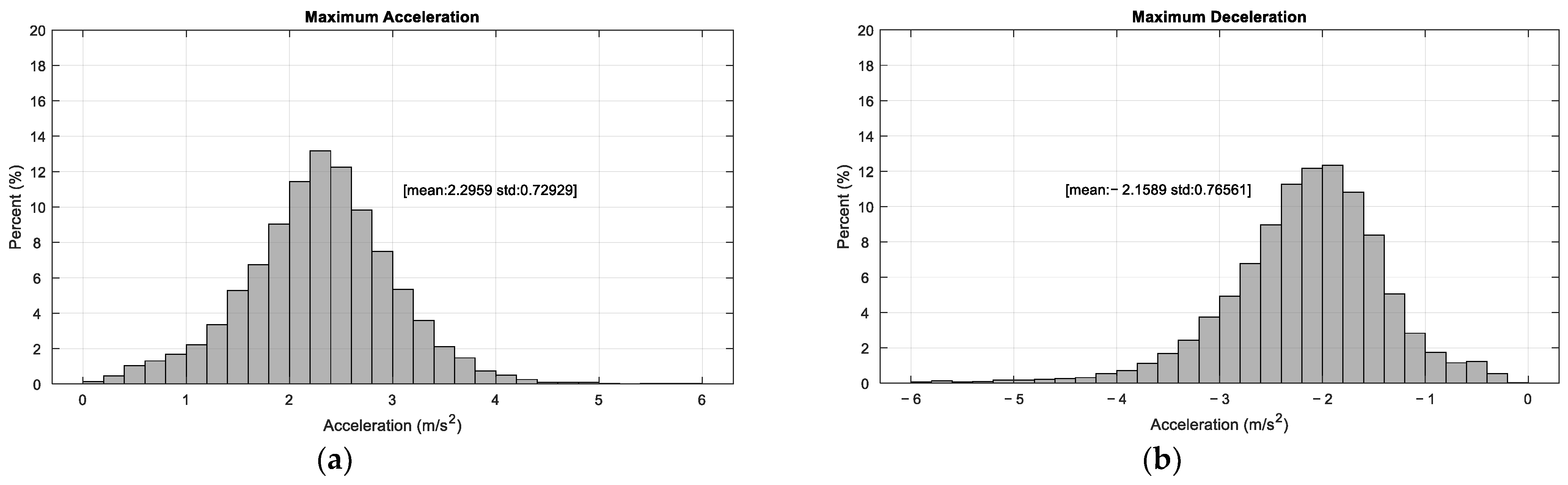
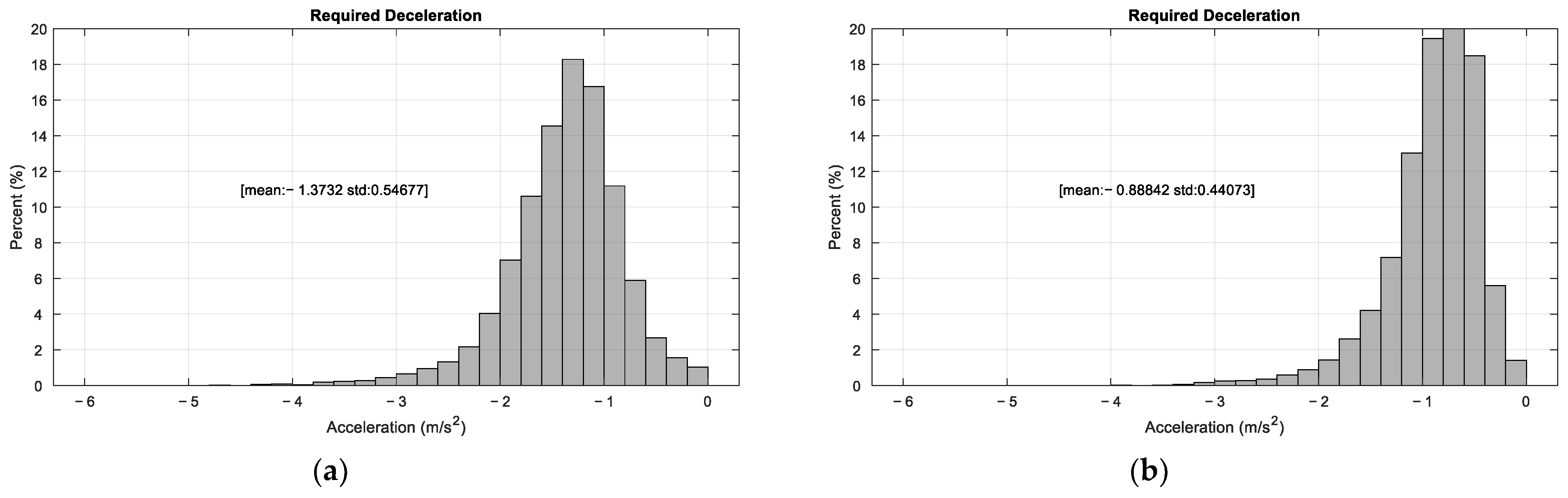
4.2. Analysis of Free Acceleration/Deceleration Point
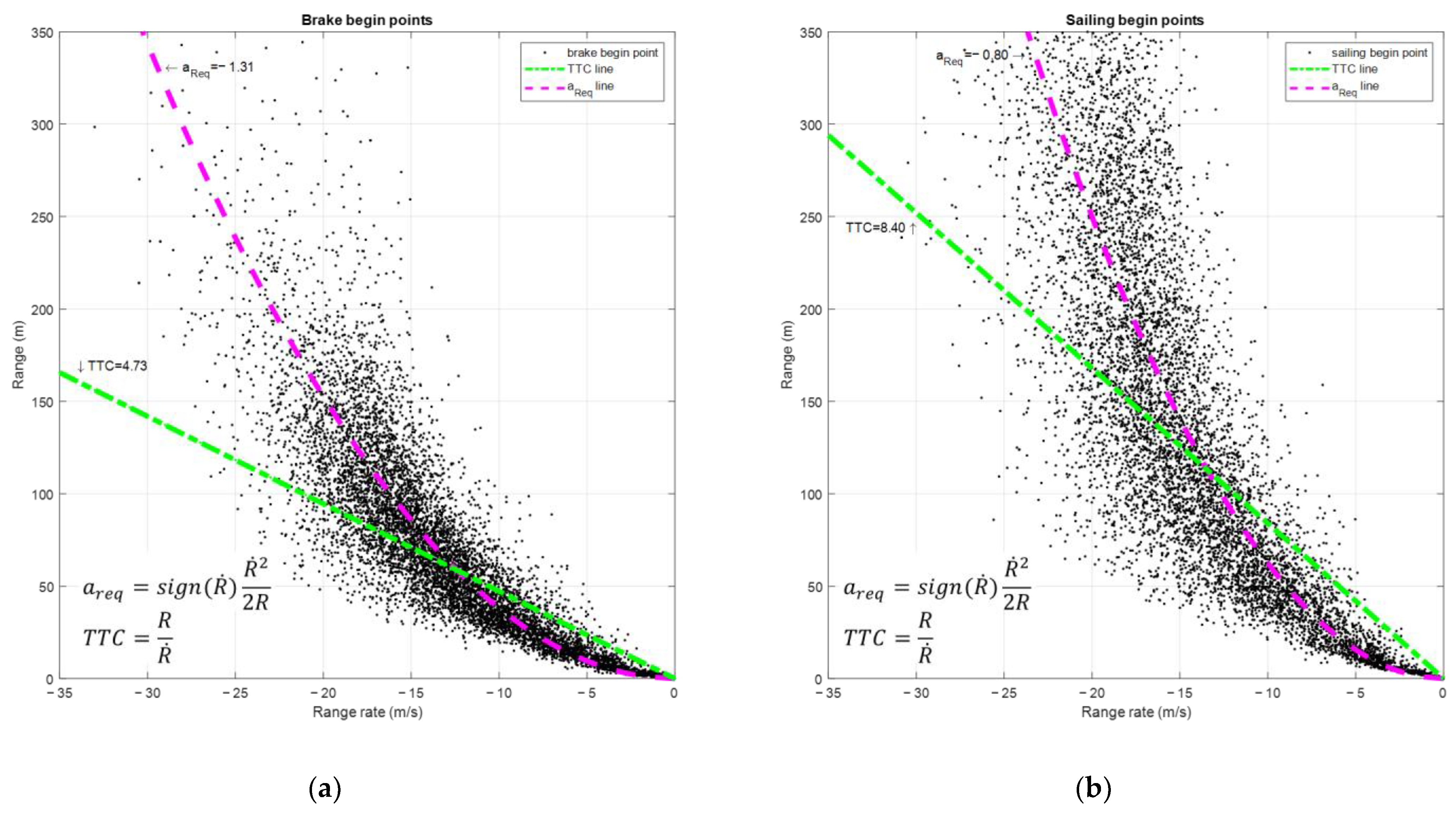
4.3. Analysis of Sailing/Braking Start Time
4.4. Driver Model Parameter Adaptation from the Analysis of Driving Data
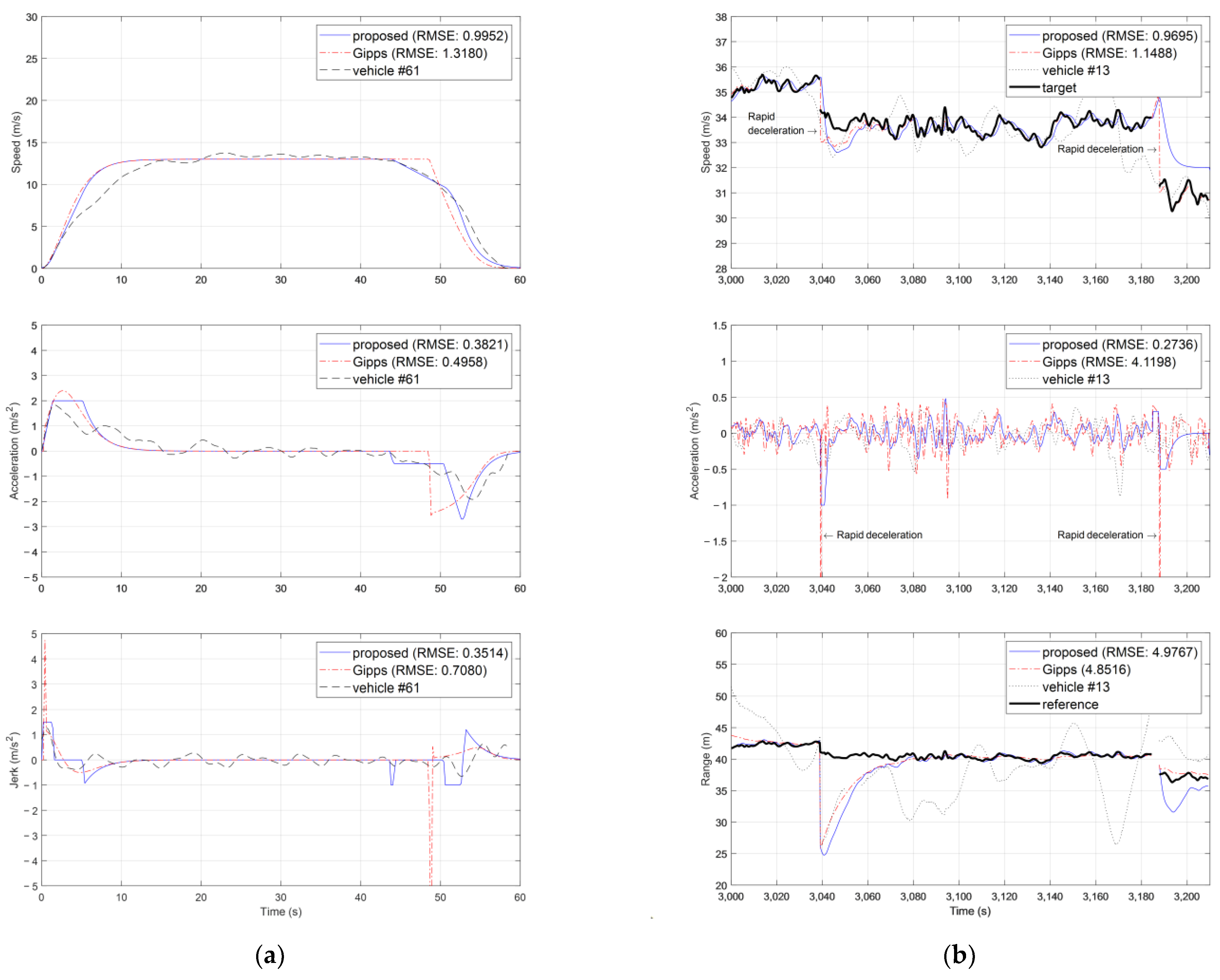
5. Computer Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Range (m/s) | Bottom | 75% | Med. | 25% | Top |
|---|---|---|---|---|---|
| 10 | 0.13 | 1.11 | 1.57 | 2.06 | 3.47 |
| 10–20 | 1.03 | 2.04 | 2.38 | 2.76 | 3.83 |
| 20–30 | 1.23 | 2.32 | 2.67 | 3.09 | 4.24 |
| 30–40 | 1.63 | 2.39 | 2.73 | 3.18 | 4.076 |
| ALL | 0.567 | 1.86 | 2.30 | 2.73 | 4.02 |
| Range (m/s) | Bottom | 75% | Med. | 25% | Top |
|---|---|---|---|---|---|
| 10 | −4.85 | −1.90 | −1.49 | −1.08 | −0.15 |
| 10–20 | −3.73 | −2.57 | −2.16 | −1.80 | −0.95 |
| 20–30 | −4.36 | −3.03 | −2.52 | −2.13 | −0.98 |
| 30–40 | −3.99 | −3.08 | −2.62 | −2.21 | −1.38 |
| ALL | −3.85 | −2.56 | −2.10 | −1.68 | −0.36 |
| Range (m/s) | Bottom | 75% | Med. | 25% | Top |
|---|---|---|---|---|---|
| 10 | −2.16 | −1.27 | −0.98 | −0.67 | −0.03 |
| 10–20 | −2.56 | −1.67 | −1.36 | −1.11 | −0.33 |
| 20–30 | −2.80 | −1.88 | −1.54 | −1.27 | −0.38 |
| 30–40 | −2.47 | −1.69 | −1.20 | −0.86 | −0.46 |
| ALL | −2.57 | −1.65 | −1.31 | −1.04 | −0.12 |
| Range (m/s) | Bottom | 75% | Med. | 25% | Top |
|---|---|---|---|---|---|
| 10 | −1.67 | −0.96 | −0.70 | −0.47 | −0.03 |
| 10–20 | −1.88 | −1.13 | −0.84 | −0.63 | −0.21 |
| 20–30 | −0.83 | −1.12 | −0.84 | −0.65 | −0.20 |
| 30–40 | −1.24 | −0.82 | −0.64 | −0.50 | −0.17 |
| ALL | −1.81 | −1.08 | −0.80 | −0.60 | −0.03 |
References
- Pendleton, S.D.; Andersen, H.; Du, X.; Shen, X.; Meghjani, M.; Eng, Y.H.; Rus, D.; Ang, M.H. Perception, Planning, Control, and Coordination for Autonomous Vehicles. Machines 2017, 5, 6. [Google Scholar] [CrossRef]
- Fényes, D.; Németh, B.; Gáspár, P. A Novel Data-Driven Modeling and Control Design Method for Autonomous Vehicles. Energies 2021, 14, 517. [Google Scholar] [CrossRef]
- Nie, Z.; Farzaneh, H. Adaptive Cruise Control for Eco-Driving Based on Model Predictive Control Algorithm. Appl. Sci. 2020, 10, 5271. [Google Scholar] [CrossRef]
- Wang, P.; Gao, S.; Li, L.; Sun, B.; Cheng, S. Obstacle Avoidance Path Planning Design for Autonomous Driving Vehicles Based on an Improved Artificial Potential Field Algorithm. Energies 2019, 12, 2342. [Google Scholar] [CrossRef] [Green Version]
- Kuutti, S.; Bowden, R.; Jin, Y.; Barber, P.; Fallah, S. A Survey of Deep Learning Applications to Autonomous Vehicle Control. IEEE Trans. Intell. Transp. Syst. 2021, 22, 712–733. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Ros, G.; Codevilla, F.; Lopez, A.; Koltun, V. CARLA: An Open Urban Driving Simulator. In Proceedings of the 1st Annual Conference on Robot Learning; PMLR, Mountain View, CA, USA, 13–15 November 2017; pp. 1–16. [Google Scholar]
- Zapridou, E.; Bartocci, E.; Katsaros, P. Runtime Verification of Autonomous Driving Systems in CARLA. In Proceedings of the Runtime Verification, Los Angeles, CA, USA, 6–9 October 2020; Deshmukh, J., Ničković, D., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 172–183. [Google Scholar]
- Arcidiacono, A. ADAS Virtual Validation: ACC and AEB Case Study with IPG CarMaker. Master’s Thesis, Politecnico di Torino, Turin, Italy, 2018. [Google Scholar]
- Zhou, J.; Schmied, R.; Sandalek, A.; Kokal, H.; del Re, L. A Framework for Virtual Testing of ADAS. SAE Int. J. Passeng. Cars Electron. Electr. Syst. 2016, 9, 66–74. [Google Scholar] [CrossRef]
- Park, C.; Chung, S.; Lee, H. Vehicle-in-the-Loop in Global Coordinates for Advanced Driver Assistance System. Appl. Sci. 2020, 10, 2645. [Google Scholar] [CrossRef] [Green Version]
- Siegl, S.; Ratz, S.; Düser, T.; Hettel, R. Vehicle-in-the-Loop at Testbeds for ADAS/AD Validation. ATZ Electron. Worldw 2021, 16, 62–67. [Google Scholar] [CrossRef]
- Tettamanti, T.; Szalai, M.; Vass, S.; Tihanyi, V. Vehicle-in-the-Loop Test Environment for Autonomous Driving with Microscopic Traffic Simulation. In Proceedings of the 2018 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Madrid, Spain, 12–14 September 2018; pp. 1–6. [Google Scholar]
- Van Ratingen, M.R. The Euro Ncap Safety Rating. In Karosseriebautage Hamburg 2017; Springer: Berlin, Germany, 2017; pp. 11–20. [Google Scholar]
- ISO. Intelligent Transport Systems–Adaptive Cruise Control Systems–Performance Requirements and Test Procedures; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Hulshof, W.; Knight, I.; Edwards, A.; Avery, M.; Grover, C. Autonomous Emergency Braking Test Results. In Proceedings of the 23rd International Technical Conference on the Enhanced Safety of Vehicles (ESV), Seoul, Republic of Korea, 27–30 May 2013; National Highway Traffic Safety Administration: Washington, DC, USA, 2013; pp. 1–13. [Google Scholar]
- Zhao, D. Accelerated Evaluation of Automated Vehicles. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2016. [Google Scholar]
- Peng, H.; Leblanc, D. Evaluation of the Performance and Safety of Automated Vehicles. White Paper on NSF Transportation CPS Work. 2012. Available online: https://cps-vo.org/sites/default/files/webform/Evaluation_of_the_Performance_and_Safety_of_Automated_Vehicles_0.pdf (accessed on 16 December 2022).
- Lee, K. Longitudinal Driver Model and Collision Warning and Avoidance Algorithms Based on Human Driving Databases; University of Michigan: Ann Arbor, MI, USA, 2004. [Google Scholar]
- Klischat, M.; Althoff, M. Generating Critical Test Scenarios for Automated Vehicles with Evolutionary Algorithms. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 2352–2358. [Google Scholar]
- Koopman, P.; Wagner, M. Challenges in Autonomous Vehicle Testing and Validation. SAE Int. J. Transp. Safety 2016, 4, 15–24. [Google Scholar] [CrossRef] [Green Version]
- Riedmaier, S.; Ponn, T.; Ludwig, D.; Schick, B.; Diermeyer, F. Survey on Scenario-Based Safety Assessment of Automated Vehicles. IEEE Access 2020, 8, 87456–87477. [Google Scholar] [CrossRef]
- Fellendorf, M.; Vortisch, P. Microscopic Traffic Flow Simulator VISSIM. In Fundamentals of Traffic Simulation; Springer: Berlin, Germany, 2010; pp. 63–93. [Google Scholar]
- Kaths, J.; Krause, S. Integrated Simulation of Microscopic Traffic Flow and Vehicle Dynamics. In Proceedings of the IPG Apply & Innovate 2016, Karlsruhe, Germany, 20–21 September 2016. [Google Scholar]
- Pipes, L.A. An Operational Analysis of Traffic Dynamics. J. Appl. Phys. 1953, 24, 274–281. [Google Scholar] [CrossRef]
- Gazis, D.C.; Herman, R.; Rothery, R.W. Nonlinear Follow-the-Leader Models of Traffic Flow. Oper. Res. 1961, 9, 545–567. [Google Scholar] [CrossRef]
- Newell, G.F. Nonlinear Effects in the Dynamics of Car Following. Oper. Res. 1961, 9, 209–229. [Google Scholar] [CrossRef]
- Tyler, J. The Characteristics of Model-Following Systems as Synthesized by Optimal Control. IEEE Trans. Autom. Control. 1964, 9, 485–498. [Google Scholar] [CrossRef]
- Gipps, P.G. A Behavioural Car-Following Model for Computer Simulation. Transp. Res. Part B Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Huang, Y.; Lu, P. A Review of Car-Following Models and Modeling Tools for Human and Autonomous-Ready Driving Behaviors in Micro-Simulation. Smart Cities 2021, 4, 314–335. [Google Scholar] [CrossRef]
- Dingus, T.A.; Klauer, S.G.; Neale, V.L.; Vicki, L.; Petersen, A.; Lee, S.E.; Sudweeks, J.; Perez, M.A.; Hankey, J.; Ramsey, D.; et al. The 100-Car Naturalistic Driving Study, Phase II Results of the 100-Car Field Experiment; National Highway Traffic Safety Administration: Washington, DC, USA, 2006.
- Ervin, R.; Sayer, J.; LeBlanc, D.; Bogard, S.; Mefford, M.; Hagan, M.; Bareket, Z.; Winkler, C. Automotive Collision Avoidance System Field Operational Test Report: Methodology and Results; Transportation Research Board: Washington, DC, USA, 2005. [Google Scholar]
- LeBlanc, D.J. Road Departure Crash Warning System Field Operational Test: Methodology and Results. Volume 1: Technical Report; Transportation Research Institute, University of Michigan: Ann Arbor, MI, USA, 2006. [Google Scholar]
- Victor, T.; Bärgman, J.; Hjälmdahl, M.; Kircher, K.; Svanberg, E.; Hurtig, S.; Gellerman, H.; Moeschlin, F. Sweden-Michigan Naturalistic Field Operational Test (Semifot) Phase 1: Final Report; Chalmers: Goteborg, Sweden, 2010. [Google Scholar]
- Sayer, J.; LeBlanc, D.; Bogard, S.; Funkhouser, D.; Bao, S.; Buonarosa, M.L.; Blankespoor, A. Integrated Vehicle-Based Safety Systems Field Operational Test: Final Program Report; Transportation Research Institute, University of Michigan: Ann Arbor, MI, USA, 2011. [Google Scholar]
- Bezzina, D.; Sayer, J. Safety Pilot Model Deployment: Test Conductor Team Report. Report No. DOT HS 2014, 812, 18. [Google Scholar]
- Traffic Analysis Tools: Next Generation Simulation-FHWA Operations. Available online: https://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm (accessed on 20 October 2022).
- Open Dataset. Available online: https://waymo.com/open/ (accessed on 20 October 2022).
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The HighD Dataset: A Drone Dataset of Naturalistic Vehicle Trajectories on German Highways for Validation of Highly Automated Driving Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2118–2125. [Google Scholar]
- Bifulco, G.N.; Simonelli, F.; Di Pace, R. Experiments toward an Human-like Adaptive Cruise Control. In Proceedings of the 2008 IEEE Intelligent Vehicles Symposium, Eindhoven, The Netherlands, 4–6 June 2008; pp. 919–924. [Google Scholar]
- Zheng, J.; Suzuki, K.; Fujita, M. Car-Following Behavior with Instantaneous Driver–Vehicle Reaction Delay: A Neural-Network-Based Methodology. Transp. Res. Part C Emerg. Technol. 2013, 36, 339–351. [Google Scholar] [CrossRef]
- He, Z.; Zheng, L.; Guan, W. A Simple Nonparametric Car-Following Model Driven by Field Data. Transp. Res. Part B Methodol. 2015, 80, 185–201. [Google Scholar] [CrossRef]
- Przybyla, J.; Taylor, J.; Jupe, J.; Zhou, X. Estimating Risk Effects of Driving Distraction: A Dynamic Errorable Car-Following Model. Transp. Res. Part C Emerg. Technol. 2015, 50, 117–129. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Mechanical Engineering Series; Springer: Boston, MA, USA, 2012; ISBN 978-1-4614-1432-2. [Google Scholar]
- Kiencke, U.; Nielsen, L. Automotive Control Systems: For Engine, Driveline, and Vehicle; IOP Publishing Ltd.: Bristol, UK, 2000. [Google Scholar]
- Yi, K.; Song, B. Automated Driving Vehicles. In Vehicle Dynamics: Fundamentals and Ultimate Trends; Lenzo, B., Ed.; CISM International Centre for Mechanical Sciences; Springer International Publishing: Cham, Switzerland, 2022; pp. 289–387. ISBN 978-3-030-75884-4. [Google Scholar]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Bosetti, P.; Da Lio, M.; Saroldi, A. On the Human Control of Vehicles: An Experimental Study of Acceleration. Eur. Transp. Res. Rev. 2014, 6, 157–170. [Google Scholar] [CrossRef]
- Xia, L.; Li, P.; Su, Z.; Chen, T.; Deng, Z.; Sun, D. Longitudinal Driving Behavior before, during, and after a Left-Turn Movement at Signalized Intersections: A Naturalistic Driving Study in China. Sustainability 2022, 14, 11630. [Google Scholar] [CrossRef]
- Loader, C. Local Regression and Likelihood; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]


| Researcher (Year) | Model |
|---|---|
| Pipe [24] (1953) | |
| Gazis [25] (1961) | |
| Newell [26] (1961) | |
| Tyler [27] (1964) | |
| Gipps [28] (1981) |
| Step | Exclusion Conditions | Remain Time (s) |
|---|---|---|
| (1) Original | - | 8,338,419.4 |
| (2) Trip time | Trip data less than 300 s | 7,589,392.0 |
| (3) Radar | Radar data nonexistence | 7,523,291.5 |
| (4) 0 to 0 | Zero speed nonexistence | 7,277,452.8 |
| (5) Data | Continuous data nonexistence over 10 s | 6,884,491.7 |
| Trip Time (s) | Max. Speed (m/s) | Max. Acceleration (m/s2) | Max. Deceleration (m/s2) | |
|---|---|---|---|---|
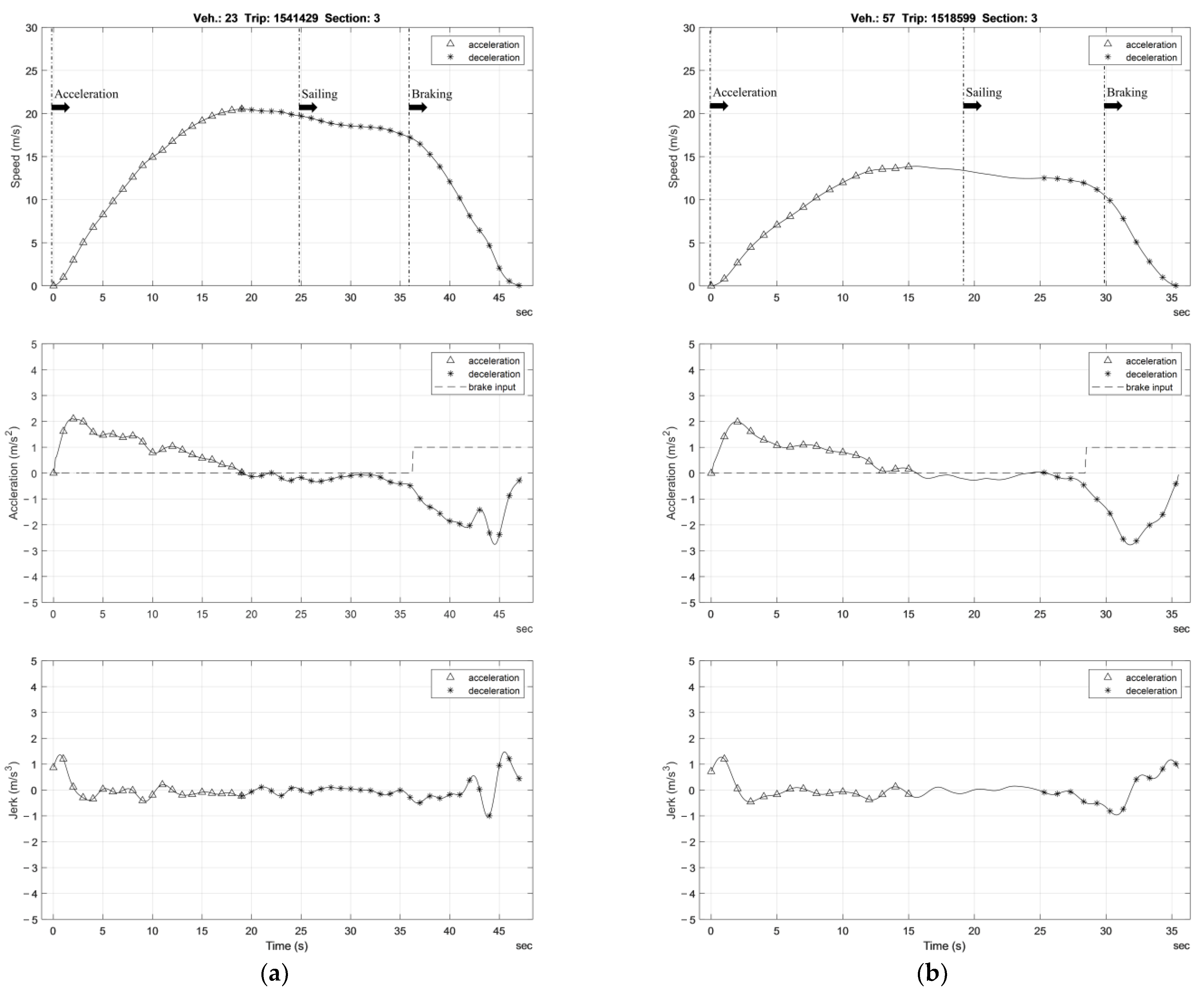
| Driver #23 | 47.2 | 20.5 | 2.10 | −2.75 |
| Driver #57 | 35.5 | 13.9 | 1.98 | −1.92 |
| Driver #23 | 2 | −2.1 | −0.5 | −0.4 | 3 | 45 |
| Driver #57 | 2 | −2.5 | −0.5 | −0.1 | 5 | 45 |
| Driver #61 | 2 | −2.7 | −0.8 | −0.5 | 2 | 40 |
| Driver #13 | 2 | −1 | −0.5 | −0.1 | 5 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, K.; Park, C.; Lee, H. A Study on Longitudinal Motion Scenario Design for Verification of Advanced Driver Assistance Systems and Autonomous Driving Systems. Appl. Sci. 2023, 13, 716. https://doi.org/10.3390/app13020716
Cho K, Park C, Lee H. A Study on Longitudinal Motion Scenario Design for Verification of Advanced Driver Assistance Systems and Autonomous Driving Systems. Applied Sciences. 2023; 13(2):716. https://doi.org/10.3390/app13020716
Chicago/Turabian StyleCho, Kunhee, Changwoo Park, and Hyeongcheol Lee. 2023. "A Study on Longitudinal Motion Scenario Design for Verification of Advanced Driver Assistance Systems and Autonomous Driving Systems" Applied Sciences 13, no. 2: 716. https://doi.org/10.3390/app13020716
APA StyleCho, K., Park, C., & Lee, H. (2023). A Study on Longitudinal Motion Scenario Design for Verification of Advanced Driver Assistance Systems and Autonomous Driving Systems. Applied Sciences, 13(2), 716. https://doi.org/10.3390/app13020716






