An Improved Passing Network for Evaluating Football Team Performance
Abstract
:1. Introduction
2. Related Work
3. Methodology
3.1. Research Object
3.2. Model Specification
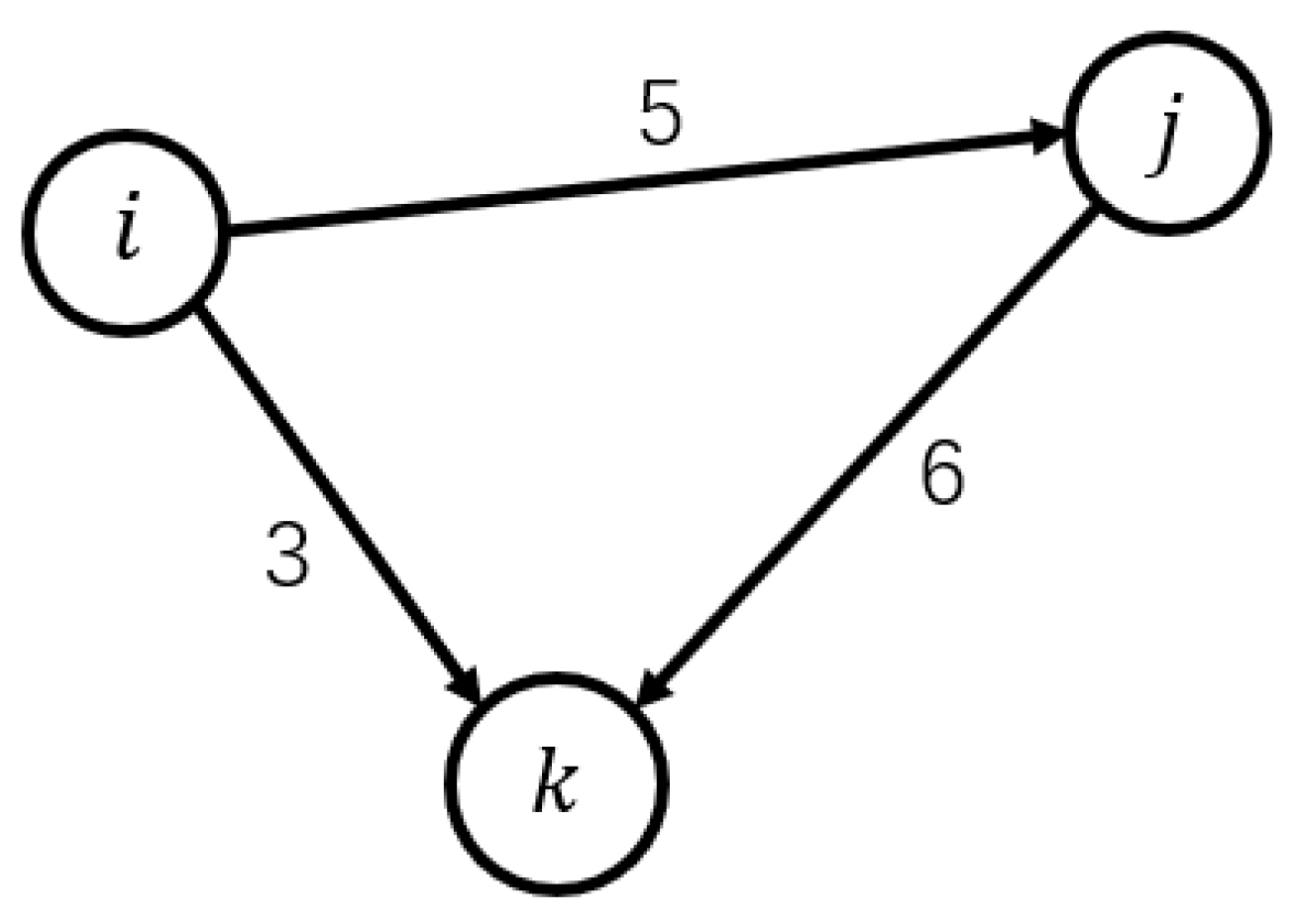
3.2.1. Basic Network Model
3.2.2. Weight Models of Directed Edges and Nodes
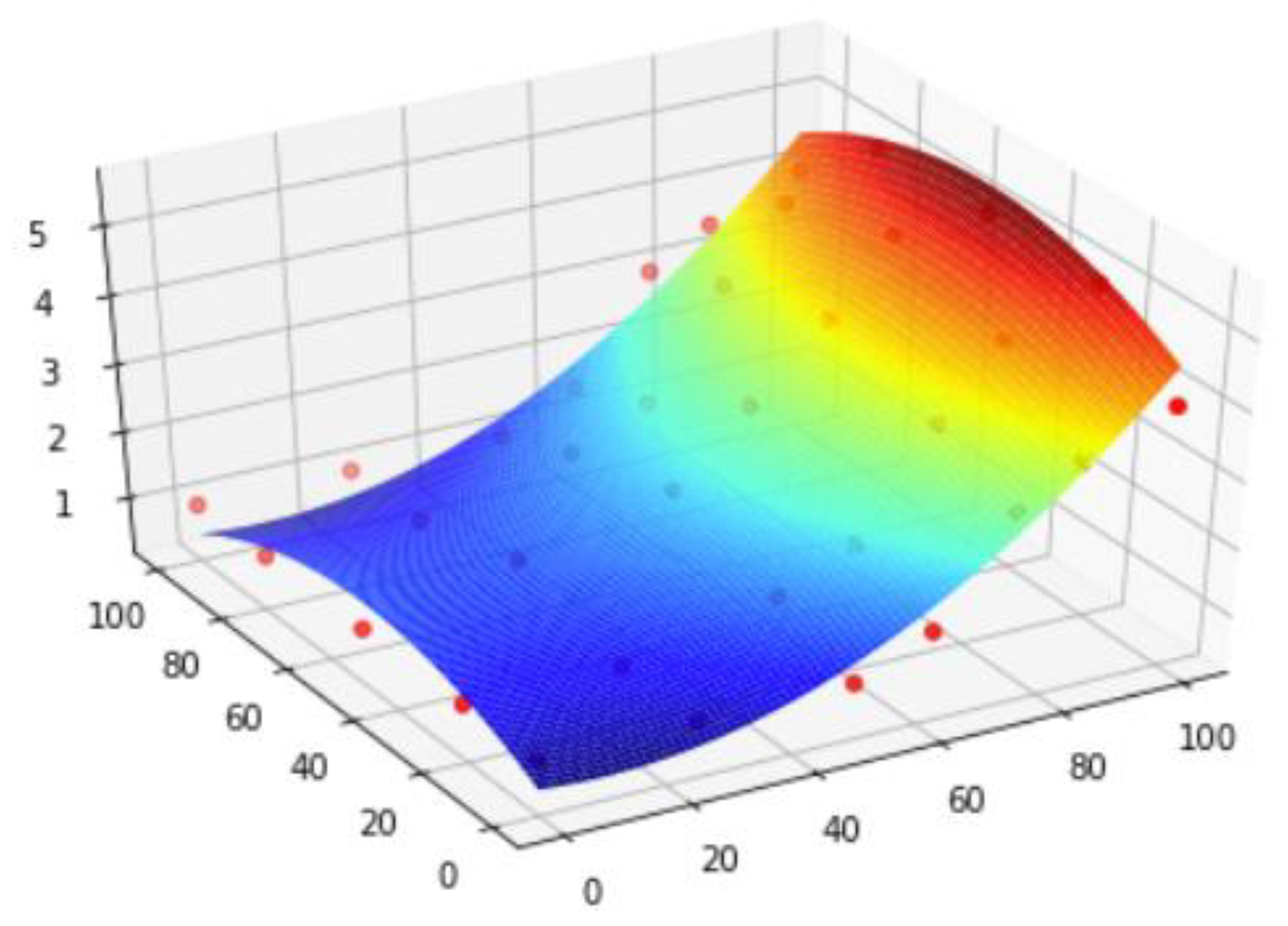
3.2.3. Establishment of Coordination Index
4. Results
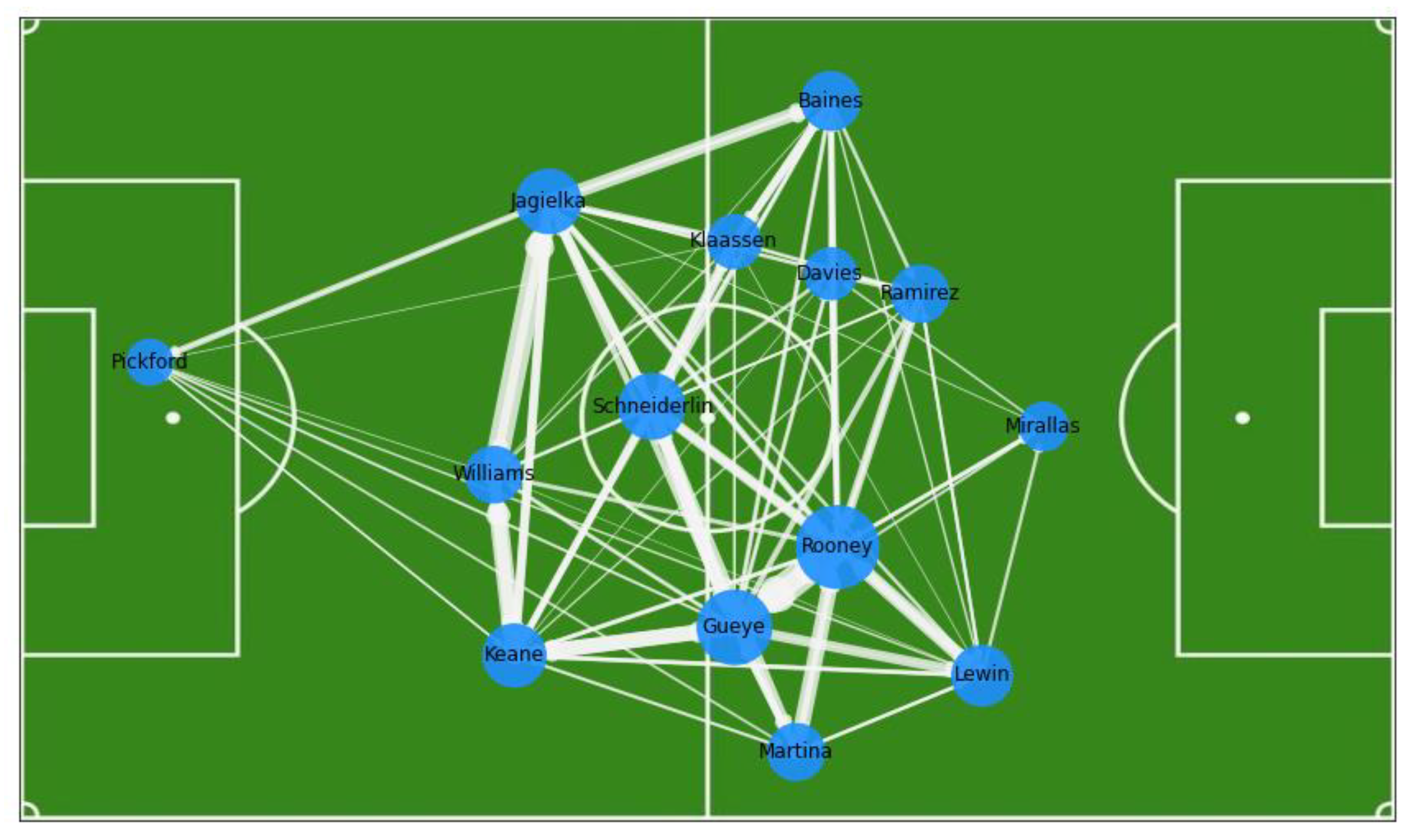
4.1. Visualization and Comparison of Passing Networks
4.2. Establish Team Coordination Index
5. Inspection
5.1. Pezzali Score Test
5.2. Control Score Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reep, C.; Benjamin, B. Skill and Chance in Association Football. J. R. Stat. Soc. Ser. A (Gen.) 1968, 131, 581–585. [Google Scholar] [CrossRef]
- Rao, Y.; Chen, L. A survey of video enhancement techniques. J. Inf. Hiding Multimed. Signal Process. 2012, 3, 71–99. [Google Scholar]
- Hild, F.; Roux, S. Digital Image Correlation: From Displacement Measurement to Identification of Elastic Properties–A Review. Strain 2010, 42, 69–80. [Google Scholar] [CrossRef] [Green Version]
- Dubitzky, W.; Lopes, P.; Davis, J.; Berrar, D. The Open International Soccer Database for machine learning. Mach. Learn. 2018, 108, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Wang, L. Statistics and analysis of goals conceded in the final stage of the 2006 World Cup soccer tournament. Acad. Discuss. 2006, 2010, 267–268. [Google Scholar]
- Xiang, Y.; Hu, W. Research on goals from set pieces in the 18th World Cup. Three Gorges Univ. J. Humanit. Soc. Sci. 2010, 199–200. [Google Scholar]
- Pappalardo, L.; Cintia, P.; Ferragina, P.; Massucco, E.; Pedreschi, D.; Giannotti, F. PlayeRank: Data-driven Performance Evaluation and Player Ranking in Soccer via a Machine Learning Approach. ACM Trans. Intell. Syst. Technol. 2019, 10, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Pappalardo, L.; Cintia, P.; Rossi, A.; Massucco, E.; Ferragina, P.; Pedreschi, D.; Giannotti, F. A public data set of spatio-temporal match events in soccer competitions–Python code to replicate plots in the paper. Sci. Data 2019, 6, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Yan, J. Research on the optimal allocation of defense and control forces based on graph theory. Univ. Math. 2013, 29, 52–55. [Google Scholar]
- Boyd, D.M.; Ellison, N.B. Social Network Sites: Definition, History, and Scholarship. J. Comput. Mediat. Commun. 2013, 13, 210–230. [Google Scholar] [CrossRef] [Green Version]
- Aral, S.; Nicolaides, C. Exercise contagion in a global social network. Nat. Commun. 2017, 8, 14753. [Google Scholar] [CrossRef] [Green Version]
- Buldú, J.M.; Busquets, J.; Martínez, J.H.; Herrera-Diestra, J.L.; Echegoyen, I.; Galeano, J.; Luque, J. Using Network Science to Analyse Football Passing Networks: Dynamics, Space, Time, and the Multilayer Nature of the Game. Front. Psychol. 2018, 9, 1900. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Zhang, D.; Cui, H. Analysis of critical foul flash voltage prediction of silicone rubber composite insulators based on BP neural network. Autom. Technol. Appl. 2020, 39, 90–93. [Google Scholar]
- Passos, P.; Davids, K.; Araújo, D.; Paz, N.; Minguéns, J.; Mendes, J. Networks as a novel tool for studying team ball sports as complex social systems. J. Sci. Med. Sport 2011, 14, 170–176. [Google Scholar] [CrossRef]
- Kong, X. Prediction of total hospitalization cost and analysis of influencing factors for patients with bronchopneumonia based on BP neural network and support vector machine. West China Med. 2021, 36, 55–60. [Google Scholar]
- Karlis, D.; Ntzoufras, I. Bayesian modelling of football outcomes: Using the Skellam’s distribution for the goal difference. Ima J. Manag. Math. 2009, 20, 133–145. [Google Scholar] [CrossRef]
- Ling, X.; Xu, L.; Yu, J. Prediction of corrosion rate in oil pipelines based on improved BP neural network. Sens. Microsyst. 2021, 40, 124–127. [Google Scholar]
- Gudmundsson, J.; Horton, M. Spatio-Temporal Analysis of Team Sports. ACM Comput. Surv. 2017, 50, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Golbeck, J. Chapter 21–Analyzing networks. In Introduction to Social Media Investigation; Golbeck, J., Ed.; Syngress: Boston, MA, USA, 2015; pp. 221–235. [Google Scholar]
- Golbeck, J. Chapter 3–Network Structure and Measures. In Analyzing the Social Web; Golbeck, J., Ed.; Morgan Kaufmann: Boston, MA, USA, 2013; pp. 25–44. [Google Scholar]
- Bonacich, P. Power and Centrality: A Family of Measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Clemente, F.M.; Martins, F.M.L.; Mendes, R.S. Analysis of scored and conceded goals by a football team throughout a season: A network analysis. Kinesiology 2016, 48, 103–114. [Google Scholar] [CrossRef]
- Clemente, F.M.; Silva, F.; Martins, F.M.L.; Kalamaras, D.; Mendes, R.S. Performance Analysis Tool for network analysis on team sports: A case study of FIFA Soccer World Cup 2014. Proc. Inst. Mech. Eng. Part P J. Sport. Eng. Technol. 2016, 230, 158–170. [Google Scholar] [CrossRef]
- Grund, T.U. Network structure and team performance: The case of English Premier League soccer teams. Soc. Netw. 2012, 34, 682–690. [Google Scholar] [CrossRef]
- Li, C.; Ji, X.; Zhi, L. Analysis of the degree of interdisciplinarity of disciplines based on E–I index—Taking five disciplines such as intelligence science as an example. Libr. Inf. Work 2011, 55, 33–36. [Google Scholar]
- Yu, Q.; Chen, L. Analysis of CSL teams’ passing performance based on social network analysis and its value to team performance. Hubei Sport. Sci. Technol. 2020, 39, 1004–1012. [Google Scholar]
- Nia, M.E.; Besharat, M.A. Comparison of athletes’ personality characteristics in individual and team sports. Procedia–Soc. Behav. Sci. 2010, 5, 808–812. [Google Scholar] [CrossRef] [Green Version]
- Lei, L. Research on the passing network before soccer goals based on the perspective of social network analysis method—Taking the 2018 World Cup as an example. Commun. Power Res. 2020, 4, 144–149. [Google Scholar]
- Haveliwala, T.H. Topic-sensitive PageRank: A context-sensitive ranking algorithm for Web search. IEEE Trans. Knowl. Data Eng. 2003, 15, 784–796. [Google Scholar] [CrossRef] [Green Version]
- Stefani, R.; Pollard, R. Football Rating Systems for Top-Level Competition: A Critical Survey. J. Quant. Anal. Sport. 2007, 3. [Google Scholar] [CrossRef]
- Li, B.; Wang, L. Feasibility analysis of social network analysis method to study the passing performance of soccer games. J. Beijing Sport. Univ. 2017, 40, 112–119. [Google Scholar]
- Ao, X.; Gong, Y.; Li, J. Soccer tournament result prediction based on handicap data. J. Chongqing Univ. Technol. Bus. Nat. Sci. Ed. 2016, 33, 85–89. [Google Scholar]
- Liang, H.; Li, X.; Li, J. The value of applying social network analysis in the sociological study of sports and its limitations. J. Chengdu Sport. Inst. 2015, 51–56. [Google Scholar]
- Telesford, Q.K.; Joyce, K.E.; Hayasaka, S.; Burdette, J.H.; Laurienti, P.J. The ubiquity of small-world networks. Brain Connect. 2011, 1, 367–375. [Google Scholar] [CrossRef] [Green Version]
- Brandes, U. On variants of shortest-path betweenness centrality and their generic computation. Soc. Netw. 2008, 30, 136–145. [Google Scholar]
- Brandes, U. A faster algorithm for betweeness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Schank, T.; Wagner, D. Approximating clustering coefficient and transitivity. J. Graph Algorithms Appl. 2005, 9, 2005. [Google Scholar] [CrossRef]
- Zhao, G.; Chen, C. Research on the research method and evaluation index system of soccer game performance. Sport. Sci. 2015, 72–81. [Google Scholar]

| Martina | Schneiderlin | … | Rooney | Gueye | |
|---|---|---|---|---|---|
| Martina | 0.00 | 1.89 | … | 19.20 | 9.16 |
| Schneiderlin | 13.80 | 0.00 | … | 13.42 | 16.18 |
| … | … | … | … | … | … |
| Rooney | 7.91 | 9.18 | … | 0.00 | 37.02 |
| Gueye | 7.72 | 14.19 | … | 22.14 | 0.00 |
| Match_ID | 1 | 2 | 3 | …… | 36 | 37 | 38 |
|---|---|---|---|---|---|---|---|
| Co_Index | 0.04986 | 0.07676 | 0.05274 | …… | 0.0479 | 0.05161 | 0.05309 |
| Match_ID | 1 | 2 | 3 | …… | 36 | 37 | 38 |
|---|---|---|---|---|---|---|---|
| Pezzali Score | 2 | 2.5 | 0.7917 | …… | 3.75 | 1.1 | 0.5333 |
| Match_ID | 1 | 2 | 3 | …… | 36 | 37 | 38 |
|---|---|---|---|---|---|---|---|
| Control Score | 0.2407 | 0.0906 | 0.0774 | …… | 0.1194 | 0.4486 | 0.1351 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Yu, G.; You, S.; Wang, Z. An Improved Passing Network for Evaluating Football Team Performance. Appl. Sci. 2023, 13, 845. https://doi.org/10.3390/app13020845
Zhou W, Yu G, You S, Wang Z. An Improved Passing Network for Evaluating Football Team Performance. Applied Sciences. 2023; 13(2):845. https://doi.org/10.3390/app13020845
Chicago/Turabian StyleZhou, Wenxuan, Guo Yu, Songhui You, and Zejun Wang. 2023. "An Improved Passing Network for Evaluating Football Team Performance" Applied Sciences 13, no. 2: 845. https://doi.org/10.3390/app13020845
APA StyleZhou, W., Yu, G., You, S., & Wang, Z. (2023). An Improved Passing Network for Evaluating Football Team Performance. Applied Sciences, 13(2), 845. https://doi.org/10.3390/app13020845









