Study on Dynamic Characteristics of the Bistable Nonlinear Damper
Abstract
1. Introduction
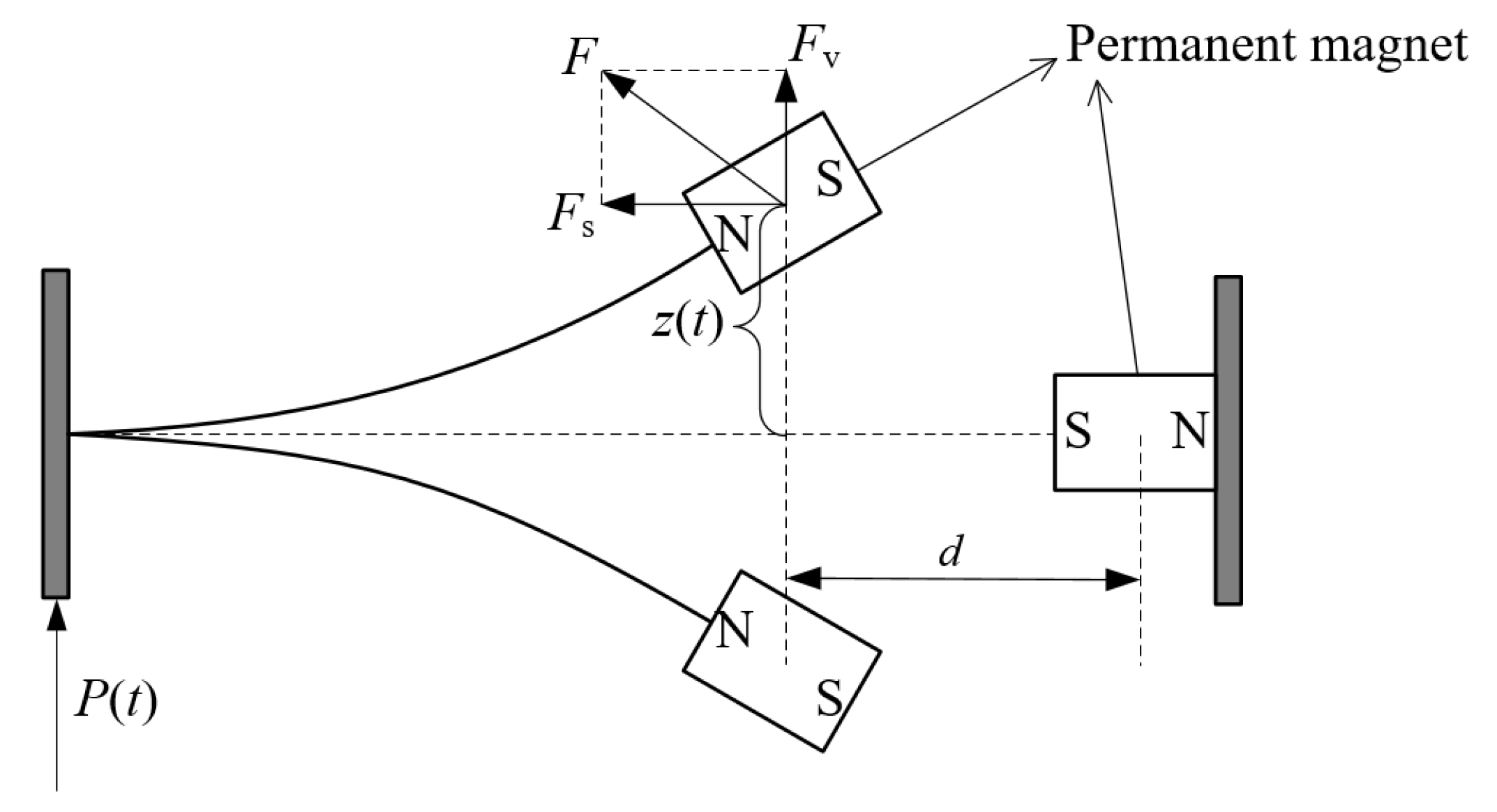
2. System Vibration Model
2.1. Dynamic Model
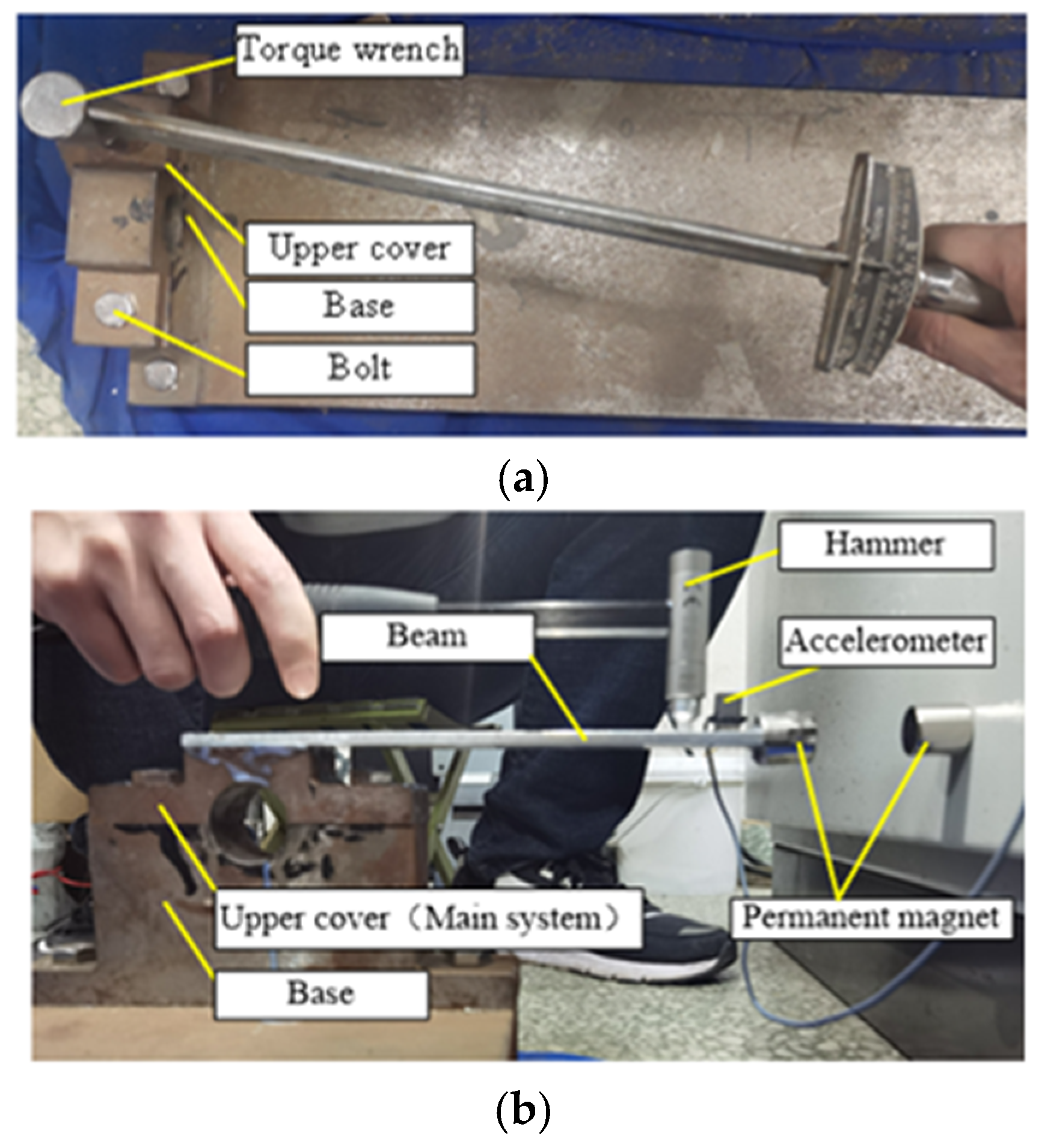
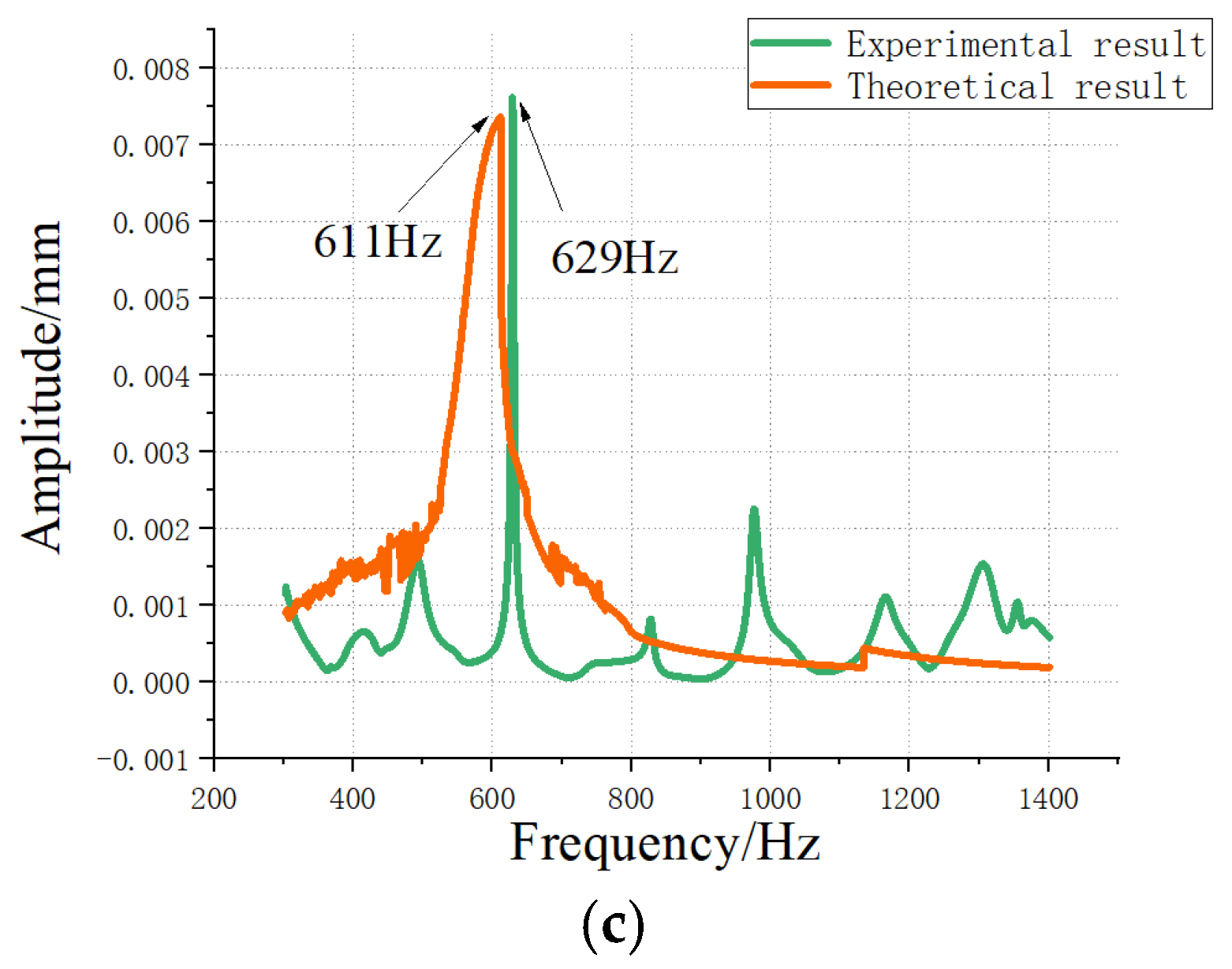
2.2. Experimental Validation
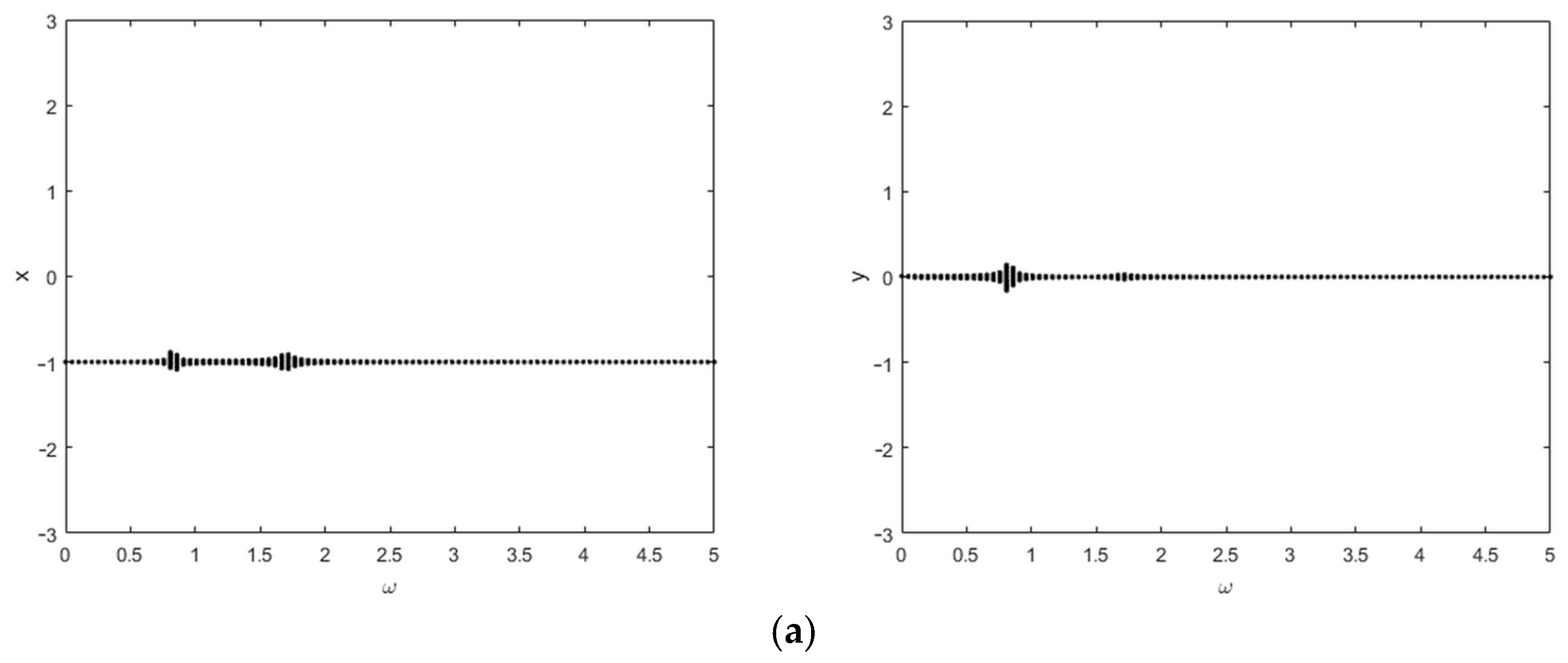
3. Analysis of Dynamic Parameters
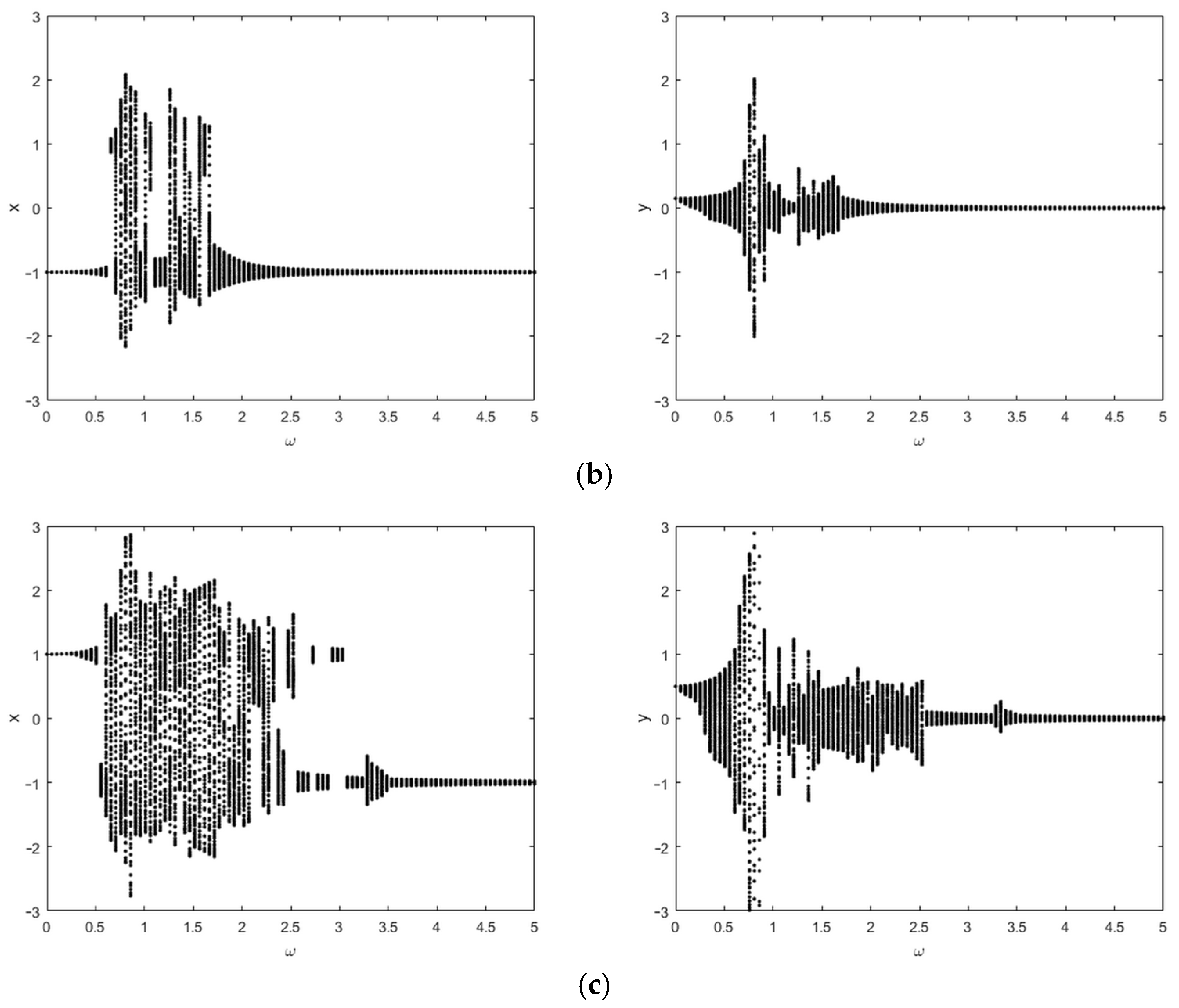
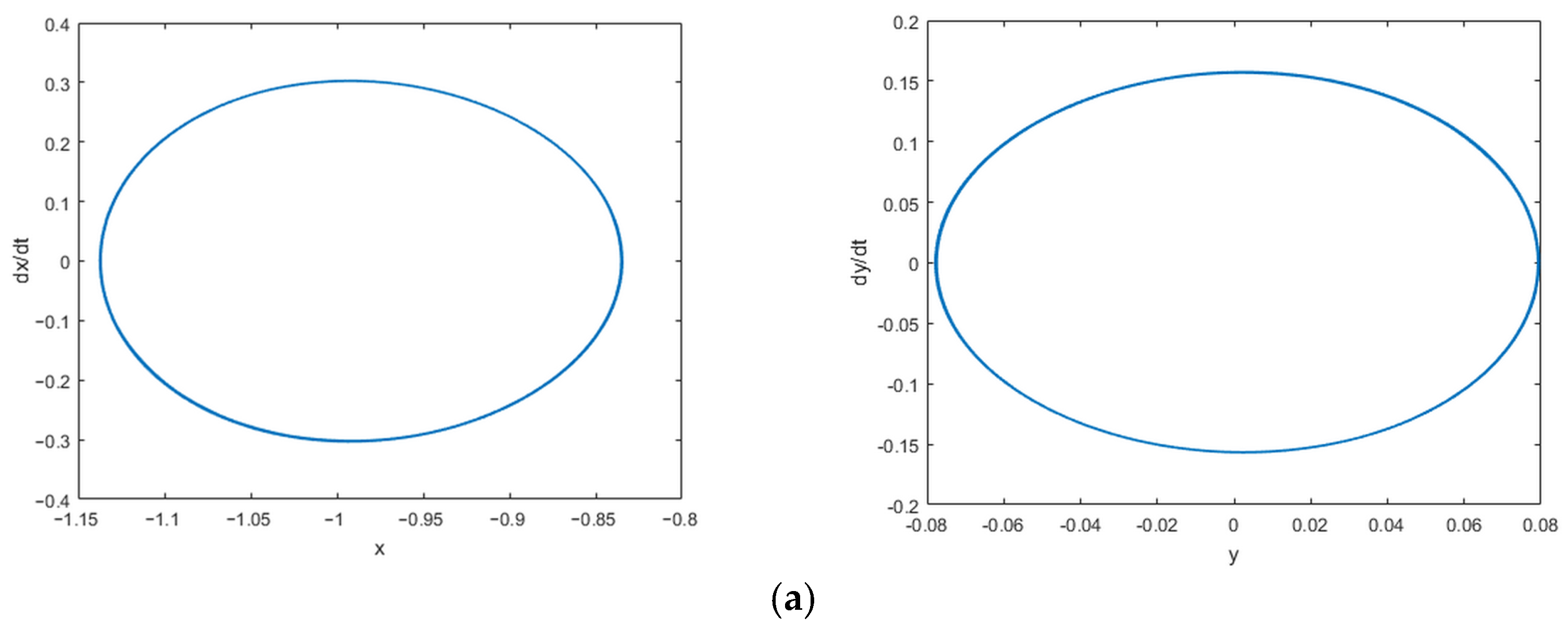
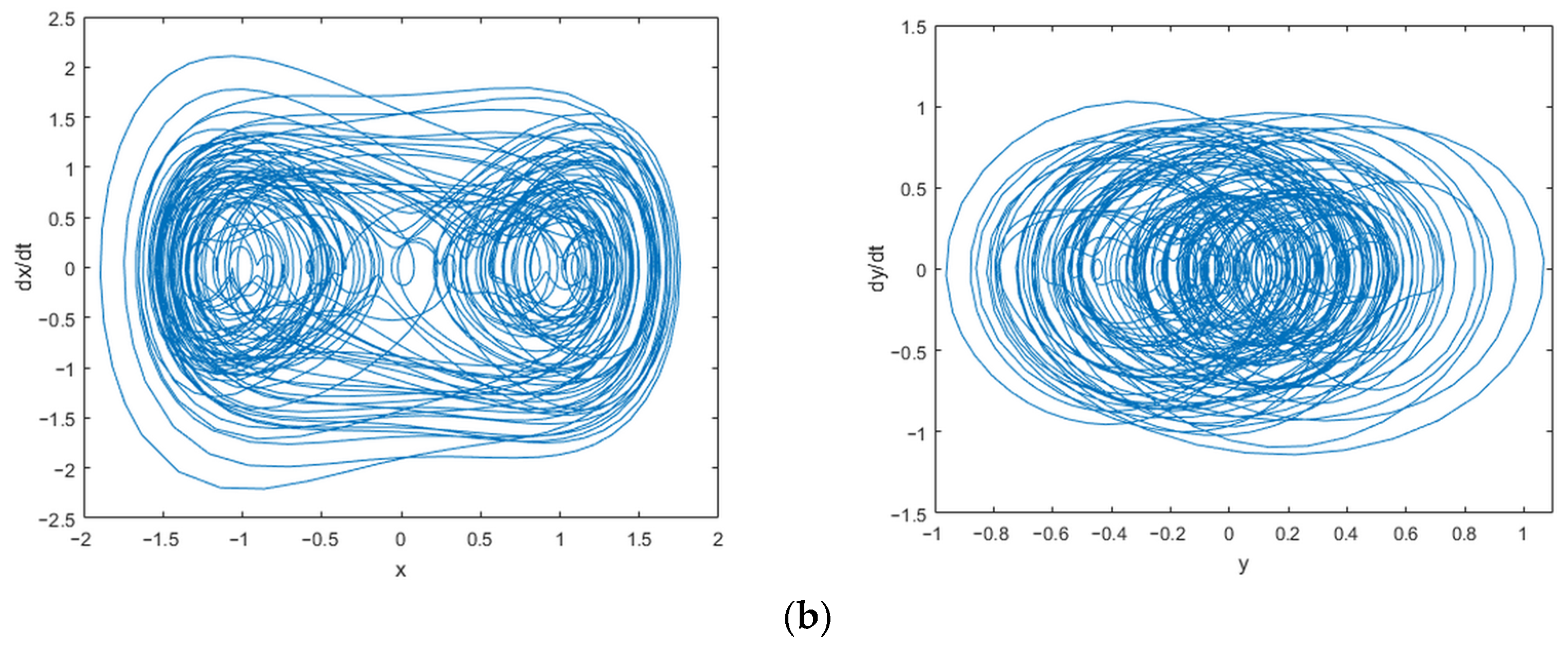
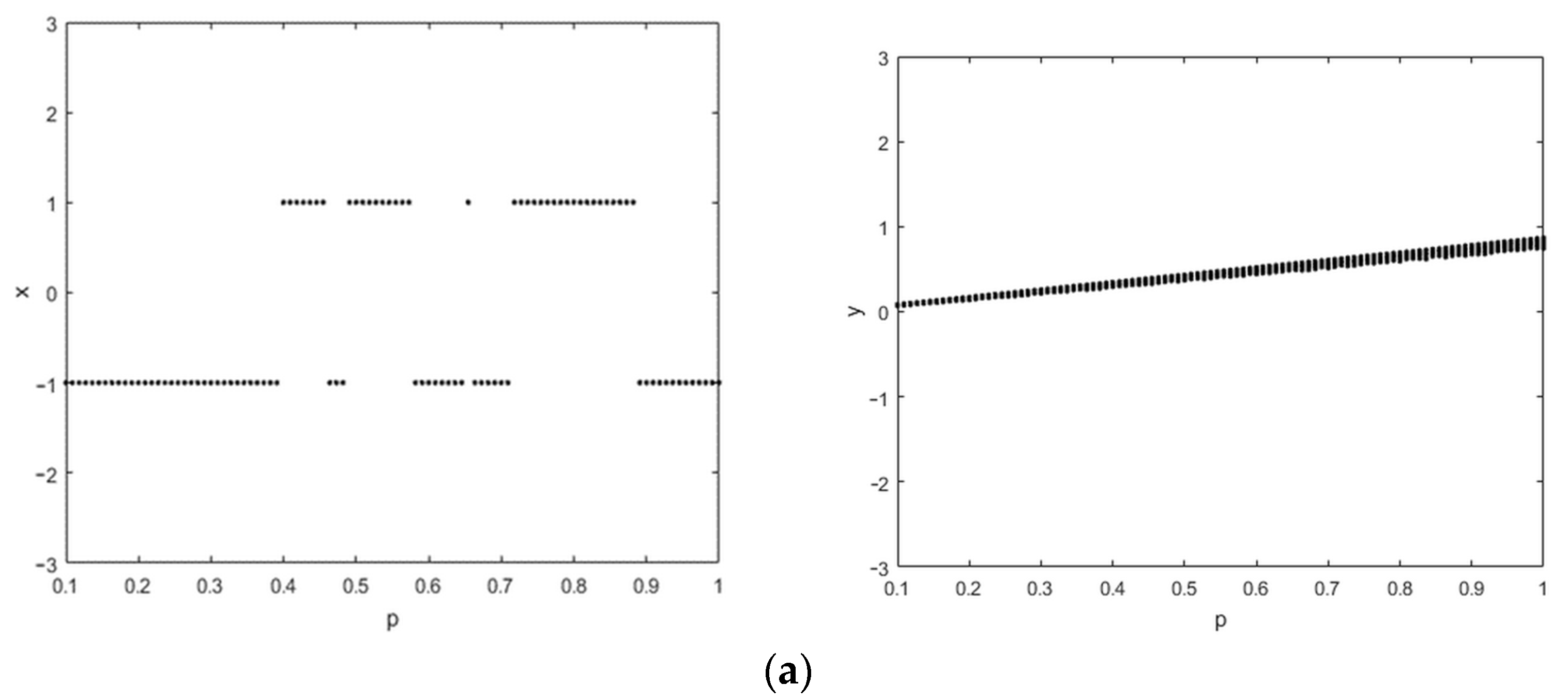
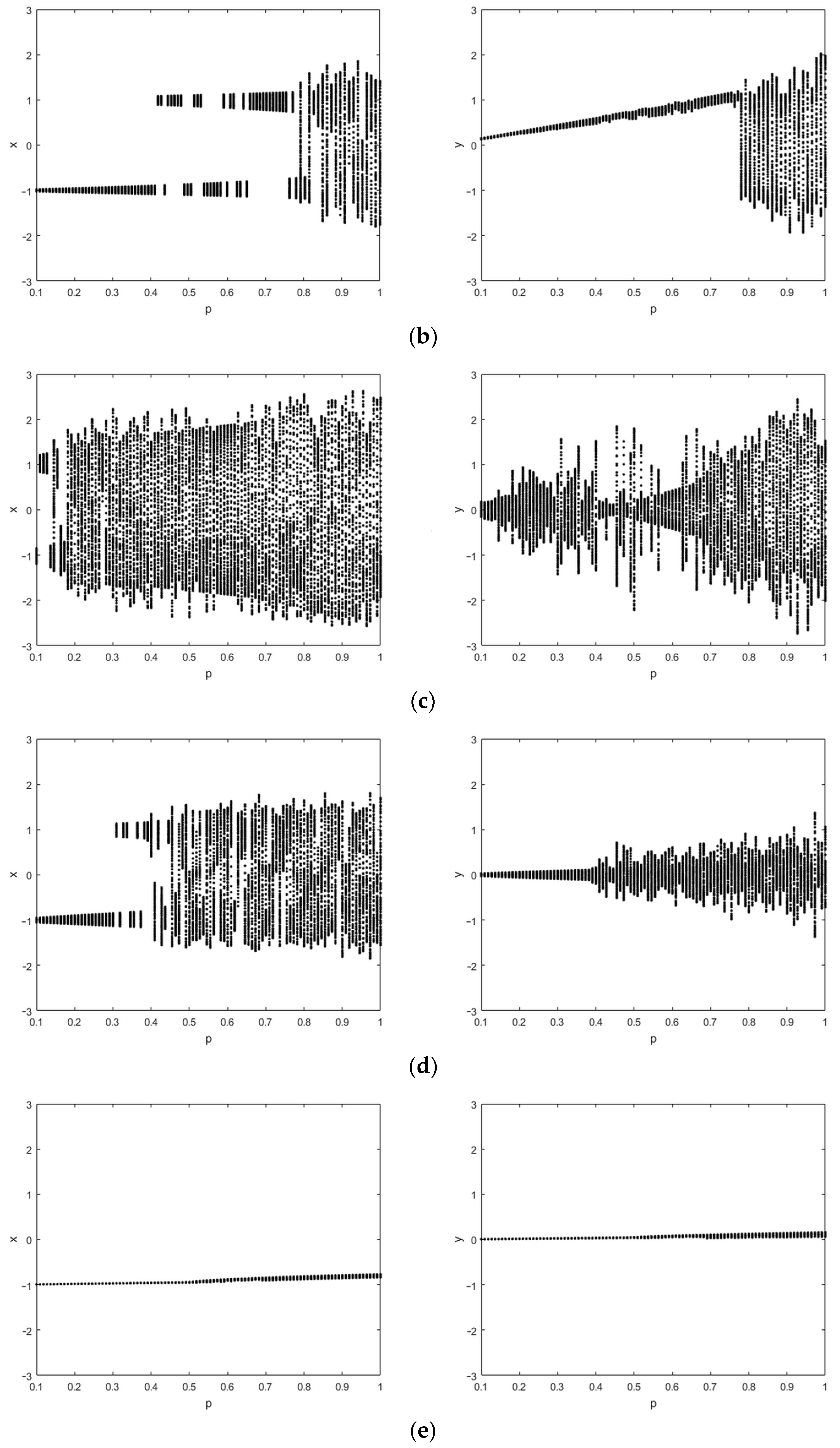
3.1. Effects of the Excitation Frequency on the Response Characteristics of the Vibration Absorber and the Main System
3.2. Effects of the Excitation Amplitude on the Response Characteristics of the Vibration Absorber and the Main System
4. Effects of the Structural Parameters
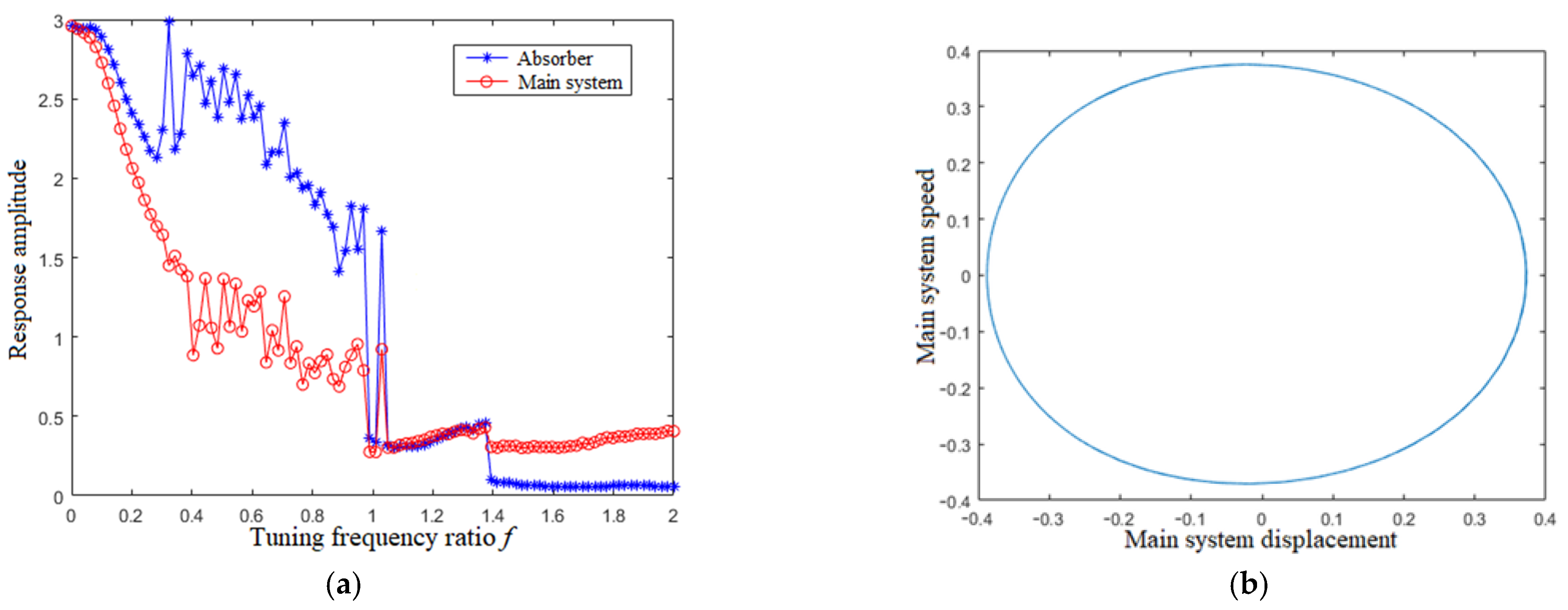
4.1. Tuning Frequency Ratio f
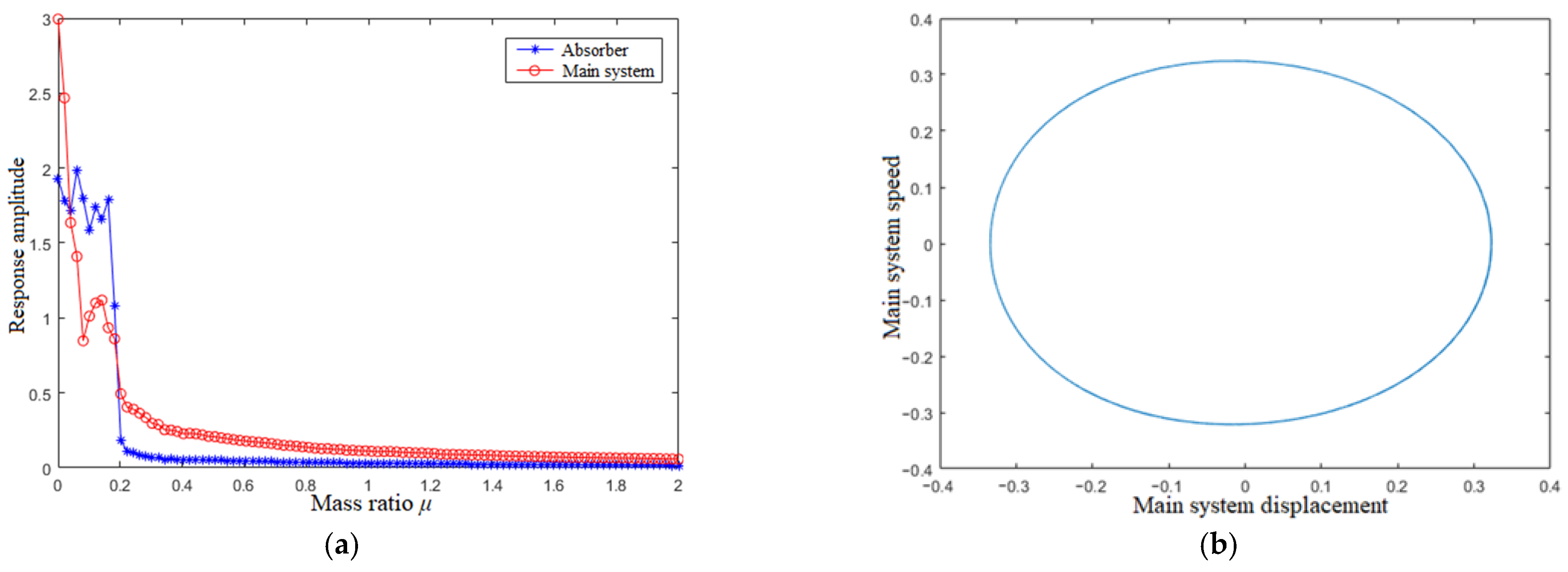
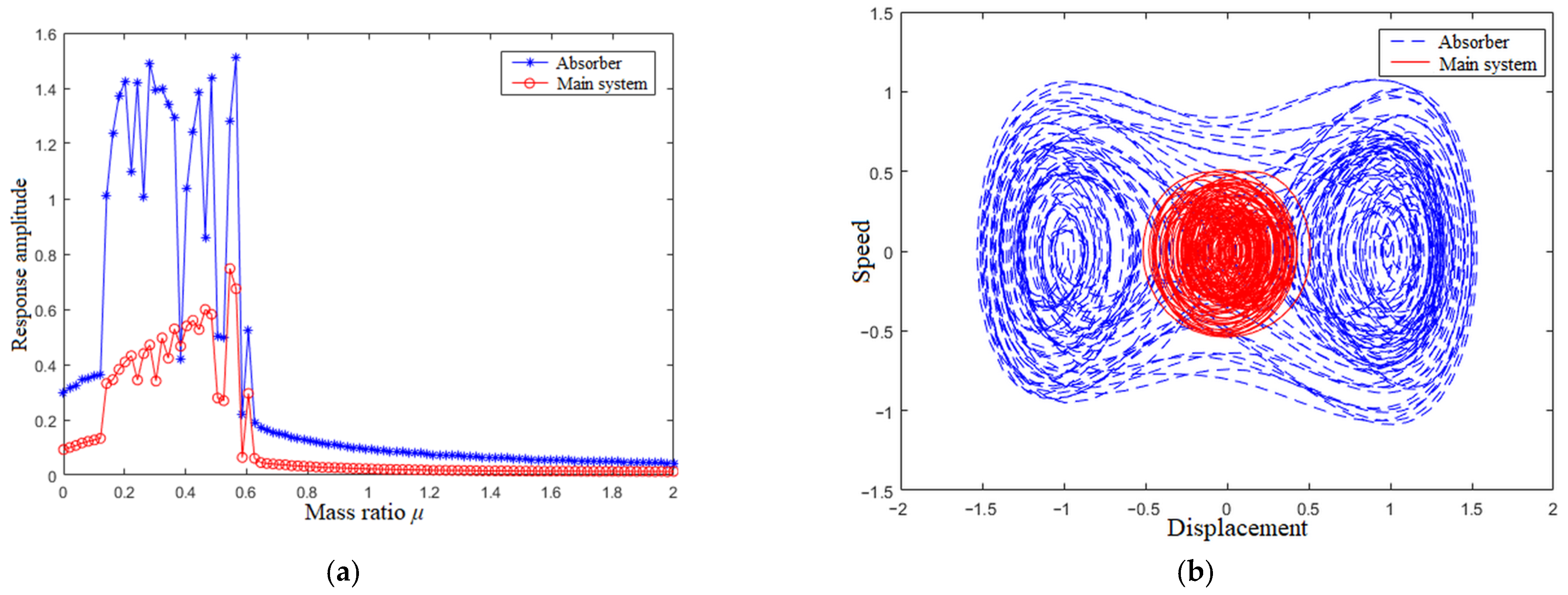
4.2. Mass Ratio μ
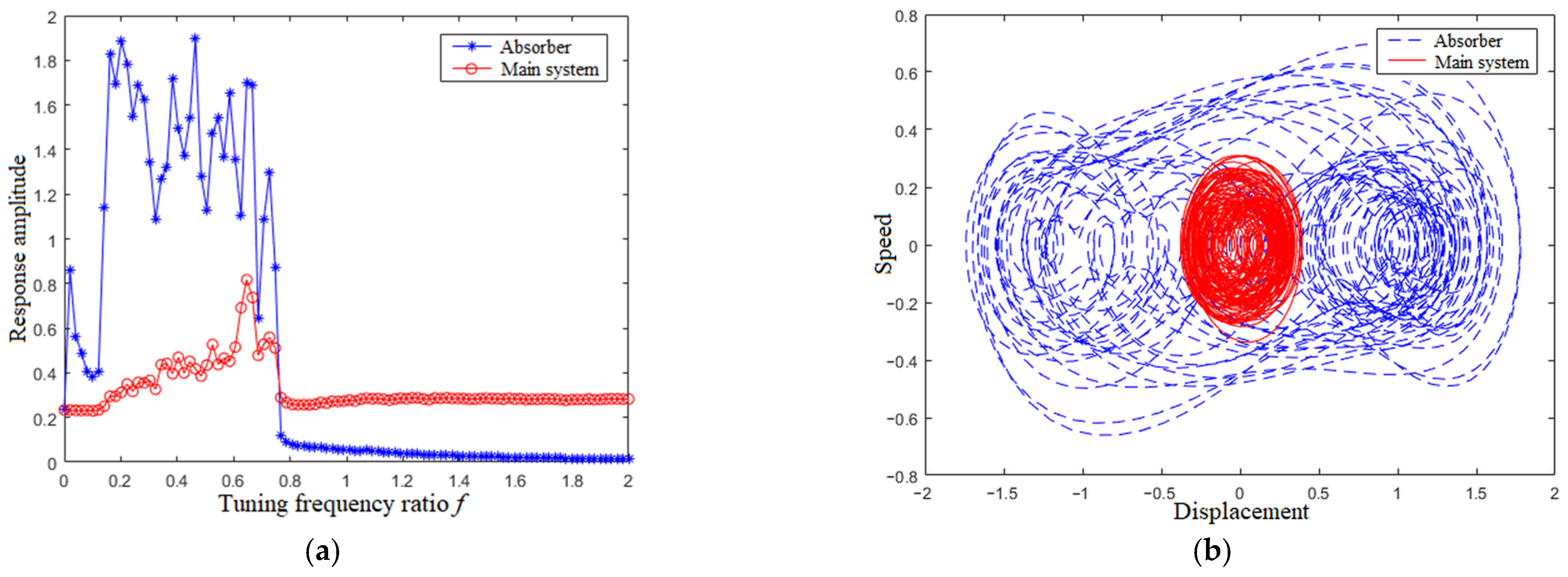
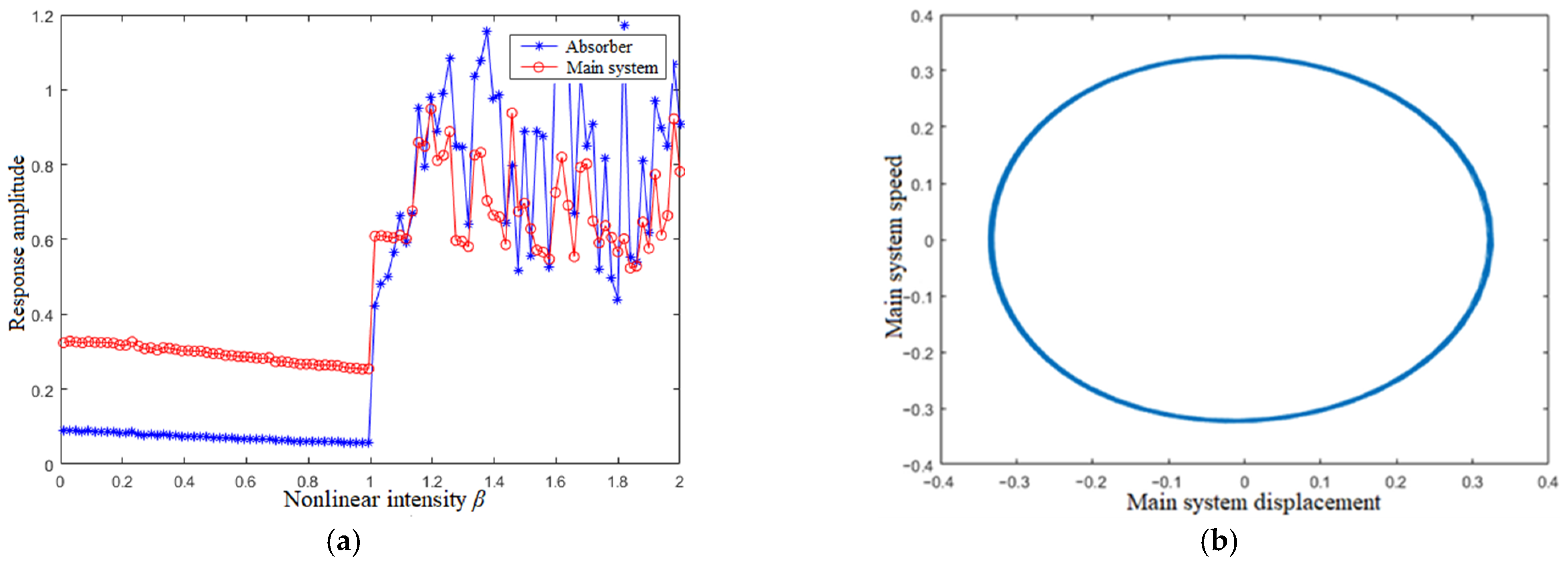
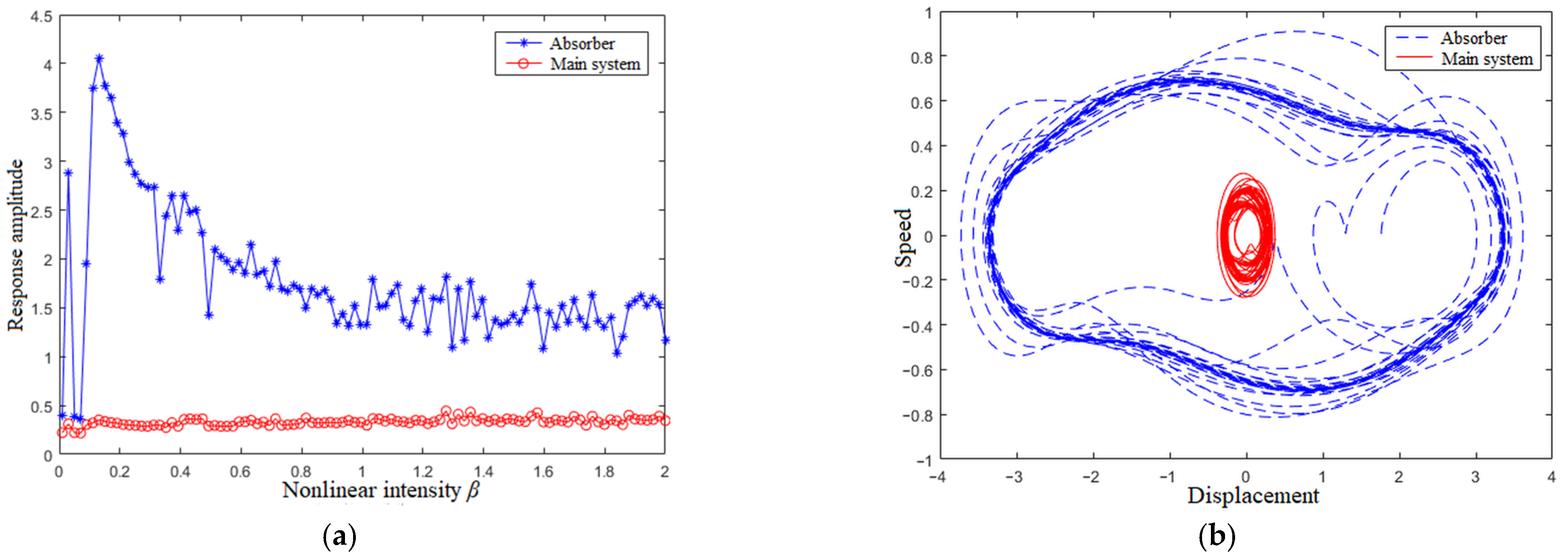
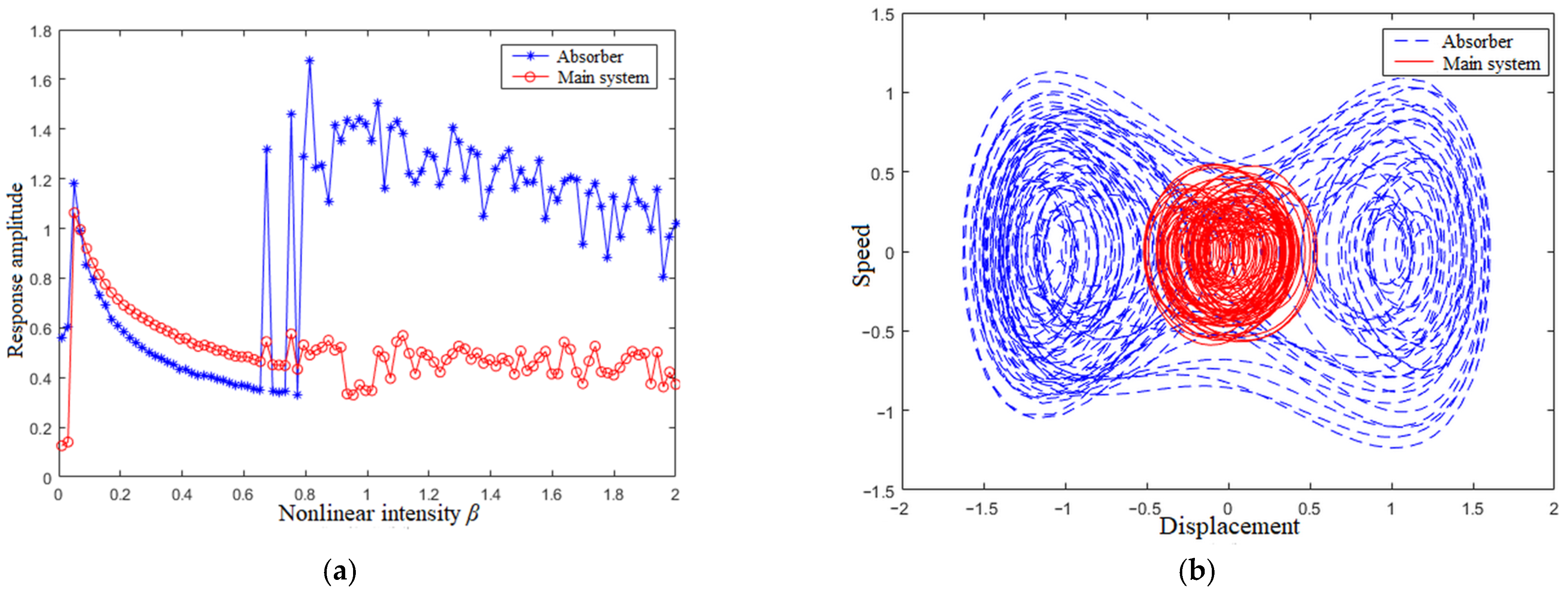
4.3. Nonlinear Intensity β
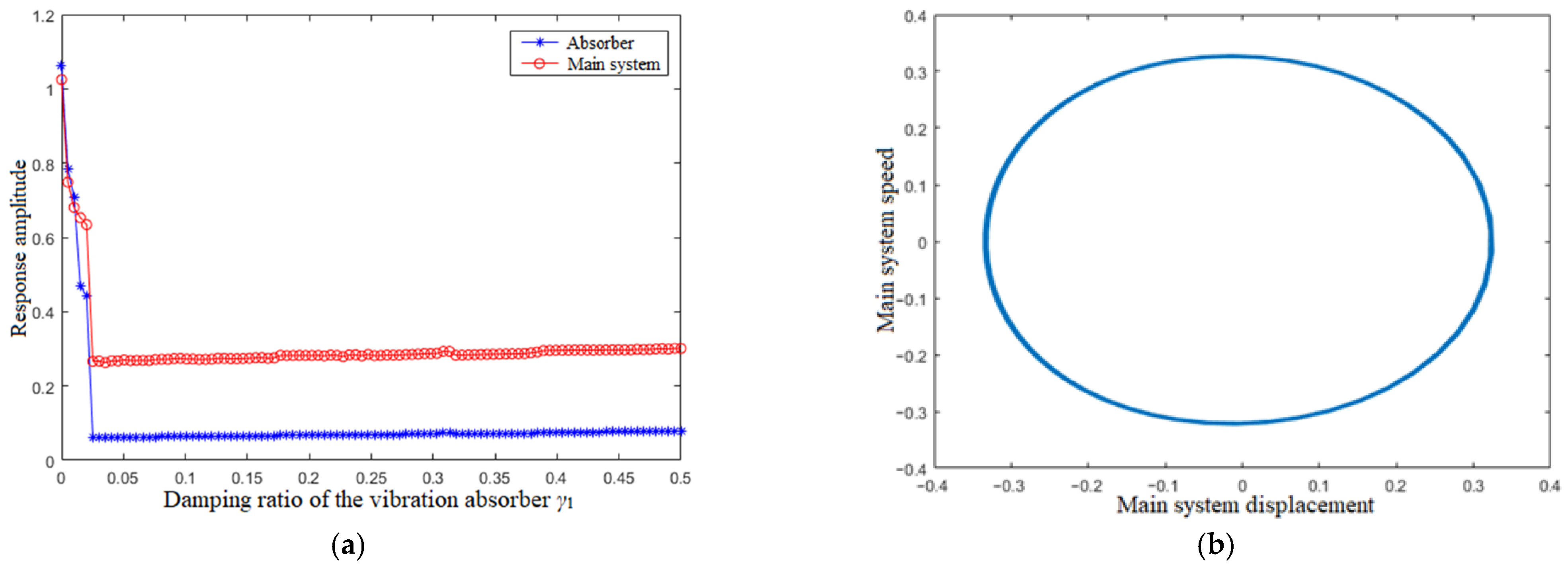
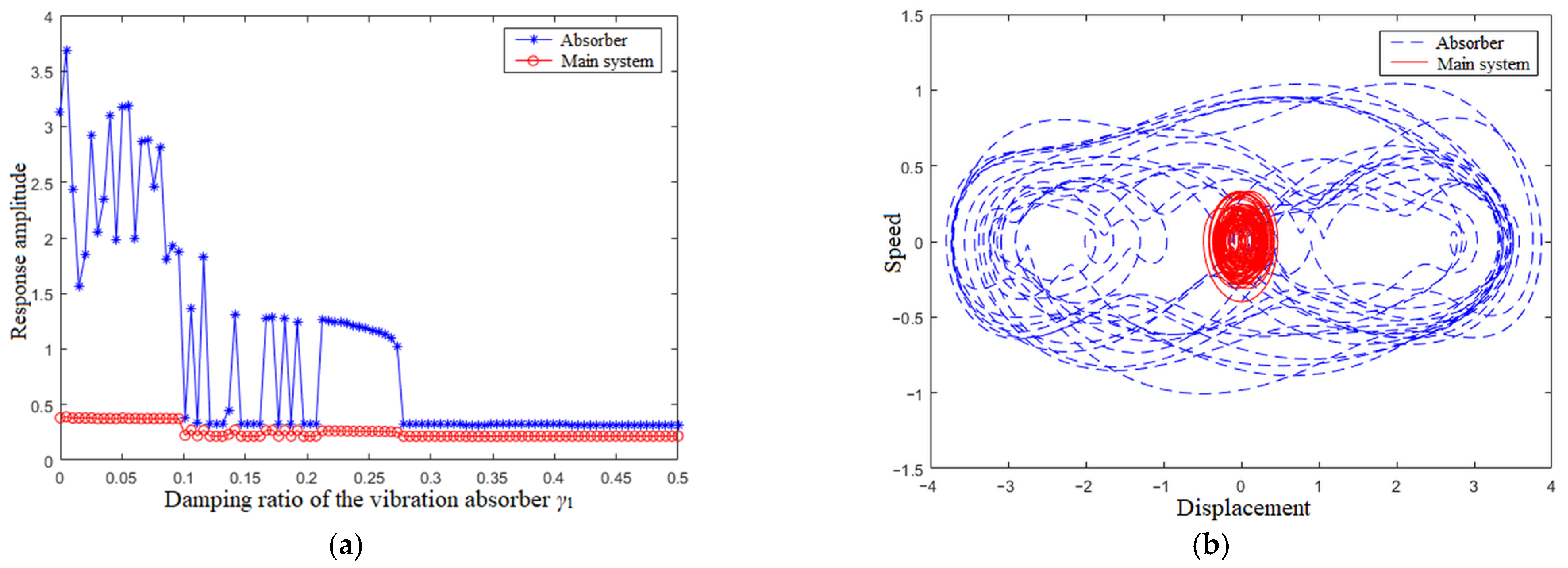
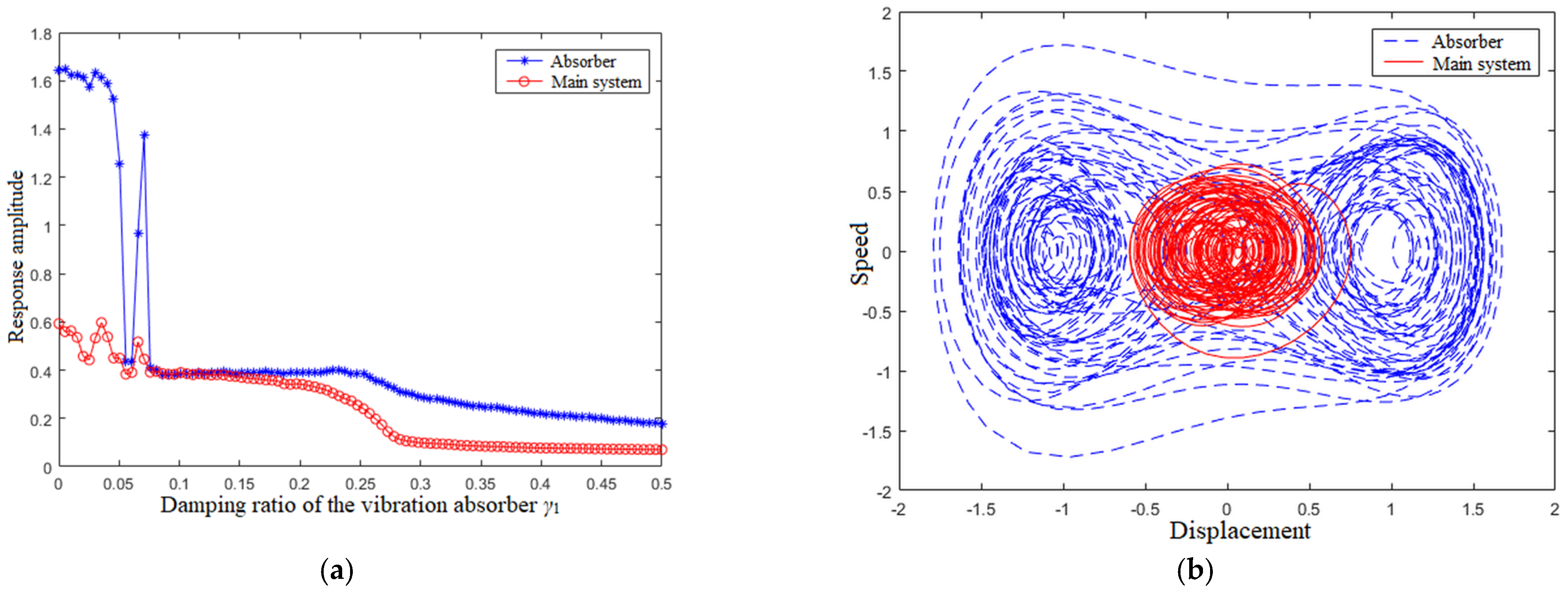
4.4. Damping Ratio of the Vibration Absorber γ1
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Luo, S.; Gao, C.; Ma, W. Research on the mechanism of a newly developed levitation frame with mid-set air spring. Veh. Syst. Dyn. 2018, 56, 1797–1816. [Google Scholar] [CrossRef]
- Zhu, H.; Yang, J.; Zhang, Y.; Feng, X.; Ma, Z. Nonlinear dynamic model of air spring with a damper for vehicle ride comfort. Nonlinear Dyn. 2017, 89, 1545–1568. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, J. Analysis on nonlinear stiffness and vibration isolation performance of scissor-like structure with full types. Nonlinear Dyn. 2016, 86, 17–36. [Google Scholar] [CrossRef]
- Fiebig, W.; Wróbel, J. Two stage vibration isolation of vibratory shake-out conveyor. Arch. Civ. Mech. Eng. 2017, 17, 199–204. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Xu, D.; Ouyang, H.; Duan, Y. Force transmissibility of a two-stage vibration isolation system with quasi-zero stiffness. Nonlinear Dyn. 2017, 87, 633–646. [Google Scholar] [CrossRef]
- Beijen, M.A.; Heertjes, M.F.; Butler, H.; Steinbuch, M. Disturbance feedforward control for active vibration isolation systems with internal isolator dynamics. J. Sound Vib. 2018, 436, 220–235. [Google Scholar] [CrossRef]
- Melik-Shakhnazarov, V.A.; Strelov, V.I.; Sofiyanchuk, D.V.; Tregubenko, A.A. Active vibration isolation devices with inertial servo actuators. Cosm. Res. 2018, 56, 140–143. [Google Scholar] [CrossRef]
- Virgin, L.N.; Santillan, S.T.; Plaut, R.H. Vibration isolation using extreme geometric nonlinearity. J. Sound Vib. 2008, 315, 721–731. [Google Scholar] [CrossRef]
- Guest, S.D.; Pellegrino, S. Analytical models for bistable cylindrical shells. Proc. R. Soc. A 2006, 462, 839–854. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Ma, Y.; Zhang, H.Y.; Pan, H.G.; Cai, Y. Free vibration analysis of a rotating graphene nanoplatelet reinforced pre-twist blade-disk assembly with a setting angle. Appl. Math. Model. 2021, 93, 578–596. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Cui, Y.S.; Pan, H.G.; Yuan, H.Q.; Yang, J. Free vibration analysis of a functionally graded graphene nanoplatelet reinforced disk-shaft assembly with whirl motion. Int. J. Mech. Sci. 2021, 197, 106335. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Yan, K.; Li, H.W.; Wang, X. Study on theoretical modeling and vibration performance of an assembled cylindrical shell-plate structure with whirl motion. Appl. Math. Model. 2022, 110, 618–632. [Google Scholar] [CrossRef]
- Nicassio, F. Shape prediction of bistable plates based on Timoshenko and Ashwell theories. Compos. Struct. 2021, 265, 113645. [Google Scholar] [CrossRef]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Transient responses. J. Sound Vib. 2014, 333, 4859–4880. [Google Scholar] [CrossRef]
- Kremer, D.; Liu, K. A nonlinear energy sink with an energy harvester: Harmonically forced responses. J. Sound Vib. 2017, 410, 287–302. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, J. Modeling and vibration control for a flexible pendulum inverted system based on a PDE observer. Int. J. Control 2016, 90, 1736–1751. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V.; Sun, H. Performance of a 3D pendulum tuned mass damper in offshore wind turbines under multiple hazards and system variations. Smart Struct. Syst. 2019, 24, 53–65. [Google Scholar]
- Taghipour, J.; Dardel, M.; Pashaei, M.H. Vibration mitigation of a nonlinear rotor system with linear and nonlinear vibration absorbers. Mech. Mach. Theory 2018, 128, 586–615. [Google Scholar] [CrossRef]
- Stanton, S.C.; Culver, D.; Mann, B.P. Tuning inertial nonlinearity for passive nonlinear vibration control. Nonlinear Dyn. 2020, 99, 495–504. [Google Scholar] [CrossRef]
- Shui, X.; Wang, S. Investigation on a mechanical vibration absorber with tunable piecewise-linear stiffness. Mech. Syst. Signal Process. 2018, 100, 330–343. [Google Scholar] [CrossRef]
- Yan, L.; Gong, X. Experimental study of vibration isolation characteristics of a geometric anti-spring isolator. Appl. Sci. 2017, 7, 711. [Google Scholar] [CrossRef]
- Shapiro, B.; Kissel, J.; Mavalvala, N.; Strain, K.; Youcef-Toumi, K. Limitations of underactuated modal damping for multistage vibration isolation systems. IEEE-ASME Trans. Mech. 2014, 20, 393–404. [Google Scholar] [CrossRef]
- Tuna, M.; Kirca, M. Exact solution of Eringen’s nonlocal integral model for vibration and buckling of Euler–Bernoulli beam. Int. J. Eng. Sci. 2016, 107, 54–67. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Yan, B.; Ma, C. Design and experiment of a high-static–low-dynamic stiffness isolator using a negative stiffness magnetic spring. J. Sound Vib. 2016, 360, 31–52. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Jiang, L.P.; Pan, H.G.; Yang, J.; Kitipornchai, S. Coupled free vibration of a functionally graded pre-twisted blade-shaft system reinforced with graphene nanoplatelets. Compos. Struct. 2021, 262, 113362. [Google Scholar] [CrossRef]
- Zhao, T.Y.; Li, K.; Ma, H. Study on dynamic characteristics of a rotating cylindrical shell with uncertain parameters. Anal. Math. Phys. 2022, 12, 97. [Google Scholar] [CrossRef]
- Yan, W.; Yu, Y.; Mehta, A. Analytical modeling for rapid design of bistable buckled beams. Theor. Appl. Mech. Lett. 2019, 9, 264–272. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, X.; Yang, M.; Zhao, J.; Wang, W. Study on Dynamic Characteristics of the Bistable Nonlinear Damper. Appl. Sci. 2023, 13, 878. https://doi.org/10.3390/app13020878
Liu Y, Li X, Yang M, Zhao J, Wang W. Study on Dynamic Characteristics of the Bistable Nonlinear Damper. Applied Sciences. 2023; 13(2):878. https://doi.org/10.3390/app13020878
Chicago/Turabian StyleLiu, Yunan, Xianhui Li, Min Yang, Junjuan Zhao, and Wenjiang Wang. 2023. "Study on Dynamic Characteristics of the Bistable Nonlinear Damper" Applied Sciences 13, no. 2: 878. https://doi.org/10.3390/app13020878
APA StyleLiu, Y., Li, X., Yang, M., Zhao, J., & Wang, W. (2023). Study on Dynamic Characteristics of the Bistable Nonlinear Damper. Applied Sciences, 13(2), 878. https://doi.org/10.3390/app13020878





