Lid Driven Triangular and Trapezoidal Cavity Flow: Vortical Structures for Steady Solutions and Hopf Bifurcations
Abstract
:1. Introduction
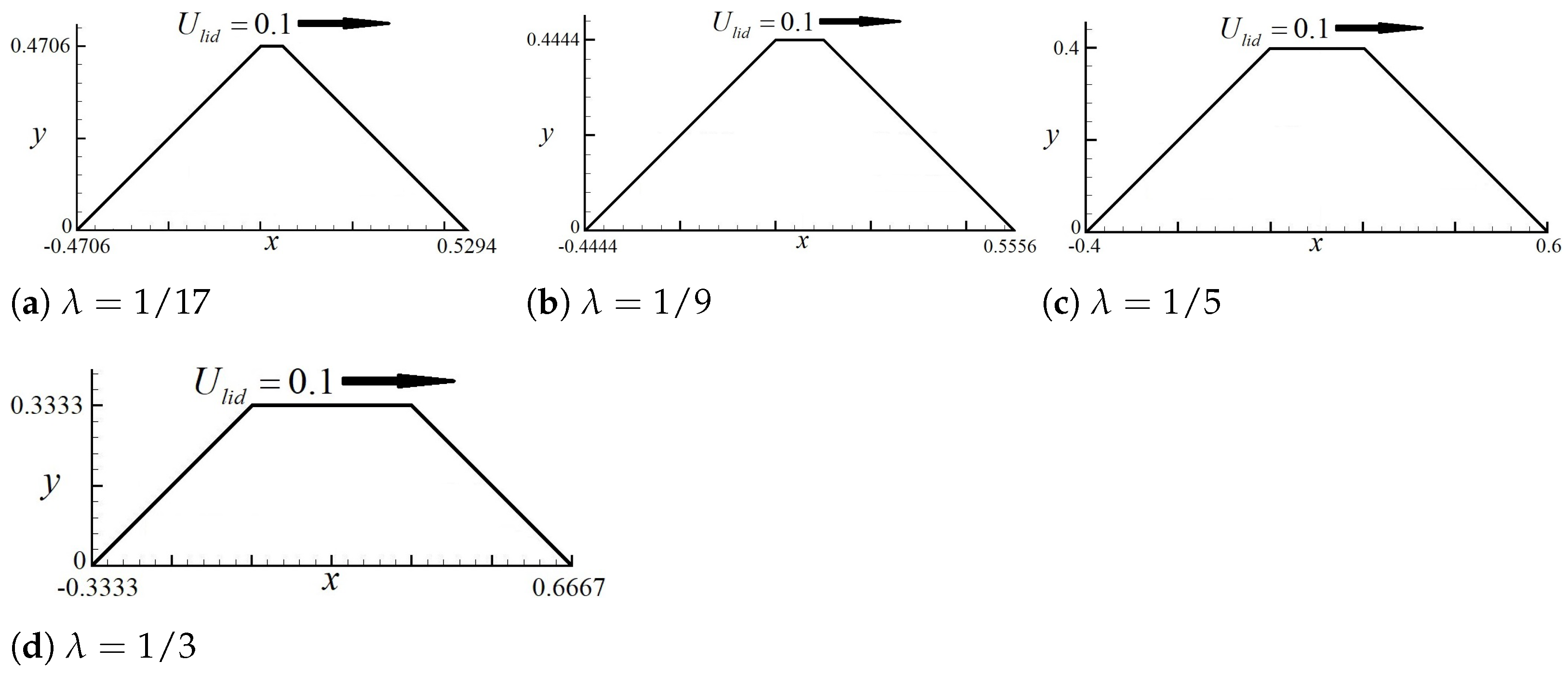
2. Numerical Approach and Boundary Treatment
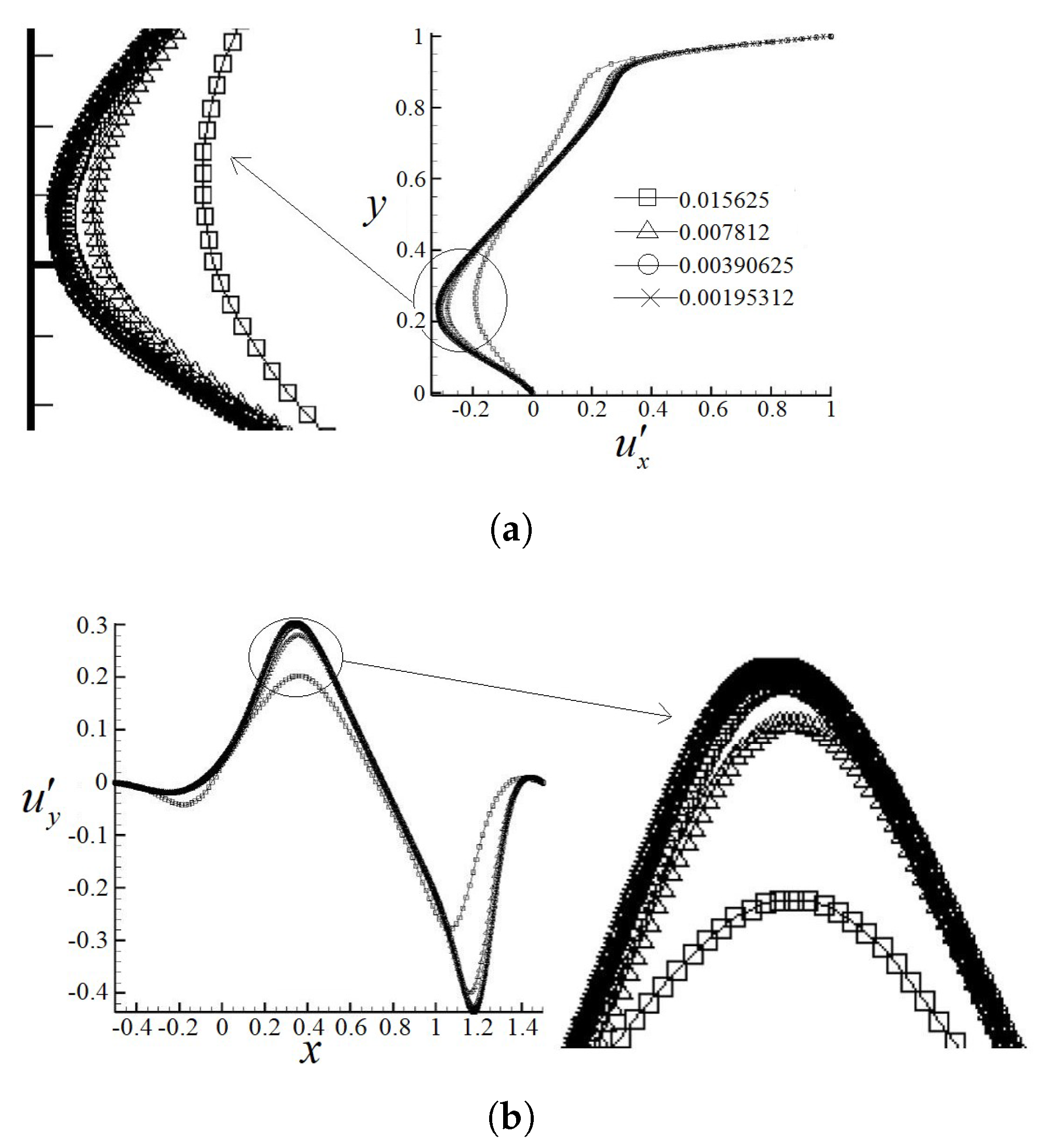
3. Code Validation
Lid Driven Flow on an Equilateral Triangular Cavity
4. Computational New Results and Analysis
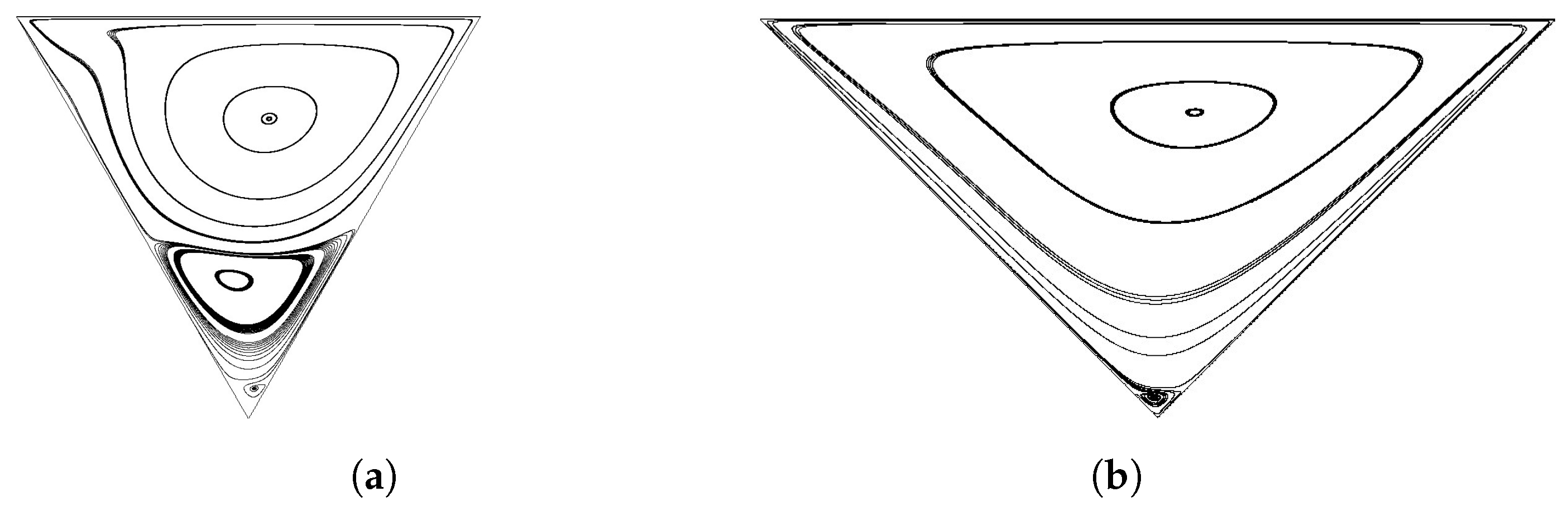
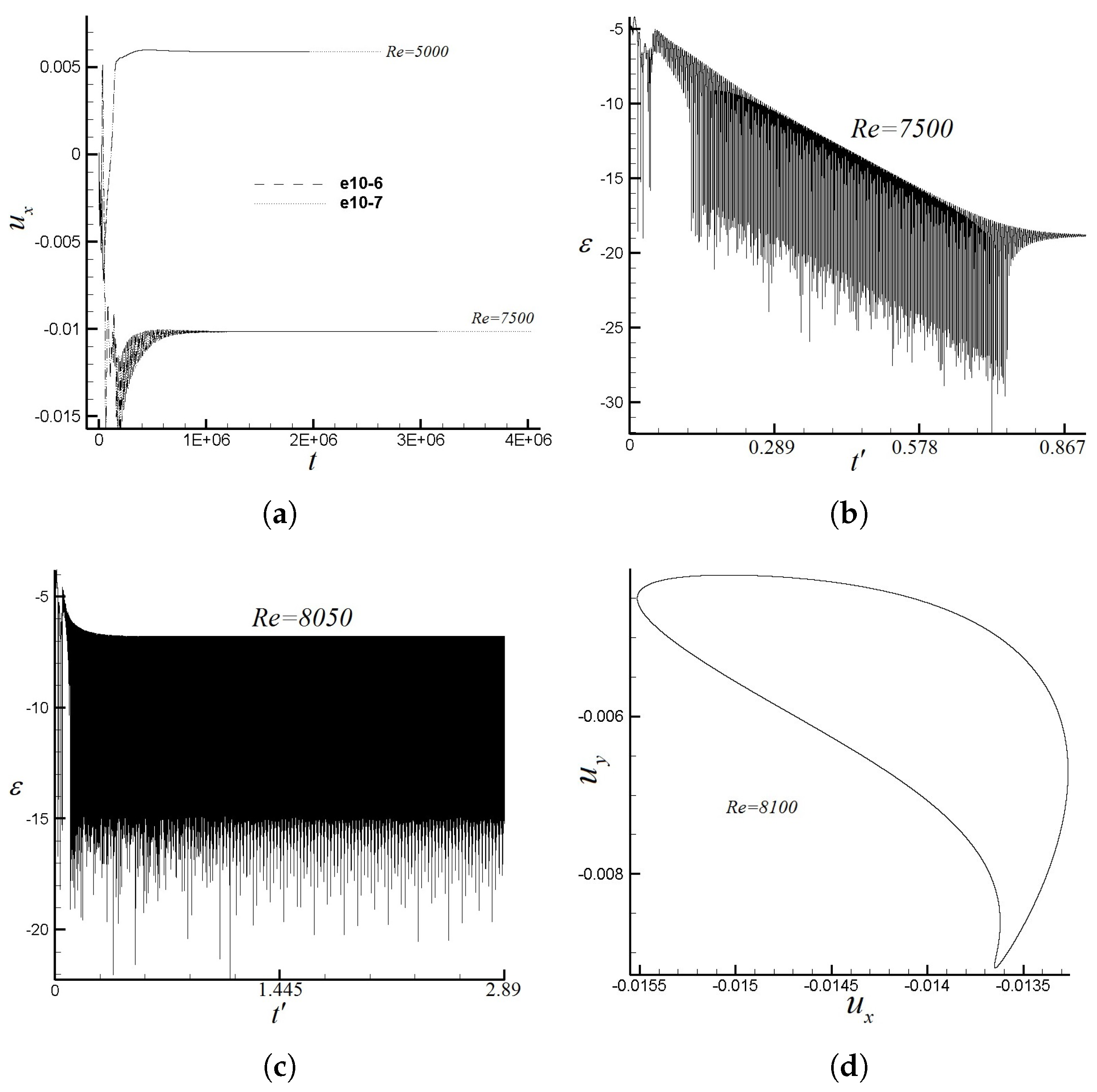
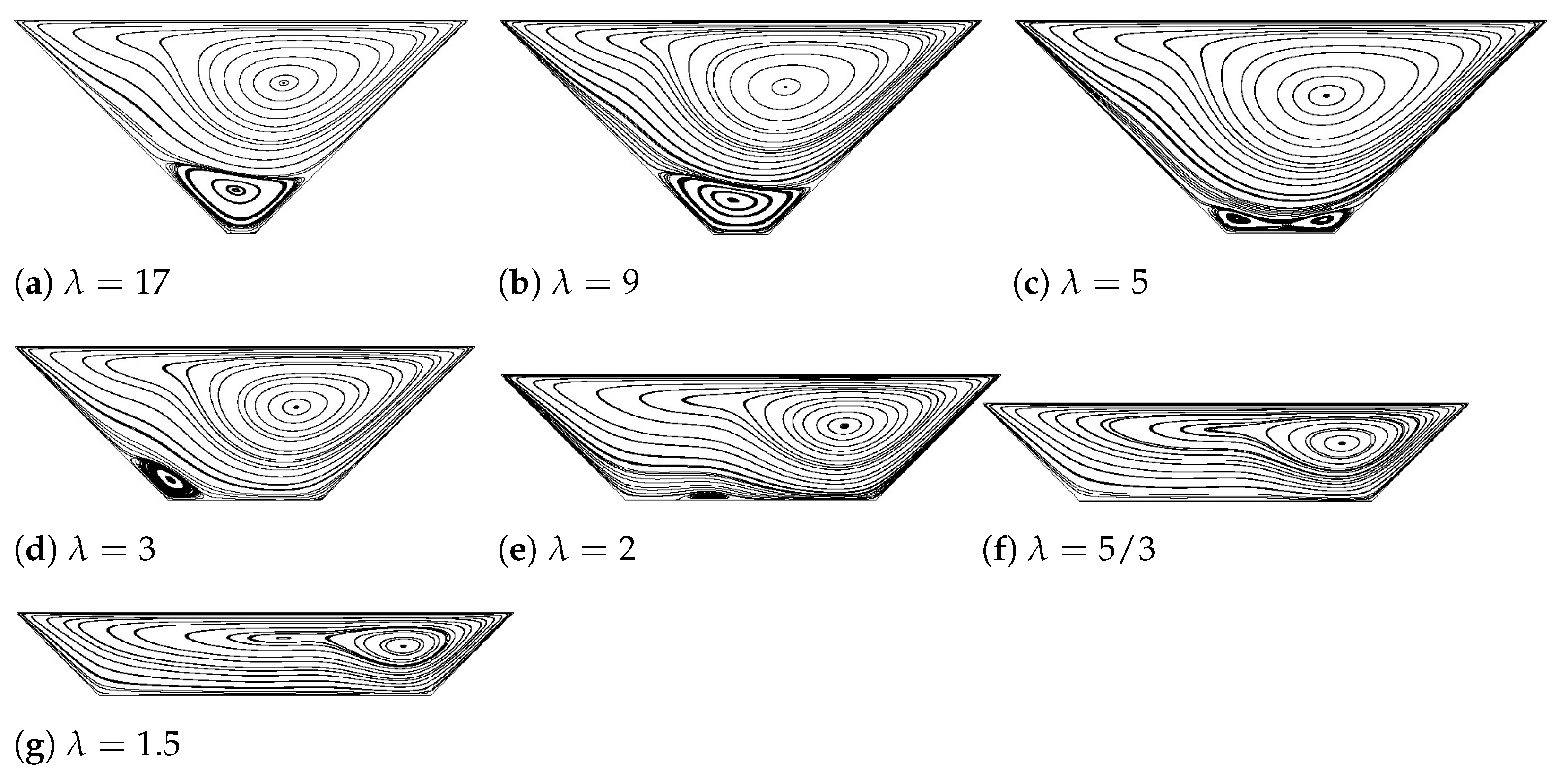
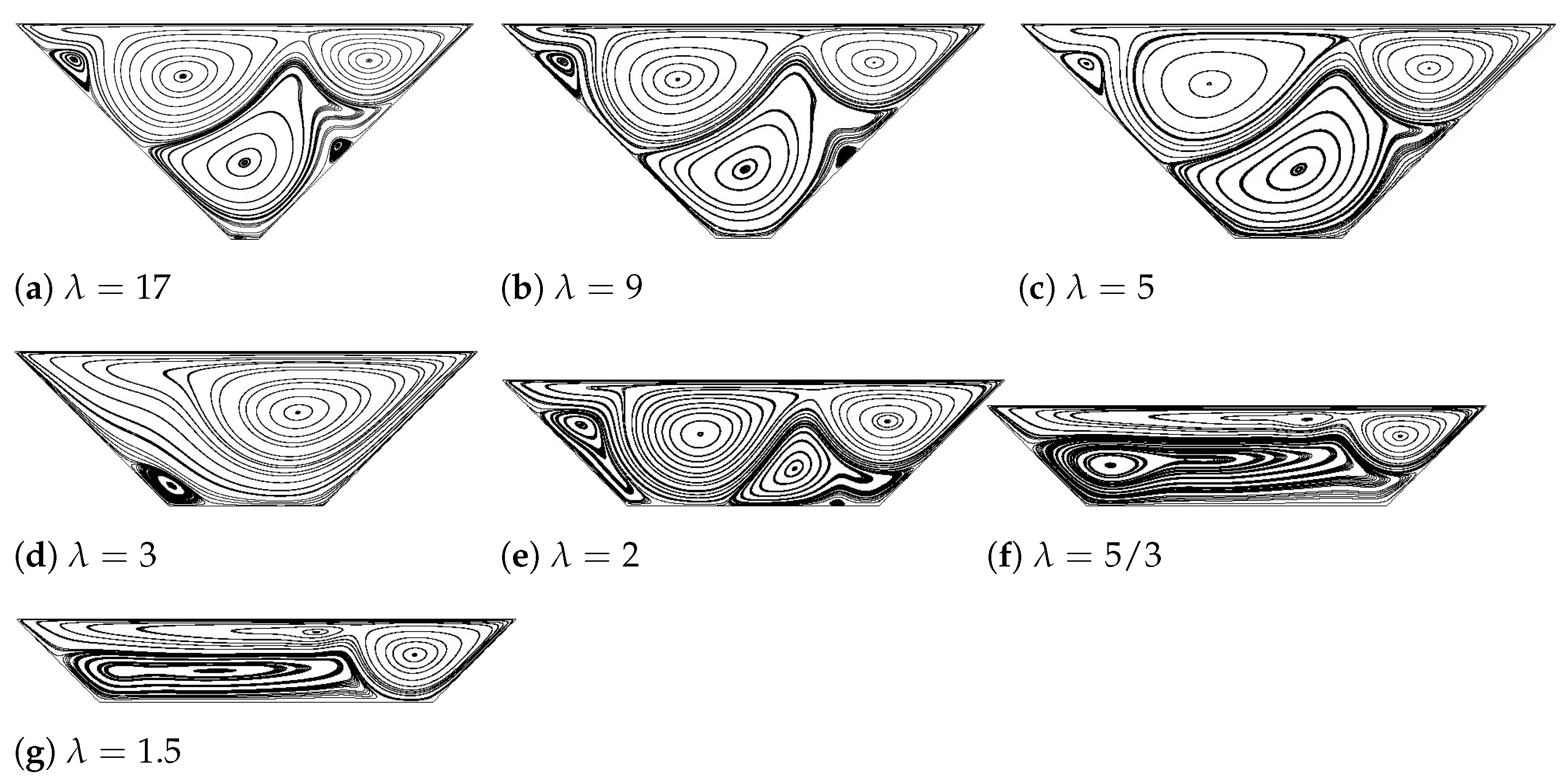
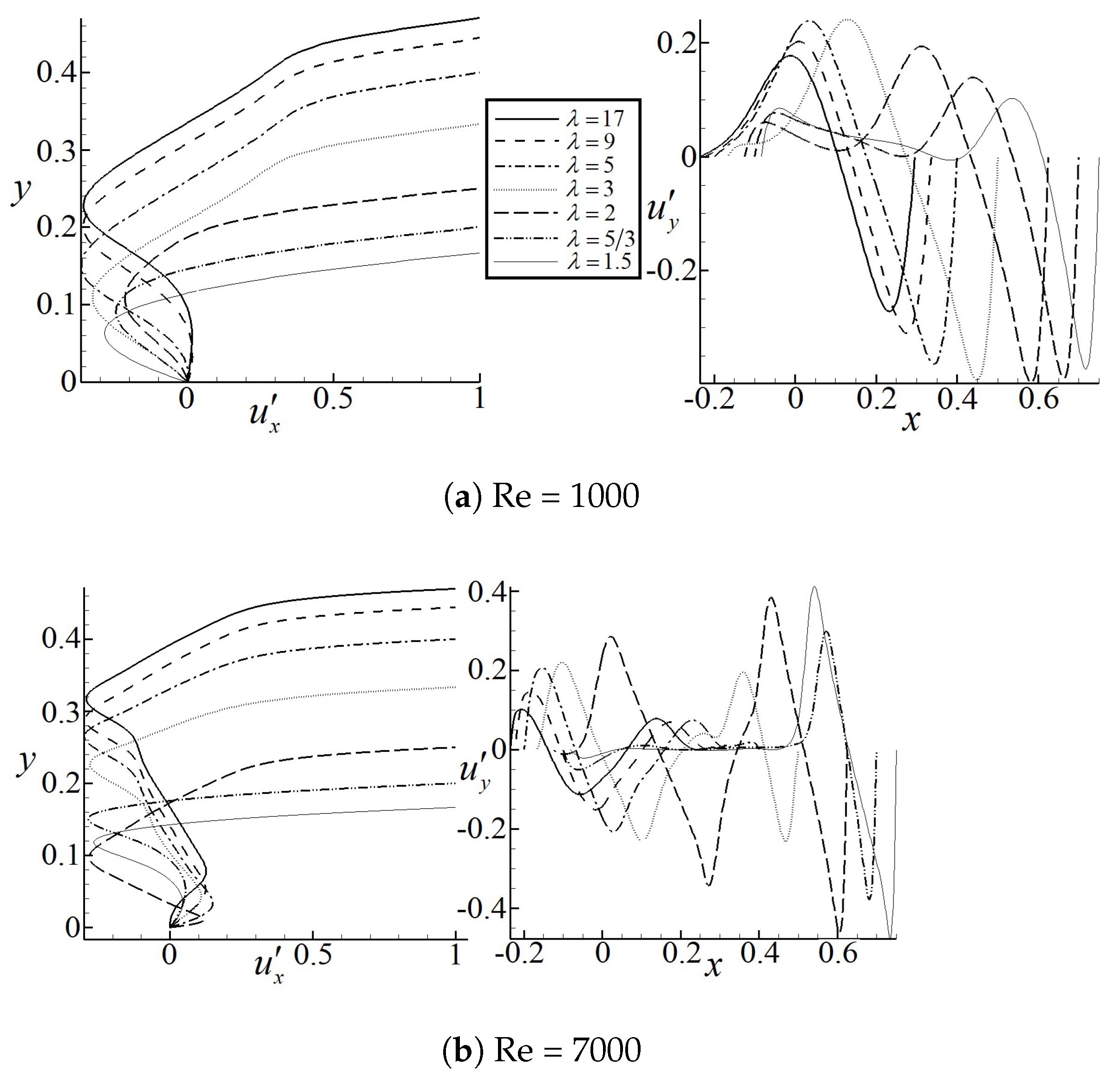
4.1. Right-Angled Isosceles Triangular Cavity
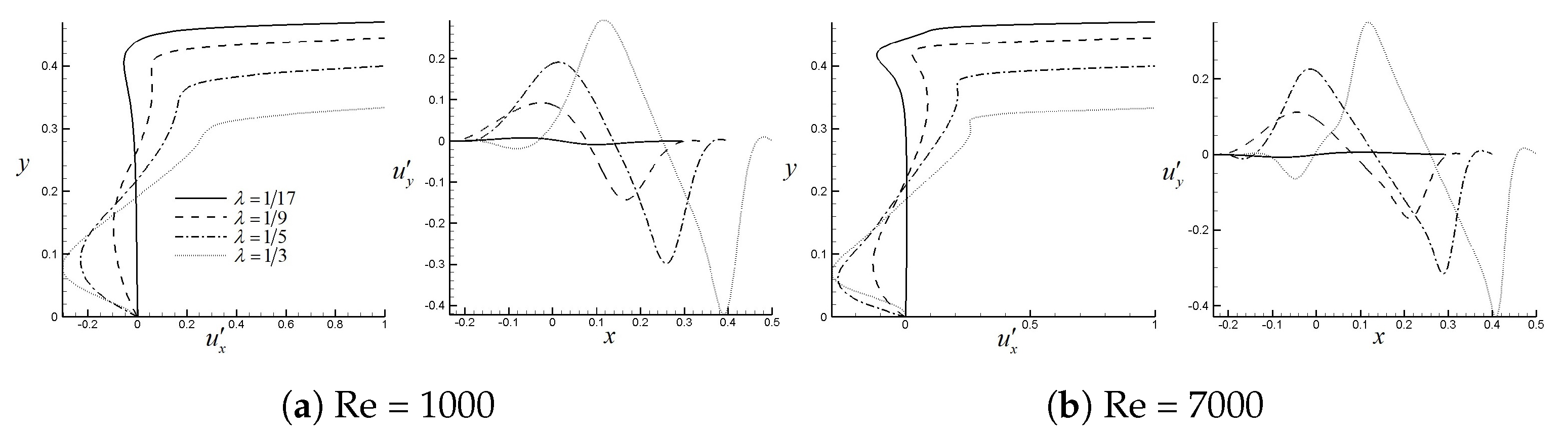
4.2. Right-Angled Isosceles Trapezoidal Cavity (Bowl Shape)
4.3. Right-Angled Isosceles Trapezoidal Cavity (Pyramid Shape)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Lattice sound speed | |
| C | Lattice velocity |
| Unit velocities vector along discrete directions | |
| Precollision distribution functions | |
| Postcollision distribution functions | |
| The discrete equilibrium distribution functions | |
| The discrete nonequilibrium distribution functions | |
| L | Characteristic length |
| Normal vector perpendicular to the walls | |
| Reynolds number | |
| Standard deviation of perturbation decay rate | |
| s | Spatial position vector |
| t | Iteration steps |
| Physical computational time | |
| Aspect ratio of the top line over the base line | |
| Velocity | |
| Lid-driven velocity | |
| Converged solution | |
| Horizontal component of velocity | |
| Vertical component of velocity | |
| Unitized horizontal component of velocity | |
| Unitized vertical component of velocity | |
| i | Discrete directions |
| Grid spacing | |
| Time step | |
| Perturbation decay rate | |
| Perturbation | |
| Density | |
| Stream function | |
| Vorticity | |
| Velocity vector | |
| Single relaxation time term | |
| Weight coefficient | |
| Discrete collision operator |
References
- Ghia, U.; Ghia, K.N.; Shin, C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Schreiber, R.; Keller, H.B. Driven cavity flows by efficient numerical techniques. J. Comput. Phys. 1983, 49, 310–333. [Google Scholar] [CrossRef]
- Bruneau, C.H.; Jouron, C. An efficient scheme for solving steady incompressible Navier-Stokes equations. J. Comput. Phys. 1990, 89, 389–413. [Google Scholar] [CrossRef]
- Peng, Y.F.; Shiau, Y.H.; Hwang, R.R. Transition in a 2-D lid-driven cavity flow. Comput. Fluids 2003, 32, 337–352. [Google Scholar] [CrossRef]
- Fortin, A.; Jardak, M.; Gervais, J.; Pierre, R. Localization of Hopf bifurcations in fluid flow problems. Int. J. Numer. Methods Fluids 1997, 24, 1185–1210. [Google Scholar] [CrossRef]
- Auteri, F.; Parolini, N.; Quartapelle, L. Numerical investigation on the stability of singular driven cavity flow. J. Comput. Phys. 2002, 183, 1–25. [Google Scholar] [CrossRef]
- Bruneau, C.H.; Saad, M. The 2D lid-driven cavity problem revisited. Comput. Fluids 2006, 35, 326–348. [Google Scholar] [CrossRef]
- Sahin, M.; Owens, R.G. A novel fully implicit finite volume method applied to the lid-driven cavity problem—Part I: High Reynolds number flow calculations. Int. J. Numer. Methods Fluids 2003, 42, 57–77. [Google Scholar] [CrossRef]
- Ribbens, C.J.; Watson, L.T.; Wang, C.Y. Steady viscous flow in a triangular cavity. J. Comput. Phys. 1994, 112, 173–181. [Google Scholar] [CrossRef] [Green Version]
- Jyotsna, R.; Vanka, S. Multigrid calculation of steady, viscous flow in a triangular cavity. J. Comput. Phys. 1995, 122, 107–117. [Google Scholar] [CrossRef]
- Li, M.; Tang, T. Steady viscous flow in a triangular cavity by efficient numerical techniques. Comput. Math. Appl. 1996, 31, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Gaskell, P.; Thompson, H.; Savage, M. A finite element analysis of steady viscous flow in triangular cavities. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1999, 213, 263–276. [Google Scholar] [CrossRef]
- Erturk, E.; Gokcol, O. Fine grid numerical solutions of triangular cavity flow. Eur. Phys. J.-Appl. Phys. 2007, 38, 97–105. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, L.; Ahmed, M.; Kühnen, J.; Kuhlmann, H.C.; Theofilis, V. Three-dimensional flow instability in a lid-driven isosceles triangular cavity. J. Fluid Mech. 2011, 675, 369–396. [Google Scholar] [CrossRef] [Green Version]
- Sidik, N.A.C.; Munir, F.A. Mesoscale numerical prediction of fluid flow in a shear driven cavity. Arab. J. Sci. Eng. 2012, 37, 1723–1735. [Google Scholar] [CrossRef]
- Ahmed, M.; Kuhlmann, H.C. Flow instability in triangular lid-driven cavities with wall motion away from a rectangular corner. Fluid Dyn. Res. 2012, 44, 025501. [Google Scholar] [CrossRef]
- Jagannathan, A.; Mohan, R.; Dhanak, M. A spectral method for the triangular cavity flow. Comput. Fluids 2014, 95, 40–48. [Google Scholar] [CrossRef]
- Gaspar, F.; Rodrigo, C.; Heidenreich, E. Geometric multigrid methods on structured triangular grids for incompressible navier-stokes equations at low reynolds numbers. Int. J. Numer. Anal. Model. 2014, 11, 400–411. [Google Scholar]
- Darr, J.H.; Vanka, S. Separated flow in a driven trapezoidal cavity. Phys. Fluids A Fluid Dyn. 1991, 3, 385–392. [Google Scholar] [CrossRef]
- McQuain, W.D.; Ribbens, C.J.; Wang, C.Y.; Watson, L.T. Steady viscous flow in a trapezoidal cavity. Comput. Fluids 1994, 23, 613–626. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Shi, B.; Chai, Z. Lattice Boltzmann simulation of lid-driven flow in trapezoidal cavities. Comput. Fluids 2010, 39, 1977–1989. [Google Scholar] [CrossRef]
- Ismael, M.A.; Chamkha, A.J. Mixed convection in lid-driven trapezoidal cavities with an aiding or opposing side wall. Numer. Heat Transf. Part A Appl. 2015, 68, 312–335. [Google Scholar] [CrossRef]
- Kareem, A.K.; Mohammed, H.; Hussein, A.K.; Gao, S. Numerical investigation of mixed convection heat transfer of nanofluids in a lid-driven trapezoidal cavity. Int. Commun. Heat Mass Transf. 2016, 77, 195–205. [Google Scholar] [CrossRef] [Green Version]
- Rashad, A.; Sivasankaran, S.; Mansour, M.; Bhuvaneswari, M. Magneto-convection of nanofluids in a lid-driven trapezoidal cavity with internal heat generation and discrete heating. Numer. Heat Transf. Part A Appl. 2017, 71, 1223–1234. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Modeling and optimization of MHD mixed convection in a lid-driven trapezoidal cavity filled with alumina–water nanofluid: Effects of electrical conductivity models. Int. J. Mech. Sci. 2018, 136, 264–278. [Google Scholar] [CrossRef]
- Mehmood, Z. Numerical simulations and linear stability analysis of mixed thermomagnetic convection through two lid-driven entrapped trapezoidal cavities enclosing ferrofluid saturated porous medium. Int. Commun. Heat Mass Transf. 2019, 109, 104345. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Selimefendigil, F.; Oztop, H.F. Pulsating flow of CNT–water nanofluid mixed convection in a vented trapezoidal cavity with an inner conductive T-shaped object and magnetic field effects. Energies 2020, 13, 848. [Google Scholar] [CrossRef] [Green Version]
- Toghraie, D. Numerical simulation on MHD mixed convection of Cu-water nanofluid in a trapezoidal lid-driven cavity. Int. J. Appl. Electromagn. Mech. 2020, 62, 683–710. [Google Scholar] [CrossRef]
- Mondal, P.; Mahapatra, T.R. Minimization of entropy generation due to MHD double diffusive mixed convection in a lid driven trapezoidal cavity with various aspect ratios. Nonlinear Anal. Model. Control 2020, 25, 545–563. [Google Scholar] [CrossRef]
- Ali, F.H.; Hamzah, H.K.; Hussein, A.K.; Jabbar, M.Y.; Talebizadehsardari, P. MHD mixed convection due to a rotating circular cylinder in a trapezoidal enclosure filled with a nanofluid saturated with a porous media. Int. J. Mech. Sci. 2020, 181, 105688. [Google Scholar] [CrossRef]
- Alshuraiaan, B.; Pop, I. Numerical simulation of mixed convection in a lid-driven trapezoidal cavity with flexible bottom wall and filled with a hybrid nanofluid. Eur. Phys. J. Plus 2021, 136, 580. [Google Scholar] [CrossRef]
- Ishak, M.S.; Alsabery, A.I.; Hashim, I.; Chamkha, A.J. Entropy production and mixed convection within trapezoidal cavity having nanofluids and localised solid cylinder. Sci. Rep. 2021, 11, 14700. [Google Scholar] [CrossRef] [PubMed]
- Prince, H.A.; Redwan, D.A.; Rozin, E.H.; Saha, S.; Mamun, M.A.H. Augmentation of Pure Mixed Convection Heat Transfer in a Non-Newtonian Power-Law Fluid Filled Lid-Driven Trapezoidal Cavity With Double Rotating Cylinders. J. Heat Transf. 2021, 143, 082601. [Google Scholar] [CrossRef]
- Shah, S.S.; Haq, R.U.; Al-Kouz, W. Mixed convection analysis in a split lid-driven trapezoidal cavity having elliptic shaped obstacle. Int. Commun. Heat Mass Transf. 2021, 126, 105448. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Laouira, H.; Hussein, A.K.; Omri, M.; Abderrahmane, A.; Kolsi, L.; Biswal, U. Mixed Convection inside a Duct with an Open Trapezoidal Cavity Equipped with Two Discrete Heat Sources and Moving Walls. Mathematics 2022, 10, 929. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, W.; Qasim, M.; Alharbi, S.; Hamid, M.; Du, M. Hybrid nanofluid flow around a triangular-shaped obstacle inside a split lid-driven trapezoidal cavity. Eur. Phys. J. Spec. Top. 2022, 231, 2749–2759. [Google Scholar] [CrossRef]
- An, B.; Bergada, J.; Mellibovsky, F. The lid-driven right-angled isosceles triangular cavity flow. J. Fluid Mech. 2019, 875, 476–519. [Google Scholar] [CrossRef]
- Bo, A.; Mellibovsky, F.; Bergadà, J.; Sang, W. Towards a better understanding of wall-driven square cavity flows using the lattice Boltzmann method. Appl. Math. Model. 2020, 82, 469–486. [Google Scholar]
- An, B.; Bergadà, J.M.; Mellibovsky, F.; Sang, W. New applications of numerical simulation based on lattice Boltzmann method at high Reynolds numbers. Comput. Math. Appl. 2020, 79, 1718–1741. [Google Scholar] [CrossRef]
- An, B.; Bergadà, J.; Mellibovsky, F.; Sang, W.; Xi, C. Numerical investigation on the flow around a square cylinder with an upstream splitter plate at low Reynolds numbers. Meccanica 2020, 55, 1037–1059. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, B.; Wang, N. Lattice BGK model for incompressible Navier–Stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Shi, B. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 2002, 11, 366. [Google Scholar]
- Moffatt, H.K. Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 1964, 18, 1–18. [Google Scholar] [CrossRef]
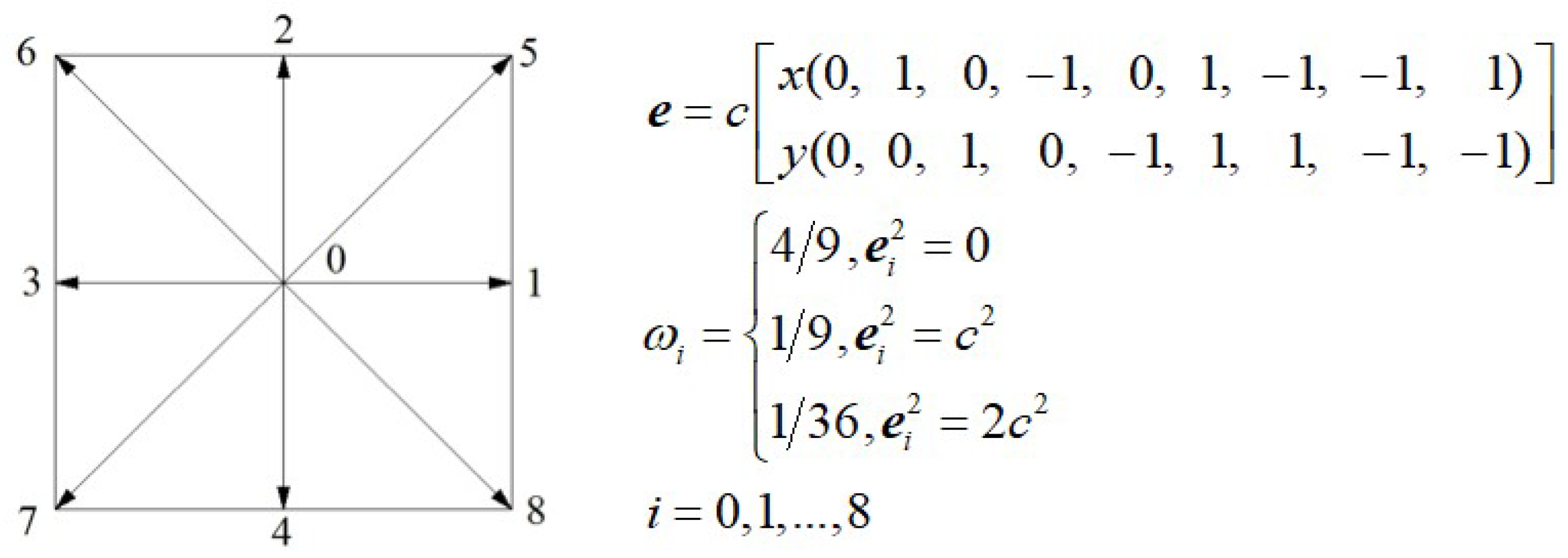




| Equilateral triangular cavity | Data source | This paper | Ref. [13] | Ref. [11] | Ref. [15] |
| Primary vortex | X = 0.5442 | X = 0.5401 | X = 0.5499 | X = 0.5266 | |
| Y = 0.6455 | Y = 0.6527 | Y = 0.6539 | Y = 0.6501 | ||
| Isosceles triangular cavity | Data source | This paper | Ref. [14] | Ref. [18] | |
| Primary vortex | X = 0.0465 | X = 0.0448 | X = 0.045 | ||
| Y = 0.3829 | Y = 0.3816 | Y = 0.38 |
| Re | 7000 | 7100 | 7200 | 7300 | 7500 | 7600 | 7700 |
| t′ | 0.47399 | 0.49084 | 0.551296 | 0.64146 | 1.0696 | 1.179 | 1.5745 |
| −4.57412 | −3.8701 | −3.40548 | −2.96897 | −1.9354 | −1.4096 | −1.03147 | |
| 0.601306 | 0.40408 | 0.454294 | 0.403031 | 0.24998 | 0.103915 | 0.0947897 | |
| Re | 7800 | 7850 | 7900 | 7950 | 8050 | ||
| t′ | 2.30165 | 2.95315 | 4.081 | 6.473 | 2.8928 | ||
| −0.69855 | −0.5528 | −0.39235 | −0.25251 | −0.0000 | |||
| 0.095591 | 0.0801 | 0.0447 | 0.031272 | 0 |
| Re = 1000 | 17 | 9 | 5 | 3 | 2 | 5/3 | 1.5 | |
| Position | X = 0.5946 | X = 0.5949 | X = 0.5862 | X = 0.6122 | X = 0.6868 | X = 0.7385 | X = 0.7790 | |
| Y = 0.3319 | Y = 0.3054 | Y = 0.2600 | Y = 0.2020 | Y = 0.1476 | Y = 0.1176 | Y = 0.0989 | ||
| −0.0527 | −0.0528 | −0.0537 | −0.0510 | −0.0426 | −0.0360 | −0.02994 | ||
| −6.393 | −6.397 | −6.274 | −6.859 | −9.066 | −11.46 | −13.804 | ||
| Re = 7000 | Position | X = 0.7714 | X = 0.7733 | X = 0.7626 | X = 0.7512 | X = 0.7665 | X = 0.8271 | X = 0.7966 |
| Y = 0.3898 | Y = 0.3638 | Y = 0.3165 | Y = 0.2458 | Y = 0.1680 | Y = 0.1395 | Y = 0.0945 | ||
| −0.0349 | −0.03475 | −0.0361 | −0.0359 | −0.0035 | −0.02461 | −0.0290 | ||
| −13.020 | −13.070 | −12.563 | −11.233 | −12.39 | −16.096 | −13.635 |
| Re = 1000 | 1/17 | 1/9 | 1/5 | 1/3 | |
| Position | X = 0.5118 | X = 0.5301 | X = 0.5382 | X = 0.5822 | |
| Y = 0.4425 | Y = 0.2764 | Y = 0.2195 | Y = 0.1830 | ||
| −0.0078 | −0.0176 | −0.0334 | −0.0426 | ||
| −23.27 | −3.566 | −4.269 | −5.794 | ||
| Re = 7000 | Position | X = 0.4828 | X = 0.5349 | X = 0.5311 | X = 0.5927 |
| Y = 0.2188 | Y = 0.2047 | Y = 0.2031 | Y = 0.1744 | ||
| 0.0128 | −0.0126 | −0.0309 | −0.0406 | ||
| 1.443 | −1.637 | −3.304 | −5.916 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, B.; Guo, S.; Bergadà, J.M. Lid Driven Triangular and Trapezoidal Cavity Flow: Vortical Structures for Steady Solutions and Hopf Bifurcations. Appl. Sci. 2023, 13, 888. https://doi.org/10.3390/app13020888
An B, Guo S, Bergadà JM. Lid Driven Triangular and Trapezoidal Cavity Flow: Vortical Structures for Steady Solutions and Hopf Bifurcations. Applied Sciences. 2023; 13(2):888. https://doi.org/10.3390/app13020888
Chicago/Turabian StyleAn, Bo, Shipeng Guo, and Josep M. Bergadà. 2023. "Lid Driven Triangular and Trapezoidal Cavity Flow: Vortical Structures for Steady Solutions and Hopf Bifurcations" Applied Sciences 13, no. 2: 888. https://doi.org/10.3390/app13020888






