Study on the Disturbance of Existing Subway Tunnels by Foundation Sloping Excavation
Abstract
:1. Introduction
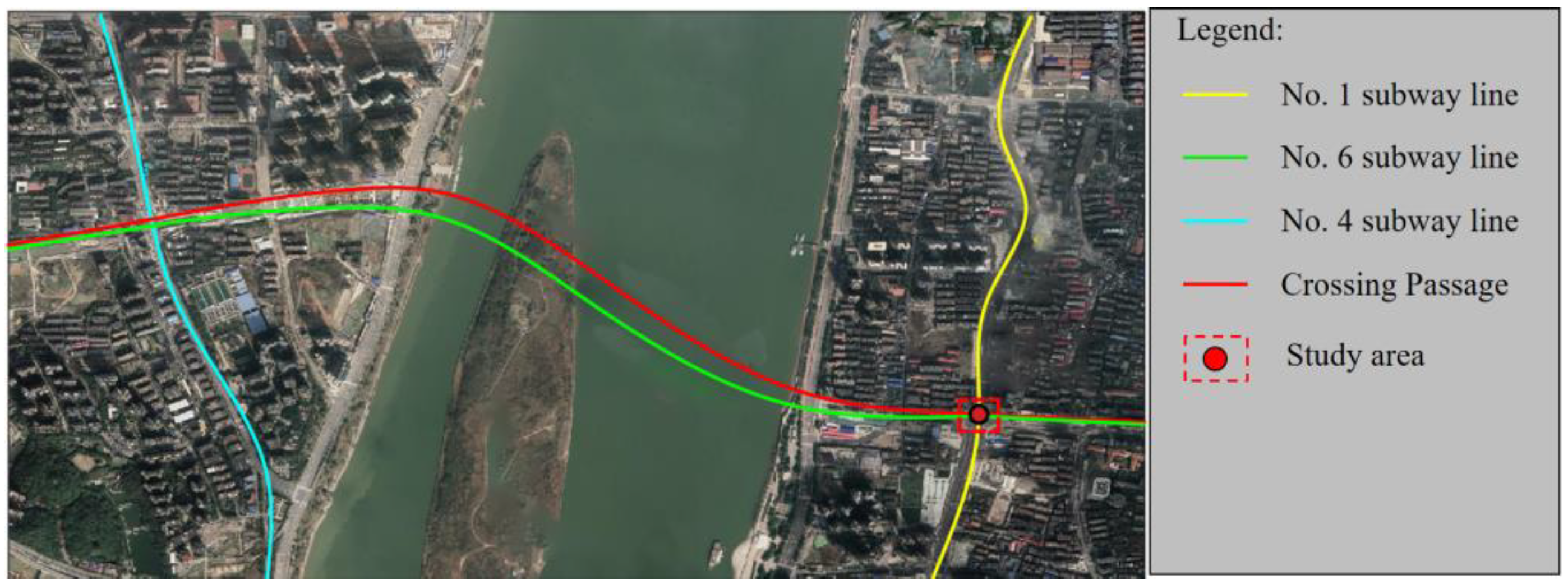
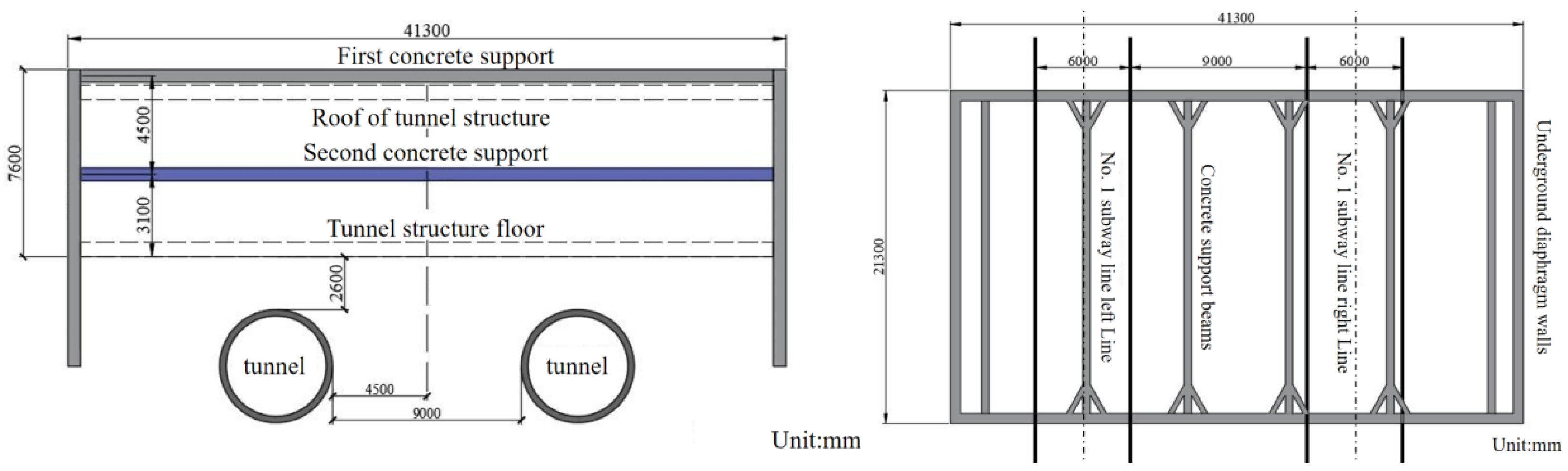
2. Engineering Background
3. The Foundations of Theory Calculation
3.1. Calculation of Additional Stress
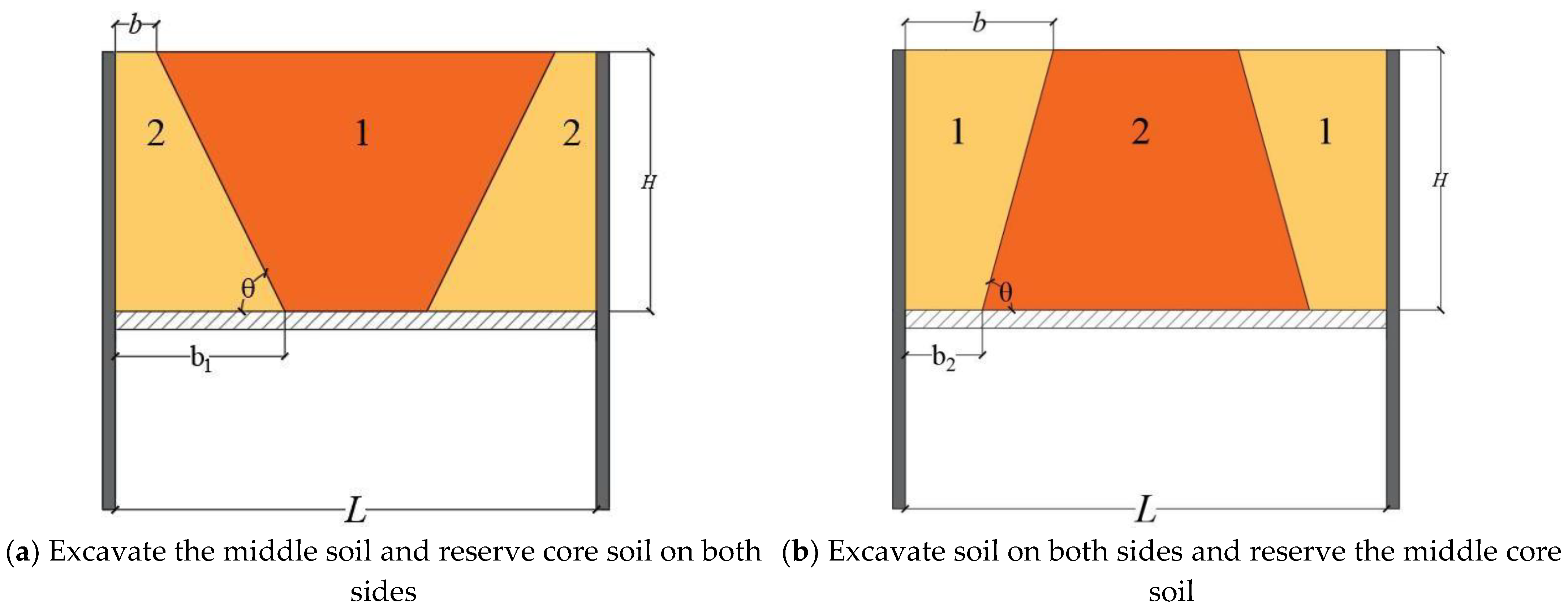
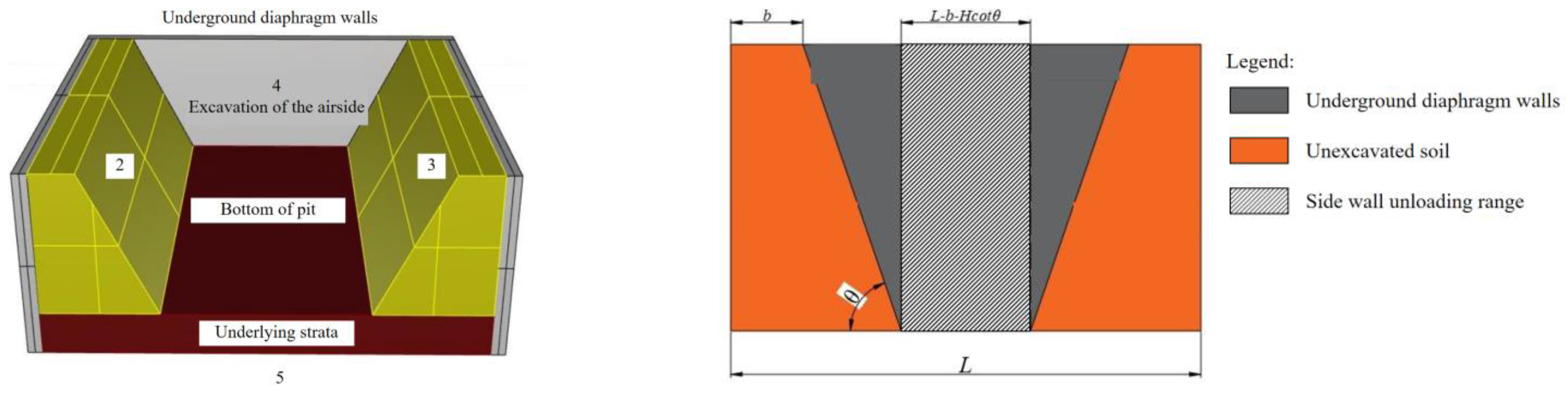
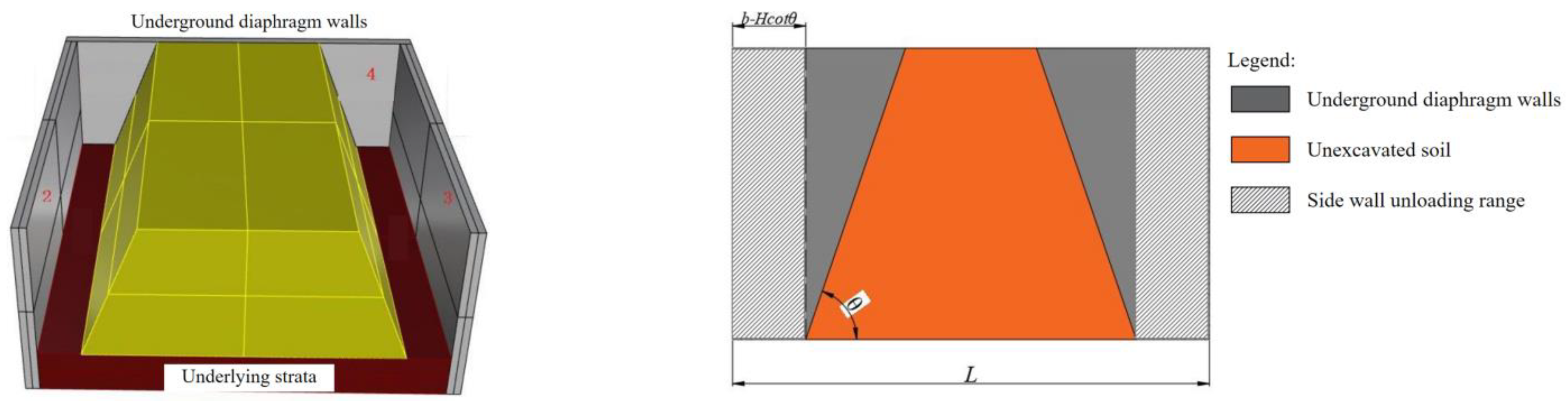
3.2. Model of Foundation Sloping
3.3. Excavate the Middle Soil and Reserve Core Soil on Both Sides
3.4. Excavate on Both Sides Soil and Reserve the Middle Core Soil
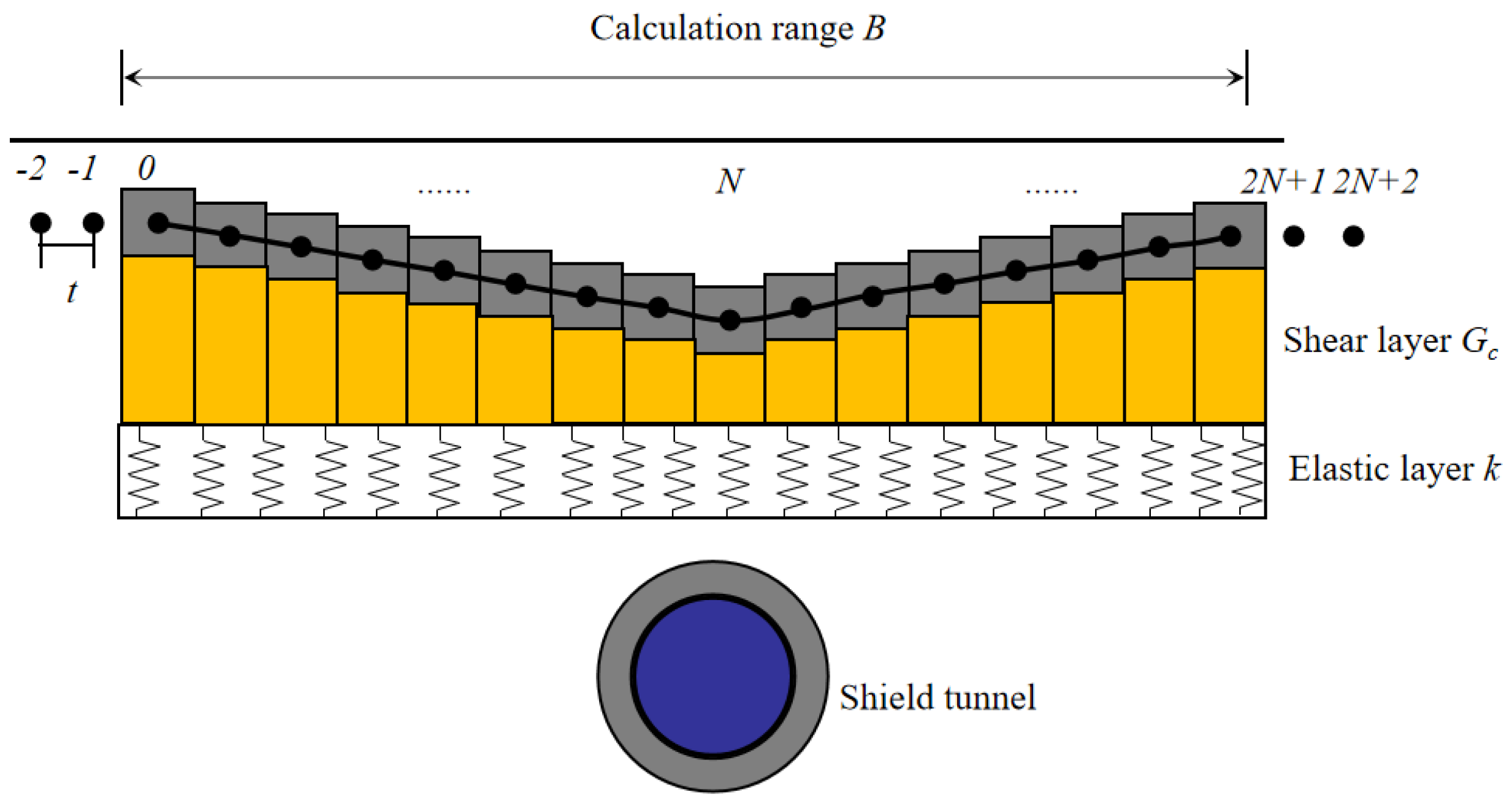
3.5. Calculation of Existing Tunnel Deformation
4. Validation of the Numerical Simulation
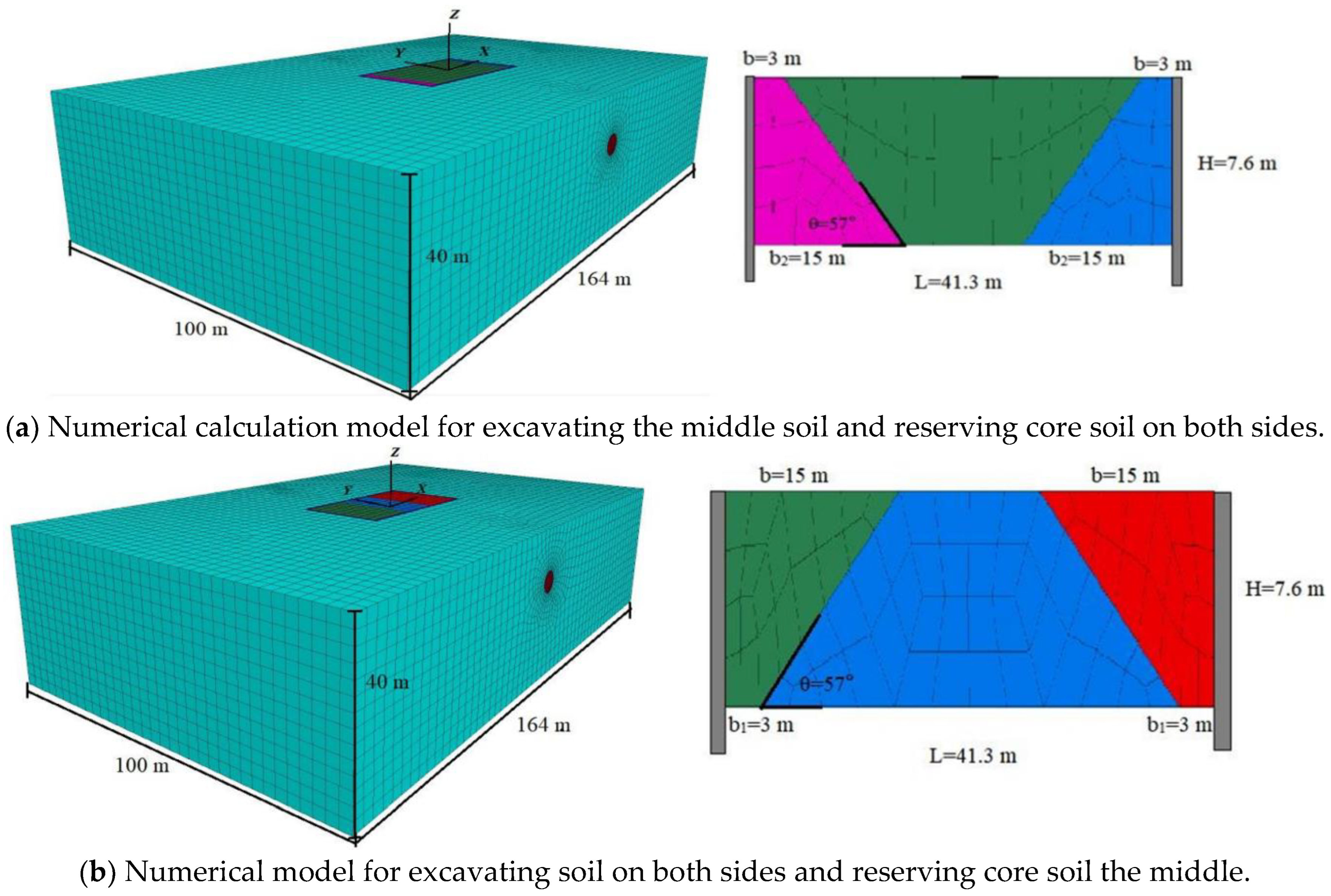
4.1. Calculation and Element Parameters
4.2. Modeling and Calculation Steps
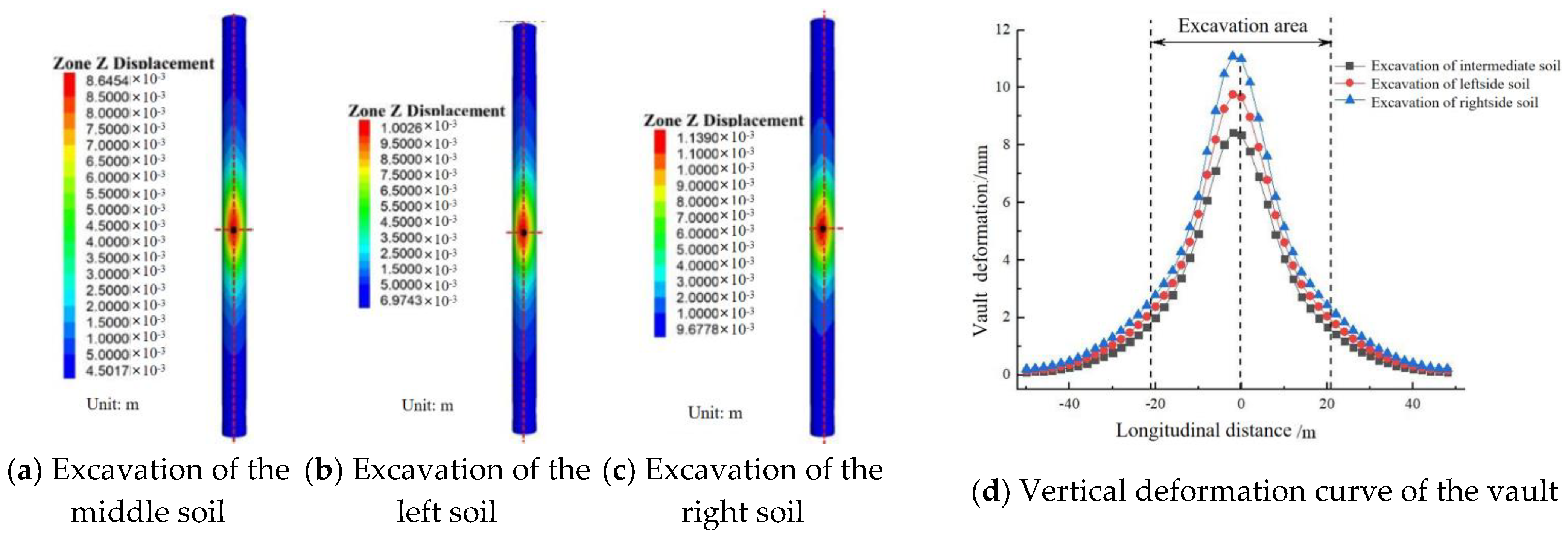
4.3. Results Analysis of Numerical Simulation
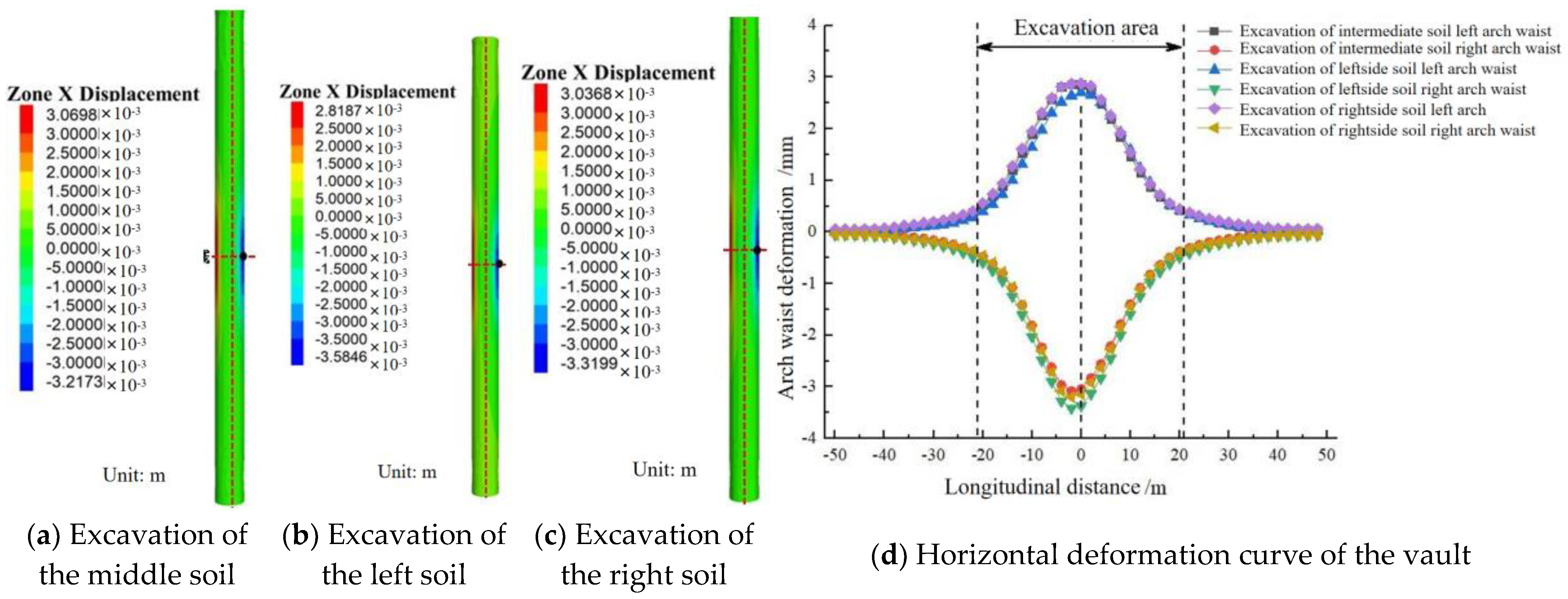
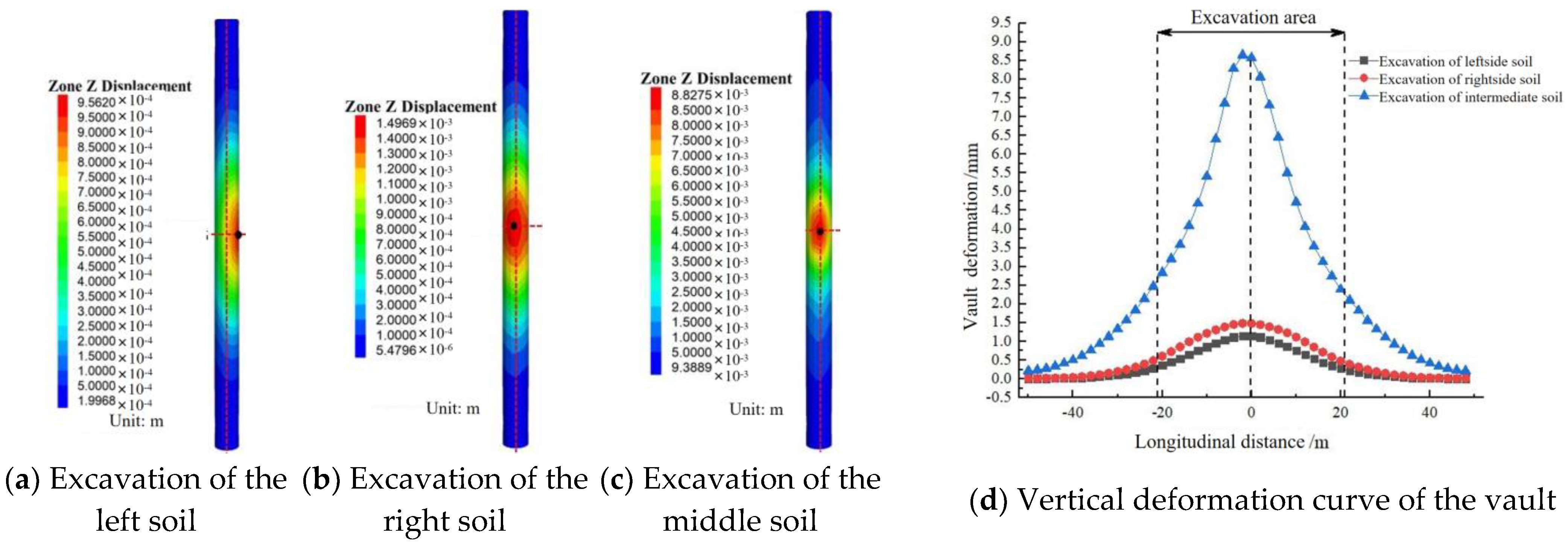
4.3.1. Excavate the Middle Soil and Reserve Core Soil on Both Sides
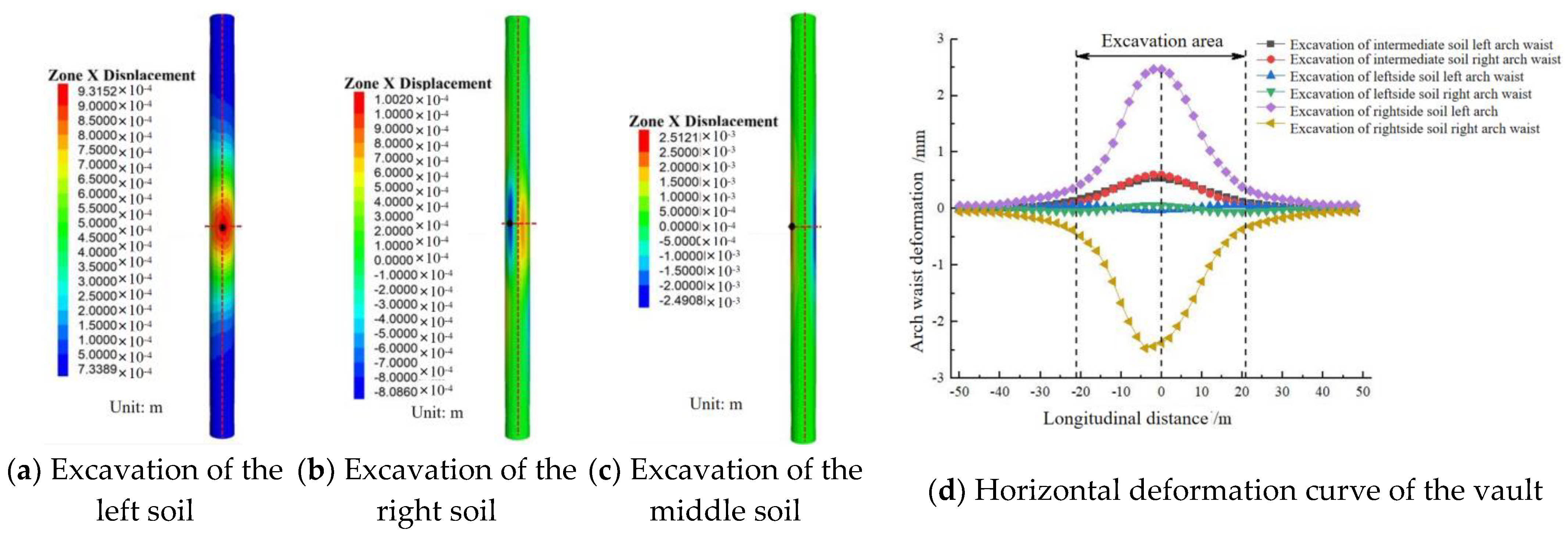
4.3.2. Excavating Soil on Both Sides and Reserving the Middle Core Soil
4.4. Comparative Analysis of Calculation Results
4.4.1. Excavate the Middle Soil and Reserve Core Soil on Both Sides
4.4.2. Excavate on Both Sides Soil and Reserve the Middle Core Soil
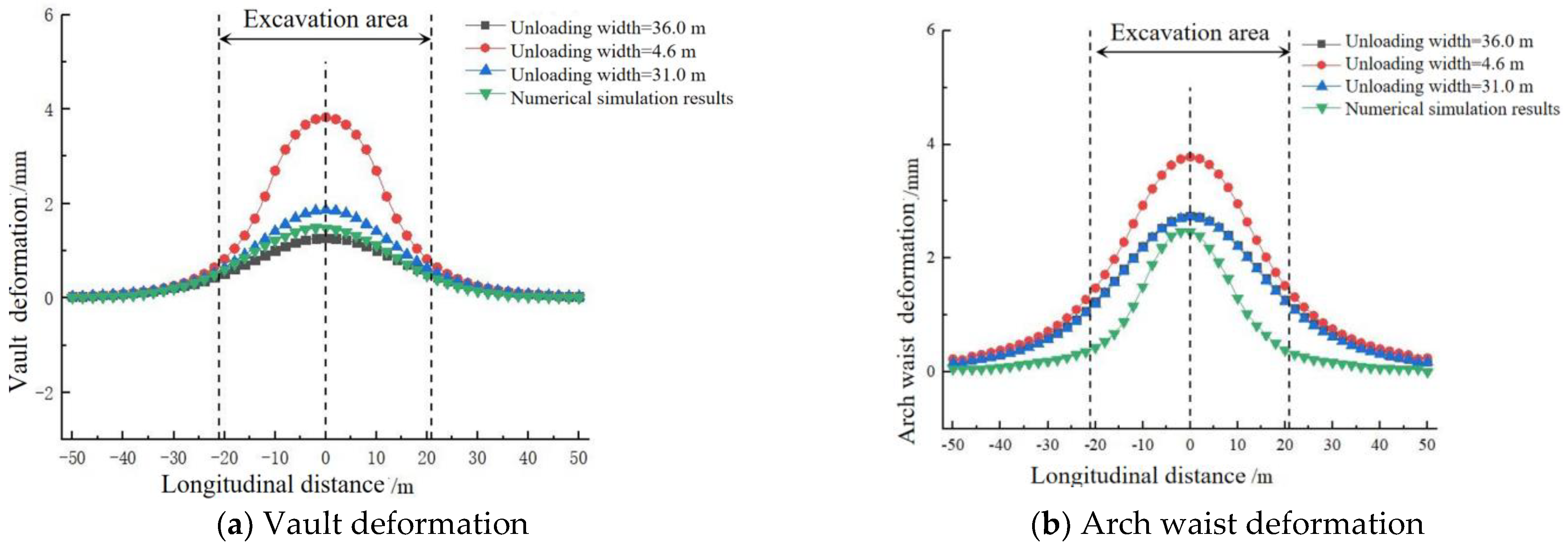
5. Parametric Analysis
5.1. Different Footings of the Slope
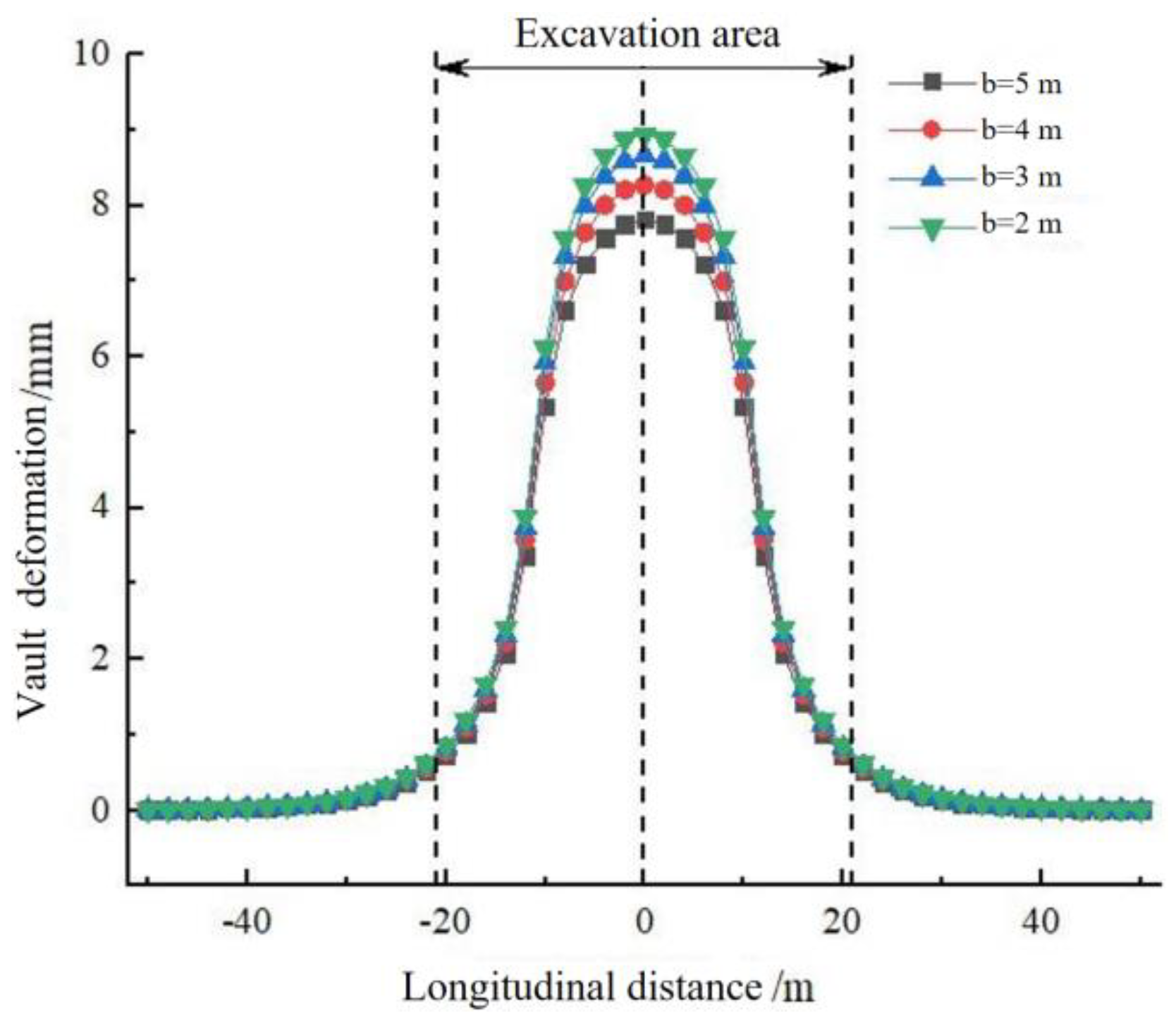
5.2. Different Slope Widths
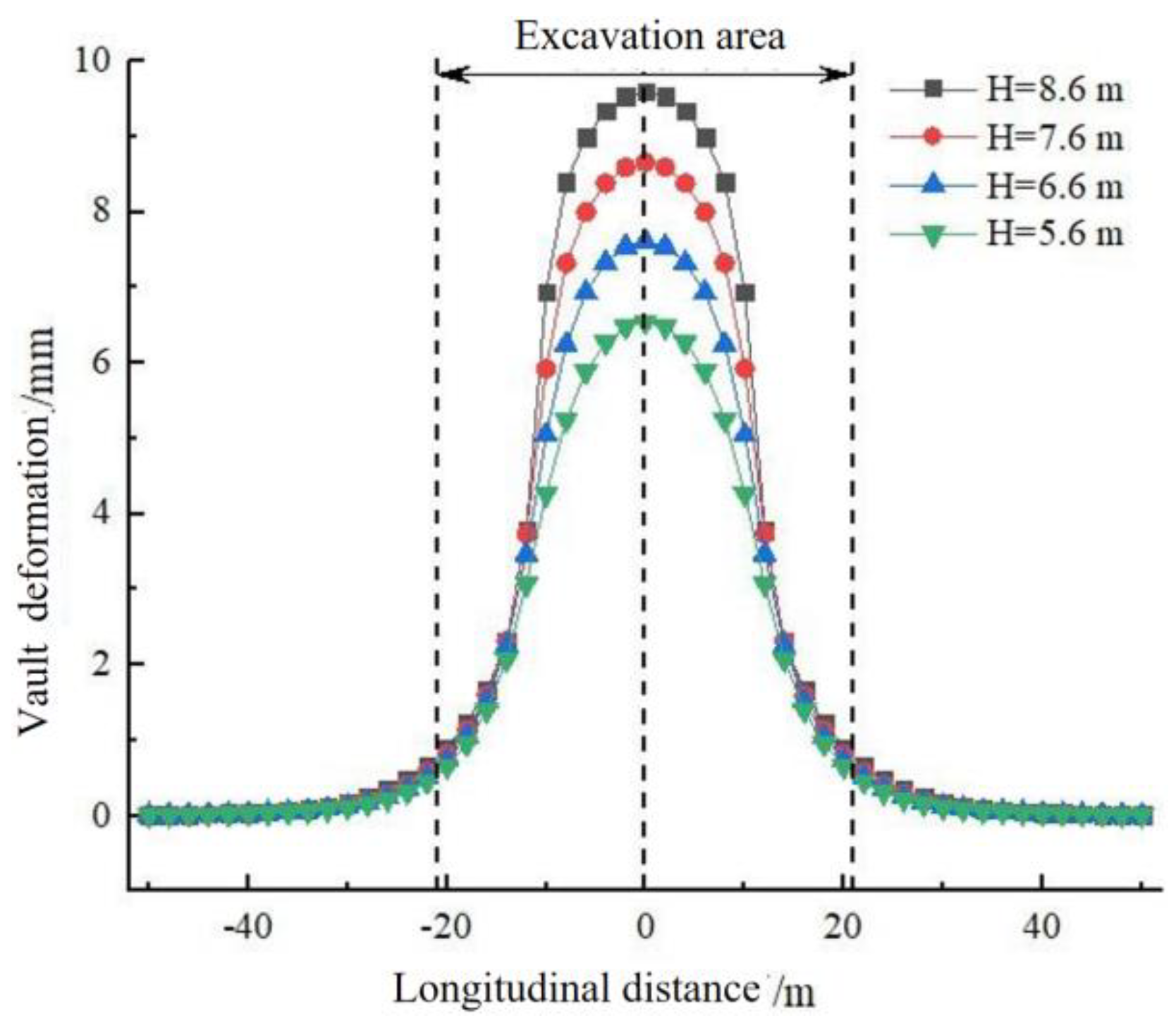
5.3. Excavation Depths
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Festa, D.; Broere, W.; Bosch, J.W. Tunnel-boring in soft soil: A study on the driving forces applied to a slurry-shield TBM. Civ. Eng. Geosci. 2012. Available online: https://www.researchgate.net/profile/Wout-Broere/publication/328981655_Tunnel-boring_in_soft_soil_a_study_on_the_driving_forces_applied_to_a_slurry-shield_TBM/links/5bee9b28a6fdcc3a8dda1a40/Tunnel-boring-in-soft-soil-a-study-on-the-driving-forces-applied-to-a-slurry-shield-TBM.pdf (accessed on 1 December 2022).
- Cheng, H.; Chen, J.; Chen, G. Analysis of ground surface settlement induced by a large EPB shield tunnelling: A case study in Beijing, China. Environ. Earth Sci. 2019, 78, 605. [Google Scholar] [CrossRef]
- Di, H.; Huang, S.; Fu, L.; Wang, B. A variational method for calculating the longitudinal deformation of a shield tunnel in soft soil caused by grouting under tunnel. Eng. Comput. 2021, 38, 2733–2754. [Google Scholar] [CrossRef]
- Liang, R.; Wu, W.; Yu, F.; Jiang, G.; Liu, J. Simplified method for evaluating shield tunnel deformation due to adjacent excavation. Tunn. Undergr. Space Technol. 2018, 71, 94–105. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Lei, M.; Cao, C.; Lin, Y. Improved analytical method for evaluating the responses of a shield tunnel to adjacent excavations and its application. Tunn. Undergr. Space Technol. 2020, 98, 103339. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, M.; Zhang, C.; Jiang, K.; Lu, M. Time-domain analyses for pile deformation induced by adjacent excavation considering influences of viscoelastic mechanism. Tunn. Undergr. Space Technol. 2019, 85, 392–405. [Google Scholar] [CrossRef]
- Shi, C.; Cao, C.; Lei, M.; Peng, L.; Ai, H. Effects of lateral unloading on the mechanical and deformation performance of shield tunnel segment joints. Tunn. Undergr. Space Technol. 2016, 51, 175–188. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; Liu, J. Numerical investigation of underlying tunnel heave during a new tunnel construction. Tunn. Undergr. Space Technol. 2011, 26, 276–283. [Google Scholar] [CrossRef]
- Li, M.-G.; Zhang, Z.-J.; Chen, J.-J.; Wang, J.-H.; Xu, A.-J. Zoned and staged construction of an underground complex in Shanghai soft clay. Tunn. Undergr. Space Technol. 2017, 67, 187–200. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, H.; Li, Z.; Dai, G.; Yin, Z.; Cao, S.; Zhou, J. Numerical Study on the Deformation of Tunnels by Excavation of Foundation Pit Adjacent to the Subway. Appl. Sci. 2022, 12, 4752. [Google Scholar] [CrossRef]
- Sun, H.; Wang, L.; Chen, S.; Deng, H.; Zhang, J. A precise prediction of tunnel deformation caused by circular foundation pit excavation. Appl. Sci. 2019, 9, 2275. [Google Scholar] [CrossRef]
- Nejjar, K.; Dias, D.; Cuira, F.; Chapron, G.; Lebissonnais, H. Experimental study of the performance of a 32 m deep excavation in the suburbs of Paris. Géotechnique 2021, 1–11. [Google Scholar] [CrossRef]
- Mitew-Czajewska, M. A study of displacements of structures in the vicinity of deep excavation. Arch. Civ. Mech. Eng. 2019, 19, 547–556. [Google Scholar] [CrossRef]
- Soomro, M.A.; Liu, K.; Mangnejo, D.A.; Mangi, N. Effects of twin excavations with different construction sequence on a brick masonry wall: 3D finite element approach. Structures 2022, 41, 866–886. [Google Scholar] [CrossRef]
- Deng, H.; Fu, H.; Shi, Y.; Huang, Z.; Huang, Q. Analysis of Asymmetrical Deformation of Surface and Oblique Pipeline Caused by Shield Tunneling along Curved Section. Symmetry 2021, 13, 2396. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Wu, C.; Li, H.; Goh, A.; Liu, H. Prediction of lining response for twin tunnels constructed in anisotropic clay using machine learning techniques. Undergr. Space 2020, 7, 122–133. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Liang, R.; Kang, C.; Xiang, L.; Li, Z.; Lin, C.; Gao, K.; Guo, Y. Responses of in-service shield tunnel to overcrossing tunnelling in soft ground. Environ. Earth Sci. 2021, 80, 183. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, M.; Zhao, Q. A simplified analysis for deformation behavior of buried pipelines considering disturbance effects of underground excavation in soft clays. Arab. J. Geosci. 2015, 8, 7771–7785. [Google Scholar] [CrossRef]
- Mindlin, R.D. Force at a Point in the Interior of a Semi-Infinite Solid. Physics 1936, 7, 195–202. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, M. Mechanical effects of tunneling on adjacent pipelines based on Galerkin solution and layered transfer matrix solution. Soils Found. 2013, 53, 557–568. [Google Scholar] [CrossRef]
- Lin, C.; Huang, M.; Nadim, F.; Liu, Z. Embankment responses to shield tunnelling considering soil-structure interaction: Case studies in Hangzhou soft ground. Tunn. Undergr. Space Technol. 2019, 96, 103230. [Google Scholar] [CrossRef]
- Zhou, R.; Fang, W.; Wu, J. A risk assessment model of a sewer pipeline in an underground utility tunnel based on a Bayesian network. Tunn. Undergr. Space Technol. 2020, 103, 103473. [Google Scholar] [CrossRef]
- Ma, S.; Li, M.; Jin, J.; Bai, K. The influence of shallow buried double-line parallel rectangular pipe jacking construction on ground settlement deformation. Alex. Eng. J. 2021, 60, 1911–1916. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, R.; Zhang, H. Mechanical response analysis of the buried pipeline due to adjacent foundation pit excavation. Tunn. Undergr. Space Technol. 2018, 78, 135–145. [Google Scholar] [CrossRef]
- Tanahashi, H. Formulas for an Infinitely Long Bernoulli-Euler Beam on the Pasternak Model. Soils Found. 2004, 44, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.-M.; Huang, Z.-K.; Li, Z.-L.; Zong, X.; Zhang, D.-M. Analytical solution for the response of an existing tunnel to a new tunnel excavation underneath. Comput. Geotech. 2019, 108, 197–211. [Google Scholar] [CrossRef]
- Vorster, T.E.; Klar, A.; Soga, K.; Mair, R.J. Estimating the Effects of Tunneling on Existing Pipelines. J. Geotech. Geoenviron. Eng. 2005, 131, 1399–1410. [Google Scholar] [CrossRef]
- Chheng, C.; Likitlersuang, S. Underground excavation behaviour in Bangkok using three-dimensional finite element method. Comput. Geotech. 2018, 95, 68–81. [Google Scholar] [CrossRef]
- Goh, A.; Zhang, F.; Zhang, W.; Zhang, Y.; Liu, H. A simple estimation model for 3D braced excavation wall deflection. Comput. Geotech. 2017, 83, 106–113. [Google Scholar] [CrossRef]
- Deng, H.-S.; Fu, H.-L.; Shi, Y.; Zhao, Y.-Y.; Hou, W.-Z. Countermeasures against large deformation of deep-buried soft rock tunnels in areas with high geostress: A case study. Tunn. Undergr. Space Technol. 2022, 119, 104238. [Google Scholar] [CrossRef]




| Soil Layer | Natural Heavy | Cohesion | Friction Angle | Shear Modulus | Poisson’s Ratio | Thickness |
|---|---|---|---|---|---|---|
| γ (KN·m−3) | c (kPa) | φ (°) | G (MPa) | μ | m | |
| Miscellaneous fill | 18.5 | 10 | 10 | 6.48 | 0.28 | 2.0 |
| Powdery clay | 19.5 | 18 | 14 | 50.00 | 0.25 | 2.1 |
| Powdery clay | 20.0 | 24 | 16 | 56.25 | 0.25 | 3.7 |
| Powdery clay | 19.5 | 20 | 15 | 62.00 | 0.24 | 3.2 |
| Mesothermal slate | 26.0 | 400 | 40 | 597.80 | 0.22 | - |
| H | L | B | α | γ | φ | l |
| 7.6 m | 41.3 m | 22.0 m | 0.9 | 18.5 kN/m3 | 15° | 1.0 |
| EI | D | Gp | μ | Es | a | η |
| 28.7 GPa | 6.0 m | 3.92 MPa | 0.25 | 11.3 MPa | 0.2 | 0.319 |
| Footings of Slope θ | 60° | 57° | 54° | 51° |
| Unloading Load (kPa) | 10,868 | 10,760 | 10,642 | 10,513 |
| Distribution Range (m) | 31.6 | 31.0 | 30.4 | 29.8 |
| Slope Width b | 5 m | 4 m | 3 m | 2 m |
| Unloading Load (kPa) | 9918 | 10,351 | 10,760 | 11,148 |
| Range of Effects (m) | 29.5 | 31.5 | 33.5 | 35.5 |
| Excavation Depth H | 8.6 m | 7.6 m | 6.6 m | 5.6 m |
| Unloading Load (kPa) | 12,028 | 10,760 | 9456 | 8116 |
| Range of Effects (m) | 33.2 | 33.5 | 33.8 | 34.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.-L.; Deng, H.-S.; Zhao, Y.-B.; Chang, X.-B.; Yi, H.-D. Study on the Disturbance of Existing Subway Tunnels by Foundation Sloping Excavation. Appl. Sci. 2023, 13, 948. https://doi.org/10.3390/app13020948
Fu H-L, Deng H-S, Zhao Y-B, Chang X-B, Yi H-D. Study on the Disturbance of Existing Subway Tunnels by Foundation Sloping Excavation. Applied Sciences. 2023; 13(2):948. https://doi.org/10.3390/app13020948
Chicago/Turabian StyleFu, He-Lin, Huang-Shi Deng, Yi-Bo Zhao, Xiao-Bing Chang, and Hai-Dong Yi. 2023. "Study on the Disturbance of Existing Subway Tunnels by Foundation Sloping Excavation" Applied Sciences 13, no. 2: 948. https://doi.org/10.3390/app13020948
APA StyleFu, H.-L., Deng, H.-S., Zhao, Y.-B., Chang, X.-B., & Yi, H.-D. (2023). Study on the Disturbance of Existing Subway Tunnels by Foundation Sloping Excavation. Applied Sciences, 13(2), 948. https://doi.org/10.3390/app13020948






