1. Introduction
Specific for its unpredictability and covering vast areas, a strong earthquake inflicts heavy damage, which can be a tremendous shock for the engaged society. Various disciplines include methods of earthquake risk reduction and hazard assessment [
1], which consider social and economic consequences of earthquakes in studying the earthquake vulnerability of the built environment [
2,
3].
Material damage can even be assessed by planning, designing, and constructing structures according to standards of earthquake resilience [
1,
4,
5,
6]. There are various levels of earthquake resistance, which determine the cost of structures and construction. The design and construction of earthquake-resistant structures are based on regulations and standards derived from earthquake studies and the effects they inflicted on existing structures.
Civil engineers strive to improve regulations of seismic resistance of structures. Experts from other branches derive similar rules and recommendations. These efforts are based on a better comprehension of seismic processes, which are usually described through seismograms and their various characteristics, often called attributes.
In this paper, it is propose a new frame for defining attributes, with the hope to define new features, which could make the picture of earthquakes more complete and more suitable, in addition to existing ones. A better understanding and description of earthquakes surely means better and more refined regulations and standards.
1.1. Earthquake “Speaks” through Seismogam(s)
Seismicity is the main source of our knowledge about the Earth’s structure. For a more elaborate general view, see [
7] “Vol. 4, paper 4.01, p. 1924”. A seismogram is almost the only source of information about an earthquake, apart from tangible effects on society and the (built) environment. It is a record of seismic effects at the site, which are the result of many complex processes in the seismic source, during wave propagation through the Earth, the influence of seismic sensors, recorders, and processing techniques applied on the seismogram [
8] “Ch. 1, Figure 1.2, p. 6; Ch. 11”.
On the other hand, the above title is just half of the story: valuable data on earthquake stem also from the cross between the seismogram itself and seismic effects on the built environment.
Various experts are interested in earthquakes and their effects, including geophysicists, seismologists and observatory personnel, civil engineers, disaster managers and risk planners, urban planners, to whole governments, not to mention related researchers, students, training personnel [
8] “Ch. 1, p. 29”, [
1,
9].
For the sake of this analysis, all complex processes standing behind a seismogram will be temporarily put aside, and attention will be focused on its waveform only. The reasons for such a formal approach will be elaborated in
Section 2.
The seismogram is by all means fluctuational in nature, representing recorded fluctuation of acceleration, velocity, or displacement. Its waveform looks like a wave train randomly composed of wavelets (from the source) mutually shifted in time [
7] “Vol. 1, paper 1.03.1.3, p. 73, p. 131”. The term ‘wavelets’ is used here just as a language item, not as a mathematical tool. If the plural of “fluctuation” is used, then, from the more formal point of view, one can consider such waveform as a sequence of impulses of random amplitude, duration, and shape, where the shape proves to be very important. This issue can be further formalized, and a seismogram be considered as the sequence of elementary fluctuations (EF) [
10].
1.2. Purpose and Categories of Attributes
A seismogram is usually a very complex transient. It contains, or hides, all the available information about an earthquake but taken at the (recording) site. As such, it is cumbersome and intricate for direct use. In addition, not all experts are interested in the information the seismogram waveform brings with them, but they seek some aspects that are the most important for their needs. So, it asks for processing, to a certain extent, to find out needed characteristics, often called attributes or features, which carry particular significance for users and reveal interesting content from raw recordings. Here it is accepted the widest definition of seismic attribute, as any information of interest that can be derived from raw seismic data [
11].
There are many references involving the notion of ‘seismic attribute’ [
12,
13,
14,
15,
16], often giving the definition of the issue. What can be noticed is a slight evolution in the meaning of the seismic attribute [
12,
13]. In close relation to the definition stands the issue of attribute classification [
12,
16]. Either with respect to definition or classification, this research relies on the broader meaning of both notions.
Only a few characteristics can be extracted directly from a seismogram, but it does not mean simply picking up the item(s) because it is not the result of a passive perception of details, but rather depends on the researcher’s recognition ability, backed by his/her knowledge and experience about waveform background, and many other conditions [
8] “Ch. 1, Section 1.3, Ch. 11”.
It may seem that the reading is burdened by subjective factors, but provided a skilled analyst instead of, e.g., a novice, this makes the description objective, quantified, and comparable to other cases because the examiner performs according to the prescribed procedure. In [
8] “Ch. 1, Section 1.3”, it is explicitly stated that to “provide properly processed and interpreted seismograms under these diverse conditions, it is necessary to establish protocols for all aspects of observatory operation that may affect the seismological data itself”. There are other interesting proposals regarding procedures of seismogram interpretation [
17].
Even for the most skillful researcher, much of the content in seismograms remains hidden. To extract such information, various (post)processing techniques are used, either performed by humans (graphically numerical methods) or by machines (usually computer programs), up to artificial intelligence [
18]. In both cases, techniques stem from respective algorithms. In the first case, the human is functioning as a ‘machine’ (following the strict protocol).
There are (too?) many attributes [
19], and each one is dedicated to something particular in seismogram or any other random signal. Such a heap of attributes needs categorization. The grade “too” and question mark definitely prove that the seismogram is a very complex matter.
They can be roughly classified into parametric and functional attributes. Parametric ones can be further divided into single-parametric and group-parametric. Single-parametric can be local and general, with the latter determined from the whole seismogram. Examples of local single-parametric are the peak-to-peak max span (
B), and the period (
T), given in, e.g., [
8] “Ch. 3, p. 47, Figure 3.19, Figure 3.28” while general single-parametric are, e.g., 5–95% duration [
20,
21,
22], seismogram energy [
8] “Ch. 3” etc.
The root-mean-square acceleration
is an important, and also interesting single-parametric attribute, which, implicitly, contains other attributes (parameters):
T1 and
T2, where the size and location of the interval
T2 −
T1 strongly influence the value of
arms for a transient signal like seismogram, so
T1 and
T2 commonly chosen to exclude insignificant shaking. There are several proposals, e.g., for
T1 as the time of S-wave arrival, and for
T2:
T2 =
T1 + 10 s, or
T2 =
T1 +
Td (
Td is the duration of faulting, or
T2 = 1/
f0) [
1] “p. 76”.
This is not the final word about duration (see [
8] “Ch. 3, p. 135, Figure 3.62”), showing the complexity of the issue. The attribute
arms only shows how the matters in seismology are far from simple.
As for functional attributes, a common one is the envelope, in simple and more complex forms. For others, see [
8] “Ch. 3”. Simple or peak envelope is related to seismogram waveform in an apparent way.
The known Husid diagram is a functional attribute:
as the integral as a function of its upper limit, normalized by the total integral. The
TD is the total duration of the earthquake, and
a(
t) is the instantaneous earthquake ground acceleration [
23,
24], where the
AD represents the total integral of squared acceleration.
In direct relationship with
H(
t) and
arms is the Arias intensity
where
TD is, again, the total duration of the record, and
a(
t) is the acceleration time series [
23,
24], so that one can write:
No wonder that all these attributes, parametric or functional, stem from acceleration seismograms. The Hurst exponent is a useful statistical method for inferring the properties of a random time series without making assumptions about stationarity. Within voluminous literature about the Hurst exponent, a quick and insight can be found in [
25]. It is also applied to seismograms [
26].
Another important functional attribute is the spectrum of seismograms, as the result of the Fourier transform. There are also parametric attributes of the spectrum (see [
27]). It is interesting to note that the spectrum, although functional, i.e., continuous, can also be defined as a group-parametric attribute, which will consider later in detail.
The envelope, as a functional attribute in various forms, is widely used, and it is at the focus in this paper.
1.3. Envelope of Seismogram—Issue of Complexity
If one draws the peak envelope over positive elementary fluctuations (EF) of a seismogram, one gets better insight into peak amplitude variation, which would not be that much visible through mere spikes (see, [
14,
28]). It has something to do with gestalt principles of perception—if spikes along a seismogram are not so dense as necessary, one’s vision cannot gather them into the shape to perceive a variation. Just the fact that the envelope is drawn as a line over the peaks, making visual continuation, helps in the perceptive grouping of impulses [
29].
The envelope is a widely used attribute of seismograms or other signals. Besides the plain (peak) envelope, there is also the envelope defined as a mixture of a signal itself and its Hilbert transform [
11]
where various labels of the operator’s action are quoted and direct and smoothed envelopes as well.
Apart from the information about P- and S-phase, seismologists often focus on the characteristics of seismogram envelopes (rms envelope in [
30]). Extensive use of envelopes can be found in many papers [
29,
31]. Another interesting kind of envelope is the signal-to-noise ratio:
which is calculated for short- and long-term averages (
STA,
LTA) to detect phases as [
32]
Seismograms are recorded for various physical quantities (acceleration, velocity displacement), orientations (e.g., Hor-1, Hor-2, and Vert, in PEER database nomenclature, or equivalent ones), and filtered (low-, band, or high-frequency) [
33].
It is obvious that the envelope, as an attribute of seismogram, gains in importance with waveform complexity or fluctuational density. Different recordings (acceleration, velocity, or displacement) of the same seismic event at the same site show different waveform densities [
33], and the same record is different with different filtering ([
7] “article 1.01, p. 22, Figure 13”).
The seismogram gains in complexity with propagation distance, which is documented in many references [
29], but the distance is not the only cause. Just to mention processes during fault rupture, the size, and geometry of the fault, emitted (delivered) energy, etc.
Seismic processes, in the whole range from the fault to the site, are ‘buried’, so they are difficult for open study. In
Section 2, a brief analysis of the specific open ‘fault’ mechanism of the Chelyabinsk event is given, and the following consequences, are as an illustration of said complexity.
Rise of seismogram complexity with the distance has its coin reverse. Comparison of accelerograms for a range of event sizes, chosen to have a hypocentral distance of approximately 25 km, shows an increase of complexity with magnitude ([
7] “article 4.18, Figure 4, p. 2437”).
In one word, the envelope seeks a critical “mass” of a waveform to justify its applicability. Otherwise, if a seismogram waveform is heavily and randomly indented (contains only a few fluctuations), its envelope is of little use (e.g., displacement record).
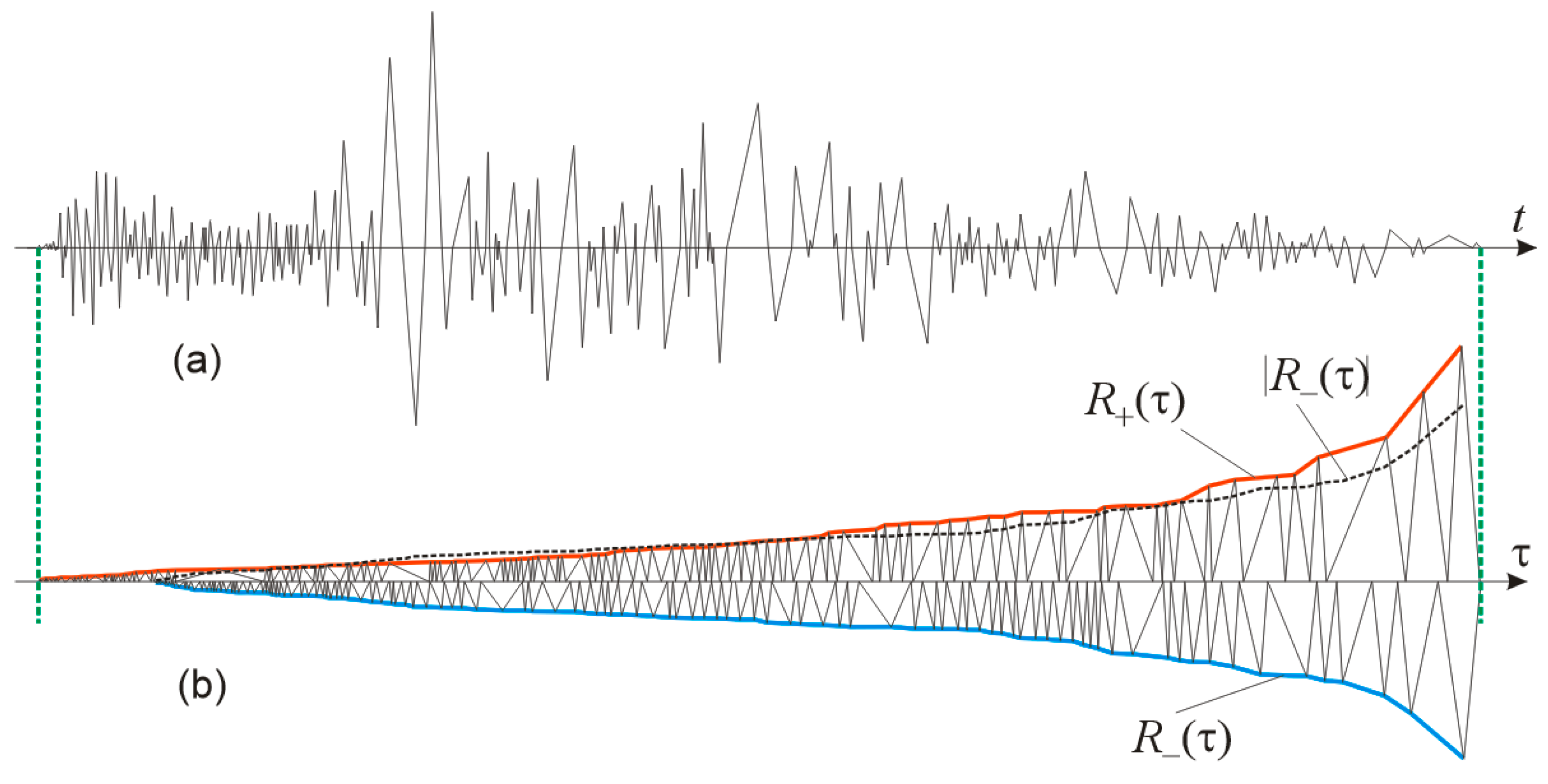
With all these various types of envelopes, it seems there is no room left for a new one. Nevertheless, in this article it is proposed a new envelope, better to say a new type of envelope, which is neither the result of some complicated mathematical transformation, such as, Fourier or Hilbert, nor it is that simple to stem from the raw waveform. The proposed new envelope is mainly based on the rearrangement (recomposition) of single fluctuations (SFs) from a raw seismogram into a new sequence, ordered by increasing or decreasing peak amplitudes. Because of that, the new envelope is named as the R-envelope (from “Rearranged”, “Recomposed”).
1.4. Article Aims and Findings
A seismogram is the result of many complex physical processes. It is very difficult to relate every detail in a seismogram with the processes standing behind. Even if it might look like an obvious fact, it is important to remember that the seismogram is the picture of seismic processes at the site. Therefore, the formalization of seismograms is inevitable—one considers what it has at hand. How, then to peer through the fluctuations of the seismogram and try to see something more behind the wiggles?
The lowest structural level of a seismogram is at the waveform elements, impulses, or wavelets (considered as small waves, not as mathematical tools). In this paper, such chunks of seismogram are defined as elementary or single fluctuations (EF and SF). The next structural level is the short train of SFs/EFs. Here, the authors perceive the next stage of research. The SFs are simpler but easier for manipulation, while the EFs are more complex but also more natural as elementary building blocks of the seismogram, as the simplest shapes still carry alternating change, which actually causes shaking (quaking) in the ‘push-pull’ pattern.
Getting to EFs/SFs means prior parsing of the seismogram. Segmentation also provides rearrangement of EFs/SFs to create new waveform structures, which can reveal new information previously invisible. As the simplest regrouping, the overlapping of EFs gave a ‘wood’, a structure which prevents ‘not see the wood for the trees’. To simplify the mess, the EF is approximated by triangles or even by structural axis, making the ‘wood’ more transparent.
Sorting the durations of SFs by the length, for both positive and negative ones, led to very interesting results, which peered not only into the seismogram waveform but also into its spectrum.
More organized, more systematic rearrangement, the ordering of SFs or of EFs by peak amplitudes, yielded the so-called R-envelope, either in natural (R) or in regular (quantized, RQ) forms. It turned out that the R-envelope represents a kind of invariant in the population of seismograms. Moreover, there is a direct correlation between the R-envelope and ordered durations of SFs.
The difference between R-envelopes, drawn over positive SFs and negative SFs, is expected to produce a rule about seismogram symmetry but enabled, for the present, only individual interpretations.
Where this approach of seismogram segmentation and rearrangement showed its potential is a new definition of seismogram duration in objective way, which excludes subjective factors but outcomes from the waveform.
2. Materials and Methods
2.1. Elementary Fluctuation—Formal and Real Meaning
The term “fluctuation” (to fluctuate) is irregular rising and falling (change) of a physical quantity in an alternating pattern, although random, which is consisted of “ups” and “downs”, separated by crossings of a certain axis (mostly the t-axis), or some constant value, or even some monotonic trend curve (e.g., change of stock price or currency exchange rate). So, one can see some regularity in such irregular behavior: alternating positive-negative pattern, in brief, random cyclic behavior.
In this research, the term “elementary fluctuation” (EF) is defined, and the seismogram is considered a sequence of EFs. Further, the EF is composed of two subsequent alternate random impulses, which are called single fluctuations (SF), as in [
10]. So, the EF, or the SF, is the basic structural element of a seismogram.
When the fault slips, the two sides of the fault move in opposite directions, which creates a different polarity of the first motion P in different directions (see [
34] “p. 217, Figure 7.3”), so one should distinguish two conventions in defining the EF composition: (1) the leading impulse is positive. Hence the other is negative, and vice versa (
Figure 1). To put it more clearly [
10],
The EFs are separated by zero-crossings (
Figure 1), the points where the random waveform crosses the actual axis, “the
t-axis, or some constant, or even some monotonic trend curve”.
Within repetitive fluctuational patterns one can distinguish regular and irregular fluctuations. Regular EFs can mean quasi-periodicity, while irregular EFs mean just repeating a general pattern [
35].
The generation of a seismogram is caused by processes during fault rupture in the hypocenter, which picture is conveyed by seismic waves to the seismograph location. In-between, seismic waves propagate through a (spherically) multilayered, inhomogeneous, anisotropic medium, which yields intricate combination of many reverberations of initial waves [
8] “Ch. 2”, [
36]. Even with the seismic kinematics (ray formalism), the picture at the site remains pretty entangled. Standard Nomenclature of Seismic Phases speaks for itself, and the distribution of seismic sources as well [
37].
Global Earth models are just statistical pictures of real mantle structure for study of teleseismic events. Top-down mantle convection brings much more complicated models and, hence, propagation pictures [
7,
38] “article 1.16, Figure 12, p. 555/576”.
At closer distances, propagation conditions can be considered as even more complex, caused by the usually very irregular structure of lithosphere, since the main propagation in these cases takes place mainly in the crust [
8] “Ch. 2; article 1.08.7, Figures 5–12, pp. 260–281”. It is not only a matter of internal but also of external irregularities since there are effects of the Earth's surface topography [
7] “article 4.18.6.13, Figure 15, p. 2453”.
The events observed at closer distances also send seismic waves toward all seismographs around the world, where usually are recorded only the basic transients. For teleseismic observations, subsequent reverberations are also recorded. This research is restricted only to close-range earthquakes.
The lithosphere is a layered structure, often corrugated (due to tectonic movements), where basins (bedrocks) are infilled with stratified deposits (soil). Bedrock-soil boundaries and soil surfaces affect the propagation of seismic waves in several ways, causing reflections, refractions, and scatterings. The geometry of the infilled basin makes a real resonator, which can create resonances of incident seismic waves and, thus, change the fluctuation pattern in the seismogram. What is interesting to note and to add to such a model of resonator is the urban (built environment) layer, situated on the soil surface, consisting mainly of concrete structures, which changes the wave impedance of the soil surface and affects the seismic picture around the site, even with possibility to amplify seismic effects [
1] “p. 29, Figure 3.1; p. 54, Figure 4.4; p. 145, Figure 5.7”, [
8] “Ch. 3, p. 224, Figure 3.113”. To get an image of possible effects which can stand in the background of seismic phenomena, see [
39,
40] “Figure 4”.
The term ‘hypocenter’ suggests a point-like source of seismic waves. It is actually a relative “point”, which size depends on distance. Fault interfacing surfaces create a large system ranging from a (few) kilometers (s) to tens or hundreds of kilometers in length. If recorded closely, then each place on the rupturing fault acts as a point source of (its own) seismic waves, so all of them create a very complex picture at the seismic sensor. What’s more, an earthquake often starts at one place of the fault, and then the perturbation also propagates along the fault, triggering other strained places to rupture, highly influencing recording conditions and the waveform of seismogram [
7] “article 4.07, Figure 5, p. 2132”.
Now, we may have an idea of what all (might) stand behind “wiggles” in seismogram, remembering the words of Professor Wiechert, “understand each wiggle” [
8] “Ch. 1, p. 6”.
It is very difficult to peer through the soil into the seismic processes. In many cases, it turns into a kind of guesswork.
A suitable case to study the seismic effects more transparently, not buried in the Earth depths, and to illustrate the effect of increasing seismogram’s complexity with the distance is Chelyabinsk/Ural meteorite (small asteroid) impact of 15 February 2013, 17 m in diameter, mass approximately 11,000 tons, which struck Earth’s atmosphere at 19.16 km/s speed and exploded in a meteor air burst at about 30 km above Earth’s surface, resulting in explosion equivalent to over 470 kilotons of TNT. The air-friction heat evaporated debris, so just 0.05% of the original rock reached the ground as meteorites. This means that the main “seismic” mechanism was the air shockwave, of a pretty simple waveform covering vast soil area and triggering detections from monitoring stations as far away as Antarctica. Seismic records, 26 in total, compiled at the GFZ, taken within the span of 227 km to 2197 km, represent a remarkable example of seismogram waveform change with distance. Instead of complex fault rupture processes superimposed to create an intricate waveform, here is a simple “fault” mechanism, providing something similar to delta short-impulse excitation. From recording distances, one can infer that the propagation of resulting seismic waves took place mostly through the mantle [
41,
42,
43,
44,
45,
46,
47,
48,
49,
50].
Details about the shockwave ‘fault’ mechanism can be found in [
48]. Apart from the GFZ graphical account of the event [
43,
45], there are recordings, mostly taken as teleseismic, with arrays in China and the USA [
49,
50]. This ‘fault’ mechanism is, by all means, very specific. It is directional, even to say one-dimensional, without direct material impact, where the whole energy is transferred by the air. It is a kind of ‘soft’ rupture. Quite the skew angle of arrival, and almost graze angle, in combination with shockwave conical pressure front, indicate the area of the ‘fault’, and time profile of perturbation [
43], which is easily seen comparing scales on the
t-axis of this event and any other usual seismogram, e.g., RSN1616. A completely Earth-originating case can be seen in [
51] “Figure 6”.
But whatever the processes, in the source or during propagation, they keep the rudimentary and general shape of a random alternation. One should stress this apparent fact just to point out fundamental phenomena and principles that generate basically the same shape. After all processes in the said seismic ‘information chain’ took their part, what a structure or, generally, the built environment experiences is written in a seismogram, i.e., in the sequence of EFs. To say it otherwise, a structure is not ‘interested’ in the origin of wiggles that shake it, but it is ‘interested’ in how to survive and withstand the incoming EFs train.
2.2. Envelope of Rearranged Individual Fluctuations
A plain (peak) envelope, drawn over a seismogram’s peak amplitudes of fluctuations, clearly shows general variation along the waveform (
Figure 2).
The segmentation of the seismogram into single fluctuations (SEs) results in sequences of random shape impulses, both positive and negative ones. Recomposition of these sets of SEs, separately for positive and negative SEs, by increasing or decreasing peak amplitudes, will produce another rearranged waveform. Thus, one gets two ordered “halves” of the original seismogram, one composed of positive SFs and the other of negative SFs (see
Figure 3). The rearrangement processes are schematically represented in [
10] “Figures 3, 5 and 11”.
Now, it is routine to draw the R-envelope along arranged SFs, both over positive and over negative SF sequences [
28,
52] “Figure 3”, which contains new information about seismogram. Also, the previous correlative content in the original seismogram is heavily disrupted by recomposition, but new information appeared, telling us something new about fluctuating content in the seismogram, which is much more easily perceived than from the raw one.
Therefore, the R-envelope can be designated as a new functional attribute of the actual seismogram, which also provides a basis for defining other new parametric attributes.
The (peak) envelope “hovers” over amplitude peaks along a waveform, making the shape of fluctuations irrelevant. This means it is sufficient to replace whatever complex form of the SF by only two numbers, one for peak amplitude and another for SF duration, which in geometrical terms means a triangle replacing (or approximating) the respective SF (see
Figure 3c).
The replacement of a SF by the approximating triangle is explained in more detail in
Figure 4. Similar idea is applied to the source time function
S(
t) for many earthquakes having body-wave magnitudes less than 6.5, which often can be adequately represented by a simple triangle-shaped pulse, where the triangle width is related to the corner frequency and fault length [
7] “article 1.05.6, Figure 20, pp. 190–182”.
In the case of approximation by triangles, one can use symmetric and asymmetric forms (
Figure 4) [
10]. There are also other approximating shapes, but no further elaboration of this issue will be given here. The triangle approximation of any shape of SF, whatever complex, evidently facilitates numerics about the R-envelope. This is equivalent to a sort of non-uniform sampling of seismograms, where samples are peak amplitudes of SFs.
To put it more formally, an elementary fluctuation EF, within a seismogram
s(
t), is decomposed into two single fluctuations, SF
+ and SF
−, and their waveforms
sfm(
t) are approximated by corresponding triangles
φm(
t), which are derived from generative (isosceles) triangular impulse
i(
t), scaled by respective parameters
p/
n (amplitude),
b (duration factor), and
tm (time shift):
This relation can be considered as a parametric transform of seismograms. The time-scaling factor of the triangle base is:
where
t0 is the duration of the referent (generative) triangle (see
Figure 4).
There is no essential difference in approximating the simple SFs or complex-shape SFs by symmetric (isosceles) or asymmetric triangles, particularly in so-called dense seismograms. Also, the plain envelope, anyway, cancels all the SF shape details beneath it, reducing the whole complex shape to one number, peak amplitude, as a peak of an approximating triangle. Would it be symmetric or asymmetric is a nuance. All said, it simplifies mathematical expressions and numerical calculations.
This does not mean the issue of approximating impulse form is not worth further research, from the aspect of e.g., pattern recognition and minimum-error description of original SF by regular shape.
2.3. Conversion of Seismogram into R-Envelope
Having a sequence of elements (e.g., numbers), which differ from each other only in size, it is possible to apply a mapping that arranges the elements from a random sequence into an ordered one, which seems to be an interesting mathematical aspect, elaborated in [
10].
The first step of the procedure is the decomposition of a raw seismogram
s(
t) into EFs and SFs, according to (9)
Approximating SFs by triangular impulses, as described earlier, we get (
Figure 3):
Graphical and numerical Approximations are equivalent. The graphical is more apparent to humans, while the numerical is more “apparent” to machines (computers). Graphical procedure is actually a combination of graphical and numerical one, very suitable in developing computer programs.
Scale factor
am (12) is closely related to the “pitch” [
53] of seismic signals. Variations of
am indicate a repeating rate of fluctuations.
The numerical variant of Equation (12) is a sequence of numbers:
representing time shifts (
tSk) and peak amplitudes (
ak) of respective triangles:
with durations and peak amplitudes of respective triangles.
The upper limit of index k is 2N, since there are N EFs and 2N SFs.
Combining the Equations (13) and (14) we get:
We then separate impulses with positive and negative amplitudes, making two subsets:
The central step of transformation is rearrangement of positive and negative triangles in respective ordered sets by increasing or decreasing peak amplitudes (
Figure 3):
where only amplitudes (superscript (
a) in
S) are considered.
Mathematical details describing only the rearrangement algorithm are omitted here for brevity.
To draw the peak R-envelopes,
R+(τ) and
R_(τ), over arranged triangles, positive and negative, as polygonal lines connecting triangles’ peaks, we need time locations of triangles’ peaks, i.e., middle points on t-axis of each triangle:
where the symmetric triangles are used. The coordinates of R-envelope are (
Figure 3):
2.4. Order—Key Feature of the R-Envelope and of the Spectrum
The seismogram, labeled with
s(
t), is a raw information about an earthquake, while its spectrum is a chief seismogram’s functional attribute, usually given in earthquake databases, e.g., [
33]:
Quite a decent survey of FT, elaborate but brief, can be found in [
54]. Being the Fourier transform of seismic signal
s(
t), the spectrum
S(
ω) is fully equivalent but not equal to
s(
t). Another notation,
s and
ŝ, emphasizes their equivalence:
Since
s(
t) and
ŝ(
ω) are equivalent but not equal, they do not contain the same quantity of information (
Q)
To get
s(
t) from
S(
ω), one must add sinusoids (through the
F−1) to the spectrum values:
which are previously removed time components in operation (21).
Whatever the “raw” domain, where one originally observes certain physical phenomena (time, length, angle, etc.), for all of them, the transformed domain will always be the frequency, or the ω-domain, because the Fourier operator itself contains sinusoids, either in complex (
eiωt) or in plain (cosω
t) forms (see Equation (24)), which the most characteristic parameter is the frequency [
55].
It might seem pretty obvious, but the ω-domain (ω-axis) is arranged by frequency. The same stands for the t-domain (the t-axis). In both cases, there is a continuous increase of numeric values along both axes. What makes the important difference between these two arrangements is the fact that a point on the ω-axis is not a simple numerical quantity, as on the t-axis—it is the basic parameter of a sinusoid component—its frequency. Figuratively, each point at the ω-axis hides a sinusoid waveform of assigned frequency since the term frequency corresponds only to sinusoid shape so that one can ascribe arrangement of sinusoid shapes along the ω-axis, with respective frequencies, and make a parallel to the arrangement in the R-envelope, which is, however, simpler and more obvious.
Moreover, there is a general tendency in the spectrum (amplitude or power, not in phase), nevertheless, its complexity, to steadily decrease with frequency, see, e.g., [
54], so that one can treat the ω-axis as the spectrum’s horizontal asymptote. In similar way, the R-envelope not only steadily, but monotonically approaches the
t-axis. This issue of R-envelope depends on several, mostly practical factors, and will be considered in
Section 4.
Although the R-envelope proposed in this paper, seems to be a continuous function (functional attribute), it is actually a group-parametric attribute (set of parameters) since it abstracts real shapes of SFs, and relies on peak amplitudes and durations of SFs, i.e., “equivalent triangles”. So, it is not possible to reconstruct the original waveform of a seismogram just from this envelope (see
Figure 3). A similar fact holds for the spectrum, which parameters need adding sinusoid waveforms to create the original signal.
Also the spectrum can be represented as a group-parametric attribute, as the line spectrum, given by the Fourier series. If a seismogram is formally periodized [
56], the result is a line (discrete) spectrum. Having on mind the general feature of any spectrum to decrease with frequency, it can be truncated to extract its significant part, and to yield a (discrete) finite set of parameters describing the seismogram. It is essentially numerical compression of seismograms, i.e., from huge recording files (thousands of numbers), having thousands of numerical values to a set of several ones, much more suitable to manipulate with. All that being said, it is obvious how organized information is more compact than in its raw form. Implications for the R-envelope are apparent.
Similarly, the R-envelope can also be considered as numerical compression of the seismogram, because it represents the impulses, i.e., SFs, by real numbers or even integers. Yet, it still contains remnants of raw structural information.
2.5. Attributes Based Directly on EFs/SFs
The original seismogram looks identical to its parsed version. Nevertheless, the latter one provides additional degree of freedom for manipulations with the waveform, just because it is segmented. There is no need at once to go up to rearrangement to get the R-envelope, but to apply more simple operations on EFs/SFs to attain some attributes.
One idea is simply to shift the EFs along the
t-axis and overlap them to coincide their inflection points (
Figure 5a,b).
The same picture could be attained with the SFs, but with the SFs, one should use all of them to create a proper picture, while with the EFs, it is possible to get the contours of the final picture with a sample of limited size.
At last, the EFs is a more natural form of earthquake acting, as is said above, reflecting the very basic form of change in the seismogram—the ‘push-pull’ action, more closely to the pattern in which an earthquake acts on structures. On the other hand, the SFs are slightly artificially separated, to give additional room for manipulations.
It is not difficult to comprehend the picture resulting from overlapping of all or from a considerable number of EFs.
The pretty entangled mesh of overlapped EFs can show a certain average picture but is very blurred. More transparency is attained by introducing, let us call it, the structural axis of the EF, as explained in
Figure 5a,c. This axis connects three characteristic points of an EF: both peaks and zero crossing (the inflection point). Note that the term ‘inflection point’ refers to the function, which would formally describe the actual EF. All these are point-like, pretty local features, so the structural axis form highly depends on the shape of EF, which is very variable.
A more adequate feature would be the slope (tangent) through the inflection point (where the EF crosses the
t-axis) (see
Figure 6a and
Figure 7). Notice the difference between ascending (blue lines) and descending (red lines) tangents, which shows a kind of statistical asymmetry of SFs.
It determines the maximum change of mechanical variables acting in the site. It has something to do with the transfer of earthquake force to structures. Let us remember the simple thing that when one says ‘earthquake,’ it is thought of as seismic effects in the site, not in the hypocenter.
The said tangent, although the most characteristic of all tangents along the EF function, does not reflect well this energy transfer, particularly in the case of complex EF shape (
Figure 6). This tangent is also a local feature, standing in the middle of the complex shape of the EF, but it is still a peripheral description of force transfer from seismic waves to the structure.
In order to take the shape of the EF into consideration, which actually carries the influence, it is more proper to speak of energy transfer since the EF shape itself shows the energy distribution contained in it.
There, one can define the instantaneous energy transfer carried by a single EF. In other words, it is the instantaneous average power, as the energy contained within the EF divided by its duration Δ
t:
where the label
EF symbolically designates the function describing the EF shape (see (9)). Of course, it is a rough measure of energy transfer. It is well known from dynamics that the inertial forces and impulse loads depend on d/dt (
Figure 6).
The first derivative of the EF shows the essential difference in the transfer rate, particularly when compared with the sin function, which provides a mild change without discontinuities (
Figure 6). The earthquake displays sharp changes, where the flection points are connected with almost linear slopes, quite opposite to sinusoid monotonic change.
Until now, the transfer rate is considered for a single (individual) EF isolated from others. The EFs never act separately but in bursts. The fact that points out the burst influence of EFs on structures are resonant characteristics of structures, having modes of vibration. Thusly, it is necessary to analyze the repetition pattern of EFs.
2.6. Attributes Based on Rearrangement of EFs/SFs
One of a few of the previous attributes was also based on the rearrangement of EFs/SFs, but it was not placed in this subsection because the rearrangement was simple, involving only gathering of EFs at one place, with coinciding their inflection points. Rearrangement as ordering (sorting) is a little ‘heavier’ operation, which enables a more potent basis for creating new attributes.
The first one is the R-envelope, for which one could even say that it is not only an attribute but also a basis for qualitatively new attributes.
2.6.1. Issue of Seismogram Symmetry
Formally considered, the seismogram fluctuates around the t-axis. Physically, the t-axis is a reference, around which seismic waves compress or extend the medium. It would be interesting to examine seismogram symmetry with respect to the t-axis. The files used for this purpose are recordings of acceleration.
The simplest method to do that is to compare peak envelopes,
A+(
t) and
A−(
t), drawn over positive and negative peaks of seismogram waveform, i.e., over peaks of EFs (
Figure 2). The difference between these two plain envelopes apparently exists, but they are very indented for a reliable visual assessment.
A more regular picture of symmetry is attained by the R-envelope, both for positive and negative SFs, see
Figure 3, and see [
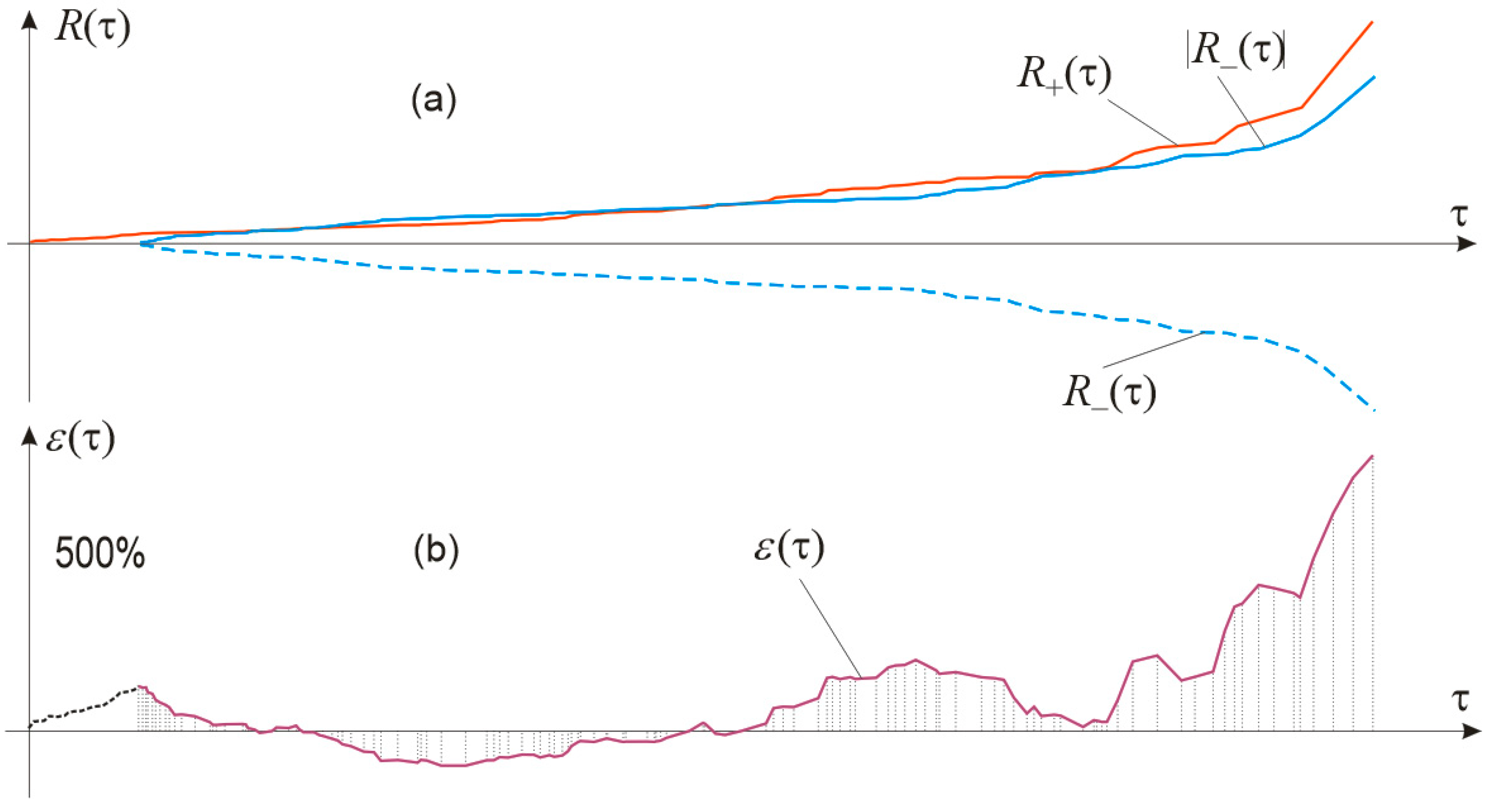
10] “Figure 20”. As can be seen, there are small differences between the envelopes
R+(τ) and
R−(τ) so that one can speak of an invariant on the population of seismograms [
10]. Additionally, one can complain about the small variation range to be useful for qualifying and quantifying the difference between the two envelopes in order to describe the seismogram symmetry.
The cause is simple: rearrangement of SFs equalizes differences, putting similar SFs face-to-face. The seismogram conveys the influence right by its waveform, not by arranged SFs, but by a sequence of EFs. Finally, the chief factor by which the earthquake acts on the environment are transitions, which means that a more proper structural element would be the EF than the SF.
It seems that it would be more proper to create the R-envelope by arranging the EFs, but it is not simple as in the case of SFs, since the EF is ambiguous, having two randomly different maximum amplitudes, and makes the ordering by peak amplitude uncertain.
Then, the better criterion for ordering would be the EF energy: firstly, to calculate the energy of each EF, then to order the EFs by increasing/decreasing energy, and then to draw the R-envelope over maximum amplitudes of respective positive and negative peak amplitudes. This approach is the square-linear combination. Of course, such an envelope would not be labeled by R, but by, e.g., RE (with E for energy).
A linear-linear version of this energy approach is described in
Figure 8. The EFs are ordered twice: once by positive peak amplitudes of EFs (not SFs) and then by negative ones. Each time, the correspondent R-envelope is drawn over the peaks by which the sorting is performed (
Figure 9).
The quantized durations Δs make the time variable τ irrelevant, so a new index variable
n can be introduced, and all the envelopes from
Figure 9 are rewritten as
RQ+(
n),
NQ+(
n), etc.
Two key elements should be noted in
Figure 8 and
Figure 9. Instead of the structural axis of the EF, already introduced in
Figure 5, here, one deals with the skeleton of EF, graphically explained in
Figure 8. The other one is the quantizing operation over EF skeleton durations (
Figure 9a), and its role is apparent—to minimize the influence of EF shape variability on the result. Consequently, after the quantization, the creation of the R-envelope is meaningless, but not the creation of the quantized envelope labeled by R
Q.
The positive RQ+(τ) is monotonic and topologically identical to the corresponding R+(τ) envelope, i.e., the R+-envelope. The reverse of the RQ+(τ) is the NQ+(τ), which clearly shows the asymmetry of ordered EFs. The similar holds for RQ−(τ) and NQ−(τ).
2.6.2. R-Envelope and New Definition of Seismogram Duration
The duration of the seismogram is a very important attribute. Some of the proposals were quoted in
Section 1.
The usual and widespread definition stems from the Husid diagram, for D5-75 and D5-95. Both intervals, determined by respective limits, seem a little arbitrary as a convention. Husid diagram is quite objective functional attribute of a seismogram—it still contains the seismogram’s waveform, although in cumulative appearance. Yet, the limits 5%, 75%, and 95% do reflect the subjectivity, where a human, more according to its biased tendency to choose rounded numbers (for example, 5, 10, etc. which has to do with the number of fingers) than in regard to mathematical objectivity, has chosen the rounded numbers. Simply, why exactly 5, but not e.g., 4.4 etc.?
With the R-envelope, one gets a more objective platform to define the seismogram duration. One limit of the seismogram’s duration is pretty well defined—it is the highest fluctuation (
Figure 3b,c). Another limit of duration is placed somewhere along the monotonic tail of the arranged seismogram (see
Figure 3).
The other limit can be defined if one considers peaks of SFs a in rearranged seismogram as the scatter plot. These points are also nodes of the other R-envelope. Linear regression, as the simplest form of regression analysis, is a universal statistical tools that can reveal hidden linear rules behind a scatter plot (diagram).
When a regression line through the “cloud” of the SFs peaks is calculated, one gets a simple geometrical description of the whole rearranged seismogram (
Figure 10).
4. Discussion
Some issues were partly discussed in previous sections, for the sake of reading continuity. The expression ‘seismogram rearrangement from the article title, not ordering or sorting, implies the previous decomposition. The very seismogram indicates elementary repeating pattern, although random, which is named the elementary fluctuation, further divided into a pair of single fluctuations. It is a fundamental concept.
The concept of elementary/single (EF/SF) fluctuation proved itself as fruitful, not only as a base for defining several new attributes, but for the further study of EF forms, particularly of the complex or composite EFs. The decomposition is a prerequisite for recomposition.
4.1. Mathematical and Physical Meaning of Decomposition
The seismogram can be formally considered as a mathematical function s(t). Decomposition into EFs/SFs means some mathematical operations, which are actually numerical, since the seismograms are available as numerical files (of some 5000 to 10,000 thousand numerical values).
The proposed approach involves two-stage processing: the prior and the main one. The prior is carried out once, ad forever. Once completed, it reduces the numerical heap of several thousand numbers into a couple of hundreds of number pairs (max amplitude and duration of SFs). This is a high-level numerical compression. Now comes the main processing—it is much easier to manipulate with this small set of numbers, producing various attributes of a seismogram.
The numerical reduction is not the main advantage of the proposed approach. A more important aspect is qualitative: the very fact of parsing (segmentation). Now, one has at disposal the basic structural elements (EFs and SFs) of seismogram and can easily manipulate them, creating unique and specific combinations, i.e., attributes, not found elsewhere, since the other attributes have another definition basis.
An earthquake does not act on a structure at once, as a whole, but sequentially, EF by EF. On the other side, the structure shows its own resonant characteristics, given as vibration modes. These are complex form damped vibrations (composite oscillations of mutually connected structure elements (beams and columns, a real small internal ‘earthquakes’, as responses to outer excitation. Damped vibrations (from pulse excitation) take some time to dwindle, which can be considered as the memory of structure. The arrival rate of exciting elements in an acting earthquake (at the location of the considered structure) and the resonances of the subjected structure create a complex interference. The concept of the EF, more than the SF, because it is of a more natural shape to reflect the ‘push-pull’ pattern of excitement, provides an opportunity to compose characteristic local (short) sequences of EFs and to examine structure response instead of applying the whole seismogram.
4.2. Attributes from Decomposition-Recomposition
In this paper, the widest definition of seismic attribute is accepted, as any information of interest that can be derived from raw seismic data. They can be roughly classified into parametric and functional attributes. Parametric ones can be single-parametric and group-parametric. As a side note, one could notice some evolution of the notion of attribute in the last two decades.
All attributes proposed in this paper are based on the decomposition approach. Some of them are the result of recomposition (rearrangement). The key value of segmentation is the recomposition, which can yield various results (attributes).
The R/R
Q-envelope is only one of these results, although a significant one. Moreover, there is a new type of random bipartite graph (see [
10]), which addresses the issue of seismogram clustering and seismic database organization. The issue of seismogram duration, which is indisputably significant, is treated in a more objective way. As for the R/R
Q -envelope, it revealed an invariant on the population of seismograms, where a small sample was enough for the conclusion. The issue of seismogram symmetry can also be treated in a simple way, without having to engage a huge population of seismograms to infer reliable results (see [
57]). Then, applying the principle of recomposition on SFs durations, it is possible to make local assessments of spectrum structure at low numerical cost.
Available attributes could address and describe many issues, but their limitations stem from the basis on which they are defined on. Similarly, the proposed attributes are capable of describing some issues, which the current attributes are not capable of, just because of the definition basis: the segmentation into SFs/EFs, giving the ability of their recomposition. Just to mention some: the ordered sequence of SFs (by SF peak amplitude, to give, e.g., the R/RQ -envelope, or by SF duration, to give period distribution); the R/RQ -envelope; the new type of random bipartite graph, as structural description of seismogram; the invariant on seismogram population; etc. There partly belongs the seismogram duration, where some of the available attributes also give very useful definitions. Also for the seismogram symmetry, since there are other ways to describe it, except for the RQ and NQ envelopes proposed in this paper, which form the difference functions εQ, as a specific description of the seismogram symmetry.
4.3. R-Envelope as Functional Attribute or Transform of Seismogram
It is said that the R/RQ-envelope is a functional attribute. This claim has the reverse. The R/RQ-envelope, represented by a polygonal continuous line drawn over SFs peaks, really seems to have a continuous function. However, each segment of a polygonal line is drawn (interpolated) between adjacent peaks. Thus, the segment does not carry any additional information which is not already contained in peak coordinates. It serves only for visual impressions to human vision. In that sense, the R/RQ-envelope actually represents a group-parametric attribute of the original seismogram, not the functional one, unless polygonal line segments are not taken as a fact of continuity. The same holds for the seismogram: a string of several thousand amplitudes (samples) expressed as real numbers, which peaks the plotting software connects by linear segments, creating a polygonal line just for the needs of the software user (human).
In plain words, a human sees the polygonal line where the computer ‘sees’ a string of numbers. The R/RQ-envelope actually does not exist as a function, nor the other ‘functions’ derived from the R/RQ-envelope, but it is very useful to treat it formally as a function, not only for the sake of human vision, but for mathematical reasons because in such case it is a single object to manipulate with, and not a string of numbers, i.e., a collection of separate mathematical objects. It is now quite clear that there is no necessity for any R/RQ-envelope in defining the seismogram duration.
R-Envelope and Spectrum Issues
There is an analogy between the spectrum of the raw seismogram and the rearranged seismogram since both are ordered sequences of elements (SFs and spectral components), although the order is the result of different operations (plain sorting in size and the Fourier transform).
In that sense, the R/R
Q-envelope, as the main product of seismogram rearrangement), can be considered as a kind of its transform. This issue is also considered in [
10].
In the case of analytic function, the FT transforms one form into the exact another, and vice versa, showing its cyclic ability. For non-analytic cases, usually expressed as numerical sets, the FT (i.e., DFT, FFT) transforms one set into strictly another one. With digital computers, even analytic cases are processed as numerical sets.
It means that the FT transform operates between two numerical domains, which are actually one and the same domain. This further means that this is not a transformation since it circles within one domain. The same situation then occurs with the DFT: it transfers one set of numbers into another one. The human is the factor that prescribes the meaning to bare numbers prior to and after the transform action. If one would ask the computer, could it tell the difference?
When parsed into SFs (raw or approximated by triangles), the seismogram becomes a finite string of real numbers (peak amplitudes and durations of SFs). When indexed, it becomes a string of integers. The above expression ‘vice versa’ designates the cyclic ability of a transform, to equally transfer mathematical objects between two domains. The R/RQ-transform shows limits of such ability. At the integer level, it works completely. At the real-number level (maximum amplitudes or SFs’ peaks), it also works, with an addition of another set of real numbers—positions of peaks along the τ-axis. On the SF level, it does not work since it cannot return SFs shapes from R/RQ-envelope.
There is one more difference between R/R
Q-envelope, as the proclaimed transform of the seismogram, and the FT. Each element (SF) in a recomposed sequence of SFs, which is the basis for creating the R/R
Q-envelope, already existed in the original sequence (seismogram), and it is just moved from the previous to the new position, according to the criterion of increasing/decreasing maximum amplitude of SF. It means that none of the SFs was subject to any transformation during this shifting operation. In other words, it already existed as the object of transformation. On the opposite, each element in the spectrum, the sinusoid component of a certain frequency, is the result of the transformation of the whole original object—seismogram
s(
t). This is because the FT (DFT/FFT) is basically defined by an integral dependent on a parameter.
This further means that one should calculate the whole integral over the variable t for each value of parameter ω. It could be called the circle transformation to disambiguate with the cyclic transformation (giving the original after two transformations, F−1{F[s(t)]} = s(t). It further means that the whole object of transformation, seismogram s(t), experiences essential change to yield just a single element (a single sin component with the parameter ω) in the ordered representation of seismogram, i.e., its spectrum. There is also an ordered sequence of SFs, i.e., an ordered picture of a seismogram, but created in a much simple way. Also, since the concept of spectrum is a pretty fundamental one and can attain various forms, one could even name the rearranged sequence of SFs as spectrum since it provides a specific picture of the content of a seismogram, but it is fundamentally different from the FT spectrum, which the frequency spectrum, indicating the main parameter of its products—sinusoid components. Further, the proposed method operates with a far less sized set of numbers, and it does so once, not all over, for each value of the main parameter.
4.4. Is Seismogram Randomness Suitable for Its Statistics?
Seismogram is the product of random processes, and as such, it is formally a random variable.
If the seismogram’s complexity is defined by the number of EFs (one attribute more), it does not always provide sufficient statistical “mass” for getting reliable statistical characteristics and conclusions, even with the large number of SFs. Moreover, the waveform complexity is very different in various recordings (acceleration, velocity, displacement) of the same event, even at the same site, and also depends on filtering conditions [
7] “article 1.01, p. 22, Figure 13”. We considered the usual file sizes of earthquakes in databases [
33], with mostly 5000–10,000 amplitudes (numerical values), taken at the rate of 0.01 s.
Although it seems to be a sufficient statistical sample, these 5000 values are not 5000 independent but considerably correlated, yielding effectively a few hundred of practically really independent ones, and, hence, suitable for statistical conclusions.
Another constraint is that we seek for the attributes to be taken from individual seismograms, not so much from a bunch of them, not to speak of a statistical ensemble of seismograms, since the earthquake is an event per se, expressing “individuality”, i.e., it is “one-shot” event.
The confirmation of the fact that it is not easy to cluster earthquakes, one can simply find classification schemes in earthquake databases, for example, the PEER database [
33]. It is enough to see under which criteria they are grouped, although it is the result of tremendous experience. This issue is considered in more details in [
10].
There is a weak homogeneity in the earthquake population. The seismograms of the same event, of the same component, taken at sites with almost equal distances from the hypocenter, show considerable variations in waveform caused by different propagation conditions between fault-site, so that they arrive at a station carrying different stochastics.
Simply, seismograms are too non-stationary events, truly transients, to be suitable for tight clustering. Seismic arrays [
8] “Ch. 9” may effectively bridge such gap, but the fact of inhomogeneity remains in power. In this aspect, see the elaboration about the random bipartite graphs as a means for organizing seismic database [
10].
4.5. Horizontal Asymptote of R-Envelope?
Since the small fluctuations dominate in seismogram, the arrangement of SFs, by decreasing peak amplitude, makes the R-envelope a monotonic function, in which the R-envelope closely approaches the t-axis, so it might be considered as a horizontal asymptote. Mathematics strictly defines the issue of asymptote.
How close the R-envelope will reach the t-axis, or how much the t-axis is a true horizontal asymptote of the R-envelope, depends on the length of seismogram, i.e., on the moment when recording is interrupted after the basic part of the event and its coda interval. If the recording would be intentionally extended, let us say for the sake of this research, then one would have a long seismogram’s tail composed of seismic noise. The one noise component generated by the recorded event will definitely become extinct with time, but not the perpetual seismic noise from other sources all around the never resting Earth. This means that neither recording truncation nor the seismic noise simply allows the R-envelope to infinitesimally reach the t-axis since there always are the smallest but not negligible fluctuations. So, one cannot speak about the asymptotic approaching (reaching) of the R-envelope in the conventional mathematical sense, but just about approaching tendency.
What is more interesting in this issue is the twofold approach the t-axis (better to say, the τ-axis), where both positive and negative R-envelopes approach the same line.
This issue finds its place in the spectrum as well, but with an essential difference: whatever is the truncation of the seismogram, its spectrum will approach the ω-axis infinitesimally close with ω tending to infinity, but the R-envelope will not. Also, the spectrum of noisy seismogram will also approach the ω-axis infinitesimally close, though more gradually since the seismic noise has a broader spectrum than the event’s seismogram.
4.6. Seismogram Duration—Linear or Non-Linear Regression?
To demonstrate the fertility of the proposed concept it is applied on the issue of seismogram duration using the simplest case of regression analysis—linear regression.
The scatter diagram, hiding certain relationships between two variables, implies that all points are of the same significance. Can one claim that for SFs peaks, which represent maximum amplitudes of SFs? This means that the peaks of the highest amplitudes are equally significant as the smallest ones. In other words, there is no ponderation. It does not make the linear regression questionable for this case since the SFs peaks already involve ponderation simply by being big or being small.
Otherwise, if one claims that the seismogram is not a sample of sufficient size for reliable statistical conclusion, then the duration determined in this way seems to be also unreliable. Here, the regression is applied to a scatter plot, which is not so stochastic one, as it would be if taken from a raw seismogram. The rearrangement of SFs, from an “unkempt” seismogram into an ordered sequence, makes averaging, equalization of original stochastics, and smooths variability, so it equivalently enlarges the sample, enabling more reliable statistical inference.
This does not mean that one cannot apply polynomial regression. A suitable polynomial form can be nothing other than the R-envelope shape fitted with a proper polynomial. It will be an issue for further research.
One of the purposes of ordered SFs, united under the R-envelope to describe them by one mathematical object, was illustrated through the proposed definition of seismogram duration, with the aim to make the definition objective, stemming from the very waveform. Linear regression gave the duration just as an interval, since the interval (duration) is determined from rearranged SFs. Where to place this interval on the raw seismogram? The answer gives the seismogram itself by its beginning, i.e., the position of the first (P-) phase.
The R-envelope and the seismogram duration, as well, are numerically extensive. To estimate its numerical demand, one could simply compare this procedure with integral calculation for, e.g., the Husid diagram.
There is a correlation in each random process. Instead of the correlation function, the usual attribute of stationary signals, the Hurst exponent is more suitable. The rearrangement operation over SFs in a seismogram perturbs the correlation between SFs up to canceling, and more than that, the separation of positive and negative SFs adds to correlation disruption.
4.7. Issue of Zero-Crossing Criterion
Decomposition of raw seismogram into SFs is based on zero crossings. After an in-depth study of the given and other SFs/EFs in the said RSN 1616 time series, one should reconsider the definition of the SF/EF in the part of the t-axis crossing, which sometimes can yield questionable results: such definition detects very small fluctuations, but can overlook considerable ones, especially those within complex SEs. One may also speak of significant and insignificant amplitudes SFs.
That means that the criterion of the t-axis crossing is a point-like one, which does not take into account the context of a random process developing around the crossing point. It also determines the number of SFs.
This criterion is sensitive to the position of the waveform with respect to the
t-axis: slight shift of the
t-axis (better to say, the reference axis) up or down yields different segmentations of a seismogram into SFs, in respect to the original position of the
t-axis. The small SFs are particularly sensitive to such shifts of reference axis (
Figure 20), which now can reach internal fluctuation(s) of SF with complex shape and add a new SF in the result of parsing. Then an issue of complex SFs approximation should be modified: complex SF shapes should not be approximated with simple triangles, either symmetric or asymmetric, but with other regular shapes, better suited for actual SF shape, even up to embedding the elements of AI (Artificial Intelligence), e.g., shape recognition in the procedure.
The t-axis crossing is an important event in random process development, which generates an actual seismogram. It indicates a transition in the process course, i.e., the pass through the neutral equilibrium, state, which we consider a very important case in random process evolution.
5. Conclusions
The decomposition of seismogram into EFs and SFs turned out to be a fruitful fundamental approach not only for defining new attributes but also for revealing some invariants in the seismogram population. It could be said that it opens the way in a promising direction of further research.
Decomposition enables rearrangement (ordering) of EFs/SFs, which have a fundamentally statistical quality, to produce preliminary mean operation over the raw sample, i.e., seismogram.
The very number of new attributes confirms the effectiveness of said platform, mainly by these presented in the paper, and also by those conceived in this research.
There is a noticeable difference between the currently available and the proposed attributes in addressing certain issues simply because they come from different definition bases. Some of them are disjunct in this sense, and some of them differently treat the same issues, e.g., the seismogram duration.
The arranging of the EFs/SFs makes the seismogram more deterministic than before, since averaging processes take place and give results with new quality, n. Nevertheless contains the same numbers of EFs/SFs before and after. This new quality manifests its effects in new attributes derived from the new arrangements. The main one is the R/RQ-envelope, showing its potential to derive several new attributes. In that sense, the R-envelope (taken as a continuous curve) can be considered as a kind of seismogram transform.
With this approach, and with the presented results of its application, it is expected to attain a more thorough description of the seismogram, besides the existing attributes, which would find its place in refining and improving regulative in the design and construction of seismic resistant structures, and in other related disciplines as well.