A New Multi-Physics Coupled Method for the Temperature Field of Dry Clutch Assembly
Abstract
:1. Introduction
2. Temperature Test of Dry Clutch Assembly
3. Multi-Physics Coupled Simulation
3.1. Geometric Model
3.2. Fluid-Solid Coupling Model
- (1)
- To ensure computational convergence, a time step of 0.1 s is set with a total of 300 steps. The energy equation is enabled.
- (2)
- The realizable turbulence model and Enhanced Wall Treatment (EWF) are used.
- (3)
- The rotational speed is applied to the coupled wall surfaces covered by the fluid domain. The fluid domain rotates around the Y-axis at a speed of 1400 rpm.
- (4)
- The material properties of the pressure plate, friction plate, transmission plate, rivets, and diaphragm spring are defined according to Table 3. The fluid domain is set to default air gas.
- (5)
- The heat flux model based on the sliding power is applied to the friction surface of the pressure plate. The sliding power is calculated using the test bench data for each engagement-disengagement cycle. The convective heat transfer coefficient required for solving the neighboring wall surface heat transfer is obtained.
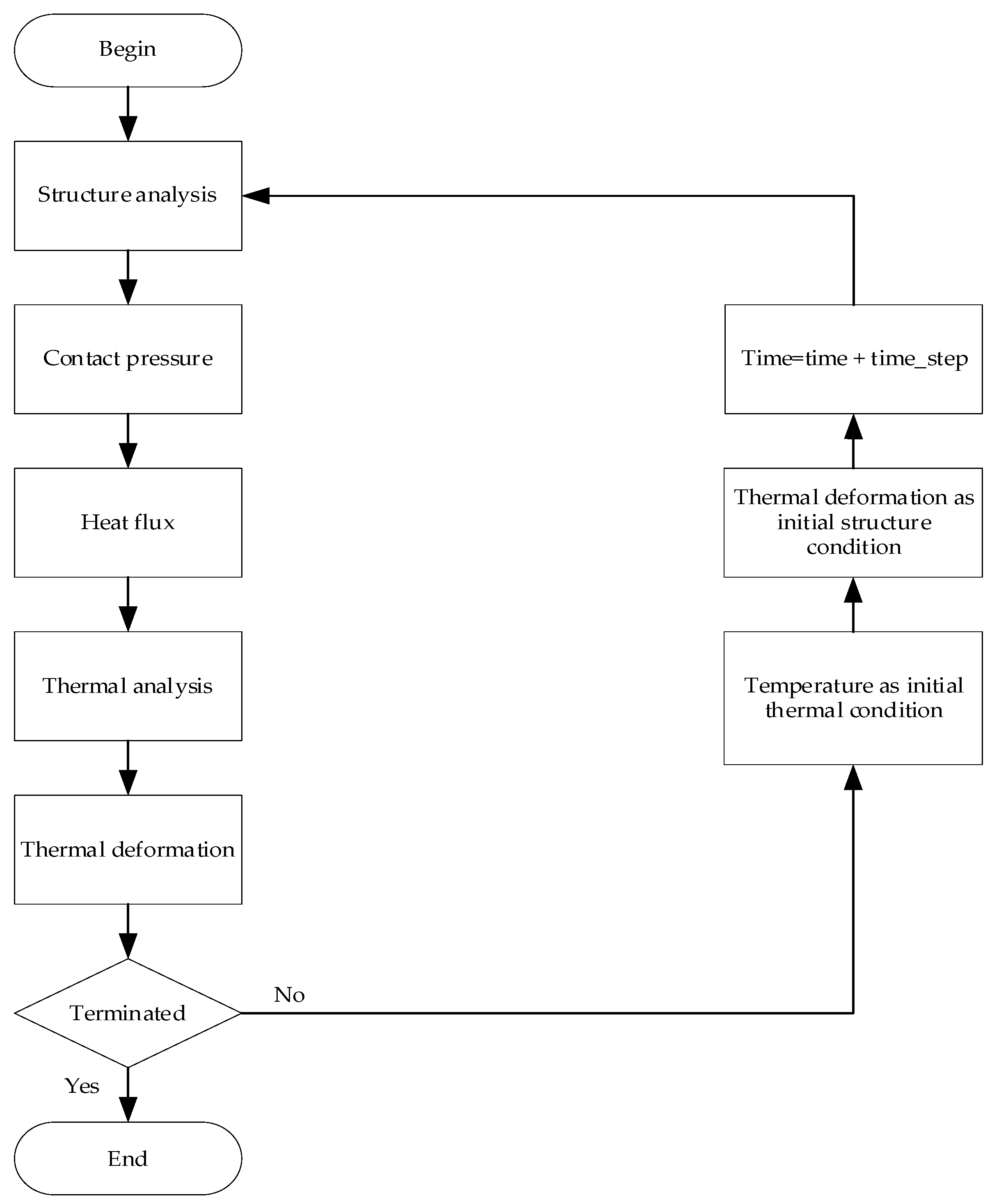
3.3. Thermal-Solid Decoupling Model
3.4. Friction Surface Heat Flux Model
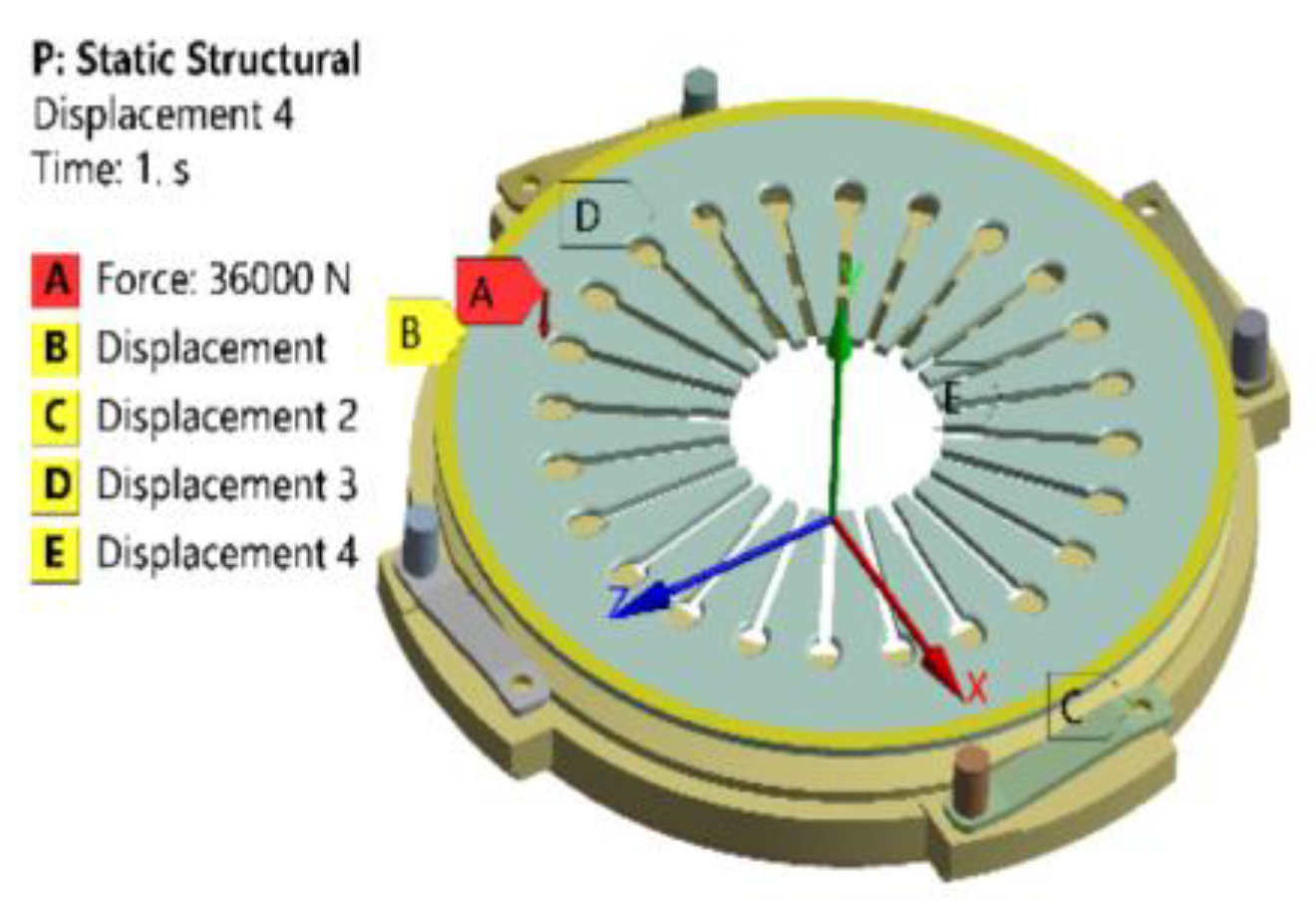
3.5. Boundary Conditions
- (1)
- For improving the computational efficiency, the engagement and sliding phase are calculated and analyzed with a time step of 0.1 s, while the synchronous rotation phase is calculated with a time step of 1 s. The material properties are set according to the thermal and physical parameters used in ANSYS-Fluent 2021 calculations.
- (2)
- In the engagement and sliding phase, a compressive force of 36,000 N is applied at the back of the pressure plate. After the synchronous rotation phase, the pressure plate and friction plate start to separate, and the compressive force is released to 0 N.
- (3)
- The displacement constraints are applied to the convex ear at the outer edge of the pressure plate and the large-end support ring surface of the diaphragm spring. The friction surface in contact with the flywheel is constrained axially, and the inner diameter of the friction plate is constrained radially and circumferentially, as shown in Figure 9.
4. Results Analysis and Discussion
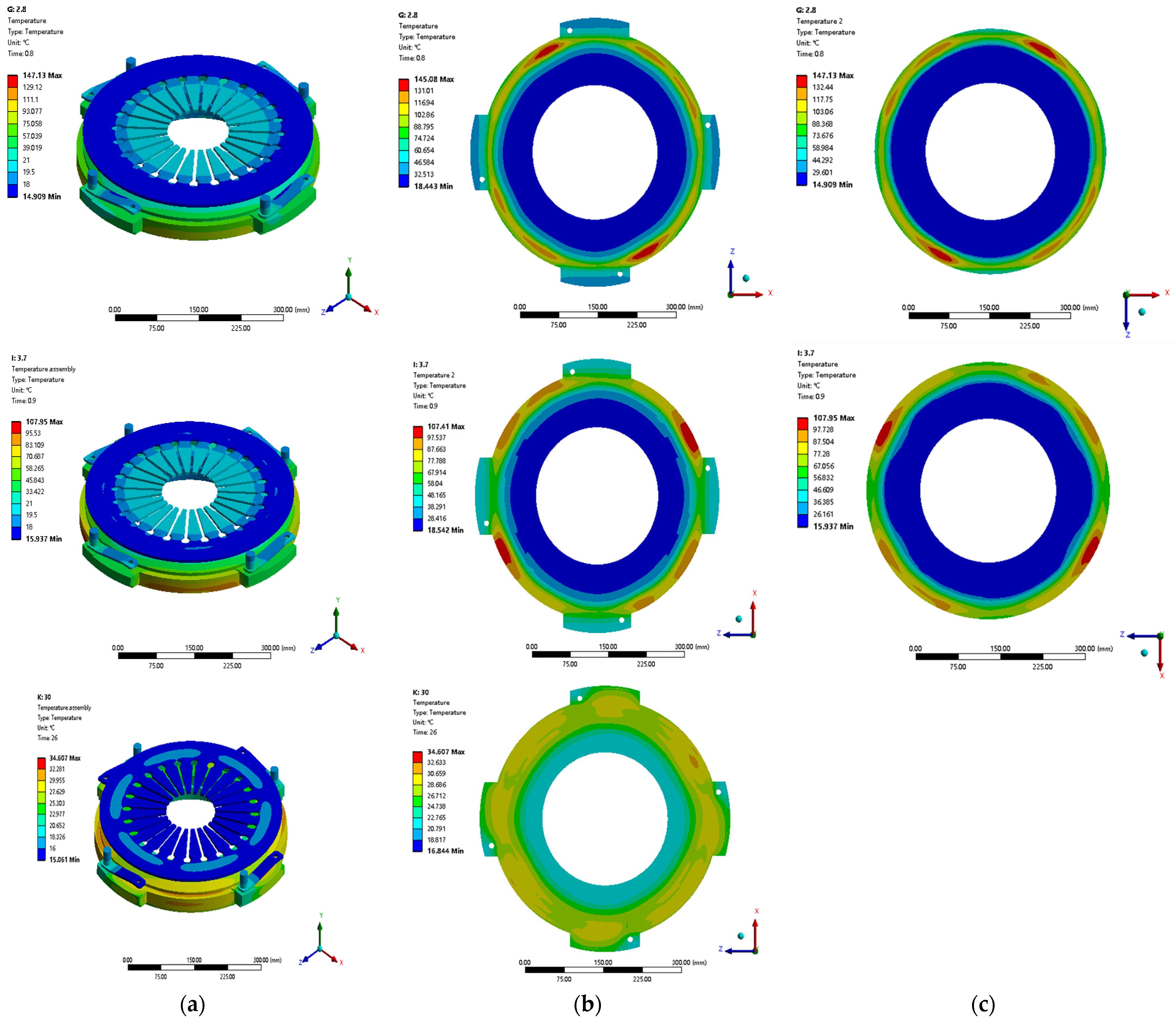
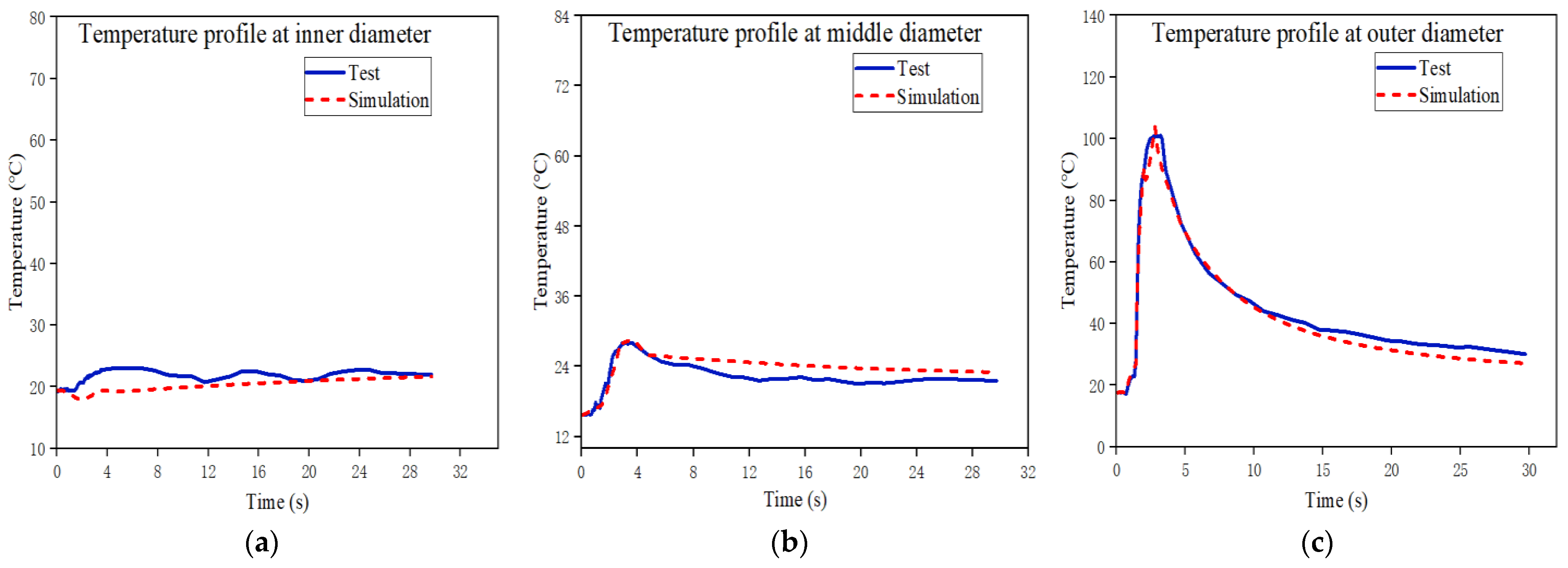
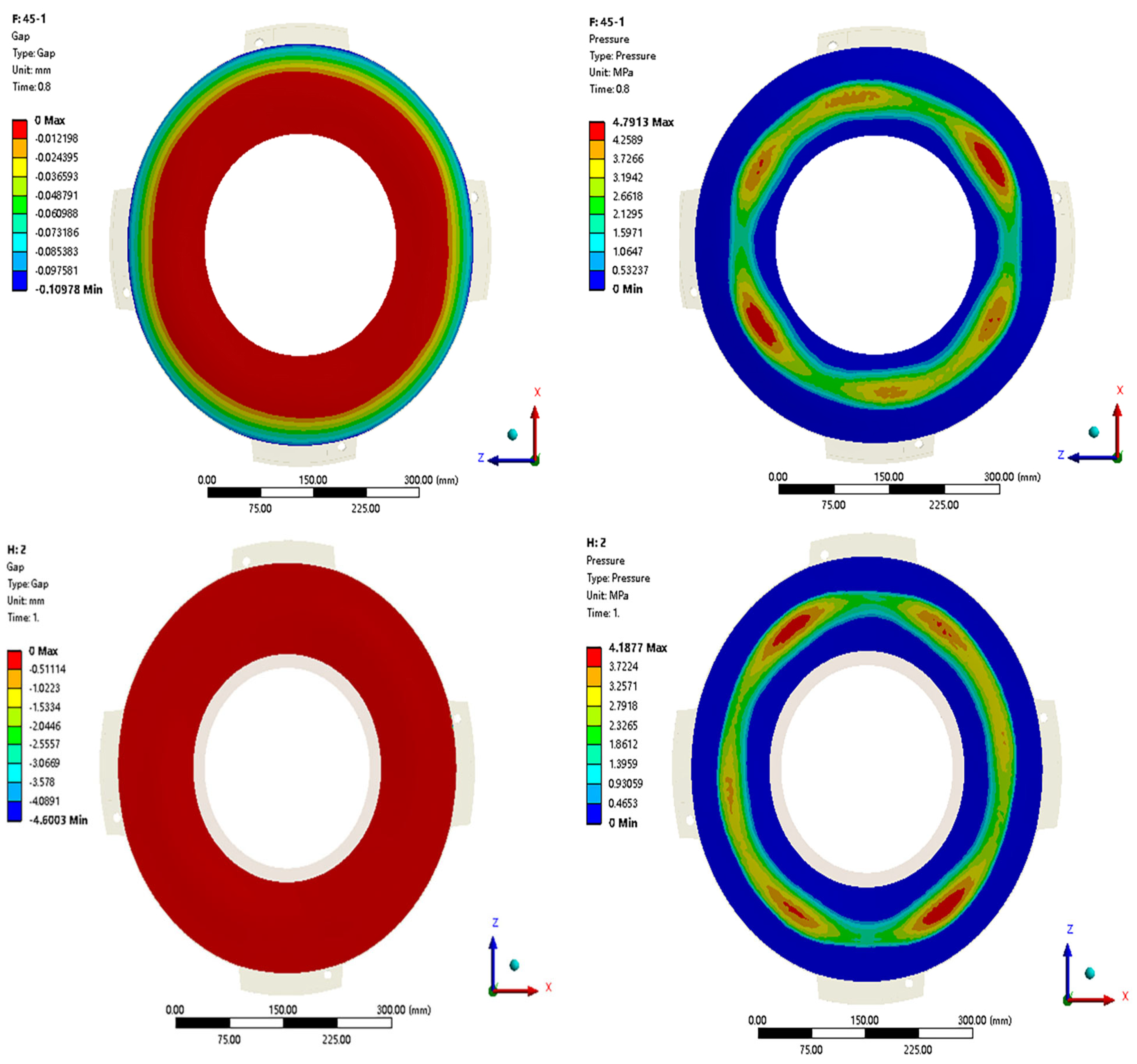
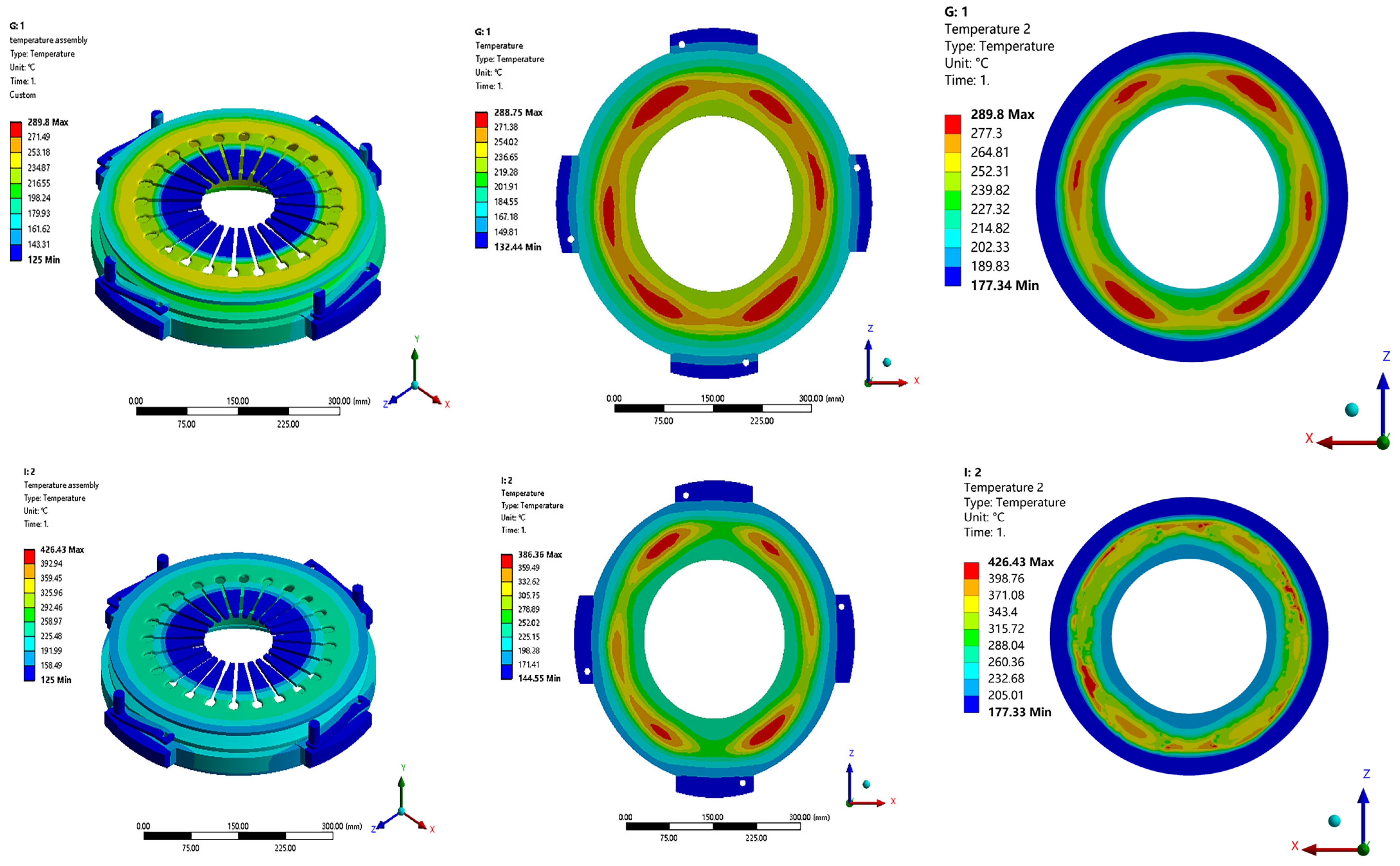
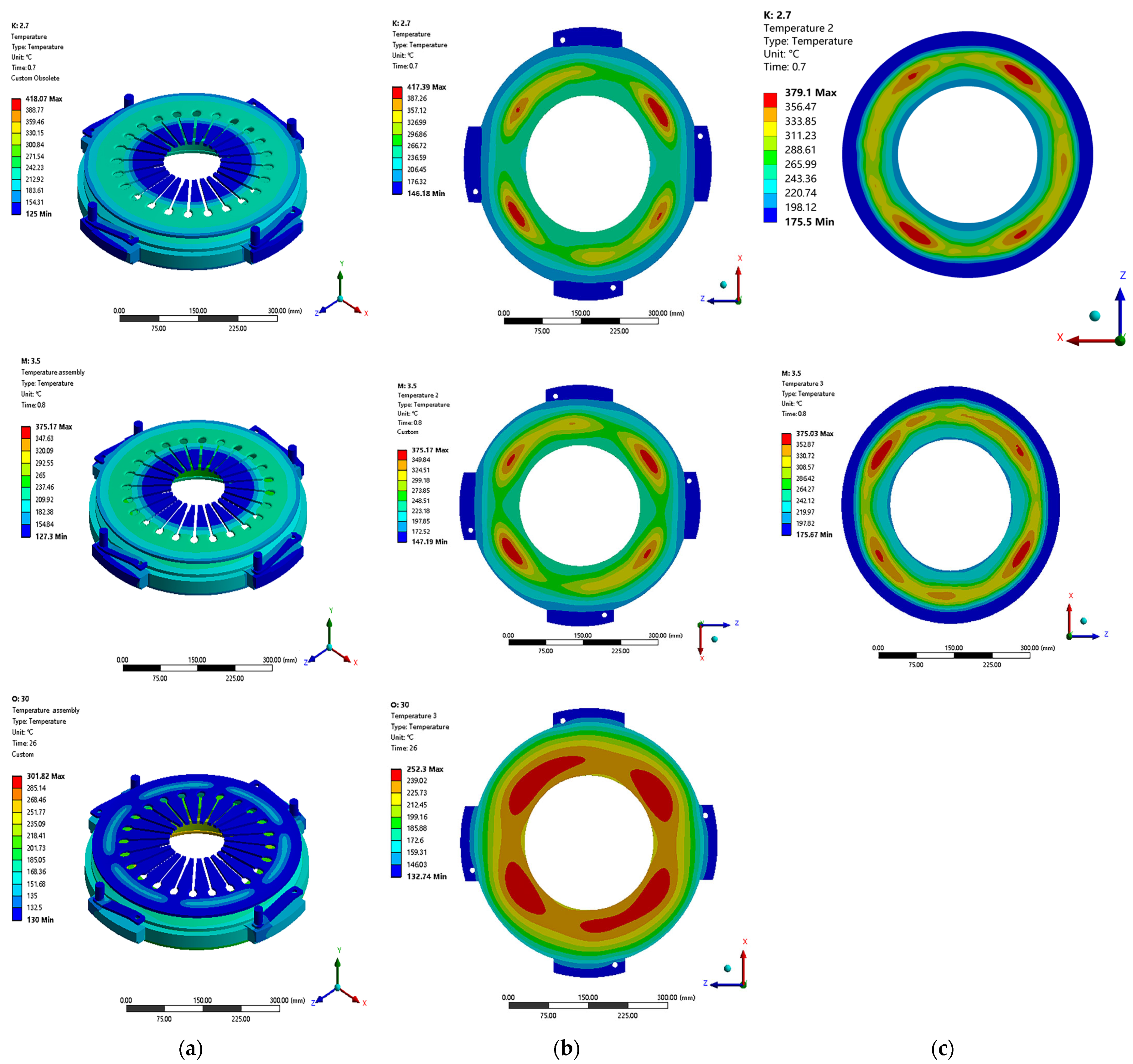
4.1. Temperature Field of the Clutch Assembly during the First Engagement
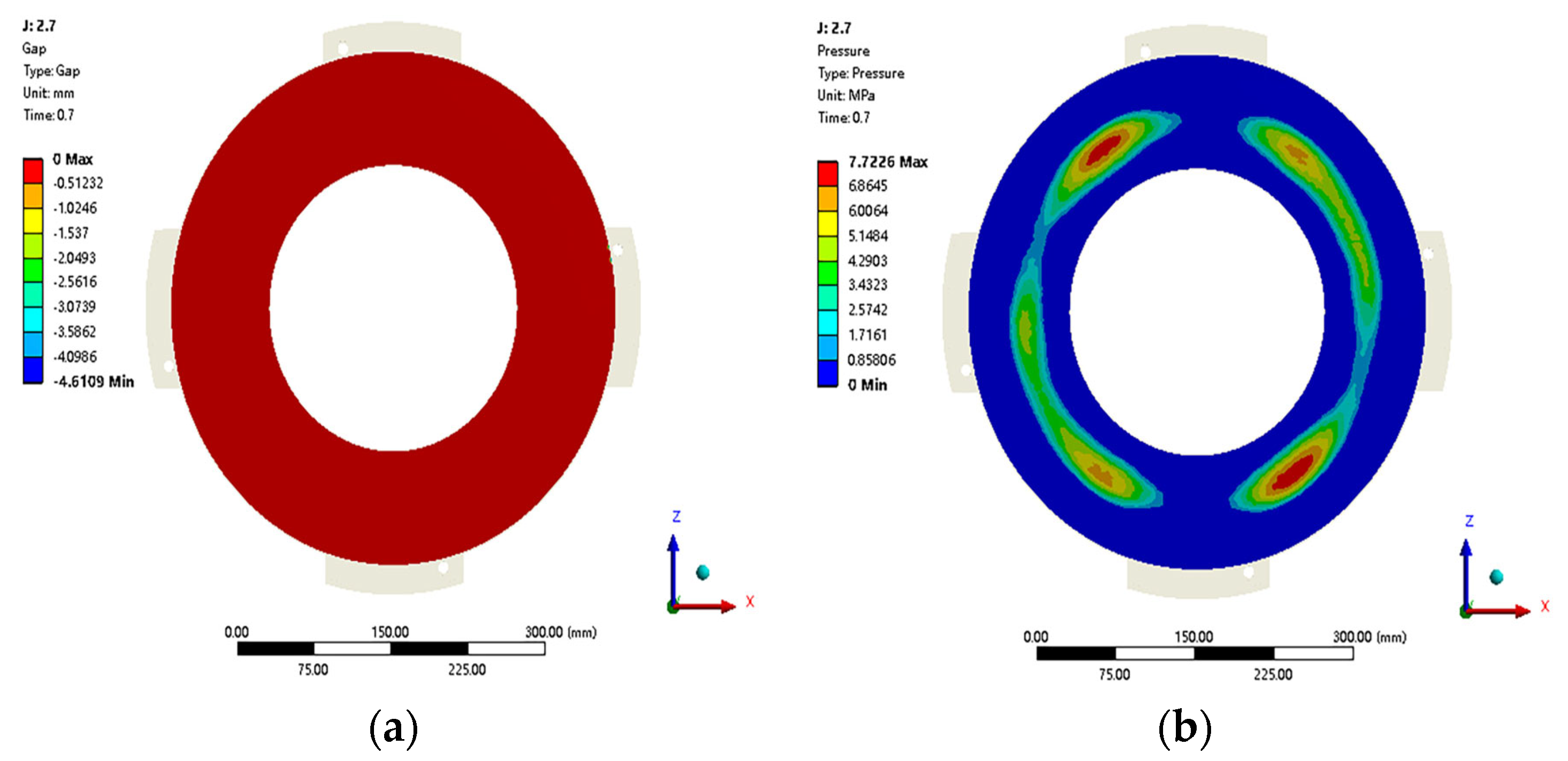
4.2. Temperature Field of the Clutch Assembly during the Last Engagement
5. Conclusions
- (1)
- To compromise the issues of long-term simulation and high model accuracy in clutch assembly temperature modeling, a numerical simulation method based on CFD simulation and decoupling theory is proposed. Firstly, the convection boundary conditions between the clutch assembly and the ambient air are determined using a fluid-thermal bidirectional coupling method for the sake of high precision. Subsequently, a thermal-solid multi-stage decoupling method is employed to achieve long-term simulation. Applying the approach, the temperature of the dry clutch assembly during the continuous engagement-disengagement process is measured.
- (2)
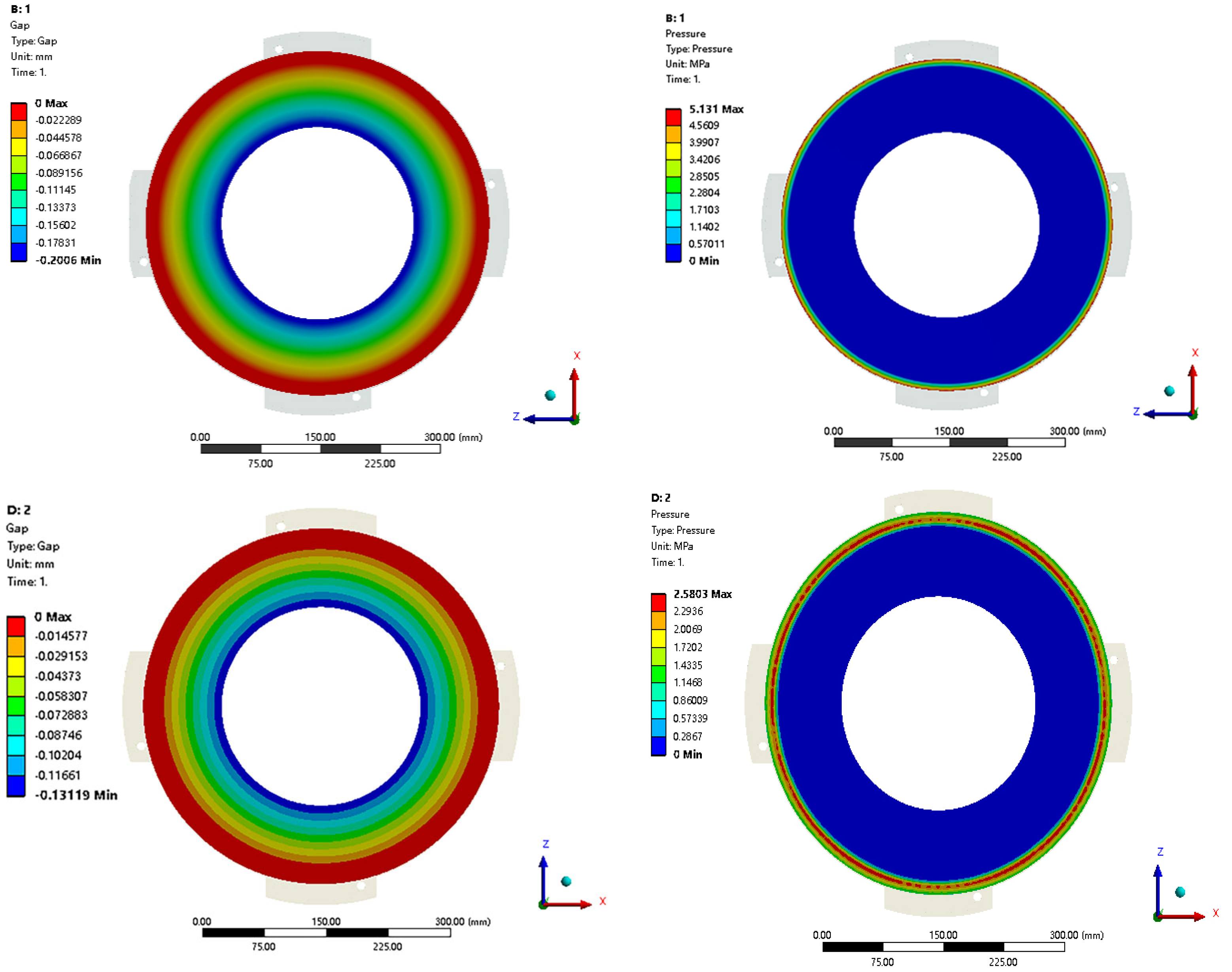
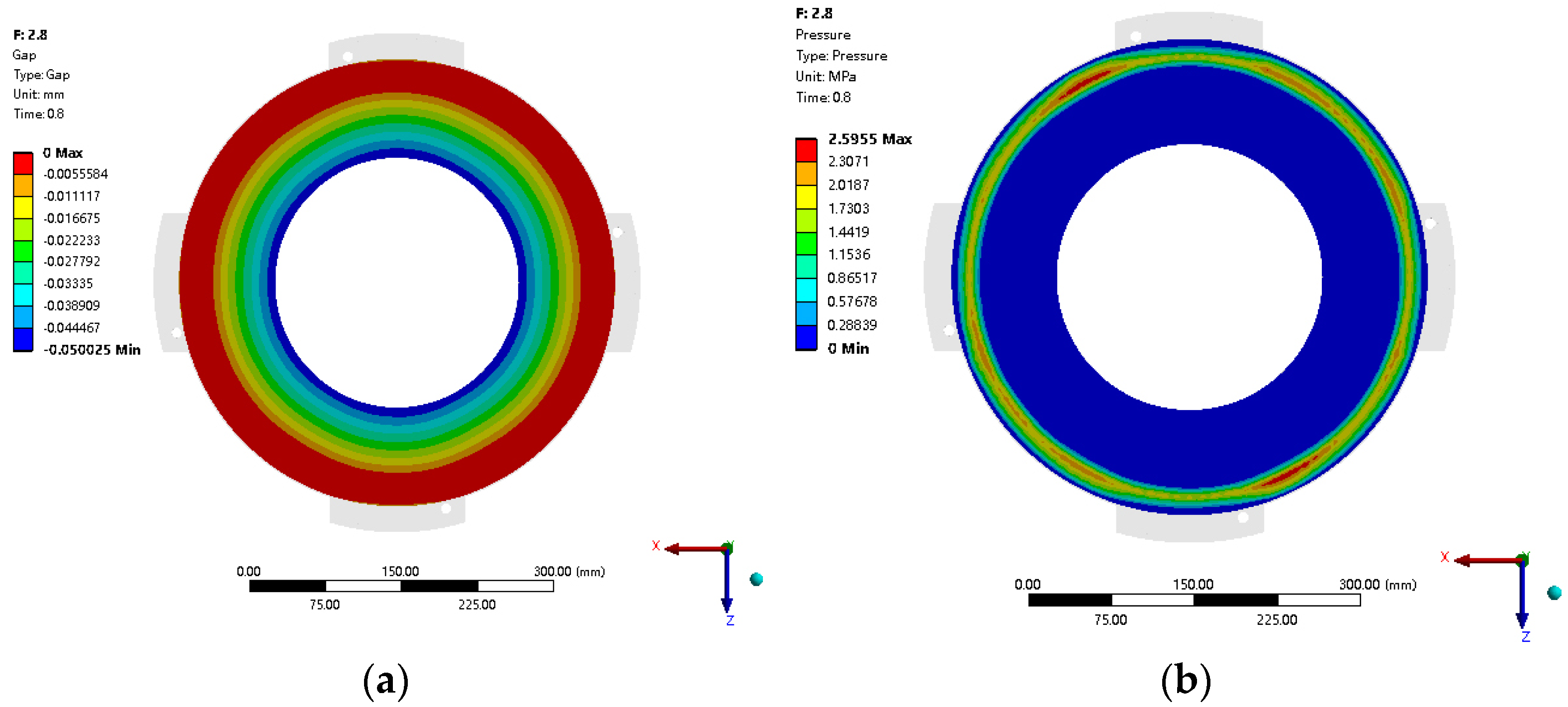
- During the continuous engagement-disengagement process, the distribution of contact between the friction surfaces of the clutch changed from the outer diameter area to the middle diameter area of the surfaces, which in turn affects the temperature distribution on the friction surface. With the continuous engagement-disengagement cycles increasing, the initial concave state of the pressure plate surface transitions to a convex state, resulting in significant deformation and warpage of the pressure plate’s outer diameter.
- (3)
- The contact pressure, thermal conductivity, and thermal deformation of the pressure plate are coupled to each other. Using the approach proposed, the temperature of the model agrees well with that of the rig test at the outer, middle, and inner diameters of the pressure plate. The average deviations in the last cycle (45th cycle) of the engagement process are 1.98%, 0.88%, and 1.05% for the outer, middle, and inner diameters, respectively. This indicates that the accuracy of the model is higher while the long-term time scale (up to 30 s) of the temperature distribution of the dry clutch assembly is achieved.
- (4)
- This article did not consider the transient processes during the engagement and disengagement of the clutch, only presenting a static Coulomb friction model. This represents one of the main limitations of the model under consideration, and further research is needed in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdullah, O.I.; Schlattmann, J. Thermal behavior of friction clutch disc based on uniform pressure and uniform wear assumptions. Friction 2016, 4, 228–237. [Google Scholar] [CrossRef]
- Abdullah, O.I.; Schlattmann, J.; Majeed, M.H.; Sabri, L.A. The temperatures distributions of a single-disc clutches using heat partitioning and total heat generated approaches. Case Stud. Therm. Eng. 2018, 11, 43–54. [Google Scholar] [CrossRef]
- Gong, Y.; Ge, W.; Yi, Y.B. Finite element analysis of thermal buckling characteristics of automotive 430 dry clutch pressure plate. Int. J. Veh. Des. 2018, 78, 108–130. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J.; Cui, H.; Wang, J.; Zhang, F. Numerical investigation into thermal buckling of friction pairs in hydro-viscous drive under nonlinear radial temperature distribution. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 36, 1081–1090. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, P.; Ge, W.; Yi, Y.-B. Numerical simulation and mechanism analysis on the concave deformation of automotive dry clutch pressure plate. Appl. Sci. 2019, 9, 5017. [Google Scholar] [CrossRef]
- Yu, L.; Zheng, C.; Wang, L.; Wu, J.; Jia, R. Influences of the Contact State between Friction Pairs on the Thermodynamic Characteristics of a Multi-Disc Clutch. Materials 2022, 15, 7758. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, M.J.A.; Abdullah, O.I.; Josef, S. Transient thermoelastic analysis of dry clutch system. Mach. Des. 2013, 5, 141–150. [Google Scholar]
- Abdullah, O.I. Stresses and deformations analysis of a dry friction clutch system. Tribol. Ind. 2013, 35, 155–162. [Google Scholar]
- Pisaturo, M.; Senatore, A. Simulation of engagement control in automotive dry-clutch and temperature field analysis through finite element model. Appl. Therm. Eng. 2016, 93, 958–966. [Google Scholar] [CrossRef]
- Ovchinnikov, A.V.; Chernova, S.A.; Pavlov, V.A. Heat transfer in the friction elements of automotive clutches. simulation and experimental study. J. Phys. Conf. Ser. 2019, 1297, 012060. [Google Scholar]
- Ding, H.; Cai, S.; Zhang, Y.; Xu, H. Transient temperature field simulation of continuously variable transmission clutch. Int. J. Automot. Technol. 2020, 21, 57–65. [Google Scholar]
- Meng, F.; Xi, J. Numerical and experimental investigation of temperature distribution for dry-clutches. Machines 2021, 9, 185. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, X.; Liu, R.; Chen, J.; Li, Z.; Xiong, X.; Liao, N. Frictional Temperature Field Study of Three Brake Rings with Copper-based Friction Material Pair. J. Powder Metall. Mater. Sci. Eng. 2022, 27, 129–139. [Google Scholar]



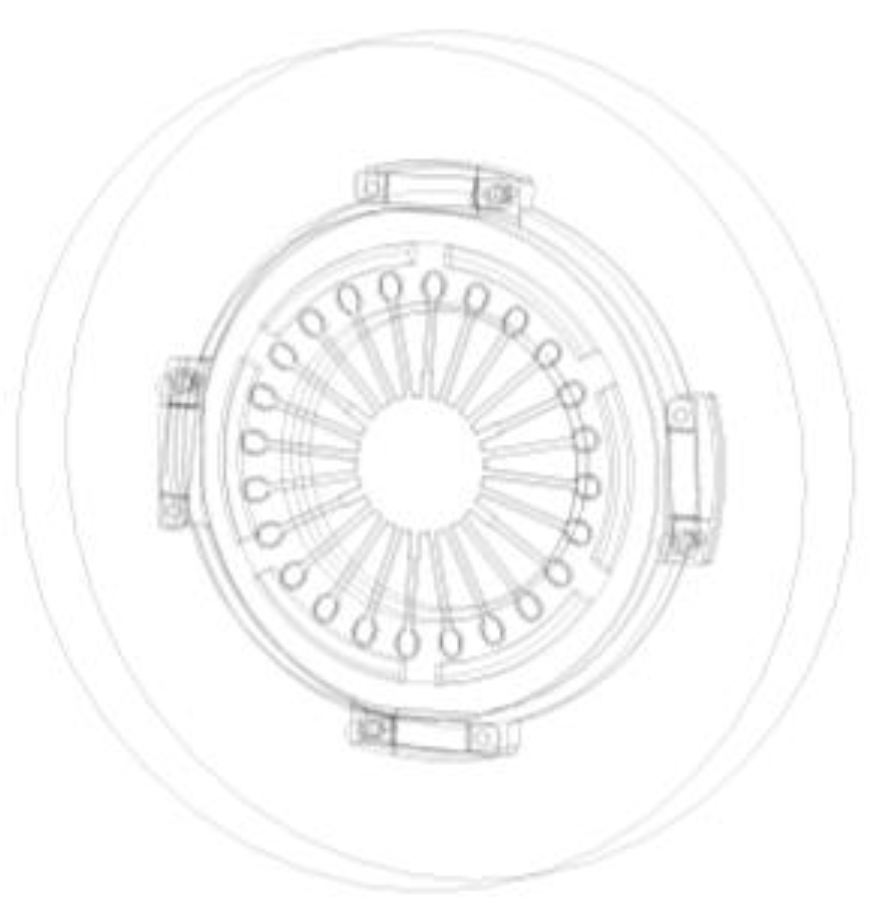
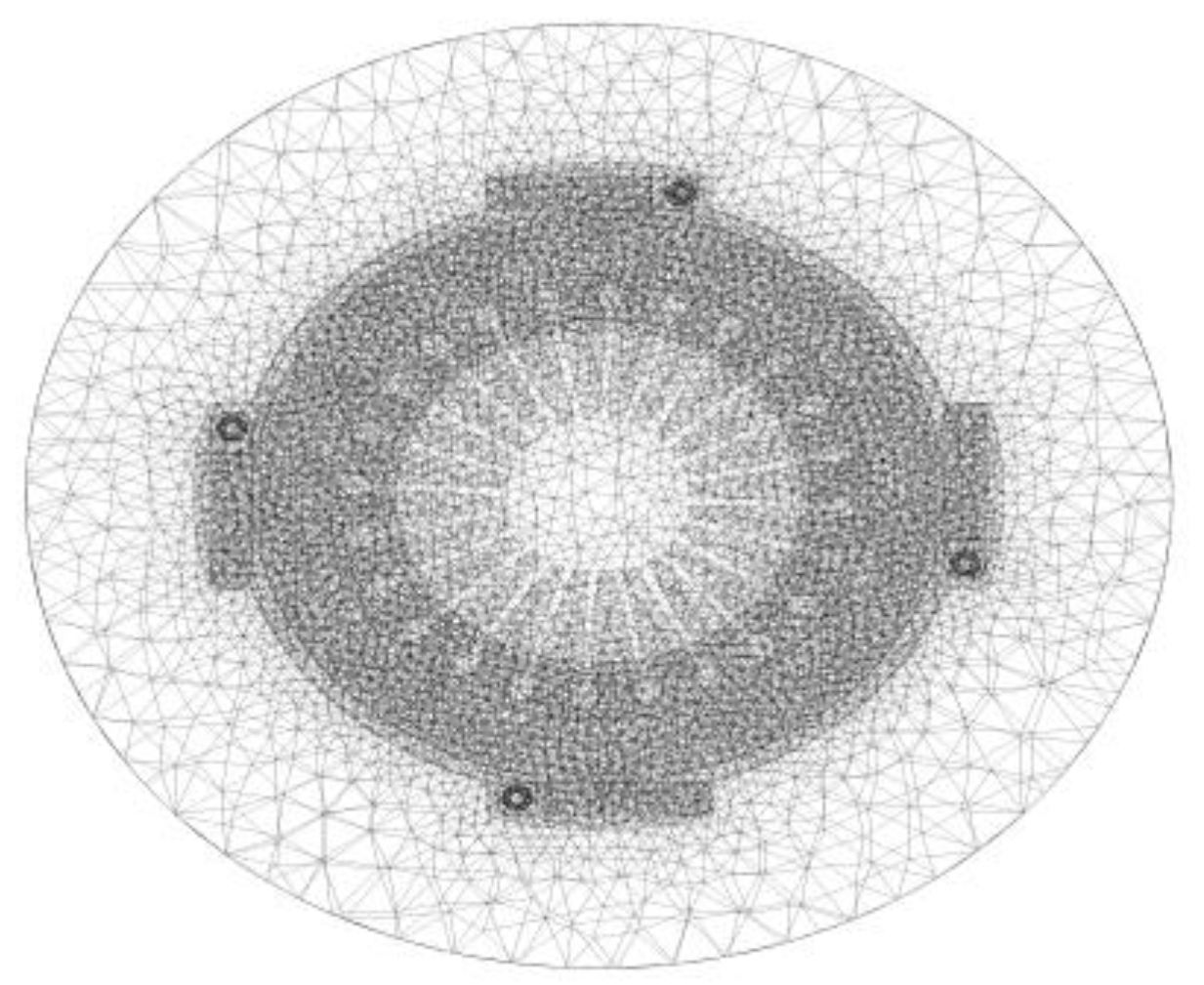

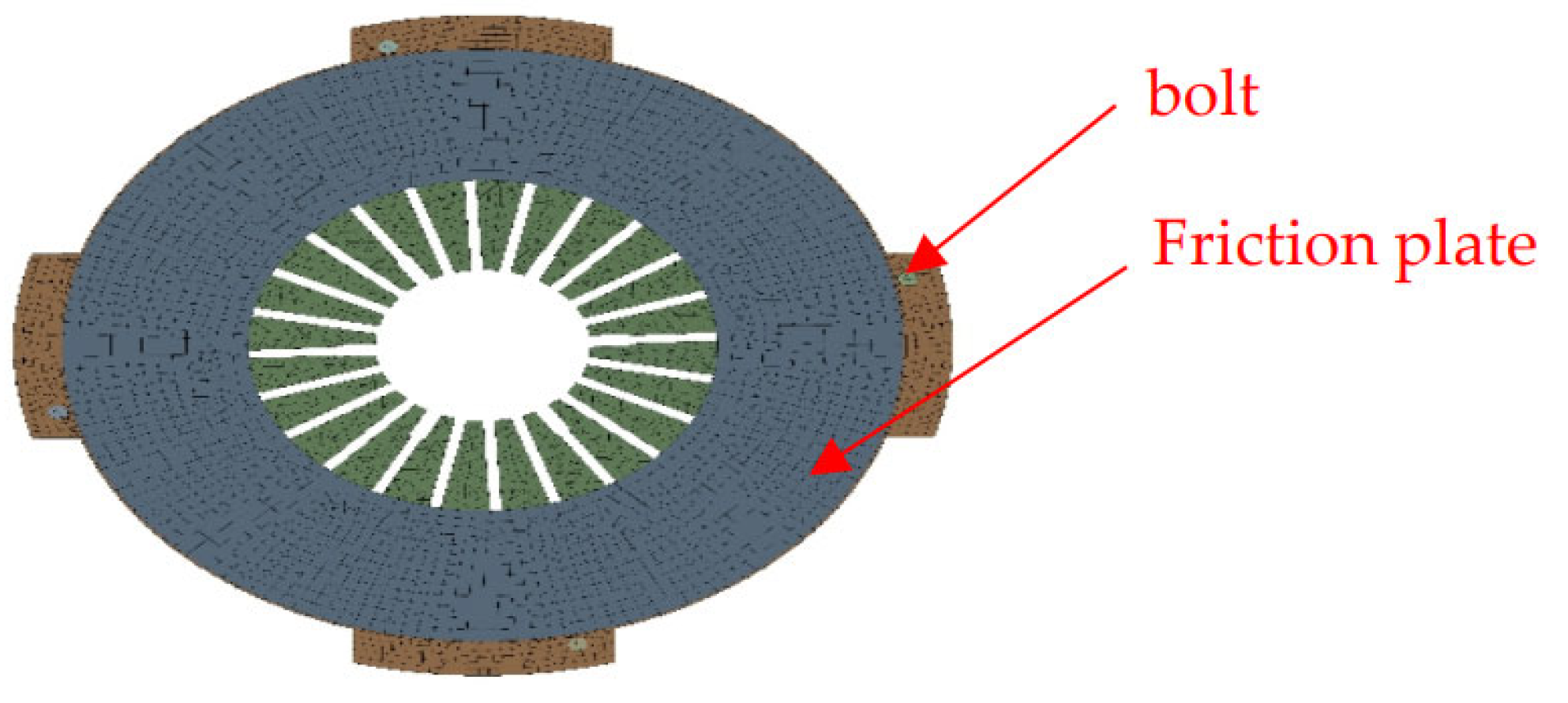



| Clutch Cover Assembly | Driven Plate Assembly | ||||
|---|---|---|---|---|---|
| Pressure Plate Weight (kg) | Pressure Plate Outer Diameter (mm) | Pressure Plate Inner Diameter (mm) | Clamping Force (N) | Friction Material | Driven Plate Outer Diameter (mm) |
| 28.5 | 430 | Φ240 | 36,000 | B8090 | 240 |
| Component | Inner Diameter R1 (mm) | Outer Diameter R2 (mm) | Thickness a (mm) |
|---|---|---|---|
| Pressure Plate | 120 | 216.5 | 39 |
| Friction Disc | 120 | 215 | 5 |
| Components | Pressure Plate | Friction Disc | Friction Disc | Drive Plate | Rivets/Bolts |
|---|---|---|---|---|---|
| Material Name | HT250 | Fiction plate | 51Crv4 | 65Mn | HT250 |
| Density (kg/m3) | 7200 | 2595 | 7860 | 7850 | 7200 |
| Young’s Modulus (Pa) | 1.1 × 1011 | 1.5 × 109 | 2.07 × 1011 | 2 × 1011 | 1.1 × 1011 |
| Poisson’s Ratio | 0.26 | 0.25 | 0.29 | 0.3 | 0.26 |
| Thermal Expansion Coefficient (°C−1) | 1.1 × 10−5 | 1.5 × 10−5 | 1.1 × 10−5 | 1.2 × 10−5 | 1.1 × 10−5 |
| Conditions | Engagement + Synchronization Stage | Disengagement Stage | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Monitoring Point | Outer Diameter Point | ||||||||||
| Time/s | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 8.0 | 13.0 | 18.0 | 23.0 | 28.0 |
| Measured Temperature/°C | 17.68 | 22.33 | 49.43 | 89.73 | 100.19 | 100.87 | 52.93 | 41.28 | 36.45 | 33.11 | 31.27 |
| Simulated Temperature/°C | 17.65 | 22.68 | 51.97 | 90.73 | 95.05 | 96.25 | 53.19 | 39.30 | 33.09 | 29.73 | 27.68 |
| Temperature Difference/°C | 0.03 | 0.35 | 2.54 | 1.00 | 5.14 | 4.62 | 0.26 | 1.98 | 3.36 | 3.38 | 3.59 |
| Deviation% | 0.17 | 1.57 | 5.14 | 1.11 | 5.13 | 4.58 | 0.49 | 4.80 | 9.22 | 10.21 | 11.48 |
| Monitoring Point | Middle Diameter Point | ||||||||||
| Measured Te-mperature/°C | 15.89 | 17.8 | 19.41 | 22.87 | 26.72 | 27.88 | 24.24 | 21.57 | 21.85 | 21.36 | 21.73 |
| Simulated Te-mperature/°C | 16.21 | 16.64 | 17.71 | 21.59 | 25.26 | 28.09 | 25.40 | 24.59 | 23.94 | 23.47 | 23.14 |
| Temperature Difference/°C | 0.32 | 1.16 | 1.70 | 1.28 | 1.46 | 0.21 | 1.16 | 3.02 | 2.09 | 2.11 | 1.41 |
| Deviation% | 2.01 | 6.52 | 8.76 | 5.60 | 5.46 | 0.75 | 4.79 | 14.00 | 9.57 | 9.88 | 6.49 |
| Monitoring Point | Inner Diameter Point | ||||||||||
| Measured Temperature/°C | 19.55 | 19.39 | 19.69 | 20.69 | 21.45 | 22.29 | 22.68 | 21.21 | 21.84 | 22.49 | 22.12 |
| Simulated Temperature/°C | 19.33 | 19.08 | 18.21 | 18.04 | 18.32 | 18.99 | 19.60 | 20.23 | 20.76 | 21.19 | 21.54 |
| Temperature Difference/°C | 0.22 | 0.31 | 1.48 | 2.65 | 3.13 | 3.3 | 3.08 | 0.98 | 1.08 | 1.3 | 0.58 |
| Deviation% | 1.13 | 1.60 | 7.52 | 12.81 | 14.59 | 14.80 | 13.58 | 4.62 | 4.95 | 5.78 | 2.62 |
| Conditions | Engagement + Synchronization Stage | Disengagement Stage | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Monitoring Point | Outer Diameter Point | ||||||||||
| Time/s | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 8.0 | 13.0 | 18.0 | 23.0 | 28.0 |
| Measured Temperature/°C | 179.45 | 181.53 | 190.64 | 193.08 | 193.54 | 193.04 | 186.58 | 183.74 | 182.48 | 181.22 | 181.06 |
| Simulated Temperature/°C | 178.42 | 181.35 | 186.98 | 194.51 | 197.12 | 198.52 | 195.89 | 191.50 | 187.62 | 184.03 | 180.70 |
| Temperature Difference/°C | 1.03 | 0.18 | 3.66 | 1.43 | 3.58 | 5.48 | 9.31 | 7.76 | 5.14 | 2.81 | 0.36 |
| Deviation% | 0.57 | 0.10 | 1.92 | 0.74 | 1.85 | 2.84 | 4.99 | 4.22 | 2.82 | 1.55 | 0.20 |
| Monitoring Point | Middle Diameter Point | ||||||||||
| Measured Temperature/°C | 247.53 | 267.7 | 332.89 | 349.76 | 351.36 | 345.98 | 295.91 | 275.67 | 263.44 | 256.41 | 250.36 |
| Simulated Temperature/°C | 248.01 | 268.77 | 332.00 | 349.88 | 350.55 | 339.96 | 293.93 | 273.60 | 261.21 | 251.71 | 243.67 |
| Temperature Difference/°C | 0.48 | 1.07 | 0.89 | 0.12 | 0.81 | 6.02 | 1.98 | 2.07 | 2.23 | 4.70 | 6.69 |
| Deviation% | 0.19 | 0.40 | 0.27 | 0.03 | 0.23 | 1.74 | 0.67 | 0.75 | 0.85 | 1.83 | 2.67 |
| Monitoring Point | Inner Diameter Point | ||||||||||
| Measured Temperature/°C | 229 | 230.01 | 237.43 | 242.55 | 244.61 | 246.25 | 243.67 | 238.78 | 237.55 | 234.41 | 234.75 |
| Simulated Temperature/°C | 229.89 | 232.09 | 235.24 | 240.06 | 241.84 | 242.90 | 244.04 | 243.18 | 241.33 | 238.72 | 235.58 |
| Temperature Difference/°C | 0.89 | 2.08 | 2.19 | 2.49 | 2.77 | 3.35 | 0.37 | 4.4 | 3.78 | 4.31 | 0.83 |
| Deviation% | 0.39 | 0.90 | 0.92 | 1.03 | 1.13 | 1.36 | 0.15 | 1.84 | 1.59 | 1.84 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yu, J.; Gong, Y. A New Multi-Physics Coupled Method for the Temperature Field of Dry Clutch Assembly. Appl. Sci. 2023, 13, 11165. https://doi.org/10.3390/app132011165
Chen J, Yu J, Gong Y. A New Multi-Physics Coupled Method for the Temperature Field of Dry Clutch Assembly. Applied Sciences. 2023; 13(20):11165. https://doi.org/10.3390/app132011165
Chicago/Turabian StyleChen, Jun, Jiali Yu, and Yubing Gong. 2023. "A New Multi-Physics Coupled Method for the Temperature Field of Dry Clutch Assembly" Applied Sciences 13, no. 20: 11165. https://doi.org/10.3390/app132011165
APA StyleChen, J., Yu, J., & Gong, Y. (2023). A New Multi-Physics Coupled Method for the Temperature Field of Dry Clutch Assembly. Applied Sciences, 13(20), 11165. https://doi.org/10.3390/app132011165





