Abstract
Providing interpretable explanations can notably enhance users’ confidence and satisfaction with regard to recommender systems. Counterfactual explanations demonstrate remarkable performance in the realm of explainable sequential recommendation. However, current counterfactual explanation models designed for sequential recommendation overlook the temporal dependencies in a user’s past behavior sequence. Furthermore, counterfactual histories should be as similar to the real history as possible to avoid conflicting with the user’s genuine behavioral preferences. This paper presents counterfactual explanations by Considering temporal dependencies (CETD), a counterfactual explanation model that utilizes a variational autoencoder (VAE) for sequential recommendation and takes into account temporal dependencies. To improve explainability, CETD employs a recurrent neural network (RNN) when generating counterfactual histories, thereby capturing both the user’s long-term preferences and short-term behavior in their real behavioral history. Meanwhile, CETD fits the distribution of reconstructed data (i.e., the counterfactual sequences generated by VAE perturbation) in a latent space, and leverages learned variance to decrease the proximity of counterfactual histories by minimizing the distance between the counterfactual sequences and the original sequence. Thorough experiments conducted on two real-world datasets demonstrate that the proposed CETD consistently surpasses current state-of-the-art methods.
1. Introduction
Sequential recommendation focuses on predicting users’ preferences by leveraging their historical behaviors [,,,]. In recent years, sequential recommendations that specifically model sequential behavior have achieved encouraging performance on various online platforms. High-quality explanations for sequential recommendation play a pivotal role in helping users comprehend the reasoning behind item recommendations, consequently enhancing their satisfaction. Therefore, explainable sequential recommendation has recently attracted the attention of researchers.
Some previous works have greatly contributed to explainable sequential recommendation. Existing methods can be broadly categorized into two groups: deep learning approaches and knowledge graph-based methods. Deep learning methods use a wide range of deep learning techniques to generate explanations [,]. Knowledge graph methods encompass abundant information about users and items, enabling the generation of more intuitive and personalized explanations for the recommended items [,]. However, these methods still have limits because an explanation is built with correlation. Extracting correlations from the observed user behavior data without the support of causal inference may lead to incorrect explanations. Furthermore, we contend that a genuine explanation of a recommendation model should possess the capability to address queries such as “Would the system alter its decision if the user purchased a different set of items”? In essence, the explanation should be cognizant of the counterfactual world, encompassing unobserved user histories and their corresponding recommendations.
As an initial attempt at applying causal inference to explainable sequential recommendation [,], a perturbation model was utilized to generate counterfactual histories as input sequences and extract causal explanations through a causal rule mining model. However, this method cannot effectively address the two following challenges when generating counterfactual histories: (i) The historical records of a user consist of a sequence arranged in chronological order—for this reason, it is important that a model is capable of considering the temporal dependencies of user–item interactions when generating counterfactual histories; (ii) Proximity requires the magnitude of the perturbation for each historical sequence to be as small as possible. Indeed, counterfactual histories that closely resemble the original input records can be the most valuable and informative for a user [].
Considering the aforementioned challenges in explainable sequential recommendation, in this paper, we propose a counterfactual explanation model CETD. When generating counterfactual histories, CETD is integrated with gated recurrent units (GRUs). Rather than passing a subset of the entire history into a latent space regardless of temporal dependencies, it passes a historical sequence subset through a GRU. This can capture temporal dependencies among the user behavior sequence for enhancing interpretability. Meanwhile, CETD fits the distribution of reconstructed data, which are sequences of item embeddings generated by VAE given latent variational information, and generates counterfactual sequences using learned latent variance, which will reduce the proximity of counterfactual histories. Through our formulated counterfactual explanation model, CETD aims to generate high-quality explanations for sequential recommendation to ensure that it can be used in a real-life setting. Figure 1 illustrates an example counterfactual explanation output by our model for the recommended item suit.
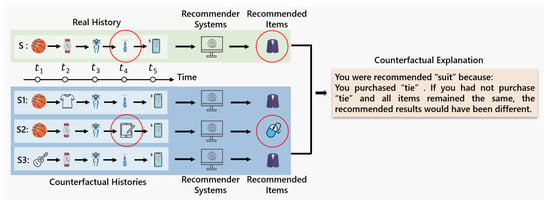
Figure 1.
An example of counterfactual explanation. In S1 and S3, we use the counterfactual replacement items T-shirt and guitar to replace watch and basketball in the Real History S, respectively, and the recommended item is still a suit. However, in S2, after replacing tie in S with iPad, the recommendation result changes to mouse. Therefore, tie could indeed be the genuine reason why the recommender systems recommend the originally recommended suit.
The key contributions of this paper are summarized as follows:
- We proposed a counterfactual explanation model based on a VAE for sequential recommendation that considers temporal dependencies. This aids in capturing both long-term preferences and short-term behavior for enhancing explainability.
- By fitting the distribution of the reconstructed data in the latent space and utilizing the learned latent variance, CETD can generate counterfactual sequences that are closer to the original sequence. This in turn reduces the proximity of the counterfactual history.
- We conducted extensive experiments to evaluate the effectiveness of our model on two real-world datasets. Results show that our model significantly outperforms state-of-the-art models.
2. Related Work
2.1. Sequential Recommendation
Studies pertaining to sequential recommendation aim to extract information regarding the transitions between items in a user’s sequence of interactions. Markov chains have been commonly employed in prior research to model the patterns of transition between items [,]. The advent of neural networks has prompted a shift in research on sequential recommendation towards the utilization of such networks, such as RNNs [,,,], convolutional neural networks [,], transformers [,,], and graph neural networks (GNNs) [,,]. To effectively model high-order sequential dependencies concealed within historical user–item interactions, e.g., RNNs in GRU4Rec [] and convolutional operations in Caser []. Inspired by the advantages of transformers, SASRec [] and BERT4Rec [] were built upon the self-attention mechanism for item–item relation modeling. GNN-based models [,] have been introduced to capture patterns that are more intricate than mere sequential patterns. While these models have demonstrated impressive performance, their utilization of complex neural network architectures can make it challenging to understand their decision-making processes, thereby motivating the need for explanation generation.
2.2. Explainable Recommendation
There is a significant body of research that attests to the crucial role of explanations in enabling users to evaluate the outcomes produced by a recommender system [,]. The employment of a knowledge graph is a widely adopted approach for generating explanations within the domain of recommendation systems [,,,]. For example, the PLM-Rec [] model is designed to generate explainable recommendations by leveraging knowledge graphs and path language modeling to capture both user behavior and item-side knowledge. There are also works that leverage sentiments and opinions to facilitate explainable recommendation. Wang et al. [] proposed a multitask learning solution for explainable recommendation that optimizes user preference for recommendation and generates opinionated content for explanation in a joint manner. Additionally, research endeavors have explored attribute-aware, explainable recommendation techniques [,]. Hou et al. [] extracted visual attributes from product images to generate interpretable recommendations. Although these existing approaches generate explanations for recommendation from different perspectives, they are built with correlation, which may not reflect the true causes of interaction. And, these approaches often necessitate redesigning the original recommendation model, which may lead to a compromise in model accuracy to attain satisfactory explanations. In this paper, we consider explainable recommendations from the causal perspective by utilizing counterfactual reasoning. In addition, our model is a model agnostic interpretable recommendation method, which considers the underlying recommendation model as a black box and does not affect the accuracy of the recommendation model.
2.3. Counterfactual Explanations
Within the domain of recommender systems, several studies have been conducted with the objective of furnishing counterfactual explanations to explicate recommendations. These approaches may involve the utilization of methods such as heterogeneous information networks [,,,], perturbation models [], or influence functions []. PRINCE [] is a recommendation model that leverages a polynomial-time optimal algorithm to identify a minimal set of user actions from a search space that is exponential in size, achieved through the use of random walks over dynamic graphs. Tran et al. [] proposed ACCENT which extends the influence function [] to generate counterfactual explanations for neural recommender systems. CountER [] is an explanation generation model that produces explanations by simulating counterfactual changes to item attributes. CCR [] integrates the power of logical reasoning and counterfactual reasoning and generates explicit counterfactual data to enhance the performance of recommendation models. In contrast to obtaining counterfactual explanations by objectives, the generation of counterfactual explanations was addressed by Xu et al. [] through the use of a perturbation model and a causal rule mining model. In contrast to the aforementioned works, our model considers temporal dependencies when generating counterfactual histories and reduces the proximity of counterfactual histories.
3. Propose Model
3.1. Notations
In the present study, the set of users is denoted as , while the set of items is denoted as . Every user u is linked to a set of purchase history represented by a series of items . In this paper, calligraphic represents a user history and straight H represents an item in the user’s history . The function represents a black-box sequential recommendation model that takes an input sequence of items and produces recommended items as its output.
3.2. Problem Formulation
Prior research on explainable sequential recommendation has predominantly focused on correlation-based approaches, with a dearth of studies investigating the potential of causal inference. Our research aims to address this gap by developing an item-level post hoc model that captures the causal relationships between historical items and recommended items for each user. Specifically, our proposed model takes into account temporal dependencies when generating counterfactual histories, thereby ensuring that the resulting sequences remain close to the real historical interactions.
3.3. The CETD Model
3.3.1. Perturbation Model
Our approach involves a perturbation-based method to generate counterfactual histories by substituting items in the original user history . The two mainstream generative models VAE and generative adversarial network (GAN) have their own strengths and weaknesses, with VAE relying on hypothetical conditions and GAN being less interpretable. Given that the user’s histories exhibit a non-random pattern, we posit the existence of a ground truth user history distribution and utilize VAE to acquire knowledge of this distribution.
Given the chronological order of a user’s historical records, the perturbation model’s ability to consider temporal and sequential user–item interactions is critical in generating meaningful counterfactual histories. Within the specified timestamp, we posit that the selection of a particular item is influenced by an underlying latent factor that captures user trends and preferences. Indeed, the latent factor is subject to influence from the user history and can be modeled to encompass both long-term preferences and short-term behavior. The basic framework VAE can be utilized to effectively model time-aware user preferences. In this scenario, we presume the presence of timing information denoted by and incorporate a temporal mark in the elements of . The term (with ) corresponds to the item in at the t-th position, whereas represents the sequence . Ideally, latent variable modeling when used to generate counterfactual histories must be able to express temporal dynamics. In a probabilistic framework, we incorporate temporal dependencies by conditioning each event on the preceding events. can be formulated as:
Note that is an initialization when is the first item in as . This specification highlights two essential aspects: (i) The existence of a recurrent relationship between and , designed by , which allows for advantageous modeling; and (ii) the capability to treat each time-step independently, specifically by employing a conditional VAE for modeling. The proposed distribution incorporates a dependency on the latent variable through a recurrent layer, enabling the retrieval of information from the previous history. The GRU model represents an advancement over the Long short-term memory (LSTM) model, as it includes storage units to retain long-term historical data. In the context of time series prediction, GRU exhibits a prediction accuracy that is at least comparable to that of the LSTM model while offering a higher computational efficiency. In this paper, we used GRU to learn the recurrent relationship between and .
As shown in Figure 2, in detail, we pass the users’ real history into the embedding layer to obtain the corresponding embedding . Then, we pass through a GRU layer, which can learn the temporal dependencies of the previous history and thus further obtain the output of enhanced long-term preference memory G. Counterfactual history can be precisely derived for any real history using the VAE, which consists of an encoder = Encoder(·) and a decoder = Decoder(·). Furthermore, the VAE extracts the encoded item sequences’ mean and variance from the latent space first, and then samples the latent embedding Z based on the above variational information. The obtained embedding is then passed to the decoder, which generates the perturbed sequence . The items embedded in are currently sampled vectors from the latent space and may not correspond to actual items. To address this, we employ dot product similarity to determine its closest neighbor in the item set \, which serves as the actual item representation. By employing the aforementioned approach, undergoes a transformation to the final counterfactual history . In order to generate w distinct counterfactual histories for each user, the perturbation process will be repeated w times. Ultimately, the original will be used as inputs to the black-box recommendation model along with the generated counterfactual data , resulting in the recommendation outcomes and , respectively. Upon completing this process, we will obtain w distinct counterfactual input–output pairs for each user u. In this context, w is manually set, but it should not exceed the total number of feasible item combinations.
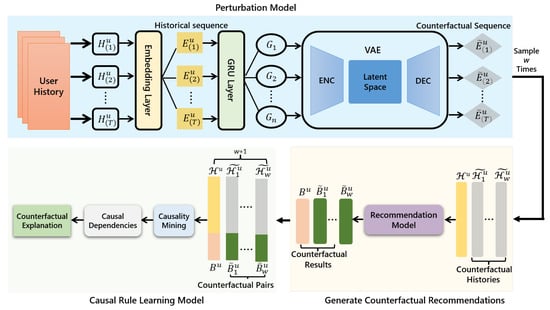
Figure 2.
Overall architecture of our proposed model CETD. represents the concatenation of item embeddings derived from the user history, while denotes the perturbed embedding.
Intuitively, a counterfactual history formed after the perturbation is as relevant as possible to the user’s interest. For a user, the proximity can be quantified as Equation (2). The distance in this case is specified in the latent space. Any historical sequence may be represented by concatenating the latent representations of all the items in the series. Any distance between two sequences is calculated based on the Euclidean distance, and the proximity value is computed by averaging across all users.
The iterative optimization objectives in our model training process include two terms: The first term will fit the mean and variance distributions of the variables in the potential space, whereas the second term can be interpreted as a (negative) reconstruction error. To ensure similarity between the generated sequences and the original sequence, it is imperative to maintain a small variance during the sampling process. We train the model using the following loss function:
The first term represents the Kullback–Leibler (KL) divergence of the approximate from the true posterior . We default , . Z is the potential variance information. is the input to the encoder. is output of the decoder. And, is a weight parameter.
3.3.2. Causal Rule Learning Model
For a user u, we define as the composite dataset that comprises the original pair and the counterfactual input–output pairs . We can define … as the input sequence of the i-th record in , where is the t-th item in . Let denote the corresponding output for this input sequence. Our goal is to construct a causal model that initially identifies causal relationships between input and output items that are present in the , and subsequently selects the causal rule by analyzing the inferred causal dependencies. Our contention is that a single output event can be represented by a logistic regression model that takes into account the causal dependencies of all input items in the sequence. It is necessary for the model to be able to suppose the causal dependency that exists between the input item and the output item .
In recommendation tasks, the proximity of a behavior is a strong predictor of a user’s future behaviors, while the impact of past behaviors diminishes over time. Specifically, earlier behaviors are given less weight in the recommendation algorithm compared to more recent behaviors. To account for the temporal effect of behaviors on the recommendation algorithm, we introduce a weight growth parameter , where is a positive value that is less than 1. For a given input–output pair in , the probability of its occurrence can be calculated by:
To scale the score to a value within the range of 0–1, we utilized the sigmoid function , which is defined as . The input value is transformed by the function to produce the desired output. According to Equation (4), the calculated probability should be close to 1. In order to derive the causal dependencies , we maximize the probability over . Once all the causal dependencies have been collected, we identify those dependencies whose output corresponds to the original input . Then, we construct counterfactual explanations based on the items with higher scores. The counterfactual explanation that is extracted is personalized as a result of the algorithm that is applied to , which only consists of records that are centered around the user’s original record . The complete algorithm is presented in Algorithm 1.
| Algorithm 1: Counterfactual explanations by considering temporal dependencies |
 |
In Algorithm 1, generating counterfactual interpretations of their recommended items for each user u can be divided into three phases: lines 5–8 are the perturbation phases, where the perturbation model perturbs the history times to generate counterfactual histories, passes them into the recommendation model to generate their corresponding recommendation results, and ultimately composes w pairs of counterfactual input–input pairs ; lines 9–14 are the causal rule learning phase, where the causal rule learning model is utilized to learn the causal dependency between each input term and the output item ; lines 15–20 are the generation of the interpretation phase, where the model generates its corresponding counterfactual explanations for the item recommended to the user u.
4. Experiments
4.1. Experimental Setup
4.1.1. Datasets
To assess the effectiveness of our proposed counterfactual explanation model, we conduct evaluations on two distinct datasets. The first dataset is MovieLens100k (https://grouplens.org/datasets/movielens/ (accessed on 30 July 2023)), while the second dataset comprises office products from Amazon (https://nijianmo.github.io/amazon/ (accessed on 30 July 2023)). In order to enable sequential recommendation with an input length of 5, we preprocess the original 5-core dataset by selecting only those users who have made at least 15 purchases and those items that have received at least 10 interactions. This filtering process enables us to generate a subset of the original dataset that is better suited for our proposed approach. To facilitate the explanation of sequential recommendation, we split the dataset chronologically, which ensures that the model is trained and tested on data that are representative of the actual order in which the interactions occurred.
4.1.2. Sequential Recommendation Models
We employ the following methodologies to train the black-box sequential recommendation models, and for each method, parameter selection is based on their corresponding implementations in the public domain.
FPMC []: This approach integrates matrix factorization with the Markov chain model to accomplish sequential recommendation.
GRU4Rec []: This approach utilizes GRUs to capture sequential dependencies and generate recommendations.
NARM []: This approach utilizes an attention mechanism to determine the user’s purpose based on their sequential behavior and purpose.
Caser []: This approach utilizes vertical and horizontal convolutions to capture sequential behavior patterns for recommendation.
4.1.3. Baselines
Traditional association rules serve as comparative explanations. Meanwhile, our model CETD is compared with the following state-of-the-art method that generates causal explanations for sequential recommendation.
AR-sup []: This model extracts association rules from user interactions and ranks them according to the support value in order to produce item-level explanations for all users.
AR-conf []: This model extracts association rules and ranks them according to their confidence values to obtain explanations
AR-lift []: This model generates explanations by ordering association rules based on lift value.
CR-VAE []: The model utilizes a perturbation model to generate counterfactual histories and extracts explanations through a causal rule mining model.
To ensure a fair comparison, the parameters of the association rule-based explanation model are set according to the recommendations in []. We select the top 100 rules as explanations based on their corresponding values. Regarding the causal rule model CR-VAE, we adopt the parameter selection from [], where for both datasets.
4.1.4. Training Details
CETD consists of an embedding layer with a size of 256, a GRU-based recurrent layer with 320 cells, two encoding layers (1024 and 512 in size), and two decoding layers (512 and 1024 in size). The number of latent factors Z for the VAE was set to 16. The optimization of the loss function was performed using Adam with a weight decay of 0.01. The number of counterfactual histories m defaults to 500. The default weight parameter is set to 0.003, and the default time growth factor is .
4.1.5. Evaluation Metrics
Specifically, our model’s evaluation is conducted from three perspectives. Firstly, the model is required to provide explanations for a significant portion of recommendations (see fidelity in the subsequent section), indicating the percentage of recommended items that the model can explain. Secondly, we will validate the significance of our counterfactual explanations as an integral component in recommending the original item. One of the commonly used methods is through the assessment of the causal impact of the model’s recommendation results [].
Two binary random variables a and b, where the average causal effect (ACE) of a on b is defined as follows: . In this context, the notation denotes an external intervention that exerts a compulsion on a variable to adopt a specific value. Given an extracted counterfactual explanation , we define the variable if occurs or 0 otherwise. We define b as a binary random variable, where if occurs and 0 otherwise. We then estimate the ACE as the Equations (5) and (6) are based on w counterfactual pairs.
Finally, our model must be able to generate counterfactual histories that are closer to the real history (proximity). CETD is a model-agnostic interpretable recommendation approach that considers the underlying recommendation model as a black-box. CETD delivers explanations after making the recommendation decision without compromising the model’s recommendation performance. As a result, we solely report the evaluation metrics for the explanation results.
4.2. Results
4.2.1. Fidelity
Table 1 presents a comprehensive summary of the best results obtained by all models on the two datasets. The information contained in Table 1 allows for several observations.

Table 1.
Results of model fidelity. CR-VAE and our model CETD are tested under (the number of candidate counterfactual explanations). The bold scores in each column represent the best results, while the underlined scores indicate the best results of the baseline.
On both datasets, our counterfactual explanation model CETD generates explanations for most of the recommended items, whereas the association explanation approach can only offer explanations for a considerably smaller number of recommendations. This is due to the number of input–output pairs being too small to match the global rules with individual interactions and recommendations, thus greatly constraining the flexibility of the association rule model. In contrast, CETD has the capability of generating numerous counterfactual histories, enabling effective causal rule learning, and allowing the extraction of counterfactual explanations beyond the constraints of the original limited data. Meanwhile, our model CETD outperforms the baseline CR-VAE; CETD can capture both long-term preferences and short-term behavior for a user’s real history when creating counterfactual histories, which can generate more counterfactual sequences with temporal dynamics. Furthermore, these counterfactual histories can better help the causal rule learning model learn causal dependencies. Although the improvement in our model CETD over CR-VAE is not remarkable, CETD will still boost the fidelity of the explanations due to the huge number of items and users in the real world.
4.2.2. Average Causal Effect
The ACE values of CETD and CR-VAE are shown in Figure 3, which verify that our counterfactual explanations are an important component for recommending the original item. As the ACE value is exclusively applicable to related causal models, it cannot be reported for the association rule baselines.
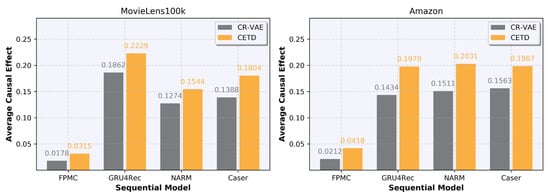
Figure 3.
Average causal effect results. CR-VAE and our model CETD are tested under (the number of candidate counterfactual explanations).
CETD achieves higher ACE values than CR-VAE for most sequential recommendation models on both datasets, which verify that the counterfactual explanations generated by CETD are a crucial component of the recommendation. This is because our perturbation model is able to capture the temporal dependencies of users’ real historical sequences during the training process, so that when using latent variable modeling to generate counterfactual histories, temporal dynamics can be expressed, which can extract the causality and dependency between users’ historical preferences more accurately and finally provide higher-quality counterfactual explanations.
Additionally, FPMC relies on the Markov chain, which solely considers the last behavior. Consequently, when altering a few input items, the FPMC model only generates a limited number of counterfactual histories that deviate from the true historical recommendation items, leading to a lower ACE value.
4.2.3. Proximity
As shown in Figure 4, the reported proximity value represents the average value across all users. However, since the association rule model does not incorporate counterfactual histories, this study only reports this indicator for CETD and CR-VAE.
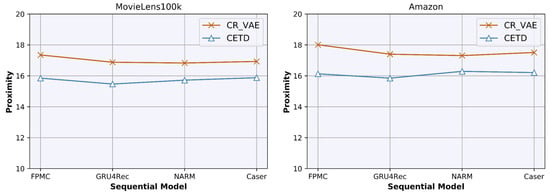
Figure 4.
Proximity results. The proximity value is calculated by Equation (2).
CETD can achieve lower proximity compared with the baseline CR-VAE. Thus, by fitting the distribution of reconstructed data to converge to a normal distribution and then using the latent variance obtained from learning to generate counterfactual sequences, the counterfactual histories can be made more similar to the real history. More specifically, we use the cross-entropy loss function to calculate the reconstruction loss during the iterative training process. And, we fit the mean and variance distributions of the variables in the potential space. CETD is able to accommodate the similarity in the Euclidean distance. Therefore, lower proximity means that the counterfactual histories generated by CETD have higher quality and are more useful for later causal learning.
4.3. Case Study
We offer a straightforward case study to compare our model of CETD with the traditional association explanation model. Specifically, we demonstrate an example involving the sequential recommendation model GRU4Rec [] on the MovieLens100k dataset, as depicted in Figure 5. Even if the recommendation system recommends the same movie (movie Pulp Fiction) to two different users, and the two users have an overlapping viewing record (commonly watched movie The Sound of Music), CETD still has the capability to generate personalized explanations for different users. Nevertheless, due to the extraction of association rules based on global records, the association model will offer the same interpretation for all users, lacking personalization.

Figure 5.
A case study on MovieLens100k by the GRU4Rec model.
4.4. Ablation Study
Here, we thoroughly demonstrate the capability of CETD to enhance the interpretability of sequential recommendations. Specifically, we discuss the capability of CETD through ablation experiments in the two following tasks.
- (i)
- Does CETD provide high-quality explanations for most of the recommendations on different sequential recommendation models?
As shown in Figure 6a,b, we remove the module capturing temporal dependencies from CETD (denoted by “CETD(w/o A)”) to see how its performance changes on different sequential recommendation models. Generating counterfactual sequences by capturing the temporal dependencies of users’ real historical sequences can provide higher-quality counterfactual explanations for most sequential recommendation models.
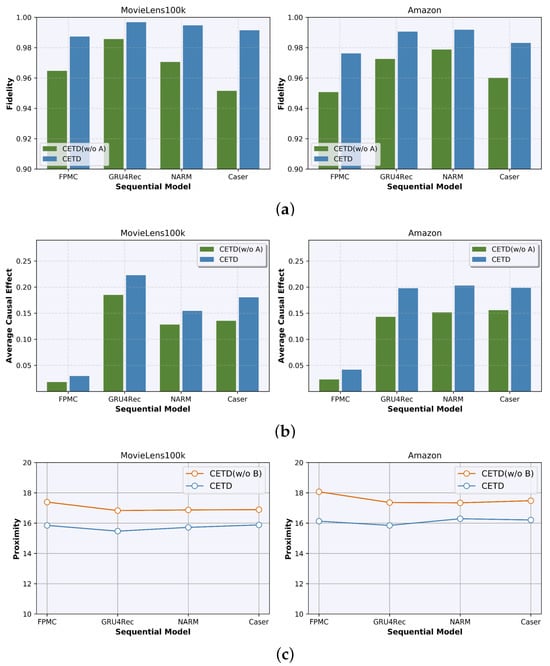
Figure 6.
Results of CETD in the ablation tests for different sequential recommendation models on the MovieLens100k and Amazon datasets, respectively. (a) Comparison between CETD and CETD (w/o A) for fidelity; (b) Comparison between CETD and CETD (w/o A) for average causal effect; and (c) Comparison between CETD and CETD (w/o B) for proximity.
- (ii)
- Can CETD generate counterfactual histories that are closer to the real history and further reduce the proximity?
We remove the module fitting reconstructed data from CETD (denoted by “CETD(w/o B)”) to observe how its performance changes on different sequential recommendation models. In Figure 6c, when CETD fits the distribution of reconstruction data to converge to a normal distribution in a latent space and generates counterfactual sequences using the learned latent variance, the proximity of the counterfactual histories can be effectively reduced.
4.5. Influence of Parameters
In this section, we will explore the impact of a crucial parameter: the time decay parameter is denoted by . In our framework, while elucidating the sequential recommendation models, it is essential to note that earlier interactions within the sequence are subject to diminishing effects on the recommended item. An appropriately tuned time decay parameter plays a pivotal role in enhancing the framework’s ability to mitigate noise signals during the process of pattern learning from the sequence.
Figure 7 illustrates the impact of parameter on various sequential recommendation models and datasets. The results reveal that the time decay factor, denoted as , significantly influences the model performance concerning fidelity. Notably, for smaller values of , earlier interactions within a sequence tend to be disregarded, resulting in a decrease in model fidelity. Conversely, for larger values of , such as , older interactions hold equal importance alongside the most recent ones, which also leads to a reduction in performance. Our findings indicate that the optimal performance is attained at approximately for both datasets.
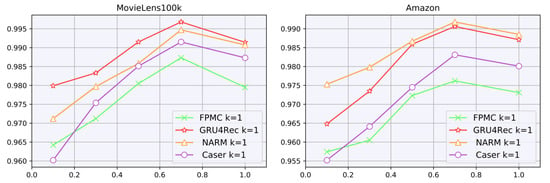
Figure 7.
CETD fidelity on the different time decay parameters . x axis is the time decay parameter and y axis is the model fidelity.
5. Conclusions
In this paper, we propose CETD, a counterfactual explanation model based on a VAE for sequential recommendation that handles temporal dependencies. Meanwhile, CETD fits the distribution of reconstructed data in a latent space and uses the learned latent variance, which can generate closer counterfactual sequences to the original sequence. Extensive experiments on two real-world datasets demonstrated that CETD is not only able to generate high-quality explanations for most sequential recommendation models, but also effectively reduce the proximity of counterfactual histories. However, the data gathered from user history interactions are observational rather than experimental, which may result in various biases within the dataset. For our future work, we will explore counterfactual reasoning for raw data debiasing and advance the research on counterfactual explanation.
Author Contributions
Writing—original draft, B.A.; Writing—review& editing, J.W. and H.W.; Supervision, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The research work in this paper uses a publicity available dataset, which can be accessed here: https://grouplens.org/datasets/movielens/, https://nijianmo.github.io/amazon/, accessed on 10 September 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, R.; McAuley, J. Fusing similarity models with markov chains for sparse sequential recommendation. In Proceedings of the IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 191–200. [Google Scholar]
- Kang, W.C.; McAuley, J. Self-attentive sequential recommendation. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 197–206. [Google Scholar]
- Ma, C.; Ma, L.; Zhang, Y.; Sun, J.; Liu, X.; Coates, M. Memory augmented graph neural networks for sequential recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 5045–5052. [Google Scholar]
- Tang, J.; Wang, K. Personalized top-n sequential recommendation via convolutional sequence embedding. In Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, Marina Del Rey, CA, USA, 5–9 February 2018; pp. 565–573. [Google Scholar]
- Gholami, E.; Motamedi, M.; Aravindakshan, A. PARSRec: Explainable personalized attention-fused recurrent sequential recommendation using session partial actions. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 454–464. [Google Scholar]
- Li, Y.; Chen, H.; Li, Y.; Li, L.; Philip, S.Y.; Xu, G. Reinforcement Learning based Path Exploration for Sequential Explainable Recommendation. IEEE Trans. Knowl. Data Eng. 2023, 35, 11801–11814. [Google Scholar] [CrossRef]
- Hou, H.; Shi, C. Explainable sequential recommendation using knowledge graphs. In Proceedings of the 5th International Conference on Frontiers of Educational Technologies, Beijing, China, 1–3 June 2019; pp. 53–57. [Google Scholar]
- Huang, X.; Fang, Q.; Qian, S.; Sang, J.; Li, Y.; Xu, C. Explainable interaction-driven user modeling over knowledge graph for sequential recommendation. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 548–556. [Google Scholar]
- Xu, S.; Li, Y.; Liu, S.; Fu, Z.; Ge, Y.; Chen, X.; Zhang, Y. Learning causal explanations for recommendation. In Proceedings of the 1st International Workshop on Causality in Search and Recommendation, Virtual Event, 15 July 2021. [Google Scholar]
- Xu, S.; Li, Y.; Liu, S.; Fu, Z.; Ge, Y.; Chen, X.; Zhang, Y. Learning post hoc causal explanations for recommendation. arXiv 2020, arXiv:2006.16977. [Google Scholar]
- Mothilal, R.K.; Sharma, A.; Tan, C. Explaining machine learning classifiers through diverse counterfactual explanations. In Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency, Barcelona, Spain, 27–30 January 2020; pp. 607–617. [Google Scholar]
- Rendle, S.; Freudenthaler, C.; Schmidt-Thieme, L. Factorizing personalized markov chains for next-basket recommendation. In Proceedings of the 19th International Conference on World Wide Web, Raleigh North, CA, USA, 26–30 April 2010; pp. 811–820. [Google Scholar]
- Hidasi, B.; Karatzoglou, A.; Baltrunas, L.; Tikk, D. Session-based recommendations with recurrent neural networks. arXiv 2015, arXiv:1511.06939. [Google Scholar]
- Hou, Y.; Mu, S.; Zhao, W.X.; Li, Y.; Ding, B.; Wen, J.R. Towards universal sequence representation learning for recommender systems. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 585–593. [Google Scholar]
- Xu, C.; Zhao, P.; Liu, Y.; Xu, J.; Sheng, V.S.S.S.; Cui, Z.; Xiong, H. Recurrent convolutional neural network for sequential recommendation. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 3398–3404. [Google Scholar]
- Li, M.; Zhang, Z.; Zhao, X.; Wang, W.; Zhao, M.; Wu, R.; Guo, R. AutoMLP: Automated MLP for Sequential Recommendations. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1190–1198. [Google Scholar]
- Yang, Y.; Huang, C.; Xia, L.; Huang, C.; Luo, D.; Lin, K. Debiased Contrastive Learning for Sequential Recommendation. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1063–1073. [Google Scholar]
- Sun, F.; Liu, J.; Wu, J.; Pei, C.; Lin, X.; Ou, W.; Jiang, P. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1441–1450. [Google Scholar]
- Hou, Y.; He, Z.; McAuley, J.; Zhao, W.X. Learning vector-quantized item representation for transferable sequential recommenders. In Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 1162–1171. [Google Scholar]
- Chang, J.; Gao, C.; Zheng, Y.; Hui, Y.; Niu, Y.; Song, Y.; Li, Y. Sequential recommendation with graph neural networks. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 378–387. [Google Scholar]
- Liu, Z.; Chen, Y.; Li, J.; Yu, P.S.; McAuley, J.; Xiong, C. Contrastive self-supervised sequential recommendation with robust augmentation. arXiv 2021, arXiv:2108.06479. [Google Scholar]
- Cai, R.; Wu, J.; San, A.; Wang, C.; Wang, H. Category-aware collaborative sequential recommendation. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 388–397. [Google Scholar]
- Yang, A.; Wang, N.; Cai, R.; Deng, H.; Wang, H. Comparative explanations of recommendations. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 3113–3123. [Google Scholar]
- Fu, Z.; Xian, Y.; Gao, R.; Zhao, J.; Huang, Q.; Ge, Y.; de Melo, G. Fairness-aware explainable recommendation over knowledge graphs. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 25–30 July 2020; pp. 69–78. [Google Scholar]
- Geng, S.; Fu, Z.; Tan, J.; Ge, Y.; De Melo, G.; Zhang, Y. Path language modeling over knowledge graphsfor explainable recommendation. In Proceedings of the ACM Web Conference, Lyon, France, 25–29 April 2022; pp. 946–955. [Google Scholar]
- Jiang, H.; Li, C.; Cai, J.; Wang, J. RCENR: A Reinforced and Contrastive Heterogeneous Network Reasoning Model for Explainable News Recommendation. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, Taipei, Taiwan, 23–27 July 2023; pp. 1710–1720. [Google Scholar]
- Shuai, J.; Wu, L.; Zhang, K.; Sun, P.; Hong, R.; Wang, M. Topic-enhanced Graph Neural Networks for Extraction-based Explainable Recommendation. In Proceedings of the 46th International ACM SIGIR Conference on Research and Development in Information Retrieval, Taipei, Taiwan, 23–27 July 2023; pp. 1188–1197. [Google Scholar]
- Wang, N.; Wang, H.; Jia, Y.; Yin, Y. Explainable recommendation via multi-task learning in opinionated text data. In Proceedings of the 41st international ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 165–174. [Google Scholar]
- Hou, M.; Wu, L.; Chen, E.; Li, Z.; Zheng, V.W.; Liu, Q. Explainable fashion recommendation: A semantic attribute region guided approach. arXiv 2019, arXiv:1905.12862. [Google Scholar]
- Wang, L.; Cai, Z.; de Melo, G.; Cao, Z.; He, L. Disentangled CVAEs with contrastive learning for explainable recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington DC, USA, 7–14 February 2023; pp. 13691–13699. [Google Scholar]
- Ghazimatin, A.; Balalau, O.; Saha Roy, R.; Weikum, G. PRINCE: Provider-side interpretability with counterfactual explanations in recommender systems. In Proceedings of the 13th International Conference on Web Search and Data Mining, Houston, TX, USA, 3–7 February 2020; pp. 196–204. [Google Scholar]
- Tan, J.; Geng, S.; Fu, Z.; Ge, Y.; Xu, S.; Li, Y.; Zhang, Y. Learning and evaluating graph neural network explanations based on counterfactual and factual reasoning. In Proceedings of the ACM Web Conference, Lyon, France, 25–29 April 2022; pp. 1018–1027. [Google Scholar]
- Prado-Romero, M.A.; Prenkaj, B.; Stilo, G. Developing and Evaluating Graph Counterfactual Explanation with GRETEL. In Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, Singapore, 27 February–3 March 2023; pp. 1180–1183. [Google Scholar]
- Guo, H.; Nguyen, T.H.; Yadav, A. CounterNet: End-to-End Training of Prediction Aware Counterfactual Explanations. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 577–589. [Google Scholar]
- Tran, K.H.; Ghazimatin, A.; Saha Roy, R. Counterfactual explanations for neural recommenders. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, 11–15 July 2021; pp. 1627–1631. [Google Scholar]
- Cheng, W.; Shen, Y.; Huang, L.; Zhu, Y. Incorporating interpretability into latent factor models via fast influence analysis. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 885–893. [Google Scholar]
- Tan, J.; Xu, S.; Ge, Y.; Li, Y.; Chen, X.; Zhang, Y. Counterfactual explainable recommendation. In Proceedings of the 30th ACM International Conference on Information & Knowledge Management, Gold Coast, Australia, 1–5 November 2021; pp. 1784–1793. [Google Scholar]
- Ji, J.; Li, Z.; Xu, S.; Xiong, M.; Tan, J.; Ge, Y.; Zhang, Y. Counterfactual Collaborative Reasoning. In Proceedings of the Sixteenth ACM International Conference on Web Search and Data Mining, Singapore, 27 February–3 March 2023; pp. 249–257. [Google Scholar]
- Li, J.; Ren, P.; Chen, Z.; Ren, Z.; Lian, T.; Ma, J. Neural attentive session-based recommendation. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 1419–1428. [Google Scholar]
- Peake, G.; Wang, J. Explanation mining: Post hoc interpretability of latent factor models for recommendation systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 2060–2069. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).