Real-Time Path Planning for Obstacle Avoidance in Intelligent Driving Sightseeing Cars Using Spatial Perception
Abstract
:1. Introduction
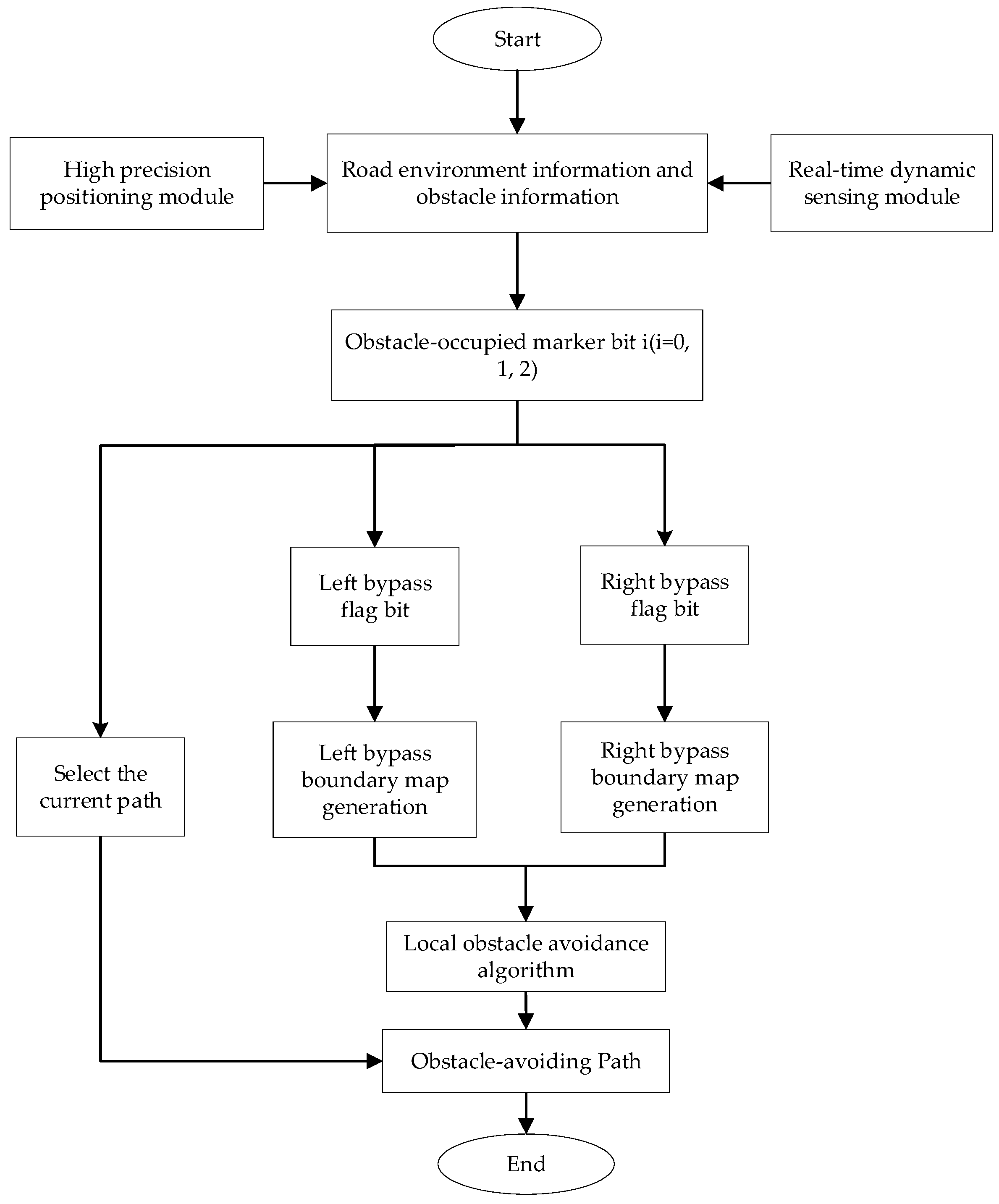
2. Local Path Generation Based on Spatial Perception
2.1. Dynamic Control Point Determination
2.1.1. Acquisition of Global Path Points
2.1.2. Determination of Control Points for Local Obstacle Avoidance Path
2.2. Dynamic Control Point Optimization
2.3. Obstacle Avoidance Path Generation
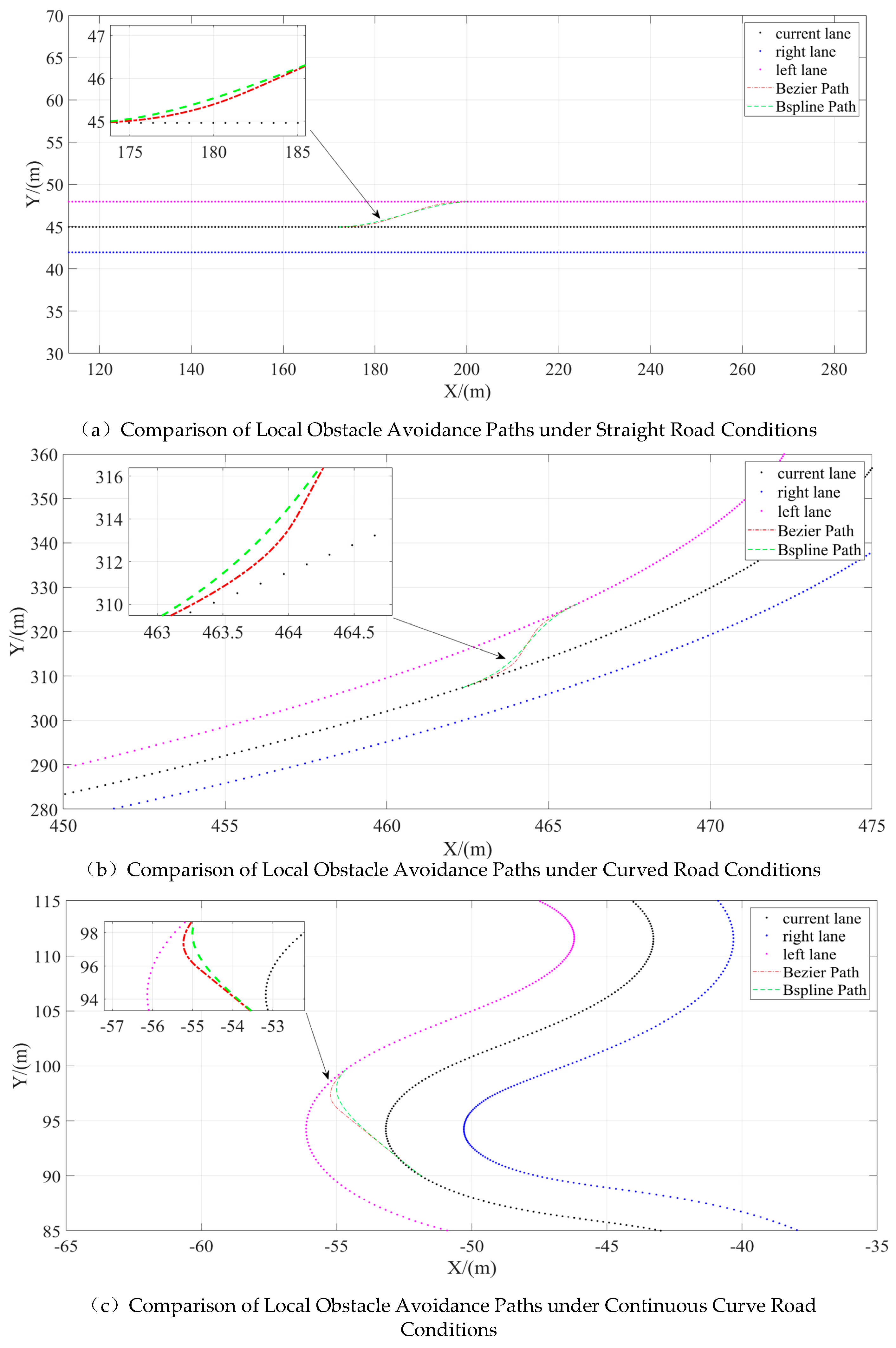
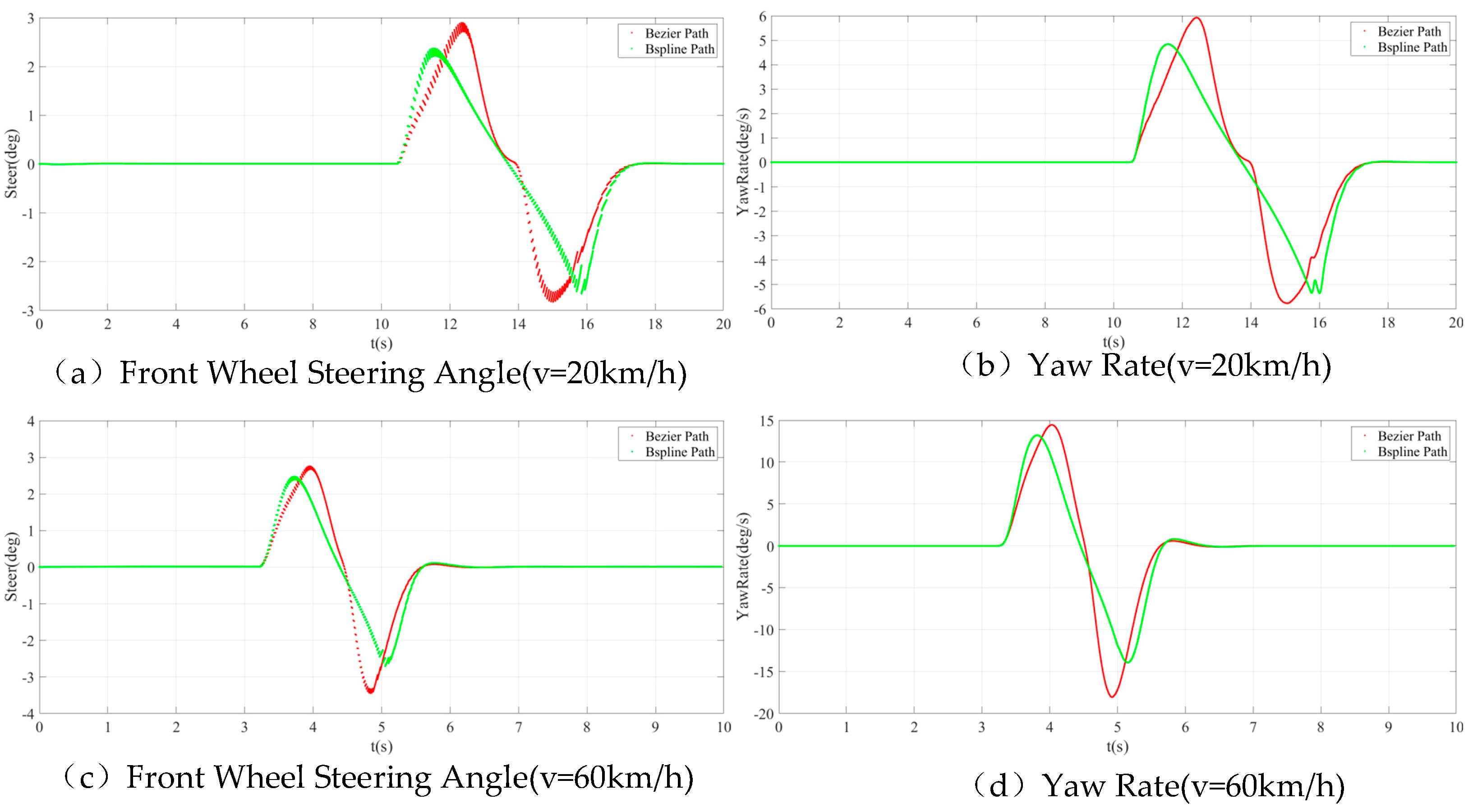
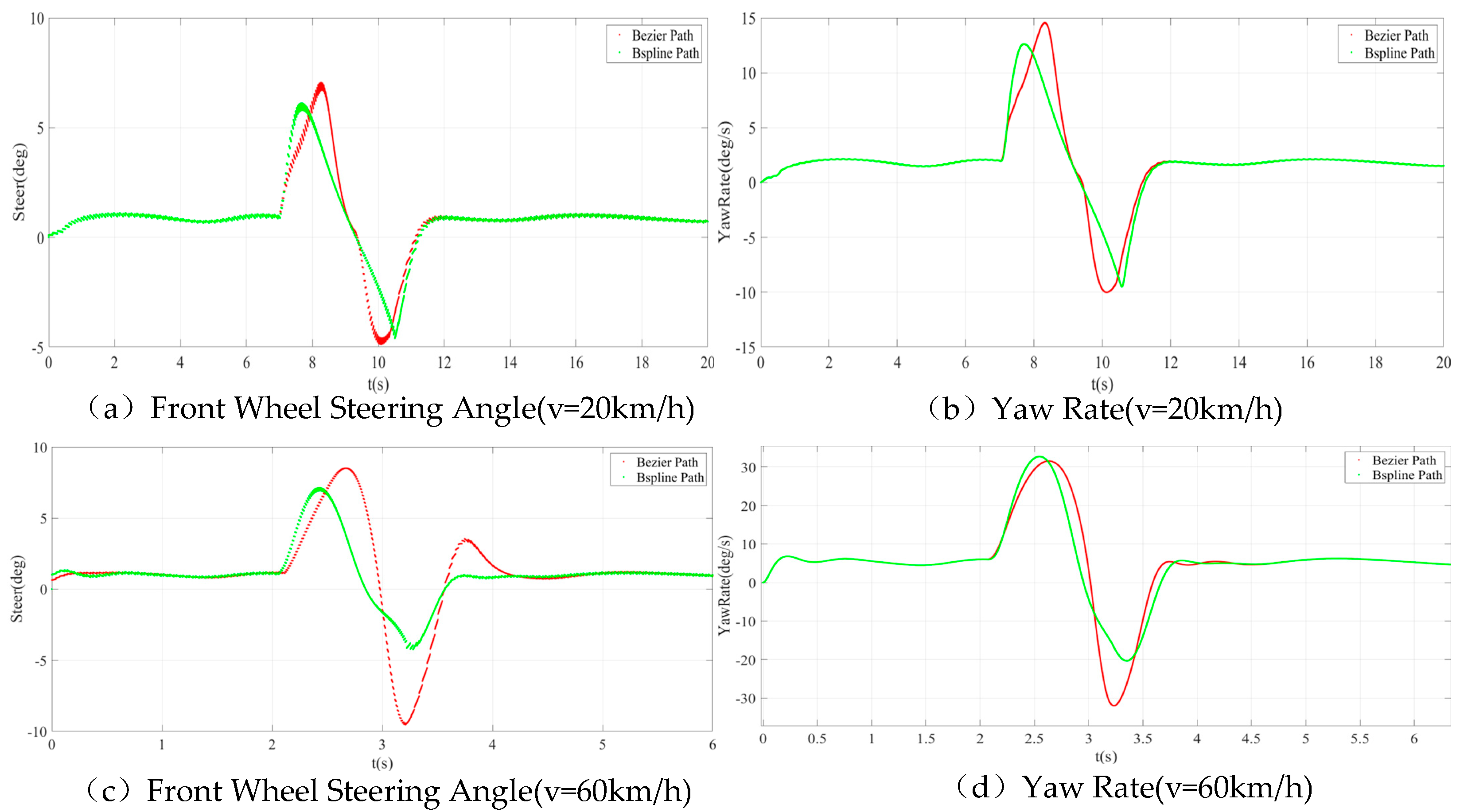
3. Simulation Analysis
3.1. Model Construction
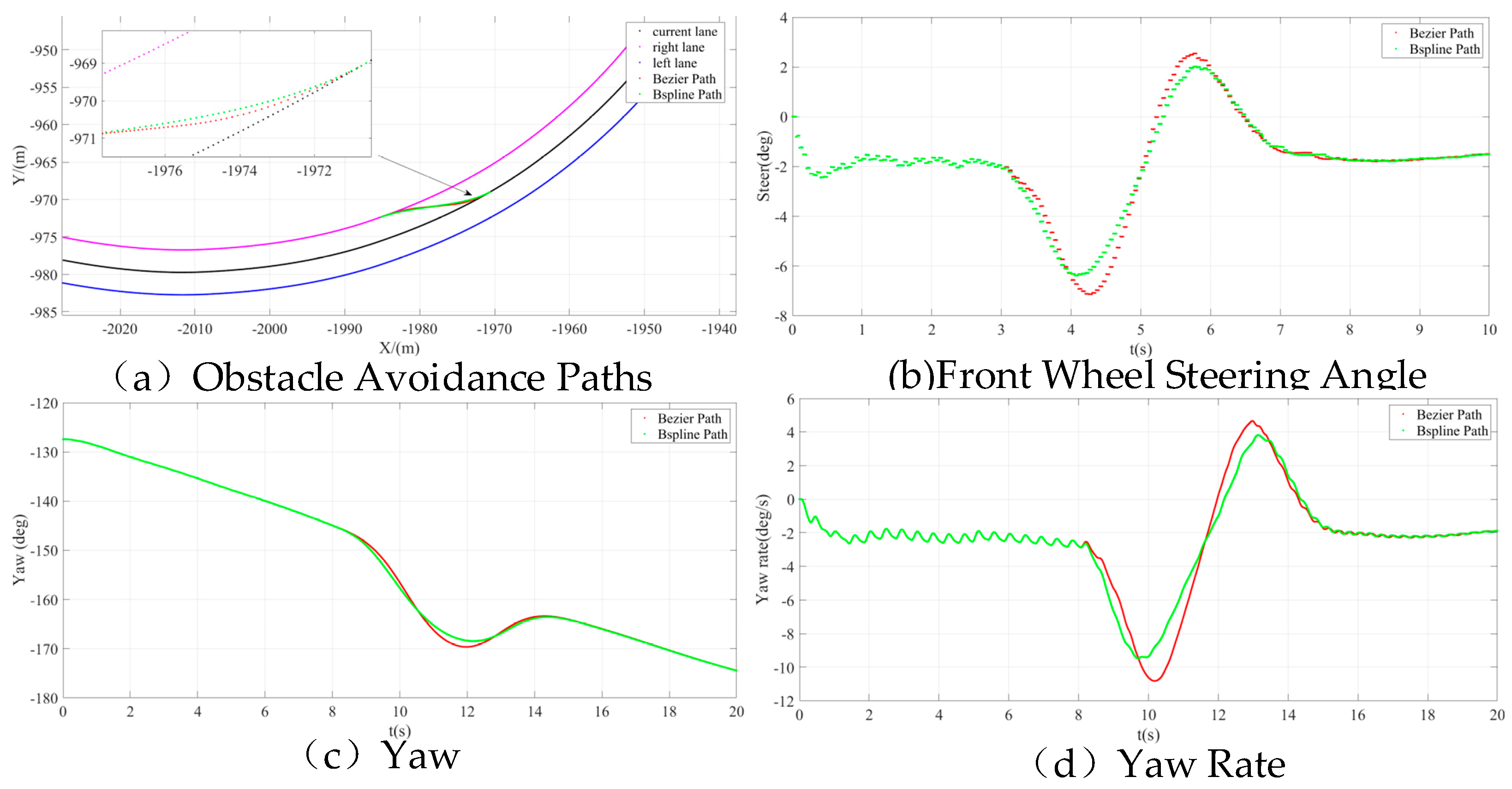
3.2. Simulation Result
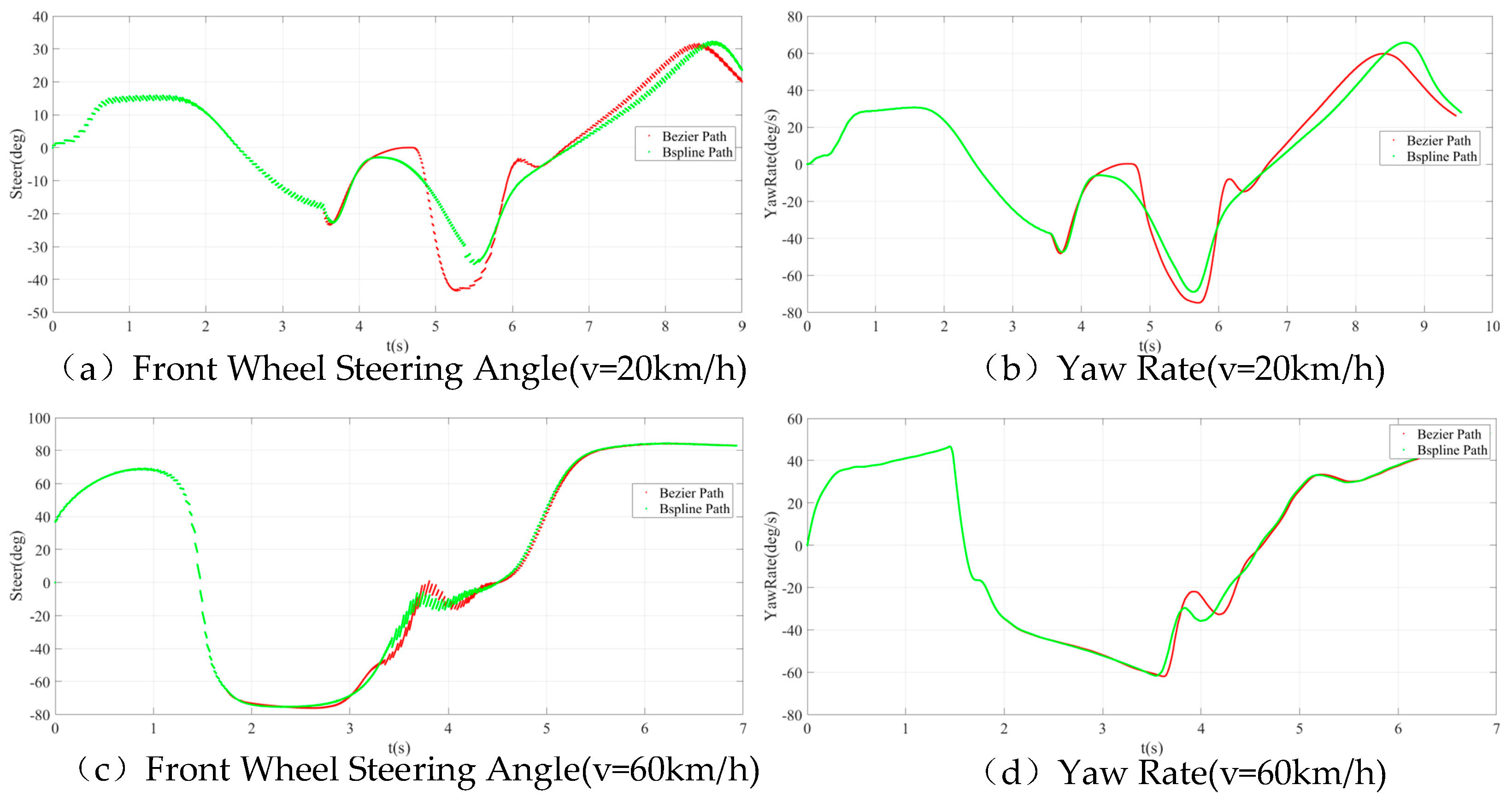
4. On-Vehicle Experiment
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Fan, J.; Liu, Y.; Wang, X. Path Planning and Path Tracking for Autonomous Vehicle Based on MPC with Adaptive Dual-Horizon-Parameters. Int. J. Automot. Technol. 2022, 23, 1239–1253. [Google Scholar] [CrossRef]
- Xiong, L.; Fu, Z.; Zeng, D.; Qian, Z.; Leng, B. A Path Planning and Tracking Framework Based on Model Predictive Control for Autonomous Vehicle Obstacle Avoidance. In Proceedings of the 27th Symposium of the International Association of Vehicle System Dynamics, IAVSD 2021, Virtual, 17–19 August 2021; pp. 1137–1143. [Google Scholar]
- Tang, P.; Yang, R.; Ni, X.; Zhao, H.; Xu, F. Research on a lightweight unmanned sightseeing vehicle frame based on multi-condition and multi-objective optimization. Adv. Mech. Eng. 2022, 14, 16878132221131748. [Google Scholar] [CrossRef]
- Jiao, M.; Song, Y. Path Planning for Unmanned Campus Sightseeing Vehicle with Linear Temporal Logic. In Proceedings of the 2018 Chinese Intelligent Systems Conference, Singapore, 23 December 2019; pp. 329–337. [Google Scholar]
- Wang, M.-L.; Luo, J.-H.; Yang, Y.; Liu, T.; Li, Y.-F. Application Analysis of GIS on UGV Autonomous Navigation. Beijing Ligong Daxue Xuebao/Trans. Beijing Inst. Technol. 2019, 39, 907–911. [Google Scholar] [CrossRef]
- Lim, K.-I.; Oh, J.-S.; Lee, J.-U.; Kim, J.-H. Development of an intelligent cruise control using path planning based on a geographic information system. J. Inst. Control Robot. Syst. 2015, 21, 217–223. [Google Scholar] [CrossRef]
- Choi, Y.-G.; Lim, K.-I.; Kim, J.-H. Lane change and path planning of autonomous vehicles using GIS. In Proceedings of the 12th International Conference on Ubiquitous Robots and Ambient Intelligence, URAI 2015, Goyang City, Republic o Korea, 28–30 October 2015; pp. 163–166. [Google Scholar]
- Hosseinyalamdary, S.; Balazadegan, Y.; Toth, C. Tracking 3D Moving Objects Based on GPS/IMU Navigation Solution, Laser Scanner Point Cloud and GIS Data. ISPRS Int. J. Geo-Inf. 2015, 4, 1301–1316. [Google Scholar] [CrossRef]
- Zhu, H.; Fu, M.; Yang, Y.; Wang, X.; Wang, M. A path planning algorithm based on fusing lane and obstacle map. In Proceedings of the 2014 17th IEEE International Conference on Intelligent Transportation Systems, ITSC 2014, Qingdao, China, 8–11 October 2014; pp. 1442–1448. [Google Scholar]
- Wang, M.-L.; Pan, Y.-H. Research on optimal path planning with constraints based on GIS. Beijing Ligong Daxue Xuebao/Trans. Beijing Inst. Technol. 2016, 36, 851–856; 861. [Google Scholar] [CrossRef]
- Fu, M.; Song, W.; Yi, Y.; Wang, M. Path Planning and Decision Making for Autonomous Vehicle in Urban Environment. In Proceedings of the 18th IEEE International Conference on Intelligent Transportation Systems, ITSC 2015, Gran Canaria, Spain, 15–18 September 2015; pp. 686–692. [Google Scholar]
- Yang, F.; Zhu, Z.; Gong, X.-J.; Liu, J.-L. Real-time dynamic obstacle detection and tracking using 3D Lidar. Zhejiang Daxue Xuebao (Gongxue Ban)/J. Zhejiang Univ. (Eng. Sci.) 2012, 46, 1565–1571. [Google Scholar] [CrossRef]
- Zhong, M.; Wu, Y.; Wan, F.; Fu, Q. Research on Dynamic Path Planning of Internet of Vehicles Based on Edge Computing. In Proceedings of the 2nd International Conference on Networking, Communications and Information Technology, NetCIT 2022, Virtual, 26–27 December 2022; pp. 453–457. [Google Scholar]
- Shi, S.; Cui, J.; Jiang, Z.; Yan, Z.; Xing, G.; Niu, J.; Ouyang, Z. VIPS: Real-Time Perception Fusion for Infrastructure-Assisted Autonomous Driving. In Proceedings of the 28th ACM Annual International Conference on Mobile Computing and Networking, MobiCom 2022, Sydney, NSW, Australia, 17–21 October 2202; pp. 133–146. [Google Scholar]
- Gamerdinger, J.; Teufel, S.; Volk, G.; Bringmann, O. CoLD Fusion: A Real-time Capable Spline-based Fusion Algorithm for Collective Lane Detection. In Proceedings of the 34th IEEE Intelligent Vehicles Symposium, IV 2023, Anchorage, AK, USA, 4–7 June 2023; IEEE Intelligent Transportation Systems Society (ITSS): Piscataway, NJ, USA, 2023. [Google Scholar]
- Gonzalez, D.; Perez, J.; Milanes, V.; Nashashibi, F. A review of motion planning techniques for automated vehicles. IEEE Intell. Transp. Syst. Mag. 2016, 17, 1135–1145. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Xu, X. Improved RRT-Connect Based Path Planning Algorithm for Mobile Robots. IEEE Access 2021, 9, 145988–145999. [Google Scholar] [CrossRef]
- Tang, X.; Zhu, Y.; Jiang, X. Improved a-star algorithm for robot path planning in static environment. In Proceedings of the 2020 International Conference on Communications, Information System and Software Engineering, CISSE 2020, Guangzhou, China, 18–20 December 2020. [Google Scholar]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A Review of Motion Planning for Highway Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1826–1848. [Google Scholar] [CrossRef]
- Kang, J.-G.; Lim, D.-W.; Choi, Y.-S.; Jang, W.-J.; Jung, J.-W. Improved RRT-connect algorithm based on triangular inequality for robot path planning. Sensors 2021, 21, 333. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Zeng, P.; Yang, W.; Li, Y.; Zhan, Z. Bézier curve-based trajectory planning for autonomous vehicles with collision avoidance. IET Intell. Transp. Syst. 2020, 14, 1882–1891. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, C.; Ma, L. Dynamic Lane-changing Trajectory Planning Model for Intelligent Vehicle Based on Quadratic Programming. Zhongguo Gonglu Xuebao/China J. Highw. Transp. 2021, 34, 79–94. [Google Scholar] [CrossRef]
- Han, L.; Yashiro, H.; Nejad, H.T.N.; Do, Q.H.; Mita, S. Bézier curve based path planning for autonomous vehicle in urban environment. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, IV 2010, La Jolla, CA, USA, 21–24 June 2010; pp. 1036–1042. [Google Scholar]
- Chen, C.; He, Y.; Bu, C.; Han, J.; Zhang, X. Quartic Bézier curve based trajectory generation for autonomous vehicles with curvature and velocity constraints. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6108–6113. [Google Scholar]
- Donatelli, M.; Giannelli, C.; Mugnaini, D.; Sestini, A. Curvature continuous path planning and path finding based on PH splines with tension. CAD Comput. Aided Des. 2017, 88, 14–30. [Google Scholar] [CrossRef]
- Yamamoto, M.; Iwamura, M.; Mohri, A. Quasi-time-optimal motion planning of mobile platforms in the presence of obstacles. Proc.–IEEE Int. Conf. Robot. Autom. 1999, 4, 2958–2963. [Google Scholar]
- Xu, W.; Yang, Y.; Yu, L.-T.; Zhu, L. A global path planning algorithm based on improved RRT. Kongzhi Yu Juece/Control Decis. 2022, 37, 829–838. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Randomized Bidirectional B-Spline Parameterization Motion Planning. IEEE Trans. Intell. Transp. Syst. 2016, 17, 406–419. [Google Scholar] [CrossRef]
- Wang, P.; Yang, J.; Zhang, Y.; Wang, Q.; Sun, B.; Guo, D. Obstacle-Avoidance Path-Planning Algorithm for Autonomous Vehicles Based on B-Spline Algorithm. World Electr. Veh. J. 2022, 13, 233. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Fan, M.; Wu, G.; Pedrycz, W.; Suganthan, P.N. An Autonomous Path Planning Method for Unmanned Aerial Vehicle based on A Tangent Intersection and Target Guidance Strategy. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3061–3073. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Wang, W. Path Planning and Obstacle Avoidance Control for Autonomous Multi-Axis Distributed Vehicle Based on Dynamic Constraints. IEEE Trans. Veh. Technol. 2023, 72, 4342–4356. [Google Scholar] [CrossRef]
- Wang, S.Z.; Xu, W. Safe Distance Model for Control of Vehicle Emergency Collision Avoidance. Int. J. Veh. Struct. Syst. 2021, 13, 598–603. [Google Scholar] [CrossRef]
- Zhang, R.; Li, K.; Wu, Y.; Zhao, D.; Lv, Z.; Li, F.; Chen, X.; Qiu, Z.; Yu, F. A Multi-Vehicle Longitudinal Trajectory Collision Avoidance Strategy Using AEBS with Vehicle-Infrastructure Communication. IEEE Trans. Veh. Technol. 2022, 71, 1253–1266. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, D.; Wang, H.; Chen, W.; Wang, Q.; Zhu, M. Study on Longitudinal Collision Avoidance with Human-machine Cooperation Based on Improved Safety Distance Model. Qiche Gongcheng/Automot. Eng. 2021, 43, 588–600. [Google Scholar]
- McNaughton, M.; Urmson, C.; Dolan, J.M.; Lee, J.-W. Motion planning for autonomous driving with a conformal spatiotemporal lattice. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, ICRA 2011, Shanghai, China, 9–13 May 2011; pp. 4889–4895. [Google Scholar]
- Maekawa, T.; Noda, T.; Tamura, S.; Ozaki, T.; Machida, K.-i. Curvature continuous path generation for autonomous vehicle using B-spline curves. CAD Comput. Aided Des. 2010, 42, 350–359. [Google Scholar] [CrossRef]
- Lu, E.; Ruan, Q.; Liu, Y.; Wang, F.; Lin, W.; Dong, B. Obstacle Avoidance Path Planning for Intelligent Forklift Truck Based on Dynamic Identification Zone and B-spline Curve. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2019, 50, 359–366. [Google Scholar] [CrossRef]
- Cao, H.; Zoldy, M. Implementing B-Spline Path Planning Method Based on Roundabout Geometry Elements. IEEE Access 2022, 10, 81434–81446. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Gangavarapu, P.T.; Kompe, N.F.; Schildbach, G.; Ernst, F. Navigation with Polytopes: A Toolbox for Optimal Path Planning with Polytope Maps and B-spline Curves. Sensors 2023, 23, 3532. [Google Scholar] [CrossRef] [PubMed]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Wu, F.; Li, R.; Yao, D.; Meng, L.; He, A. Real-Time Path Planning for Obstacle Avoidance in Intelligent Driving Sightseeing Cars Using Spatial Perception. Appl. Sci. 2023, 13, 11183. https://doi.org/10.3390/app132011183
Yang X, Wu F, Li R, Yao D, Meng L, He A. Real-Time Path Planning for Obstacle Avoidance in Intelligent Driving Sightseeing Cars Using Spatial Perception. Applied Sciences. 2023; 13(20):11183. https://doi.org/10.3390/app132011183
Chicago/Turabian StyleYang, Xu, Feiyang Wu, Ruchuan Li, Dong Yao, Lei Meng, and Ankai He. 2023. "Real-Time Path Planning for Obstacle Avoidance in Intelligent Driving Sightseeing Cars Using Spatial Perception" Applied Sciences 13, no. 20: 11183. https://doi.org/10.3390/app132011183
APA StyleYang, X., Wu, F., Li, R., Yao, D., Meng, L., & He, A. (2023). Real-Time Path Planning for Obstacle Avoidance in Intelligent Driving Sightseeing Cars Using Spatial Perception. Applied Sciences, 13(20), 11183. https://doi.org/10.3390/app132011183





