Three-Dimensional Limited-Memory BFGS Inversion of Magnetic Data Based on a Multiplicative Objective Function
Abstract
:1. Introduction
2. Forward and Inversion Theory
2.1. Three Dimensional Forward Modelling of the Magnetic Method
2.2. Magnetic Three-Dimensional Inversion
2.2.1. Traditional Magnetic Three-Dimensional Inversion
2.2.2. Three-Dimensional Limited-Memory BFGS Inversion Using a Magnetic Method Based on a Multiplicative Objective Function
- 1.
- Determine the initial inversion model, set the maximum number of inversion iterations and the minimum fitting difference, calculate the model item and add the constant value, and carry out depth weighting on the initial model;
- 2.
- Take the natural logarithm of the initial model and ;
- 3.
- Calculate the objective function and the gradient ;
- 4.
- Calculate the inverse matrix and the quasi-Newtonian direction ;
- 5.
- Set the initial step size, and perform a linear search from the initial step size to find the relative best iteration step size ;
- 6.
- Update the inversion model by the determined iteration step size and quasi-Newtonian direction;
- 7.
- Transform the updated models and using the exponential e;
- 8.
- Determine whether the data fitting difference of the current model is less than the set minimum fitting difference. If it is less, the iteration is stopped, and the depth-weighted inverse transformation is performed on the obtained model ; otherwise, the third step is performed again, and the iteration is continued.
3. Example of Theoretical Model Synthesis
3.1. Example of Single Prism Synthesis
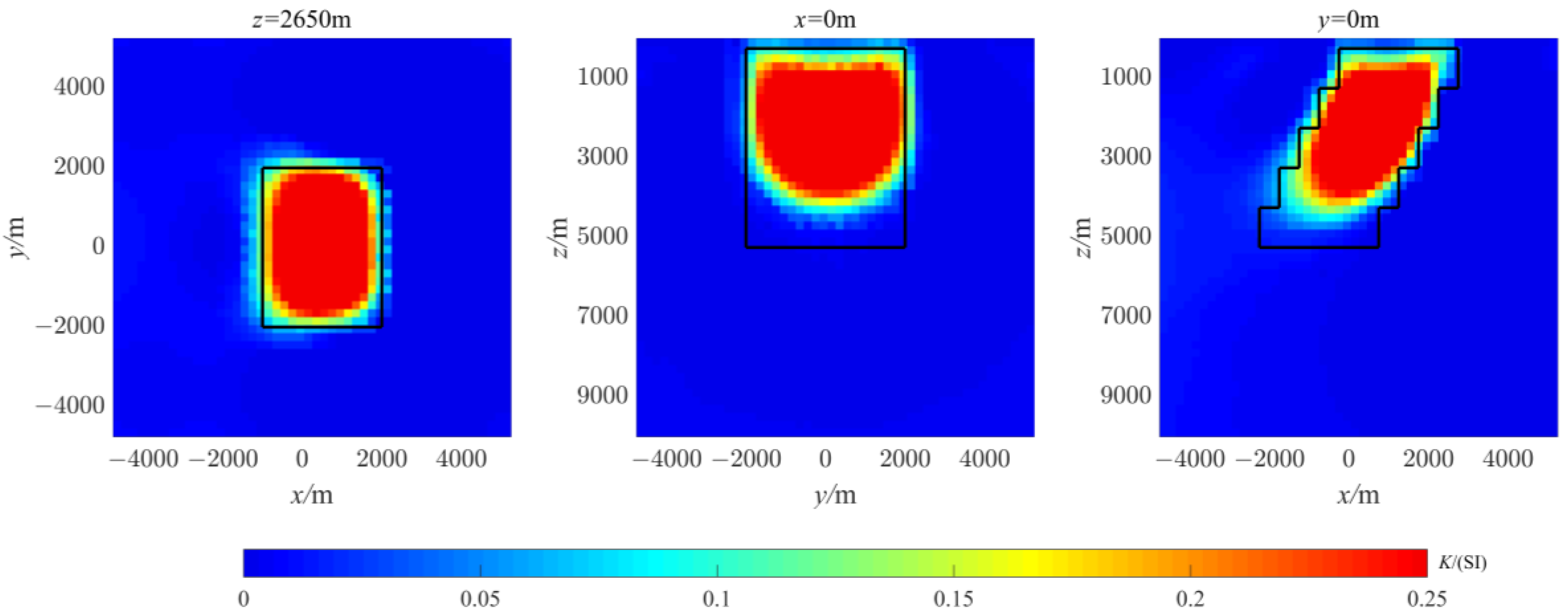
3.2. Examples of Oblique Prismatic Synthesis
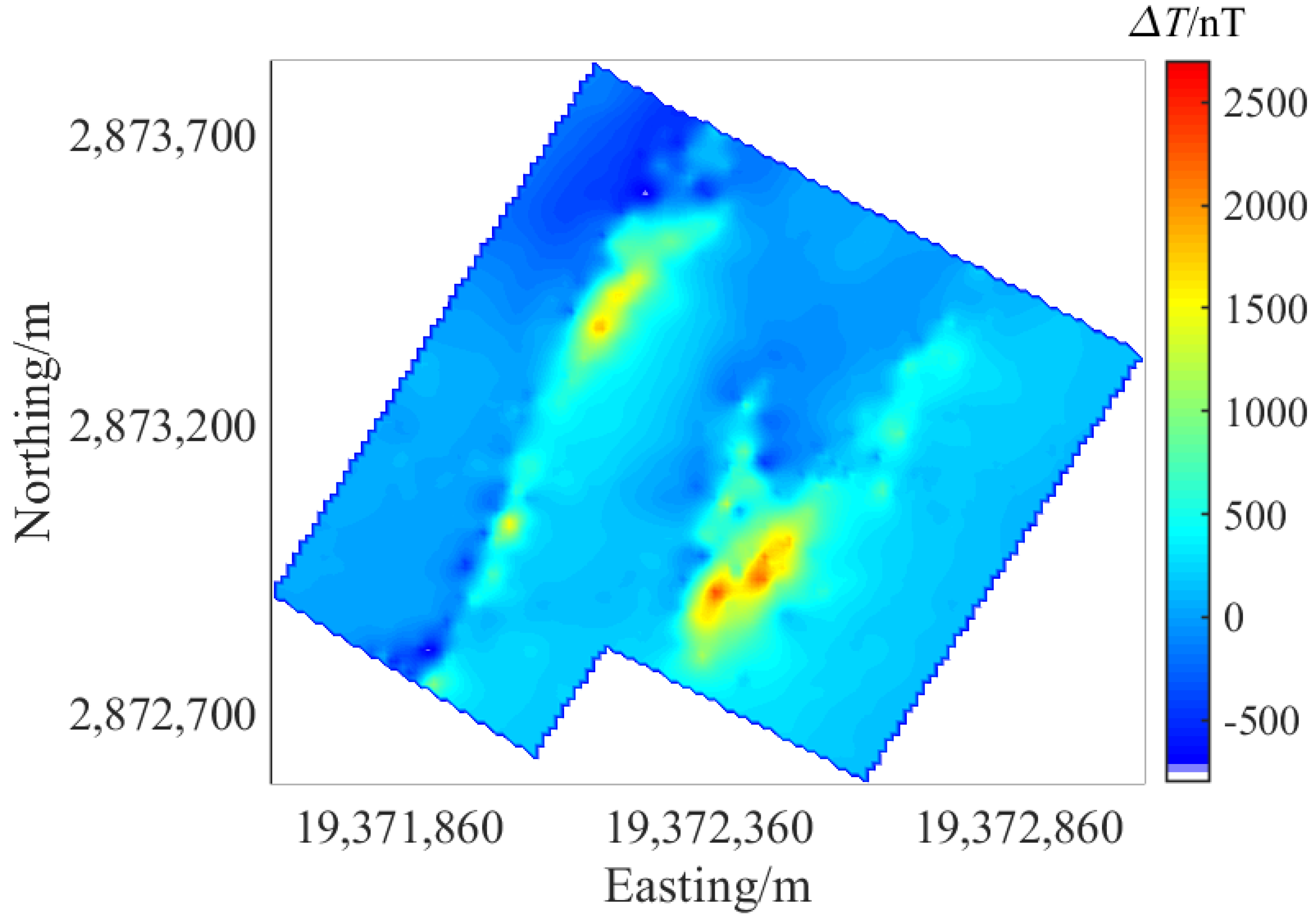
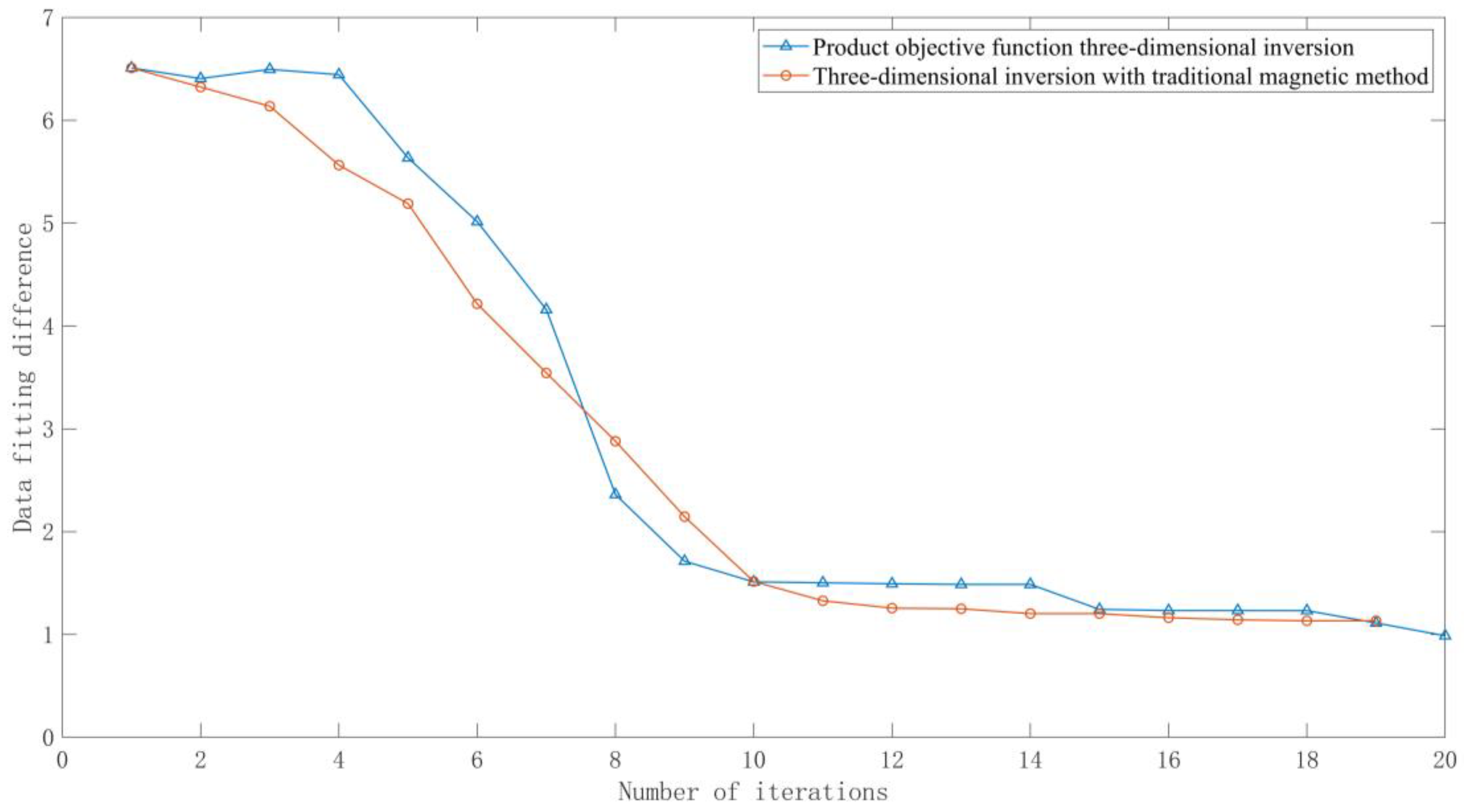
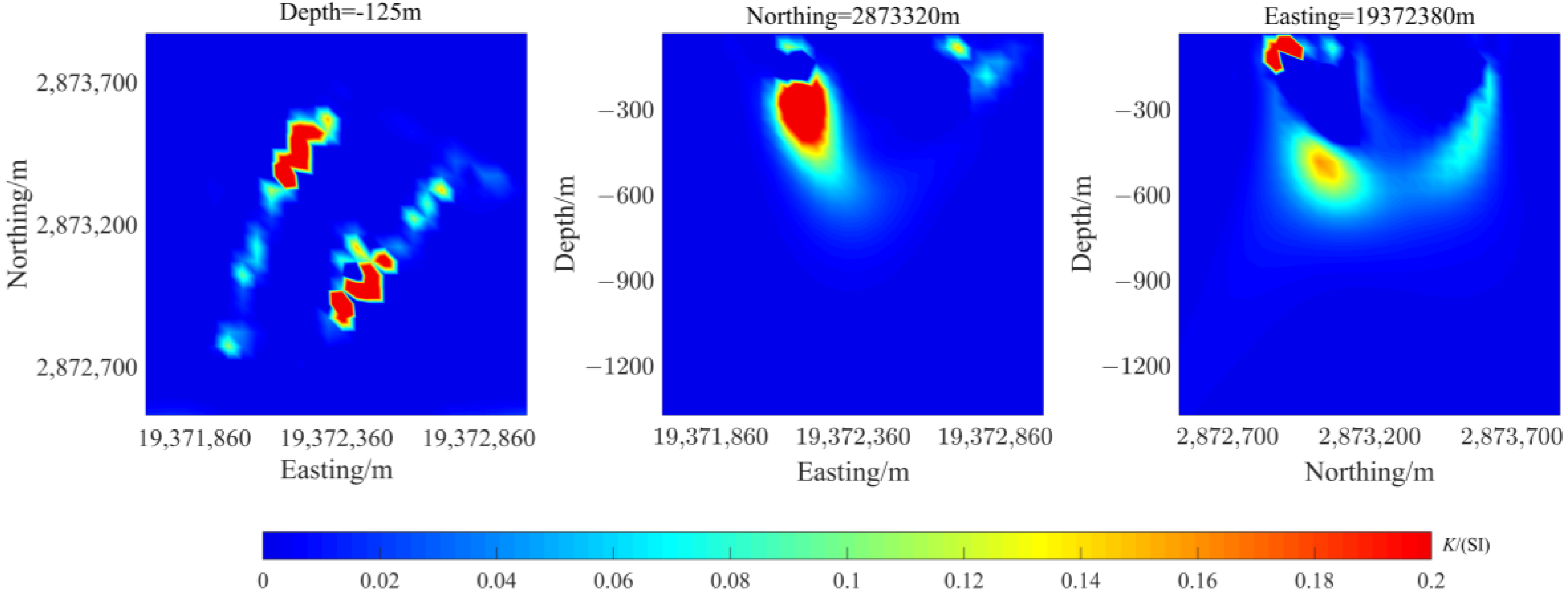
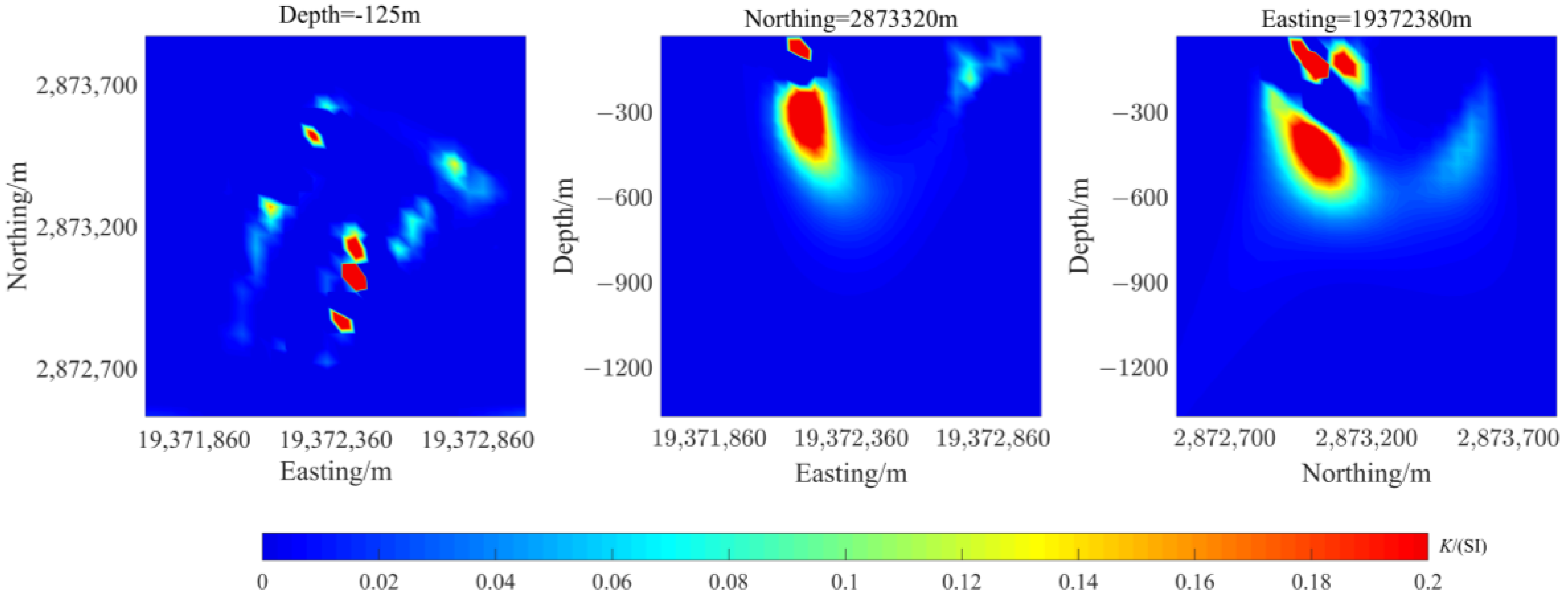
4. Measured Data Test
5. Conclusions
- (1)
- The initial inversion model was developed, the maximum number of inversion iterations and the minimum fitting difference were set, the model item was calculated, the constant value was added, and depth weighting on the initial model was carried out;
- (2)
- Inversion based on a multiplicative objective function can be used to more easily determine the weight factor of the regularization constraint term in the inversion objective function, which has obvious advantages compared with traditional inversion based on an additive objective function.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maksimov, M.A.; Surodina, I.V. Three-dimensional forward and inverse modelling of multi-height magnetic data using the relief maps. Russ. J. Geophys. Technol. 2020, 2, 4–11. [Google Scholar] [CrossRef]
- Liu, S.; Fedi, M.; Hu, X. 3D inversion of magnetic data in the simultaneous presence of significant remanent magnetization and self-demagnetization: Example from Daye iron-ore deposit, Hubei province, China. Geophys. J. Int. 2018, 215, 614–634. [Google Scholar] [CrossRef]
- Geng, M.; Ali, M.Y.; Fairhead, J.D.; Pilia, S.; Bouzidi, Y.; Barkat, B. Crustal structure of the United Arab Emirates and northern Oman Mountains from constrained 3D inversion of gravity and magnetic data: The Moho and basement surfaces. J. Asian Earth Sci. 2022, 231, 1–19. [Google Scholar] [CrossRef]
- Yan, J.; Lü, Q.; Qi, G.; Fu, G.; Zhang, K.; Lan, X.; Guo, X.; Wei, J.; Luo, F.; Wang, H.; et al. A 3D Geological Model Constrained by Gravity and Magnetic Inversion and its Exploration Implications for the World-class Zhuxi Tungsten Deposit, South China. Acta Geol. Sin. Engl. Ed. 2020, 94, 1940–1959. [Google Scholar]
- Dandan, J.; Zhaofa, Z.; Shuai, Z.; Guan, Y.; Lin, T.; Lu, P. Three-Dimensional Magnetic Inversion Based on an Adaptive Quadtree Data Compression. Appl. Sci. 2020, 10, 7636. [Google Scholar]
- Emad, G.; Jan, D. Joint gravity and magnetic inversion with trans-dimensional alpha shapes and autoregressive noise models. Inverse Probl. 2022, 38, 890–892. [Google Scholar]
- Wolde, M.T. Applications of Magnetic Method in Mapping Subsurface Structures in the Ziway Langano Corridor Central Main Ethiopian Rift. J. Geol. Geophys. 2021, 10, 991. [Google Scholar]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar]
- Li, Y.; Oldenburg, D.W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys. J. Int. 2003, 152, 251–265. [Google Scholar] [CrossRef]
- Yan, Z.; Tan, H.; Peng, M.; Kong, W.; Wu, P. Three-dimensional joint inversion of gravity, magnetic and magnetotelluric data based on cross-gradient theory. Chin. J. Geophys. 2020, 63, 736–752. [Google Scholar]
- Alpak, F.; Gao, G.; Florez, H.; Shi, S.; Vink, J.; Blom, C.; Saaf, F.; Wells, T. A machine-learning-accelerated distributed LBFGS method for field development optimization: Algorithm, validation, and applications. Comput. Geosci. 2023, 27, 425–450. [Google Scholar]
- Wang, K.; Tan, H.; Lin, C.; Yuan, J.; Wang, C.; Tang, J. Three-dimensional tensor controlled-source audio-frequency magnetotelluric inversion using LBFGS. Explor. Geophys. 2017, 49, 268–284. [Google Scholar] [CrossRef]
- Abubakar, A.; Van den Berg, P.M.; Mallorqui, J.J. Imaging of biomedical data using a multiplicative regularized contrast source inversion method. IEEE Trans. Microw. Theory Tech. 2002, 50, 1761–1771. [Google Scholar] [CrossRef]
- Li, M.; Abubakar, A.; Van den Berg, P.M. Application of the multiplicative regularized contrast source inversion method on 3D experimental Fresnel data. Inverse Probl. 2009, 25, 24006–24028. [Google Scholar] [CrossRef]
- van den Berg, P.M.; van Broekhoven, A.L.; Abubakar, A. Extended contrast source inversion. Inverse Probl. 1999, 15, 1325–1344. [Google Scholar] [CrossRef]
- Alpak, F.O.; Habashy, T.; Abubakar, A.; Torres-Verdin, C.; Sepehrnoori, K. A multiplicative regularized gauss-newton algorithm and its application to the joint inversion of induction logging and near-borehole pressure measurements. Prog. Electromagn. Res. B 2011, 29, 105–138. [Google Scholar] [CrossRef]
- Xie, H.; Tan, H.; Ma, F. Three-dimensional resistivity inversion based on product type objective function. Geoscience 2023, 37, 67–73. [Google Scholar]
- Guan, Z. Geomagnetic Field and Magnetic Exploration; Geological Publishing House: Beijing, China, 2005; Volume 7, pp. 119–121. [Google Scholar]
- Abubakar, A.; Li, M.; Pan, G.; Liu, J.; Habashy, T.M. Joint MT and CSEM data inversion using a multiplicative cost function approach. Geophysics 2011, 76, 203–214. [Google Scholar] [CrossRef]
- Chen, J. Modern Geodetic datum of China: China Geodetic Coordinate System 2000(CGCS 2000) and its framework. Acta Geod. Et Cartogr. Sin. 2008, 3, 269–271. [Google Scholar]
- Li, Z.; Yao, C.; Zheng, Y.; Wang, J.; Zhang, Y. 3D magnetic sparse inversion using an interior-point method. Geophysics 2018, 83, 15–32. [Google Scholar] [CrossRef]



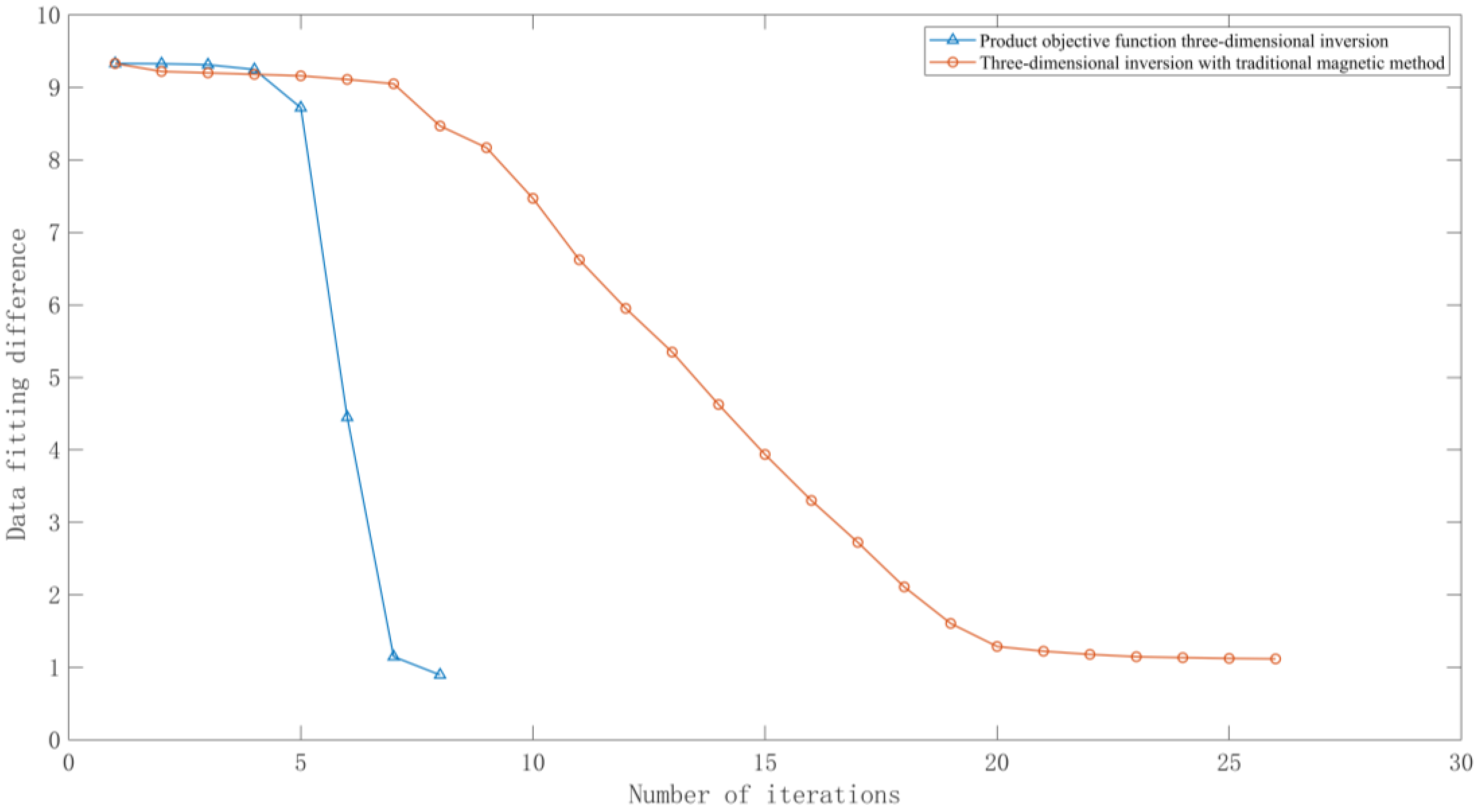
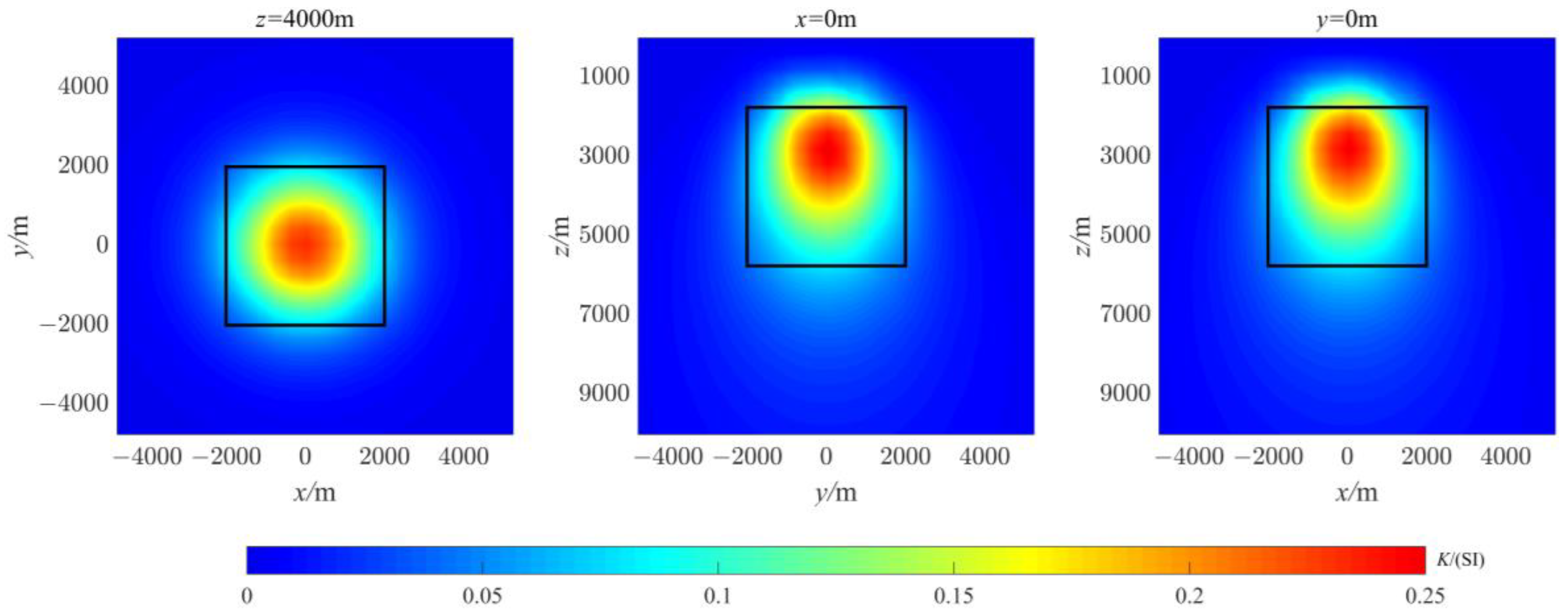

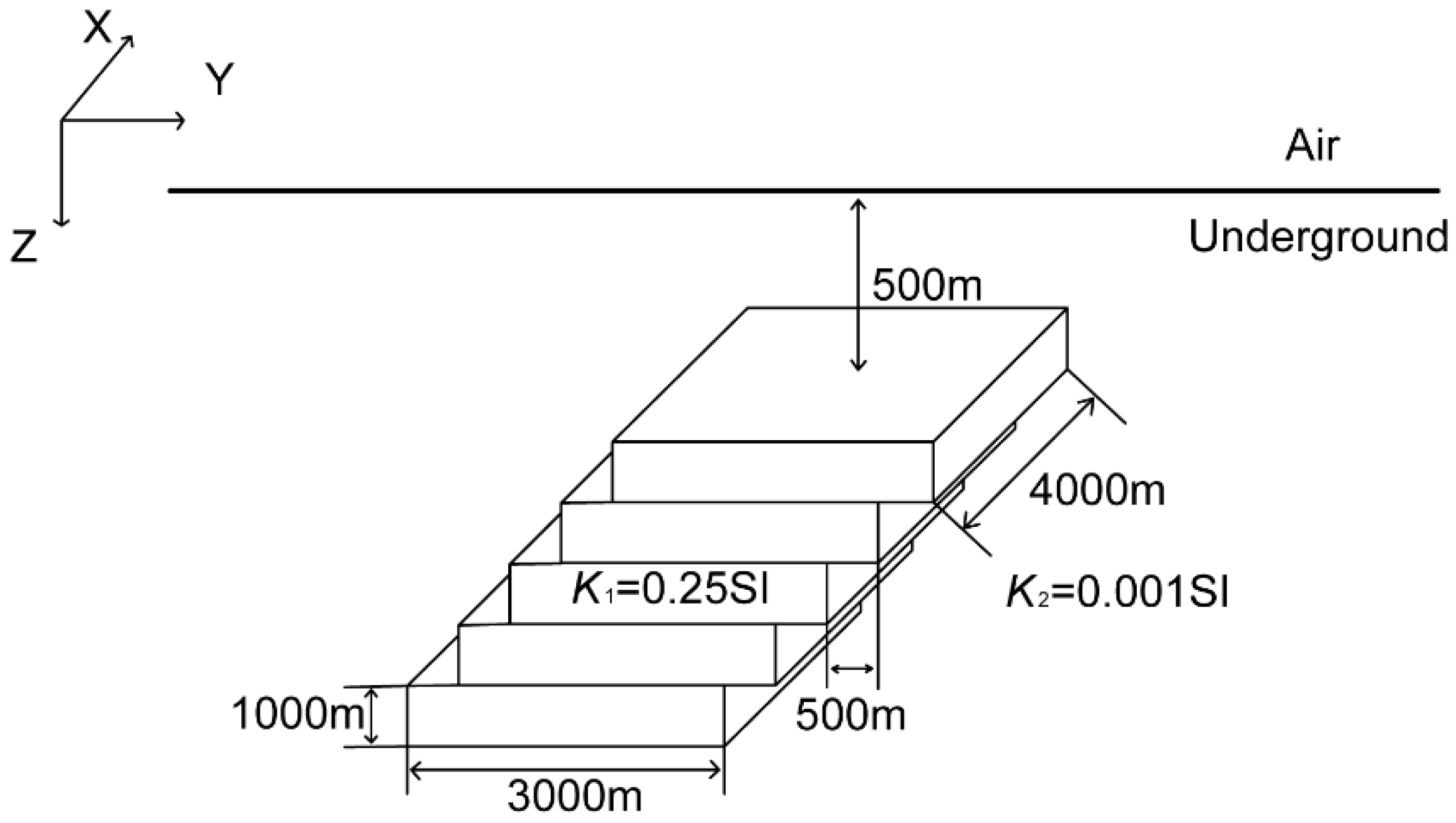
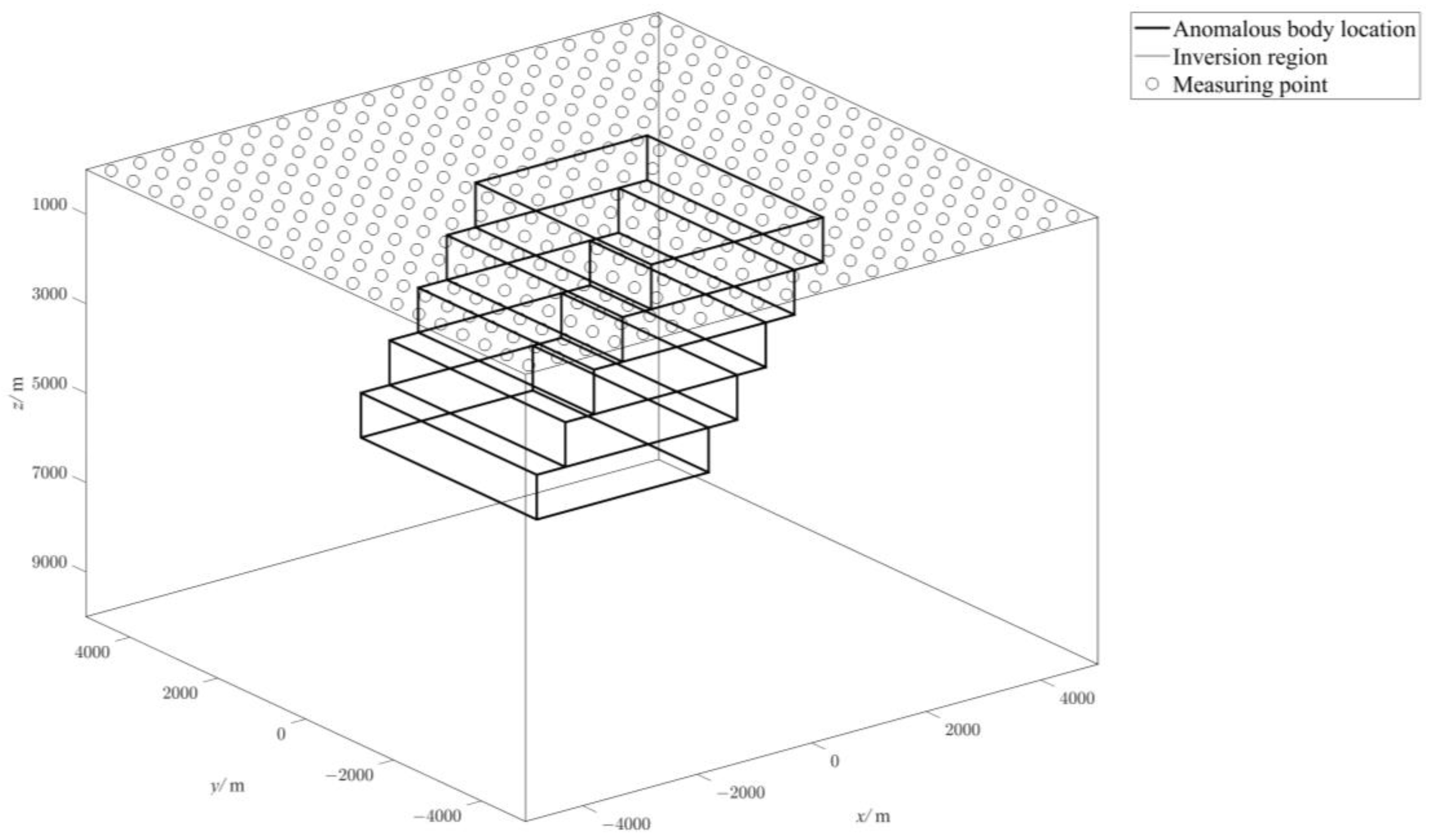


| Single Prism | Iterations Number/Times | Inversion Time/Seconds | Final RMS |
|---|---|---|---|
| Limited-memory BFGS three-dimensional inversion | 8 | 3.7 | 0.84 |
| Traditional magnetic three-dimensional inversion | 26 | 1800.2 | 0.92 |
| Single Prism | Iterations Number/Times | Inversion Time/Seconds | Final RMS |
|---|---|---|---|
| Limited-memory BFGS three-dimensional inversion | 11 | 26.9 | 0.88 |
| Traditional magnetic three-dimensional inversion | 36 | 1600.6 | 0.98 |
| Single Prism | Iterations Number/Times | Inversion Time/Seconds | Final RMS |
|---|---|---|---|
| Limited-memory BFGS three-dimensional inversion | 20 | 35 | 0.98 |
| Traditional magnetic three-dimensional inversion | 19 | 2600 | 1.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Tan, H.; Peng, M.; Li, Y. Three-Dimensional Limited-Memory BFGS Inversion of Magnetic Data Based on a Multiplicative Objective Function. Appl. Sci. 2023, 13, 11198. https://doi.org/10.3390/app132011198
Liu S, Tan H, Peng M, Li Y. Three-Dimensional Limited-Memory BFGS Inversion of Magnetic Data Based on a Multiplicative Objective Function. Applied Sciences. 2023; 13(20):11198. https://doi.org/10.3390/app132011198
Chicago/Turabian StyleLiu, Shuaishuai, Handong Tan, Miao Peng, and Yanxing Li. 2023. "Three-Dimensional Limited-Memory BFGS Inversion of Magnetic Data Based on a Multiplicative Objective Function" Applied Sciences 13, no. 20: 11198. https://doi.org/10.3390/app132011198
APA StyleLiu, S., Tan, H., Peng, M., & Li, Y. (2023). Three-Dimensional Limited-Memory BFGS Inversion of Magnetic Data Based on a Multiplicative Objective Function. Applied Sciences, 13(20), 11198. https://doi.org/10.3390/app132011198





