Robust 3D Joint Inversion of Gravity and Magnetic Data: A High-Performance Computing Approach
Abstract
:1. Introduction
2. Methods
2.1. Regularized Least Squares 3D Joint Inversión with Gramian-Based Constraint
2.2. Gravity and Magnetic Inversion Using Conjugate Gradient Algorithm
2.3. Coding Guidelines
3. Results and Validation
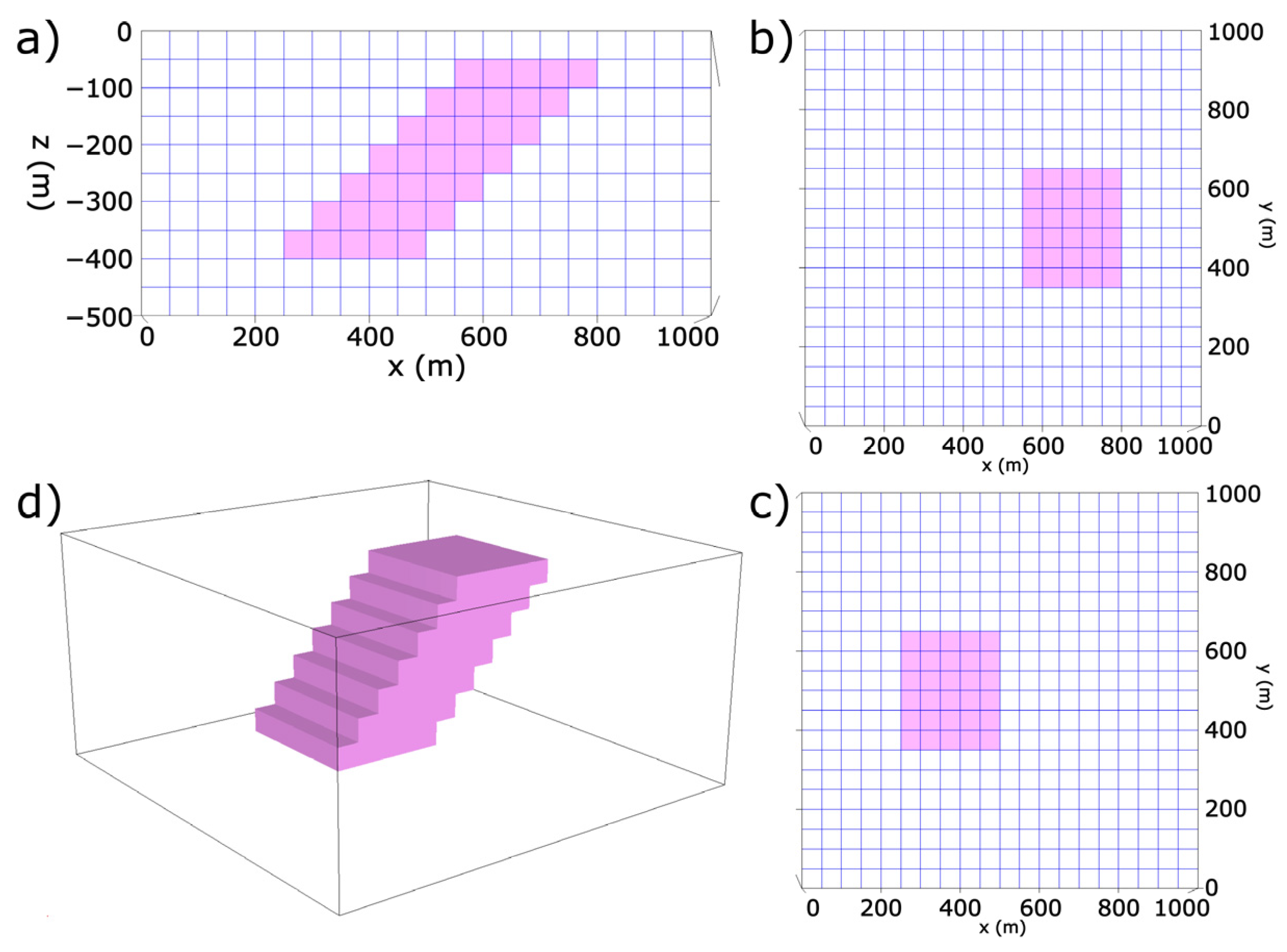
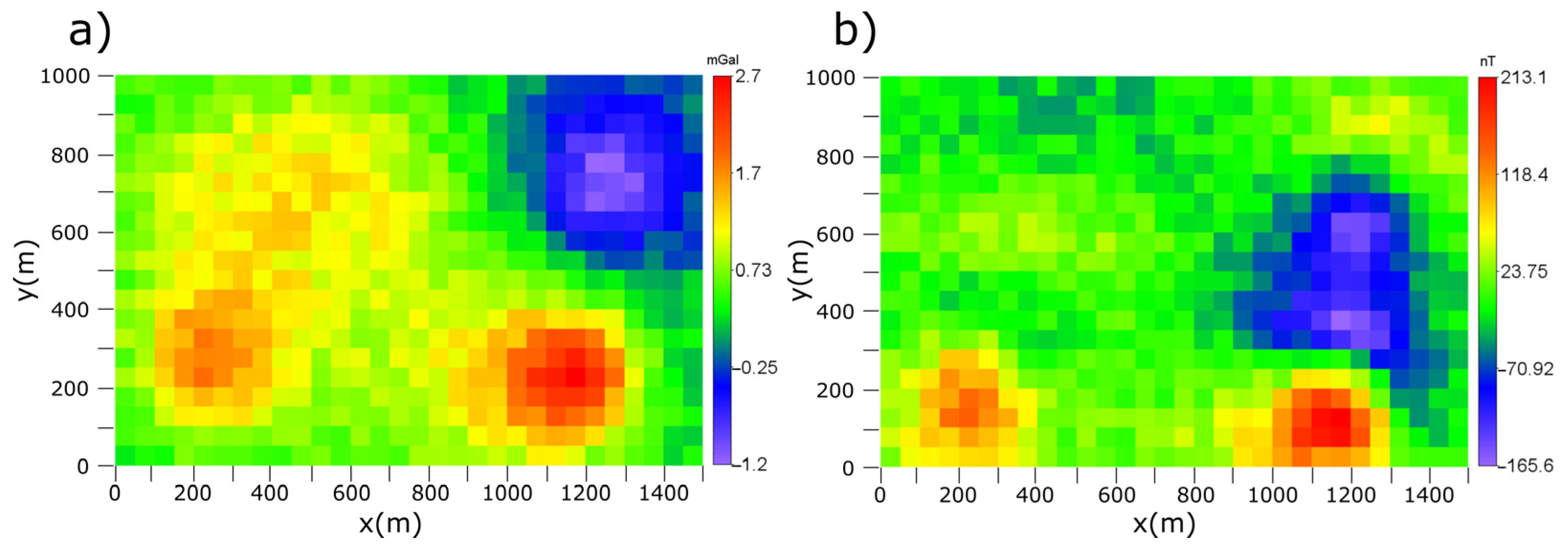
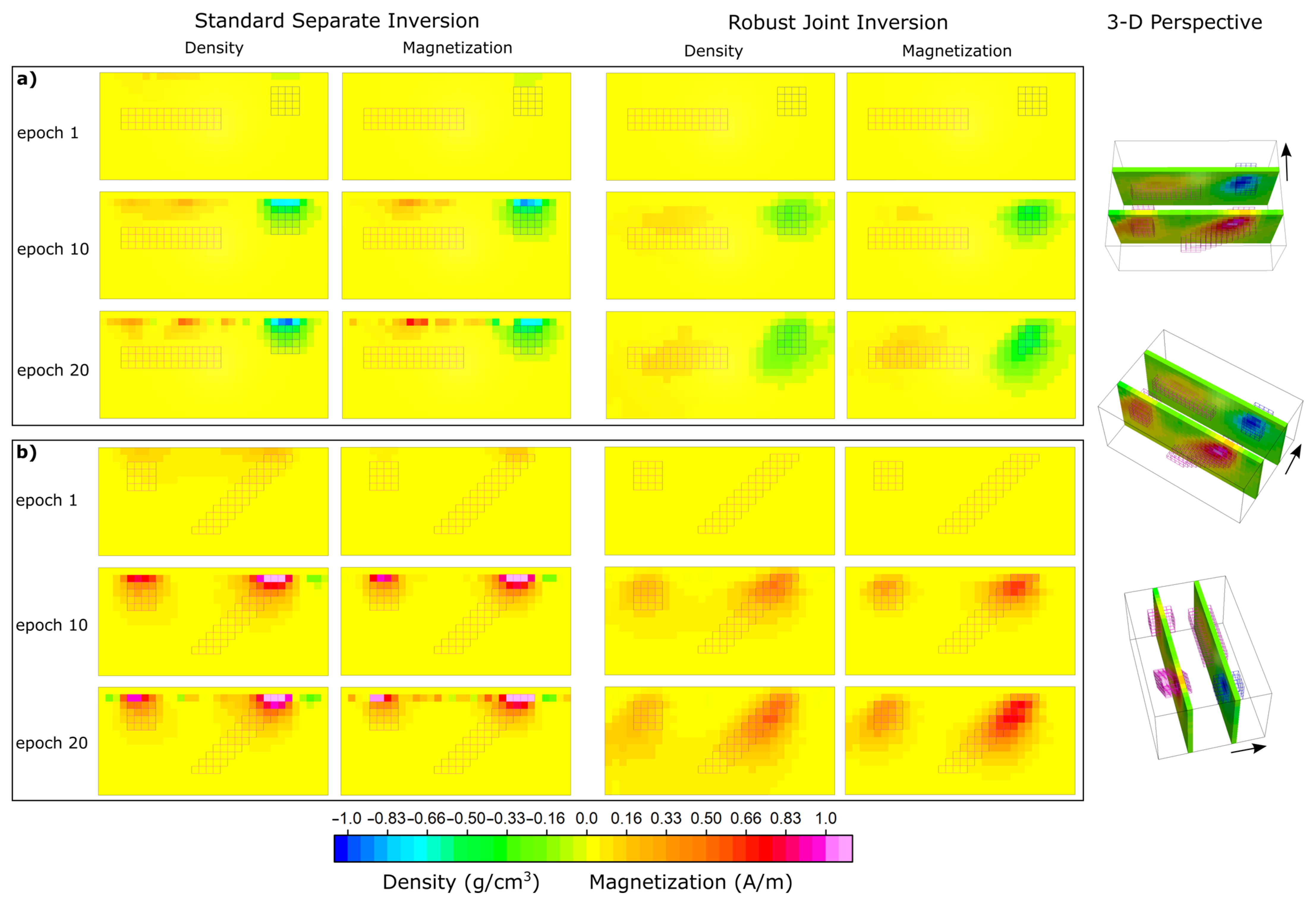
3.1. Synthetic Test Model 1
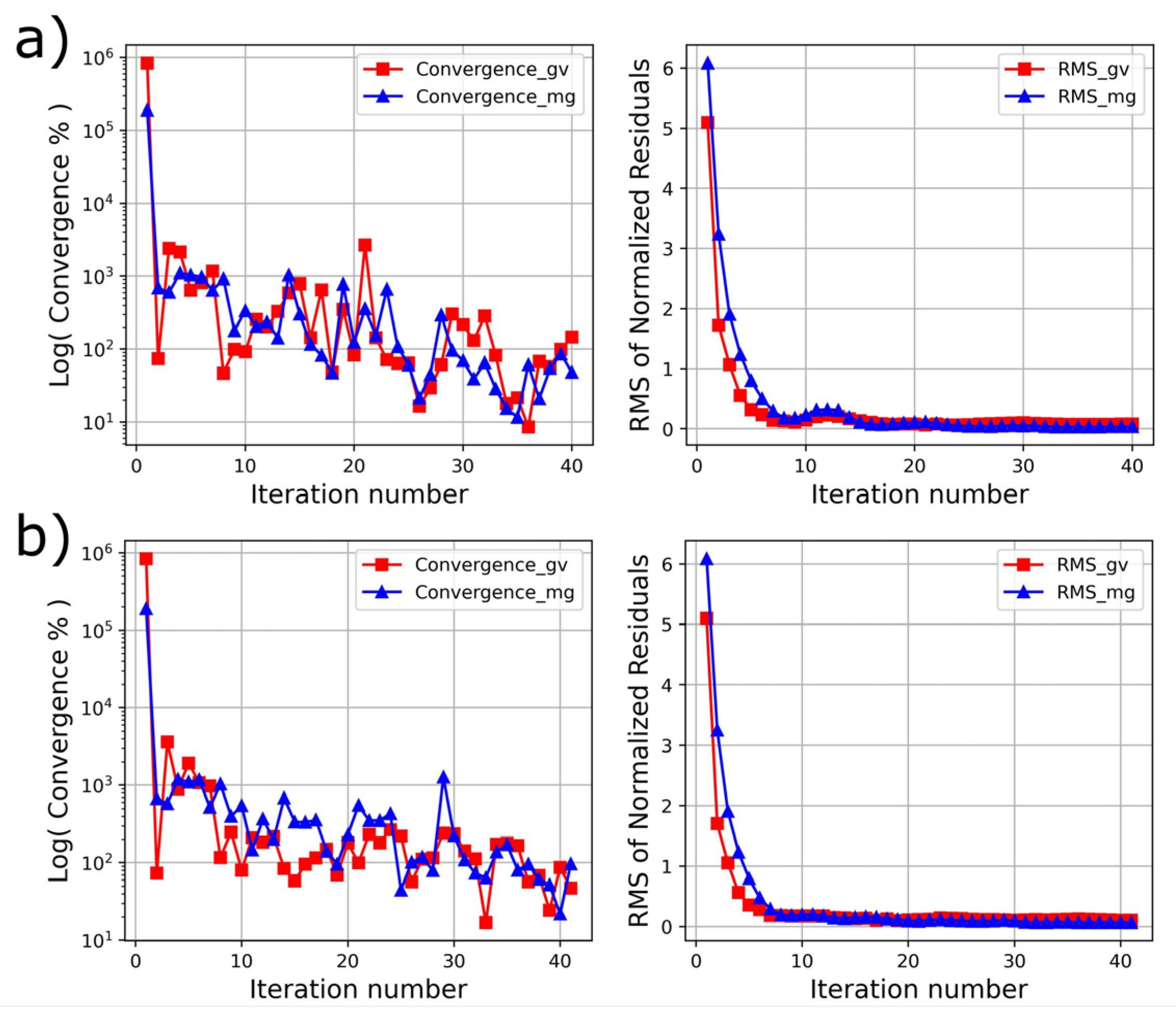
Standard Separate versus Robust Joint Inversion Results of Test Data 1
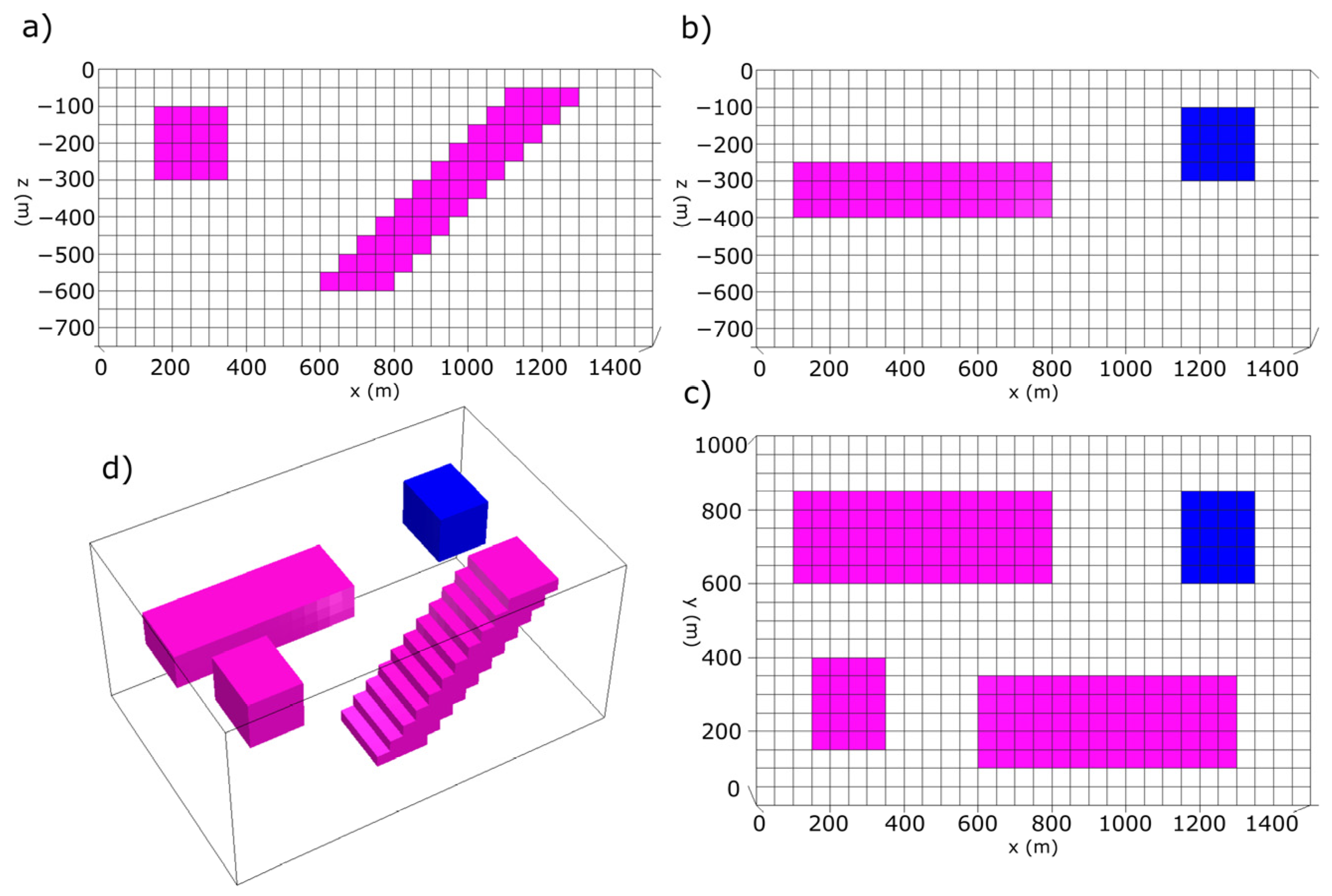
3.2. Synthetic Test Model 2
Standard Separate versus Robust Joint Inversion Results of Test Data 2
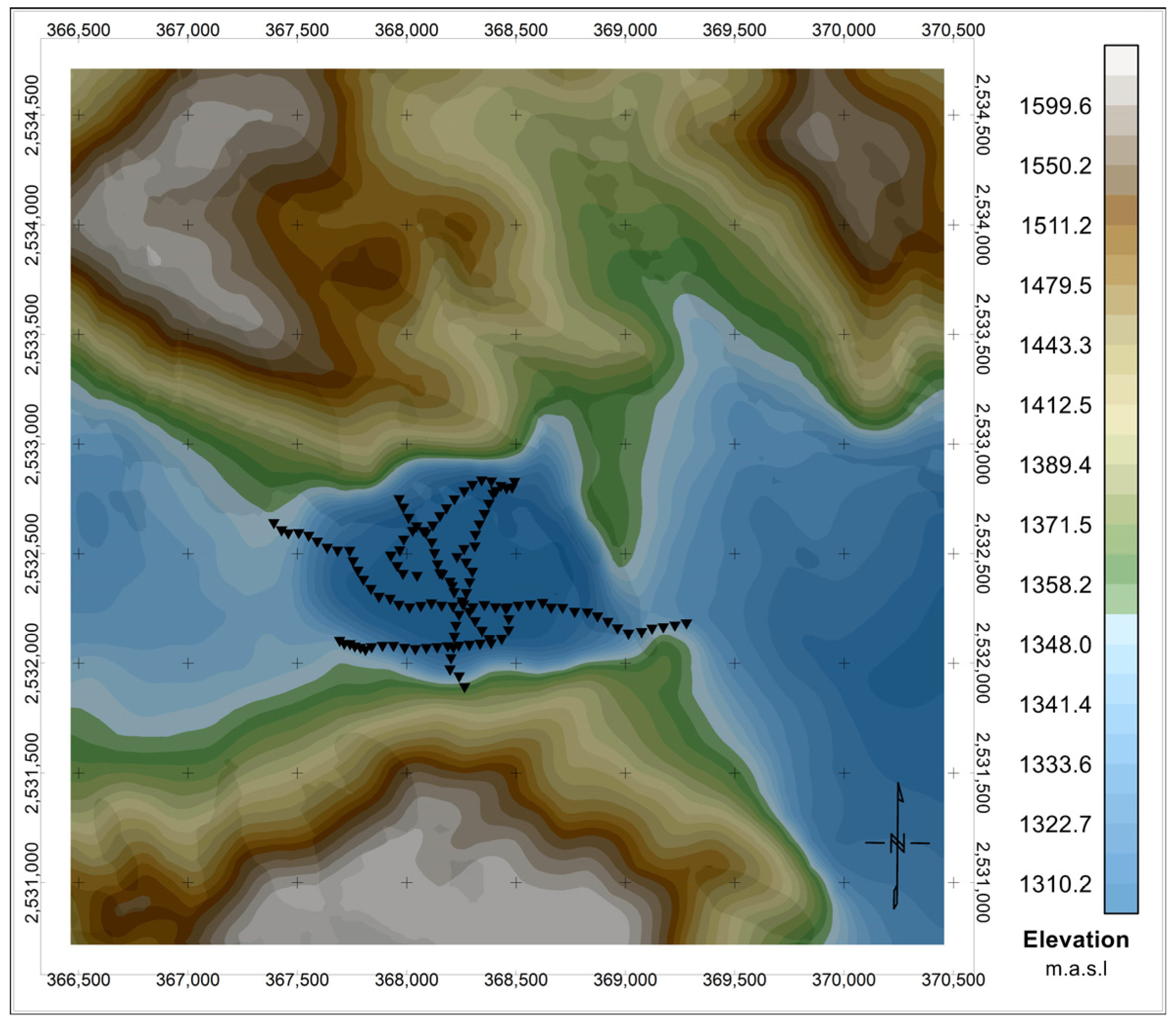
3.3. Field Data Testing
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Linear Operators for Gravimetric and Magnetic Direct Modeling
Appendix B. Development of the 1st Variation of the Objective Function
Appendix C. First Variation of the Structural Coupling Term of the Parametric Functional
References
- Wiederhold, H.; Kallesøe, A.J.; Kirsch, R.; Mecking, R.; Pechnig, R.; Skowronek, F. Geophysical methods help to assess potential groundwater extraction sites. Grund.-Z. Der Fachsekt. Hydrogeol. 2021, 26, 367–378. [Google Scholar] [CrossRef]
- Xu, M.L.; Yang, C.B.; Wu, Y.G.; Chen, J.Y.; Huan, H.F. Edge detection in the potential field using the correlation coefficients of multidirectional standard deviations. Appl. Geophys. 2015, 12, 23–34. [Google Scholar] [CrossRef]
- Mauriello, P.; Patella, D. Localization of magnetic sources underground by a probability tomography approach. Prog. Electromagn. Res. 2008, 3, 27–56. [Google Scholar] [CrossRef]
- Blakely, R.J. Potential Theory in Gravity and Magnetic Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E. Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA; Port Chester, NY, USA; Melbourne, Australia; Sydney, Australia, 1991; 770p, ISBN 0-521-3269-3-1/0-521-33938-3. [Google Scholar]
- Kearey, P.; Brooks, M.; Hill, I. An Introduction to Geophysical Exploration; John Wiley & Sons: Hoboken, NJ, USA, 2002; Volume 4. [Google Scholar]
- Lowrie, W.; Fichtner, A. Fundamentals of Geophysics; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Jackson, D.D. The use of a priori data to resolve non-uniqueness in linear inversion. Geophys. J. Int. 1979, 57, 137–157. [Google Scholar] [CrossRef]
- Grana, A.; Passos de Figueiredo, L.; Azevedo, L. Uncertainty quantification in Bayesian inverse problems with model and data dimension reduction. Geophysics 2019, 84, M15–M24. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Ellis, R.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- Pallero, J.L.G.; Fernández-Martínez, J.L.; Bonvalot, S.; Fudym, O. Gravity inversion and uncertainty assessment of basement relief via Particle Swarm Optimization. J. Appl. Geophys. 2015, 116, 180–191. [Google Scholar] [CrossRef]
- Abubakar, A.; Gao, G.; Habashy, T.M.; Liu, J. Joint inversion approaches for geophysical electromagnetic and elastic full-waveform data. Inverse Prob. 2012, 28, 055016. [Google Scholar] [CrossRef]
- Gao, G.; Abubakar, A.; Habashy, T.M. Joint petrophysical inversion of electromagnetic and full-waveform seismic data. Geophysics 2012, 77, WA3–WA18. [Google Scholar] [CrossRef]
- Habashy, T.M.; Abubakar, A. A general framework for constraint minimization for the inversion of electromagnetic measurements. Prog. Electromagn. Res. Symp. 2004, 46, 265–312. [Google Scholar] [CrossRef]
- Spichak, V. Modern Methods for Joint Analysis and Inversion of Geophysical Data. Russ. Geol. Geophys. 2020, 61, 341–357. [Google Scholar] [CrossRef]
- Lelièvre, P.G.; Farquharson, C.G.; Hurich, C.A. Joint inversion of seismic travel times and gravity data on unstructured grids with application to mineral exploration. Geophysics 2012, 77, K1–K15. [Google Scholar] [CrossRef]
- Franz, G.; Moorkamp, M.; Jegen, M.; Berndt, C.; Rabbel, W. Comparison of Different Coupling Methods for Joint Inversion of Geophysical Data: A Case Study for the Namibian Continental Margin. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022092. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional cross-gradient imaging of magnetotelluric and seismic traveltime data for structural and lithological classification. Geophys. J. Int. 2007, 169, 261–1272. [Google Scholar] [CrossRef]
- Dell‘Aversana, P. Integration of seismic, MT and gravity data in a thrust belt interpretation. First Break 2001, 6, 335–341. [Google Scholar]
- Dell’Aversana, P.; Bernasconi, G.; Miotti, F.; Rovetta, D. Joint inversion of rock properties from sonic, resistivity and density welllog measurements. Geophys. Prosp. 2011, 59, 1144–1154. [Google Scholar] [CrossRef]
- Reimann, C.; Filzmoser, P.; Garrett, R.; Dutter, R. Statistical Data Analysis Explained; John Wiley & Sons: London, UK, 2008. [Google Scholar]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data; John Wiley & Sons: London, UK, 2005. [Google Scholar]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2, Number 3. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Huberty, C.J. Applied Discriminant Analysis; John Wiley & Sons, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Scales, J.A.; Snieder, R. The anatomy of inverse problems. Geophysics 2000, 65, 1708–1710. [Google Scholar] [CrossRef]
- Fernández-Martínez, J.L.; Mukerji, T.; García-Gonzalo, E.; Suman, A. Reservoir characterization and inversion uncertainty via a family of particle swarm optimizers. Geophysics 2012, 77, M1–M16. [Google Scholar] [CrossRef]
- Fernández-Martínez, J.L.; Fernández-Muñiz, Z.; Pallero, J.L.G.; Pedruelo-González, L.M. From Bayes to Tarantola: New insights to understand uncertainty in inverse problems. J. Appl. Geophys. 2013, 98, 62–72. [Google Scholar] [CrossRef]
- Fernández-Martínez, J.L.; Pallero, J.L.G.; Fernández-Muñiz, Z.; Pedruelo-González, L.M. The effect of noise and Tikhonov’s regularization in inverse problems. Part I: The linear case. J. Appl. Geophys. 2014, 108, 176–185. [Google Scholar] [CrossRef]
- Abdelrahman, E.; El-Arby, H.; El-Arby, T.; Essa, K.S. A Least-squares Minimization Approach to Depth Determination from Magnetic Data. Pure Appl. Geophys. 2003, 160, 1259–1271. [Google Scholar] [CrossRef]
- Abdullahi, M.; Singh, U.K.; Roshan, R. Mapping magnetic lineaments and subsurface basement beneath parts of Lower Benue Trough (LBT), Nigeria: Insights from integrating gravity, magnetic and geologic data. J. Earth Syst. Sci. 2019, 128, 17. [Google Scholar] [CrossRef]
- Kumar, C.R.; Kesiezie, N.; Pathak, B.; Maiti, S.; Tivar, R.K. Mapping of basement structure beneath the Kohima Synclinorium, north-east India via Bouguer gravity data modelling. J. Earth Syst. Sci. 2020, 129, 56. [Google Scholar] [CrossRef]
- Alatorre-Zamora, M.A.; Campos-Enriquez, J.O.; Fregoso, E.; Belmonte-Jiménez, S.I.; Chávez-Segura, R.; Gaona-Mota, M. Basement faults deduction at a dumpsite using advanced analysis of gravity and magnetic anomalies. Near Surf. Geophys. 2020, 18, 307–331. [Google Scholar] [CrossRef]
- Jishun, P.; Wang, X.; Zhang, X.; Xu, Z.; Zhao, P.; Tian, X.; Pan, S. 2D multi-scale hybrid optimization method for geophysical inversion and its application. Appl. Geophys. 2009, 6, 337–348. [Google Scholar] [CrossRef]
- Oldenburg, D. Inversion of electromagnetic data: An overview of new techniques. Surv. Geophys. 1990, 11, 231–270. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Parameter Estimation; Society of Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005; ISBN 10:0898715725/13:9780898715729. [Google Scholar]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Parameter Estimation and Inverse Problems, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2019; 392p, ISBN 978-0-12-804651-7. Library of Congress Cataloging-in-Publication Data; Available online: https://gr.xjtu.edu.cn/c/document_library/get_file?folderId=2777518&name=DLFE-136223.pdf (accessed on 15 August 2023).
- Salem, A.; Ravat, D.; Martin, F.M.; Ushijima, R. Linearized least-squares method for interpretation of potential-field data from sources of simple geometry. Geophysics 2004, 69, 783–788. [Google Scholar] [CrossRef]
- Witter, J.B.; Siler, D.L.; Faulds, J.E.; Hinz, N.H. 3D geophysical inversion modeling of gravity data to test the 3D geologic model of the Bradys geothermal area, Nevada, USA. Geotherm. Energy 2016, 4, 14. [Google Scholar] [CrossRef]
- Panzera, F.; Alber, J.; Imperatori, W.; Bergamo, P.; Fah, D. Reconstructing a 3D model from geophysical data for local amplification modelling: The study case of the upper Rhone valley, Switzerland. Soil Dyn. Earthq. Eng. 2022, 155, 107163. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Characterization of heterogeneous near-surface materials by joint 2D inversion of dc resistivity and seismic data. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Liu, S.; Jin, S.; Xuan, S.; Liu, X. Three-dimensional data-space joint inversion of gravity and magnetic data with correlation-analysis constrains. Ann. Geophys. 2022, 65. [Google Scholar] [CrossRef]
- Zhang, R.; Li, T.; Liu, C.; Huang, X.; Jensen, K.; Sommer, M. 3-D Joint Inversion of Gravity and Magnetic Data Using Data-Space and Truncated Gauss–Newton Methods. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8012105. [Google Scholar] [CrossRef]
- Jacoby, W.; Smilde, P.L. Gravity Interpretation. In Fundamentals and Application of Gravity Inversion and Geological Interpretation; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-85328-2/978-3-540-85329-9. [Google Scholar]
- Al-Garni, M.A. Inversion of residual gravity anomalies using neural network. Arab. J. Geosci. 2013, 6, 1509–1516. [Google Scholar] [CrossRef]
- Al-Garni, M.A. Inversion of magnetic anomalies due to isolated thin dike-like sources using artificial neural networks. Arab. J. Geosci. 2017, 10, 337. [Google Scholar] [CrossRef]
- Núñez-Demarco, P.; Bonilla, A.; Sánchez-Bettucci, L.; Prezzi, C. Potential-Field Filters for Gravity and Magnetic Interpretation: A Review. Surv. Geophys. 2023, 44, 603–664. [Google Scholar] [CrossRef]
- Shang, Y.-J.; Yang, C.-G.; Jin, W.-J.; Chen, Y.-W.; Hasan, M.; Wang, Y.; Li, K.; Lin, D.-M.; Zhou, M. Application of Integrated Geophysical Methods for Site Suitability of Research Infrastructures (RIs) in China. Appl. Sci. 2021, 11, 8666. [Google Scholar] [CrossRef]
- Linde, N.; Tryggvason, A.; Peterson, J.E.; Hubbard, S.S. Joint inversion of crosshole radar and seismic traveltimes acquired at the south oyster bacterial transport site. Geophysics 2008, 73, G29–G37. [Google Scholar] [CrossRef]
- Fregoso, E.; Gallardo, L.A. Cross-gradients joint 3D inversion with applications to gravity and magnetic data. Geophysics 2009, 74, L31–L42. [Google Scholar] [CrossRef]
- Moorkamp, M.; Heincke, B.; Jegen, M. A framework for 3D joint inversion of MT, gravity and seismic refraction data. Geophys. J. Int. 2011, 184, 477–493. [Google Scholar] [CrossRef]
- Moorkamp, M.; Roberts, A.W.; Jegen, M.; Heincke, B.; Hobbs, R.W. Verification of velocity-resistivity relationships derived from structural joint inversion with borehole data. Geophys. Res. Lett. 2013, 40, 3596–3601. [Google Scholar] [CrossRef]
- Liu, S.; Wan, X.; Jin, S.; Jia, B.; Xuan, S.; Lou, Q.; Qin, B.; Peng, R.; Sun, D. 2023. Fast 3D joint inversion of gravity and magnetic data based on cross gradient constraint. Geod. Geodyn. 2023, 14, 331–346. [Google Scholar] [CrossRef]
- Newman, G.A. A review of high-performance computational strategies for modeling and imaging of electromagnetic induction data. Surv. Geophys. 2014, 35, 85–100. [Google Scholar] [CrossRef]
- Martin, R.; Monteiller, V.; Komatitsch, D.; Perrouty, S.; Jessell, M.; Bonvalot, S.; Lindsay, M. Gravity inversion using wavelet-based compression on parallel hybrid CPU/GPU systems: Application to southwest Ghana. Geophys. J. Int. 2013, 195, 1594–1619. [Google Scholar] [CrossRef]
- Hou, Z.; Huang, D.; Wei, X. Fast inversion of probability tomography with gravity gradiometry data based on hybrid parallel programming. J. Appl. Geophys. 2016, 124, 27–38. [Google Scholar] [CrossRef]
- Rücker, C.; Günther, T.; Wagner, F.M. pyGIMLi: An open-source library for modelling and inversion in geophysics. Comput. Geosci. 2017, 109, 106–123. [Google Scholar] [CrossRef]
- Ravasi, M.; Vasconcelos, I. An open-source framework for the implementation of large-scale integral operators with flexible, modern high-performance computing solutions: Enabling 3D Marchenko imaging by least-squares inversion. Geophysics 2021, 86, WC177–WC194. [Google Scholar] [CrossRef]
- Fu, N.; Tai, H.M. Accelerated Geophysical Inversion for Airborne Transient Electromagnetic Data Using GPU. In Proceedings of the 2023 IEEE International Conference on Industrial Technology (ICIT), Orlando, FL, USA, 4–6 April 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Epov, M.I.; Nechaev, O.V.; Glinskikh, V.N.; Danilovskiy, K.N. Pulsed Electromagnetic Sounding of the Bazhenov Formation: High-Performance Computing to Justify a New Geophysical Technology. Russ. Geol. Geophys. 2023, 64, 102–108. [Google Scholar] [CrossRef]
- Zhou, S.; Jia, H.; Lin, T.; Zeng, Z.; Yu, P.; Jiao, J. An Accelerated Algorithm for 3D Inversion of Gravity Data Based on Improved Conjugate Gradient Method. Appl. Sci. 2023, 13, 10265. [Google Scholar] [CrossRef]
- Laloy, E.; Linde, N.; Ruffino, C.; Hérault, R.; Gasso, G.; Jacques, D. Gradient-based deterministic inversion of geophysical data with generative adversarial networks: Is it feasible? Comput. Geosci. 2019, 133, 104333. [Google Scholar] [CrossRef]
- Isaev, I.; Obornev, I.; Obornev, E.; Rodionov, E.; Shimelevich, M.; Dolenko, S. Integration of Geophysical Methods for Solving Inverse Problems of Exploration Geophysics Using Artificial Neural Networks. In Problems of Geocosmos; Springer Proceedings in Earth and Environmental Sciences; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Liu, M.; Vashisth, D.; Grana, D.; Mukerji, T. Joint Inversion of Geophysical Data for Geologic Carbon Sequestration Monitoring: A Differentiable Physics-Informed Neural Network Model. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025372. [Google Scholar] [CrossRef]
- Wu, X.; Ma, J.; Si, X.; Bi, Z.; Yang, J.; Gao, H.; Zhang, J. Sensing prior constraints in deep neural networks for solving exploration geophysical problems. Proc. Natl. Acad. Sci. USA 2023, 120, e2219573120. [Google Scholar] [CrossRef] [PubMed]
- Dukalski, M.; Rovetta, D.; van der Linde, S.; Möller, M.; Neumann, N.; Phillipson, F. Quantum computer-assisted global optimization in geophysics illustrated with stack-power maximization for refraction residual statics estimation. Geophysics 2023, 88, V75–V91. [Google Scholar] [CrossRef]
- Benning, M.; Burger, M. Modern Regularization Methods for Inverse Problems. arXiv 2017, arXiv:1801.09922. [Google Scholar] [CrossRef]
- Hansen, P.C. Regularization tools: A Matlab package for analysis and solution of discrete ill-posed problems. Numer. Algorithms 1994, 6, 1–35. [Google Scholar] [CrossRef]
- Vozoff, K.; Jupp, D.L.B. Joint Inversion of Geophysical Data. Geophys. J. R. Astron. Soc. 1975, 42, 977–991. [Google Scholar] [CrossRef]
- Zhang, J.; Morgan, F.D. Joint Seismic and Electrical Tomography. In Proceedings of the Symposium on the Applicatión of Geophysical to Engineering and Environmental Problems SAGEEP, Houston, TX, USA, 23–26 March 1997; pp. 391–396. [Google Scholar] [CrossRef]
- Haber, E.; Oldenburg, D. Joint inversion: A structural approach. Inverse Probl. 1997, 13, 63–77. [Google Scholar] [CrossRef]
- Gallardo, L.A. Multiple cross-gradient joint inversion for geospectral imaging. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Gribenko, A.; Wilson, G. Generalized joint inversion of multimodal geophysical data using Gramian constraints. Geophys. Res. Lett. 2012, 39, 1–7. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Fontes, S.L.; Meju, M.A.; Buonora, M.P.; de Lugao, P.P. Robust geophysical integration through structure-coupled joint inversion and multispectral fusion of seismic reflection, magnetotelluric, magnetic, and gravity images: Example from Santos Basin, offshore Brazil. Geophysics 2012, 77, B237–B251. [Google Scholar] [CrossRef]
- Zhdanov, M.S. Inverse Theory and Applications in Geophysics, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Tu, X.; Zhdanov, M.S. Joint Gramian inversion of geophysical data with different resolution capabilities: Case study in Yellowstone. Geophys. J. Int. 2021, 226, 1058–1085. [Google Scholar] [CrossRef]
- Banerjee, B.; Das Gupta, S.P. Gravitational Attraction of a Rectangular Parallelepiped. Geophysics 1977, 42, 1053–1055. [Google Scholar] [CrossRef]
- Bhattacharya, B.K. Magnetic Anomalies Due to Prism Shaped Bodies with Arbitrary Polarization. Geophysics 1964, 29, 517–531. [Google Scholar] [CrossRef]
- Reid, J. The new features of Fortran 2008. ACM SIGPLAN Fortran Forum 2008, 27, 8–21. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Varfinezhad, R.; Parnow, S.; Florio, G.; Fedi, M.; Mohammadi Vizheh, M. DC resistivity inversion constrained by magnetic method through sequential inversion. Acta Geophys. 2023, 71, 247–260. [Google Scholar] [CrossRef]
- Aranda-Gómez, J.J.; Luhr, J.F.; Housh, T.B.; Valdez-Moreno, G.; Chávez-Cabello, G. El volcanismo tipo intraplaca del Cenozoico tardío en el centro y norte de México: Una revisión. Bol. Soc. Geol. Mex. 2005, 57, 187–225. [Google Scholar] [CrossRef]
- Peredo, C.R.; Yutsis, V.; Martin, A.J.; Aranda-Gómez, J.J. Crustal structure and Curie point depth in Central Mexico deduced from the spectral analysis and forward modeling of potential field data. J. S. Am. Earth Sci. 2021, 112, 103565. [Google Scholar] [CrossRef]

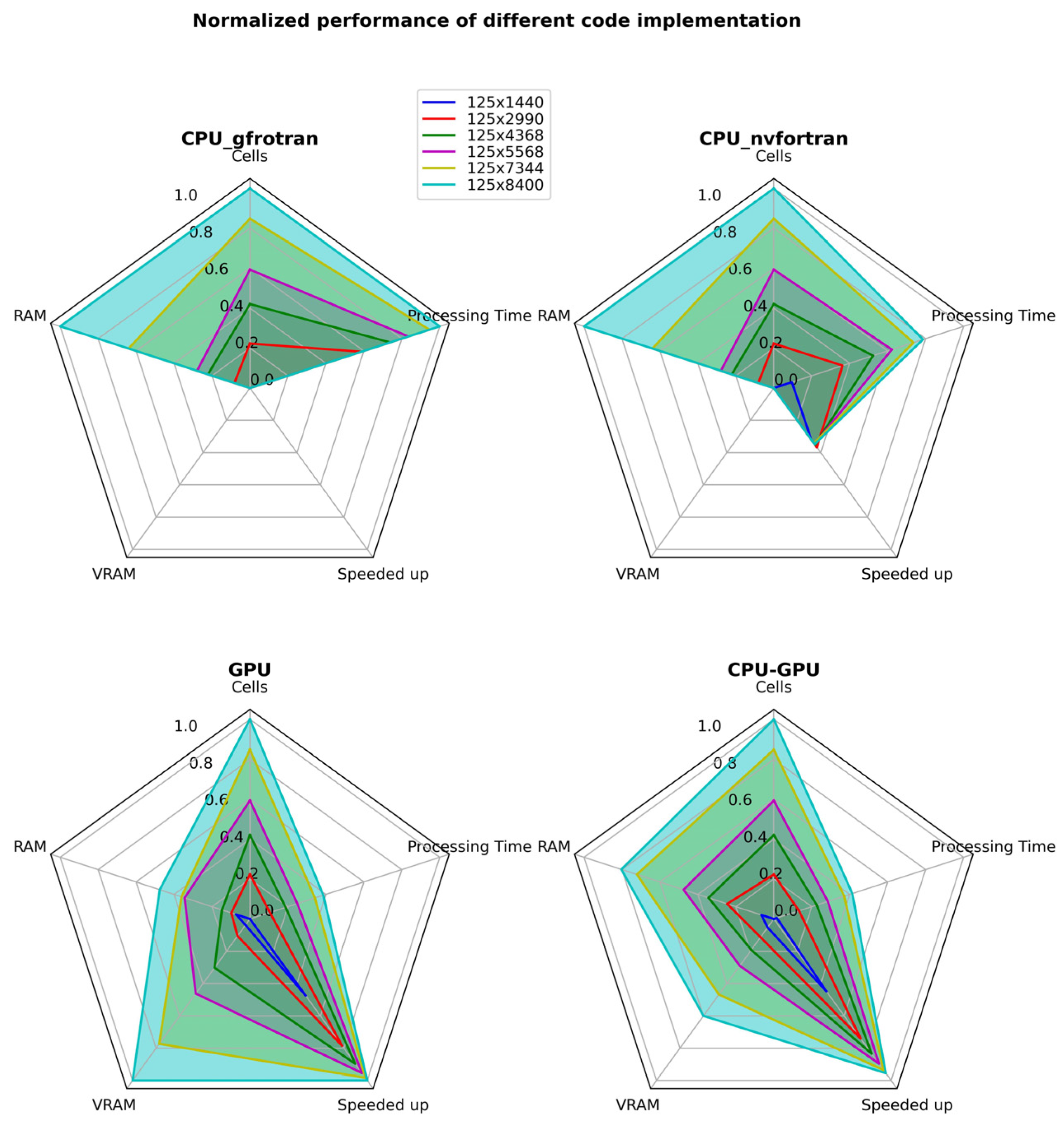





| Cells | RAM Usage (Gb) | VRAM Usage (Gb) | Processing Time (s) | Speeded Up 1 | |
|---|---|---|---|---|---|
| CPU (gfortran) | 1440 | 0.30 | 0.00 | 6.24 | 1.00 |
| 2990 | 0.80 | 0.00 | 57.57 | 1.00 | |
| 4368 | 1.65 | 0.00 | 179.32 | 1.00 | |
| 5568 | 2.00 | 0.00 | 369.85 | 1.00 | |
| 7344 | 4.20 | 0.00 | 848.76 | 1.00 | |
| 8400 | 6.40 | 0.00 | 1274.86 | 1.00 | |
| CPU (nvfortran) | 1440 | 0.30 | 0.00 | 1.43 | 4.36 |
| 2990 | 0.80 | 0.00 | 10.62 | 5.42 | |
| 4368 | 1.65 | 0.00 | 35.49 | 5.05 | |
| 5568 | 2.00 | 0.00 | 74.81 | 4.94 | |
| 7344 | 4.20 | 0.00 | 175.11 | 4.85 | |
| 8400 | 6.40 | 0.00 | 256.38 | 4.97 | |
| GPU | 1440 | 0.75 | 0.25 | 0.7 | 8.91 |
| 2990 | 0.90 | 0.70 | 1.54 | 37.38 | |
| 4368 | 1.20 | 2.00 | 2.87 | 62.48 | |
| 5568 | 2.40 | 3.06 | 4.56 | 81.11 | |
| 7344 | 2.50 | 5.12 | 9.13 | 92.96 | |
| 8400 | 3.20 | 6.62 | 12.72 | 100.22 | |
| CPU-GPU | 1440 | 0.70 | 0.35 | 0.79 | 7.90 |
| 2990 | 1.80 | 0.75 | 1.9 | 30.30 | |
| 4368 | 2.40 | 1.27 | 3.83 | 46.82 | |
| 5568 | 3.20 | 1.92 | 5.94 | 62.26 | |
| 7344 | 4.70 | 3.10 | 11.35 | 74.78 | |
| 8400 | 5.20 | 3.97 | 15.63 | 81.56 |
| Parameters | Standard Separate Inversion | Robust Joint Inversion |
|---|---|---|
| α(1) | 1 × 102 | 1 × 102 |
| α(2) | 1 × 102 | 1 × 102 |
| β(1) | 2 × 100 | 2 × 100 |
| β(2) | 9 × 10−1 | 9 × 10−1 |
| γ(1) | 0 | 1 × 105 |
| γ(2) | 0 | 1 × 105 |
| η(1) | 0 | 0 |
| η(2) | 0 | 0 |
| μ(1) | 0 | 1 × 103 |
| μ(2) | 0 | 1 × 107 |
| Strike | 0 | 0 |
| Dip | 0 | −45 |
| Std_ | 0.3 top z cell and 1 × 108 rest of domain | 0.3 top z cell and 1 × 108 rest of domain |
| Std_ | 0.3 top z cell and 1 × 108 rest of domain | 0.3 top z cell and 1 × 108 rest of domain |
| Std_ | 2% 1 | 2% 1 |
| Std_ | 2% 1 | 2% 1 |
| Parameters | Standard Separate Inversion | Robust Joint Inversion |
|---|---|---|
| α(1) | 1 × 104 | 1 × 104 |
| α(2) | 1 × 104 | 1 × 104 |
| β(1) | 1 × 101 | 1 × 101 |
| β(2) | 1 × 101 | 1 × 105 |
| γ(1) | 0 | 3 × 105 |
| γ(2) | 0 | 3 × 105 |
| η(1) | 0 | 1 × 100 |
| η(2) | 0 | 1 × 100 |
| μ(1) | 0 | 1 × 107 |
| μ(2) | 0 | 1 × 102 |
| Strike | 0 | 0 |
| Dip | 0 | −45 |
| Std_ | 0.2 top z cell and 1× 108 rest of domain | 0.2 top z cell and 1× 108 rest of domain |
| Std_ | 0.2 top z cell and 1× 108 rest of domain | 0.2 top z cell and 1× 108 rest of domain |
| Std_ | 2% 1 | 2% 1 |
| Std_ | 2% 1 | 2% 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Razo Gonzalez, A.; Yutsis, V. Robust 3D Joint Inversion of Gravity and Magnetic Data: A High-Performance Computing Approach. Appl. Sci. 2023, 13, 11292. https://doi.org/10.3390/app132011292
Del Razo Gonzalez A, Yutsis V. Robust 3D Joint Inversion of Gravity and Magnetic Data: A High-Performance Computing Approach. Applied Sciences. 2023; 13(20):11292. https://doi.org/10.3390/app132011292
Chicago/Turabian StyleDel Razo Gonzalez, Abraham, and Vsevolod Yutsis. 2023. "Robust 3D Joint Inversion of Gravity and Magnetic Data: A High-Performance Computing Approach" Applied Sciences 13, no. 20: 11292. https://doi.org/10.3390/app132011292
APA StyleDel Razo Gonzalez, A., & Yutsis, V. (2023). Robust 3D Joint Inversion of Gravity and Magnetic Data: A High-Performance Computing Approach. Applied Sciences, 13(20), 11292. https://doi.org/10.3390/app132011292






