Topology Optimisation of Structural Steel with Non-Penalisation SEMDOT: Optimisation, Physical Nonlinear Analysis, and Benchmarking
Abstract
:1. Introduction
2. Related Work
3. Non-Penalisation Smooth-Edged Material Distribution for Optimising Topology
4. Case-Study
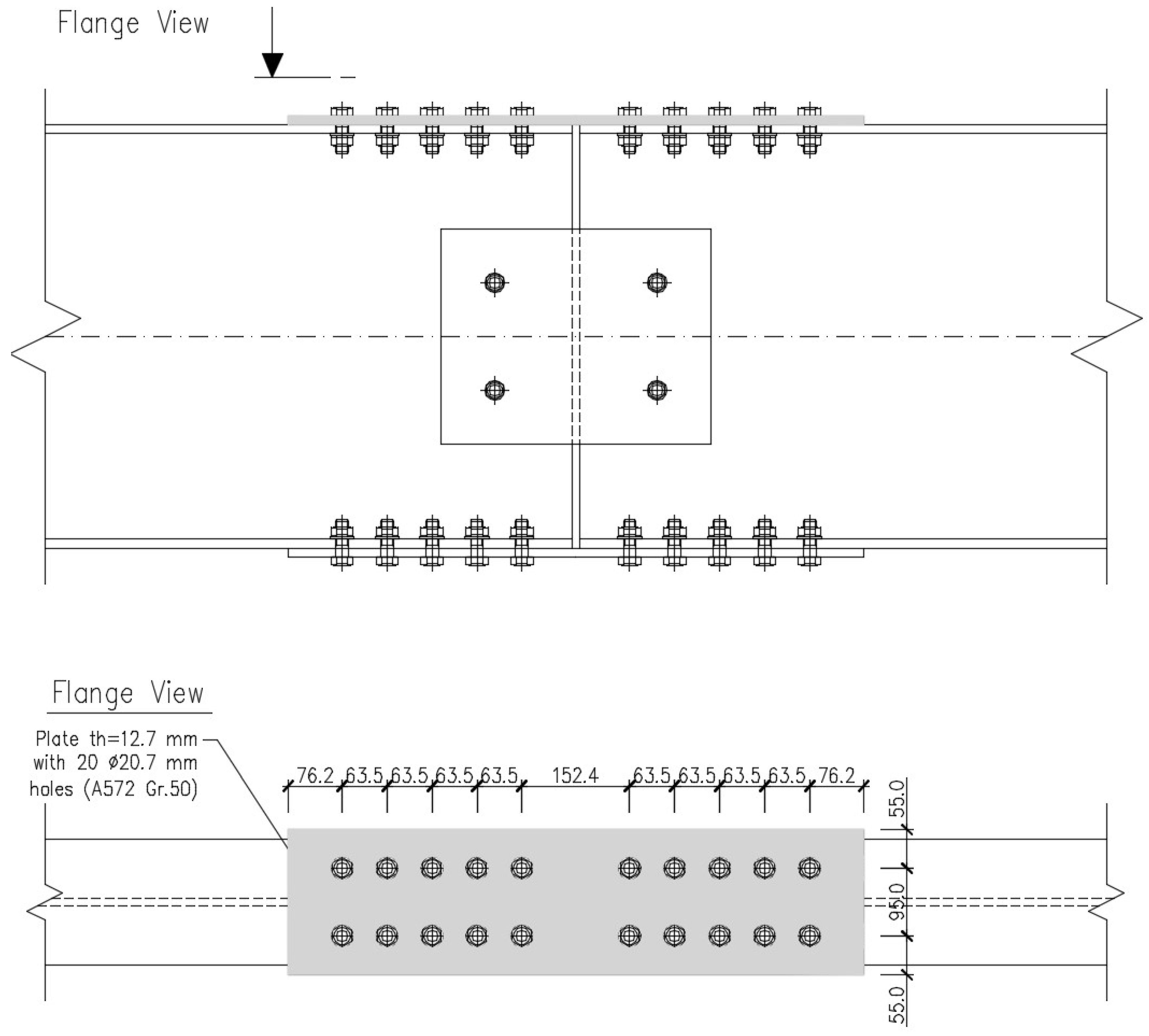
4.1. Sheikh-Ibrahim’s Steel Beam Splice Connection
4.1.1. Geometry
4.1.2. Material Modelling
5. Methods
5.1. General Optimisation Methodology
5.2. SEMDOT Optimisation Protocol
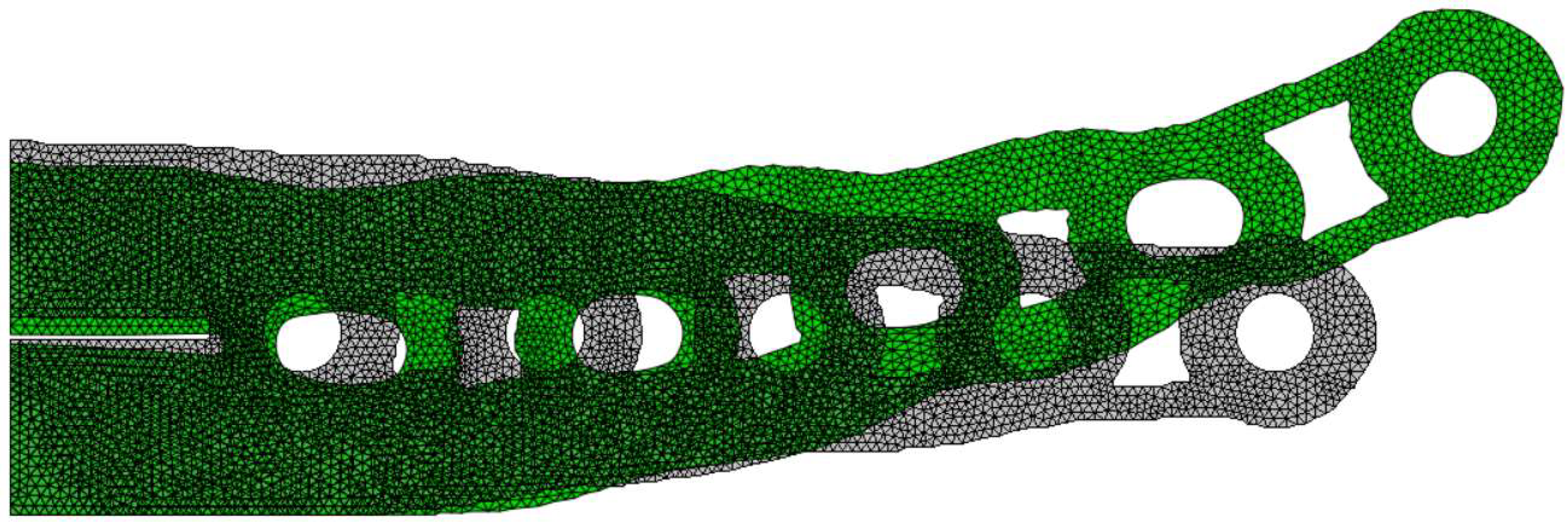
5.3. Structural Assessment with Physically Nonlinear Finite Element Analyses
5.4. Benchmarking
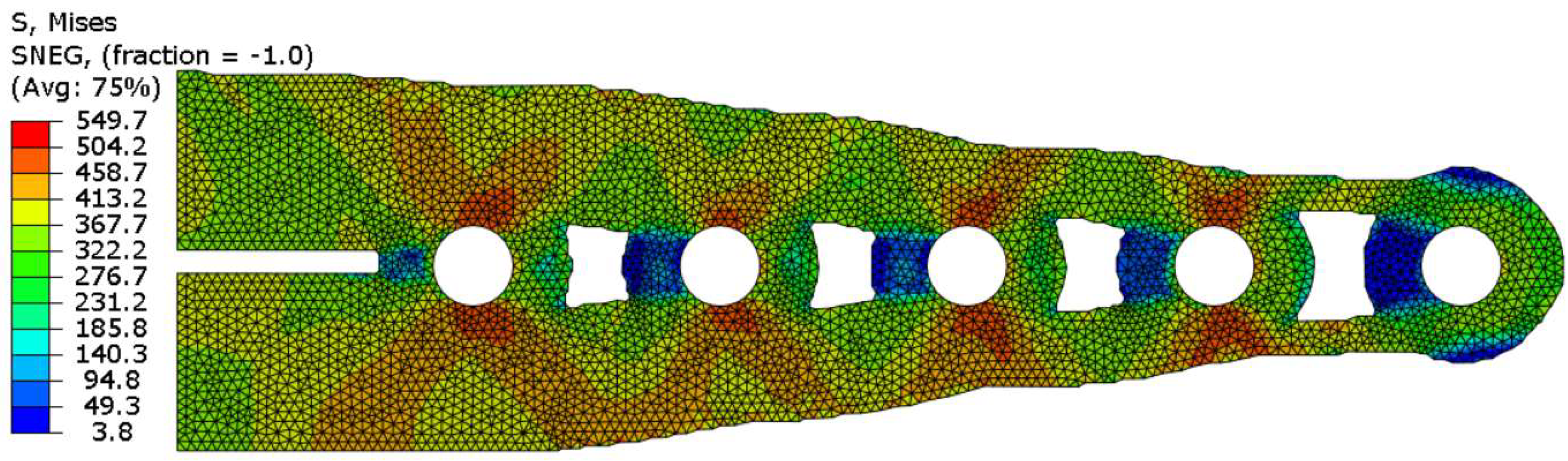
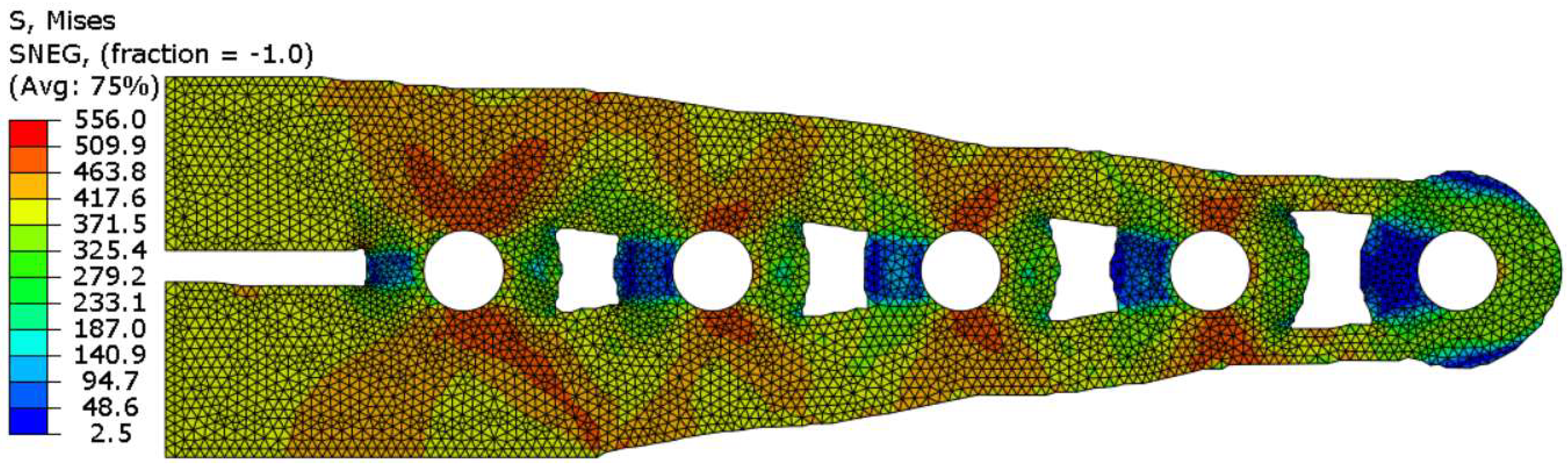
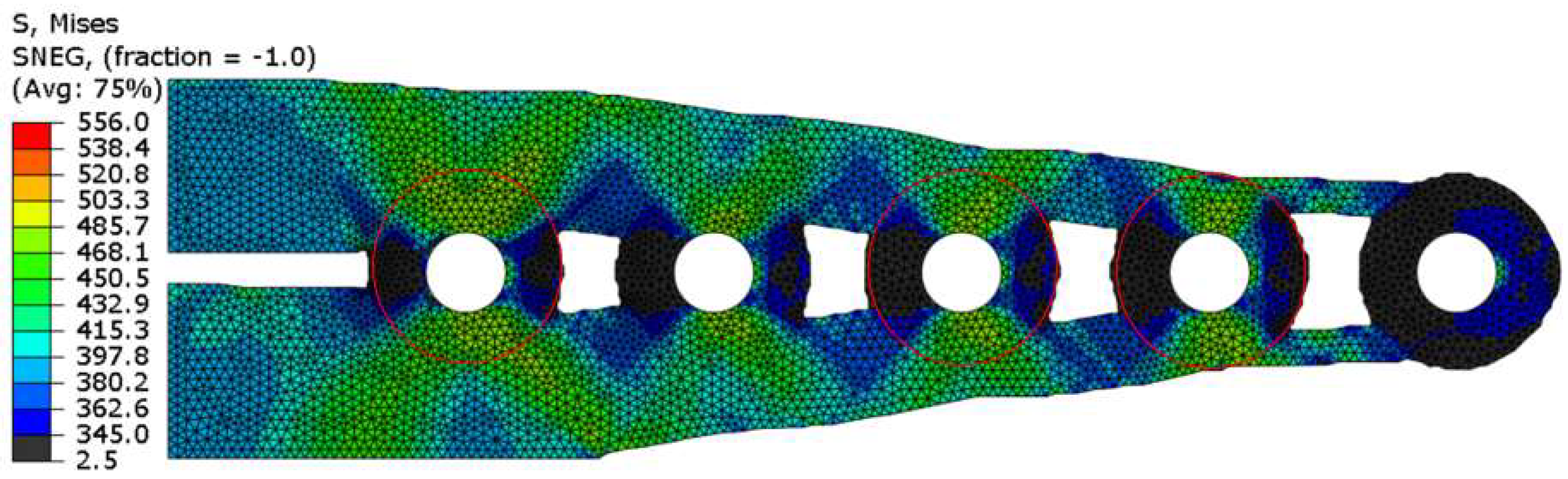
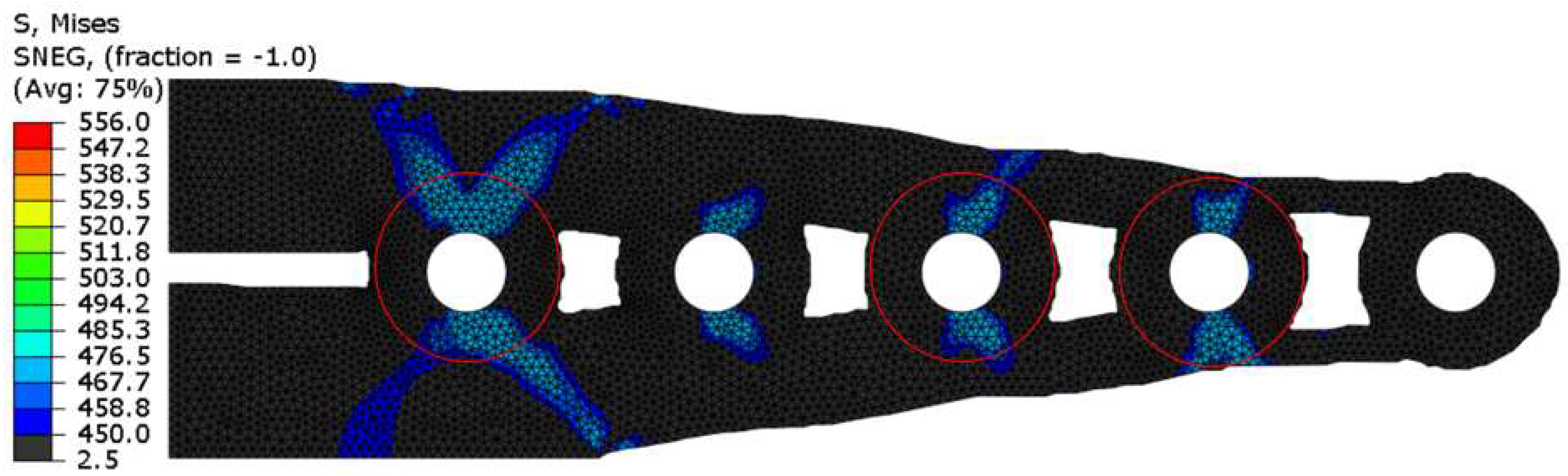
6. Results and Discussion
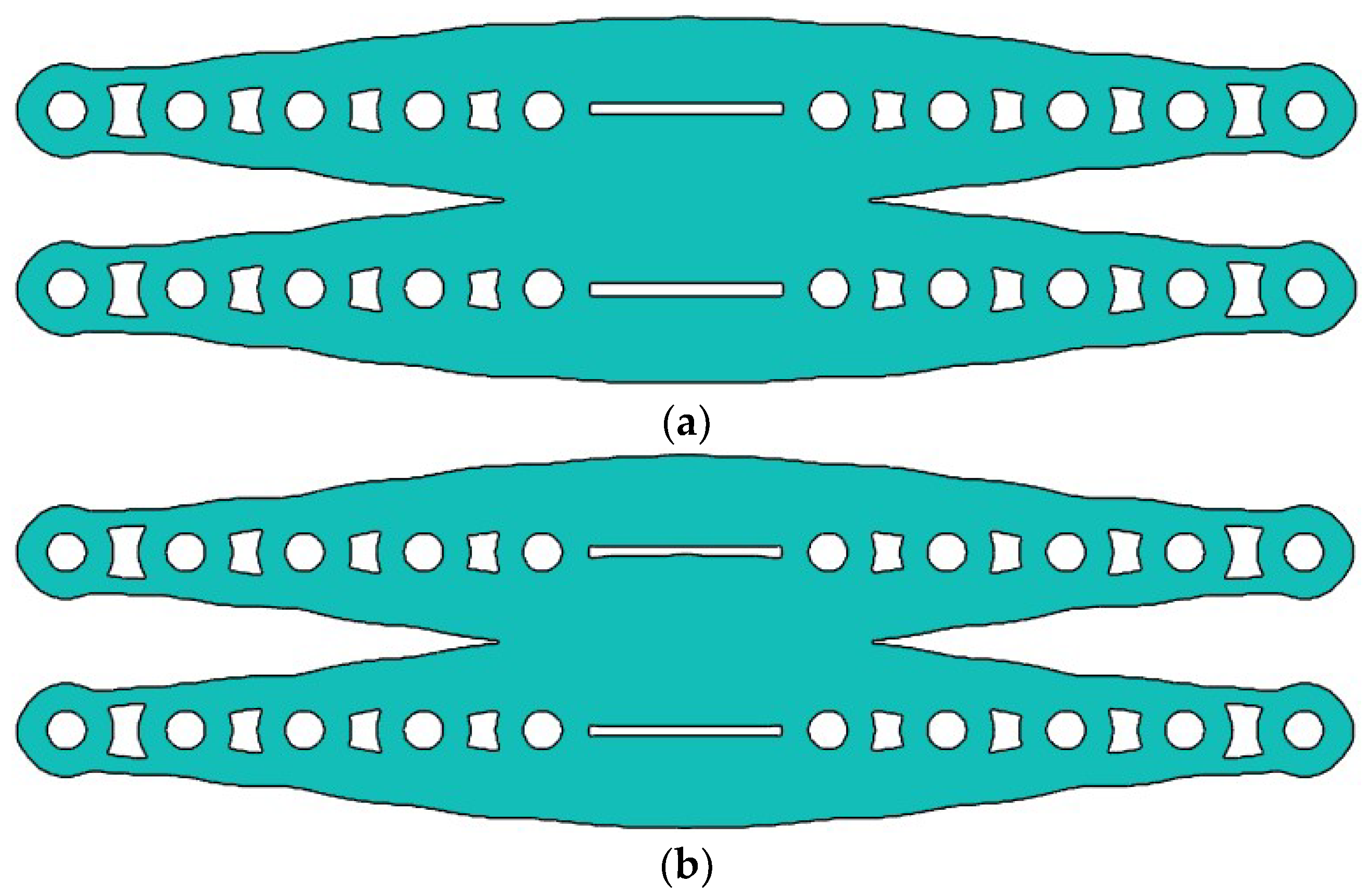
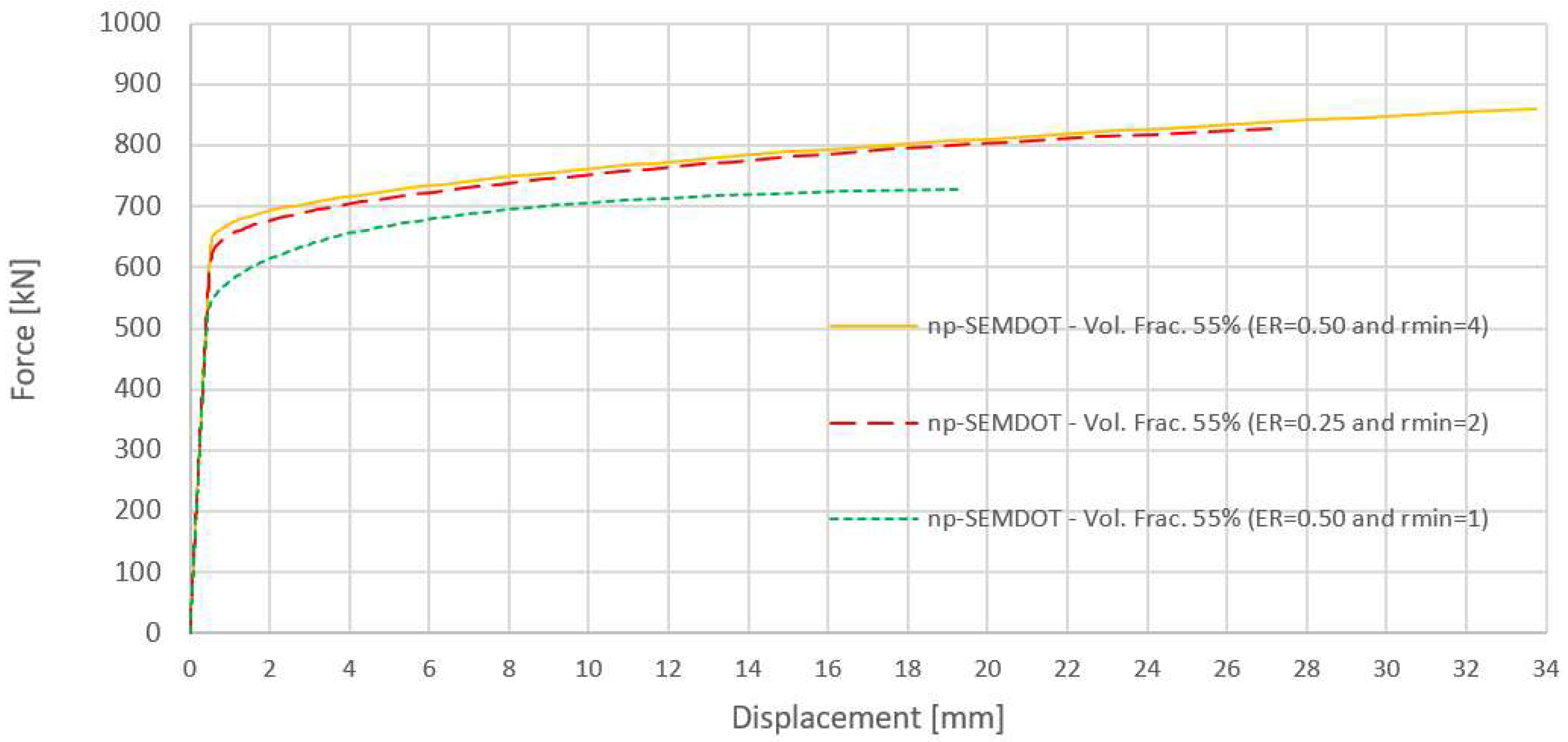
6.1. Optimised Topologies Using Non-Penalisation SEMDOT
6.2. Optimised Topologies Using Non-Penalisation SEMDOT
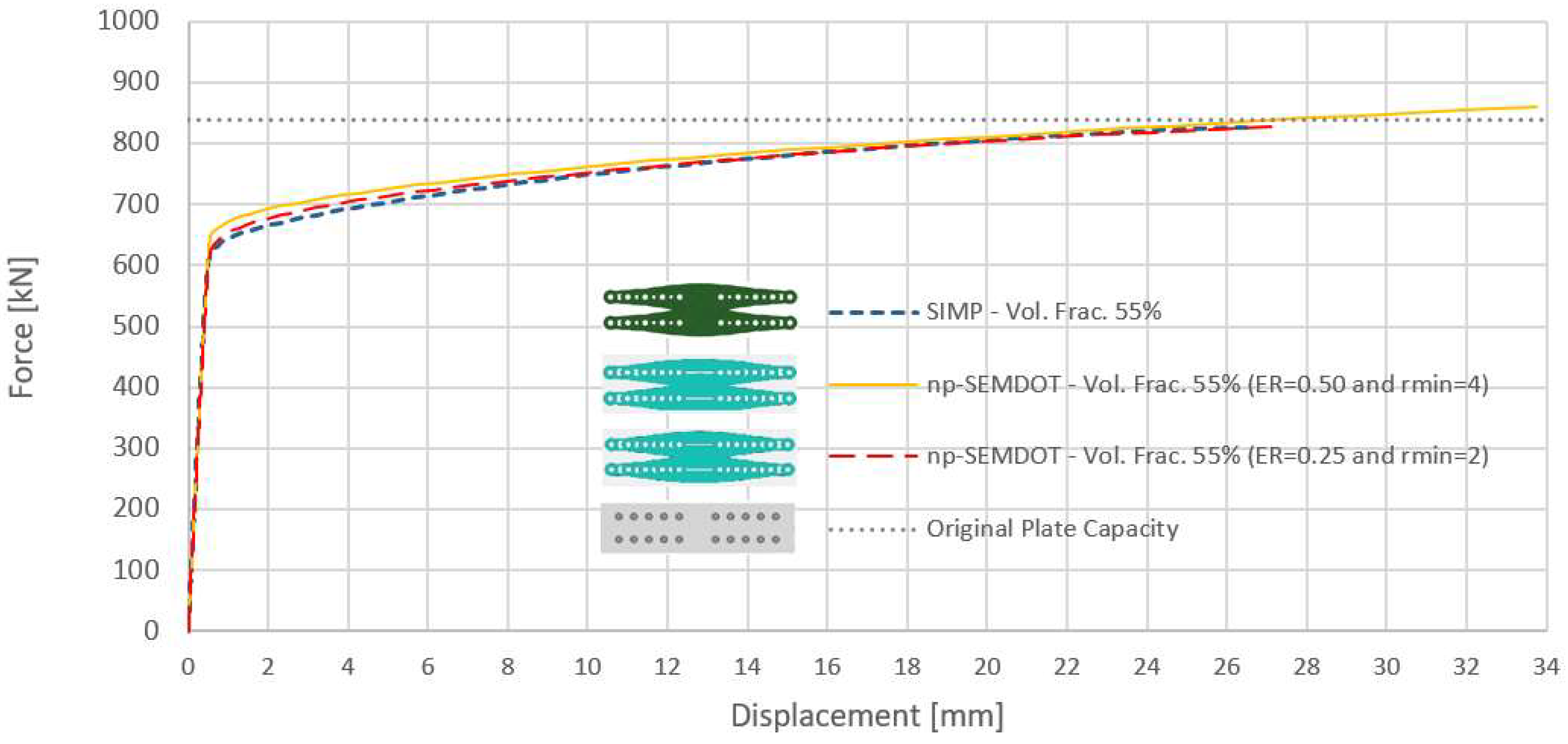
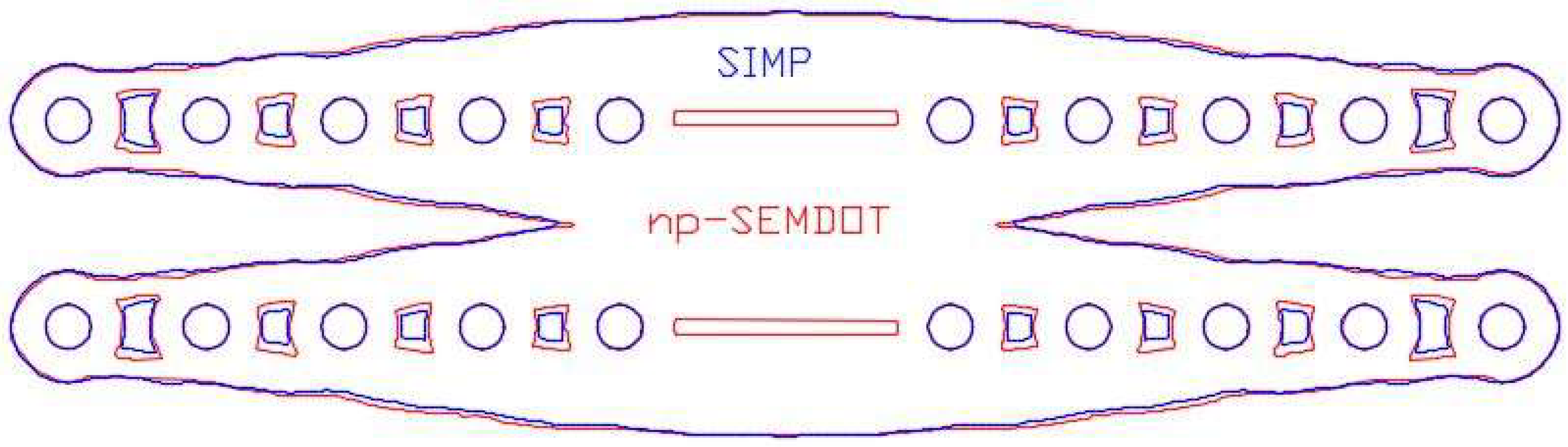
6.3. Benchmarking SEMDOT Solutions against SIMP-Based TOSCA Optimisations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ribeiro, T.; Bernardo, L.; Andrade, J. Topology Optimisation in Structural Steel Design for Additive Manufacturing. Appl. Sci. 2021, 11, 2112. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization—Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2012; ISBN 9783642076985. [Google Scholar]
- Haftka, R.T.; Gurdal, Z. Elements of Structural Optimization; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 2002. [Google Scholar]
- Rozvany, G.I.N.; Lewiński, T. Topology Optimization in Structural and Continuum Mechanics; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-7091-1642-5. [Google Scholar]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Suzuki, K.; Kikuchi, N. Shape and topology optimization by a homogenization method. Am. Soc. Mech. Eng. Appl. Mech. Div. AMD 1990, 115, 15–30. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal Design and Relaxation of Variational Problems, I. Commun. Pure Appl. Math. 1986, 39, 113–137. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal design and relaxation of variational problems, II. Commun. Pure Appl. Math. 1986, 39, 139–182. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal design and relaxation of variational problems, III. Commun. Pure Appl. Math. 1986, 39, 113–137. [Google Scholar] [CrossRef]
- Strang, G.; Kohn, R. Optimal Design in Elasticity and Plasticity. Int. J. Numer. Methods Eng. 1986, 22, 183–188. [Google Scholar] [CrossRef]
- Fu, Y.F.; Rolfe, B.; Chiu, L.N.S.; Wang, Y.; Huang, X.; Ghabraie, K. SEMDOT: Smooth-edged material distribution for optimizing topology algorithm. Adv. Eng. Softw. 2020, 150, 102921. [Google Scholar] [CrossRef]
- Fu, Y.F.; Long, K.; Rolfe, B. On Non-Penalization SEMDOT Using Discrete Variable Sensitivities. J. Optim. Theory Appl. 2023, 198, 644–677. [Google Scholar] [CrossRef]
- Sarkisian, M.; Beghini, A.; Long, E.; Shook, D.; Krebs, A.; Diaz, A. Innovation in the sustainable design process of Earthquake resistant buildings: From topology optimization to staged construction analysis. Eng. Prog. Nat. People 2014, 102, 1192–1199. [Google Scholar] [CrossRef]
- Spaeth, A.B. Editorial. Archit. Sci. Rev. 2020, 63, 103–104. [Google Scholar] [CrossRef]
- Brown, N.C.; Mueller, C.T. Design for structural and energy performance of long span buildings using geometric multi-objective optimization. Energy Build. 2016, 127, 748–761. [Google Scholar] [CrossRef]
- Baker, W.F.; Beghini, A.; Mazurek, A. Applications of Structural Optimization in Architectural Design. In Proceedings of the 20th Analysis & Computation Specialty Conference, Chicago, IL, USA, 29–31 March 2012; pp. 207–218. [Google Scholar]
- Beghini, A.; Beghini, L.L.; Baker, W.F. Applications of structural optimization in architectural design. In Proceedings of the Structures Congress 2013: Bridging Your Passion with Your Profession—Proceedings of the 2013 Structures Congress, Pittsburgh, PA, USA, 2–4 May 2013; pp. 2499–2507. [Google Scholar]
- Kravanja, S.; Žula, T. Cost optimization of industrial steel building structures. Adv. Eng. Softw. 2010, 41, 442–450. [Google Scholar] [CrossRef]
- Ribeiro, T.; Bernardo, L.; Carrazedo, R.; Domenico, D. De Eurocode-compliant Topology Optimisation and Analysis of a Steel Cover-plate in a Splice Moment Connection. In Proceedings of the Materials Today: Proceedings—Recent Advancements in Construction Materials & Structures, ICCMS-2021, Kerala, India, 15–17 December 2021; Elsevier: Amsterdam, The Netherlands. [Google Scholar]
- Ribeiro, T.; Bernardo, L.; Carrazedo, R.; De Domenico, D. Eurocode-compliant topology optimisation of steel moment splice connections. J. Build. Eng. 2022, 62, 105346. [Google Scholar] [CrossRef]
- Simões, L.; Templeman, A. Entropy-based Synthesis of Pretensioned Cable Net Structures. Eng. Opt. 1989, 15, 121–140. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, L.P.; Yang, J.; Zhang, Y.Q.; Abdel-Malek, K. Fuzzy tolerance multilevel approach for structural topology optimization. Comput. Struct. 2006, 84, 127–140. [Google Scholar] [CrossRef]
- Li, H.; Gao, L.; Li, P. Topology optimization of structures under multiple loading cases with a new compliance-volume product. Eng. Optim. 2014, 46, 725–744. [Google Scholar] [CrossRef]
- Alkalla, M.G.; Helal, M.; Fouly, A. Revolutionary Superposition Layout Method for Topology Optimization of Non-Concurrent Multi-load Models: Connecting-Rod Case Study. Int. J. Numer. Methods Eng. 2020, 122, 1378–1400. [Google Scholar] [CrossRef]
- Pintér, E.; Lengyel, A.; Lógó, J. Structural topology optimization with stress constraint considering loading uncertainties. Period. Polytech. Civ. Eng. 2015, 59, 559–565. [Google Scholar] [CrossRef]
- Lógó, J.; Balogh, B.; Pintér, E. Topology optimization considering multiple loading. Comput. Struct. 2018, 207, 233–244. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; Efthymiou, E.; Adugu, A.; Hughes, J.A.; Grekavicius, L. Application of structural topology optimisation in aluminium cross-sectional design. Thin-Walled Struct. 2019, 139, 372–388. [Google Scholar] [CrossRef]
- Sheikh-Ibrahim, F. Development of Design Procedures for Steel Girder Bolted Splices. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 1995. [Google Scholar]
- Jacobsen, R.S.; Andersen, K.N.; Borel, P.I.; Fage-Pedersen, J.; Frandsen, L.H.; Hansen, O.; Kristensen, M.; Lavrinenko, A.V.; Moulin, G.; Ou, H.; et al. Strained silicon as a new electro-optic material. Nature 2006, 441, 199–202. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Topology optimization for nano-photonics. Laser Photonics Rev. 2011, 5, 308–321. [Google Scholar] [CrossRef]
- Alexandersen, J.; Aage, N.; Andreasen, C.S.; Sigmund, O. Topology optimisation for natural convection problems. Int. J. Numer. Methods Fluids 2014, 76, 699–721. [Google Scholar] [CrossRef]
- Clausen, A.; Wang, F.; Jensen, J.S.; Sigmund, O.; Lewis, J.A. Topology Optimized Architectures with Programmable Poisson’s Ratio over Large Deformations. Adv. Mater. 2015, 27, 5523–5527. [Google Scholar] [CrossRef]
- Sousa, A.M.; Andrade, T.A.; Errico, M.; Coelho, P.; Filipe, R.M.; Matos, H.A. Fatty Acid Content in Biomasses: State-of-the-Art and Novel Physical Property Estimation Methods. Int. J. Chem. Eng. 2019, 2019, 2430234. [Google Scholar] [CrossRef]
- Alexandersen, J.; Andreasen, C.S. A review of topology optimisation for fluid-based problems. Fluids 2020, 5, 29. [Google Scholar] [CrossRef]
- Andersen, M.N.; Wang, F.; Sigmund, O. On the competition for ultimately stiff and strong architected materials. Mater. Des. 2021, 198, 109356. [Google Scholar] [CrossRef]
- Sousa, A.M.; Matos, H.A.; Pereira, M.J. Properties of Crude Oil-in-Water and Water-in-Crude Oil Emulsions: A Critical Review. Ind. Eng. Chem. Res. 2022, 61, 1–20. [Google Scholar] [CrossRef]
- Wang, Y.; Sigmund, O. Multi-material topology optimization for maximizing structural stability under thermo-mechanical loading. Comput. Methods Appl. Mech. Eng. 2023, 407, 115938. [Google Scholar] [CrossRef]
- Kazakis, G.; Kanellopoulos, I.; Sotiropoulos, S.; Lagaros, N.D. Topology optimization aided structural design: Interpretation, computational aspects and 3D printing. Heliyon 2017, 3, e00431. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Tsavdaridis, K.D. A Review of Optimised Additively Manufactured Steel Connections for Modular Building Systems. Ind. Addit. Manuf. 2021, 1, 357–373. [Google Scholar] [CrossRef]
- Lange, J.; Feucht, T.; Erven, M. 3D printing with steel: Additive Manufacturing for connections and structures. Steel Constr. 2020, 13, 144–153. [Google Scholar] [CrossRef]
- Wang, L.; Du, W.; He, P.; Yang, M. Topology Optimization and 3D Printing of Three-Branch Joints in Treelike Structures. J. Struct. Eng. 2020, 146, 04019167. [Google Scholar] [CrossRef]
- Kanyilmaz, A.; Berto, F. Robustness-oriented topology optimization for steel tubular joints mimicking bamboo structures. Mater. Des. Process. Commun. 2019, 1, e43. [Google Scholar] [CrossRef]
- Kanyilmaz, A.; Berto, F.; Paoletti, I.; Caringal, R.J.; Mora, S. Nature-inspired optimization of tubular joints for metal 3D printing. Struct. Multidiscip. Optim. 2020, 63, 767–787. [Google Scholar] [CrossRef]
- Hassani, V.; Khabazi, Z.; Mehrabi, H.A.; Gregg, C.; O’Brien, R.W. Rationalization algorithm for a topologically-optimized multi-branch node for manufacturing by metal printing. J. Build. Eng. 2020, 29, 101146. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Li, H.; Liang, J.; Wang, R.; Li, H.; Nishiwaki, S. An 89-line code for geometrically nonlinear topology optimization written in FreeFEM. Struct. Multidiscip. Optim. 2021, 63, 1015–1027. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, G.; Zuo, W. MATLAB implementations for 3D geometrically nonlinear topology optimization: 230-line code for SIMP method and 280-line code for MMB method. Struct. Multidiscip. Optim. 2023, 66, 146. [Google Scholar] [CrossRef]
- Sun, Y.; Lueth, T.C. Enhancing Torsional Stiffness of Continuum Robots Using 3-D Topology Optimized Flexure Joints. IEEE/ASME Trans. Mechatron. 2023, 28, 1844–1852. [Google Scholar] [CrossRef]
- Habashneh, M.; Rad, M.M.; Fischer, S. Bi-directional Evolutionary, Reliability-based, Geometrically Nonlinear, Elasto-Plastic Topology Optimization, of 3D Structures. Acta Polytech. Hung. 2023, 20, 169–186. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, Z.; Guo, H.; Park, G.J.; Zuo, W. Nonlinear dynamic topology optimization with explicit and smooth geometric outline via moving morphable components method. Struct. Multidiscip. Optim. 2021, 64, 2465–2487. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Tao, N.L.; Nguyen, T.T.; Bui, N.T. Adaptive Plan Using Sigmoid Function for Nonlinear Topology Optimization. Int. J. Mech. Eng. Robot. Res. 2021, 10. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, R.; Zhang, H.; Li, H.; Liang, J.; Zhang, X.; Li, H.; Nishiwaki, S. An Approach for Geometrically Nonlinear Topology Optimization Using Moving Wide-Beìzier Components with Constrained Ends. J. Mech. Des. 2021, 144, 4051872. [Google Scholar] [CrossRef]
- Paulino, D.M.S.; Leonel, E.D. Topology optimization and geometric nonlinear modeling using positional finite elements. Optim. Eng. 2022, 23, 1439–1469. [Google Scholar] [CrossRef]
- Fu, Y.F.; Ghabraie, K.; Rolfe, B.; Wang, Y.; Chiu, L.N.S. Smooth design of 3d self-supporting topologies using additive manufacturing filter and semdot. Appl. Sci. 2021, 11, 238. [Google Scholar] [CrossRef]
- Yi, L.; Wu, X.; Nawaz, A.; Glatt, M.; Aurich, J.C. Improving energy performance in the product design for additive manufacturing using a multi-player competition algorithm. J. Clean. Prod. 2023, 391, 136173. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Y.; Wei, Q.; Ma, X.; Zhang, K.; Li, X.; Bao, C.; Du, B. Topology optimization for reducing stress shielding in cancellous bone scaffold. Comput. Struct. 2023, 288, 107132. [Google Scholar] [CrossRef]
- Sheikh-Ibrahim, F.I.; Frank, K.H. The ultimate strength of symmetric beam bolted splices. Eng. J. 2001, 38, 100–117. [Google Scholar]
- Richter, C. Behavior of a Steel Girder Bolted Splice Connection; US Department of Transportation, Federal Highway Administration, McLean: Washington, DC, USA, 2017.
- ASTM A36/A36M-19; Standard Specification for Carbon Structural Steel. ASTM: West Conshohocken, PA, USA, 2019.
- ASTM A572/A572M-15; High-Strength Low-Alloy Columbium-Vanadium Structural Steel. ASTM: West Conshohocken, PA, USA, 2015.
- Rex, C.; Samuel Easterling, W. Behavior and Modeling of Mild and Reinforcing Steel; Department of Civil and Environmental Engineering, Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1996. [Google Scholar]
- Barbosa, V.S.; Ruggieri, C. Effects of increased span on fracture toughness using non-standard PCVN specimens and implications for the reference temperature, T 0. Procedia Struct. Integr. 2018, 13, 367–372. [Google Scholar] [CrossRef]
- Wang, Y.; Pasiliao, C.L. Modeling ablation of laminated composites: A novel manual mesh moving finite element analysis procedure with ABAQUS. Int. J. Heat Mass Transf. 2018, 116, 306–313. [Google Scholar] [CrossRef]
- Lee, S.H.; Abolmaali, A.; Shin, K.J.; Lee, H. Du ABAQUS modeling for post-tensioned reinforced concrete beams. J. Build. Eng. 2020, 30, 101273. [Google Scholar] [CrossRef]
- Yussof, M.M.; Silalahi, J.H.; Kamarudin, M.K.; Chen, P.S.; Parke, G.A.R. Numerical evaluation of dynamic responses of steel frame structures with different types of haunch connection under blast load. Appl. Sci. 2020, 10, 1815. [Google Scholar] [CrossRef]
- Sreenivas, A.; Abeyrathna, B.; Rolfe, B.; Weiss, M. Development of a reversible top-hat forming approach for reducing flange wrinkling in flexible roll forming. Int. J. Mech. Sci. 2023, 252, 108359. [Google Scholar] [CrossRef]
- Fedulov, B.; Fedorenko, A.; Khaziev, A.; Antonov, F. Optimization of parts manufactured using continuous fiber three-dimensional printing technology. Compos. Part B Eng. 2021, 227, 109406. [Google Scholar] [CrossRef]
- Tyflopoulos, E.; Steinert, M. Messing with boundaries—Quantifying the potential loss by pre-set parameters in topology optimization. Procedia CIRP 2019, 84, 979–985. [Google Scholar] [CrossRef]
- Pedersen, C.B.W.; Allinger, P. Industrial implementation and applications of topology optimization and future needs. Solid Mech. Its Appl. 2006, 137, 229–238. [Google Scholar] [CrossRef]
- Matos, M. Sizing Optimization for Industrial Applications. In Proceedings of the 11th World Congress on Structural and Multidisciplinary Optimization (WCSMO-11), Sydney, Australia, 7–12 June 2015; Volume 51, pp. 799–800. [Google Scholar]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, T.; Fu, Y.-F.; Bernardo, L.; Rolfe, B. Topology Optimisation of Structural Steel with Non-Penalisation SEMDOT: Optimisation, Physical Nonlinear Analysis, and Benchmarking. Appl. Sci. 2023, 13, 11370. https://doi.org/10.3390/app132011370
Ribeiro T, Fu Y-F, Bernardo L, Rolfe B. Topology Optimisation of Structural Steel with Non-Penalisation SEMDOT: Optimisation, Physical Nonlinear Analysis, and Benchmarking. Applied Sciences. 2023; 13(20):11370. https://doi.org/10.3390/app132011370
Chicago/Turabian StyleRibeiro, Tiago, Yun-Fei Fu, Luís Bernardo, and Bernard Rolfe. 2023. "Topology Optimisation of Structural Steel with Non-Penalisation SEMDOT: Optimisation, Physical Nonlinear Analysis, and Benchmarking" Applied Sciences 13, no. 20: 11370. https://doi.org/10.3390/app132011370
APA StyleRibeiro, T., Fu, Y.-F., Bernardo, L., & Rolfe, B. (2023). Topology Optimisation of Structural Steel with Non-Penalisation SEMDOT: Optimisation, Physical Nonlinear Analysis, and Benchmarking. Applied Sciences, 13(20), 11370. https://doi.org/10.3390/app132011370









