Depth Evaluation of Tiny Defects on or near Surface Based on Convolutional Neural Network
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental System and Methods
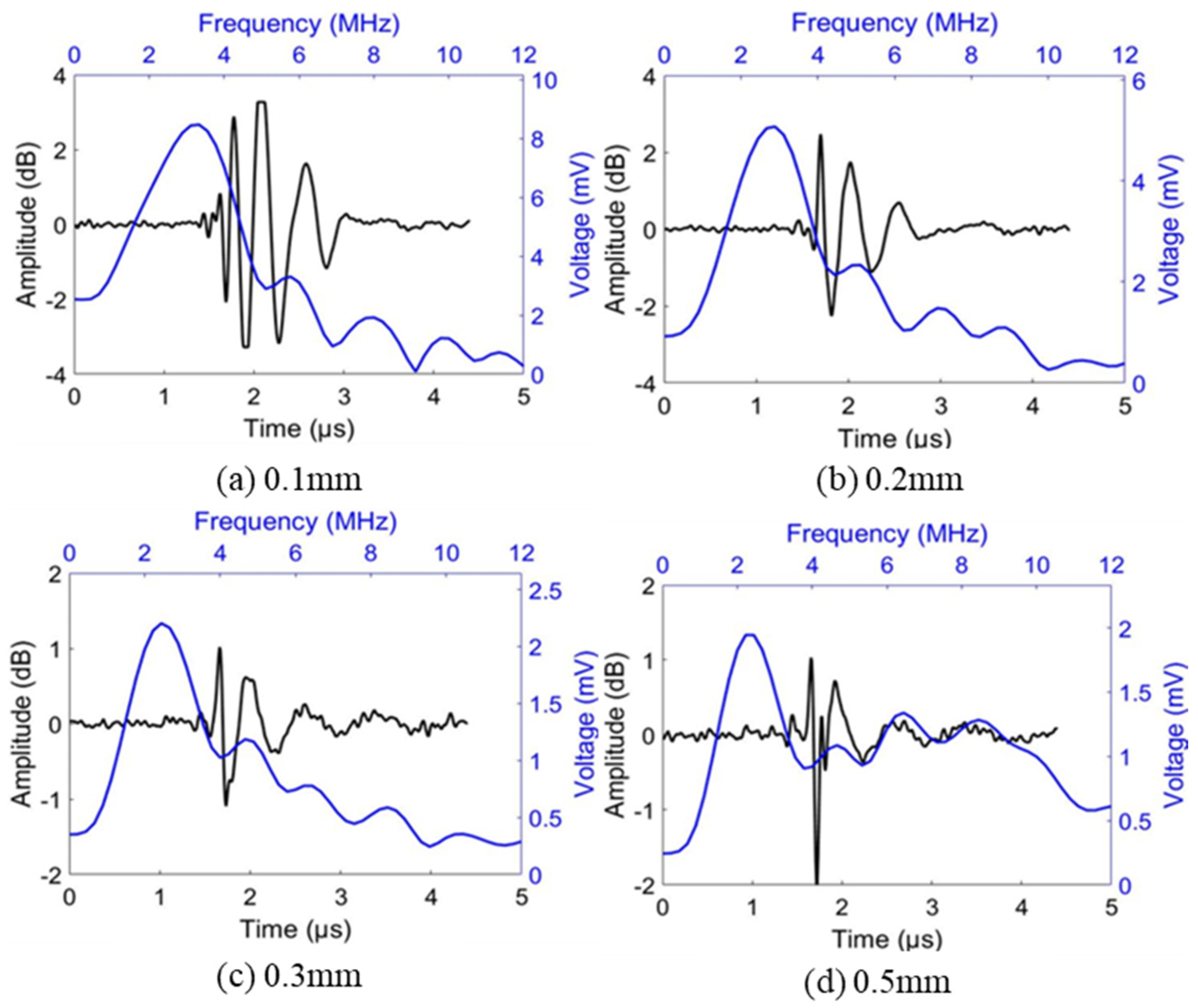
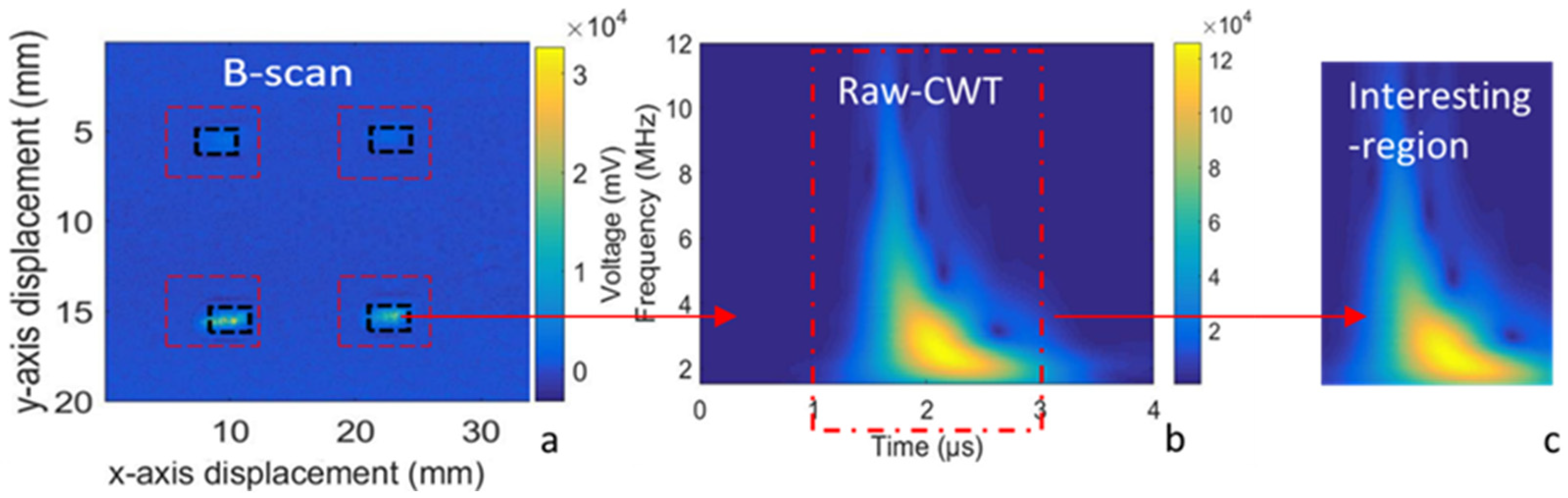
2.3. Signal Processing Methods
3. Results and Discussion
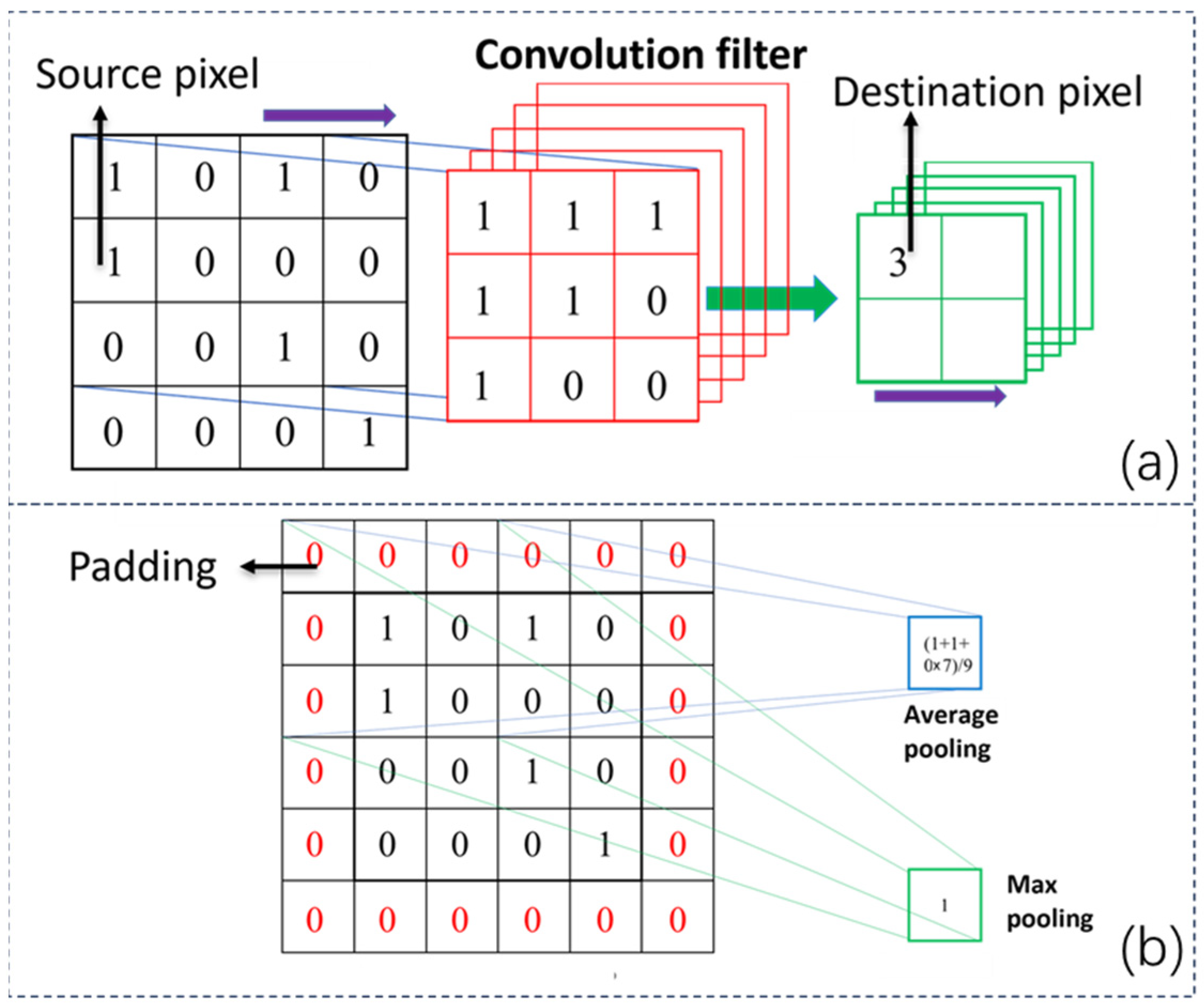
3.1. Neural Network Architecture
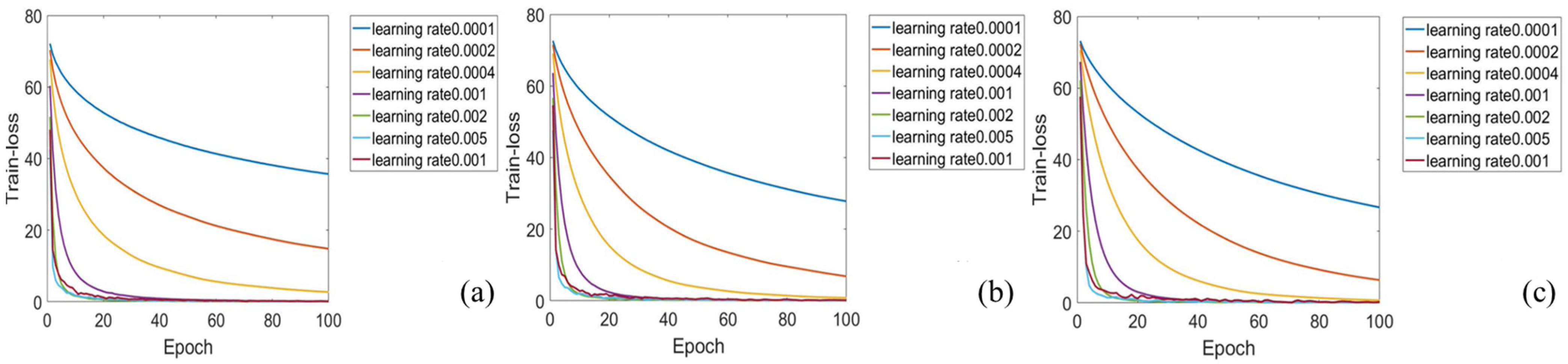
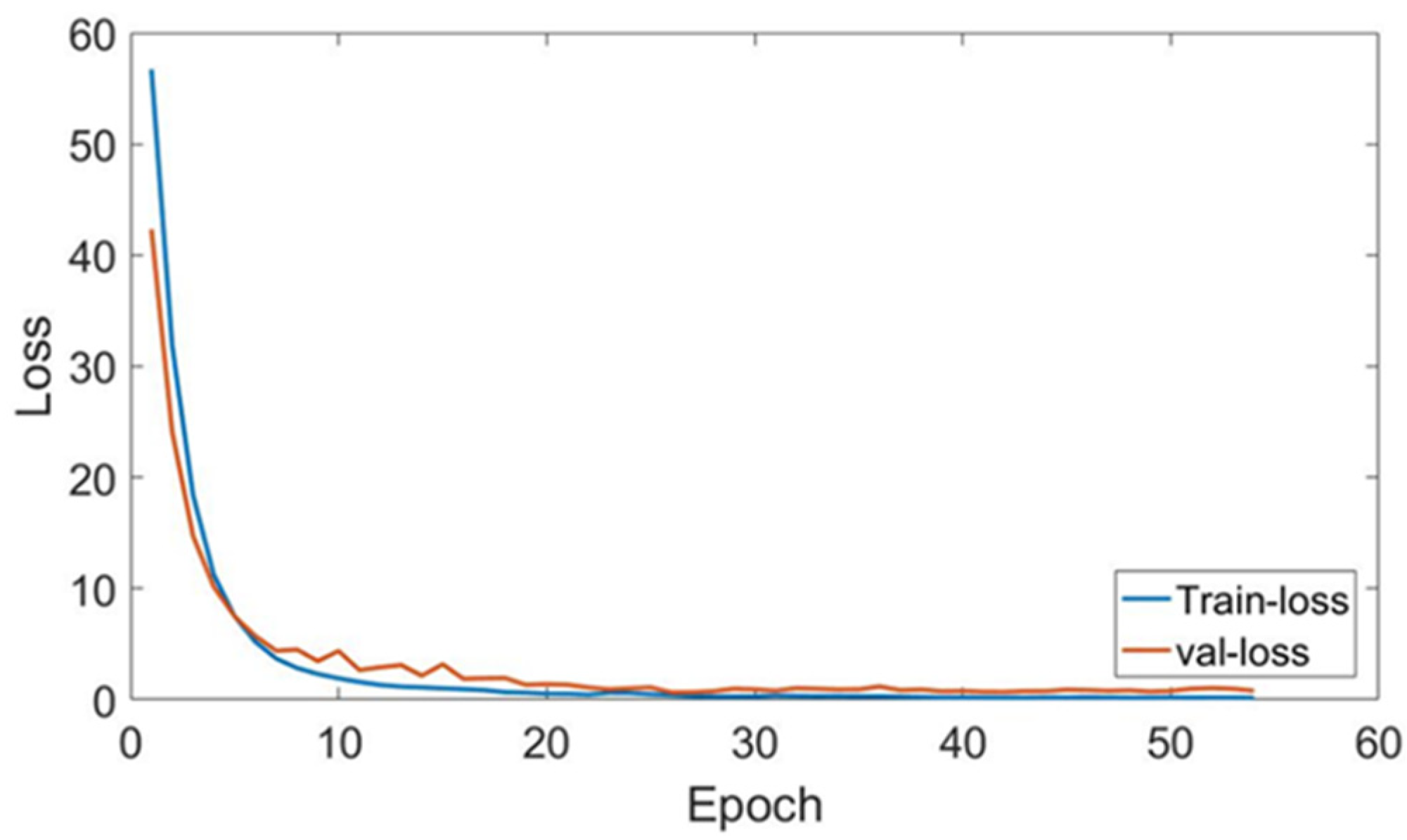
3.2. Neural Network Optimization
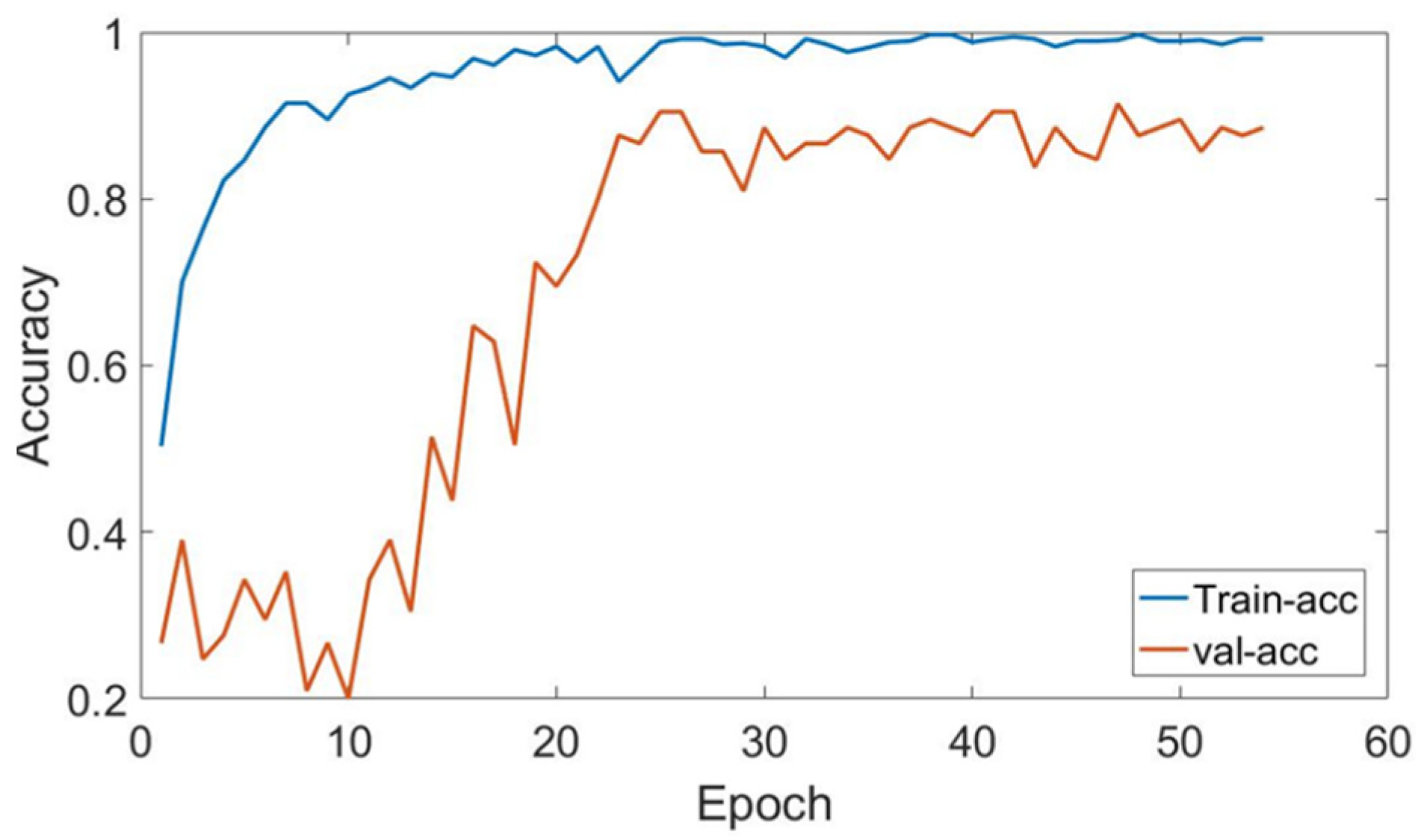
3.3. Depth Measurement Results
4. Conclusions
Future Research Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- García-Martínez, M.; del Hoyo Gordillo, J.C.; Valles González, M.P.; Pastor Muro, A.; González Caballero, B. Failure study of an aircraft engine high pressure turbine (HPT) first stage blade. Eng. Fail. Anal. 2023, 149, 107251. [Google Scholar] [CrossRef]
- Qin, C.; He, S.; Zhong, L.; Feng, W.; Pang, J.; Li, Q.; He, W. Fracture failure analysis of pressure gauge bolt on fuel gas system of offshore platform. Eng. Fail. Anal. 2020, 117, 104959. [Google Scholar] [CrossRef]
- Zobaer Shah, Q.M.; Chowdhury, M.A.; Kowser, M.A. The aspect of the corrosion pitting with fretting fatigue on Aluminum Alloy: A nuclear reactor safety or an aerospace structural failure phenomenon. Results Eng. 2022, 15, 100483. [Google Scholar] [CrossRef]
- Wu, W.P.; Li, Z.Z.; Chu, X. Peridynamics study on crack propagation and failure behavior in Ni/Ni3Al bi-material structure. Compos. Struct. 2023, 323, 117453. [Google Scholar] [CrossRef]
- Oshima, S.; Higuchi, R.; Kobayashi, S. Experimental characterization of cracking behavior initiating from microdefects in cross-ply CFRP laminates. Eng. Fract. Mech. 2023, 281, 109116. [Google Scholar] [CrossRef]
- Kenderian, S.; Djordjevic, B.B.; Green, R.E. Point and line source laser generation of ultrasound for inspection of internal and surface flaws in rail and structural materials. Res. Nondestruct. Eval. 2001, 13, 189–200. [Google Scholar] [CrossRef]
- Liao, D.; Yin, M.; Yi, J.; Zhong, M.; Wu, N. A nondestructive testing method for detecting surface defects of Si3N4-Bearing cylindrical rollers based on an optimized convolutional neural network. Ceram. Int. 2022, 48, 31299–31308. [Google Scholar] [CrossRef]
- He, J.; Liu, X.; Cheng, Q.; Yang, S.; Li, M. Quantitative detection of surface defect using laser-generated Rayleigh wave with broadband local wavenumber estimation. Ultrasonics 2023, 132, 106983. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, J.; Pan, Y. Surface circular-arc defects interacted by laser-generated Rayleigh wave. Ultrasonics 2020, 103, 106085. [Google Scholar] [CrossRef] [PubMed]
- Masserey, B.; Fromme, P. Surface defect detection in stiffened plate structures using Rayleigh-like waves. NDT E Int. 2009, 42, 564–572. [Google Scholar]
- Cheng, W.; Sun, H.H.; Wan, L.S.; Fan, Z.; Tan, K.H. Corrosion damage detection in reinforced concrete using Rayleigh wave-based method. Cement Concrete Comp. 2023, 143, 105253. [Google Scholar] [CrossRef]
- Thring, C.B.; Fan, Y.; Edwards, R.S. Focused Rayleigh wave EMAT for characterization of surface-breaking defects. NDT E Int. 2016, 81, 20–27. [Google Scholar]
- Chen, H.; Zhang, G.; Fan, D.; Fang, L.; Huang, L. Nonlinear Lamb wave analysis for microdefect identification in mechanical structural health assessment. Measurement 2020, 164, 108026. [Google Scholar] [CrossRef]
- Dehghan-Niri, E.; Al-Beer, H. Phase-space topography characterization of nonlinear ultrasound waveforms. Ultrasonics 2018, 84, 446–458. [Google Scholar] [CrossRef]
- Fu, L.L.; Yang, J.S.; Li, S.; Luo, H.; Wu, J.H. Artificial neural network-based damage detection of composite material using laser ultrasonic technology. Measurement 2023, 220, 113435. [Google Scholar] [CrossRef]
- Chen, D.; Zhou, Y.; Wang, W.; Zhang, Y.; Deng, Y. Ultrasonic signal classification and porosity testing for CFRP materials via artificial neural network. Mater. Today Commun. 2022, 30, 103021. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Tian, T.; Deng, D.; Hu, M.; Ma, J.; Gao, D.; Zhang, J.; Ma, S.; Yang, L.; et al. A review on guided-ultrasonic-wave-based structural health monitoring: From fundamental theory to machine learning techniques. Ultrasonics 2023, 133, 107014. [Google Scholar] [CrossRef] [PubMed]
- Amiri, N.; Farrahi, G.H.; Kashyzadeh, K.R.; Chizari, M. Applications of ultrasonic testing and machine learning methods to predict the static & fatigue behavior of spot-welded joints. J. Manuf. Process 2020, 52, 26–34. [Google Scholar]
- Czarnecki, S.; Shariq, M.; Nikoo, M.; Sadowski, Ł. An intelligent model for the prediction of the compressive strength of cementitious composites with ground granulated blast furnace slag based on ultrasonic pulse velocity measurements. Measurement 2021, 172, 108951. [Google Scholar] [CrossRef]
- Tenza-Abril, A.J.; Villacampa, Y.; Solak, A.M.; Baeza-Brotons, F. Prediction and sensitivity analysis of compressive strength in segregated lightweight concrete based on artificial neural network using ultrasonic pulse velocity. Constr. Build. Mater. 2018, 189, 1173–1183. [Google Scholar] [CrossRef]
- Wang, F.; Song, G. Looseness detection in cup-lock scaffolds using percussion-based method. Automat. Constr. 2020, 118, 103266. [Google Scholar] [CrossRef]
- Wang, F.; Mobiny, A.; Van Nguyen, H.; Song, G. If structure can exclaim: A novel robotic-assisted percussion method for spatial bolt-ball joint looseness detection. Struct. Health Monit. 2020, 20, 1597–1608. [Google Scholar] [CrossRef]
- Valizadeh, M.; Wolff, S.J. Convolutional Neural Network applications in additive manufacturing: A review. Adv. Indust. Manufact. Eng. 2022, 4, 100072. [Google Scholar] [CrossRef]
- Hema, C.; Garcia Marquez, F.P. Emotional speech Recognition using CNN and Deep learning techniques. Appl. Acoust. 2023, 211, 109492. [Google Scholar] [CrossRef]
- Habib, G.; Qureshi, S. Optimization and acceleration of convolutional neural networks: A survey. J. King Saud Univ. Com. Infor. Sci. 2022, 34, 4244–4268. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
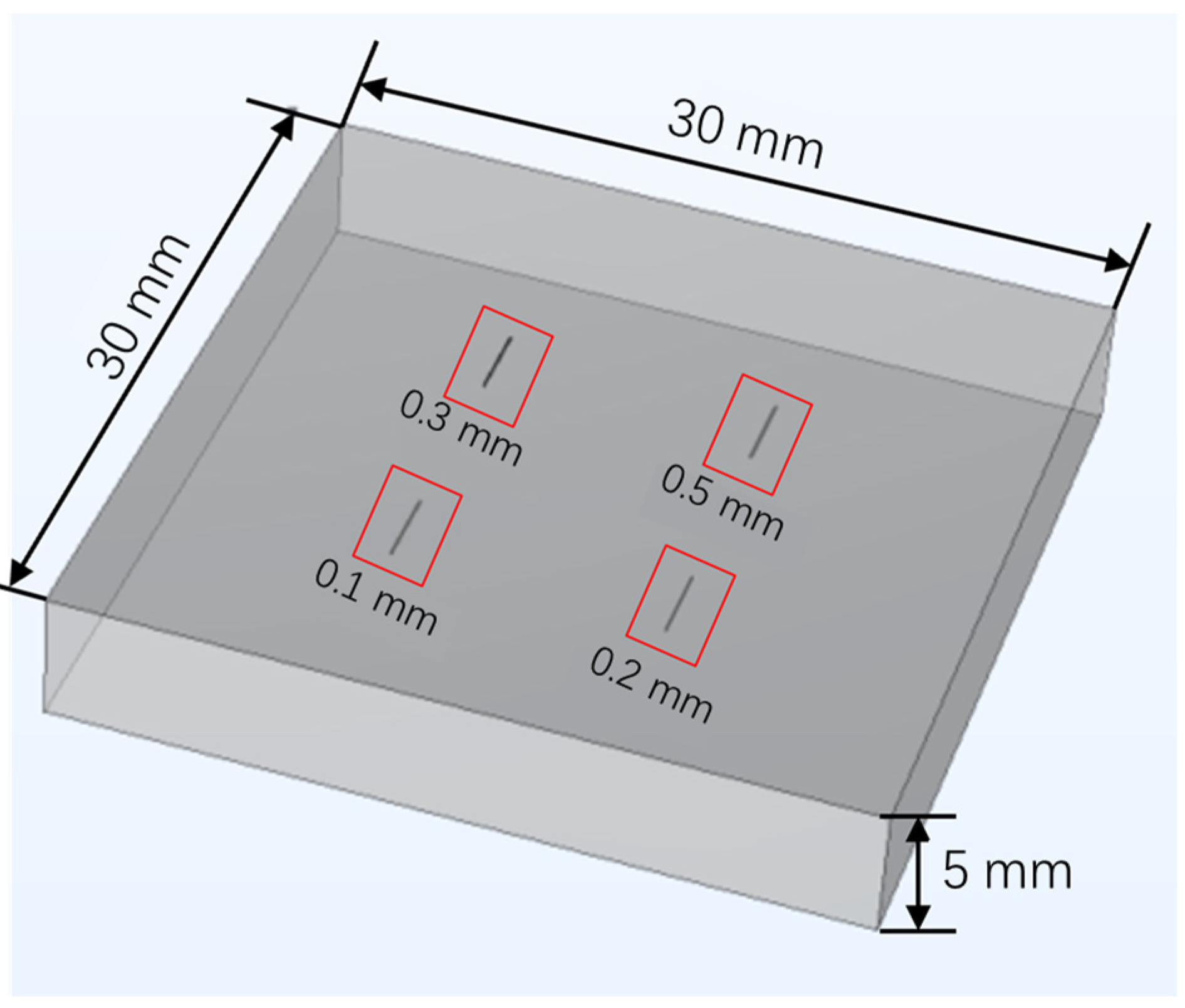
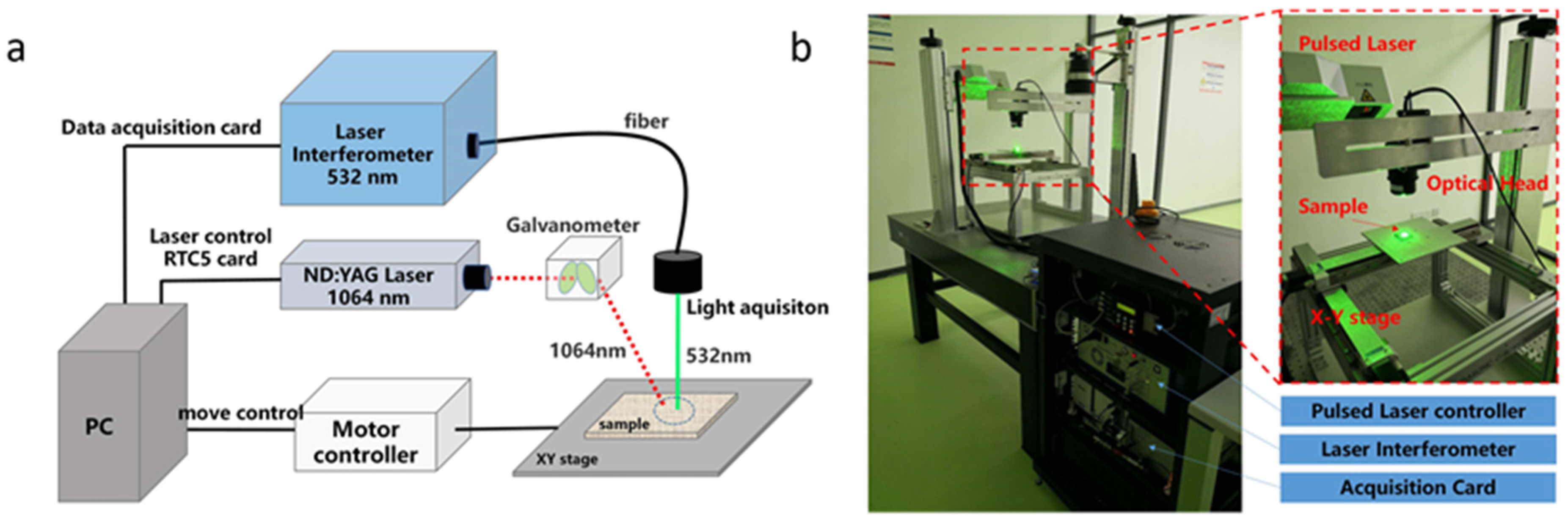





| Type | 0.1 mm | 0.2 mm | 0.3 mm | 0.5 mm | No Defect |
|---|---|---|---|---|---|
| Training set | 140 | 140 | 140 | 140 | 140 |
| Test set | 40 | 40 | 40 | 40 | 40 |
| Validation set | 20 | 20 | 20 | 20 | 20 |
| Layer | Type | Parameter Settings |
|---|---|---|
| L1 | Conv | Filter number = 64, kernel size = 11 × 11, stride = 4, activation = ’ReLU’, padding = ’same’ |
| L2 | Max-pooling | Kernel size = 3 × 3, stride = 4, padding = ’invalid’ |
| L3 | Conv | Filter number = 128, kernel size = 7 × 7, stride = 4, activation = ’ReLU’, padding = ’same’ |
| L4 | Max-pooling | Kernel size = 3 × 3, stride = 2, padding = ’valid’ |
| L5 | Conv | Filter number = 256, kernel size = 3 × 3, stride = 1, activation = ’ReLU’, padding = ’same’ |
| L6 | Max-pooling | Kernel size = 3 × 3, stride = 2, padding = ’valid’ |
| L7 | FC | Units = 1024, activation = ’ReLU’ |
| L8 | FC | Units = 1024, activation = ’ReLU’ |
| L9 | FC | Units = 5, activation = ’Softmax’ |
| Learning Rate | 0.01 | 0.005 | 0.001 | 0.002 | 0.0004 | 0.0002 | 0.0001 | |
|---|---|---|---|---|---|---|---|---|
| Batch Size | ||||||||
| 64 | 88.7% | 87.8% | 88.2% | 90.5% | 81.9% | 77.8% | 86.0% | |
| 32 | 88.7% | 86.9% | 88.7% | 91.9% | 83.7% | 83.7% | 82.8% | |
| 16 | 87.8% | 83.7% | 88.7% | 86.0% | 73.8% | 84.2% | 80.1% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, Q.; Cao, J.; Xu, W.; Jiang, L.; Zhang, J.; Ding, H.; Li, X.; Yan, J. Depth Evaluation of Tiny Defects on or near Surface Based on Convolutional Neural Network. Appl. Sci. 2023, 13, 11559. https://doi.org/10.3390/app132011559
Fei Q, Cao J, Xu W, Jiang L, Zhang J, Ding H, Li X, Yan J. Depth Evaluation of Tiny Defects on or near Surface Based on Convolutional Neural Network. Applied Sciences. 2023; 13(20):11559. https://doi.org/10.3390/app132011559
Chicago/Turabian StyleFei, Qinnan, Jiancheng Cao, Wanli Xu, Linzhao Jiang, Jun Zhang, Hui Ding, Xiaohong Li, and Jingli Yan. 2023. "Depth Evaluation of Tiny Defects on or near Surface Based on Convolutional Neural Network" Applied Sciences 13, no. 20: 11559. https://doi.org/10.3390/app132011559
APA StyleFei, Q., Cao, J., Xu, W., Jiang, L., Zhang, J., Ding, H., Li, X., & Yan, J. (2023). Depth Evaluation of Tiny Defects on or near Surface Based on Convolutional Neural Network. Applied Sciences, 13(20), 11559. https://doi.org/10.3390/app132011559







