Curved-Line Path-Following Control of Fixed-Wing Unmanned Aerial Vehicles Using a Robust Disturbance-Estimator-Based Predictive Control Approach
Abstract
:1. Introduction
- (1)
- A path-following control scheme for FWUAVs is perfected.
- (2)
- A robust control approach is proposed for attitude control.
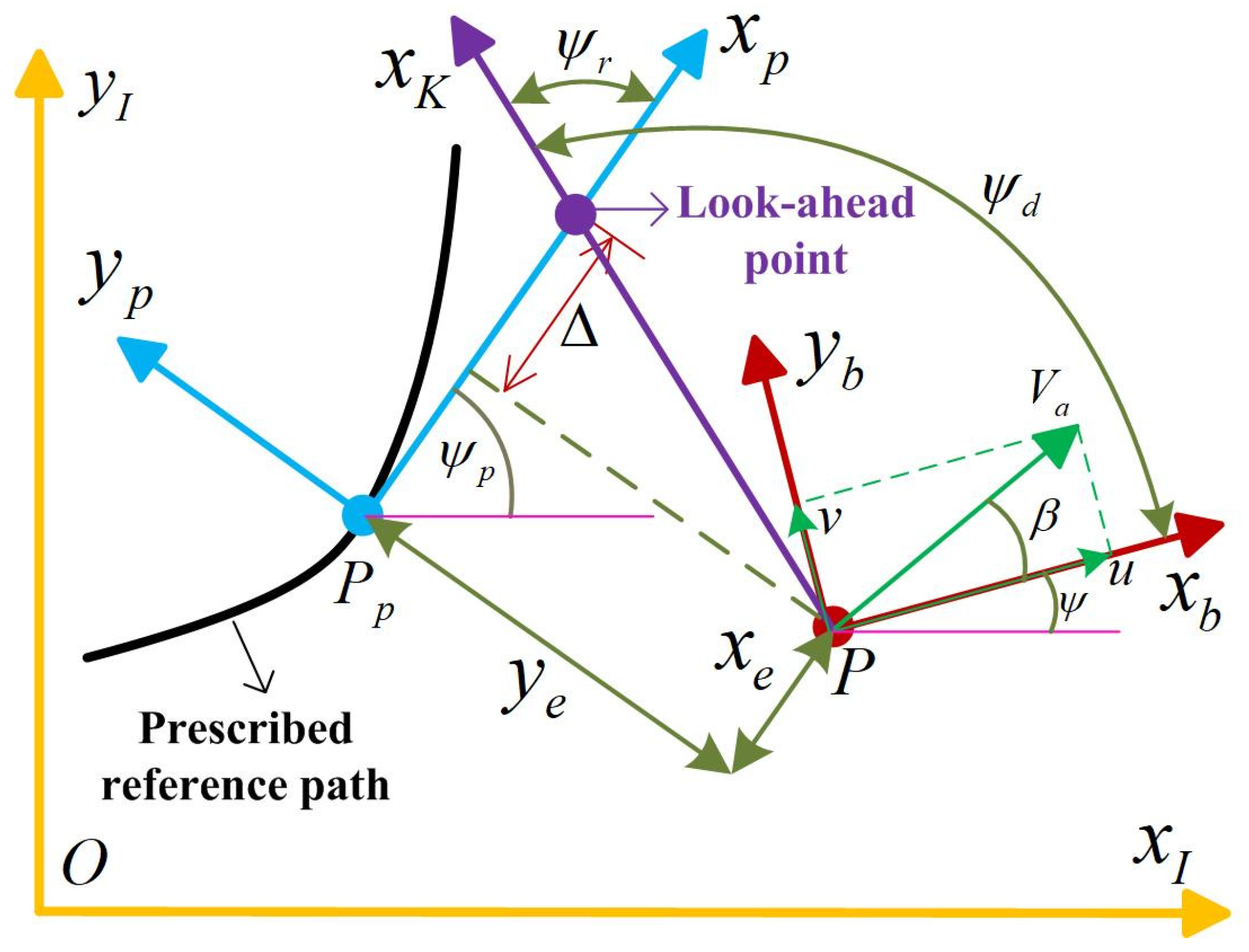
2. System Modeling
2.1. Computation of Desired Attitude Angles
2.2. Yaw System Model
2.3. Existing Approaches and Defects
3. Yaw Angle Control Design
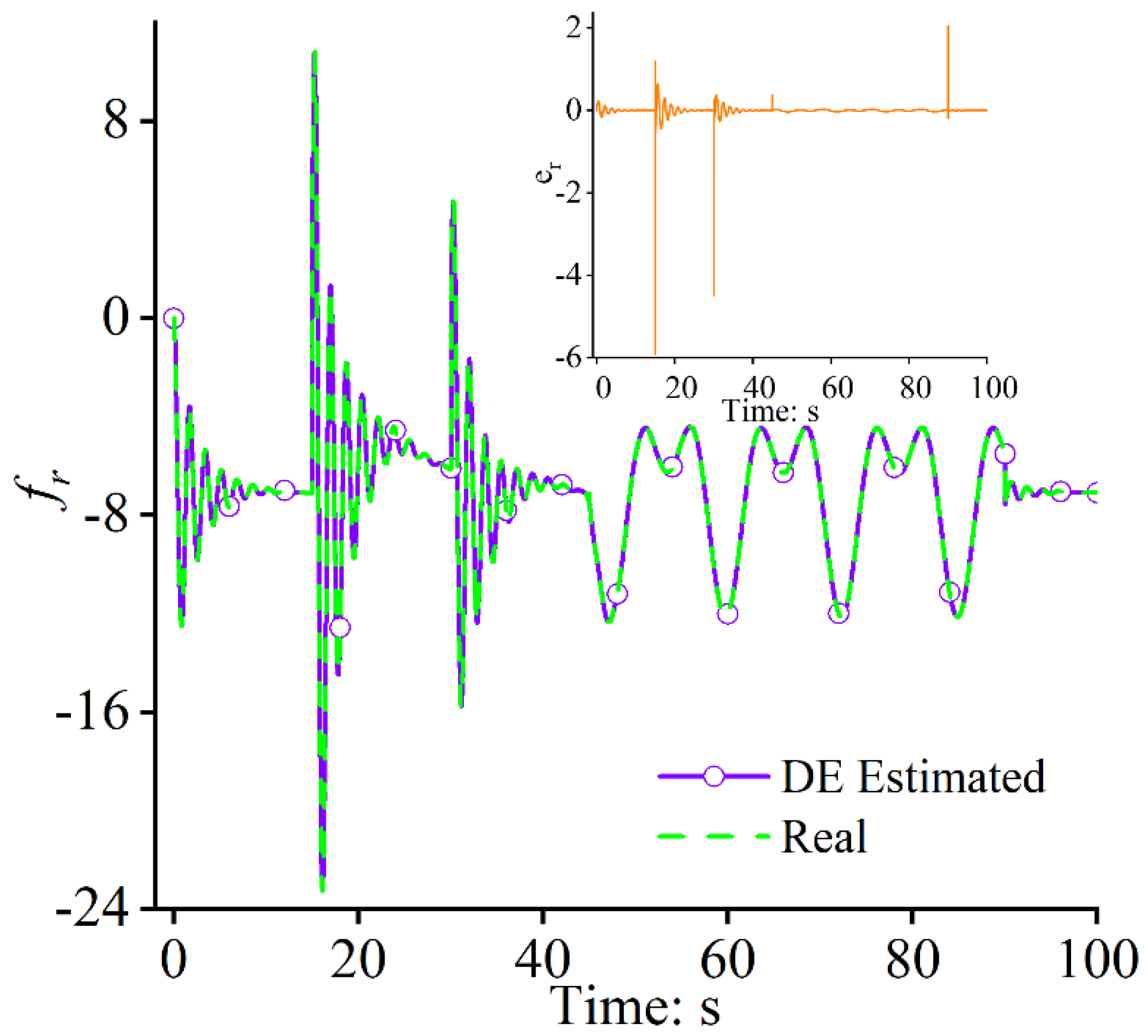
3.1. Design of DE
3.2. Controller Design
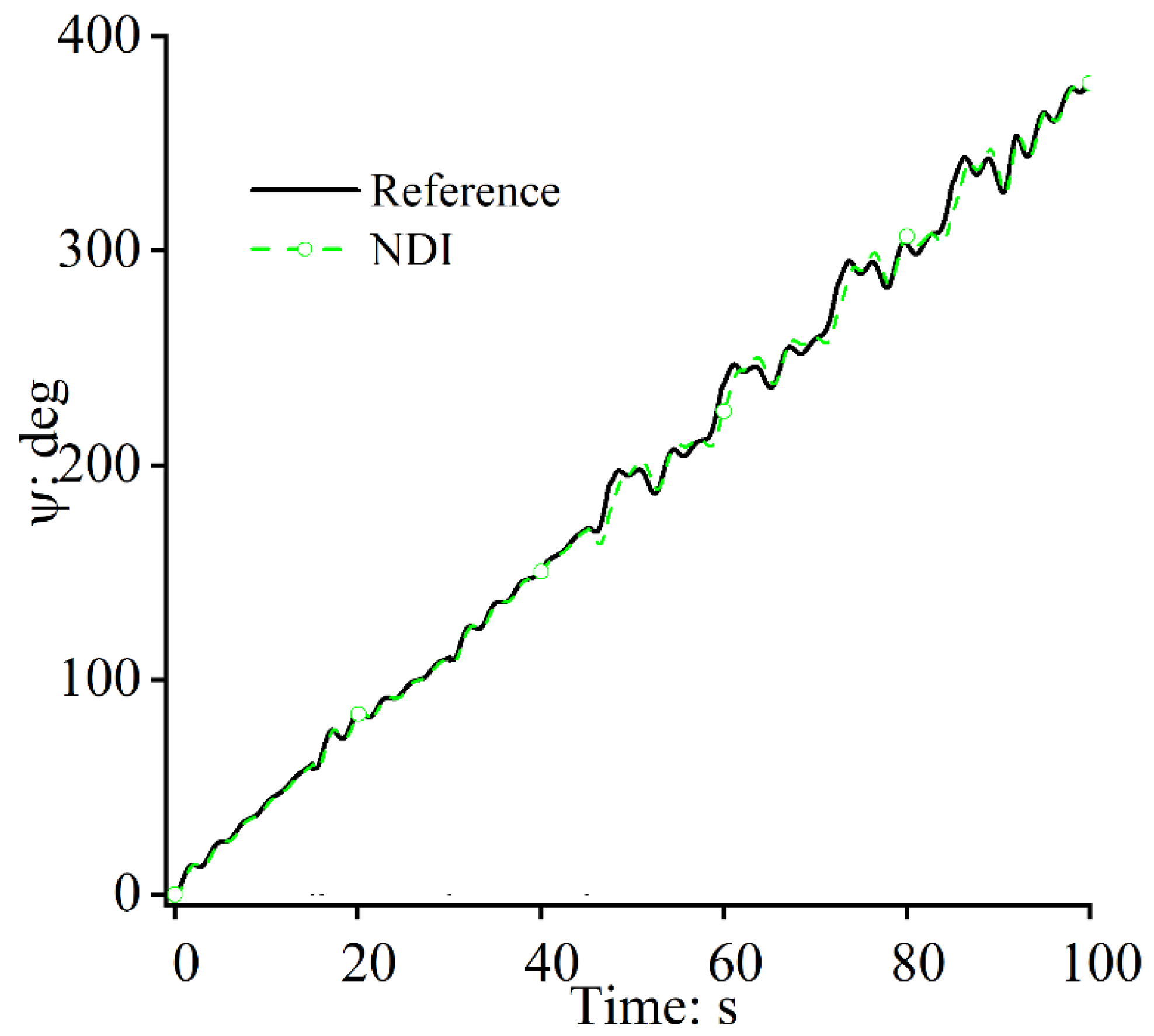
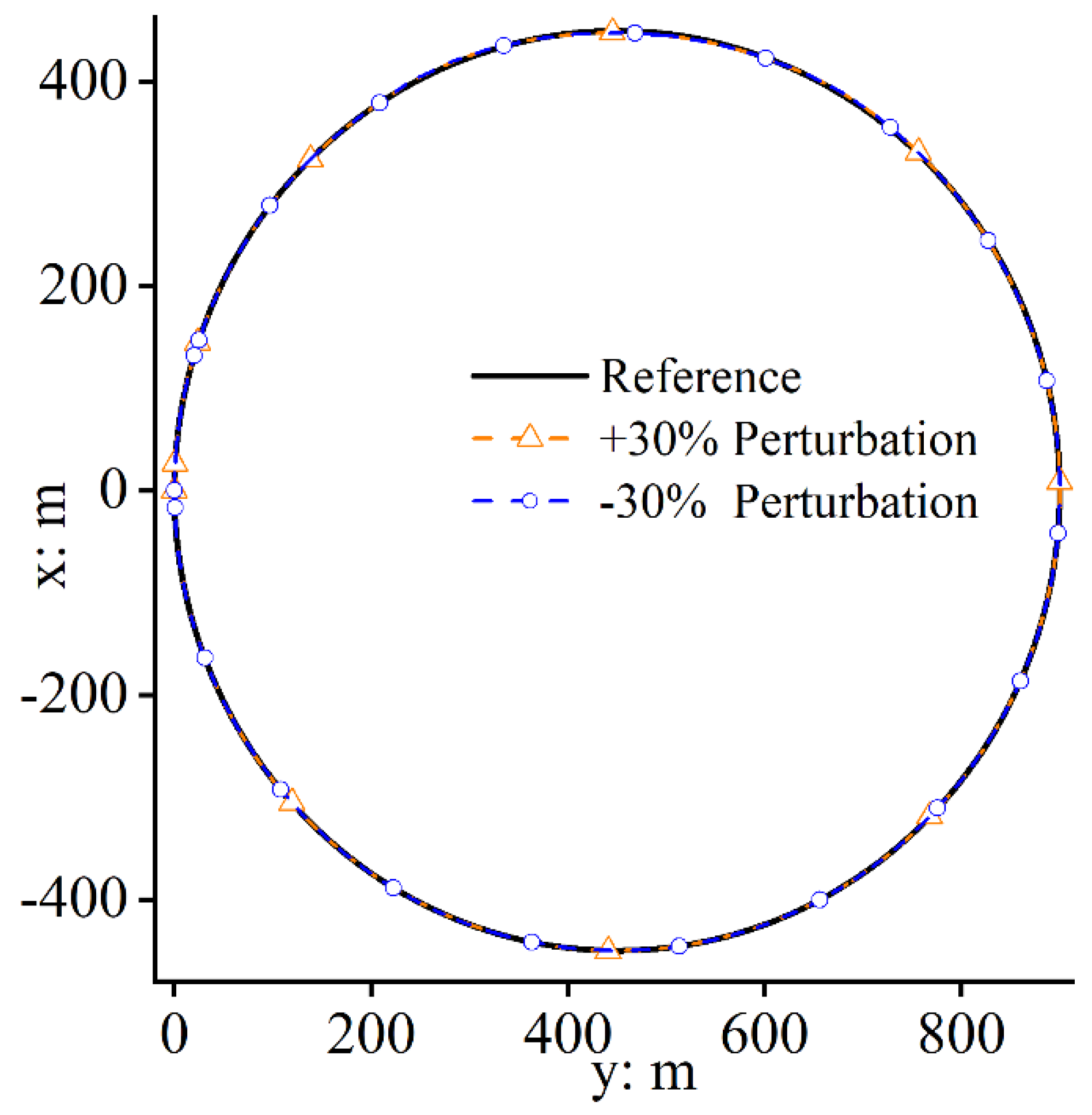
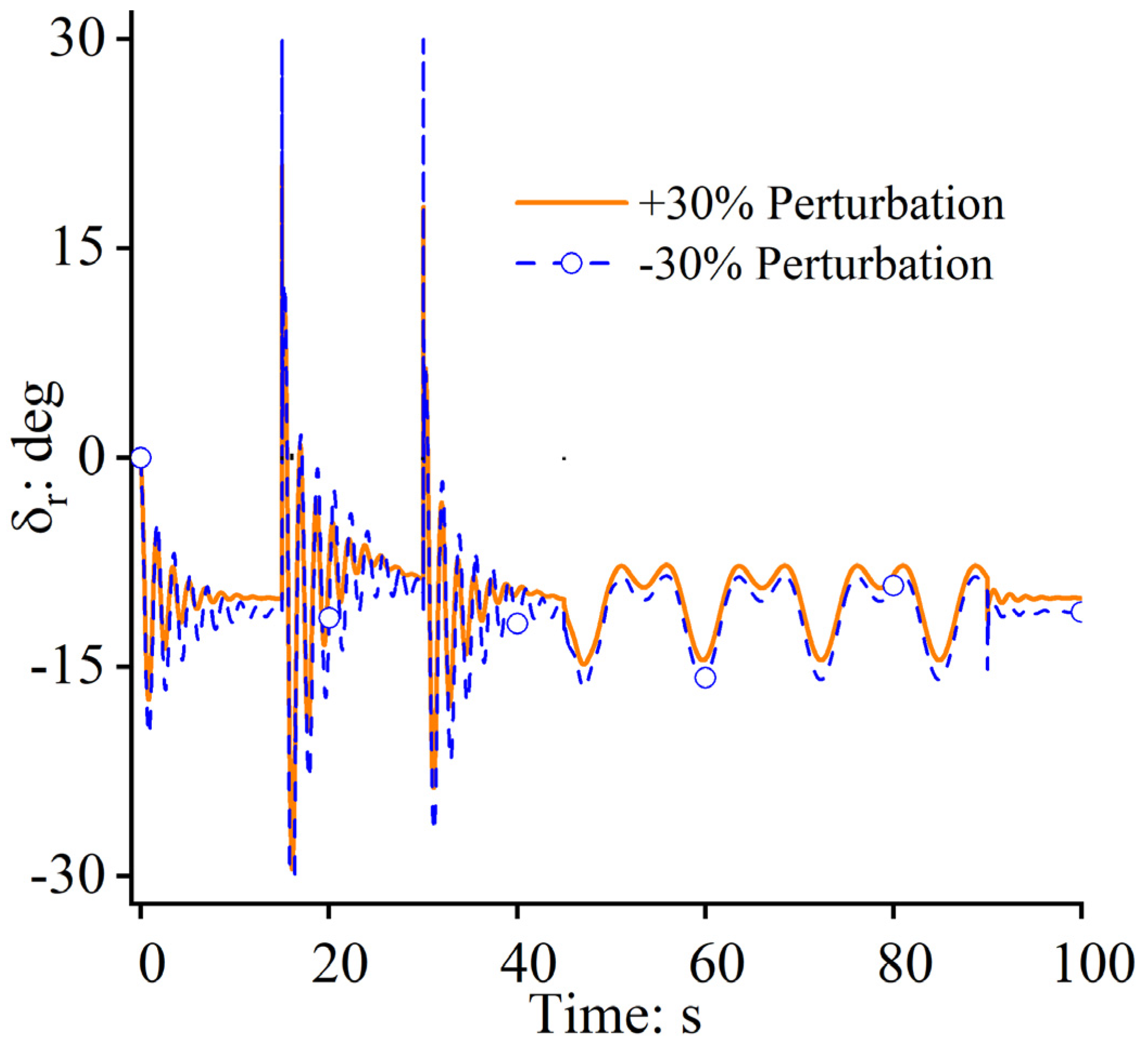
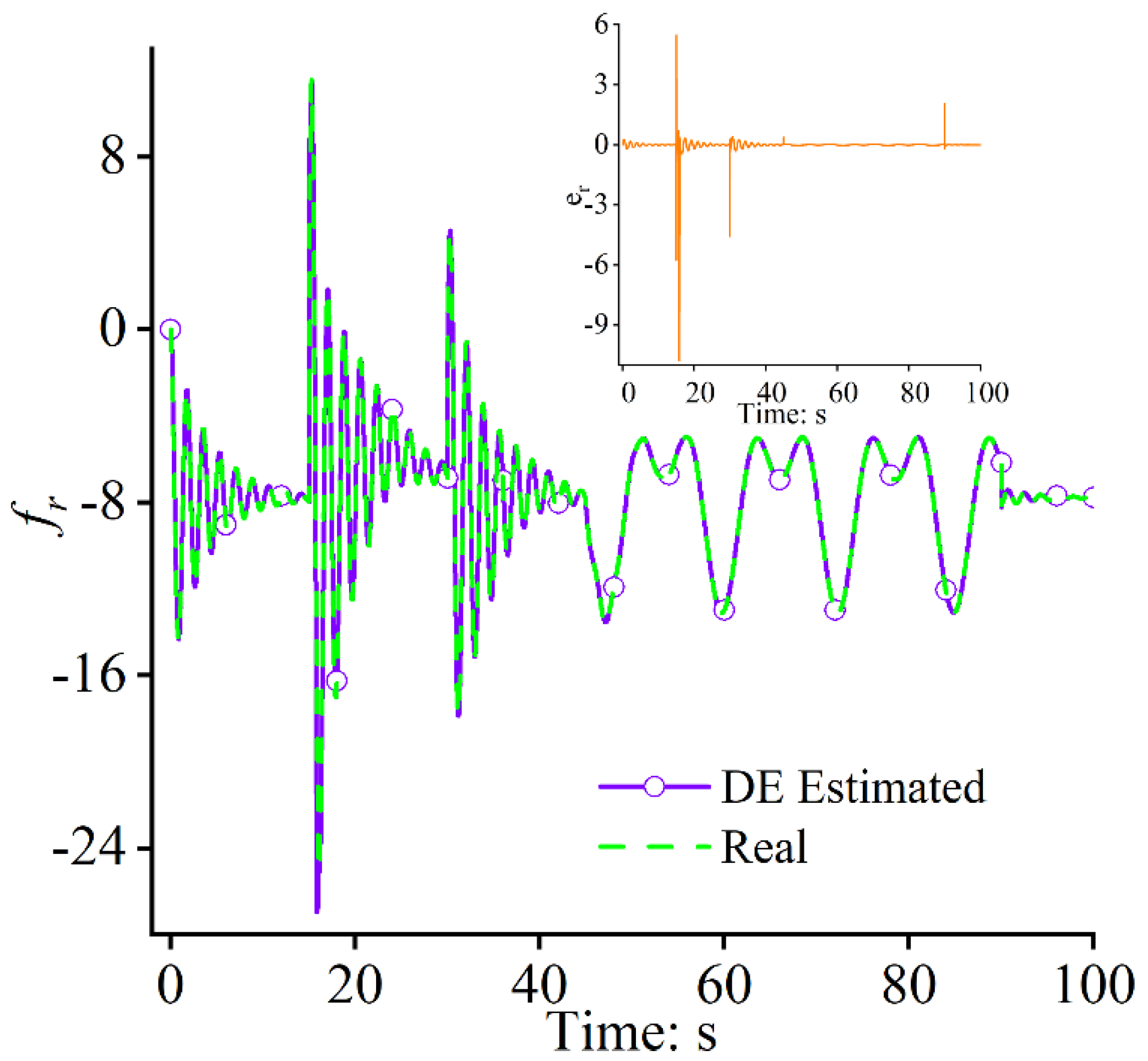
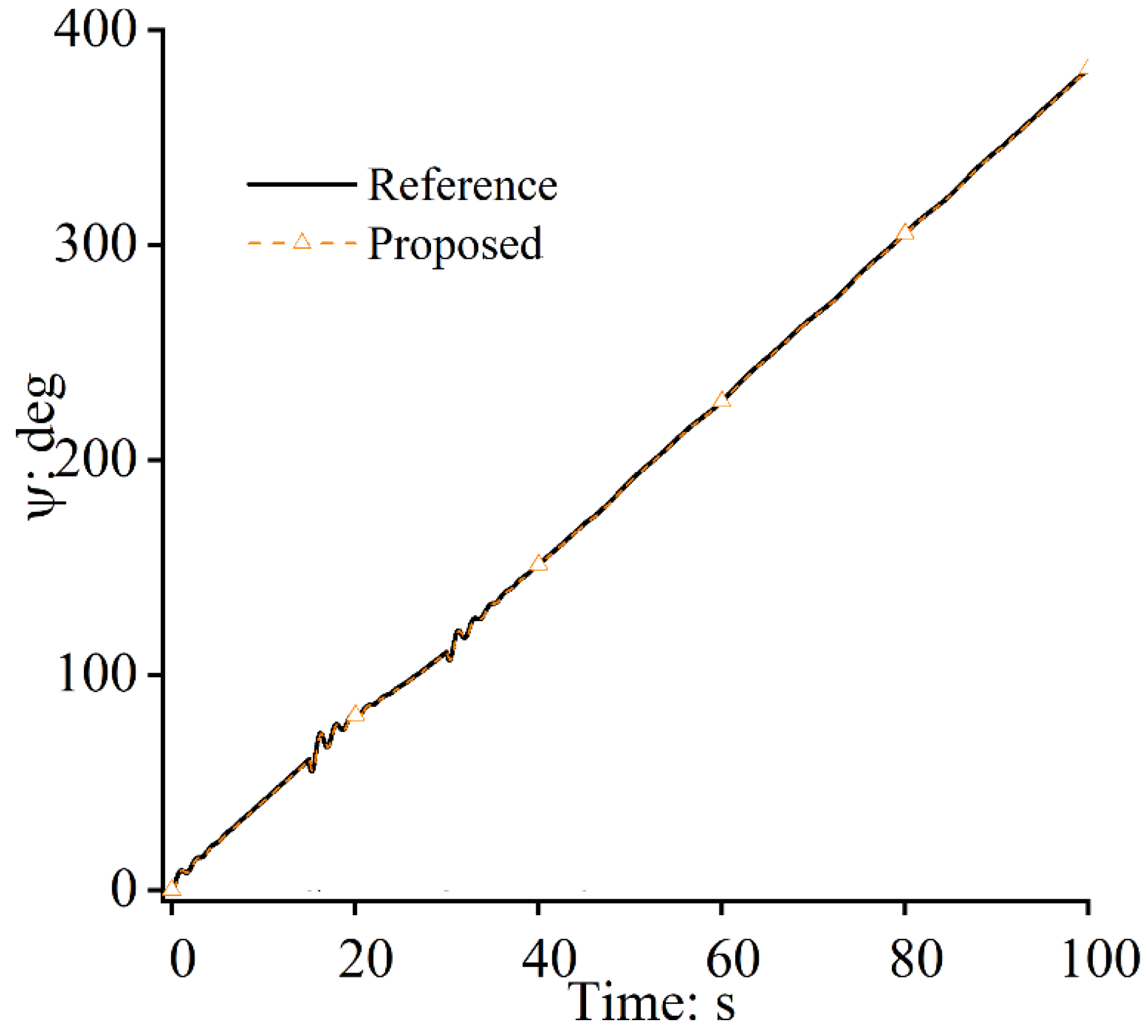
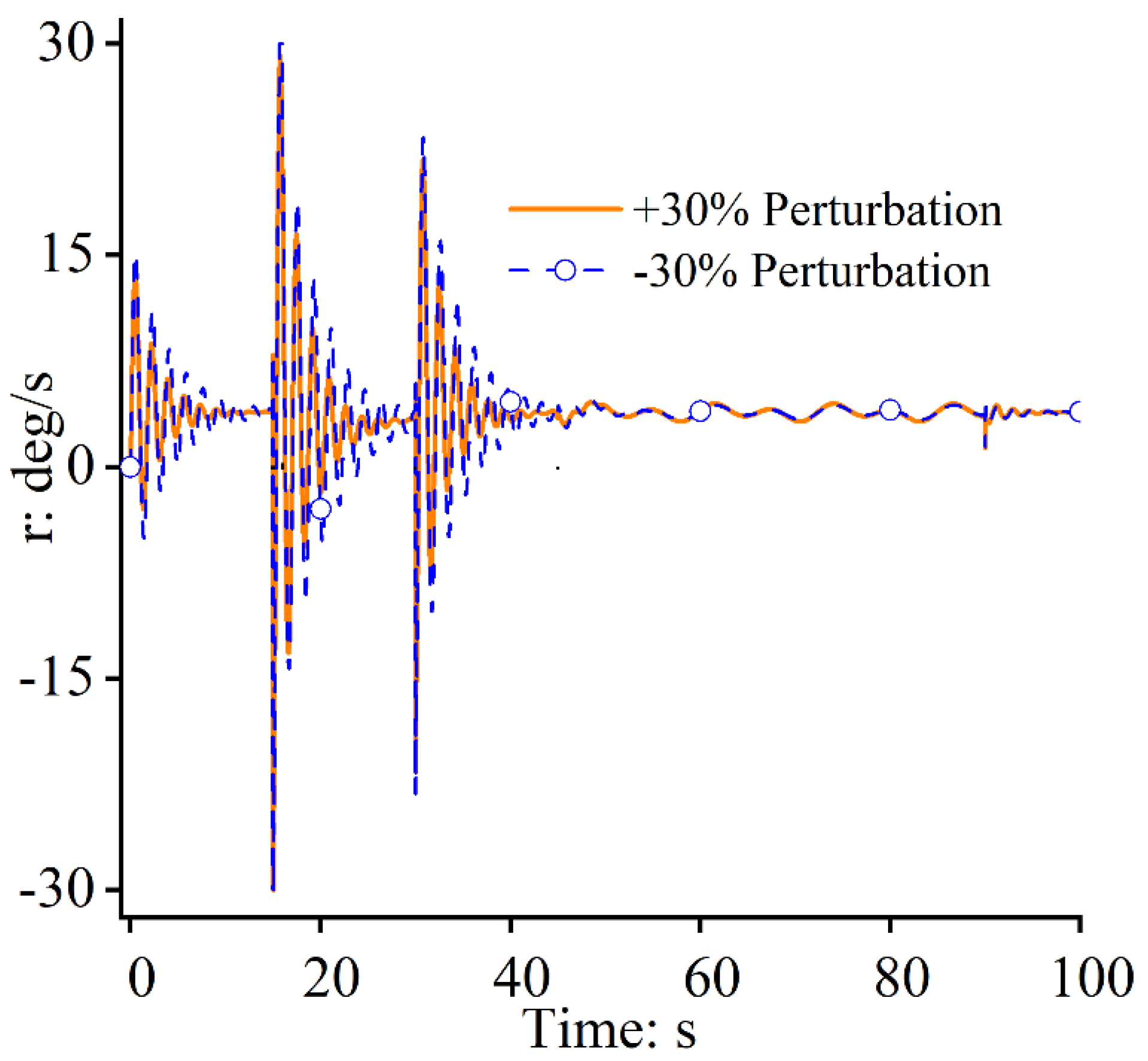
4. Numerical Simulations
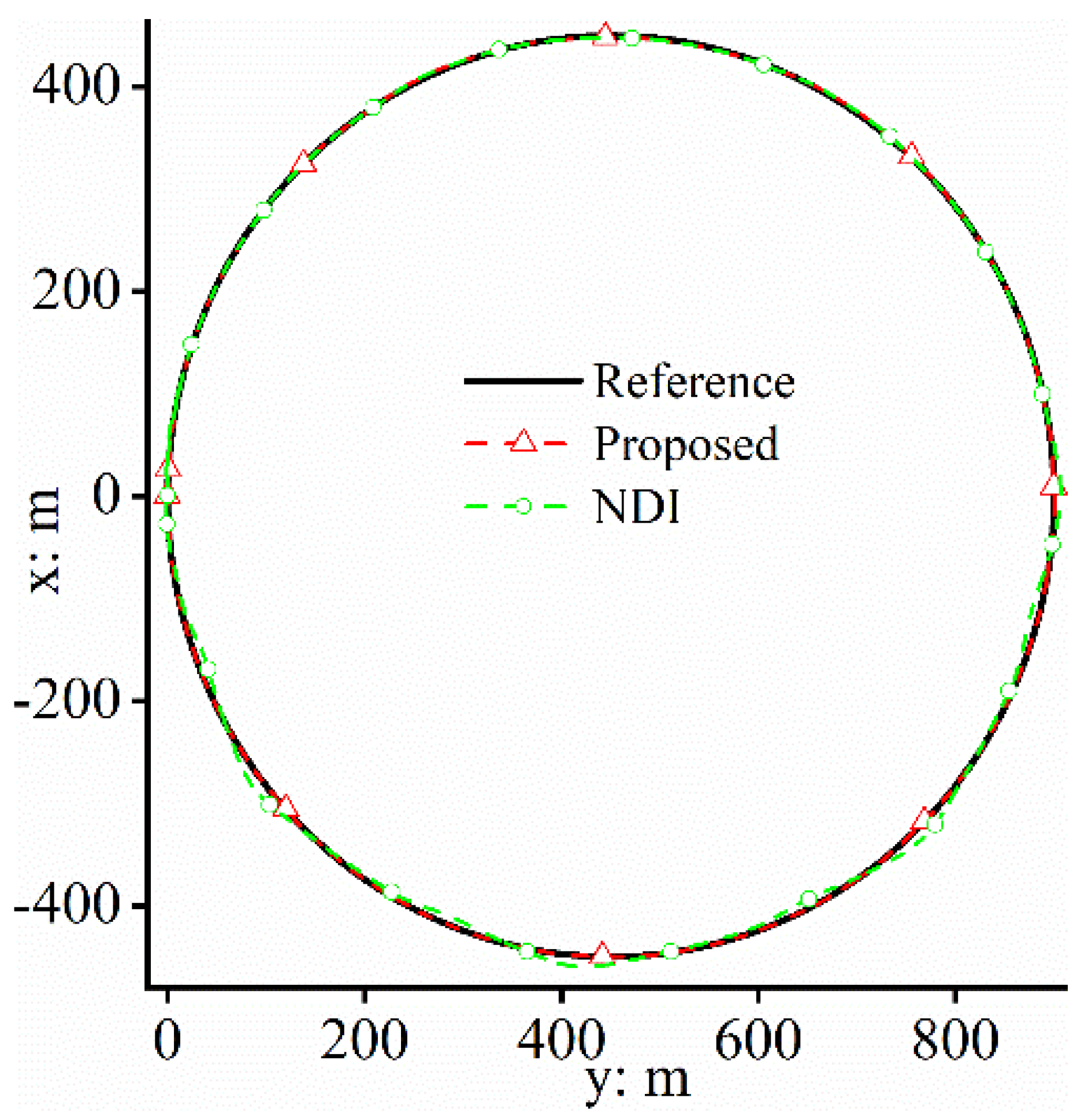
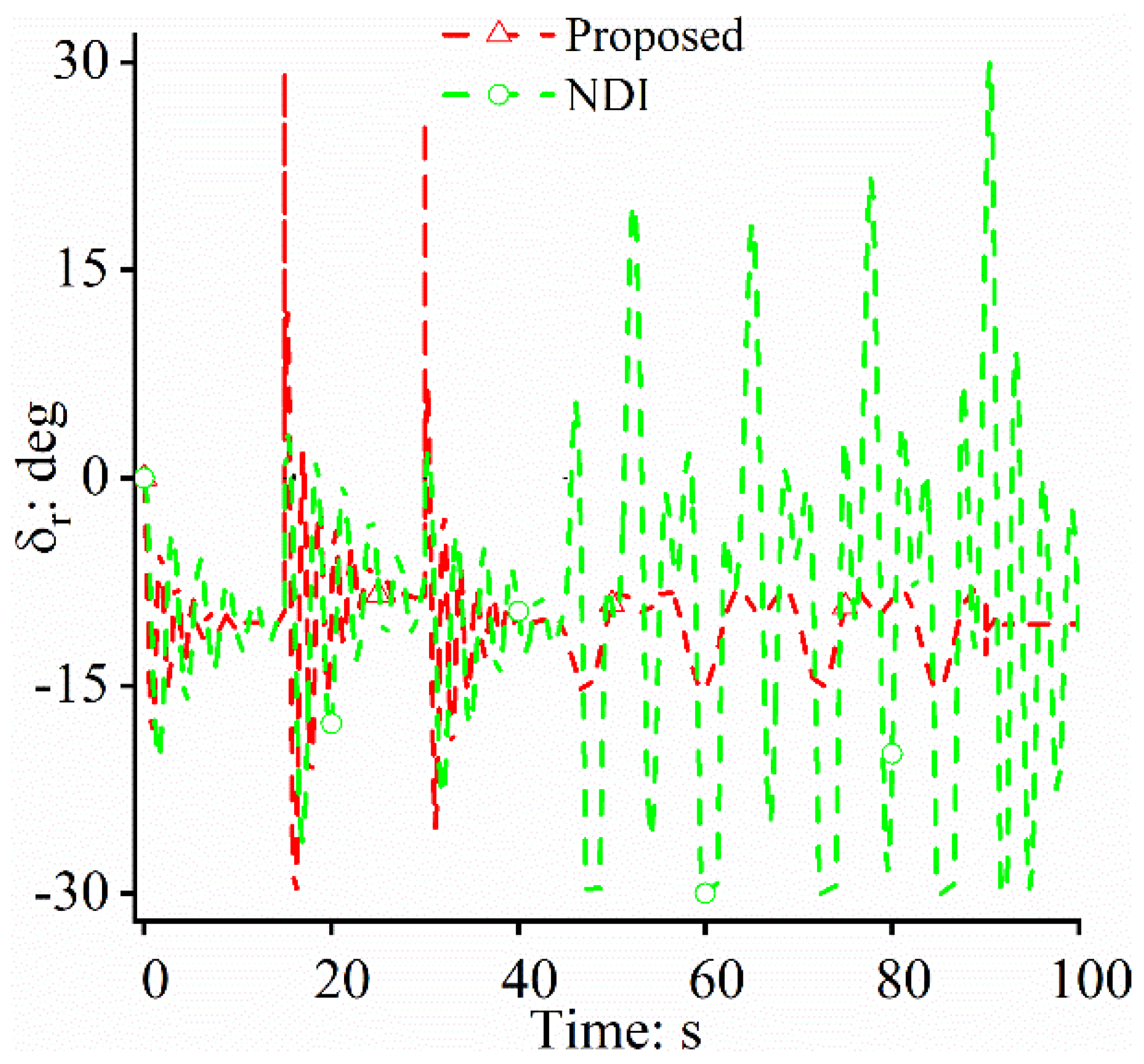
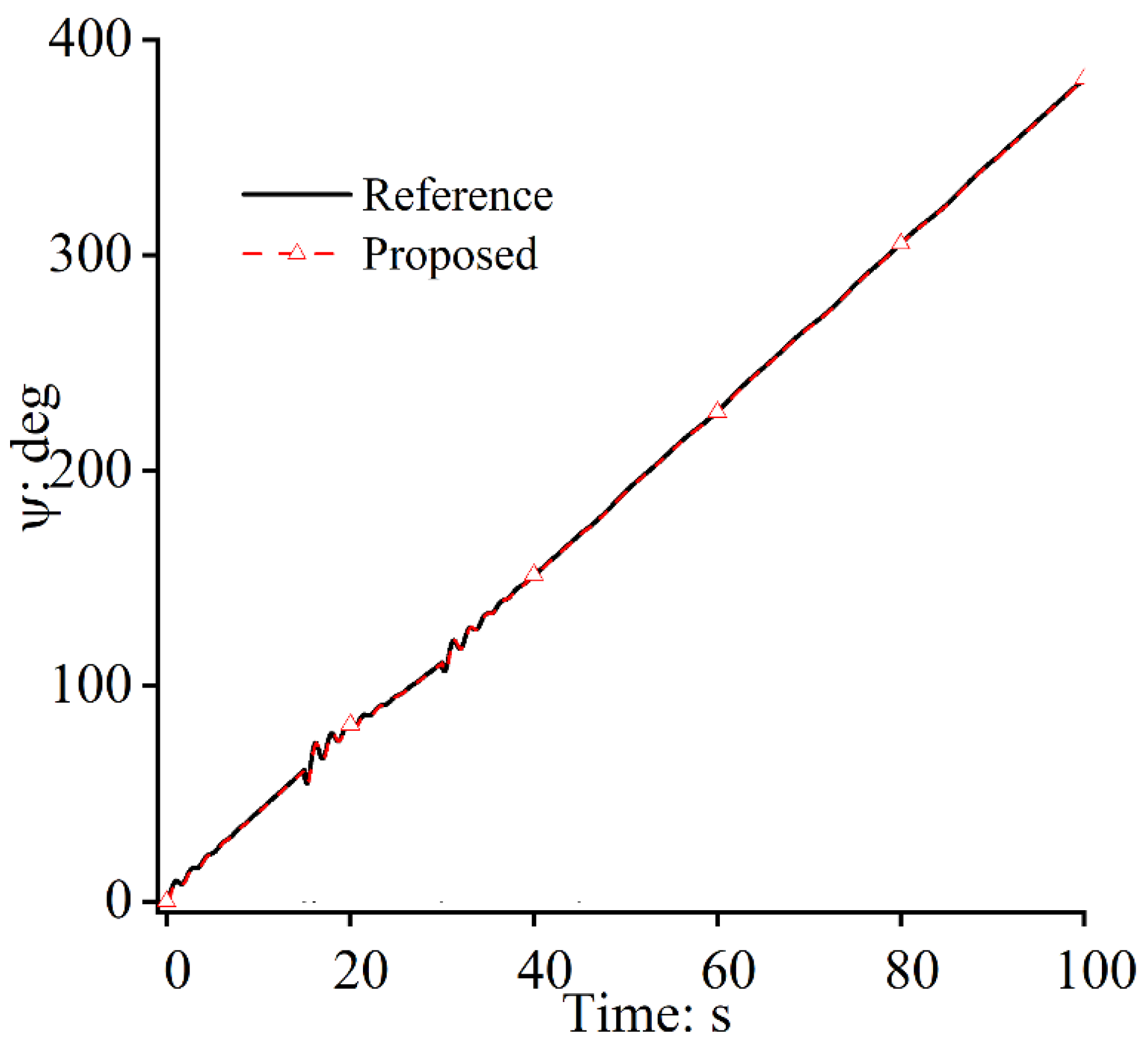
4.1. Case Study 1
4.2. Case Study 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nelson, R.C. Flight Stability and Automatic Control; The McGraw-Hill Companies Press: New York, USA, 1989. [Google Scholar]
- Ambrosino, G.; Ariola, M.; Ciniglio, U.; Corraro, F.; De Lellis, E.; Pironti, A. Path generation and tracking in 3-D for UAVs. IEEE Trans. Control Syst. Technol. 2009, 17, 980–988. [Google Scholar] [CrossRef]
- Woo, J.W.; An, J.Y.; Cho, M.G.; Kim, C.J. Integration of path planning, trajectory generation and trajectory tracking control for aircraft mission autonomy. Aerosp. Sci. Technol. 2021, 118, 107014. [Google Scholar] [CrossRef]
- Tan, G.Y.; Luo, H.B.; Liao, F.; Wang, X.H.; Ji, H.B. Cooperative Strategy for Aircraft Defense Line-of-Sight Guidance in Three-Dimensional Space. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 3398–3403. [Google Scholar]
- Gu, J.C.; Ding, G.R.; Xu, Y.T.; Wang, H.C.; Wu, Q.H. Proactive optimization of transmission power and 3D trajectory in UAV-assisted relay systems with mobile ground users. Chin. J. Aeronaut. 2021, 34, 129–144. [Google Scholar] [CrossRef]
- Rymer, N.; Moore, A.J.; Young, S.; Glaab, L.; Smalling, K.; Consiglio, M. Demonstration of Two Extended Visual Line of Sight Methods for Urban UAV Operations. In Proceedings of the AIAA AVIATION 2020 Forum, Virtual, 15–19 June 2020; p. 2889. [Google Scholar]
- Li, S.W.; Gu, Y.X.; Subedi, B.; He, C.Y.; Wan, Y.; Miyaji, A.; Higashino, A. Beyond Visual Line of Sight UAV Control for Remote Monitoring using Directional Antennas. In Proceedings of the 2019 IEEE Globecom Workshops, Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Nelson, D.R.; Blake Barber, D.; McLain, T.W.; Beard, R.W. Vector Field Path Following for Miniature Air Vehicles. IEEE Trans. Robot. 2007, 23, 519–529. [Google Scholar] [CrossRef]
- Wilhelm, J.; Clem, G.; Casbeer, D.; Gerlach, A. Circumnavigation and obstacle avoidance guidance for UAVs using Gradient Vector Fields. In Proceedings of the AIAA Sci tech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; pp. 1–15. [Google Scholar]
- Wilhelm, J.P.; Clem, G. Vector Field UAV Guidance for Path Following and Obstacle Avoidance with Minimal Deviation. J. Guid. Control Dyn. 2019, 42, 1848–1856. [Google Scholar] [CrossRef]
- Chang, K.; Ma, D.L.; Han, X.B.; Liu, N.; Zhang, B.B. Lyapunov vector-based formation tracking control for unmanned aerial vehicles with obstacle/collision avoidance. Trans. Inst. Meas. Control 2020, 42, 1–8. [Google Scholar] [CrossRef]
- Luo, Y.L.; Huang, X.Y.; Wu, C.F.; Leng, S.P. Enhanced Artificial Potential Field-based Moving Obstacle Avoidance for UAV in Three-Dimensional Environment. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Singapore, 9–11 October 2020; pp. 177–182. [Google Scholar]
- Zheng, X.; Galland, S.; Tu, X.; Yang, Q.; Lombard, A.; Gaud, N. Obstacle avoidance model for UAVs with joint target based on multi-strategies and follow-up vector field. In Proceedings of the 11th International Conference on Ambient Systems, Networks and Technologies (ANT), Warsaw, Poland, 6–9 April 2020; pp. 257–264. [Google Scholar]
- Wang, X.; Wang, H.; Lun, Y.B. Shortest Path Planning of UAV for Target Tracking and Obstacle Avoidance in 3D Environment. In Proceedings of the 39th Chinese Control Conference, Shenyang, China, 27–29 July 2020; pp. 3385–3390. [Google Scholar]
- Park, S.; Deyst, J.; How, J.P. Performance and Lyapunov stability and of a nonlinear path following guidance method. J. Guid. Control Dyn. 2007, 30, 1718–1728. [Google Scholar] [CrossRef]
- Rucco, A.; Aguiar, A.P.; Pereira, F.L.; de Sousa, J.B. A Predictive Path-Following Approach for Fixed-Wing Unmanned Aerial Vehicles in Presence of Wind Disturbances. In Proceedings of the Robot 2015: Second Iberian Robotics Conference, Lisbon, Portugal, 2 December 2015; pp. 623–634. [Google Scholar]
- Yamasaki, T.; Balakrishnan, S.N.; Takano, H. Separate-Channel Integrated Guidance and Autopilot for Automatic Path-Following. J. Guid. Control Dyn. 2013, 36, 25–34. [Google Scholar] [CrossRef]
- Rysdyk, R. Unmanned Aerial Vehicle Path Following for Target Observation in Wind. J. Guid. Control Dyn. 2006, 29, 1092–1100. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, X.G.; Yang, J.; Wang, Z.Y. Trajectory-following guidance based on a virtual target and an angle constraint. Aerosp. Sci. Technol. 2019, 87, 448–458. [Google Scholar] [CrossRef]
- Cai, Z.H.; Wang, L.H.; Zhao, J.; Wu, K.; Wang, Y.X. Virtual target guidance-based distributed model 4 predictive control for formation control of multiple 5 UAVs. Chin. J. Aeronaut. 2020, 33, 1037–1056. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.K.; Shen, L.C.; Cong, Y.R. Formation flight of fixed-wing UAV swarms: A 4 group-based hierarchical approach. Chin. J. Aeronaut. 2021, 34, 504–515. [Google Scholar] [CrossRef]
- Mao, Y.H.; Chen, Q.Y.; Hou, Z.X.; Zheng, G. An improved nonlinear guidance law for unmanned aerial vehicles path following. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 5271–5276. [Google Scholar]
- Park, S.; Deyst, J.; How, J. A New Nonlinear Guidance Logic for Trajectory Tracking. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 1–16. [Google Scholar]
- Zhou, W.H.; Li, J.; Liu, Z.H.; Shen, L.C. Improving multi-target cooperative tracking guidance for UAV swarms using multi-agent reinforcement learning. Chin. J. Aeronaut. 2022, 35, 100–112. [Google Scholar] [CrossRef]
- Ueba, M.; Takaku, Y.; Takahashi, K.; Kamata, T. Design and Tests of Guidance and Control Systems for Autonomous Flight of a Low-Speed Model Airplane for Application to a Small-Scale Unmanned Supersonic Airplane. Trans. Jpn. Soc. Aeronaut. Space Sci. Aerosp. Technol. Jpn. 2019, 17, 220–226. [Google Scholar] [CrossRef]
- Modali, S.; Ghosh, S. Terminal-Angle-Constrained Guidance based on Sliding Mode Control for UAV Soft Landing on Ground Vehicles. Electr. Eng. Syst. Sci. 2020, 2009, 14748. [Google Scholar]
- Yin, H.; Li, D.G.; Wang, Y.; Li, X.P. Adaptive Dynamic Occupancy Guidance for Air Combat of UAV. Unmanned Syst. 2023, 11, 1–18. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Tang, W.X. Guidance Strategy for UAV Tracking Target Based on Reference Point Guidance Method. J. Northwest. Polytech. Univ. 2020, 38, 176–182. [Google Scholar] [CrossRef]
- Cui, Z.Y.; Wang, Y. Nonlinear Adaptive Line-of-Sight Path Following Control of Unmanned Aerial Vehicles considering Sideslip Amendment and System Constraints. Math. Probl. Eng. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Wang, D.W.; Zhu, S.Q. Cooperative moving path following for multiple fixed-wing unmanned aerial vehicles with speed constraints. Automatica 2019, 100, 82–89. [Google Scholar] [CrossRef]
- Ma, C.; Yang, J.; Chen, J.Y.; Zhou, C. Path following identification of unmanned aerial vehicles for navigation spoofing and its application. ISA Trans. 2021, 108, 393–405. [Google Scholar] [CrossRef]
- Sedlmair, N.; Theis, J.; Thielecke, F. Design and Experimental Validation of UAV Control Laws—3D Spline-Path-Following and Easy-Handling Remote Control. In Proceedings of the 5th CEAS Conf. Guid., Navigation, Control, Milano, Italy, 3–5 April 2019; pp. 1–20. [Google Scholar]
- Kaminer, I.; Pascoa, A.; Xargay, E.; Hovakimyan, N.; Cao, C.Y.; Dobrokhodov, V. Path following for unmanned aerial vehicles using L1 adaptive augmentation of commercial autopilots. J. Guid. Control Dyn. 2010, 33, 550–564. [Google Scholar] [CrossRef]
- Liu, C.J.; McAree, O.; Chen, W.H. Path-following control for small fixed-wing unmanned aerial vehicles under wind disturbances. Int. J. Robust. Nonlinear Control 2013, 23, 1682–1698. [Google Scholar] [CrossRef]
- Beard, R.W.; Ferrin, J.; Humpherys, J. Fixed wing UAV path following in wind with input constraints. IEEE Trans. Control Syst. Technol. 2014, 22, 2103–2117. [Google Scholar] [CrossRef]
- Gavilan, F.; Vazquez, R.; Camacho, E.F. An iterative model predictive control algorithm for UAV guidance. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2406–2419. [Google Scholar] [CrossRef]
- Yang, J.; Liu, C.J.; Coombes, M.; Yan, Y.D.; Chen, W.H. Optimal path following for small fixed-wing UAVs under wind disturbances. IEEE Trans. Control Syst. Technol. 2020, 29, 996–1008. [Google Scholar] [CrossRef]
- Jackson, S.; Tisdale, J.; Kamgarpour, M.; Basso, B.; Karl Hedrick, J. Tracking controllers for small UAVs with wind disturbances: Theory and flight results. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 564–569. [Google Scholar]
- Kothari, M.; Postlethwaite, I.; Gu, D.W. A suboptimal path planning algorithm using rapidly-exploring random trees. Int. J. Aerosp. Innov. 2010, 2, 93–104. [Google Scholar]
- Brezoescu, A.; Espinoza, T.; Castillo, P.; Lozano, R. Adaptive trajectory following for a fixed-wing UAV in presence of crosswind. J. Intell. Robot. Syst. 2013, 69, 257–271. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, H.M.; Zhang, J.M.; Li, X.B. Disturbance attenuation predictive optimal control for quad-rotor transporting unknown varying payload. IEEE Access 2020, 8, 44671–44686. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y.M. Path following of Nano quad-rotors using a novel disturbance observer-enhanced dynamic inversion approach. Aeronaut. J. 2019, 123, 1122–1134. [Google Scholar] [CrossRef]
- Abro, G.E.M.; Zulkifli, S.A.B.M.; Asirvadam, V.S. Dual-loop single dimension fuzzy-based sliding mode control design for robust tracking of an underactuated quadrotor craft. Asian J. Control 2023, 25, 144–169. [Google Scholar] [CrossRef]
- Zhao, S.L.; Wang, X.K.; Zhang, D.B.; Shen, L.C. Curved Path Following Control for Fixed-wing Unmanned Aerial Vehicles with Control Constraint. J. Intell. Robot. Syst. 2017, 89, 107–119. [Google Scholar] [CrossRef]
- Abro, G.E.M.; Zulkifli, S.A.B.M.; Ali, Z.A.; Asirvadam, V.S.; Chowdhry, B.S. Fuzzy Based Backstepping Control Design for Stabilizing an Underactuated Quadrotor Craft under Unmodelled Dynamic Factors. Electronics 2022, 11, 999. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Shen, L.; Yu, Y. Coordinated path following control of fixed-wing unmanned aerial vehicles in wind. ISA Trans. 2022, 122, 260–270. [Google Scholar] [CrossRef] [PubMed]
- Sujit, P.B.; Saripalli, S.; Sousa, J.B. Unmanned aerial vehicle path following: A survey and analysis of algorithms for fixed-wing unmanned aerial vehicles. IEEE Control Syst. Mag. 2014, 34, 42–59. [Google Scholar]
- Mustafa Abro, G.E.; Ali, Z.A.; Zulkifli, S.A.; Asirvadam, V.S. Performance evaluation of different control methods for an underactuated quadrotor unmanned aerial vehicle (QUAV) with position estimator and disturbance observer. Math. Probl. Eng. 2021, 2021, 1–22. [Google Scholar] [CrossRef]
- Beard, R.W.; Mclain, T.W. Small Unmanned Airplane: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Zhou, L.; Lin, J.; Sun, J.Z.; Fu, H.M.; Wan, Q. Predictive Functional Control for Linear Motor Speed System Based on Repetitive Sliding Mode Observer. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 2633–2638. [Google Scholar]
- Xiang, Y.; Liu, Z.L.; Wang, L.M. Genetic-algorithm-optimization-based predictive functional control for chemical industry processes against partial actuator faults. IEEE Access 2020, 8, 214586–214595. [Google Scholar] [CrossRef]
- Zhou, Y.; Ho, H.W.; Chu, Q.P. Extended incremental nonlinear dynamic inversion for optical flow control of micro air vehicles. Aerosp. Sci. Technol. 2021, 116, 106889. [Google Scholar] [CrossRef]
- Fan, Z.H.; Liu, L. The high angle of attack aerodynamic modeling and nonlinear dynamic inversion flight control law design. In Proceedings of the 2012 IEEE 10th International Conference on Industrial Informatics, Beijing, China, 25–27 July 2012; pp. 901–905. [Google Scholar]
- Jayaraman, B.; Ghosh, A.K. Cascaded and Non-Cascaded Incremental Nonlinear Dynamic Inversion Flight Control Applied to a Light Aircraft. In Proceedings of the 2021 Australian & New Zealand Control Conference (ANZCC), Gold Coast, Australia, 25–26 November 2021; pp. 189–194. [Google Scholar]




| Approach Category | Literatures | Defects |
|---|---|---|
| LOS | [2,3,4,5,6,7] | Poor robustness, no attitude control system |
| vector field | [8,9,10,11,12,13,14] | Complicated theories, Poor robustness, no attitude control system |
| virtual target following | [15,16,17,18,19,20,21] | Too many virtual targets, poor robustness, no attitude control system |
| L1 guidance | [22,23,24,25,26,27,28] | Poor robustness, no attitude control system |
| Frenet | [21,29,30,31,32] | Poor robustness, no attitude control system |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, W.; Tong, M.; Wang, Q.; Song, W.; Ying, H. Curved-Line Path-Following Control of Fixed-Wing Unmanned Aerial Vehicles Using a Robust Disturbance-Estimator-Based Predictive Control Approach. Appl. Sci. 2023, 13, 11577. https://doi.org/10.3390/app132011577
Qi W, Tong M, Wang Q, Song W, Ying H. Curved-Line Path-Following Control of Fixed-Wing Unmanned Aerial Vehicles Using a Robust Disturbance-Estimator-Based Predictive Control Approach. Applied Sciences. 2023; 13(20):11577. https://doi.org/10.3390/app132011577
Chicago/Turabian StyleQi, Weiwei, Mingbo Tong, Qi Wang, Wei Song, and Hunan Ying. 2023. "Curved-Line Path-Following Control of Fixed-Wing Unmanned Aerial Vehicles Using a Robust Disturbance-Estimator-Based Predictive Control Approach" Applied Sciences 13, no. 20: 11577. https://doi.org/10.3390/app132011577
APA StyleQi, W., Tong, M., Wang, Q., Song, W., & Ying, H. (2023). Curved-Line Path-Following Control of Fixed-Wing Unmanned Aerial Vehicles Using a Robust Disturbance-Estimator-Based Predictive Control Approach. Applied Sciences, 13(20), 11577. https://doi.org/10.3390/app132011577







