Event-Based Security Control for Markov Jump Cyber–Physical Systems under Denial-of-Service Attacks: A Dual-Mode Switching Strategy
Abstract
:1. Introduction
- (1)
- A novel resilient event-triggering rule that relies on DoS signals is designed to select corresponding control strategies on demand based on the current network service quality.
- (2)
- By analyzing the inner relationship between the system mode and the triggering instant under DoS attacks, the minimum and maximum inter-execution intervals are calculated to avoid Zeno behavior and singular triggering.
- (3)
- Based on the LMI method and Lyapunov stability theory, sufficient conditions for the existence of security controller gains and resilient triggering parameters are given in the form of concise LMIs simultaneously.
2. Preliminaries and Problem Formulation
2.1. System Framework
2.2. Dual-Mode Security Control Scheme
2.3. Control Objective
3. Stability Analysis under Resilient Event-Triggered Rule and DoS Attacks
3.1. Stability Criterion
3.2. Feasibility Criterion
4. Design of Dual-Mode Security Controller under Resilient Event-Triggered Rule
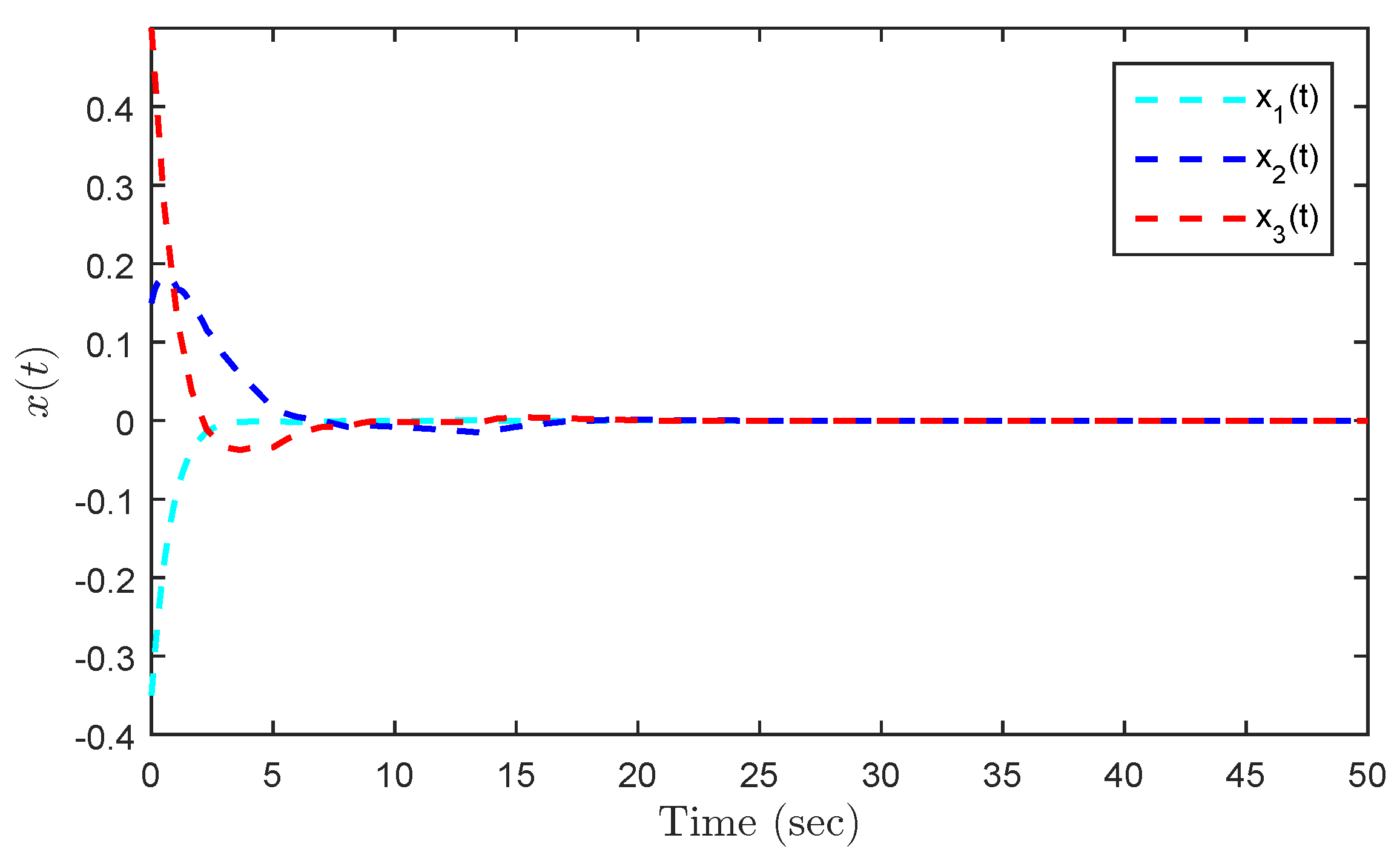
5. Simulation Example
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- DoS attacks are not activated by malicious attackers. This indicates that and .
- DoS attacks are injected remotely by malicious attackers. This means that and .
References
- Mollah, M.B.; Zhao, J.; Niyato, D.; Lam, K.-Y.; Zhang, X.; Ghias, A.M.Y.M.; Koh, L.H.; Yang, L. Blockchain for Future Smart Grid: A Comprehensive Survey. IEEE Internet Things J. 2020, 8, 18–43. [Google Scholar] [CrossRef]
- Humayed, A.; Lin, J.; Li, F.; Luo, B. Cyber-physical systems security—A survey. IEEE Internet Things J. 2017, 4, 1802–1831. [Google Scholar] [CrossRef]
- Sisinni, E.; Saifullah, A.; Han, S.; Jennehag, U.; Gidlund, M. Industrial internet of things: Challenges, opportunities, and directions. IEEE Trans. Ind. Inform. 2018, 14, 4724–4734. [Google Scholar] [CrossRef]
- Teixeira, A.; Shames, I.; Sandberg, H.; Johansson, K.H. A secure control framework for resource-limited adversaries. Automatica 2015, 51, 135–148. [Google Scholar] [CrossRef]
- Molnar, T.G.; Kiss, A.K.; Ames, A.D.; Orosz, G. Safety-Critical Control With Input Delay in Dynamic Environment. IEEE Trans. Control Syst. Technol. 2023, 31, 1507–1520. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Dorfler, F.; Bullo, F. Attack Detection and Identification in Cyber-Physical Systems. IEEE Trans. Autom. Control 2013, 58, 2715–2729. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Chang, V.; Hawash, H.; Chakrabortty, R.K.; Ryan, M. Deep-IFS: Intrusion Detection Approach for Industrial Internet of Things Traffic in Fog Environment. IEEE Trans. Ind. Inform. 2020, 17, 7704–7715. [Google Scholar] [CrossRef]
- Qaddoura, R.; Al-Zoubi, A.M.; Almomani, I.; Faris, H. A Multi-Stage Classification Approach for IoT Intrusion Detection Based on Clustering with Oversampling. Appl. Sci. 2021, 11, 3022. [Google Scholar] [CrossRef]
- Jovanov, I.; Pajic, M. Relaxing Integrity Requirements for Attack-Resilient Cyber-Physical Systems. IEEE Trans. Autom. Control 2019, 64, 4843–4858. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.-L.; Ge, X.; Wang, J. Secure State Estimation and Control of Cyber-Physical Systems: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 176–190. [Google Scholar] [CrossRef]
- Incremona, G.P.; Rubagotti, M.; Tanelli, M.; Ferrara, A. A General Framework for Switched and Variable Gain Higher Order Sliding Mode Control. IEEE Trans. Autom. Control 2021, 66, 1718–1724. [Google Scholar] [CrossRef]
- De Persis, C.; Tesi, P. Input-to-State Stabilizing Control Under Denial-of-Service. IEEE Trans. Autom. Control 2015, 60, 2930–2944. [Google Scholar] [CrossRef]
- Lu, A.-Y.; Yang, G.-H. Input-to-State Stabilizing Control for Cyber-Physical Systems With Multiple Transmission Channels Under Denial of Service. IEEE Trans. Autom. Control 2018, 63, 1813–1820. [Google Scholar] [CrossRef]
- Lu, A.-Y.; Yang, G.-H. Stability Analysis for Cyber-Physical Systems Under Denial-of-Service Attacks. IEEE Trans. Cybern. 2021, 51, 5304–5313. [Google Scholar] [CrossRef]
- Umlauft, J.; Hirche, S. Feedback Linearization Based on Gaussian Processes With Event-Triggered Online Learning. IEEE Trans. Autom. Control 2020, 65, 4154–4169. [Google Scholar] [CrossRef]
- Doostmohammadian, M.; Meskin, N. Finite-Time Stability Under Denial of Service. IEEE Syst. J. 2021, 15, 1048–1055. [Google Scholar] [CrossRef]
- Tahoun, A.H.; Arafa, M. Secure control design for nonlinear cyber–physical systems under DoS, replay, and deception cyber-attacks with multiple transmission channels. ISA Trans. 2022, 128, 294–308. [Google Scholar] [CrossRef]
- Lu, A.-Y.; Yang, G.-H. Resilient Observer-Based Control for Cyber-Physical Systems With Multiple Transmission Channels Under Denial-of-Service. IEEE Trans. Cybern. 2020, 50, 4796–4807. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, J. Resilient adaptive control of switched nonlinear cyber-physical systems under uncertain deception attacks. Inf. Sci. 2021, 543, 398–409. [Google Scholar] [CrossRef]
- Kim, S.; Park, K.-J.; Lu, C. A Survey on Network Security for Cyber–Physical Systems: From Threats to Resilient Design. IEEE Commun. Surv. Tutor. 2022, 24, 1534–1573. [Google Scholar] [CrossRef]
- Cosentino, F.; Oberhauser, H.; Abate, A. Grid-free computation of probabilistic safety with malliavin calculus. IEEE Trans. Autom. Control 2023, 68, 6369–6376. [Google Scholar] [CrossRef]
- Li, T.; Chen, B.; Yu, L.; Zhang, W.-A. Active Security Control Approach Against DoS Attacks in Cyber-Physical Systems. IEEE Trans. Autom. Control 2021, 66, 4303–4310. [Google Scholar] [CrossRef]
- Feng, S.; Cetinkaya, A.; Ishii, H.; Tesi, P.; Persis, C.D. Networked control under DoS attacks: Tradeoffs between resilience and data rate. IEEE Trans. Autom. Control 2020, 66, 460–467. [Google Scholar] [CrossRef]
- Feng, Z.; Wen, G.H.; Hu, G.Q. Distributed secure coordinated control for multiagent systems under strategic attacks. IEEE Trans. Cybern. 2017, 47, 1273–1284. [Google Scholar] [CrossRef]
- Senejohnny, D.; Tesi, P.; De Persis, C. A Jamming-Resilient Algorithm for Self-Triggered Network Coordination. IEEE Trans. Control Netw. Syst. 2018, 5, 981–990. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, H.; Yue, D. Observer-Based Distributed Secure Consensus Control of a Class of Linear Multi-Agent Systems Subject to Random Attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 66, 3089–3099. [Google Scholar] [CrossRef]
- Deng, C.; Wen, C. MAS-Based Distributed Resilient Control for a Class of Cyber-Physical Systems With Communication Delays Under DoS Attacks. IEEE Trans. Cybern. 2021, 51, 2347–2358. [Google Scholar] [CrossRef]
- Zhang, D.; Ye, Z.; Dong, X. Co-Design of Fault Detection and Consensus Control Protocol for Multi-Agent Systems Under Hidden DoS Attack. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2158–2170. [Google Scholar] [CrossRef]
- Persis, C.D.; Tesi, P. Formulas for data-driven control: Stabilization, optimality, and robustness. IEEE Trans. Autom. Control 2020, 65, 909–924. [Google Scholar] [CrossRef]
- Gabriel, G.W.; Goncalves, T.R.; Geromel, J.C. Optimal and robust sampled-data control of Markov jump linear systems: A differential LMI approach. IEEE Trans. Autom. Control 2018, 63, 3054–3060. [Google Scholar] [CrossRef]
- Gunasekaran, N.; Joo, Y.H. Robust Sampled-data Fuzzy Control for Nonlinear Systems and Its Applications: Free-Weight Matrix Method. IEEE Trans. Fuzzy Syst. 2019, 27, 2130–2139. [Google Scholar] [CrossRef]
- De Persis, C.; Rotulo, M.; Tesi, P. Learning Controllers From Data via Approximate Nonlinearity Cancellation. IEEE Trans. Autom. Control 2023, 68, 6082–6097. [Google Scholar] [CrossRef]
- Amini, A.; Asif, A.; Mohammadi, A. Formation-containment control using dynamic event-triggering mechanism for multi-agent systems. IEEE/CAA J. Autom. Sin. 2020, 7, 1235–1248. [Google Scholar] [CrossRef]
- Peng, C.; Sun, H. Switching-Like Event-Triggered Control for Networked Control Systems Under Malicious Denial of Service Attacks. IEEE Trans. Autom. Control 2020, 65, 3943–3949. [Google Scholar] [CrossRef]
- Xu, W.; Hu, G.; Ho, D.W.C.; Feng, Z. Distributed Secure Cooperative Control Under Denial-of-Service Attacks From Multiple Adversaries. IEEE Trans. Cybern. 2020, 50, 3458–3467. [Google Scholar] [CrossRef]
- Peng, C.; Wu, J.; Tian, E. Stochastic Event-Triggered H∞ Control for Networked Systems Under Denial of Service Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4200–4210. [Google Scholar] [CrossRef]
- Qi, W.; Hou, Y.; Zong, G.; Ahn, C.K. Finite-Time Event-Triggered Control for Semi-Markovian Switching Cyber-Physical Systems With FDI Attacks and Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2665–2674. [Google Scholar] [CrossRef]
- Sun, H.; Peng, C.; Zhang, W.; Yang, T.; Wang, Z. Security-based resilient event-triggered control of networked control systems under denial of service attacks. J. Frankl. Inst. 2019, 356, 10277–10295. [Google Scholar] [CrossRef]
- Xu, Y.; Fang, M.; Shi, P.; Wu, Z.-G. Event-based secure consensus of multiagent systems against DoS attacks. IEEE Trans. Cybern. 2020, 50, 3468–3476. [Google Scholar] [CrossRef]
- Feng, Z.; Hu, G. Secure Cooperative Event-Triggered Control of Linear Multiagent Systems Under DoS Attacks. IEEE Trans. Control Syst. Technol. 2020, 28, 741–752. [Google Scholar] [CrossRef]
- Deng, C.; Wen, C. Distributed resilient observer-based fault-tolerant control for heterogeneous multiagent systems under actuator faults and DoS attacks. IEEE Trans. Control Netw. Syst. 2020, 7, 1308–1318. [Google Scholar] [CrossRef]
- Behera, A.K.; Bandyopadhyay, B. Robust sliding mode control: An event-triggering approach. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 146–150. [Google Scholar] [CrossRef]
- Xiong, J.; Lam, J.; Shu, Z.; Mao, X. Stability Analysis of Continuous-Time Switched Systems With a Random Switching Signal. IEEE Trans. Autom. Control 2014, 59, 180–186. [Google Scholar] [CrossRef]
- Zhang, L.; Cui, N.; Liu, M.; Zhao, Y. Asynchronous filtering of discrete-time switched linear systems with average dwell time. IEEE Trans. Circuits Syst. Regul. Pap. 2011, 58, 1109–1118. [Google Scholar] [CrossRef]
- Lian, J.; Li, C.; Liu, D. Input-to-state stability for discrete-time nonlinear switched singular systems. IET Control Theory Appl. 2017, 11, 2893–2899. [Google Scholar] [CrossRef]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Li, Z.; Pang, T.; Xu, H.; Chen, S. Event-Based Security Control for Markov Jump Cyber–Physical Systems under Denial-of-Service Attacks: A Dual-Mode Switching Strategy. Appl. Sci. 2023, 13, 11815. https://doi.org/10.3390/app132111815
Gao M, Li Z, Pang T, Xu H, Chen S. Event-Based Security Control for Markov Jump Cyber–Physical Systems under Denial-of-Service Attacks: A Dual-Mode Switching Strategy. Applied Sciences. 2023; 13(21):11815. https://doi.org/10.3390/app132111815
Chicago/Turabian StyleGao, Mingke, Zhiqiang Li, Tao Pang, Hong Xu, and Siji Chen. 2023. "Event-Based Security Control for Markov Jump Cyber–Physical Systems under Denial-of-Service Attacks: A Dual-Mode Switching Strategy" Applied Sciences 13, no. 21: 11815. https://doi.org/10.3390/app132111815
APA StyleGao, M., Li, Z., Pang, T., Xu, H., & Chen, S. (2023). Event-Based Security Control for Markov Jump Cyber–Physical Systems under Denial-of-Service Attacks: A Dual-Mode Switching Strategy. Applied Sciences, 13(21), 11815. https://doi.org/10.3390/app132111815





