Speed Reduction Capabilities of Two-Geometry Roundabouts
Abstract
:1. Introduction
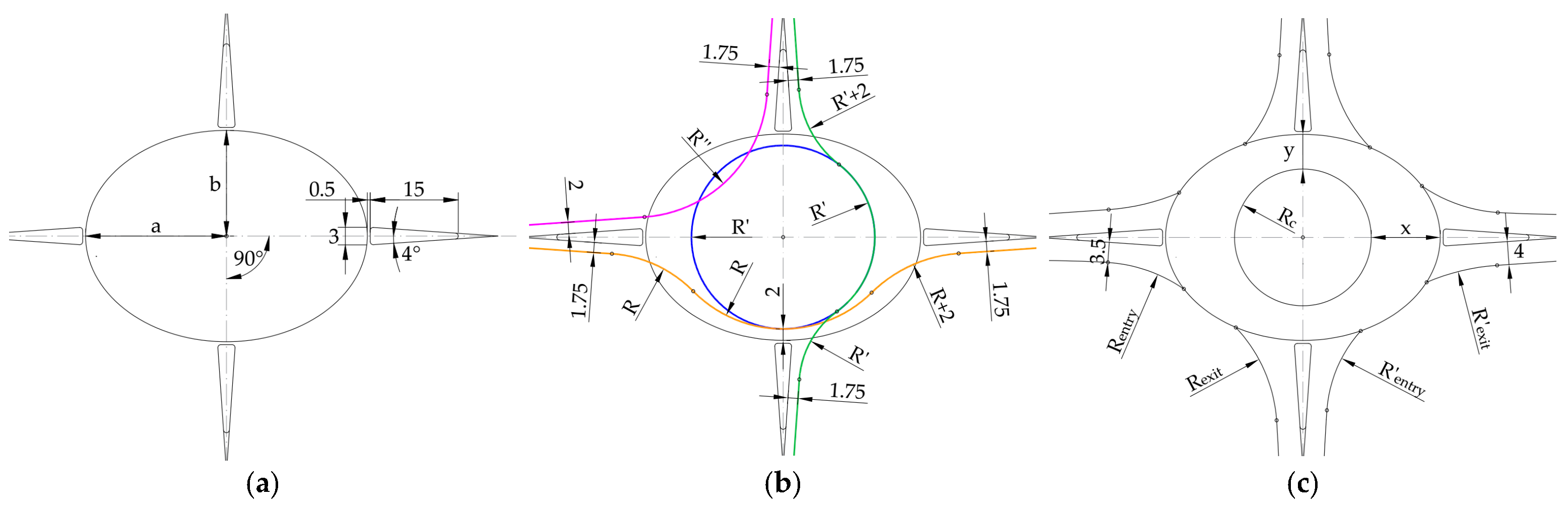
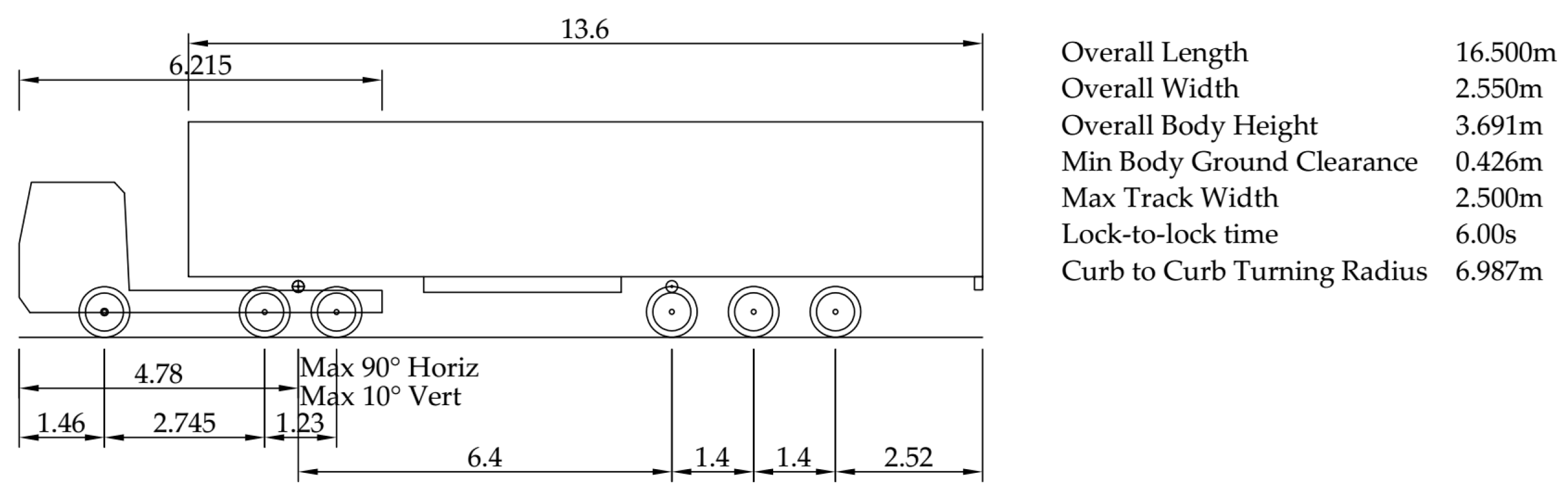
2. Experiment Design and Methodology
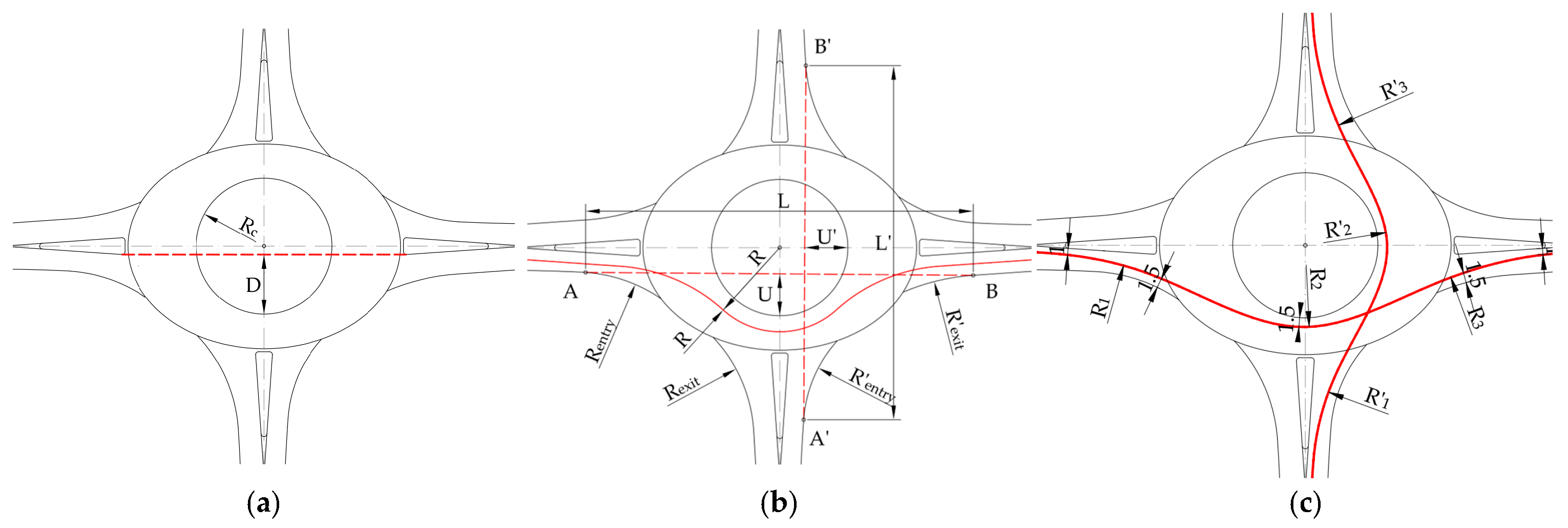
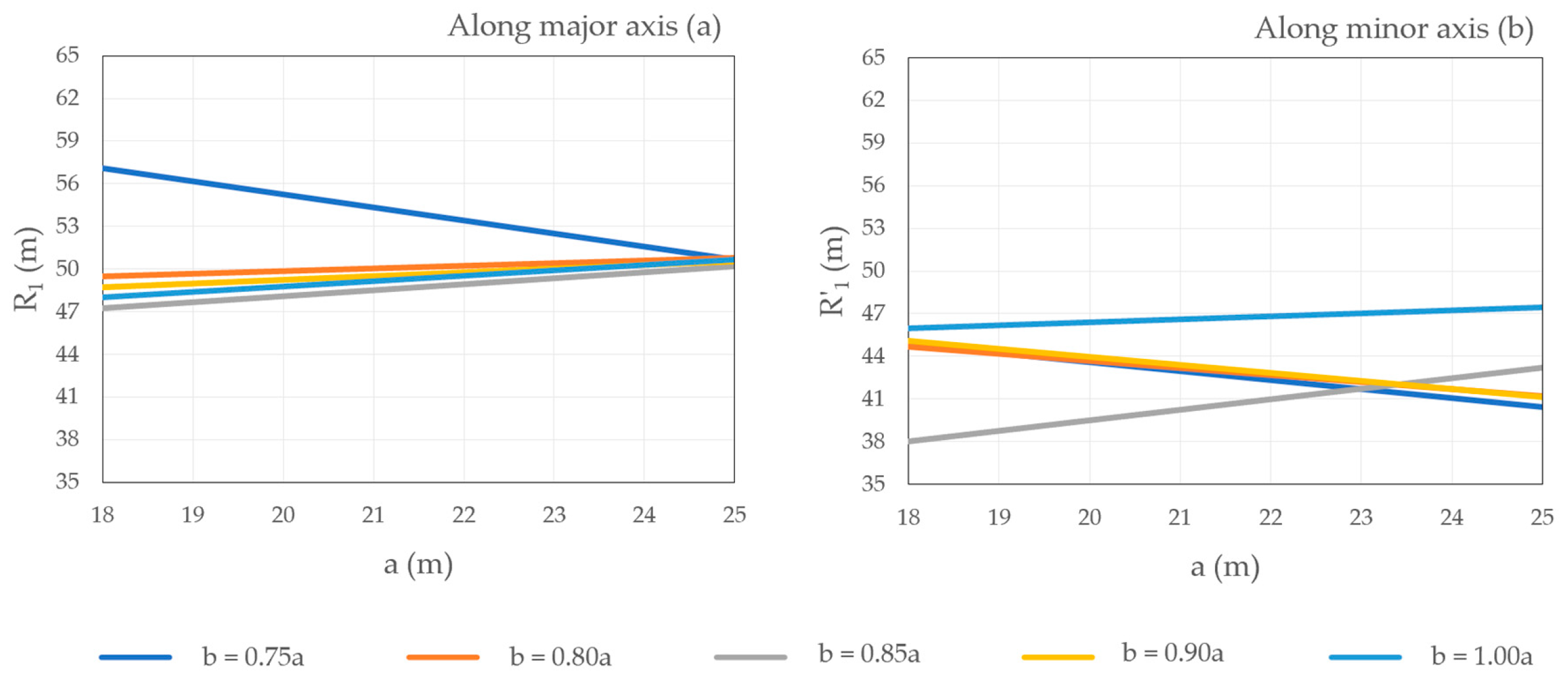
- the entry path radii (R1 and R′1), which are the minimum radii on the fastest through paths before the entrance line;
- the circulating path radii (R2 and R′2), which are the minimum radii on the fastest through paths around the central island; and
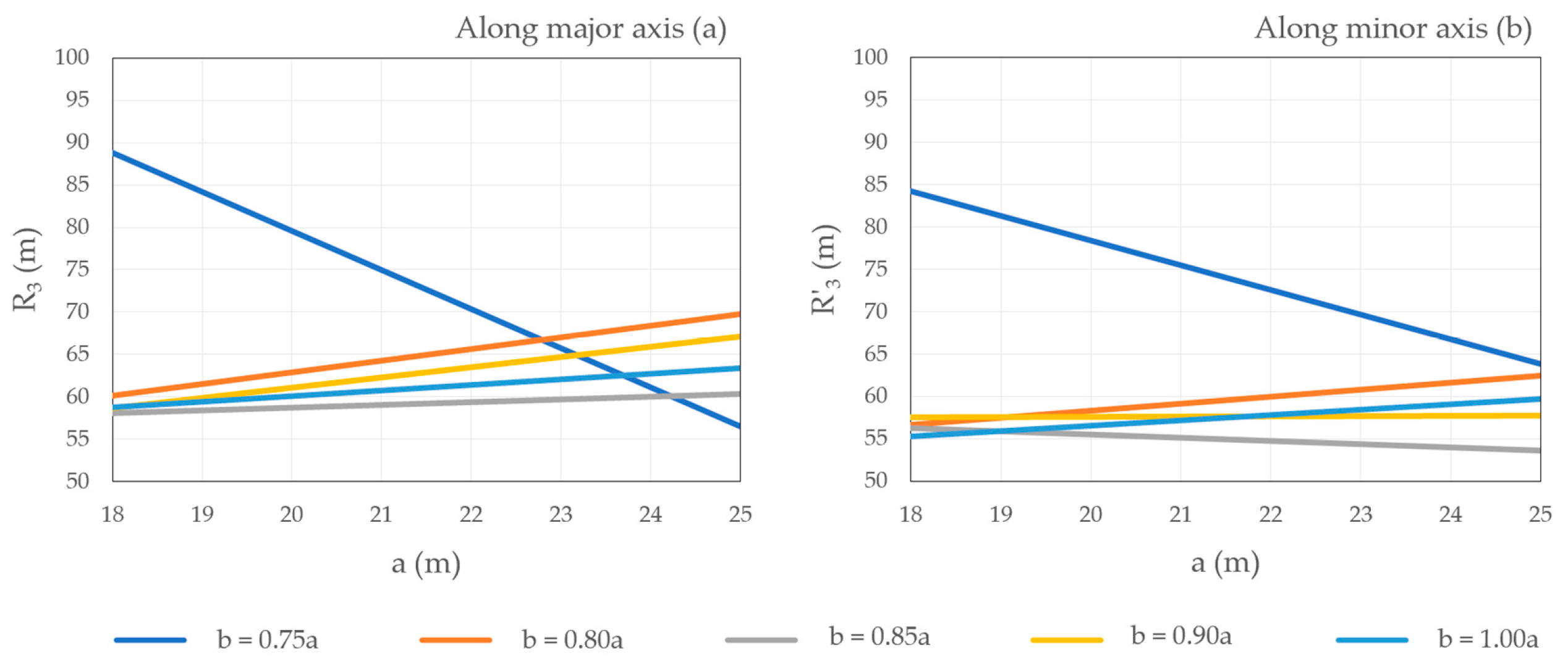
- the exit path radii (R3 and R′3), which are the minimum radii on the fastest through paths into the exit.
- Condition 1: circulatory roadway width in single-lane roundabouts (x and y) should be smaller than 5.5 m so that drivers do not use a wide roadway as two lanes and sufficient deflection is achieved [1].
- Condition 2: circulatory roadway width in the direction of the minor axis (y) should be between 4 and 6 m [22].
- Condition 3: vehicle path deflection around the central island (D) should be greater or equal to double the entrance width (which is 7.0 m in this investigation) for the roundabout’s design to be deemed satisfactory [10].
- Condition 4: the deflected vehicle path radius (R1) should not exceed 80–100 m [22].
- Condition 5: the calculated expected driving speed through the roundabout for the major and minor axis directions (V) should be lower than 35 km/h [14].
- Condition 6: for vehicles to safely negotiate the roundabout, the maximum relative speed between consecutive fastest path elements (V1–V2 and V3–V2) should not exceed 25 km/h [16].
3. Results
3.1. Roundabout Schemes with Variable (y)
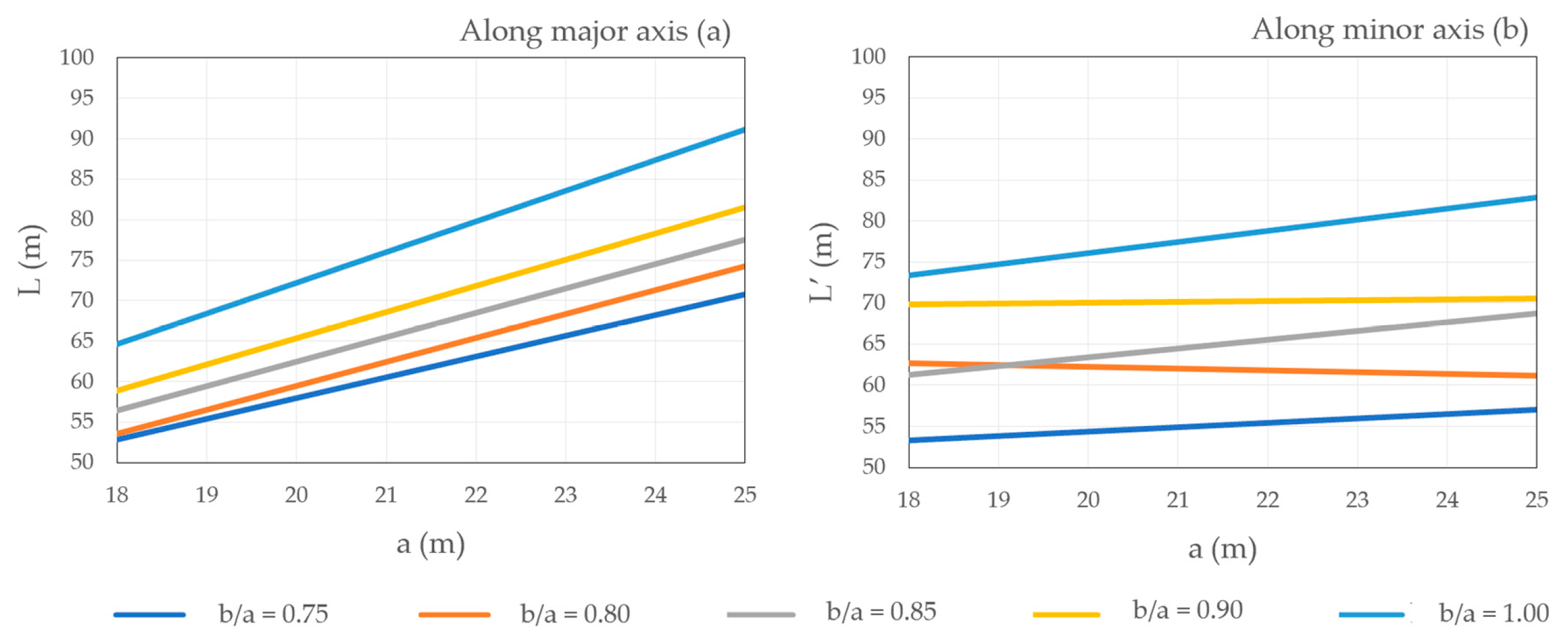
- radii for (b/a = 0.75) showed the greatest discrepancy caused by large path radii values in roundabouts with the smallest major and minor axes,
- for (b/a = 1.00), either no influence could be noted, or radii were inversely proportional to (a), and
- for the rest of the roundabout schemes, either no influence could be noted, or radii were proportional to (a).
- major axis (a) of 18 m and (b/a = 0.75, 0.80), and
- major axis (a) of 19 and 20 m and (b/a = 0.75).
- major axis (a) of 18 m and (b/a = 0.75, 0.80) for both directions,
- major axis (a) of 19 m and (b/a = 0.75) for both directions, and
- major axis (a) of 20 and 21 m and (b/a = 0.75) for the major axis direction.
- major axis (a) of 18 m and (b/a = 0.75) for both directions,
- major axis (a) of 18 m and (b/a = 0.80) for the major axis direction, and
- major axis (a) of 19 m and (b/a = 0.75) for the major axis direction.
3.2. Roundabout Schemes with Fixed (y)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Major Axis | Minor Axis | Major Axis Direction (Axis a) | Minor Axis Direction (Axis b) | Standard Geometry (b = a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a (m) | b (m) | R (m) | R1 (m) | R2 (m) | R3 (m) | R′ (m) | R′1 (m) | R′2 (m) | R′3 (m) | R = R′ (m) | R1 = R′1 (m) | R2 = R′2 (m) | R3 = R′3 (m) |
| 18 | 13.50 | 48.05 | 130.92 | 40.51 | 371.82 | 45.69 | 150.86 | 34.53 | 315.26 | 29.47 | 45.66 | 14.85 | 67.69 |
| 14.40 | 38.71 | 91.76 | 29.73 | 99.72 | 33.89 | 64.38 | 24.93 | 101.60 | |||||
| 15.30 | 35.07 | 65.64 | 22.84 | 94.27 | 31.58 | 59.00 | 19.45 | 94.89 | |||||
| 16.20 | 33.61 | 59.84 | 19.58 | 88.86 | 30.04 | 48.54 | 18.12 | 92.57 | |||||
| 19 | 14.25 | 42.23 | 83.36 | 29.92 | 138.70 | 36.51 | 68.39 | 24.89 | 168.35 | 30.66 | 49.90 | 14.60 | 70.50 |
| 15.20 | 36.38 | 65.94 | 22.83 | 96.03 | 30.78 | 52.76 | 18.93 | 81.92 | |||||
| 16.15 | 31.91 | 60.28 | 20.73 | 78.96 | 29.49 | 47.90 | 16.00 | 76.77 | |||||
| 17.10 | 31.21 | 53.41 | 17.81 | 69.81 | 31.40 | 48.39 | 15.84 | 67.25 | |||||
| 20 | 15.00 | 37.06 | 68.11 | 25.21 | 103.99 | 32.16 | 56.33 | 20.84 | 114.37 | 29.31 | 44.69 | 13.47 | 88.76 |
| 16.00 | 33.45 | 55.07 | 20.34 | 85.04 | 31.80 | 51.71 | 17.78 | 84.18 | |||||
| 17.00 | 31.94 | 53.82 | 18.43 | 71.26 | 28.98 | 47.00 | 17.00 | 74.80 | |||||
| 18.00 | 30.02 | 51.13 | 17.10 | 71.38 | 28.77 | 46.91 | 15.57 | 75.42 | |||||
| 21 | 15.75 | 39.27 | 59.77 | 24.96 | 157.55 | 29.94 | 49.33 | 17.92 | 79.59 | 30.51 | 43.29 | 14.74 | 88.76 |
| 16.80 | 32.00 | 53.36 | 20.32 | 79.49 | 28.49 | 42.22 | 15.13 | 64.06 | |||||
| 17.85 | 30.87 | 51.23 | 17.45 | 65.08 | 27.97 | 40.78 | 15.00 | 60.47 | |||||
| 18.90 | 26.75 | 47.83 | 17.29 | 57.12 | 26.92 | 43.37 | 16.68 | 66.65 | |||||
| 22 | 16.50 | 35.04 | 59.72 | 21.45 | 80.99 | 30.50 | 44.36 | 15.84 | 68.63 | 30.92 | 47.46 | 14.13 | 59.25 |
| 17.60 | 32.22 | 53.04 | 20.17 | 73.93 | 29.35 | 47.44 | 14.45 | 58.97 | |||||
| 18.70 | 31.30 | 50.24 | 16.96 | 63.65 | 28.80 | 43.70 | 14.85 | 61.35 | |||||
| 19.80 | 32.04 | 49.63 | 16.00 | 66.26 | 29.72 | 44.17 | 15.93 | 60.10 | |||||
| 23 | 17.25 | 32.70 | 55.51 | 21.70 | 68.36 | 28.90 | 54.55 | 17.13 | 70.06 | 31.82 | 50.04 | 14.20 | 85.30 |
| 18.40 | 31.94 | 53.99 | 20.39 | 65.73 | 28.48 | 43.66 | 14.73 | 62.15 | |||||
| 19.55 | 30.57 | 47.12 | 16.11 | 60.73 | 28.35 | 42.11 | 15.25 | 57.34 | |||||
| 20.70 | 30.61 | 47.74 | 14.97 | 58.53 | 29.38 | 44.67 | 14.64 | 56.25 | |||||
| 24 | 18.00 | 33.27 | 54.61 | 20.22 | 72.43 | 28.40 | 43.16 | 15.01 | 54.66 | 32.91 | 52.95 | 14.69 | 65.82 |
| 19.20 | 32.09 | 50.17 | 18.49 | 63.01 | 29.73 | 39.81 | 17.92 | 55.36 | |||||
| 20.40 | 31.61 | 48.64 | 16.43 | 58.72 | 29.27 | 47.30 | 14.80 | 57.27 | |||||
| 21.60 | 31.59 | 45.62 | 15.42 | 60.27 | 32.29 | 50.89 | 14.98 | 58.21 | |||||
| 25 | 18.75 | 34.02 | 53.65 | 19.81 | 68.22 | 28.01 | 41.56 | 13.81 | 55.61 | 33.96 | 52.93 | 14.70 | 68.15 |
| 20.00 | 32.21 | 49.88 | 18.17 | 60.91 | 28.10 | 48.20 | 14.51 | 53.60 | |||||
| 21.25 | 31.38 | 46.14 | 16.90 | 59.83 | 30.65 | 51.84 | 14.66 | 57.81 | |||||
| 22.50 | 32.33 | 48.26 | 15.11 | 58.62 | 31.44 | 44.28 | 14.45 | 55.48 | |||||
| Major Axis | Minor Axis | Major Axis Direction (Axis a) | Minor Axis Direction (Axis b) | Standard Geometry (b = a) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a (m) | b (m) | D (m) | V (km/h) | V2 (km/h) | V1–V2 (km/h) | V3–V2 (km/h) | D′ (m) | V′ (km/h) | V′2 (km/h) | V′1–V′2 (km/h) | V′3–V′2 (km/h) | D (m) | V (km/h) | V2 (km/h) | V1–V2 (km/h) | V3–V2 (km/h) |
| 18 | 13.50 | 4.7 | 51 | 47 | 38 | 96 | 4.7 | 50 | 43 | 47 | 88 | 10.5 | 40 | 29 | 21 | 32 |
| 14.40 | 5.9 | 46 | 40 | 31 | 34 | 5.9 | 43 | 37 | 22 | 38 | ||||||
| 15.30 | 7.2 | 44 | 35 | 25 | 36 | 7.2 | 42 | 33 | 24 | 39 | ||||||
| 16.20 | 8.3 | 43 | 33 | 24 | 37 | 8.3 | 41 | 32 | 20 | 40 | ||||||
| 19 | 14.25 | 5.8 | 48 | 40 | 27 | 47 | 5.8 | 45 | 37 | 24 | 59 | 11.6 | 41 | 28 | 24 | 34 |
| 15.20 | 7.0 | 45 | 35 | 25 | 37 | 7.0 | 41 | 32 | 22 | 35 | ||||||
| 16.15 | 8.2 | 42 | 34 | 24 | 32 | 8.2 | 40 | 30 | 22 | 35 | ||||||
| 17.10 | 9.4 | 41 | 31 | 23 | 31 | 9.4 | 41 | 29 | 22 | 31 | ||||||
| 20 | 15.00 | 6.8 | 45 | 37 | 24 | 38 | 6.8 | 42 | 34 | 22 | 45 | 12.7 | 40 | 27 | 22 | 43 |
| 16.00 | 8.1 | 43 | 33 | 22 | 35 | 8.1 | 42 | 31 | 22 | 37 | ||||||
| 17.00 | 9.3 | 42 | 32 | 23 | 31 | 9.3 | 40 | 31 | 20 | 33 | ||||||
| 18.00 | 10.5 | 41 | 31 | 22 | 32 | 10.5 | 40 | 29 | 21 | 35 | ||||||
| 21 | 15.75 | 7.7 | 46 | 37 | 20 | 56 | 7.7 | 40 | 31 | 21 | 35 | 13.8 | 41 | 28 | 20 | 41 |
| 16.80 | 9.1 | 42 | 33 | 21 | 33 | 9.1 | 39 | 29 | 19 | 30 | ||||||
| 17.85 | 10.3 | 41 | 31 | 22 | 29 | 10.3 | 39 | 29 | 19 | 29 | ||||||
| 18.90 | 11.4 | 38 | 31 | 20 | 25 | 11.4 | 38 | 30 | 19 | 30 | ||||||
| 22 | 16.50 | 8.7 | 44 | 34 | 23 | 32 | 8.7 | 41 | 29 | 20 | 32 | 14.9 | 41 | 28 | 23 | 29 |
| 17.60 | 10.0 | 42 | 33 | 21 | 30 | 10.0 | 40 | 28 | 23 | 29 | ||||||
| 18.70 | 11.3 | 41 | 30 | 22 | 29 | 11.3 | 40 | 29 | 20 | 29 | ||||||
| 19.80 | 12.6 | 42 | 30 | 23 | 31 | 12.6 | 40 | 30 | 20 | 28 | ||||||
| 23 | 17.25 | 9.6 | 42 | 34 | 21 | 27 | 9.6 | 40 | 31 | 24 | 31 | 16.1 | 42 | 28 | 24 | 40 |
| 18.40 | 11.0 | 42 | 33 | 21 | 27 | 11.0 | 39 | 28 | 20 | 30 | ||||||
| 19.55 | 12.3 | 41 | 30 | 21 | 28 | 12.3 | 39 | 29 | 19 | 27 | ||||||
| 20.70 | 13.6 | 41 | 29 | 22 | 28 | 13.6 | 40 | 28 | 21 | 27 | ||||||
| 24 | 18.00 | 10.5 | 43 | 33 | 21 | 30 | 10.5 | 39 | 29 | 20 | 26 | 17.1 | 42 | 28 | 25 | 32 |
| 19.20 | 11.9 | 42 | 32 | 21 | 27 | 11.9 | 40 | 31 | 15 | 24 | ||||||
| 20.40 | 13.3 | 42 | 30 | 22 | 27 | 13.3 | 40 | 28 | 22 | 28 | ||||||
| 21.60 | 14.6 | 42 | 29 | 21 | 28 | 14.6 | 42 | 29 | 24 | 28 | ||||||
| 25 | 18.75 | 11.3 | 43 | 33 | 21 | 28 | 11.3 | 39 | 27 | 20 | 28 | 18.2 | 43 | 28 | 25 | 33 |
| 20.00 | 12.8 | 42 | 32 | 21 | 26 | 12.8 | 39 | 28 | 23 | 26 | ||||||
| 21.25 | 14.2 | 41 | 30 | 20 | 27 | 14.2 | 41 | 28 | 25 | 28 | ||||||
| 22.50 | 15.6 | 42 | 29 | 23 | 28 | 15.6 | 41 | 28 | 21 | 27 | ||||||
| Major Axis | Minor Axis | Major Axis Direction (Axis a) | Minor Axis Direction (Axis b) | Standard Geometry (b = a) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a (m) | b (m) | R (m) | R1 (m) | R2 (m) | R3 (m) | R′ (m) | R′1 (m) | R′2 (m) | R′3 (m) | R = R′ (m) | R1 = R′1 (m) | R2 = R′2 (m) | R3 = R′3 (m) |
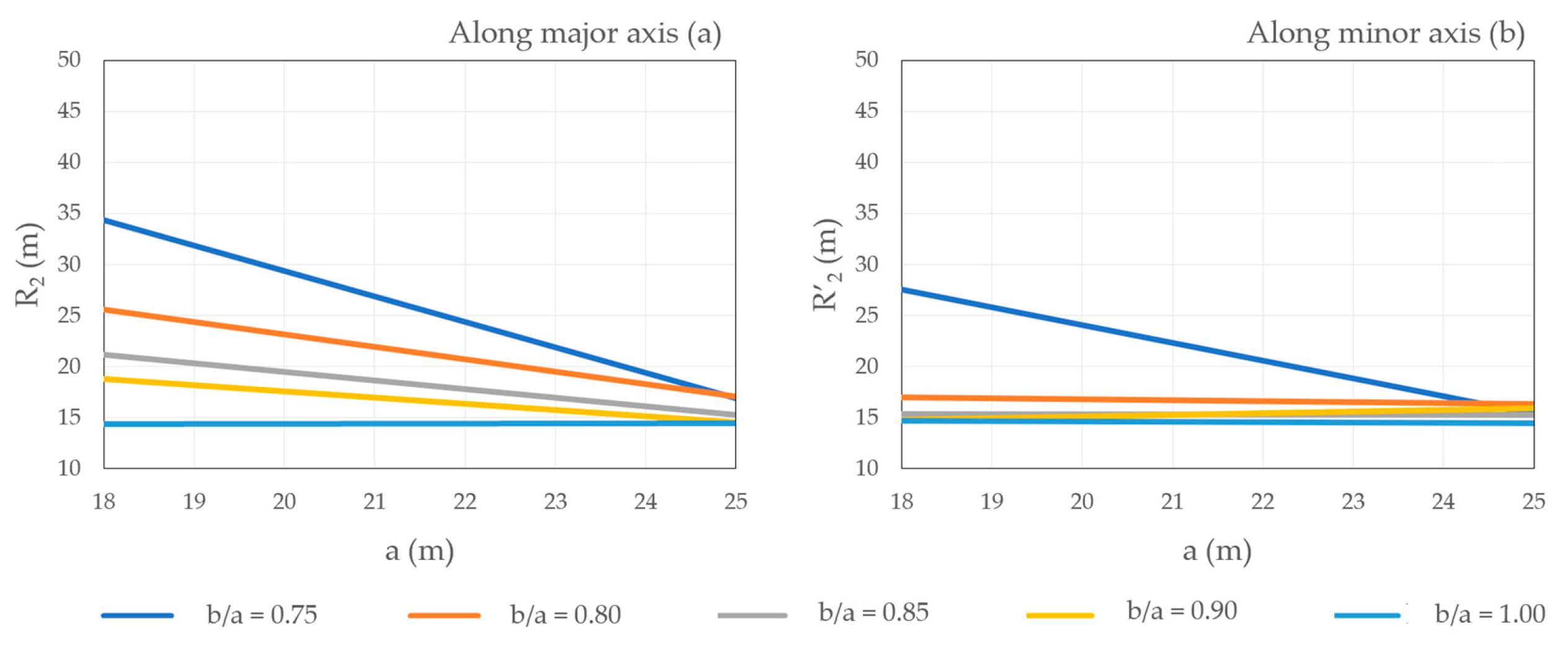
| 18 | 13.50 | 35.54 | 63.89 | 22.51 | 94.80 | 31.23 | 48.43 | 20.93 | 98.98 | 28.14 | 41.43 | 13.52 | 59.55 |
| 14.40 | 30.11 | 55.88 | 19.78 | 89.05 | 26.56 | 41.43 | 17.18 | 81.73 | |||||
| 15.30 | 30.02 | 52.71 | 17.62 | 68.98 | 27.99 | 43.34 | 14.29 | 63.58 | |||||
| 16.20 | 30.37 | 49.41 | 16.39 | 70.01 | 27.21 | 41.36 | 14.78 | 70.97 | |||||
| 19 | 14.25 | 32.36 | 61.38 | 20.54 | 81.97 | 28.44 | 42.98 | 16.99 | 80.96 | 29.66 | 45.95 | 14.17 | 60.26 |
| 15.20 | 30.75 | 55.47 | 18.24 | 62.73 | 26.20 | 39.80 | 14.74 | 70.03 | |||||
| 16.15 | 28.59 | 50.60 | 16.45 | 54.14 | 26.52 | 42.21 | 13.11 | 66.55 | |||||
| 17.10 | 29.17 | 49.54 | 15.96 | 63.04 | 29.38 | 43.68 | 13.83 | 56.75 | |||||
| 20 | 15.00 | 30.78 | 56.47 | 19.36 | 72.59 | 27.00 | 42.44 | 13.47 | 58.32 | 29.01 | 42.42 | 14.12 | 58.06 |
| 16.00 | 29.86 | 51.24 | 18.09 | 60.79 | 28.53 | 42.45 | 14.03 | 55.19 | |||||
| 17.00 | 29.63 | 50.22 | 16.57 | 57.28 | 26.95 | 43.57 | 15.30 | 61.64 | |||||
| 18.00 | 28.65 | 46.57 | 16.06 | 60.67 | 27.48 | 43.50 | 14.08 | 59.41 | |||||
| 21 | 15.75 | 34.16 | 58.60 | 20.64 | 86.78 | 25.79 | 39.63 | 15.64 | 66.74 | 30.06 | 43.56 | 16.10 | 62.28 |
| 16.80 | 29.60 | 50.39 | 17.94 | 61.17 | 26.44 | 38.09 | 13.26 | 51.27 | |||||
| 17.85 | 29.41 | 44.78 | 16.07 | 56.19 | 26.70 | 37.56 | 12.79 | 53.00 | |||||
| 18.90 | 25.72 | 45.40 | 16.21 | 51.73 | 25.94 | 39.03 | 15.80 | 63.38 | |||||
| 22 | 16.50 | 31.89 | 58.24 | 19.01 | 63.03 | 27.90 | 39.92 | 13.52 | 52.34 | 30.76 | 46.94 | 14.26 | 58.82 |
| 17.60 | 30.34 | 49.85 | 18.40 | 62.14 | 27.71 | 40.91 | 13.34 | 51.08 | |||||
| 18.70 | 30.21 | 49.03 | 16.28 | 56.96 | 27.83 | 42.36 | 13.32 | 52.85 | |||||
| 19.80 | 31.50 | 48.47 | 16.01 | 59.88 | 29.22 | 43.24 | 14.61 | 53.39 | |||||
| 23 | 17.25 | 30.51 | 52.63 | 20.04 | 58.67 | 27.01 | 46.24 | 13.83 | 55.59 | 31.82 | 50.04 | 14.20 | 85.30 |
| 18.40 | 30.77 | 51.44 | 18.71 | 60.75 | 27.49 | 40.04 | 13.42 | 55.18 | |||||
| 19.55 | 29.93 | 47.06 | 16.78 | 57.51 | 27.78 | 40.01 | 13.09 | 51.75 | |||||
| 20.70 | 30.33 | 46.19 | 15.48 | 58.97 | 29.12 | 41.00 | 13.36 | 55.16 | |||||
| 24 | 18.00 | 31.69 | 50.62 | 19.48 | 64.34 | 27.12 | 41.84 | 13.30 | 48.86 | 32.91 | 52.95 | 14.69 | 65.82 |
| 19.20 | 31.26 | 52.26 | 17.77 | 58.47 | 28.99 | 38.88 | 13.38 | 50.55 | |||||
| 20.40 | 31.31 | 47.51 | 16.88 | 56.57 | 29.00 | 46.14 | 13.81 | 52.81 | |||||
| 21.60 | 31.50 | 44.54 | 16.14 | 59.31 | 32.20 | 47.47 | 14.75 | 61.02 | |||||
| 25 | 18.75 | 32.67 | 52.84 | 18.92 | 60.86 | 26.97 | 38.92 | 13.34 | 49.11 | 33.96 | 52.93 | 14.70 | 68.15 |
| 20.00 | 31.67 | 49.85 | 17.86 | 61.17 | 27.65 | 44.51 | 13.84 | 50.82 | |||||
| 21.25 | 31.20 | 45.76 | 16.86 | 58.12 | 30.48 | 46.37 | 14.15 | 56.48 | |||||
| 22.50 | 32.33 | 48.26 | 15.11 | 58.62 | 31.44 | 44.28 | 14.45 | 55.48 | |||||
| Major Axis | Minor Axis | Major Axis Direction (Axis a) | Minor Axis Direction (Axis b) | Standard Geometry (b = a) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a (m) | b (m) | D (m) | V (km/h) | V2 (km/h) | V1–V2 (km/h) | V3–V2 (km/h) | D′ (m) | V′ (km/h) | V′2 (km/h) | V′1–V′2 (km/h) | V′3–V′2 (km/h) | D (m) | V (km/h) | V2 (km/h) | V1–V2 (km/h) | V3–V2 (km/h) |
| 18 | 13.50 | 6.5 | 44 | 35 | 24 | 37 | 6.5 | 41 | 34 | 18 | 40 | 11.4 | 39 | 27 | 20 | 30 |
| 14.40 | 7.4 | 41 | 33 | 22 | 37 | 7.4 | 38 | 31 | 17 | 36 | ||||||
| 15.30 | 8.3 | 41 | 31 | 23 | 30 | 8.3 | 39 | 28 | 21 | 31 | ||||||
| 16.20 | 9.2 | 41 | 30 | 22 | 32 | 9.2 | 39 | 28 | 19 | 34 | ||||||
| 19 | 14.25 | 7.3 | 42 | 34 | 24 | 33 | 7.3 | 39 | 31 | 18 | 36 | 12.0 | 40 | 28 | 22 | 30 |
| 15.20 | 8.2 | 41 | 32 | 24 | 27 | 8.2 | 38 | 28 | 18 | 34 | ||||||
| 16.15 | 9.2 | 40 | 30 | 23 | 24 | 9.2 | 38 | 27 | 21 | 34 | ||||||
| 17.10 | 10.1 | 40 | 30 | 23 | 29 | 10.1 | 40 | 28 | 21 | 28 | ||||||
| 20 | 15.00 | 8.0 | 41 | 33 | 23 | 30 | 8.0 | 38 | 27 | 21 | 29 | 13.0 | 40 | 28 | 20 | 29 |
| 16.00 | 9.0 | 40 | 31 | 21 | 26 | 9.0 | 40 | 28 | 20 | 27 | ||||||
| 17.00 | 10.0 | 40 | 30 | 22 | 26 | 10.0 | 38 | 29 | 20 | 29 | ||||||
| 18.00 | 11.0 | 40 | 30 | 21 | 28 | 11.0 | 39 | 28 | 21 | 29 | ||||||
| 21 | 15.75 | 8.8 | 43 | 34 | 23 | 35 | 8.8 | 38 | 29 | 17 | 31 | 14.0 | 41 | 30 | 19 | 29 |
| 16.80 | 9.8 | 40 | 31 | 21 | 27 | 9.8 | 38 | 27 | 19 | 26 | ||||||
| 17.85 | 10.9 | 40 | 30 | 20 | 26 | 10.9 | 38 | 26 | 19 | 27 | ||||||
| 18.90 | 11.9 | 38 | 30 | 20 | 23 | 11.9 | 38 | 29 | 17 | 29 | ||||||
| 22 | 16.50 | 9.5 | 42 | 32 | 24 | 26 | 9.5 | 39 | 27 | 20 | 26 | 15.0 | 41 | 28 | 23 | 29 |
| 17.60 | 10.6 | 41 | 32 | 21 | 27 | 10.6 | 39 | 27 | 20 | 26 | ||||||
| 18.70 | 11.7 | 41 | 30 | 22 | 26 | 11.7 | 39 | 27 | 21 | 27 | ||||||
| 19.80 | 12.8 | 42 | 30 | 22 | 28 | 12.8 | 40 | 28 | 20 | 26 | ||||||
| 23 | 17.25 | 10.3 | 41 | 33 | 21 | 24 | 10.3 | 38 | 28 | 23 | 28 | 16.1 | 42 | 28 | 24 | 40 |
| 18.40 | 11.4 | 41 | 32 | 21 | 26 | 11.4 | 39 | 27 | 20 | 28 | ||||||
| 19.55 | 12.6 | 40 | 30 | 20 | 26 | 12.6 | 39 | 27 | 20 | 26 | ||||||
| 20.70 | 13.7 | 41 | 29 | 21 | 28 | 13.7 | 40 | 27 | 20 | 28 | ||||||
| 24 | 18.00 | 11.0 | 42 | 33 | 20 | 27 | 11.0 | 39 | 27 | 21 | 25 | 17.1 | 42 | 28 | 25 | 32 |
| 19.20 | 12.2 | 41 | 31 | 22 | 25 | 12.2 | 40 | 27 | 19 | 26 | ||||||
| 20.40 | 13.4 | 41 | 30 | 21 | 25 | 13.4 | 40 | 27 | 23 | 26 | ||||||
| 21.60 | 14.6 | 42 | 30 | 20 | 27 | 14.6 | 42 | 28 | 23 | 29 | ||||||
| 25 | 18.75 | 11.8 | 42 | 32 | 22 | 26 | 12.0 | 38 | 27 | 19 | 25 | 18.2 | 43 | 28 | 25 | 33 |
| 20.00 | 13.0 | 42 | 31 | 21 | 27 | 13.0 | 39 | 28 | 22 | 25 | ||||||
| 21.25 | 14.3 | 41 | 30 | 20 | 26 | 14.3 | 41 | 28 | 23 | 28 | ||||||
| 22.50 | 15.6 | 42 | 29 | 23 | 28 | 15.6 | 41 | 28 | 21 | 27 | ||||||
References
- Ahac, S.; Dragčević, V. Geometric Design of Suburban Roundabouts. Encyclopedia 2021, 1, 720–743. [Google Scholar] [CrossRef]
- Hydén, C.; Várhelyi, A. The effects on safety, time consumption and environment of large scale use of roundabouts in an urban area: A case study. Accid. Anal. Prev. 2000, 32, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, P.; Teixeira, J.; Guarnaccia, C.; Bandeira, J.M.; Macedo, E.; Coelho, M.C. The Potential of Metering Roundabouts: Influence in Transportation Externalities. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 21–34. [Google Scholar] [CrossRef]
- Distefano, N.; Leonardi, S. Experimental Investigation of the Effect of Roundabouts on Noise Emission Level from Motor Vehicles. Noise Control Engr. J. 2019, 67, 282–294. Available online: https://hdl.handle.net/20.500.11769/371965 (accessed on 19 July 2023). [CrossRef]
- Jandacka, D.; Decky, M.; Hodasova, K.; Pisca, P.; Briliak, D. Influence of the Urban Intersection Reconstruction on the Reduction of Road Traffic Noise Pollution. Appl. Sci. 2022, 12, 8878. [Google Scholar] [CrossRef]
- Ziolkowski, R. Roundabouts as an effective tool of traffic management. J. Sustain. Archit. Civ. Eng. 2014, 9, 26–34. [Google Scholar] [CrossRef]
- Macioszek, E. The road safety at turbo roundabouts in Poland. Arch. Transp. 2015, 33, 57–67. [Google Scholar] [CrossRef]
- Chen, Y.; Persaud, B.; Sacchi, E.; Bassani, M. Investigation of models for relating roundabout safety to predicted speed. Accid. Anal. Prev. 2013, 50, 196–203. [Google Scholar] [CrossRef] [PubMed]
- Šurdonja, S.; Dragčević, V.; Deluka-Tibljaš, A. Analyses of maximum-speed path definition at single-lane roundabouts. J. Traffic Transp. Eng. (Engl. Ed.) 2018, 5, 83–95. [Google Scholar] [CrossRef]
- Merkblatt für die Anlage von Kreisverkehren, K 10000; FGSV (Forschungsgesellschaft für Strassen-und Verkehrswesen): Köln, Germany, 2006.
- Gallelli, V.; Vaiana, R.; Iuele, T. Comparison between simulated and experimental crossing speed profiles on roundabout with different geometric features. Procedia -Social Behav. Sci. 2014, 111, 117–126. [Google Scholar] [CrossRef]
- Bastos, S.A.; Seco, A. Trajectory deflection influence on the performance of roundabouts. In Proceedings of the European Transport Conference (ETC) Association for European Transport, Strasbourg, France, 18–20 September 2005. [Google Scholar]
- Rodegerdts, L.; Bansen, J.; Tiesler, C.; Knudsen, J.; Myers, E.; Johnson, M.; Moule, M.; Persaud, B.; Lyon, C.; Hallmark, S.; et al. NCHRP Report 672: ROUNDABOUTS: An Informational Guide, 2nd ed.; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar]
- CROW: Eenheid in Rotondes; CROW Publication no.126; CROW: Ede, The Netherlands, 1998.
- Bassani, M.; Sacchi, E. Experimental investigation into speed performance and consistency of urban roundabouts: An Italian case study. In Proceedings of the 3rd International Conference on Roundabouts, Transportation Research Board, Carmel, IN, USA, 18–20 May 2011. [Google Scholar]
- Ahac, S.; Džambas, T.; Dragčević, V. Review of fastest path procedures for single-lane roundabouts. In Road and Rail Infrastructure IV; Lakušić, S., Ed.; The University of Zagreb Faculty of Civil Engineering: Zagreb, Croatia, 2016; pp. 885–891. [Google Scholar]
- Ahmed, H.; Easa, S.M. Multi-Objective Evaluation Model of Single-Lane Roundabouts. Transp. Res. Rec. 2021, 2675, 395–410. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Guidelines for roundabout circulatory and entry widths based on vehicle dynamics. J. Traffic Transp. Eng. 2018, 5, 361–371. [Google Scholar] [CrossRef]
- Ahac, S. Design of Suburban Roundabouts Based on Rules of Vehicle Movement Geometry. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, April 2014. [Google Scholar]
- Tollazzi, T. Alternative Types of Roundabouts: An Informational Guide, Springer Tracts on Transportation and Traffc; Series editor Roger P. Roess; Springer: New York, NY, USA, 2015; Volume 6. [Google Scholar]
- Alozi, A.R.; Hussein, M. Multi-criteria comparative assessment of unconventional roundabout designs. Int. J. Transp. Sci. Technol. 2022, 11, 158–173. [Google Scholar] [CrossRef]
- Pratelli, A.; Souleyrette, R.R.; Brocchinia, L. Two-Geometry Roundabouts: Design Principles. Transp. Res. Procedia 2022, 64, 299–307. [Google Scholar] [CrossRef]
- Džambas, T.; Dragčević, V.; Bezina, Š.; Grgić, M. Reliability of vehicle movement simulation results in roundabout design procedure based on the rules of design vehicle movement geometry. In Road and Rail Infrastructure VI; Lakušić, S., Ed.; The University of Zagreb Faculty of Civil Engineering: Zagreb, Croatia, 2021; pp. 507–515. [Google Scholar] [CrossRef]
- Carrasco, M.S. Turning vehicle simulation: Interactive computer-aided design and drafting application. Transp. Res. Rec. 1995, 1500, 1–11. [Google Scholar]
- Ahac, S.; Ahac, M.; Džambas, T.; Dragčević, V. The Design Vehicle Steering Path Construction Based on the Hairpin Bend Geometry—Application in Roundabout Design. Appl. Sci. 2022, 12, 11019. [Google Scholar] [CrossRef]
- Stančerić, I.; Dobrica, T.; Ahac, S.; Dragčević, V.; Tenžera, D. Offtracking control requirements for quality roundabout design. In Road and Rail Infrastructure III; Lakušić, S., Ed.; The University of Zagreb Faculty of Civil Engineering: Zagreb, Croatia, 2014; pp. 263–268. [Google Scholar]
- Novák, J.; Ambros, J.; Frič, J. How Roundabout Entry Design Parameters Influence Safety. Transp. Res. Rec. 2018, 2672, 73–84. [Google Scholar] [CrossRef]
- Čudina Ivančev, A.; Ahac, M.; Ahac, S.; Dragčević, V. Comparison of Single-Lane Roundabout Entry Degree of Saturation Estimations from Analytical and Regression Models. Algorithms 2023, 16, 164. [Google Scholar] [CrossRef]



| a | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 |
|---|---|---|---|---|
| 18 | 13.50 | 14.40 | 15.30 | 16.20 |
| 19 | 14.25 | 15.20 | 16.15 | 17.10 |
| 20 | 15.00 | 16.00 | 17.00 | 18.00 |
| 21 | 15.75 | 16.80 | 17.85 | 18.90 |
| 22 | 16.50 | 17.60 | 18.70 | 19.80 |
| 23 | 17.25 | 18.40 | 19.55 | 20.70 |
| 24 | 18.00 | 19.20 | 20.40 | 21.60 |
| 25 | 18.75 | 20.00 | 21.25 | 22.50 |
| a (m) | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 | b/a = 1.00 | ||||
|---|---|---|---|---|---|---|---|---|---|
| x (m) | y (m) | x (m) | y (m) | x (m) | y (m) | x (m) | y (m) | x = y (m) | |
| 18 | 11.85 | 7.35 | 10.60 | 7.00 | 9.35 | 6.65 | 8.20 | 6.40 | 6.05 |
| 19 | 11.75 | 7.00 | 10.50 | 6.70 | 9.30 | 6.45 | 8.10 | 6.20 | 5.95 |
| 20 | 11.75 | 6.75 | 10.45 | 6.45 | 9.25 | 6.25 | 8.05 | 6.05 | 5.80 |
| 21 | 11.85 | 6.60 | 10.45 | 6.25 | 9.20 | 6.05 | 8.10 | 6.00 | 5.75 |
| 22 | 11.85 | 6.35 | 10.55 | 6.15 | 9.25 | 5.95 | 7.95 | 5.75 | 5.60 |
| 23 | 11.95 | 6.20 | 10.55 | 5.95 | 9.25 | 5.80 | 7.95 | 5.65 | 5.45 |
| 24 | 12.05 | 6.05 | 10.65 | 5.85 | 9.25 | 5.65 | 7.95 | 5.55 | 5.45 |
| 25 | 12.25 | 6.00 | 10.75 | 5.75 | 9.35 | 5.60 | 7.95 | 5.45 | 5.35 |
| a (m) | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 | b/a = 1.00 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| L (m) | U (m) | L (m) | U (m) | L (m) | U (m) | L (m) | U (m) | L (m) | U (m) | |
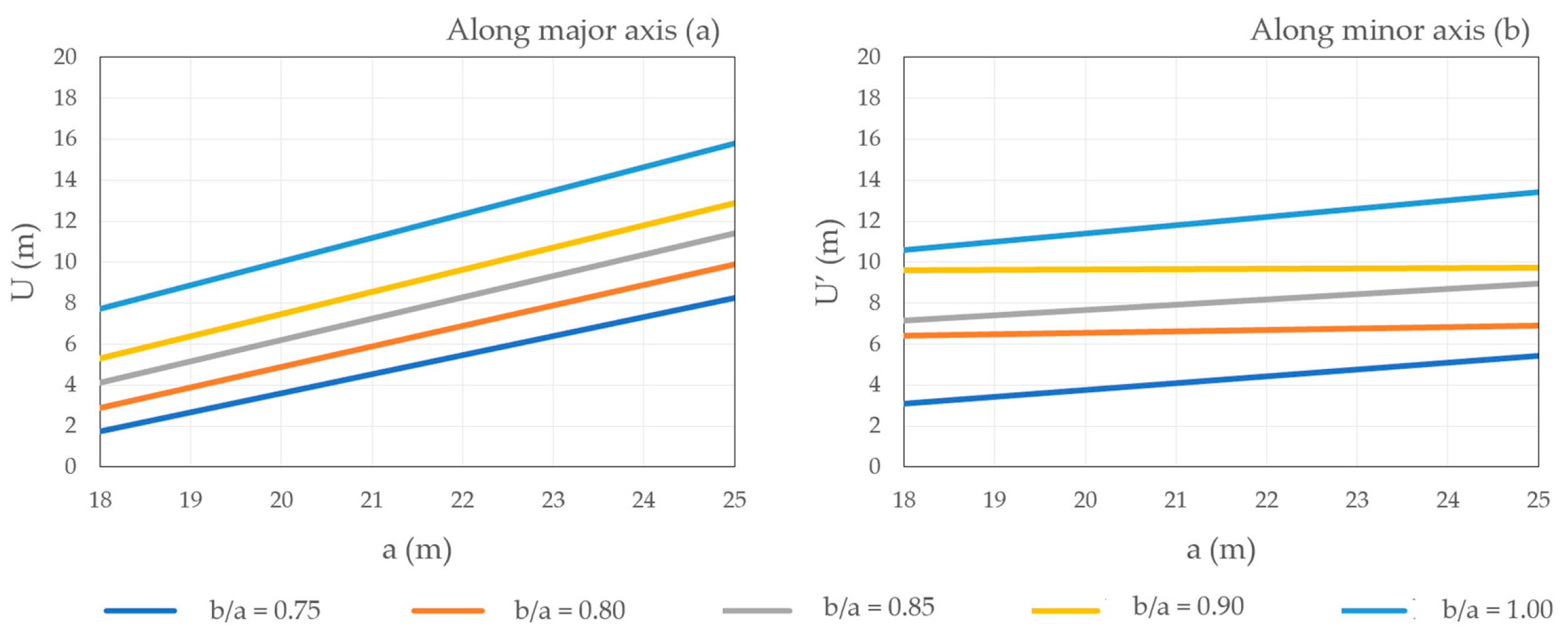
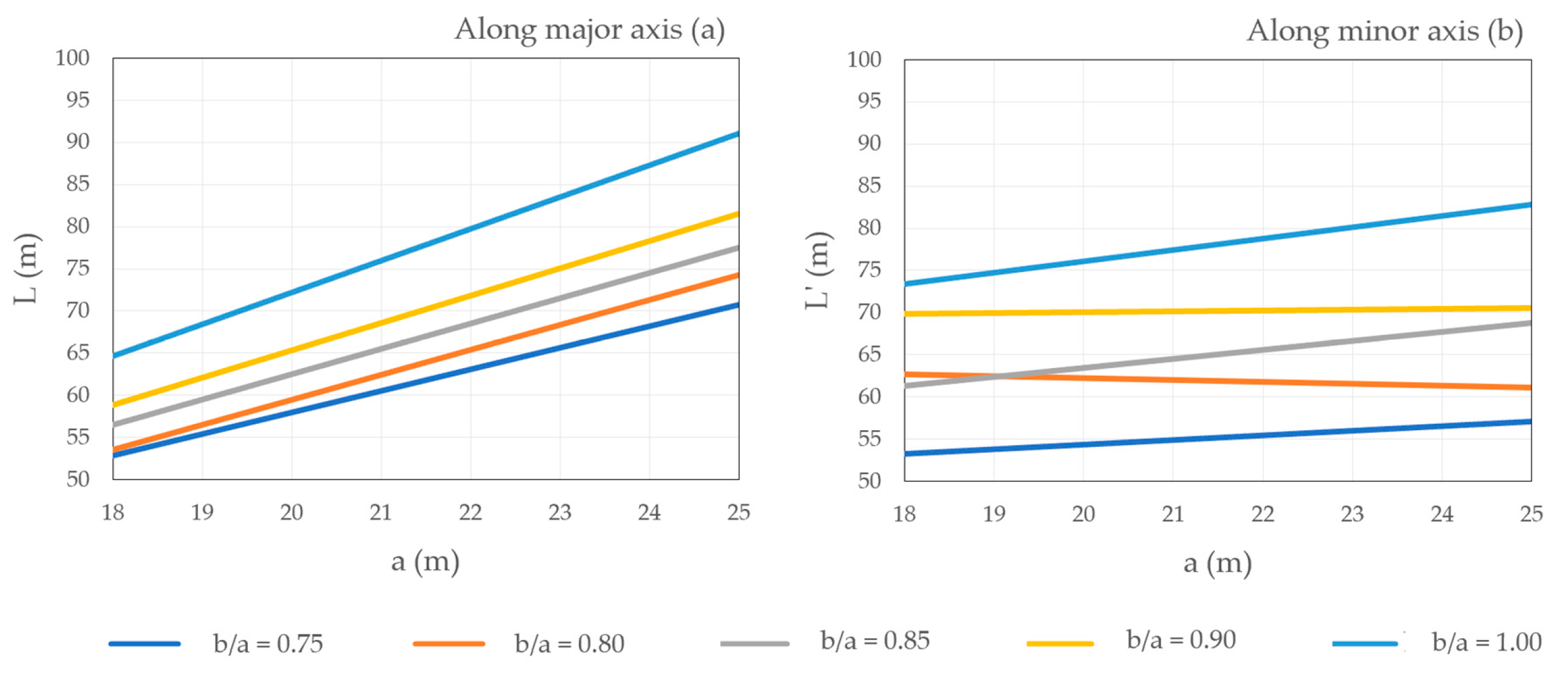
| 18 | 54.06 | 1.88 | 53.51 | 2.77 | 57.17 | 4.09 | 61.20 | 5.37 | 64.63 | 7.65 |
| 19 | 54.52 | 2.52 | 57.26 | 3.87 | 58.47 | 5.09 | 62.76 | 6.46 | 69.66 | 8.85 |
| 20 | 56.09 | 3.51 | 59.26 | 4.92 | 62.76 | 6.24 | 64.89 | 7.52 | 71.44 | 10.14 |
| 21 | 62.98 | 4.59 | 61.75 | 5.94 | 65.20 | 7.31 | 62.37 | 8.03 | 75.60 | 11.12 |
| 22 | 63.13 | 5.51 | 65.32 | 6.89 | 68.83 | 8.31 | 74.11 | 9.80 | 79.15 | 12.32 |
| 23 | 64.02 | 6.37 | 68.38 | 7.92 | 70.85 | 9.31 | 74.80 | 10.75 | 83.36 | 13.55 |
| 24 | 67.99 | 7.34 | 71.44 | 8.86 | 75.21 | 10.40 | 78.90 | 11.83 | 87.44 | 14.62 |
| 25 | 71.66 | 8.20 | 74.33 | 9.80 | 77.27 | 11.30 | 82.53 | 12.88 | 91.66 | 15.79 |
| a (m) | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 | b/a = 1.00 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| L′ (m) | U′ (m) | L′ (m) | U′ (m) | L′ (m) | U′ (m) | L′ (m) | U′ (m) | L′ (m) | U′ (m) | |
| 18 | 51.48 | 1.70 | 50.41 | 2.86 | 55.53 | 4.43 | 57.74 | 5.39 | 64.63 | 7.65 |
| 19 | 51.92 | 2.77 | 52.98 | 3.99 | 56.66 | 5.25 | 63.51 | 6.62 | 69.66 | 8.85 |
| 20 | 53.21 | 3.76 | 58.71 | 5.18 | 59.97 | 6.36 | 63.70 | 7.62 | 71.44 | 10.14 |
| 21 | 54.93 | 4.67 | 58.66 | 6.13 | 62.14 | 7.42 | 63.86 | 8.49 | 75.60 | 11.12 |
| 22 | 59.62 | 5.78 | 62.82 | 7.11 | 66.17 | 8.45 | 71.22 | 9.85 | 79.15 | 12.32 |
| 23 | 59.92 | 6.37 | 64.85 | 8.13 | 68.39 | 9.47 | 73.38 | 10.86 | 83.36 | 13.55 |
| 24 | 63.19 | 7.60 | 69.24 | 9.12 | 72.44 | 10.55 | 80.40 | 12.04 | 87.44 | 14.62 |
| 25 | 65.05 | 8.41 | 69.34 | 9.97 | 76.86 | 11.54 | 81.57 | 13.02 | 91.66 | 15.79 |
| a (m) | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 | b/a = 1.00 | ||||
|---|---|---|---|---|---|---|---|---|---|
| x (m) | y (m) | x (m) | y (m) | x (m) | y (m) | x (m) | y (m) | x = y (m) | |
| 18 | 10.00 | 5.50 | 9.10 | 5.50 | 8.20 | 5.50 | 7.30 | 5.50 | 5.50 |
| 19 | 10.25 | 5.50 | 9.30 | 5.50 | 8.35 | 5.50 | 7.40 | 5.50 | 5.50 |
| 20 | 10.50 | 5.50 | 9.50 | 5.50 | 8.50 | 5.50 | 7.50 | 5.50 | 5.50 |
| 21 | 10.75 | 5.50 | 9.70 | 5.50 | 8.65 | 5.50 | 7.60 | 5.50 | 5.50 |
| 22 | 11.00 | 5.50 | 9.90 | 5.50 | 8.80 | 5.50 | 7.70 | 5.50 | 5.50 |
| 23 | 11.25 | 5.50 | 10.10 | 5.50 | 8.95 | 5.50 | 7.80 | 5.50 | 5.50 |
| 24 | 11.50 | 5.50 | 10.30 | 5.50 | 9.10 | 5.50 | 7.90 | 5.50 | 5.50 |
| 25 | 11.75 | 5.50 | 10.50 | 5.50 | 9.25 | 5.50 | 8.00 | 5.50 | 5.50 |
| a (m) | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 | b/a = 1.00 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| L (m) | U (m) | L (m) | U (m) | L (m) | U (m) | L (m) | U (m) | L (m) | U (m) | |
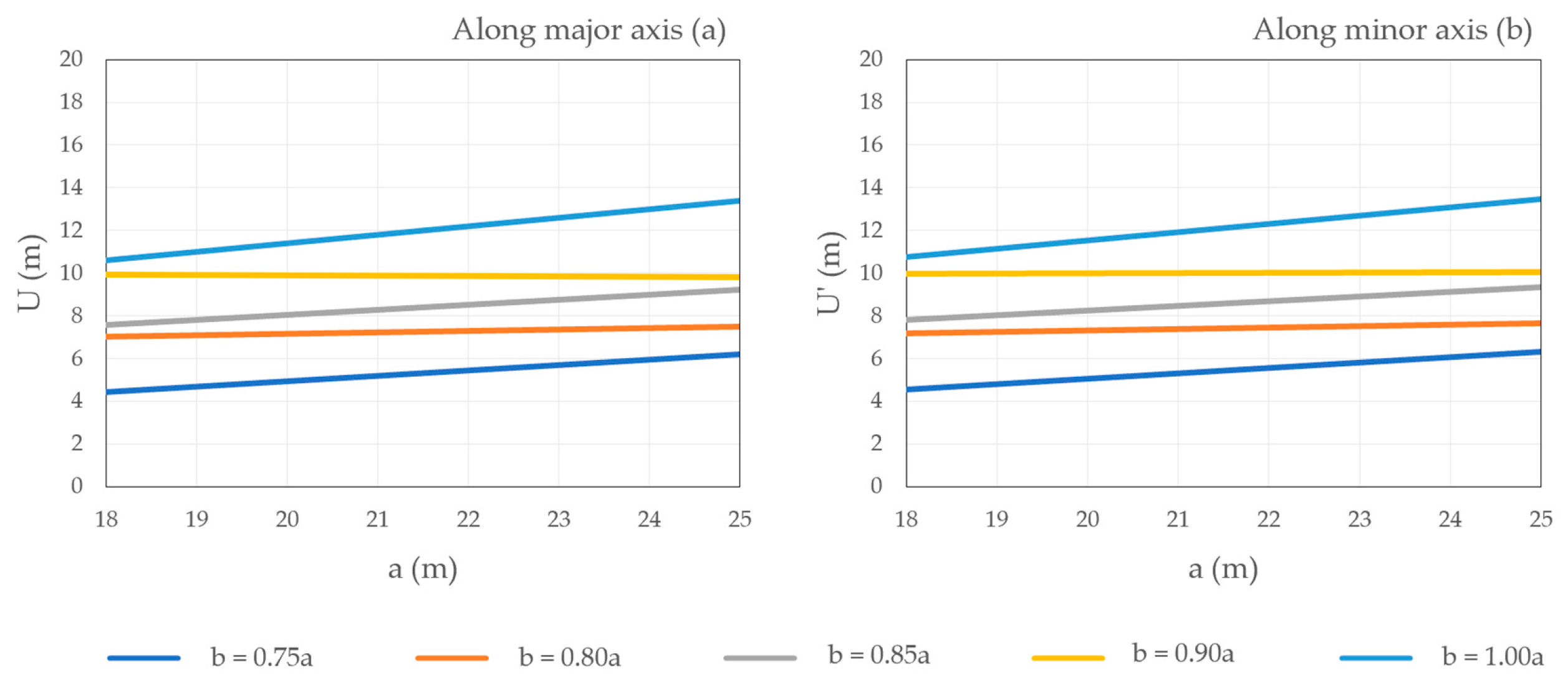
| 18 | 54.06 | 3.34 | 53.51 | 4.27 | 57.17 | 5.24 | 61.20 | 6.27 | 64.63 | 8.20 |
| 19 | 54.52 | 4.02 | 57.26 | 5.07 | 58.47 | 6.04 | 62.76 | 7.16 | 69.66 | 9.30 |
| 20 | 56.09 | 4.76 | 59.26 | 5.87 | 62.76 | 6.99 | 64.89 | 8.07 | 71.44 | 10.30 |
| 21 | 62.98 | 5.69 | 61.75 | 6.69 | 65.20 | 7.86 | 62.37 | 8.53 | 75.60 | 11.37 |
| 22 | 63.13 | 6.36 | 65.32 | 7.54 | 68.83 | 8.76 | 74.11 | 10.05 | 79.15 | 12.42 |
| 23 | 64.02 | 7.07 | 68.38 | 8.37 | 70.85 | 9.61 | 74.80 | 10.90 | 83.36 | 13.55 |
| 24 | 67.99 | 7.89 | 71.44 | 9.21 | 75.21 | 10.55 | 78.90 | 11.88 | 87.44 | 14.62 |
| 25 | 71.66 | 8.70 | 74.33 | 10.05 | 77.27 | 11.40 | 82.53 | 12.88 | 91.66 | 15.79 |
| a (m) | b/a = 0.75 | b/a = 0.80 | b/a = 0.85 | b/a = 0.90 | b/a = 1.00 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| L′ (m) | U′ (m) | L′ (m) | U′ (m) | L′ (m) | U′ (m) | L′ (m) | U′ (m) | L′ (m) | U′ (m) | |
| 18 | 51.48 | 3.55 | 50.41 | 4.36 | 55.53 | 5.37 | 57.74 | 6.29 | 64.63 | 8.20 |
| 19 | 51.92 | 4.27 | 52.98 | 5.19 | 56.66 | 6.20 | 63.51 | 7.32 | 69.66 | 9.30 |
| 20 | 53.21 | 5.01 | 58.71 | 6.13 | 59.97 | 7.11 | 63.70 | 8.17 | 71.44 | 10.30 |
| 21 | 54.93 | 5.92 | 58.66 | 6.88 | 62.14 | 7.97 | 63.86 | 8.99 | 75.60 | 11.37 |
| 22 | 59.62 | 6.63 | 62.82 | 7.76 | 66.17 | 8.90 | 71.22 | 10.10 | 79.15 | 12.42 |
| 23 | 59.92 | 7.07 | 64.85 | 8.58 | 68.39 | 9.77 | 73.38 | 11.01 | 83.36 | 13.55 |
| 24 | 63.19 | 8.15 | 69.24 | 9.47 | 72.44 | 10.70 | 80.40 | 12.09 | 87.44 | 14.62 |
| 25 | 65.05 | 8.91 | 69.34 | 10.22 | 76.86 | 11.64 | 81.57 | 13.02 | 91.66 | 15.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahac, S.; Ahac, M.; Majstorović, I.; Bašić, S. Speed Reduction Capabilities of Two-Geometry Roundabouts. Appl. Sci. 2023, 13, 11816. https://doi.org/10.3390/app132111816
Ahac S, Ahac M, Majstorović I, Bašić S. Speed Reduction Capabilities of Two-Geometry Roundabouts. Applied Sciences. 2023; 13(21):11816. https://doi.org/10.3390/app132111816
Chicago/Turabian StyleAhac, Saša, Maja Ahac, Igor Majstorović, and Silvio Bašić. 2023. "Speed Reduction Capabilities of Two-Geometry Roundabouts" Applied Sciences 13, no. 21: 11816. https://doi.org/10.3390/app132111816
APA StyleAhac, S., Ahac, M., Majstorović, I., & Bašić, S. (2023). Speed Reduction Capabilities of Two-Geometry Roundabouts. Applied Sciences, 13(21), 11816. https://doi.org/10.3390/app132111816








