Fractal Behavior of Size Distribution and Specific Surface Area of Blasting Fragments
Abstract
:1. Introduction
2. Material and Methods
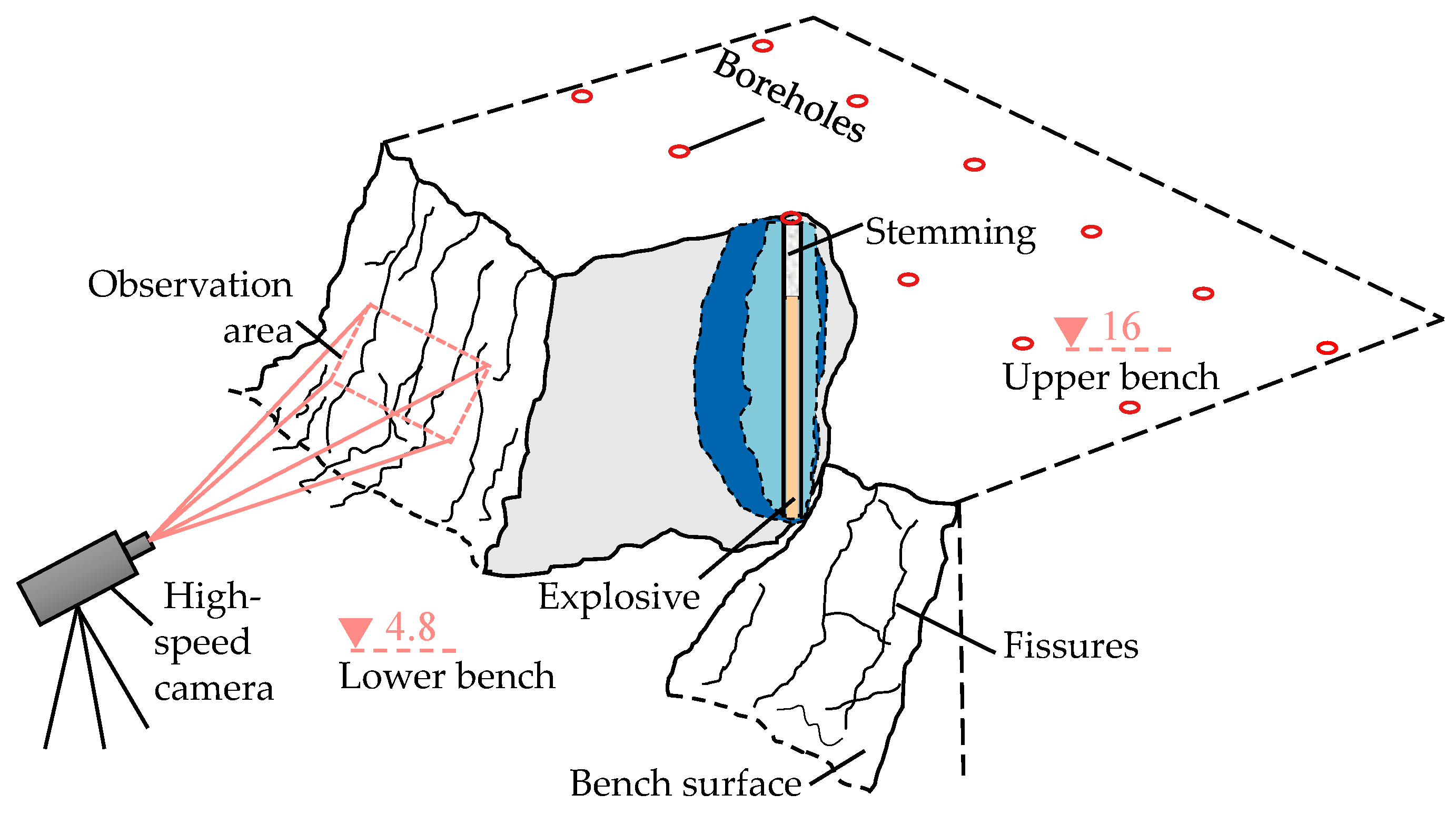
2.1. Field Blasting Experiments
2.2. Blasting Fragmentation Distribution Curve Detection Experiments
2.3. Shape Characteristics and SSA Measurement Experiments
3. Theory and Calculation Results
3.1. Theory for Fractal Dimensions of Particle Size Distribution
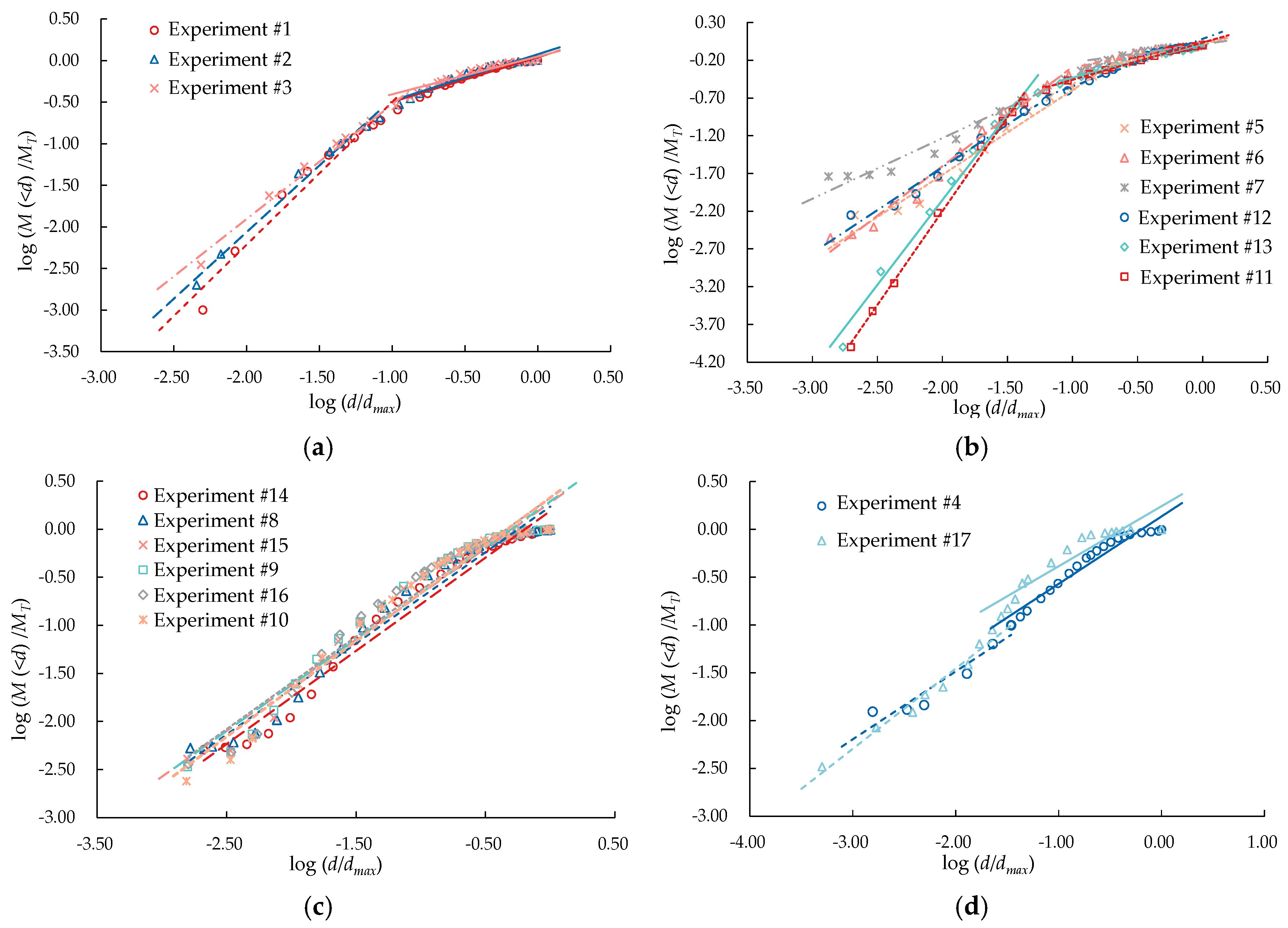
3.2. Calculation of Fractal Dimensions of Particle Size Distribution
3.3. Calculation of Fractal Dimensions of Blasting Fragmentation
3.4. Calculation of Probability of Blasting Fragmentation
4. SSA and Fractal Dimensions
5. Conclusions
- (1)
- According to the particle size–frequency relationship, the fractal dimensions of the particle size distribution calculated using different characteristic sizes were all less than 2, and the characteristic size significantly affected the computed fractal dimensions of the particle size distribution.
- (2)
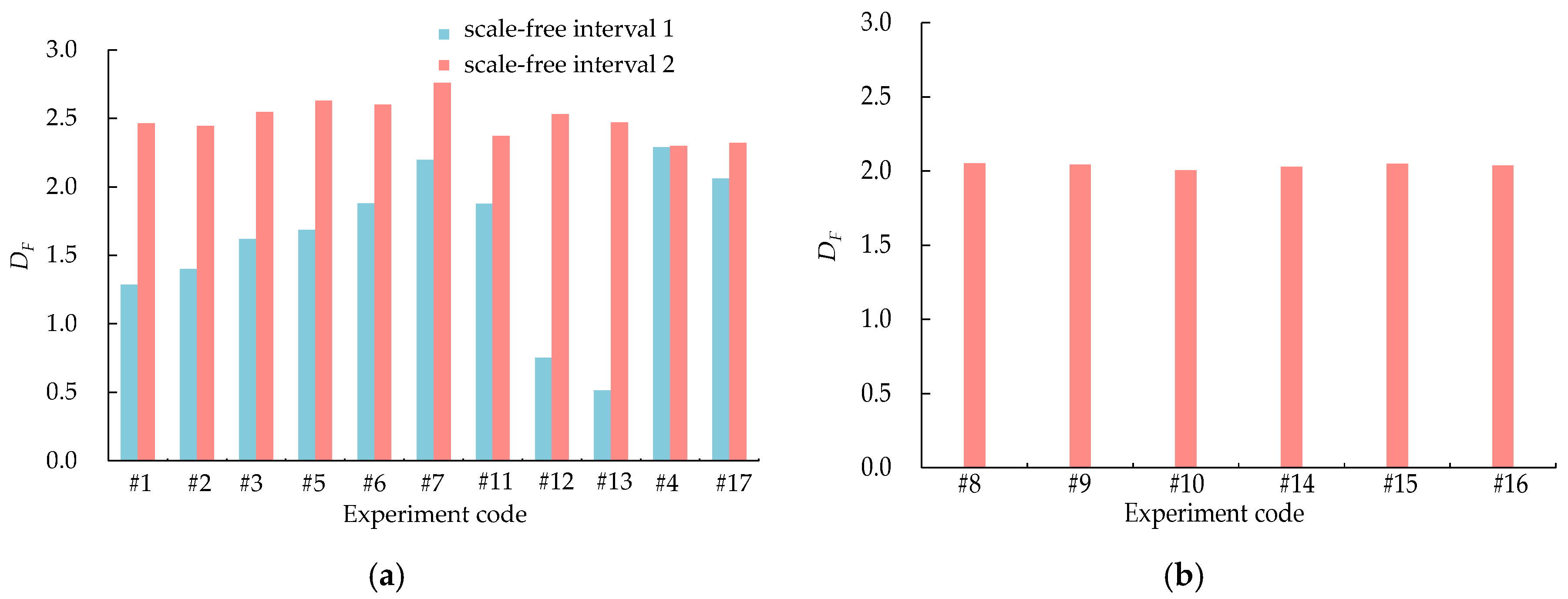
- Depending on the excavation methods, blasting parameters, and other factors, blasting experiments with multifractal characteristics exhibited significant variations in the scale-free intervals and fragmentation fractal dimensions. In the larger scale-free interval, the fragmentation fractal dimensions were mostly greater than 2.3, whereas in the smaller scale-free interval, they were often less than 2.0.
- (3)
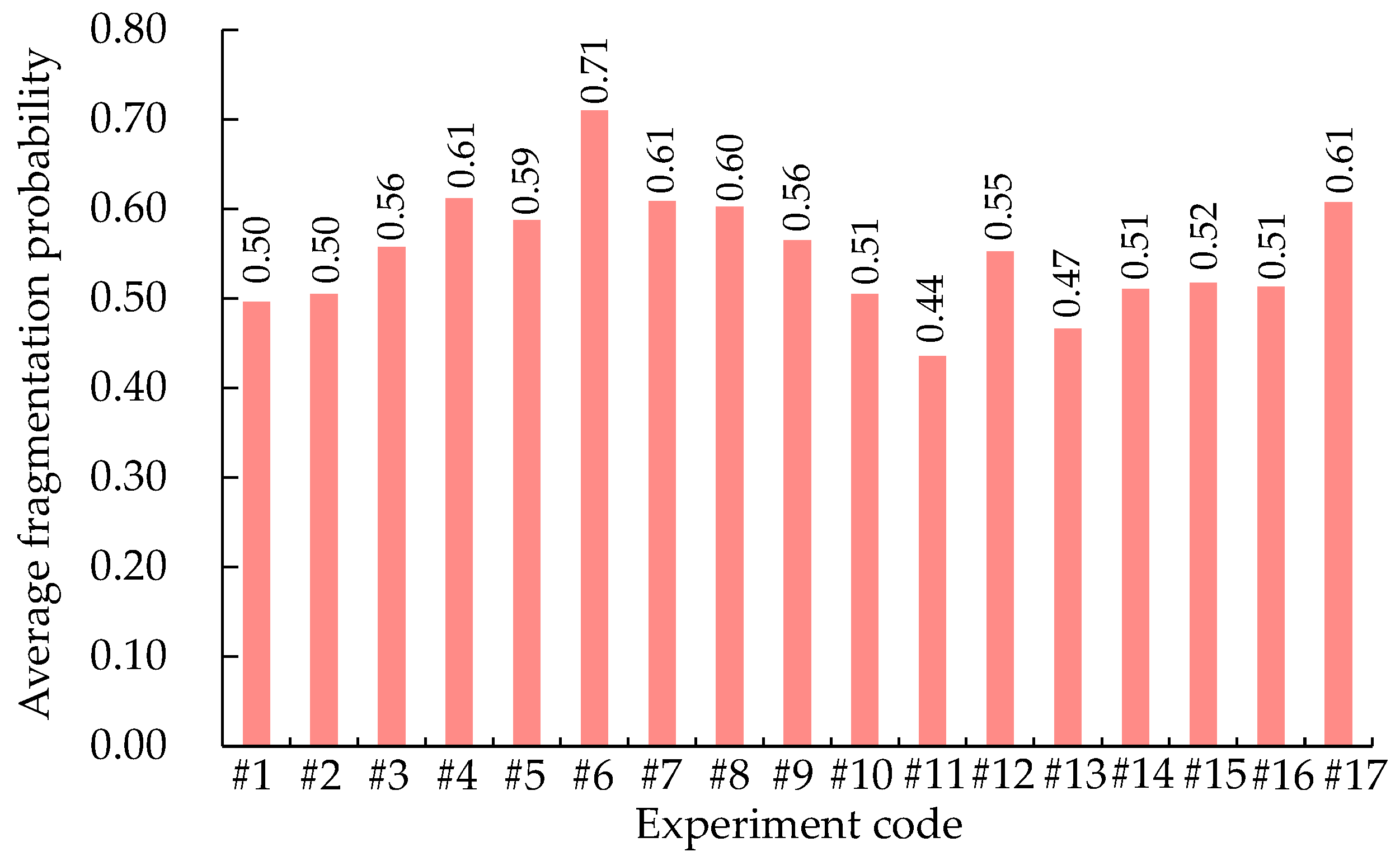
- Rock blasting fragmentation mainly involved two or three stages of fragmentation, with a similarity ratio of 0.5. The calculated average fragmentation probabilities of rock blasting ranged from 0.44 to 0.71. At the same bench height, blasting fragmentation with shock-reflection devices strengthened the transmission and reflective effects of stress waves, increasing the fragmentation probability and fragmentation efficiency of the rock mass.
- (4)
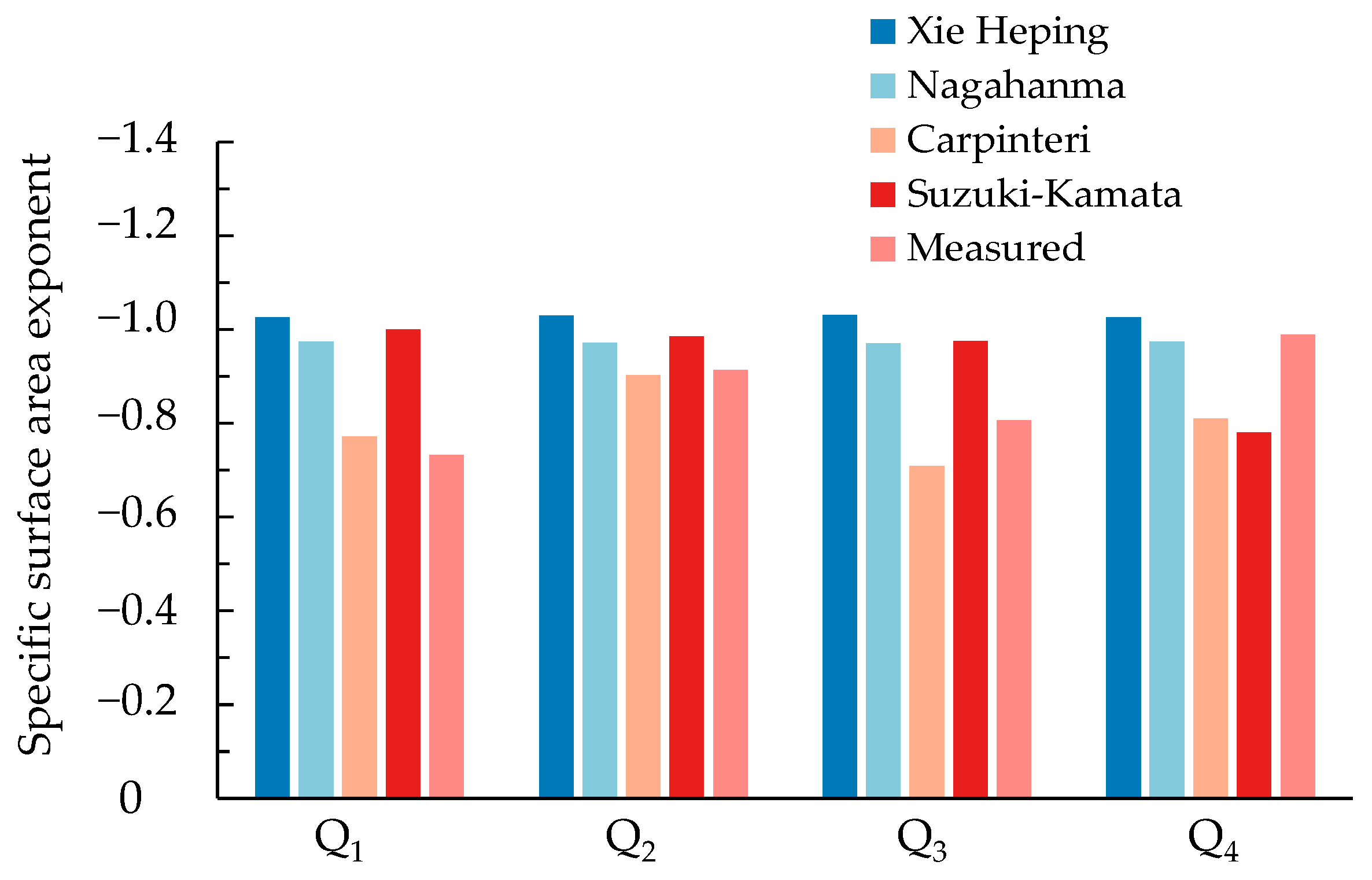
- The SSA of blasting fragments was closely related to the fragmentation fractal dimension and median particle size. By determining the SSA of blasting fragments with large particle sizes using 3D laser scanning technology in advance, the SSA of blasting fragments with a wide grading range can be easily calculated via the SSA predictive formula.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shim, H.J.; Ryu, D.W.; Chung, S.K.; Syn, J.H.; Song, J.J. Optimized blasting design for large-scale quarrying based on a 3-D spatial distribution of rock factor. Int. J. Rock Mech. Min. Sci. 2009, 46, 326–332. [Google Scholar] [CrossRef]
- Faramarzi, F.; Mansouri, H.; Farsangi, M.A.E. A rock engineering systems based model to predict rock fragmentation by blasting. Int. J. Rock Mech. Min. Sci. 2013, 60, 82–94. [Google Scholar] [CrossRef]
- Li, R.Z.; Lu, W.B.; Chen, M.; Wang, G.H.; Xia, W.J.; Yan, P. Quantitative analysis of shapes and specific surface area of blasted fragments using image analysis and three-dimensional laser scanning. Int. J. Rock Mech. Min. Sci. 2021, 141, 104710. [Google Scholar] [CrossRef]
- Ouchterlony, F. Influence of Blasting on the Size Distribution and Properties of Muckpile Fragments, a State-of-the Art Review: MinFo Project P2000-10: Energy Optimisation during Comminution; Swedish Mineral Research Organisation: Stockholm, Sweden, 2003. [Google Scholar]
- De Cola, F. Mechanical Characterisation and Modelling of Statistically Representative Granular Materials Subjected to Impact Loading. Ph.D. Thesis, University of Oxford, Oxford, UK, 2017. [Google Scholar]
- Taylor, M.A. Quantitative measures for shape and size of particles. Powder Technol. 2002, 124, 94–100. [Google Scholar] [CrossRef]
- Ouchterlony, F.; Sanchidrián, J.A. A review of development of better prediction equations for blast fragmentation. J. Rock Mech. Geotech. Eng. 2019, 11, 1094–1109. [Google Scholar] [CrossRef]
- Wills, B.A.; Finch, J.A. Wills’ Mineral Processing Technology, 8th ed.; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Snowsill, W.L. Particle sizing. In Instrumentation Reference Book, 4th ed.; Boyes, W., Ed.; Butterworth-Heinemann: Oxford, UK, 2003; pp. 175–189. [Google Scholar]
- Asl, P.F.; Monjezi, M.; Hamidi, J.K.; Armaghani, D.J. Optimization of flyrock and rock fragmentation in the Tajareh limestone mine using metaheuristics method of firefly algorithm. Eng. Comput. 2018, 34, 241–251. [Google Scholar] [CrossRef]
- Dimitraki, L.; Christaras, B.; Marinos, V.; Vlahavas, I.; Arampelos, N. Predicting the average size of blasted rocks in aggregate quarries using artificial neural networks. Bull. Eng. Geol. Environ. 2019, 78, 2717–2729. [Google Scholar] [CrossRef]
- Babaeian, M.; Ataei, M.; Sereshki, F.; Sotoudeh, F.; Mohammadi, S. A new framework for evaluation of rock fragmentation in open pit mines. J. Rock Mech. Geotech. Eng. 2019, 11, 325–336. [Google Scholar] [CrossRef]
- Onederra, I.; Thurley, M.J.; Catalan, A. Measuring blast fragmentation at Esperanza mine using high-resolution 3D laser scanning. Min. Technol. 2015, 124, 34–36. [Google Scholar] [CrossRef]
- Chen, N.; Kemeny, J.; Jiang, Q.H.; Pan, Z.W. Automatic extraction of blocks from 3D point clouds of fractured rock. Comput. Geosci. 2017, 109, 149–161. [Google Scholar] [CrossRef]
- Campbell, A.D.; Thurley, M.J. Application of laser scanning to measure fragmentation in underground mines. Min. Technol. 2017, 126, 240–247. [Google Scholar] [CrossRef]
- Masad, E.; Saadeh, S.; Al-Rousan, T.; Garboczi, E.; Little, D. Computations of particle surface characteristics using optical and X-ray CT images. Comput. Mater. Sci. 2005, 34, 406–424. [Google Scholar] [CrossRef]
- Al Rousan, T.M. Characterization of Aggregate Shape Properties Using a Computer Automated System. Doctoral Dissertation, Texas A&M University, College Station, TX, USA, 2005. [Google Scholar]
- Masad, E.; Button, J.W. Unified imaging approach for measuring aggregate angularity and texture. Comput.-Aided Civ. Infrastruct. Eng. 2000, 15, 273–280. [Google Scholar] [CrossRef]
- Liu, Y.F.; Sun, W.J.; Nair, H.; Lane, D.S.; Wang, L.B. Quantification of aggregate morphologic characteristics with the correlation to uncompacted void content of coarse aggregates in Virginia. Constr. Build. Mater. 2016, 124, 645–655. [Google Scholar] [CrossRef]
- Hryciw, R.D.; Zheng, J.; Shetler, K. Particle roundness and sphericity from images of assemblies by chart estimates and computer methods. J. Geotech. Geoenviron. Eng. 2016, 142, 04016038. [Google Scholar] [CrossRef]
- Blott, S.J.; Pye, K. Particle shape: A review and new methods of characterization and classification. Sedimentology 2008, 55, 31–63. [Google Scholar] [CrossRef]
- Tunwal, M.; Mulchrone, K.F.; Meere, P.A. Quantitative characterization of grain shape: Implications for textural maturity analysis and discrimination between depositional environments. Sedimentology 2018, 65, 1761–1776. [Google Scholar] [CrossRef]
- Zhu, H.J.; Fang, H.Y.; Cai, Y.Y.; Lv, N. Development of a rapid measurement system for coarse aggregate morphological parameters. Particuology 2020, 50, 181–188. [Google Scholar] [CrossRef]
- Barrett, P.J. The shape of rock particles, a critical review. Sedimentology 1980, 27, 291–303. [Google Scholar] [CrossRef]
- Tromans, D.; Meech, J.A. Fracture toughness and surface energies of minerals: Theoretical estimates for oxides, sulphides, silicates and halides. Miner. Eng. 2002, 15, 1027–1041. [Google Scholar] [CrossRef]
- Ouhbi, N.; Voivret, C.; Perrin, G.; Roux, J.-N. 3D particle shape modelling and optimization through proper orthogonal decomposition. Granul. Matter 2017, 19, 86. [Google Scholar] [CrossRef]
- Hyslip, J.P.; Vallejo, L.E. Fractal analysis of the roughness and size distribution of granular materials. Eng. Geol. 1997, 48, 231–244. [Google Scholar] [CrossRef]
- Xie, H.P. Introduction to Fractals and Rock Mechanics; China Science Publishing & Media Ltd. (CPSM): Beijing, China, 1996. [Google Scholar]
- Su, D.; Wang, X.; Yang, H.W.; Hong, C.Y. Roughness analysis of general-shape particles, from 2D closed outlines to 3D closed surfaces. Powder Technol. 2019, 356, 423–438. [Google Scholar] [CrossRef]
- Guo, Y.L.; Markine, V.; Zhang, X.H.; Qiang, W.L.; Jing, G.Q. Image analysis for morphology, rheology and degradation study of railway ballast: A review. Transp. Geotech. 2019, 18, 173–211. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Liu, H.M.; Wang, J.D.; Zeng, Z.P.; Xie, Y.T. Study on meso-damage damage mechanism of shale reservoir rock based on digital core. Chin. J. Rock Mech. Eng. 2022, 41, 1103–1113. [Google Scholar]
- Wang, L.; Yuan, Q.P.; Xie, G.X.; Gu, S.H.; Jiao, Z.H.; Liu, H.Q.; Chen, L.P. Length-diameter ratio effect of energy dissipation and fractals of coal samples under impact loading. J. China Coal Soc. 2022, 47, 1534–1546. [Google Scholar]
- Luo, H.H.; Yang, R.S.; Ma, X.M.; Yang, G.L.; Zhu, P.X.; Feng, W.Y. Study on distribution characteristics of deep hole in the fan-shaped hole of Shilu Iron Mine. J. Min. Saf. Eng. 2023, 40, 371–378. [Google Scholar]
- Sun, Q.; Duan, F.B.; Xie, H.P. Study on fractal dimension evaluation measurement of coal rock blasting. Chin. J. Rock Mech. Eng. 2000, 19, 505–508. [Google Scholar]
- Ouchterlony, F.; Nyberg, U.; Olsson, M.; Bergqvist, I.; Granlund, L.; Grind, H. Where does the explosive energy in rock blasting rounds go? Sci. Technol. Energetic Mater. 2004, 65, 54–63. [Google Scholar]
- Hamdi, E.; Romdhane, N.B.; du Mouza, J.; Le Cleac’h, J.M. Fragmentation energy in rock blasting. Geotech. Geol. Eng. 2008, 26, 133–146. [Google Scholar] [CrossRef]
- Jiang, S.; Shen, L.M.; Guillard, F.; Einav, I. Energy dissipation from two-glass-bead chains under impact. Int. J. Impact Eng. 2018, 114, 160–168. [Google Scholar] [CrossRef]
- Merkus, H.G. Sieves and sieving. In Particle Size Measurements; Particle Technology Series; Springer: Dordrecht, The Netherlands, 2009; Volume 17, pp. 219–240. [Google Scholar]
- Singh, P.K.; Roy, M.P.; Paswan, R.K.; Sarim, M.; Kumar, S.; Jha, R.R. Rock fragmentation control in opencast blasting. J. Rock Mech. Geotech. Eng. 2016, 8, 225–237. [Google Scholar] [CrossRef]
- Li, R.Z.; Lu, W.B.; Yin, Y.J.; Yu, Y.J.; Chen, M.; Xia, W.J.; Yan, P. Study on the shape and specific surface area characteristics of blasting gravel particles of limestone in Hangudi quarry of Baihetan. Chin. J. Rock Mech. Eng. 2019, 38, 1344–1354. [Google Scholar]
- Wu, Y.; Ma, G.; Zhou, W.; Yang, L.F. Optimization of gradation of rockfill materials based on the fractal theory. Rock Soil Mech. 2016, 37, 1977–1985. [Google Scholar]
- Li, D.J.; Jia, X.N.; Miao, J.L.; He, M.C.; Li, D.D. Analysis of fractal characteristics of fragment from rockburst test of granite. Chin. J. Rock Mech. Eng. 2010, 29, 3280–3289. [Google Scholar]
- Tyler, S.W.; Wheatcraft, S.W. Fractal scaling of soil particle-size distributions: Analysis and limitations. Soil Sci. Soc. Am. J. 1992, 56, 362–369. [Google Scholar] [CrossRef]
- Sammis, C.G.; Biegel, R.L. Fractals, fault-gouge, and friction. Pure Appl. Geophys. 1989, 131, 255–271. [Google Scholar] [CrossRef]
- Nagahama, H. Fractal scalings of rock fragmentation. Earth Sci. Front. 2000, 7, 169–177. [Google Scholar]
- Suzuki-Kamata, K.; Kusano, T.; Yamasaki, K. Fractal analysis of the fracture strength of lava dome material based on the grain size distribution of block-and-ash flow deposits at Unzen Volcano, Japan. Sediment. Geol. 2009, 220, 162–168. [Google Scholar] [CrossRef]
- Carpinteri, A.; Lacidogna, G.; Pugno, N. Scaling of energy dissipation in crushing and fragmentation: A fractal and statistical analysis based on particle size distribution. Int. J. Fract. 2004, 129, 131–139. [Google Scholar] [CrossRef]


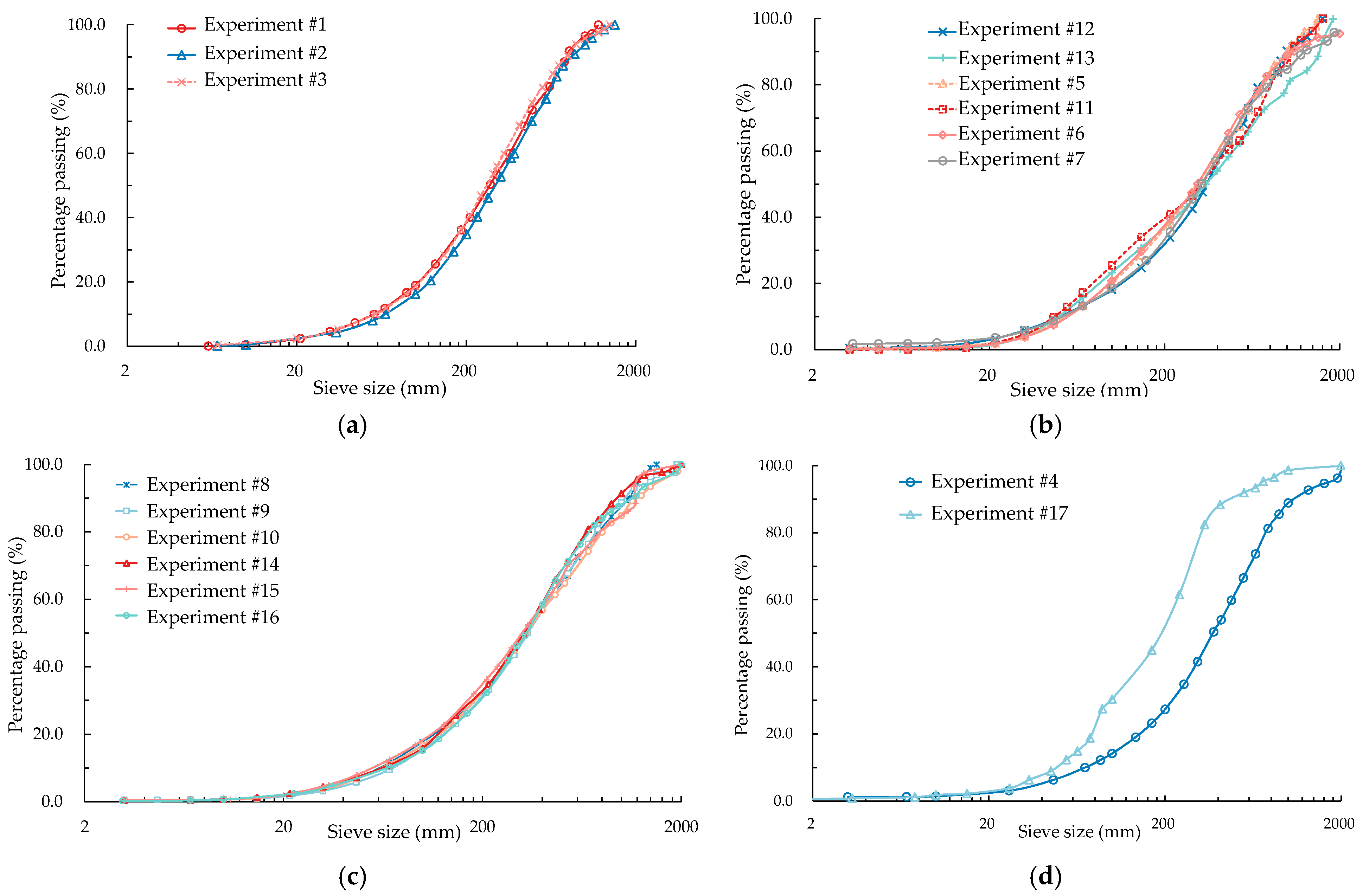
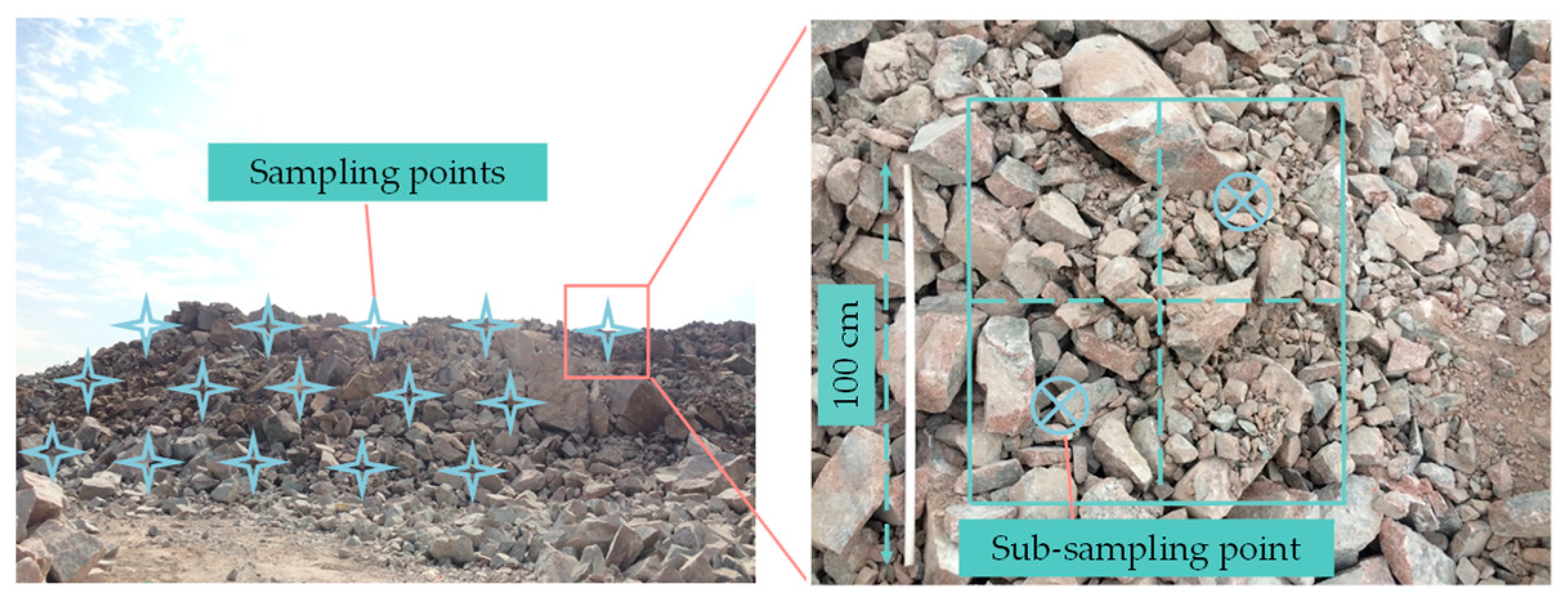
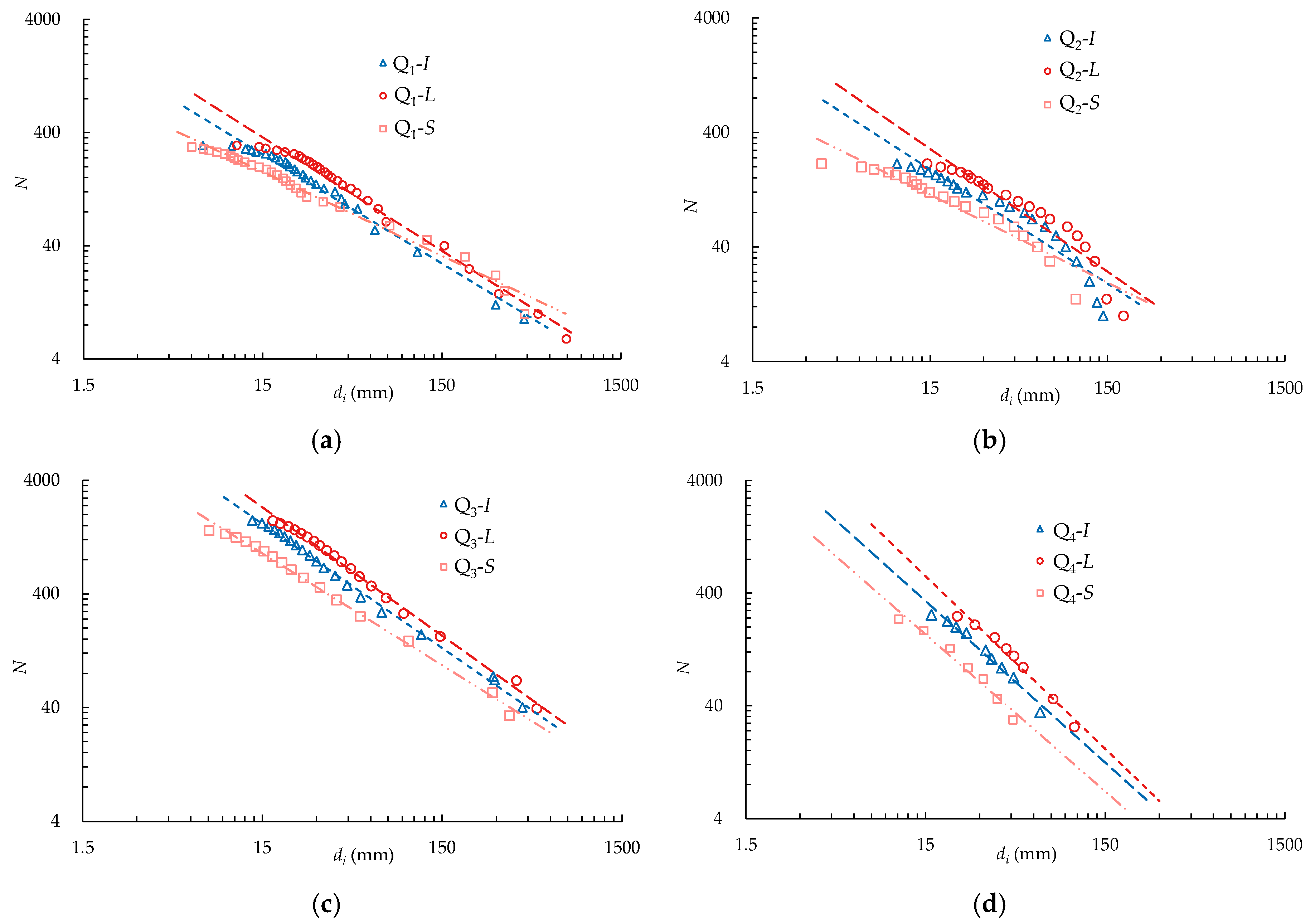



| Quarry Code | Code | Bench Height (m) | Hole Diameter (mm) | Explosive Diameter (mm) | Hole Depth (m) | Subdrill (m) | Specific Charge (kg/m3) | Hole Spacing (m) | Row Spacing (m) | Stemming Length (m) |
|---|---|---|---|---|---|---|---|---|---|---|
| Q1 | #1 | 15 | 115 | 70 | 14.8–17.0 | 1.0 | 0.38 | 6.0 | 4.0 | 4.5 |
| #2 | 15 | 115 | 70 | 16.2–18.0 | 1.0 | 0.35 | 5.0 | 4.0 | 4.5 | |
| #3 | 15 | 115 | 70 | 15.5–18.4 | 1.0 | 0.35 | 6.0 | 4.0 | 5.0 | |
| Q2 | #4 | 12 | 115 | 90/70 | 13.0–15.0 | 1.0 | 0.32 | 4.5 | 4.5 | 4.5–5.0 |
| Q3 | #5 | 12 | 115 | 90 | 10.6–13.4 | 0.8–1.0 | 0.35 | 4.0 | 3.5 | 3.5–4.0 |
| #6 | 12 | 115 | 90 | 10.6–13.4 | 0.8–1.0 | 0.35 | 4.0 | 3.5 | 3.5–4.0 | |
| #7 | 12 | 115 | 90 | 10.6–13.4 | 0.8–1.0 | 0.35 | 4.0 | 4.0 | 3.5–4.0 | |
| #8 | 8 | 115 | 60 | 8.0–9.4 | 0.4–0.6 | 0.36 | 2.3 | 2.0 | 2.0–2.5 | |
| #9 | 8 | 115 | 60 | 5.9–8.0 | 0.4–0.6 | 0.36 | 2.0 | 2.0 | 1.0–2.5 | |
| #10 | 8 | 115 | 60 | 8.0–9.4 | 0.4–0.6 | 0.36 | 2.0 | 1.8 | 2.0–2.5 | |
| #11 | 12 | 115 | 90 | 11.0–13.4 | 0.8–1.0 | 0.35 | 4.0 | 3.5 | 3.5–4.0 | |
| #12 | 12 | 115 | 90 | 10.6–13.4 | 0.8–1.0 | 0.35 | 4.0 | 4.0 | 3.5–4.0 | |
| #13 | 12 | 115 | 90 | 10.6–13.4 | 0.8–1.0 | 0.35 | 4.0 | 4.0 | 3.5–4.0 | |
| #14 | 8 | 115 | 60 | 8.0–9.4 | 0.4–0.6 | 0.36 | 2.3 | 2.0 | 2.0–2.5 | |
| #15 | 8 | 115 | 60 | 8.0–9.4 | 0.4–0.6 | 0.36 | 2.0 | 2.0 | 1.0–2.5 | |
| #16 | 8 | 115 | 60 | 8.0–9.4 | 0.4–0.6 | 0.36 | 2.0 | 1.8 | 2.0–2.5 | |
| Q4 | #17 | 15 | 160 | 160 | 16.5 | 1.5 | 0.36 | 7.5 | 5.0 | 3.5 |
| Experiment Area | Rock Type | Natural Density (g/cm3) | Young’s Modulus (GPa) | Poisson’s Ratio | Unconfined Uniaxial Compressive Strength (MPa) |
|---|---|---|---|---|---|
| Quarry Q1 | Mildly weathered limestone | 2.69–2.71 | 45–55 | 0.23 | 113–140 |
| Quarry Q2 | Mildly weathered tuff | 2.60 | 80 | 0.21 | 140–190 |
| Quarry Q3 | Mild to moderately weathered granite | 2.61 | 50 | 0.22 | 45–75 |
| Quarry Q4 | Mildly weathered limestone | 2.68–2.70 | 16 | 0.22 | 31.4–94.6 |
| Quarry Location | L | I | S | ||||||
|---|---|---|---|---|---|---|---|---|---|
| D | N0 | R2 | D | N0 | R2 | D | N0 | R2 | |
| Q1 | 1.03 | 9176.3 | 0.99 | 1.00 | 4074.2 | 0.99 | 0.74 | 1340.5 | 0.98 |
| Q2 | 1.12 | 6296.7 | 0.91 | 1.03 | 3252.4 | 0.91 | 0.83 | 1142.3 | 0.94 |
| Q3 | 1.09 | 41,866 | 0.98 | 1.05 | 25,638 | 0.98 | 1.99 | 13,112 | 0.99 |
| Q4 | 1.23 | 35,819 | 0.97 | 1.44 | 16,557 | 0.97 | 1.39 | 7470.3 | 0.97 |
| Quarry Location | Lithology | Experiment Code | Scale-Free Interval (mm) | Slope | R2 | DF |
|---|---|---|---|---|---|---|
| Q1 | Limestone | #1 | 6–131 | 1.72 | 0.97 | 1.28 |
| 131–1100 | 0.54 | 0.97 | 2.46 | |||
| #2 | 6.8–123 | 1.60 | 0.99 | 1.40 | ||
| 123–1400 | 0.56 | 0.94 | 2.44 | |||
| #3 | 6.8–186 | 1.38 | 0.99 | 1.62 | ||
| 186–1400 | 0.45 | 0.94 | 2.55 | |||
| Q2 | Tuff | #4 | 3.2–70.1 | 0.71 | 0.94 | 2.19 |
| 70.1–2030 | 0.71 | 0.91 | 2.30 | |||
| Q3 | Granite | #5 | 3.2–215 | 1.31 | 0.98 | 1.69 |
| 215–2400 | 0.37 | 0.94 | 2.63 | |||
| #6 | 3.3–389 | 0.80 | 0.98 | 2.20 | ||
| 389–2480 | 0.24 | 0.92 | 2.76 | |||
| #7 | 3.2–310 | 1.12 | 0.98 | 1.88 | ||
| 310–1500 | 0.40 | 0.97 | 2.60 | |||
| #11 | 3.2–68 | 2.49 | 0.99 | 0.51 | ||
| 68–1600 | 0.53 | 0.98 | 2.47 | |||
| #12 | 3.2–68 | 1.12 | 0.97 | 1.88 | ||
| 68–1600 | 0.63 | 0.96 | 2.37 | |||
| #13 | 3.2–100 | 2.25 | 0.98 | 0.75 | ||
| 100–1840 | 0.47 | 0.98 | 2.53 | |||
| Q4 | Limestone | #17 | 3.35–55.2 | 0.94 | 0.97 | 2.06 |
| 55.2–1988 | 0.68 | 0.88 | 2.32 |
| Quarry Location | Lithology | Experiment Code | Scale-Free Interval (mm) | Slope | R2 | DF |
|---|---|---|---|---|---|---|
| Q3 | Granite | #8 | 3.2–1900 | 0.95 | 0.97 | 2.05 |
| #9 | 6.8–2030 | 0.96 | 0.96 | 2.04 | ||
| #10 | 3.1–2080 | 1.00 | 0.95 | 2.00 | ||
| #14 | 3.2–1500 | 0.97 | 0.97 | 2.03 | ||
| #15 | 3.5–2000 | 0.95 | 0.96 | 2.05 | ||
| #16 | 6.8–1970 | 0.96 | 0.96 | 2.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Zhu, P.; Li, S.; Ding, C.; Lu, W.; Liu, Y. Fractal Behavior of Size Distribution and Specific Surface Area of Blasting Fragments. Appl. Sci. 2023, 13, 11832. https://doi.org/10.3390/app132111832
Li R, Zhu P, Li S, Ding C, Lu W, Liu Y. Fractal Behavior of Size Distribution and Specific Surface Area of Blasting Fragments. Applied Sciences. 2023; 13(21):11832. https://doi.org/10.3390/app132111832
Chicago/Turabian StyleLi, Ruize, Peng Zhu, Shuyi Li, Cong Ding, Wenbo Lu, and Yijia Liu. 2023. "Fractal Behavior of Size Distribution and Specific Surface Area of Blasting Fragments" Applied Sciences 13, no. 21: 11832. https://doi.org/10.3390/app132111832
APA StyleLi, R., Zhu, P., Li, S., Ding, C., Lu, W., & Liu, Y. (2023). Fractal Behavior of Size Distribution and Specific Surface Area of Blasting Fragments. Applied Sciences, 13(21), 11832. https://doi.org/10.3390/app132111832





