The Vibration Analysis Based on Experimental and Finite Element Modeling for Investigating the Effect of a Multi-Notch Location of a Steel Plate
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Characterization
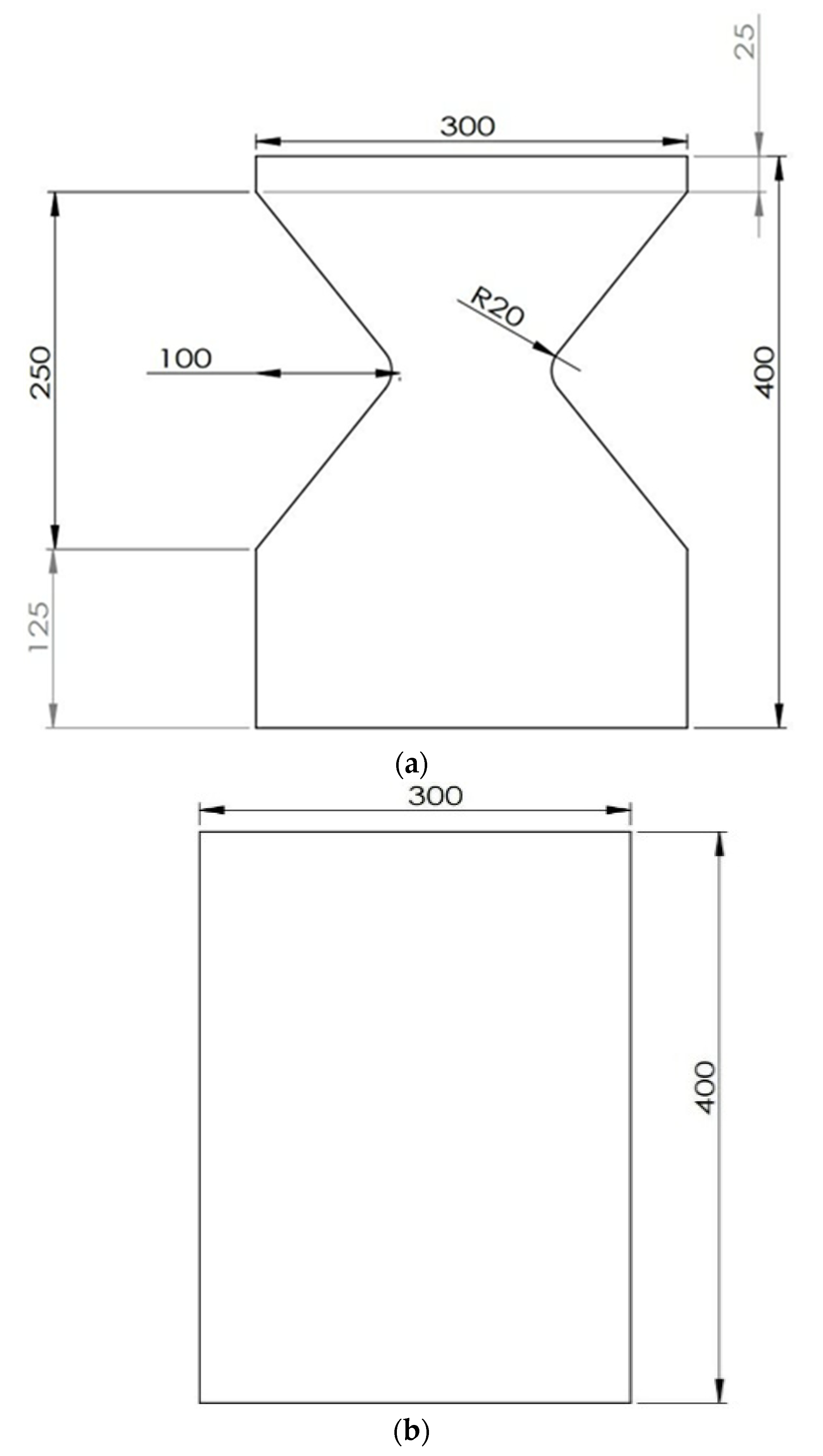
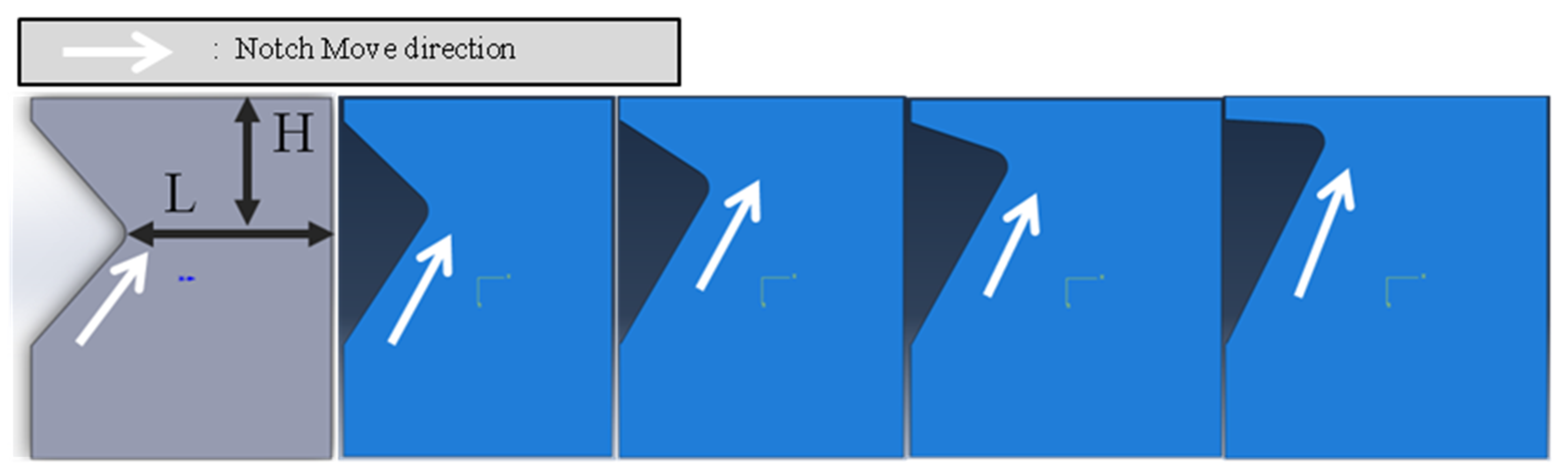
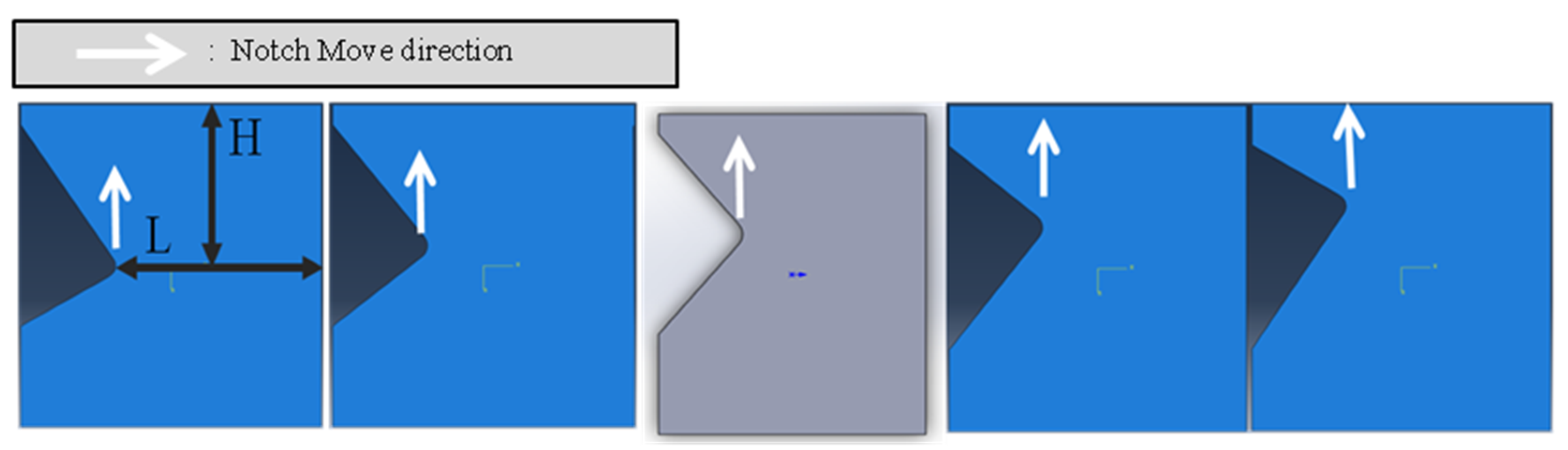
2.2. Geometry Designed and Condition
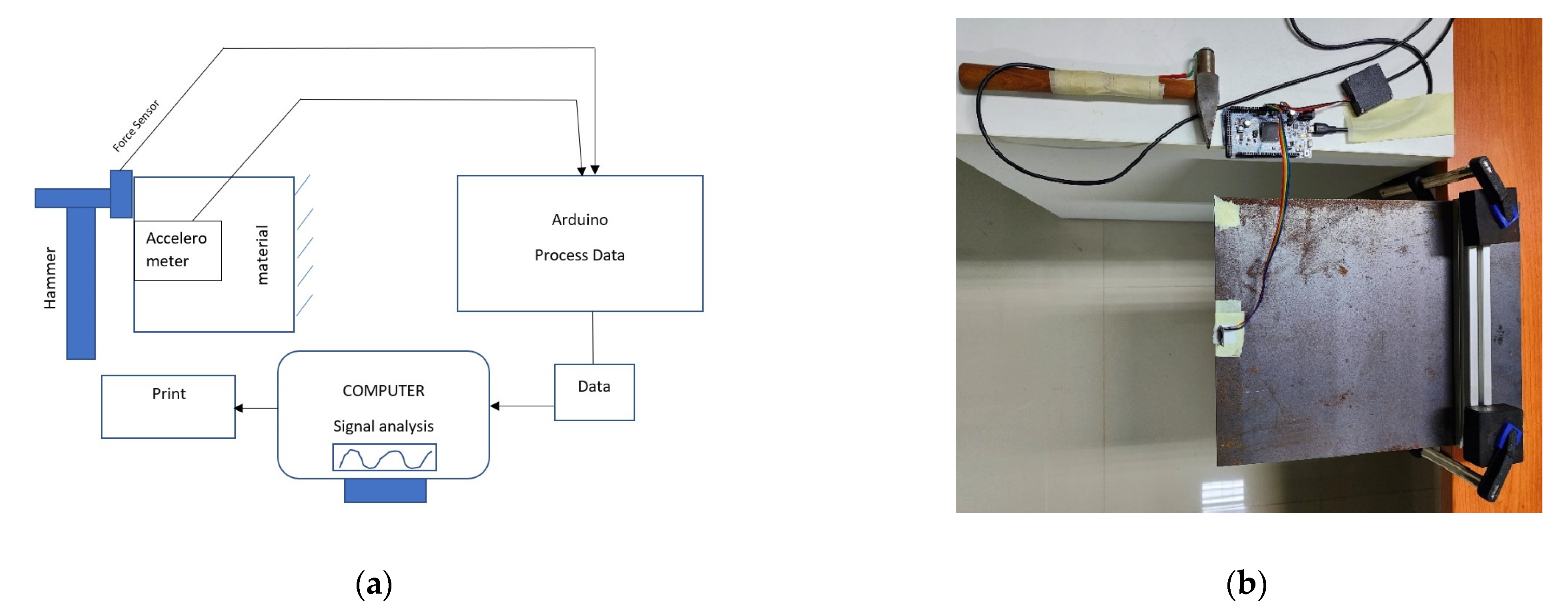
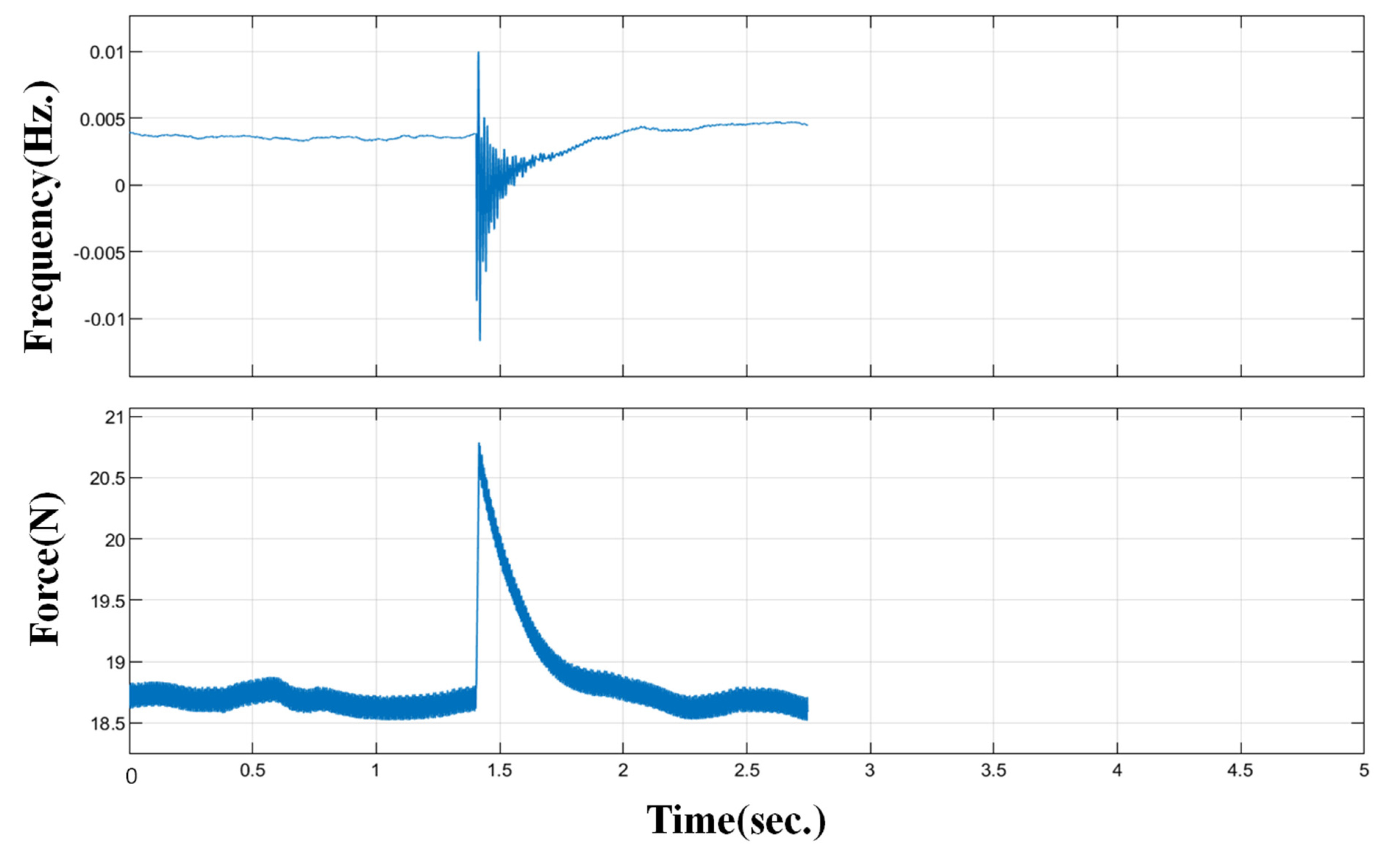
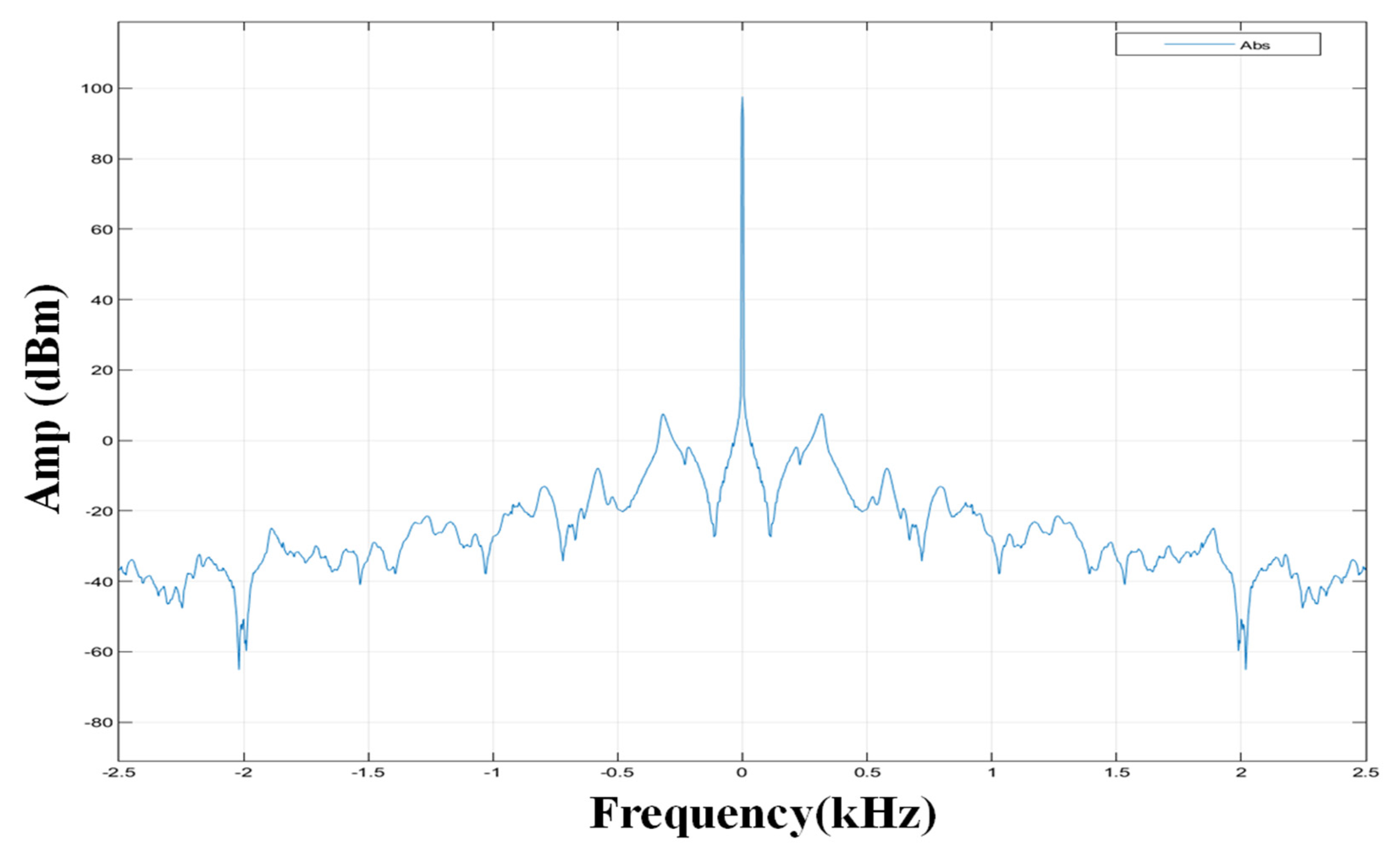
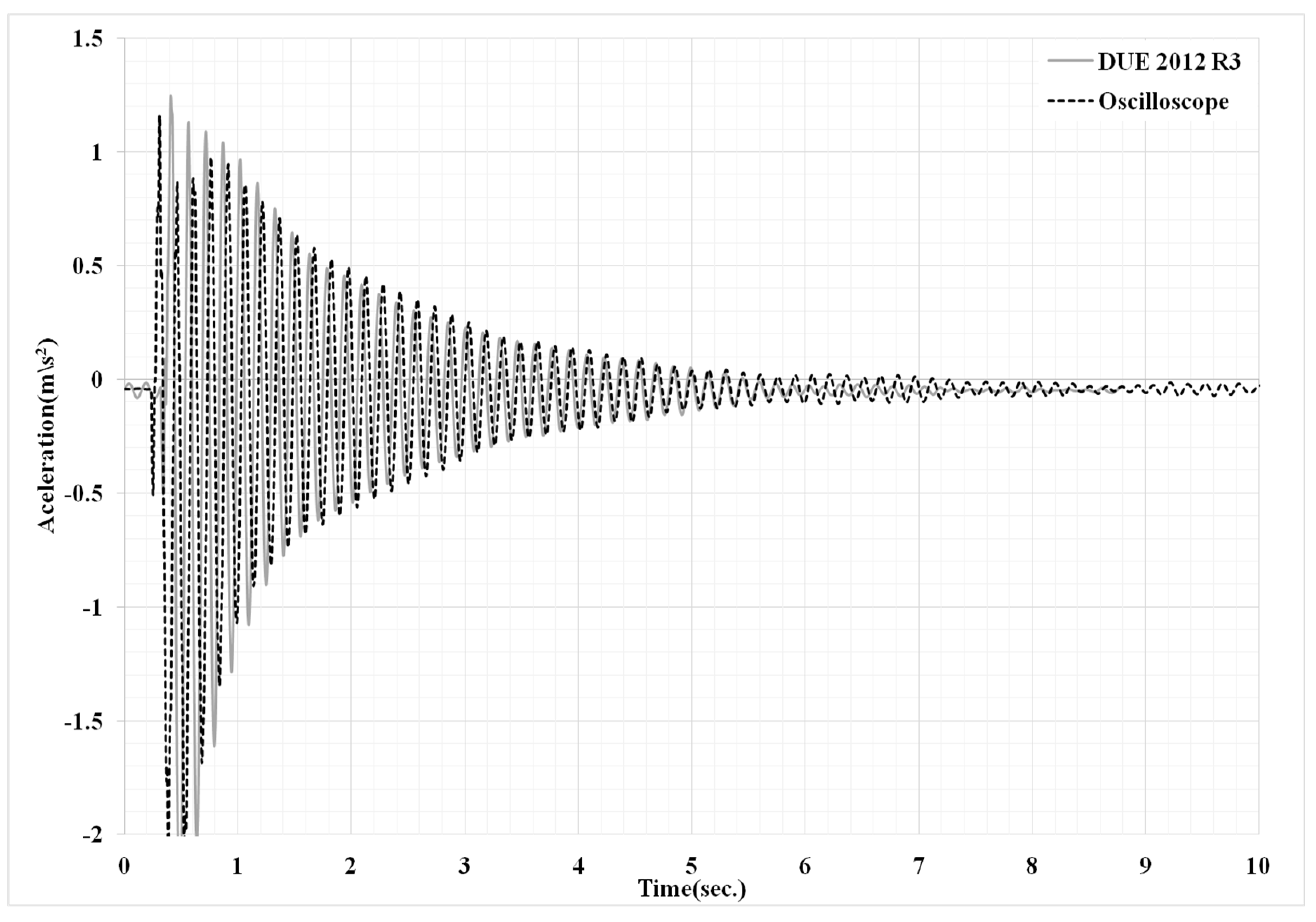
2.3. Identification of Natural Frequency in Experiments
3. Results and Discussion
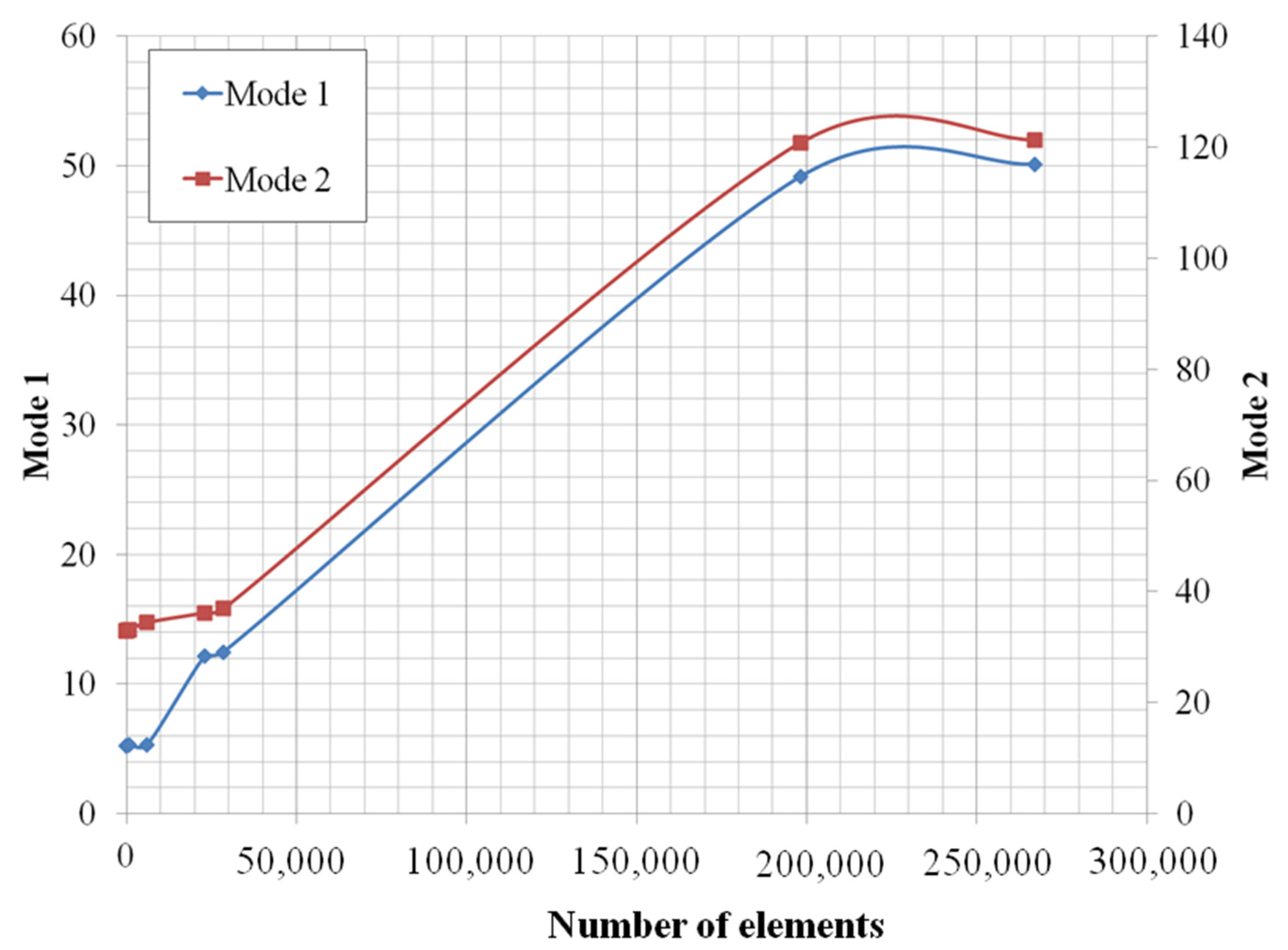
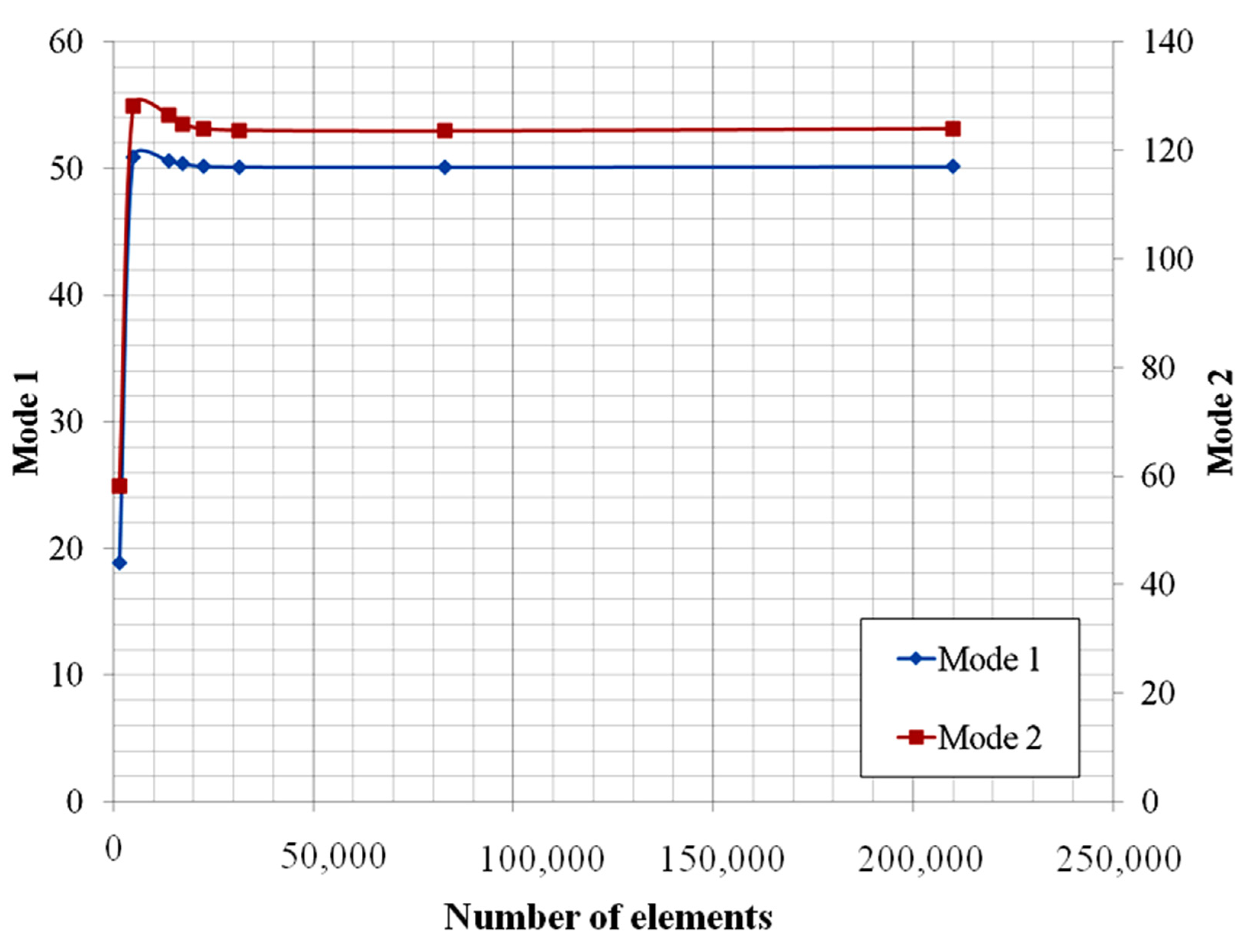
3.1. Verification for Experiment and FE Models
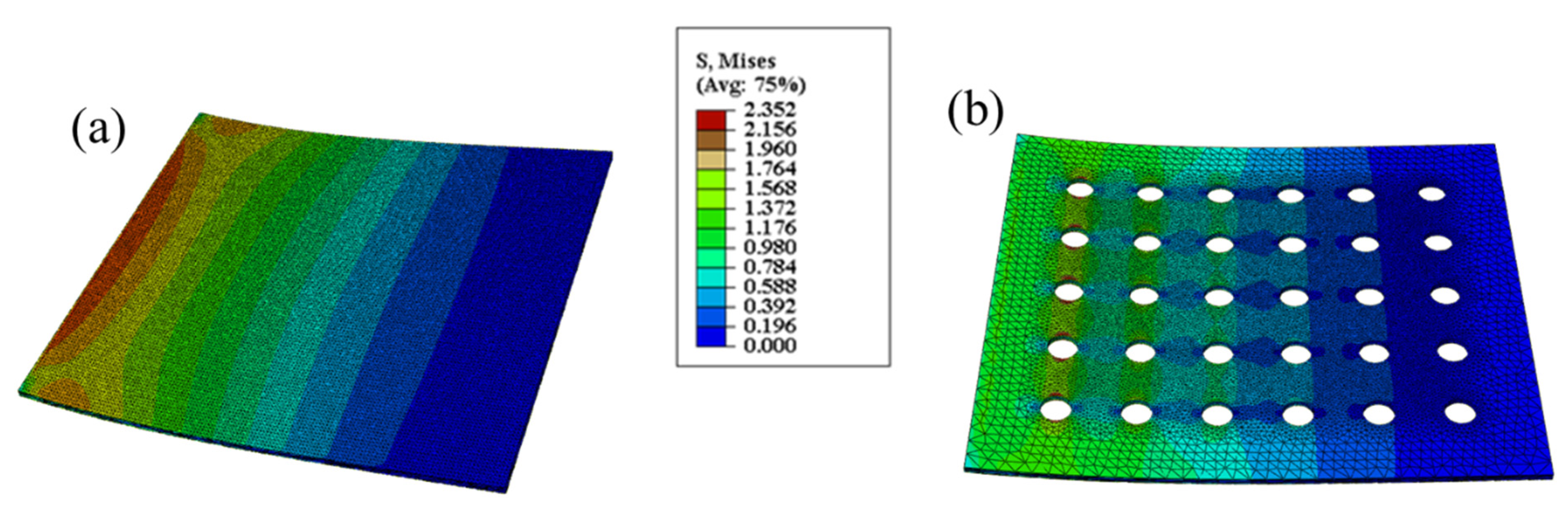
3.2. Discussion
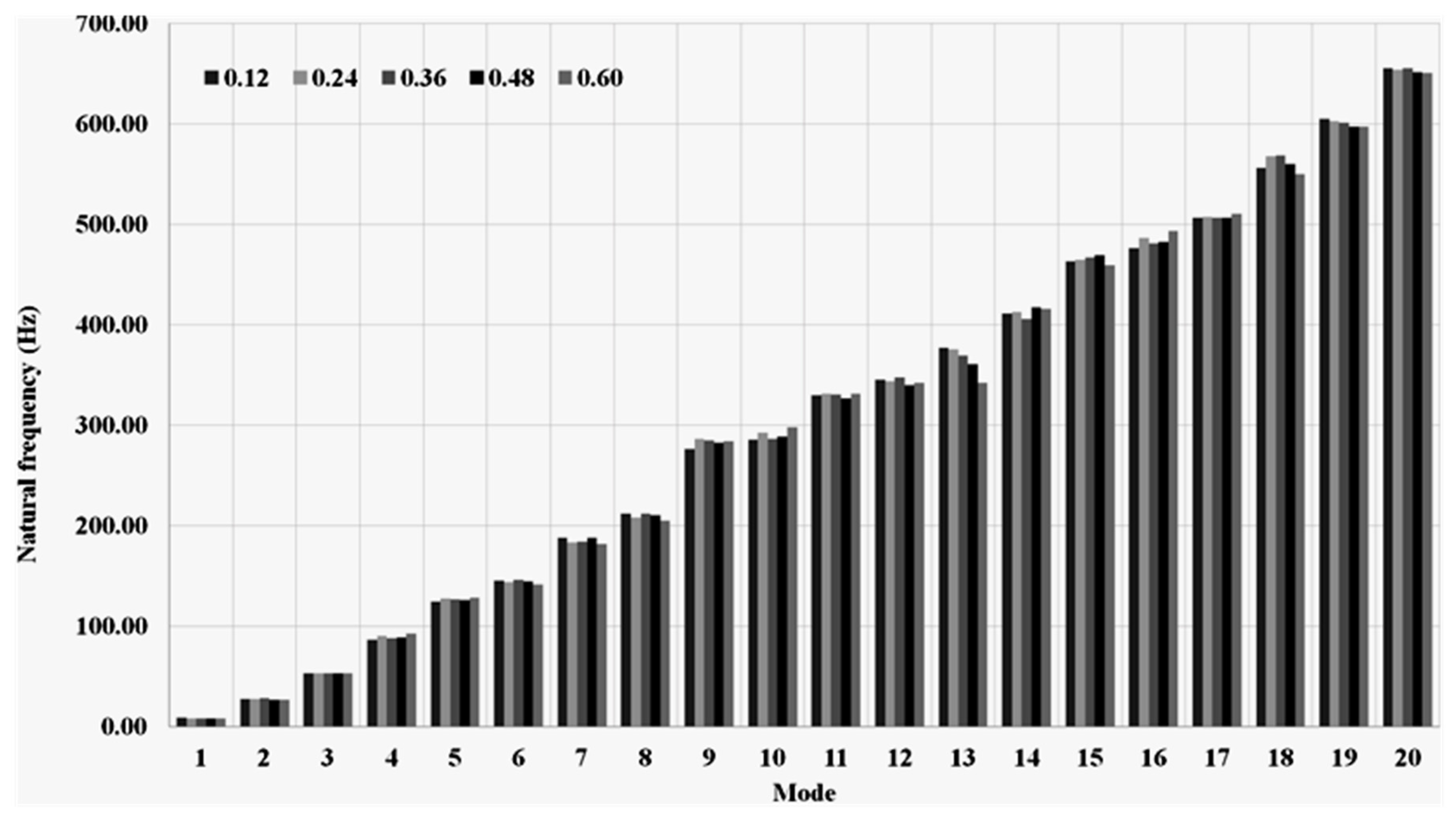
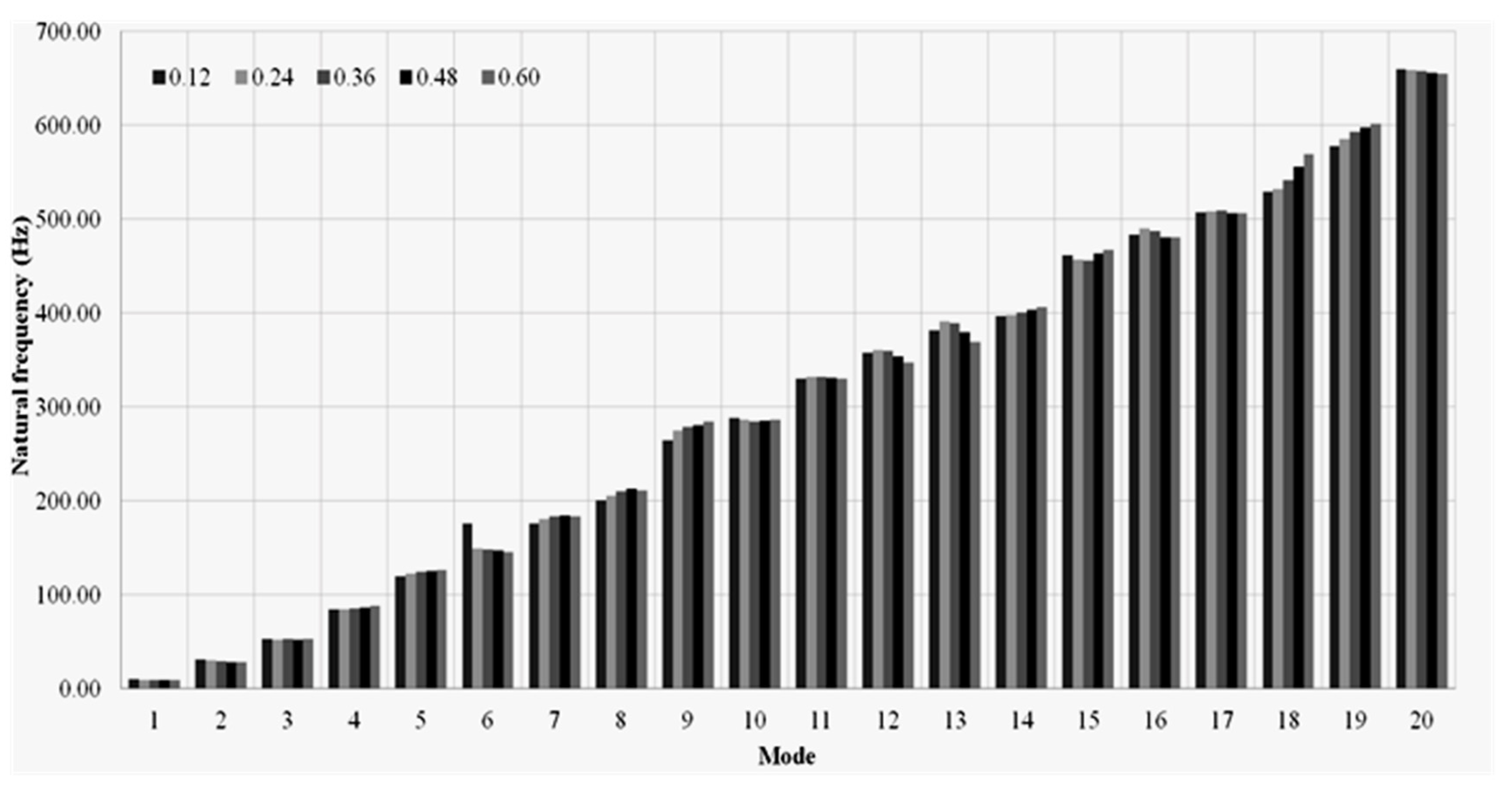
4. Influence of Notch Location on the Vibration Characteristics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chan, T.H.T.; Ashebo, D.B. Theoretical study of moving force identification on continuous bridges. J. Sound Vib. 2006, 295, 870–883. [Google Scholar] [CrossRef]
- Law, S.S.; Bu, J.Q.; Zhu, X.Q.; Chan, S.L. Moving load identification on a simply supported orthotropic plate. Int. J. Mech. Sci. 2007, 49, 1262–1275. [Google Scholar] [CrossRef]
- Kim, T.; Lee, U. Vibration analysis of thin plate structures subjected to a moving force using frequency-domain spectral element method. Shock. Vib. 2018, 2018, 1908508. [Google Scholar] [CrossRef]
- Ghafoori, E.; Kargarnovin, M.; Ghahremani, A.R. Dynamic responses of a rectangular plate under motion of an oscillator using a semi-analytical method. J. Vib. Control. 2010, 17, 1310–1324. [Google Scholar] [CrossRef]
- Amiri, J.V.; Nikkhoo, A.; Davoodi, M.R.; Hassanabadi, M.E. Vibration analysis of a Mindlin elastic plate under a moving mass excitation by eigenfunction expansion method. Thin-Walled Struct. 2013, 62, 53–64. [Google Scholar] [CrossRef]
- Bajer, C.I.; Dyniewicz, B. Numerical Analysis of Vibrations of Structures under Moving Inertial Load; Springer: Berlin, Germany, 2012. [Google Scholar]
- Shadnam, M.R.; Rofooei, F.R.; Mofid, M.; Mehri, B. Periodicity in the response of nonlinear plate, under moving mass. Thin-Walled Struct. 2002, 40, 283–295. [Google Scholar] [CrossRef]
- Yang, Y.; Ding, H.; Chen, L.-Q. Dynamic response to a moving load of a Timoshenko beam resting on a nonlinear viscoelastic foundation. Acta Mech. Sin. 2013, 29, 718–727. [Google Scholar] [CrossRef]
- Vosoughi, A.R.; Malekzadeh, P.; Razi, H. Response of moderately thick laminated composite plates on elastic foundation subjected to moving load. Compos. Struct. 2013, 97, 286–295. [Google Scholar] [CrossRef]
- Wang, X.; Jin, C. Differential Quadrature Analysis of Moving Load Problems. Adv. Appl. Math. Mech. 2016, 8, 536–555. [Google Scholar] [CrossRef]
- Wu, J.-S.; Lee, M.-L.; Lai, T.-S. The dynamic analysis of a flat plate under a moving load by the finite element method. Int. J. Numer. Methods Eng. 1987, 24, 743–762. [Google Scholar] [CrossRef]
- Ghafoori, E.; Asghari, M. Dynamic analysis of laminated composite plates traversed by a moving mass based on a first-order theory. Compos. Struct. 2010, 92, 1865–1876. [Google Scholar] [CrossRef]
- Baltzis, K.B. The finite element method magnetics (FEMM) freeware package: May it serve as an educational tool in teaching electromagnetics? Educ. Inf. Technol. 2010, 15, 19–36. [Google Scholar] [CrossRef]
- Chondros, T.G.; Dimorogonas, A.D.; Yao, J. Vibration of a beam with a breathing crack. J. Sound Vib. 2001, 239, 457–475. [Google Scholar] [CrossRef]
- Wu, J.-J. Free vibration characteristics of a rectangular plate carrying multiple three-degree-of-freedom spring–mass systems using equivalent mass method. Int. J. Solids Struct. 2006, 43, 727–746. [Google Scholar] [CrossRef]
- Gawande, S.H.; More, R.R. Effect of Notch Depth & Location on Modal Natural Frequency of Cantilever Beams. Structures 2016, 8, 121–129. [Google Scholar] [CrossRef]
- Wang, J.; Fu, M.; Shi, S. Influences of size effect and stress condition on ductile fracture behavior in micro-scaled plastic deformation. Mater. Des. 2017, 131, 69–80. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Wan, Y.; Zhang, C.; Ran, J.; Fu, M. Size effect on the shear damage under low stress triaxiality in micro-scaled plastic deformation of metallic materials. Mater. Des. 2020, 196, 109107. [Google Scholar] [CrossRef]
- Jing, C.; Wang, J.; Zhang, C.; Sun, Y.; Shi, Z. Influence of Size Effect on Dynamic Mechanical Properties of OFHC Copper at Micro/Mesoscopic Scale. Res. Sq. 2021, 1–32. [Google Scholar] [CrossRef]
- Djidrov, M.; Gavriloski, V.; Jovanova, J. Vibration analysis of cantilever beam for damage detection. FME Trans. 2014, 42, 311–316. [Google Scholar] [CrossRef]
- Liang, R.Y.; Choy, F.K.; Hu, J. Detection of cracks in beam structures using measurements of natural frequencies. J. Frankl. Inst. 1991, 328, 505–518. [Google Scholar] [CrossRef]
- Li, B.; Chen, X.; Ma, J.; He, Z. Detection of crack location and size in structures using wavelet finite element methods. J. Sound Vib. 2005, 285, 767–782. [Google Scholar] [CrossRef]
- Barad, K.H.; Sharma, D.S.; Vyas, V. Crack Detection in Cantilever Beam by Frequency based method. Procedia Eng. 2013, 51, 770–775. [Google Scholar] [CrossRef]
- Reddy, L.R.; Debora, S.N. Damage detection in structural elements using frequency contour method. In Proceedings of the 2017 First International Conference on Recent Advances in Aerospace Engineering (ICRAAE), Coimbatore, India, 3–4 March 2017; pp. 1–6. [Google Scholar]
- Rizos, P.; Aspragathos, N.; Dimarogonas, A.D. Identification of crack location and magnitude in a cantilever beam from the vibration modes. J. Sound Vib. 1990, 138, 381–388. [Google Scholar] [CrossRef]
- Labib, A.; Kennedy, D.; Featherston, C. Free vibration analysis of beams and frames with multiple cracks for damage detection. J. Sound Vib. 2014, 333, 4991–5003. [Google Scholar] [CrossRef]
- Agarwalla, D.; Parhi, D.R. Effect of Crack on Modal Parameters of a Cantilever Beam Subjected to Vibration. Procedia Eng. 2013, 51, 665–669. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Krawczuk, M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam. J. Sound Vib. 1991, 150, 191–200. [Google Scholar] [CrossRef]
- Owolabi, G.; Swamidas, A.; Seshadri, R. Crack detection in beams using changes in frequencies and amplitudes of frequency response functions. J. Sound Vib. 2003, 265, 1–22. [Google Scholar] [CrossRef]
- Yaman, Y. Vibrations of open-section channels: A coupled flexural and torsional wave analysis. J. Sound Vib. 1997, 204, 131–158. [Google Scholar] [CrossRef]
- Piana, G.; Lofrano, E.; Manuello, A.; Ruta, G. Natural frequencies and buckling of compressed non-symmetric thin-walled beams. Thin-Walled Struct. 2017, 111, 189–196. [Google Scholar] [CrossRef]
- Augello, R.; Daneshkhah, E.; Xu, X.; Carrera, E. Efficient CUF-based method for the vibrations of thin-walled open cross-section beams under compression. J. Sound Vib. 2021, 510, 116232. [Google Scholar] [CrossRef]
- Mohri, F.; Azrar, L.; Potier-Ferry, M. Vibration analysis of buckled thin-walled beams with open sections. J. Sound Vib. 2004, 275, 434–446. [Google Scholar] [CrossRef]
- William, D.; Callister, J.; Rethwisch, D.G. Materials Science and Engineering, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Zheng, D.Y. Free Vibration Analysis of a Cracked Beam by finite Element Method. J. Sound Vib. 2004, 273, 457–475. [Google Scholar] [CrossRef]
- Gudmunson, P. Eigen frequency changes of structures due to cracks, notches or other geometrical changes. J. Mech. Phys. Solids 1982, 30, 339–353. [Google Scholar] [CrossRef]
- Khalkar, V.; Ramachandran, S. Analysis of the effect of V-shape and Rectangular Shape cracks on the natural frequencies of a spring steel cantilever beam. Mater. Today Proc. 2018, 5, 855–862. [Google Scholar] [CrossRef]
- Endo, A.; Itoyama, R.; Kuroda, J.; Uchino, D.; Ogawa, K.; Ikeda, K.; Kato, T.; Narita, T.; Kato, H. Vibration Characteristics of Flexible Steel Plate on Proposed Magnetic Levitation System Using Gravity. Vibration 2022, 5, 936–945. [Google Scholar] [CrossRef]
- Lenggana, B.W.; Prabowo, A.R.; Ubaidillah, U.; Imaduddin, F.; Surojo, E.; Nubli, H.; Adiputra, R. Effects of mechanical vibration on designed steel-based plate geometries: Behavioral estimation subjected to applied material classes using finite-element method. Curved Layer Struct. 2021, 8, 225–240. [Google Scholar] [CrossRef]
- González, A.; Olazagoitia, J.L.; Vinolas, J. A Low-Cost Data Acquisition System for Automobile Dynamics Applications. Sensors 2018, 18, 366. [Google Scholar] [CrossRef] [PubMed]
- Ghazali, M.H.M.; Rahiman, W. An Investigation of the Reliability of Different Types of Sensors in the Real-Time Vibration-Based Anomaly Inspection in Drone. Sensors 2022, 22, 6015. [Google Scholar] [CrossRef]
- Grębowski, K.; Rucka, M.; Wilde, K. Non-Destructive Testing of a Sport Tribune under Synchronized Crowd-Induced Excitation Using Vibration Analysis. Mater. Today Proc. 2019, 12, 2148. [Google Scholar] [CrossRef]
- Melosh, R.J. Modeling Accuracy in FEA of Vibrations of a Drumhead. Shock. Vib. 1993, 1, 15–20. [Google Scholar] [CrossRef]
- Ridwan, R.; Prabowo, A.R.; Muhayat, N.; Putranto, T.; Sohn, J.M. Tensile analysis and assessment of carbon and alloy steels using FE approach as an idealization of material fractures under collision and grounding. Curved Layer Struct. 2020, 7, 188–198. [Google Scholar] [CrossRef]
- Orhan, S. Analysis of free and forced vibration of a cracked cantilever beam. NDT E Int. 2007, 40, 443–450. [Google Scholar] [CrossRef]
- Zsolt, H. Vibration of cracked reinforced and prestressed concrete beams. Archit. Civ. Eng. 2008, 6, 155–164. [Google Scholar]
- Meghdari, A.; Behzad, M.; Ebrahimi, A. A continuous vibration theory for beams with a vertical edge crack. Mech. Eng. 2010, 2010, 194–204. [Google Scholar]
- Logan, D.L. A First Course in the Finite Element Method, 4th ed.; Thomson: Stamford, CT, USA, 2004. [Google Scholar]
- Komarizadehasl, S.; Mobaraki, B.; Ma, H.; Lozano-Galant, J.-A.; Turmo, J. Development of a Low-Cost System for the Accurate Measurement of Structural Vibrations. Sensors 2021, 21, 6191. [Google Scholar] [CrossRef]
- Kumar, S.; Kolekar, T.; Patil, S.; Bongale, A.; Kotecha, K.; Zaguia, A.; Prakash, C. A Low-Cost Multi-Sensor Data Acquisition System for Fault Detection in Fused Deposition Modelling. Sensors 2022, 22, 517. [Google Scholar] [CrossRef]
- Yoon, H.-I.; Son, I.-S.; Ahn, S.-J. Vibration analysis of Euler-Bernoulli beam with double cracks. J. Mech. Sci. Technol. 2007, 21, 476–485. [Google Scholar] [CrossRef]
- Prabowo, A.R.; Laksono, F.B.; Sohn, J.M. Investigation of structural performance subjected to impact loading using finite element approach: Case of ship-container collision. Curved Layer Struct. 2020, 7, 17–28. [Google Scholar] [CrossRef]
- Dumond, P.; Monette, D.; Alladkani, F.; Akl, J.; Chikhaoui, I. Simplified setup for the vibration study of plates with simply-supported boundary conditions. MethodsX 2019, 6, 2106–2117. [Google Scholar] [CrossRef]
- Luo, K.; Lei, X.; Ou, K. Study on the influence of damping plates on structural vibration and radiation characteristics of the railway box girder. J. Low Freq. Noise Vib. Act. Control 2021, 40, 252–262. [Google Scholar] [CrossRef]
- Ahmed, E.; Badaruzzaman, W.W.; Wright, H. Experimental and finite element study of profiled steel sheet dry board folded plate structures. Thin-Walled Struct. 2000, 28, 125–143. [Google Scholar] [CrossRef]
- Ahmed, E.; Badaruzzaman, W.H.W. Vibration Performance of Profiled Steel Sheet Dry Board Composite Floor Panel. KSCE J. Civ. Eng. 2013, 17, 133–138. [Google Scholar] [CrossRef]
- Cawley, P.; Adams, R.D. The location of defects in structures from measurements of natural frequencies. J. Strain Alysis Eng. Des. 1979, 14, 49–57. [Google Scholar] [CrossRef]
- Nguyen, K.V. Mode shapes analysis of a cracked beam and its application for crack detection. J. Sound Vib. 2014, 333, 848–872. [Google Scholar] [CrossRef]
- Aye, W.P.P.; Htike, T.M. Inverse method for identification of edge crack using correlation model. SN Appl. Sci. 2019, 1, 590. [Google Scholar] [CrossRef]
- Kumar, C.S.; Rao, M.P.; Rao, L.G.; Chintala, D. Numerical Simulation of Cantilever Beam with Multiple Cracks Using Neural Networks and Multiple Regression Analysis Tool. Int. J. Innov. Res. Sci. Eng. Technol. 2016, 5, 12502–12511. [Google Scholar]
- Huang, C.; Leissa, A.; Liao, S. Vibration analysis of rectangular plates with edge V-notches. Int. J. Mech. Sci. 2008, 50, 1255–1262. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, C.; Niu, Z.; Hu, Z. Free vibration analysis for V-notched Mindlin plates with free or clamped radial edges. Acta Mech. 2022, 233, 2271–2285. [Google Scholar] [CrossRef]
- Leissa, A.; McGee, O.; Huang, C. Vibrations Of Circular Plates Having V-notches Or Sharp Radial Cracks. J. Sound Vib. 1993, 16, 227–239. [Google Scholar] [CrossRef]
- Leissa, A.W.; Huang, C.S.; Chang, M.J. Accurate frequencies and mode shapes for moderately thick, cantilevered, skew plates. Int. J. Struct. Stab. Dyn. 2007, 7, 425–440. [Google Scholar] [CrossRef]









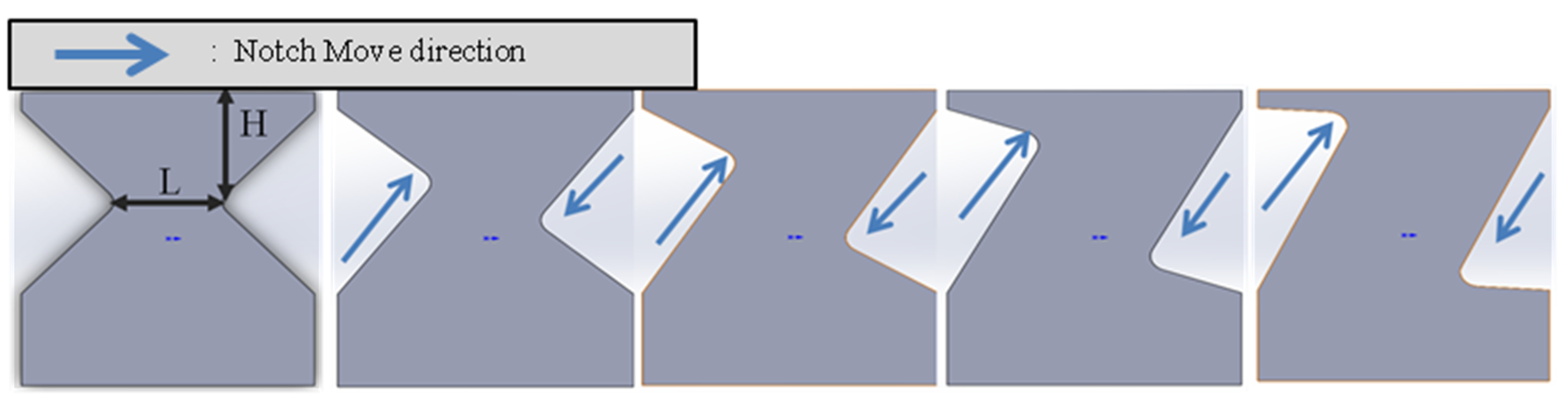

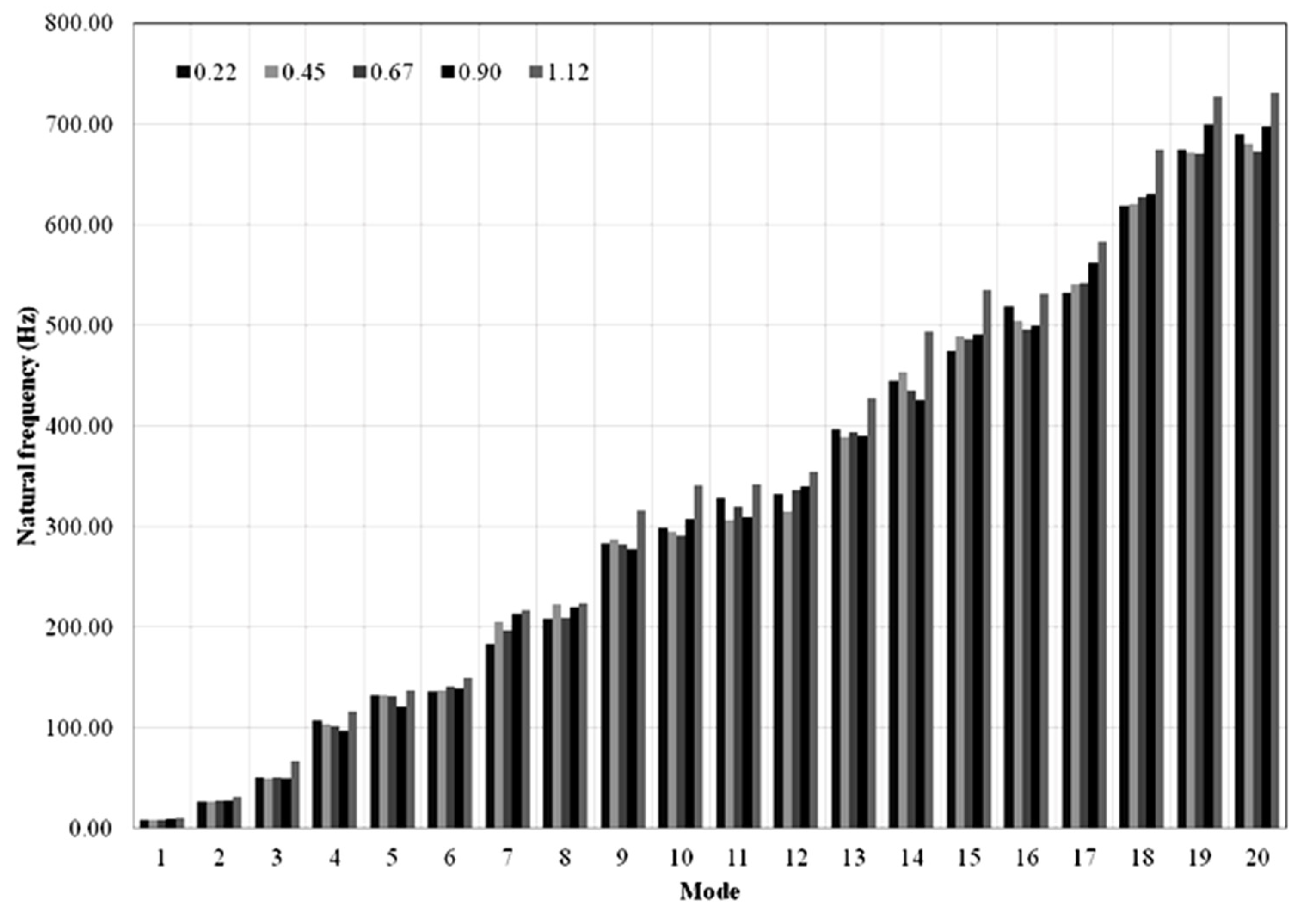
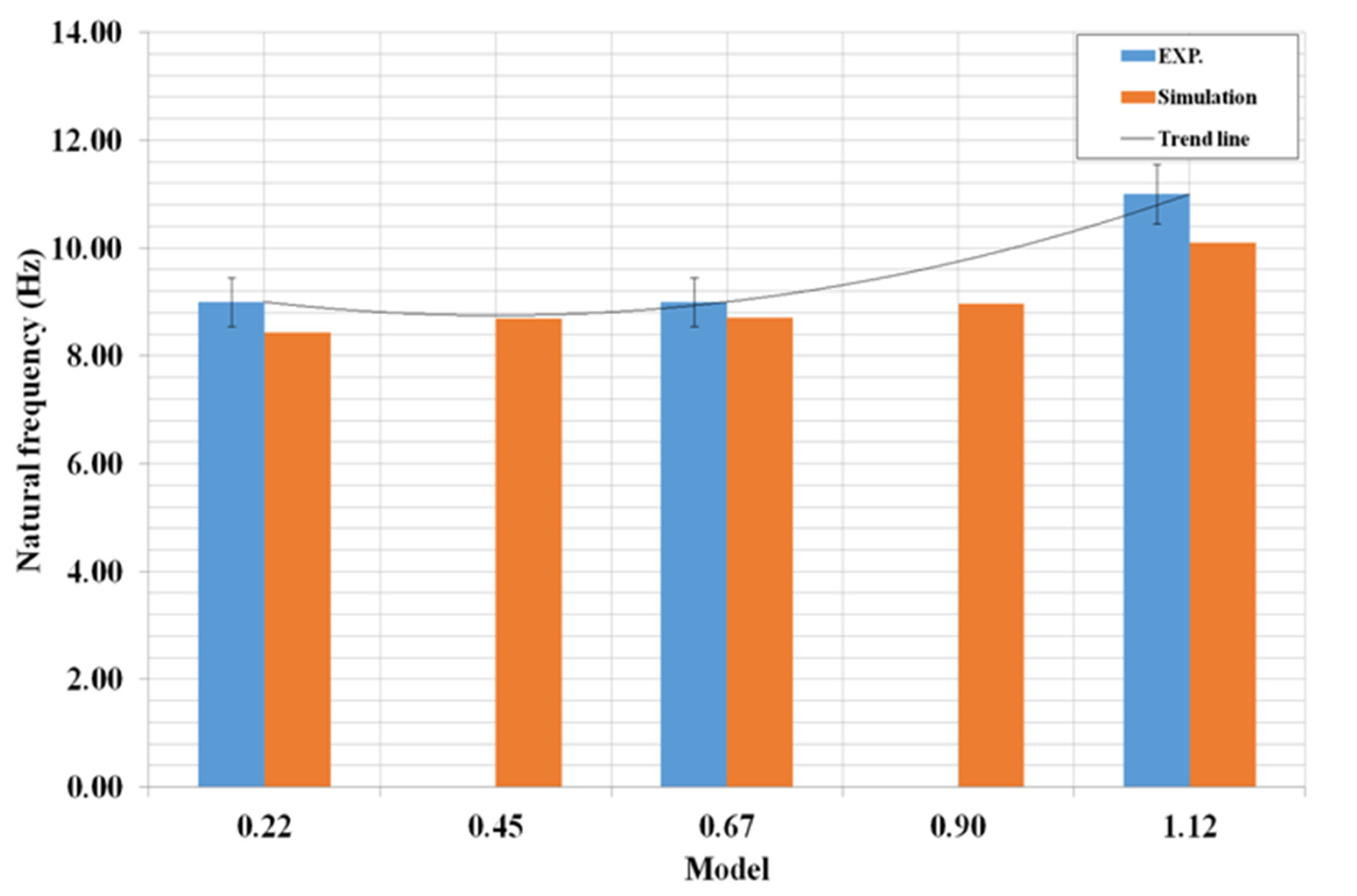

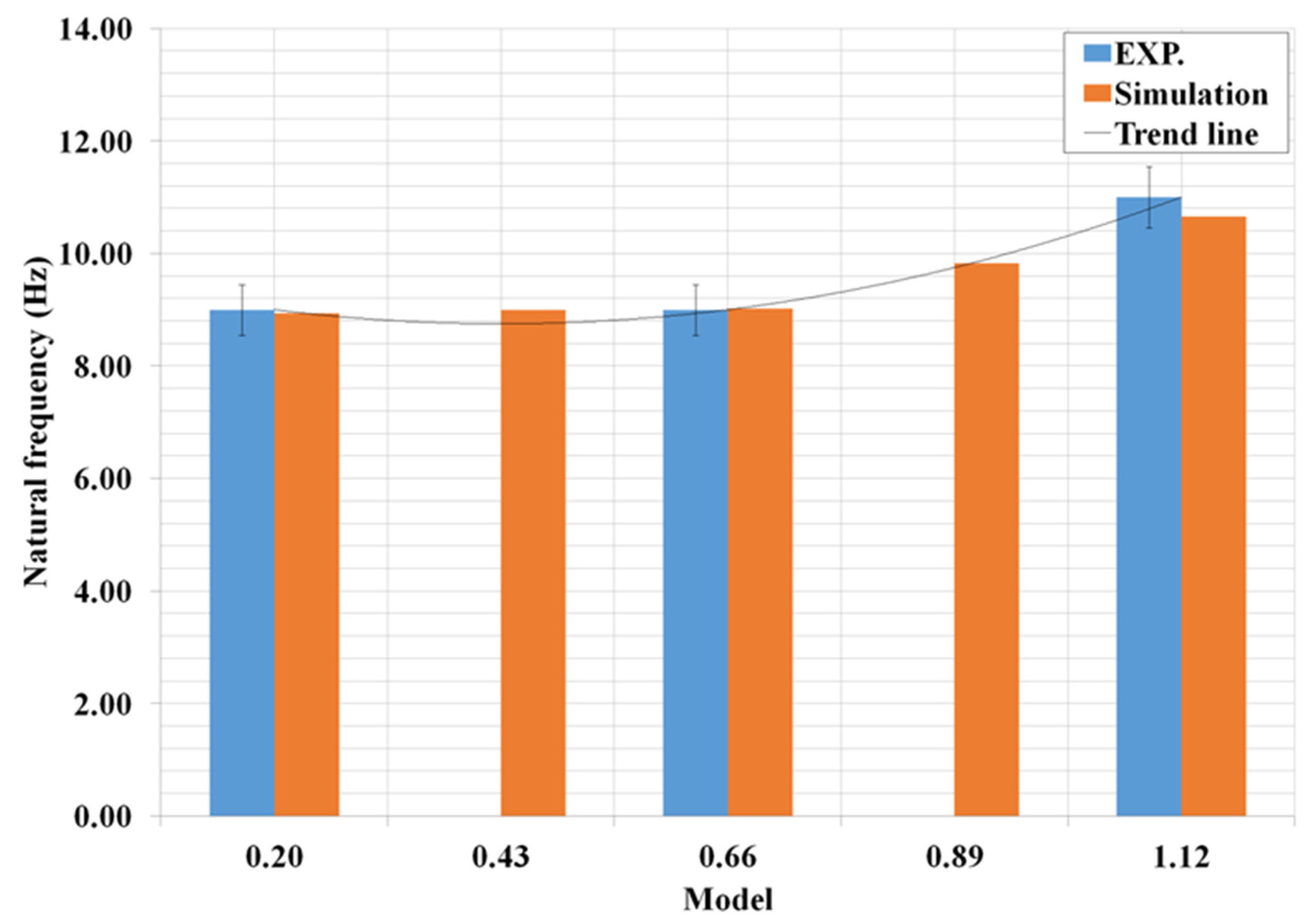

| Steel Grade | C | Si | Mn | P | S | Al |
|---|---|---|---|---|---|---|
| Low carbon | 0.055 | 0.175 | 0.253 | 0.00114 | 0.0021 | 0.0126 |
| Steel Grade | Tensile Strength, Ultimate [MPa] | Tensile Strength, Yield [MPa] | Modulus Elasticity [GPa] | Poisson’s Ratio | Shear Modulus [MPa] | Density [g/cm3] |
|---|---|---|---|---|---|---|
| Low carbon | 418 | 321 | 207 | 0.29 | 82 | 7.533 |
| Number of Element | Mode 1 | Mode 2 | ||||
|---|---|---|---|---|---|---|
| FEM | Exp. | Research Article [36,42] | FEM | Exp. | Research Article [36,42] | |
| 16 | 5.1988 | 53.63 | 52.506 | 32.908 | 129.5 | 125.2 |
| 21 | 5.2578 | 32.973 | ||||
| 907 | 5.2848 | 33.106 | ||||
| 6045 | 5.286 | 34.415 | ||||
| 23,022 | 12.163 | 36.146 | ||||
| 28,523 | 12.457 | 36.868 | ||||
| 198,367 | 49.176 | 120.78 | ||||
| 267,062 | 50.1 | 121.26 | ||||
| Number of Element | Mode 1 | Mode 2 | ||||
|---|---|---|---|---|---|---|
| FEM | Exp. | Research Article [36,42] | FEM | Exp. | Research Article [36,42] | |
| 16 | 54.107 | 53.63 | 52.506 | 138.69 | 129.5 | 125.2 |
| 21 | 53.227 | 142.91 | ||||
| 907 | 52.573 | 130.16 | ||||
| 6045 | 52.298 | 128.48 | ||||
| 23,022 | 52.163 | 128.04 | ||||
| 28,523 | 52.156 | 128.02 | ||||
| 198,367 | 52.149 | 127.98 | ||||
| 267,062 | 52.144 | 127.95 | ||||
| The Number of Elements | Mode 1 | Mode 2 | ||||
|---|---|---|---|---|---|---|
| FEM | Exp. | Research Article [36,42] | FEM | Exp. | Research Article [36,42] | |
| 16 | 18.882 | 50.3 | 51.63 | 58.098 | 125.2 | 121.95 |
| 21 | 50.901 | 128.23 | ||||
| 907 | 50.578 | 126.53 | ||||
| 6045 | 50.372 | 124.88 | ||||
| 23,022 | 50.184 | 123.98 | ||||
| 28,523 | 50.131 | 123.71 | ||||
| 198,367 | 50.111 | 123.59 | ||||
| 267,062 | 50.154 | 123.99 | ||||
| Mode Shape | Natural Frequency (Hz) | ||
|---|---|---|---|
| Virgin | Hole | V-Notch | |
| 1 | 11.290 | 10.791 | 11.103 |
| 2 | 30.998 | 29.893 | 31.598 |
| 3 | 69.777 | 66.958 | 66.780 |
| 4 | 109.030 | 105.290 | 135.950 |
| 5 | 113.250 | 105.290 | 137.140 |
| 6 | 196.580 | 187.710 | 179.880 |
| 7 | 207.780 | 197.530 | 237.470 |
| 8 | 235.790 | 228.010 | 273.760 |
| 9 | 283.370 | 262.370 | 326.380 |
| 10 | 349.350 | 334.550 | 340.700 |
| 11 | 372.390 | 351.560 | 372.360 |
| 12 | 388.460 | 370.180 | 394.620 |
| 13 | 427.970 | 412.120 | 467.720 |
| 14 | 460.690 | 425.960 | 543.900 |
| 15 | 527.640 | 500.530 | 575.640 |
| 16 | 534.370 | 502.340 | 631.090 |
| 17 | 550.890 | 525.430 | 643.730 |
| 18 | 623.230 | 586.710 | 694.660 |
| 19 | 643.370 | 612.000 | 807.460 |
| 20 | 677.860 | 653.520 | 831.250 |
| Mode Shape | Natural Frequency (Hz) | ||
|---|---|---|---|
| Virgin | Hole | V-Notch | |
| 1 | 10 | 11 | 11 |
| 2 | 39 | 33 | 49 |
| 3 | 65 | 46 | 59 |
| 4 | 98 | 95 | 107 |
| 5 | 121 | 109 | 137 |
| 6 | 189 | 195 | 202 |
| 7 | 225 | 213 | 278 |
| Mode Shape | Natural Frequency (Hz) | |||||
|---|---|---|---|---|---|---|
| Virgin | Hole | V-Notch | ||||
| Experiment | Simulation | Experiment | Simulation | Experiment | Simulation | |
| 1 | 10 | 11.290 | 11 | 10.791 | 11 | 11.103 |
| 2 | 39 | 30.998 | 33 | 29.893 | 49 | 31.598 |
| 3 | 65 | 69.777 | 66 | 66.958 | 59 | 66.780 |
| 4 | 98 | 109.030 | 95 | 105.290 | 107 | 135.950 |
| 5 | 121 | 113.250 | 109 | 105.290 | 137 | 137.140 |
| 6 | 189 | 196.580 | 195 | 187.710 | 202 | 179.880 |
| 7 | 225 | 207.780 | 213 | 197.530 | 278 | 237.470 |
| Direction | Specimen Label | L/H |
|---|---|---|
| Direct | V_D_1 | 0.22 |
| V_D_2 | 0.45 | |
| V_D_3 | 0.67 | |
| V_D_4 | 0.90 | |
| V_D_5 | 1.12 | |
| Slide | V_S_1 | 0.20 |
| V_S_2 | 0.43 | |
| V_S_3 | 0.66 | |
| V_S_4 | 0.86 | |
| V_S_5 | 1.12 |
| Direction | Specimen Label | L/H |
|---|---|---|
| Direct | V_DH_1 | 0.12 |
| V_DH_2 | 0.24 | |
| V_DH_3 | 0.36 | |
| V_DH_4 | 0.48 | |
| V_DH_5 | 0.60 | |
| Slide | V_SH_1 | 0.12 |
| V_SH_2 | 0.24 | |
| V_SH_3 | 0.36 | |
| V_SH_4 | 0.48 | |
| V_SH_5 | 0.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charoensuk, K.; Sethaput, T. The Vibration Analysis Based on Experimental and Finite Element Modeling for Investigating the Effect of a Multi-Notch Location of a Steel Plate. Appl. Sci. 2023, 13, 12073. https://doi.org/10.3390/app132112073
Charoensuk K, Sethaput T. The Vibration Analysis Based on Experimental and Finite Element Modeling for Investigating the Effect of a Multi-Notch Location of a Steel Plate. Applied Sciences. 2023; 13(21):12073. https://doi.org/10.3390/app132112073
Chicago/Turabian StyleCharoensuk, Kritchanan, and Thunyaseth Sethaput. 2023. "The Vibration Analysis Based on Experimental and Finite Element Modeling for Investigating the Effect of a Multi-Notch Location of a Steel Plate" Applied Sciences 13, no. 21: 12073. https://doi.org/10.3390/app132112073
APA StyleCharoensuk, K., & Sethaput, T. (2023). The Vibration Analysis Based on Experimental and Finite Element Modeling for Investigating the Effect of a Multi-Notch Location of a Steel Plate. Applied Sciences, 13(21), 12073. https://doi.org/10.3390/app132112073





